Applied Mathematics
Vol.3 No.8(2012), Article ID:21488,6 pages DOI:10.4236/am.2012.38122
Non-Traveling Wave Solutions for the (2+1)-Dimensional Breaking Soliton System
College of Sciences, Zhejiang Lishui University, Lishui, China
Email: chenyuanming98@163.com
Received June 6, 2012; revised July 9, 2012; accepted July 16, 2012
Keywords: 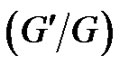 -Expansion Method; Variable Separation Approach; Breaking Soliton System; Non-Traveling Wave Solution
-Expansion Method; Variable Separation Approach; Breaking Soliton System; Non-Traveling Wave Solution
ABSTRACT
In this work, starting from the 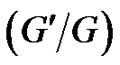 -expansion method and a variable separation method, a new non-traveling wave general solutions of the (2+1)-dimensional breaking soliton system are derived. By selecting appropriately the arbitrary functions in the solutions, special soliton-structure excitations and evolutions are studied.
-expansion method and a variable separation method, a new non-traveling wave general solutions of the (2+1)-dimensional breaking soliton system are derived. By selecting appropriately the arbitrary functions in the solutions, special soliton-structure excitations and evolutions are studied.
1. Introduction
Modern soliton theory is widely applied in many natural sciences [1-4] such as chemistry, biology, mathematics, communication, and particularly in almost all branches of physics like fluid dynamics, plasma physics, field theory, optics, and condensed matter physics, etc. [5-8]. In order to find new exact solutions of nonlinear equations, much methods have been proposed, such as the Lie group method of infinitesimal transformations, the nonclassical Lie group method, the Clarkson and Kruskal direct method (CK) [9,10], the conditional similarity reduction method [11-13] and the improved mapping approach, etc. [14-23].
Recently, the  -expansion method was proposed to obtain the new exact solutions of the nonlinear evolution equations [24]. Subsequently the powerful
-expansion method was proposed to obtain the new exact solutions of the nonlinear evolution equations [24]. Subsequently the powerful  -expansion method has been widely used by many differential such as in [25-30]. However, the previous works have mainly concentrated on obtaining new exact traveling wave solutions for the nonlinear evolution equations.
-expansion method has been widely used by many differential such as in [25-30]. However, the previous works have mainly concentrated on obtaining new exact traveling wave solutions for the nonlinear evolution equations.
In this paper, by using the  -expansion method, we construct non-traveling wave solutions with arbitrary functions in the (2+1)-dimensional breaking soliton system
-expansion method, we construct non-traveling wave solutions with arbitrary functions in the (2+1)-dimensional breaking soliton system
 (1)
(1)
 (2)
(2)
where  is an arbitrary constant, the system (1)-(2) was used to describes the (2+1)-dimensional interaction of Riemann wave propagated along the
is an arbitrary constant, the system (1)-(2) was used to describes the (2+1)-dimensional interaction of Riemann wave propagated along the  -axis with long wave propagated along the
-axis with long wave propagated along the  -axis and it seems to have been investigated extensively where overlapping solutions have been derived [31]. In the past, we have obtained the Annihilation solitons and chaotic solitons by the improved mapping approach [32]. Since the detailed physical background of the breaking soliton system has been given in [31], we neglect the corresponding description.
-axis and it seems to have been investigated extensively where overlapping solutions have been derived [31]. In the past, we have obtained the Annihilation solitons and chaotic solitons by the improved mapping approach [32]. Since the detailed physical background of the breaking soliton system has been given in [31], we neglect the corresponding description.
2. The (G'/G)-Expansion Method and Non-Traveling Wave Solutions to the (2+1)-Dimensional Breaking Soliton System
Before starting to apply the 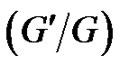 -expansion method, we will give a simple description of the method. For doing this, suppose that a (2+1)-dimensional nonlinear equation, say in three independent variables
-expansion method, we will give a simple description of the method. For doing this, suppose that a (2+1)-dimensional nonlinear equation, say in three independent variables , y and t, is given by
, y and t, is given by
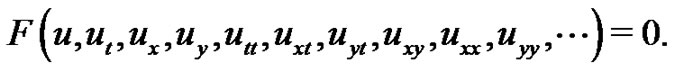 (3)
(3)
The fundamental idea of the  -expansion method is that the solutions of equation (3) can be expressed by a polynomial in
-expansion method is that the solutions of equation (3) can be expressed by a polynomial in  as follows [24,29,30]:
as follows [24,29,30]:
 (4)
(4)
where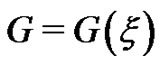 ,
,  is traveling wave transformation, and
is traveling wave transformation, and 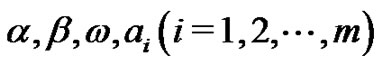 are constants to be determined later, G satisfies the second order LODE as follow:
are constants to be determined later, G satisfies the second order LODE as follow:
 (5)
(5)
In order to construct the non-traveling wave solutions with arbitrary function 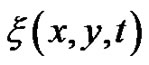 for the (2+1)-dimensional breaking soliton system (1)-(2), we suppose its solutions can be express as follow:
for the (2+1)-dimensional breaking soliton system (1)-(2), we suppose its solutions can be express as follow:
 (6)
(6)
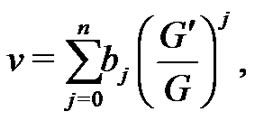 (7)
(7)
where ,
, 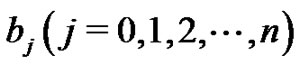 are the functions of
are the functions of  to be determined later,
to be determined later,
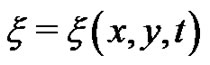 is the arbitrary function of x, y, t, and
is the arbitrary function of x, y, t, and  satisfies the second order LODE (5).
satisfies the second order LODE (5).
Applying the homogenous balance principle, we obtain . Thus (6)-(7) can be converted into
. Thus (6)-(7) can be converted into
 (8)
(8)
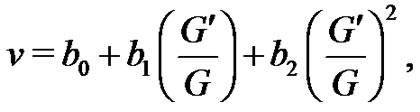 (9)
(9)
For simplifying the computation, we seek for the variable separation solutions of the breaking soliton system (2) by taking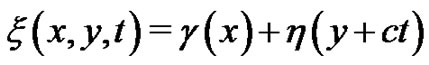 .
.
Substituting (8)-(9) into the system (1)-(2), collecting all terms with the same power of  together. Then setting each coefficient of the polynomials to zero, we can derive a set of over-determined partial differential equation for
together. Then setting each coefficient of the polynomials to zero, we can derive a set of over-determined partial differential equation for  and
and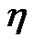 .
.
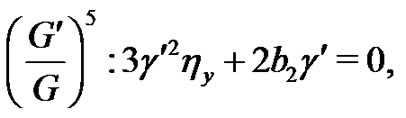 (10)
(10)
 (11)
(11)
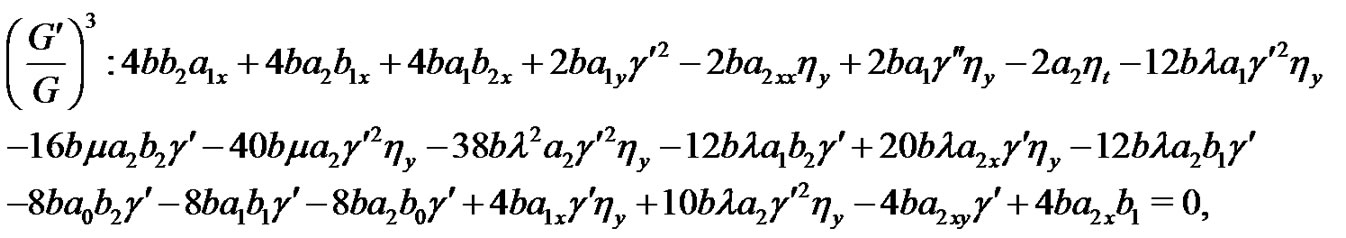 (12)
(12)
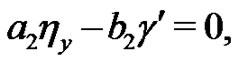 (13)
(13)
 (14)
(14)
 (15)
(15)
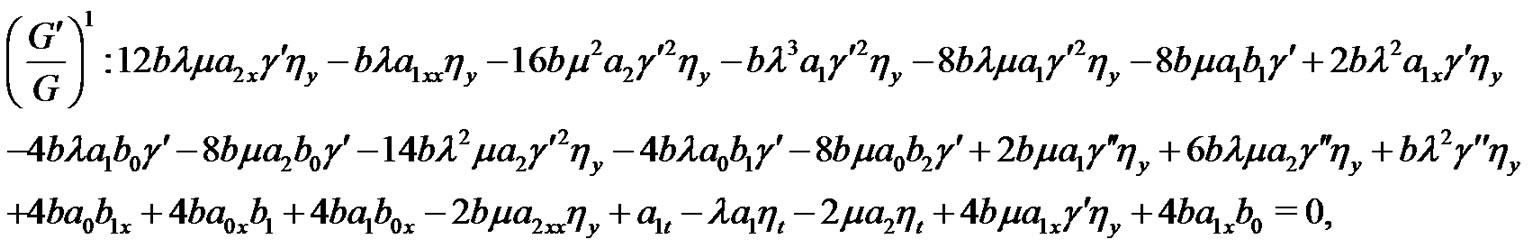 (16)
(16)
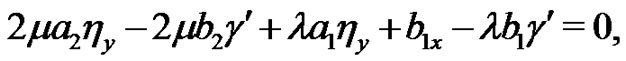 (17)
(17)
 (18)
(18)
 (19)
(19)
Solving the Equations (10)-(19) yields
 (20)
(20)
Substituting (20) and the general solutions of Equation
(5) into (6)-(7), we can obtain the general non-traveling wave solutions for the (2+1)-dimensional breaking soliton system (1)-(2).
Case 1. When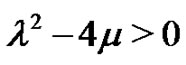 , by the general solutions of Equation (5) we can derive
, by the general solutions of Equation (5) we can derive
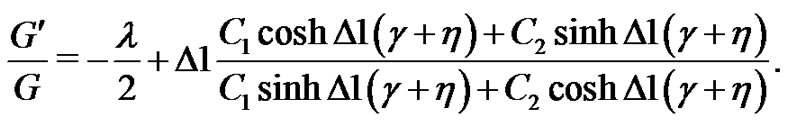 (21)
(21)
Thus, the hyperbolic solutions of the system (1)-(2) are expressed as follows:
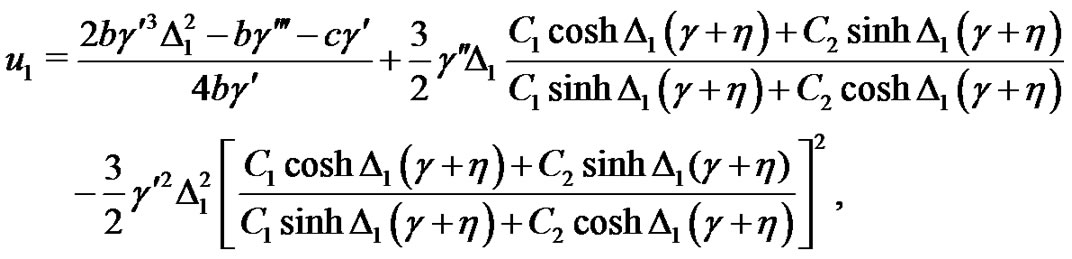 (22)
(22)
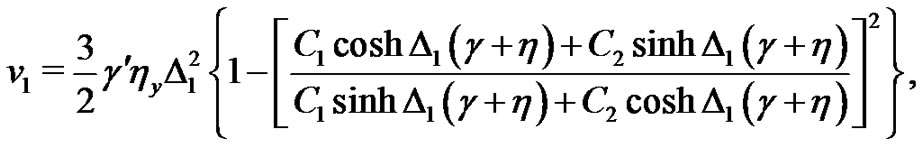 (23)
(23)
where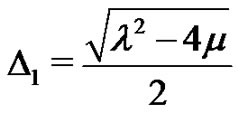 ,
,  ,
,  ,
, 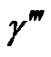 and
and 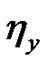 existand
existand ,
,  ,
, 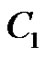 and
and  are arbitrary constants.
are arbitrary constants.
Case 2. When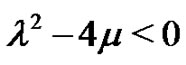 , by the general solutions of Equation (5) we can derive
, by the general solutions of Equation (5) we can derive
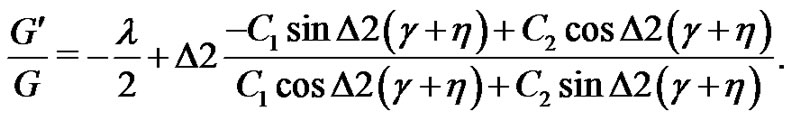 (24)
(24)
So the trigonometric solutions of the system (1)-(2) are expressed as follows:
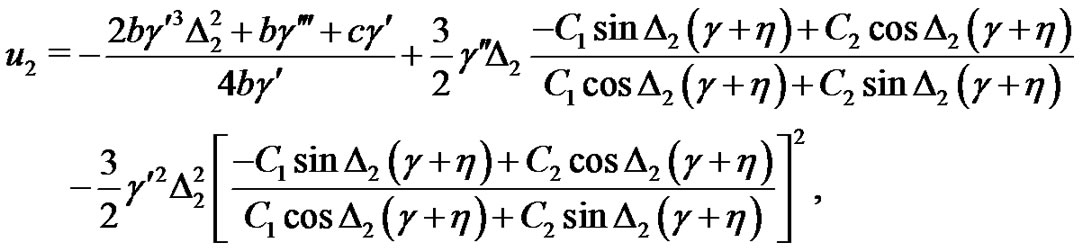 (25)
(25)
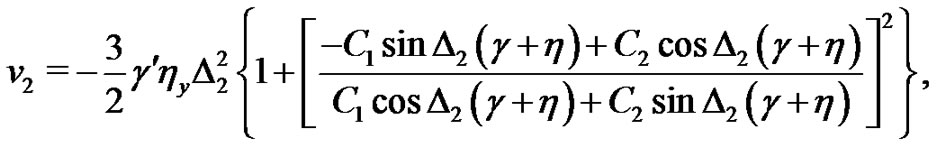 (26)
(26)
where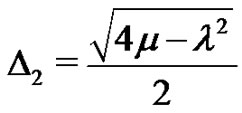 ,
,  ,
,  ,
, 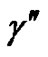 and
and 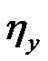 existand
existand ,
,  ,
, 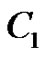 and
and  are arbitrary constants.
are arbitrary constants.
Case 3. When , by the general solutions of Equation (5) we can derive
, by the general solutions of Equation (5) we can derive
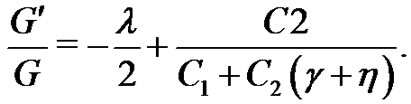 (27)
(27)
In this case, the rational solutions of the system (1)-(2) are showed as:
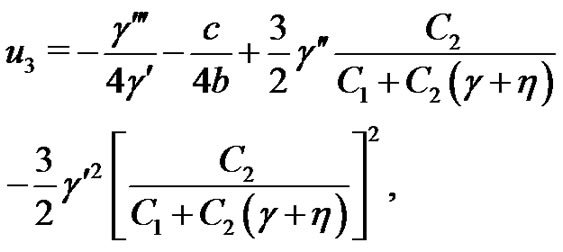 (28)
(28)
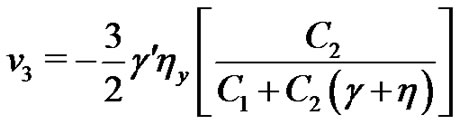 (29)
(29)
where ,
, 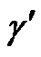 ,
,  and
and 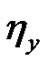 exist, and
exist, and ,
,  ,
,  and
and  are arbitrary constants.
are arbitrary constants.
3. Soliton Structure Excitation of the System (1)-(2)
Due to the arbitrary functions 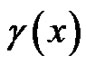 and
and  in the solutions (22)-(29), it is convenient to excite abundant soliton structures. We take the solution (23) as an example to study the soliton excitations for the (2+1)- dimensional breaking soliton system (1)-(2). For instance, if we choose
in the solutions (22)-(29), it is convenient to excite abundant soliton structures. We take the solution (23) as an example to study the soliton excitations for the (2+1)- dimensional breaking soliton system (1)-(2). For instance, if we choose  and
and  as
as
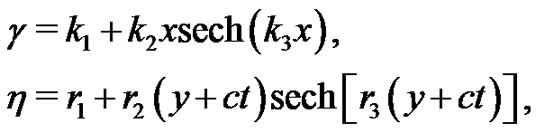 (30)
(30)
where  are arbitrary constants, and all are non-zero.
are arbitrary constants, and all are non-zero.
Substituting (30) into (23) leads to a soliton structure for the system (1)-(2). Figures 1(a)-(d) are the evolution plots of the solution (23) with time under the parameters as
 (31)
(31)
Figures 2(a)-(b) are the plots with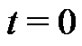 , and we choose the following special values of the parameters
, and we choose the following special values of the parameters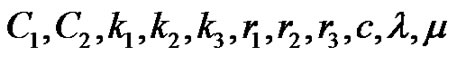 . There are
. There are
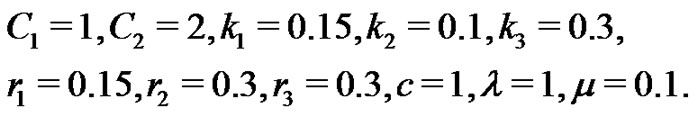 (32)
(32)
 (33)
(33)
Above we show the excitation process of a special dromion soliton structure of the solution (23) for the (2+1)- dimensional breaking soliton system (1)-(2). It is clear
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 1. The evolution plots of the solution (23) under the parameters (31) with time: (a) t = 0; (b) t = 5; (c) t = 10; and (d) t = 20.
 (a)
(a) (b)
(b)
Figure 2. (a) A plot of the soliton for the Equation (23) with condition (32) at t = 0; (b) A plot of the soliton for the Equation (23) with condition (33) at t = 0.
that other selections of the arbitrary  and
and  in (23) may generate rich localized soliton structures. On the other hand, the solutions (22), (25)- (26), (28)-(29) may also be used to excite abundant soliton structures.
in (23) may generate rich localized soliton structures. On the other hand, the solutions (22), (25)- (26), (28)-(29) may also be used to excite abundant soliton structures.
4. Summary and Discussion
In summary, via extending the 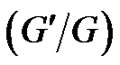 -expansion method, more rich types explicit and exact non-traveling wave solutions of the (2+1)-dimensional breaking soliton system (1)-(2) are found out, and the traveling wave solutions are included by these non-traveling wave solutions. So the non-traveling wave solutions are more general. Furthermore, by choosing appropriately the arbitrary function
-expansion method, more rich types explicit and exact non-traveling wave solutions of the (2+1)-dimensional breaking soliton system (1)-(2) are found out, and the traveling wave solutions are included by these non-traveling wave solutions. So the non-traveling wave solutions are more general. Furthermore, by choosing appropriately the arbitrary function 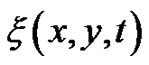 included in its solutions, one can study various interesting localized soliton excitations. Since the wide applications of the soliton theory, to learn more about the localized excitations and their applications in reality is worthy of study further.
included in its solutions, one can study various interesting localized soliton excitations. Since the wide applications of the soliton theory, to learn more about the localized excitations and their applications in reality is worthy of study further.
5. Acknowledgements
The authors would like to thank professor Zheng-yi Ma for his fruitful and helpful suggestions. The Scientific Research Foundation of Lishui University, China (Grant No. KZ201110).
REFERENCES
- S. Y. Lou and X. Y. Tang, “Fractal Solutions of the Nizhnik-Novikov-Veselov Equation,” Chinese Physica Letter, Vol. 19, No. 6, 2002, pp. 769-771. doi:10.1088/0256-307X/19/6/308
- S. Y. Lou and X. B. Hu, “Infinitely Many Lax Pairs and Symmetry Constraints of the KP Equation,” Journal of Mathematical Physics, Vol. 38, No. 6, 1997, Article ID: 6401. doi:10.1063/1.532219
- X. Y. Tang and S. Y. Lou, “Localized Excitations in (2+ 1)-Dimensional Systems,” Physical Review E, Vol. 66, No. 4, 2002, Article ID: 046601. doi:10.1103/PhysRevE.66.046601
- S. Wang, X. Y. Tang and S. Y. Lou, “Soliton Fission and Fusion: Burgers Equation and Sharma-Tasso-Olver Equation,” Chaos, Solitons & Fractals, Vol. 19, No. 1, 2004, pp. 231-239. doi:10.1016/j.chaos.2003.10.014
- C. L. Zheng, “Localized Coherent Structures with Chaotic and Fractal Behaviors in a (2+1)-Dimensional Modified Dispersive Water-Wave System,” Communications in Theoretial Physics, Vol. 40, No. 2, 2003, pp. 25-32.
- C. L. Zheng and J. M. Zhu, “Fractal Dromion, Fractal Lump, and Multiple Peakon Excitations in a New (2+1)- Dimensional Long Dispersive Wave System,” Communications in Theoretial Physics, Vol. 39, No. 1, 2003, pp. 261-266.
- C. L. Zheng and J. F. Zhang, “Folded Localized Excitations in a Generalized (2+l)-Dimensional Perturbed Nonlinear Schrodinger System,” Communications in Theoretial Physics, Vol. 40, No. 2, 2003, p. 385.
- P. A. Clarkson and M. D. Kruskal, “New Similarity Reductions of the Boussinesq Equation,” Journal of Mathematical Physics, Vol. 30, No. 10, 1989, Article ID: 2201. doi:10.1063/1.528613
- S. Y. Lou, “A Note on the New Similarity Reductions of the Boussinesq Equation,” Physica Letter A, Vol. 151, No. 3-4, 1990, pp. 133-135. doi:10.1016/0375-9601(90)90178-Q
- X. Y. Tang, J. Lin and S. Y. Lou, “Conditional Similarity Solutions of the Boussinesq Equation,” Communications in Theoretial Physics, Vol. 35, No. 3, 2001, pp. 399-404.
- S. Y. Lou and X. Y. Tang, “Conditional Similarity Reduction Approach: Jimbo-Miwa Equation,” Chinese Physics, Vol.10, No. 10, 2001, p. 897. doi:10.1088/1009-1963/10/10/303
- S. Y. Lou, X. Y. Tang and J. Lin, “Similarity and Conditional Similarity Reductions of a (2+1)-Dimensional KdV Equation via a Direct Method,” Journal Mathematical Physics, Vol. 41, No. 12, 2000, Article ID: 8286. doi:10.1063/1.1320859
- S. H. Ma and J. P. Fang, “New Exact Solutions for the Related Schrödinger Equation and the Temporal-Soliton and Soliton-Impulse,” Acta Physica Sinica, Vol. 55, No. 11, 2006, pp. 5611-5616.
- S. H. Ma, X. H. Wu, J. P. Fang and C. L. Zheng, “Chaotic Solitons for the (2+1)-Dimensional Modified Dispersive Water-Wave System,” Zeitschrift für Nnturforschung A, Vol. 61, No. 1, 2006, pp. 249-252.
- S. H. Ma, J. P. Fang and C. L. Zheng, “Folded Locailzed Excitations and Chaotic Patterns in a (2+1)-Dimensional Soliton System,” Zeitschrift für Nnturforschung A, Vol. 62, No. 1, 2008, pp. 121-126.
- S. H. Ma, J. Y. Qiang and J. P. Fang, “The Interaction between Solitons and Chaotic Behaviours of (2+1)-Dimensional Boiti-Leon-Pempinelli System,” Acta Physics Sinica, Vol. 56, No. 2, 2007, pp. 620-626.
- S. H. Ma, J. P. Fang and H. P. Zhu, “Dromion Soliton Waves and the Their Evolution in the Background of Jacobi Sine Waves,” Acta Physics Sinica, Vol. 56, No. 8, 2007, pp. 4319-4325.
- S. L. Zhang, X. N. Zhu, Y. M. Wang and S. Y. Lou, “Extension of Variable Separable Solutions for Nonlinear Evolution Equations,” Communications in Theoretial Physics, Vol. 49, No. 1, 2008, pp. 829-832.
- S. L. Zhang and S. Y. Lou, “Functional Variable Separation for Extended Nonlinear Elliptic Equations,” Communications in Theoretial Physics, Vol. 48, No. 3, 2007, pp. 385-390. doi:10.1088/0253-6102/48/3/001
- D. J. Zhang, “Singular Solutions in Casoratian Form for Two Differential-Difference Equations,” Chaos, Solitons and Fractals, Vol. 23, No. 4, 2005, pp. 1333-1350.
- D. J. Zhang, “The N-Soliton Solutions of Some Soliton Equations with Self-Consistent Sources,” Chaos, Solitons and Fractals, Vol. 18, No. 1, 2003, pp. 31-43. doi:10.1016/S0960-0779(02)00636-7
- C. L. Zheng and L. Q. Chen, “Solitons with Fission and Fusion Behaviors in a Variable Coefficient BroerCKaup System,” Chaos, Solitons and Fractals, Vol. 24, No. 5, 2005, pp. 1347-1351. doi:10.1016/j.chaos.2004.09.069
- C. L. Zheng and J. P. Fang, “New Exact Solutions and Fractal Patterns of Generalized BroerCKaup System via a Mapping Approach,” Chaos, Solitons and Fractals, Vol. 27, No. 5, 2006, pp. 1321-1327. doi:10.1016/j.chaos.2005.04.114
- M. L. Wang, X. Z. Li and J. L. Zhang, “The (G'/G)-Expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics,” Physics Letter A, Vol. 372, No. 4, 2008, pp. 417-423. doi:10.1016/j.physleta.2007.07.051
- S. Zhang and J. L. Tong, “A Generalized (G'/G)-Expansion Method for the mKdV Equation with Variable Coefficients,” Physics Letter A, Vol. 372, No. 13, 2008, pp. 2254-2257. doi:10.1016/j.physleta.2007.11.026
- A. Bekir, “Application of the (G'/G)-Expansion Method for Nonlinear Evolution Equations,” Physics Letter A, Vol. 372, No. 19, 2008, pp. 3400-3406. doi:10.1016/j.physleta.2008.01.057
- J. Zhang, X. L. Wei and Y. J. Lu, “A Generalized (G'/G)- Expansion Method and Its Applications,” Physics Letter A, Vol. 372, No. 20, 2008, pp. 3653-3658. doi:10.1016/j.physleta.2008.02.027
- E. M. E. Zayed and K. A. Gepreel, “The (G'/G)-Expansion Method for Finding Traveling Wave Solutions of Nonlinear Partial Differential Equations in Mathematical Physics,” Journal of Mathematical Physics, Vol. 50, No. 1, 2009, Article ID: 013502. doi:10.1063/1.3033750
- B. Q. Li, Y. L. Ma, C. Wang, M. P. Xu and Y. Li, “Folded Soliton with Periodic Vibration for a Nonlinear Coupled Schrödinger System,” Acta Physica Sinica, Vol. 60, No. 6, 2011, Article ID: 060203.
- B. Q. Li, Y. L. Ma and M. P. Xu, “(G'/G)-Expansion Method and Novel Fractal Structures for High-Dimensional Nonlinear Physical Equation,” Acta Physica Sinica, Vol. 59, No. 3, 2010, pp. 1409-1415.
- R. Radha and M. Laskshmanan, “Dromion Like Structures in the (2+1)-Dimensional Breaking Soliton Equation,” Physics Letter A, Vol. 197, No. 1, 1995, pp. 7-12. doi:10.1016/0375-9601(94)00926-G
- S. H. Ma, J. Y. Qiang and J. P. Fang, “Annihilation Solitons and Chaotic Solitons for the (2+1)-Dimensional Breaking Soliton System,” Communications in Theoretial Physics, Vol. 48, No. 2, 2007, p. 662.

