Applied Mathematics
Vol.4 No.10(2013), Article ID:37367,4 pages DOI:10.4236/am.2013.410184
The Change of Physical-Mechanical Properties of Viscoelastic Liquids in Consideration of Nanoparticles
1Baku State University, Baku, Azerbaijan
2Azerbaijan Technical University, Baku, Azerbaijan
Email: nanomaterials@bsu.az, mamed_r50@mail.ru
Copyright © 2013 M. A. Ramazanov, M. S. Aslanov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 16, 2013; revised June 16, 2013; accepted June 23, 2013
Keywords: Viscoelastic Body; The Maxwell Model; Nanoparticle; Value of the Deformation Points
ABSTRACT
The paper studies the viscoelastic body described by the generalized Maxwell model. This model consists of several parallel-connected simple models of Maxwell. Assuming the interaction of atoms of the body with embedded nanoparticles leads to a change in model parameters. It is shown that with the addition of nanoparticles with a specific property, it can change the value of the deformation points of a viscoelastic body. This change depends on the number of elements.
1. Introduction
This paper highly evaluated the creation of efficient technologies on the basis of nanotechnologies in the areas of oil industry, automobile industry, shipbuilding, construction, aviation and examples. For example, the application of nanotechnologies in oil industry is connected with the increasing of oil productive rate of high-viscous oil deposits. There are many efforts carried out in this direction [1-5].
It is known that one of the most important directions of nanotechnologies in the paint-and-lacquer coating is developing new special materials on the basis of sol-gel technology [6]. It permits to create systems with specified properties from inorganic and organic 3D structures as well as the task that designs nanoparticles for specific application areas. The most important drive for investment in nanotechnology from paint-and-lacquer companies is strict ecologically international and national requirements, which prohibit using many rust-preventing pigments and biocide in primer-sealer and enamel. Nanotechnologies allow refusing the application of six valent chromium in rust-preventing marine primer-sealer as well as tin organic compounds in anti fouling coating. These compounds are dangerous for ecosystem and are prohibited by International Marine Organization (IМО).
Effectiveness of suggested technology is connected with changing of physical chemical properties of paint-andlacquer systems. Taking into consideration that such systems are described by viscoelastic and visco-plastic models, there is a task of describing the model medium with interaction on atomic and molecular level. To describe such a medium, no nanoparticle is taken as a model that is detailed studied [7]. For studying nanoparticles influence, it is reasonable to modernize the existing models of viscoelastic medium by introducing parameters that define the properties of tiny sized nanoparticles. The construction of model of viscoelastic liquids containing nanoparticles is the urgent problem of nanotechnology.
The presented work is considered the generalized model of viscoelastic liquid [4,7] based on simple Maxwell model.
2. Formulation
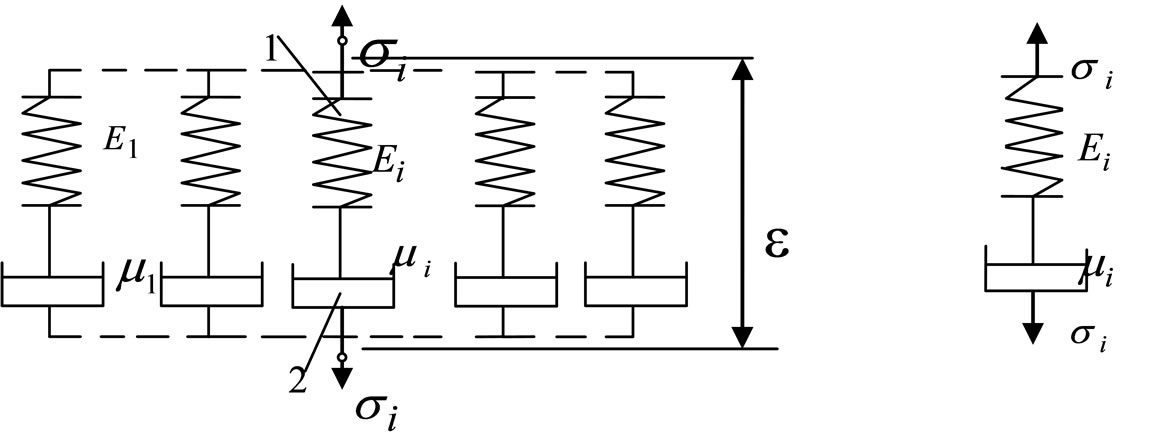
Let us consider the generalized model of viscoelastic liquid that is known as generalized Maxwell model (Figure 1(а)). It consists of parallel-connected n simple Maxwell models. The simple Maxwell model consists of successsively jointed viscous and elastic elements (Figure 1(b)).
As have been above mentioned the generalized Maxwell model consists of parallel-connected 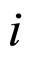 -numbered models of Maxwell. Simple
-numbered models of Maxwell. Simple 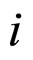 -model of Maxwell is described by successively jointed elastic
-model of Maxwell is described by successively jointed elastic  -element with the ratio
-element with the ratio 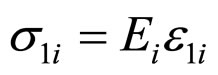 is true and viscous
is true and viscous  -element with ratio
-element with ratio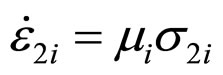 .
.
Here is taken the following designations: indexes “1”
 (a) (b)
(a) (b)
Figure 1. Maxwell model. (а) Generalized Maxwell model; (b) Simple Maxwell model. 1: elastic element; 2: viscous element.
and “2” relate to elastic and viscous element of i-model correspondingly, 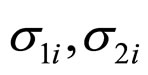 and
and  tension and deformation of each above mentioned elements,
tension and deformation of each above mentioned elements, 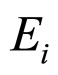 -elastic modulus,
-elastic modulus, 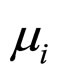 is viscosity factor of corresponding simple
is viscosity factor of corresponding simple 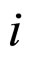 -model of Maxwell. The dot indicates the time derivative
-model of Maxwell. The dot indicates the time derivative .
.
At successive joining in simple 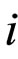 -model of Maxwell we accept
-model of Maxwell we accept  and designate
and designate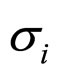 , i.e.
, i.e. 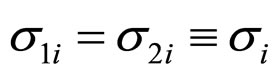 . Then for generalized model on the assumption of elements joining follows,
. Then for generalized model on the assumption of elements joining follows, 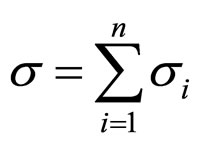 , where
, where ![]() -tension, applied to whole body,
-tension, applied to whole body, ![]() -number of simple models (Figure 1(а)). The deformation of
-number of simple models (Figure 1(а)). The deformation of 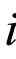 -model of Maxwell is defined by correlation
-model of Maxwell is defined by correlation
 (1)
(1)
where ![]() -lump sum deformation of
-lump sum deformation of 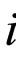 -model of Maxwell (Figure 1). Correlation (1) comes out from condition of successful joining of elastic and viscous elements. It should be noted that at parallel connection the deformation of generalized model is lump sum for all elements, i.e.
-model of Maxwell (Figure 1). Correlation (1) comes out from condition of successful joining of elastic and viscous elements. It should be noted that at parallel connection the deformation of generalized model is lump sum for all elements, i.e. .
.
Then accept 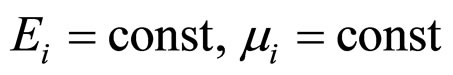 for definition
for definition ![]() at time:
at time:
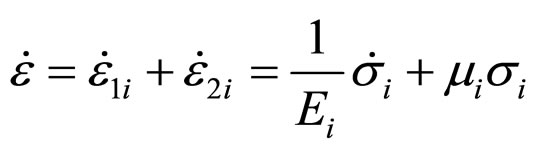 . (2)
. (2)
This equation is solved at the following initial condition:
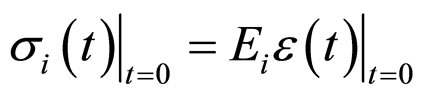 , (3)
, (3)
i.e. at initial moment the viscous element does not work.
The decision of Equation (2), satisfying to initial condition (3) is:
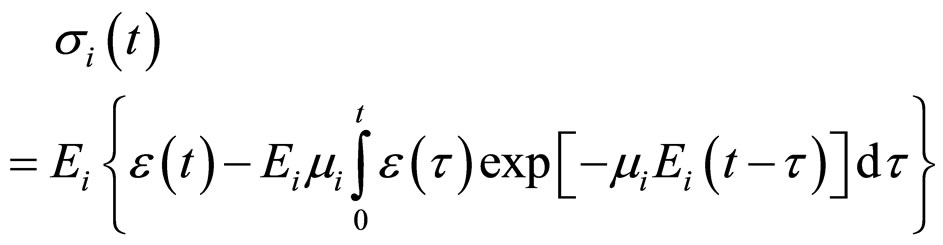 . (4)
. (4)
Based on obtained equation and dependence of ![]() from
from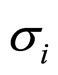 :
:
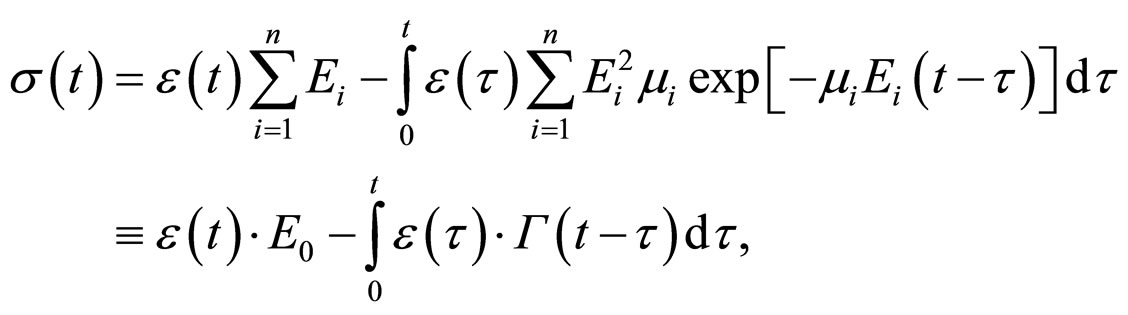 ,(5)
,(5)
where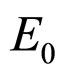 : generalized elastic modulus,
: generalized elastic modulus,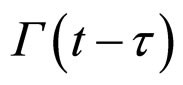 : generalized fluidity nuclei.
: generalized fluidity nuclei.
This expression makes possible to establish the dependence between ![]() and
and![]() . Usually such correlations describe the behavior of viscoelastic “liquid” medium [7]. Some nanotechnologies applied for production of lacquer coating use pressurizing of nanoparticles in medium. It leads to changing of coating behavior and consequently to changing of parameters, describing viscoelastic liquids. Assume that the structure of initial model at addition of nanoparticles does not change, i.e. the initial model is the generalization of Maxwell model but with other parameters. Define the parameters of this model. The analysis of results show that addition of nanoparticles changes the elastic as well as viscous parameters of the model [4,5]. For its definition let construct the model, permit to describe these changes at some approximation.
. Usually such correlations describe the behavior of viscoelastic “liquid” medium [7]. Some nanotechnologies applied for production of lacquer coating use pressurizing of nanoparticles in medium. It leads to changing of coating behavior and consequently to changing of parameters, describing viscoelastic liquids. Assume that the structure of initial model at addition of nanoparticles does not change, i.e. the initial model is the generalization of Maxwell model but with other parameters. Define the parameters of this model. The analysis of results show that addition of nanoparticles changes the elastic as well as viscous parameters of the model [4,5]. For its definition let construct the model, permit to describe these changes at some approximation.
3. Solving of Problem
Assume that elastic element of Maxwell model can be presented like one-dimensional “chain” of atoms, interacting to each other (Figure 2). Such representation is characteristic for polymeric compounds (PC).
Assume that each embedded nanoparticle take intermediate position between atoms (possibility of embedding several nanoparticles). The structure of elastic element does not change it is still rectilinear (not branched) “chain”. It follows from assumption of Maxwell model preservation at nanoparticles addition. Assume that particles interact only with neighboring particles. Then without consideration of nanoparticles follow
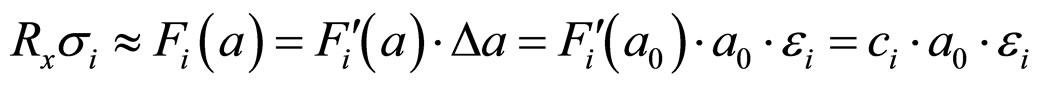 ; (6)
; (6)
where : atom interactions force,
: atom interactions force,![]() : distance between atoms after deformation,
: distance between atoms after deformation, : before deformation,
: before deformation, : elasticity factor,
: elasticity factor,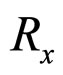 : characteristic size of cross-sectional area of atom exposed to force, stroke—
: characteristic size of cross-sectional area of atom exposed to force, stroke—
 (a)
(a) (b)
(b)
Figure 2. Elastic Maxwell element. (a) Without of nanoparticles; (b) With nanoparticles.
shows coordinate derivative, 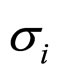 and
and![]() : tension and deformation of each of above mentioned elements.
: tension and deformation of each of above mentioned elements.
Then have the following correlation:
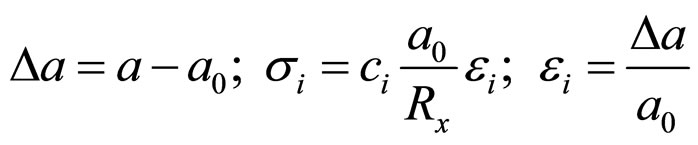 .
.
Using formula (8) let us generalize for case with nanoparticles consideration.
Assume that each of embedded nanoparticle takes intermediate position between atoms (Figure 2(b) it shown by shade circles’). The structure of elastic element does not change it is still rectilinear (not branched) “chain”. It follows from assumption of Maxwell model preservation at nanoparticles addition. Assume that particles interact only with neighboring particles.
Then with consideration of nanoparticles we have
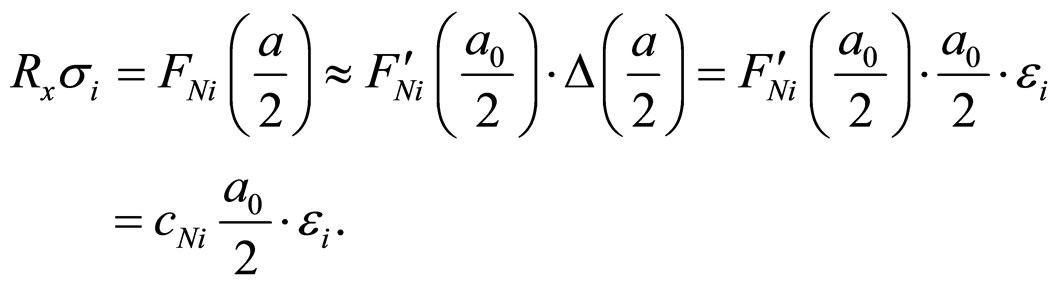
Hence we have correlation of “chain” elasticity with consideration of nanoparticles.
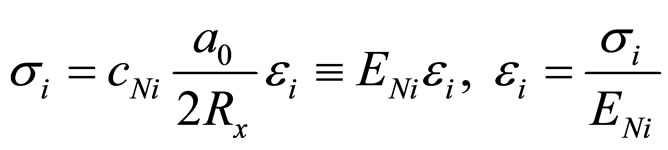 , (7)
, (7)
where “i” and “N”: mean, that given value relates to 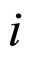 -model of Maxwell and to nanoparticle. Here assumed that nanoparticle is between atoms in the middle of “chain”. Note that this position is efficient in terms of energy.
-model of Maxwell and to nanoparticle. Here assumed that nanoparticle is between atoms in the middle of “chain”. Note that this position is efficient in terms of energy.
Let us present the viscous element of 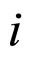 -model of Maxwell as cylinder filled by viscous liquid compressed by piston. Assume nanoparticles are distributed in viscous liquid that leads to prevention of Maxwell model element. In this case the influence of nanoparticles is similar to the influence of solid particles in viscous liquid [3]. The influence of nanoparticles become apparent differently: growth of friction force of liquid to cylinder wall, change of liquid properties, combination of these effects. Exept this it is possible the absence of influence. Choice of effect depends of interconnections between physical-chemical properties of nanoparticles and liquid and condition of interaction. All above mentioned influences of nanoparticles for considered model can be reduced to change of viscosity factor i.e. to introduce the value
-model of Maxwell as cylinder filled by viscous liquid compressed by piston. Assume nanoparticles are distributed in viscous liquid that leads to prevention of Maxwell model element. In this case the influence of nanoparticles is similar to the influence of solid particles in viscous liquid [3]. The influence of nanoparticles become apparent differently: growth of friction force of liquid to cylinder wall, change of liquid properties, combination of these effects. Exept this it is possible the absence of influence. Choice of effect depends of interconnections between physical-chemical properties of nanoparticles and liquid and condition of interaction. All above mentioned influences of nanoparticles for considered model can be reduced to change of viscosity factor i.e. to introduce the value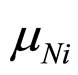 . Based on physic phenomena
. Based on physic phenomena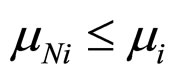 . Indeed let us consider the first variant. Assume that introduction of nanoparticles in the liquid leads to increasing of friction force of liquide. At tension of piston with same force the motion rate decrease due to tension, i.e.
. Indeed let us consider the first variant. Assume that introduction of nanoparticles in the liquid leads to increasing of friction force of liquide. At tension of piston with same force the motion rate decrease due to tension, i.e.
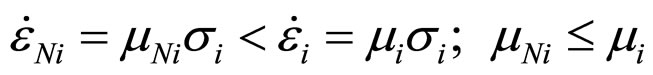 .
.
So, based on correlation (1), defining the equation of Maxwell model with nanoparticles is:
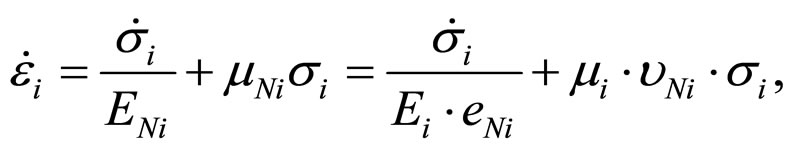 (8)
(8)
where introduced the following designations:
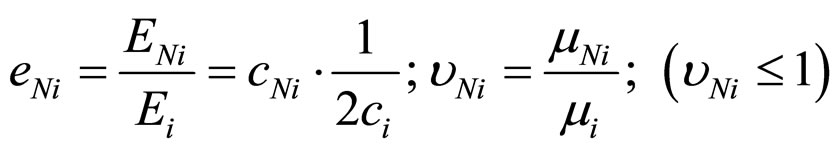 .
.
The decision of Equation (8) is:
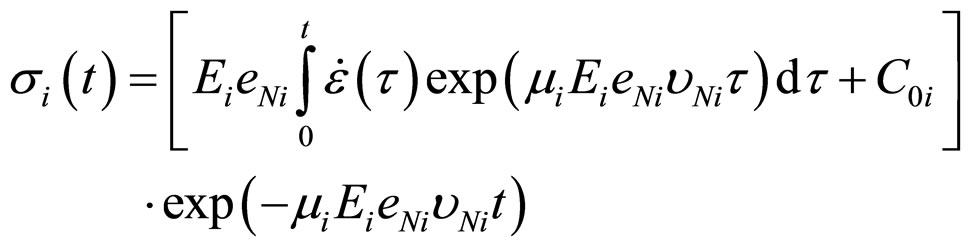 (9)
(9)
or
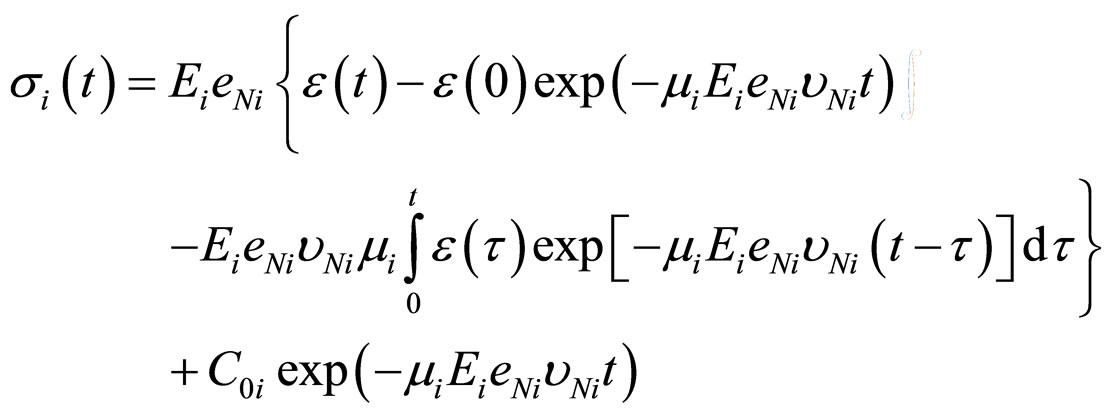 .
.
Due to the essence of initial condition does not change the Equation (9), satisfying to initial condition (3), is:
 . (10)
. (10)
Taking into consideration that lump sum tension ![]() is equal to sum of tensions
is equal to sum of tensions , based on (10), we receive:
, based on (10), we receive:
 (11)
(11)
where E0N: generalized elasticity modulus,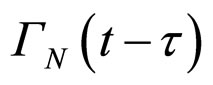 : generalized fluidity nuclei with nanoparticles.
: generalized fluidity nuclei with nanoparticles.
So on example of generalized Maxwell model it is shown that presence of nanoparticles in constituent elements leads to change of parameters of model. The character of these changes and its values are described in the frame of assumptions about interactions of nanoparticles with atoms of elastic element and viscous liquid.
Accepting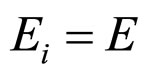 ,
, 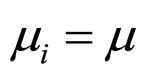 ,
, 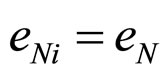 ,
, 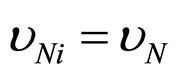 , then from (11) we receive:
, then from (11) we receive:
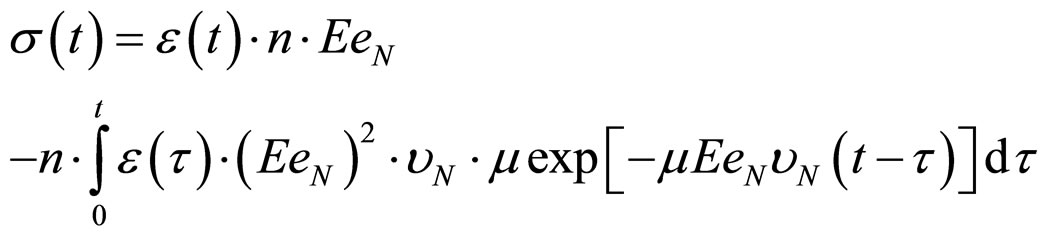 .(12)
.(12)
Differentiate the Equation (12), we receive the following differential equation:
 . (13)
. (13)
The decision of differential Equation (13) with condition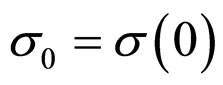 , for any
, for any ![]() is:
is:
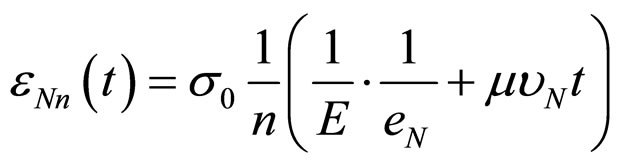 . (14)
. (14)
Define the influence of number of elements n on deformation value. For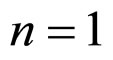 , based on (14) follow:
, based on (14) follow:
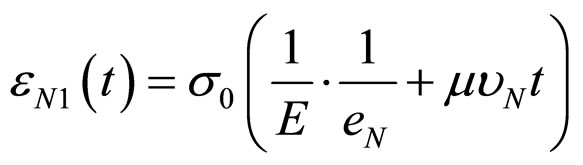 .
.
then
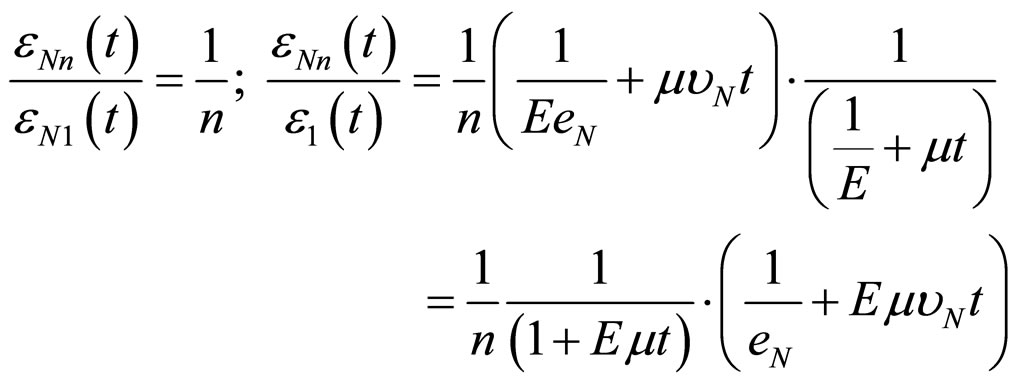 .
.
Figure 3 gives dependence of  from
from ![]()
for different values .
.
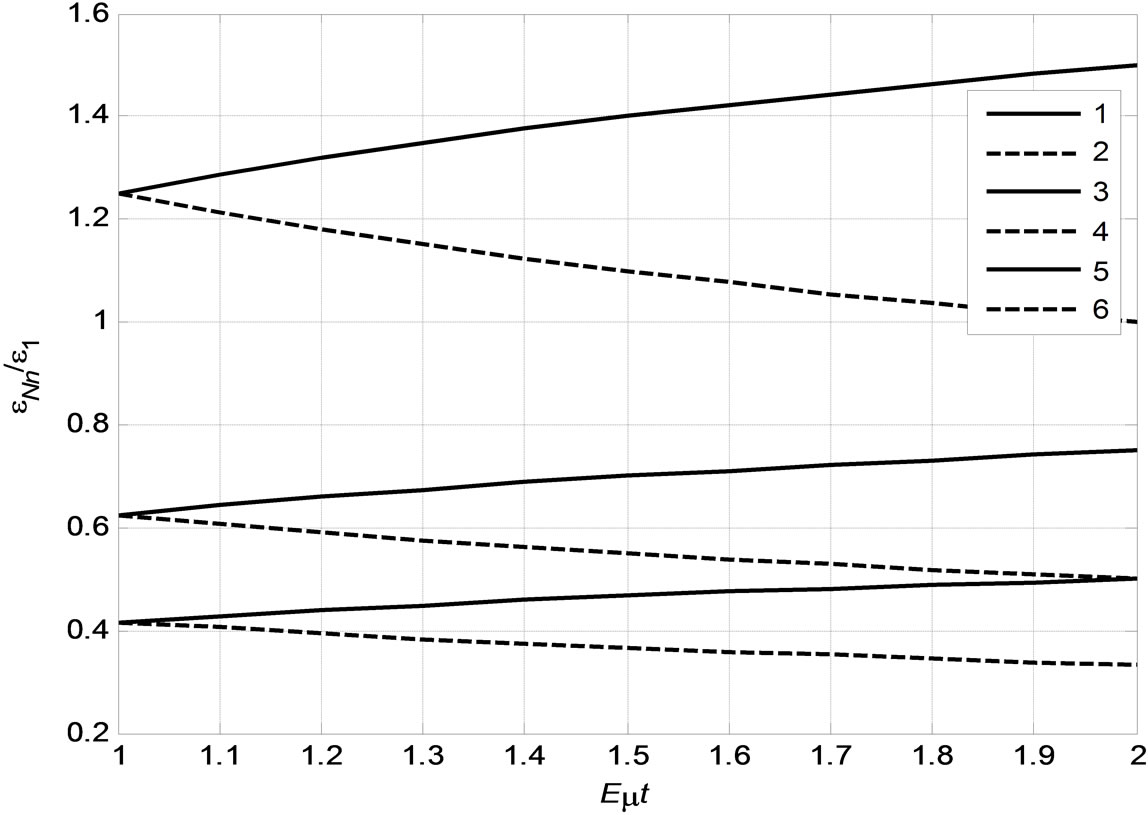
Figure 3. Dependence  from Eμt. Value of parameters: n = 1, 2, 3. eN = υN = 2, 0.5.
from Eμt. Value of parameters: n = 1, 2, 3. eN = υN = 2, 0.5.
From diagram follows at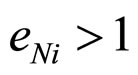 , the deformation steadily increases, and at
, the deformation steadily increases, and at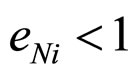 , deformation steadily decreases. The increasing of elements number leads to decreasing of deformation value.
, deformation steadily decreases. The increasing of elements number leads to decreasing of deformation value.
So if elastic bonds of nanoparticles satisfy the following inequality , i.e.
, i.e.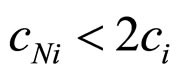 , then addition of nanoparticles in visco-elastic liquids leads to increasing of deformation. Otherwise, i.e. if
, then addition of nanoparticles in visco-elastic liquids leads to increasing of deformation. Otherwise, i.e. if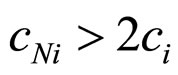 , then addition of nanoparticles in visco-elastic liquids leads to decreasing of deformation. Thereby the addition of nanoparticles with specific properties to Maxwell model of viscoelastic liquid can change the deformation value, i.e. can change the properties of model.
, then addition of nanoparticles in visco-elastic liquids leads to decreasing of deformation. Thereby the addition of nanoparticles with specific properties to Maxwell model of viscoelastic liquid can change the deformation value, i.e. can change the properties of model.
4. Conclusion
This work carries out the model generalization of the viscoelasticity theory with nanoparticle consideration. The type of model preserved for Maxwell model generalization equates the basic correlations. This model shows the influence of number of elements and nanoparticles on mechanic properties.
REFERENCES
- Q. B. Sergeev, “Nanochimiya,” М.: KDU, 2007, 336p.
- A. N. Alizadeh, “Tension of a Plate with Nanomaterial Coating,” Reports of National Academy of Sciences of Azerbaijan, Vol. 66, No. 5, 2010, pp. 34-43.
- S. Abdullayev, “Nanohydromechanica,” Baku, 2011, 158 p.
- М. А. Ramazanov and М. S. Aslanov, “Synthesis of the Maxwell Model Based on Nanoparticles,” Digest Journal of Nanomaterials and Biostructures, Vol. 7, No. 2, 2012, pp. 817-822.
- M. A. Ramazanov and M. S. Aslanov, “Article title,” Proceedings of International Scientific Conference “Nanotechnology and Its Application in Engineering”, Baku, 15-16 December 2010, pp. 72-75.
- A. D. Pomogailo, A. S. Rosenberg and I. E. Uflyand, “Metal Nanoparticles in Polymers,” М.:Chemstry, Moscow, 2000.
- R. M. Christensen, “Introduction to the Theory of Viscoelasticity,” М.:Mir, 1974, 338p.

