Applied Mathematics
Vol.4 No.1(2013), Article ID:27088,5 pages DOI:10.4236/am.2013.41001
Application of αδ-Closed Sets
1Department of Mathematics, Kongunadu Arts and Science College, Coimbatore, India
2Department of Mathematics, Kalaivani College of Technology, Coimbatore, India
Email: *baskiii2math@gmail.com
Received January 4, 2012; revised November 29, 2012; accepted December 4, 2012
Keywords: αδ-US Spaces; αδ-Convergence; Sequentially αδ-Compactness; Sequentially αδ-Continuity; Sequentially αδ-Sub-Continuity
ABSTRACT
In this paper, we introduce the notion of αδ-US spaces. Also we study the concepts of αδ-convergence, sequentially αδ-compactness, sequentially αδ-continunity and sequentially αδ-sub-continuity and derive some of their properties.
1. Introduction
In 1967, A. Wilansky [1] introduced and studied the concept of  spaces. Also, the notion of αδ-closed sets of a topological space is discussed by R. Devi, V. Kokilavani and P. Basker [2,3]. The concept of slightly continuous functions is introduced and investigated by Erdal Ekici et al. [4]. In this paper, we define that a sequence
spaces. Also, the notion of αδ-closed sets of a topological space is discussed by R. Devi, V. Kokilavani and P. Basker [2,3]. The concept of slightly continuous functions is introduced and investigated by Erdal Ekici et al. [4]. In this paper, we define that a sequence 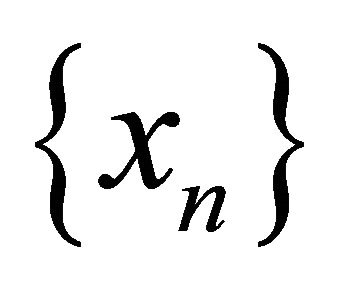 in a space
in a space 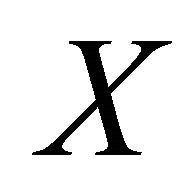 is αδ-converges to a point
is αδ-converges to a point 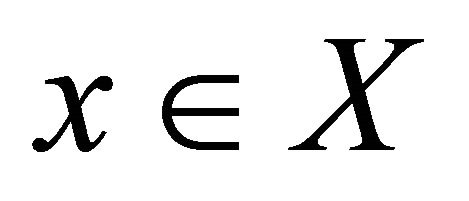 if
if 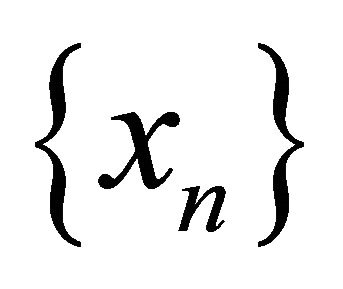 is eventually in every αδ-open set containing
is eventually in every αδ-open set containing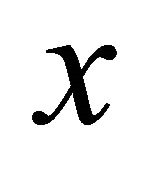 . Using this concept, we define the αδ-US space, Sequentially-αδ-continuous, Sequentially-Nearly- αδ-continuous, Sequentially-Sub-αδ-continuous and Sequentially-αδO-compact of a topological space
. Using this concept, we define the αδ-US space, Sequentially-αδ-continuous, Sequentially-Nearly- αδ-continuous, Sequentially-Sub-αδ-continuous and Sequentially-αδO-compact of a topological space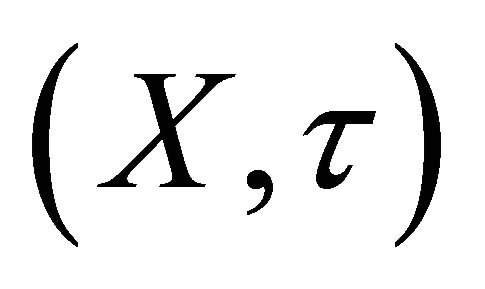 .
.
2. Preliminaries
Throughout this paper, spaces X and Y always mean topological spaces. Let X be a topological space and A, a subset of X. The closure of A and the interior of A are denoted by 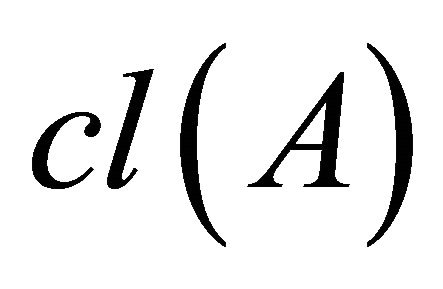 and
and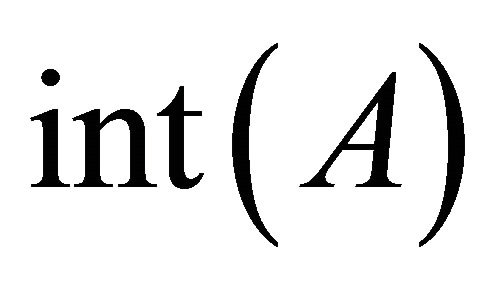 , respectively. A subset A is said to be regular open (resp. regular closed) if
, respectively. A subset A is said to be regular open (resp. regular closed) if 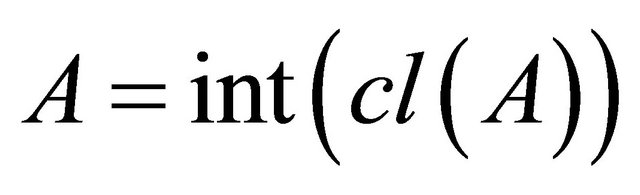 (resp.
(resp.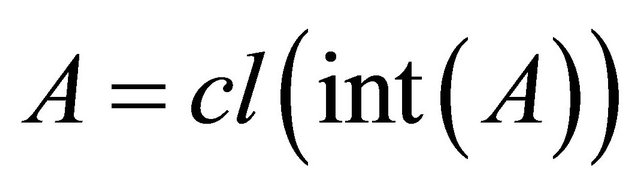 , the δ-interior [5] of a subset A of X is the union of all regular open sets of X contained in A and is denoted by
, the δ-interior [5] of a subset A of X is the union of all regular open sets of X contained in A and is denoted by . The subset A is called δ-open if
. The subset A is called δ-open if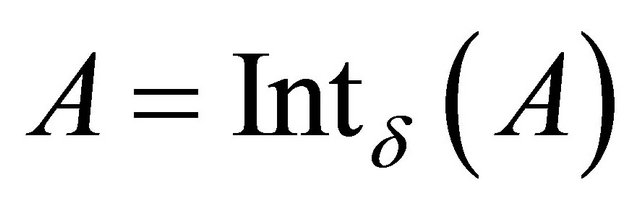 , i.e., a set is δ-open if it is the union of regular open sets. The complement of a δ-open set is called δ-closed.
, i.e., a set is δ-open if it is the union of regular open sets. The complement of a δ-open set is called δ-closed.
Alternatively, a set 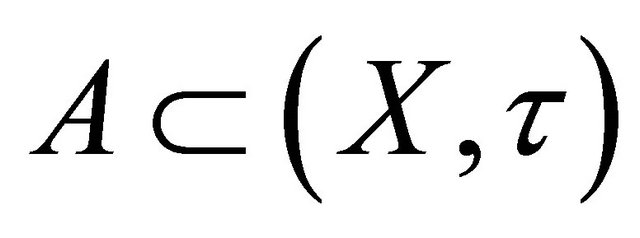 is called δ-closed if
is called δ-closed if , where
, where
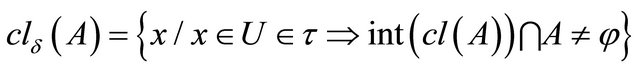 . The family of all δ-open (resp. δ-closed) sets in
. The family of all δ-open (resp. δ-closed) sets in 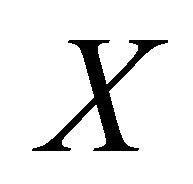 is denoted by
is denoted by 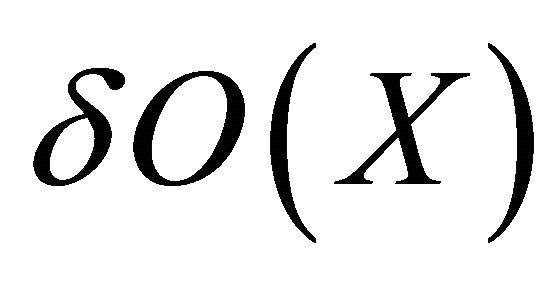 (resp.
(resp. ). A subset
). A subset  of
of 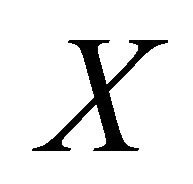
is called α-open [6] if  and the complement of a α-open are called α-closed. The intersection of all α-closed sets containing A is called the α-closure of A and is denoted by
and the complement of a α-open are called α-closed. The intersection of all α-closed sets containing A is called the α-closure of A and is denoted by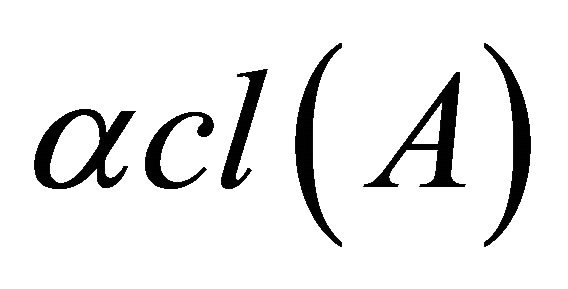 , Dually, α-interior of A is defined to be the union of all α-open sets contained in A and is denoted by
, Dually, α-interior of A is defined to be the union of all α-open sets contained in A and is denoted by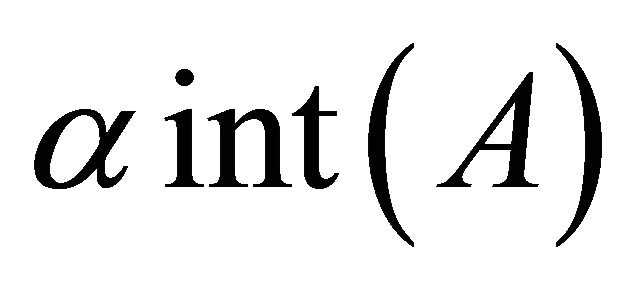 .
.
We recall the following definition used in sequel.
Definition 2.1. A subset  of a space X is said to be
of a space X is said to be
(a) An α-generalized closed [7] (αg-closed) set if  whenever
whenever  and
and  is α-open in
is α-open in 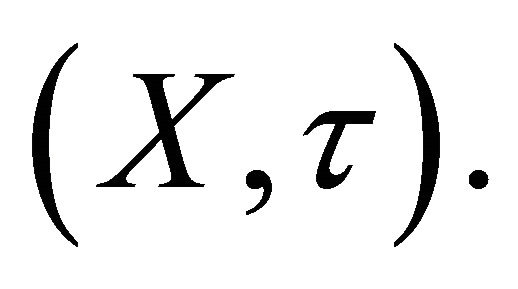
(b) An αδ-closed [8] set if 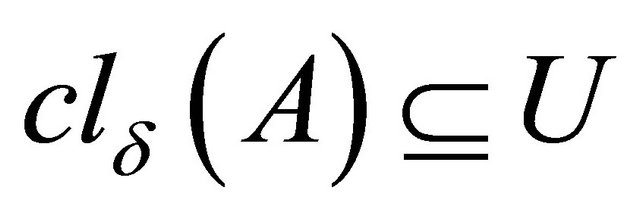 whenever
whenever 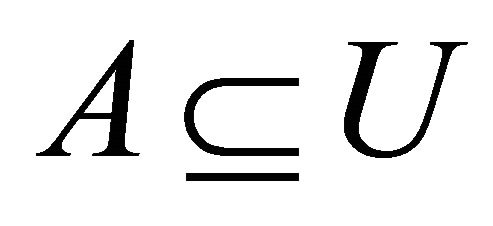 and
and  is αg-open in
is αg-open in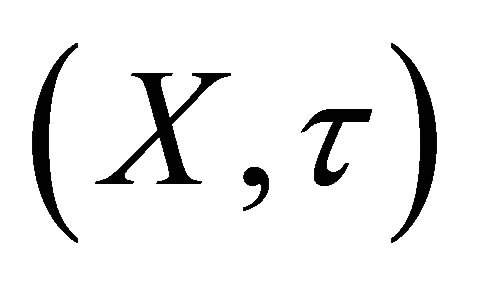 .
.
The complement of a αδ-closed set is said to be 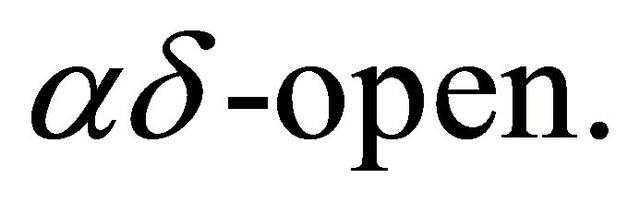 The intersection of all αδ-closed sets of X containing A is called αδ-closure of A and is denoted by
The intersection of all αδ-closed sets of X containing A is called αδ-closure of A and is denoted by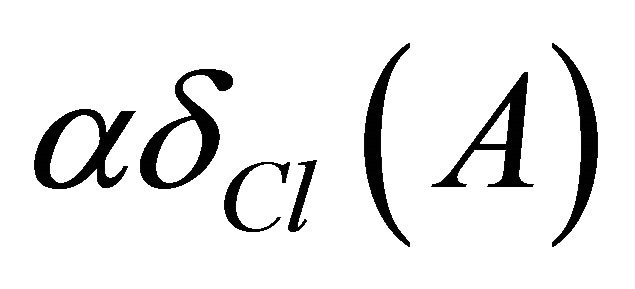 . The union of all αδ-open sets of X contained in A is called αδ-interior of A and is denoted by
. The union of all αδ-open sets of X contained in A is called αδ-interior of A and is denoted by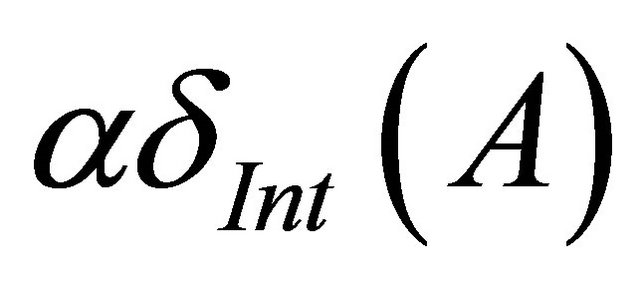 .
.
3. αδ-US Spaces
Definition 3.1. A sequence 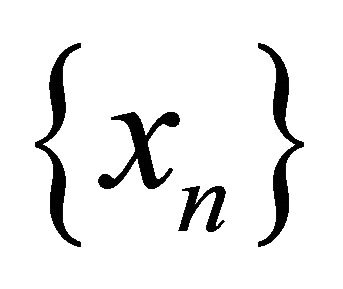 in a space
in a space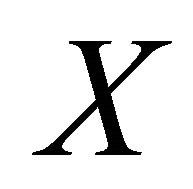 , αδ-converges to a point
, αδ-converges to a point 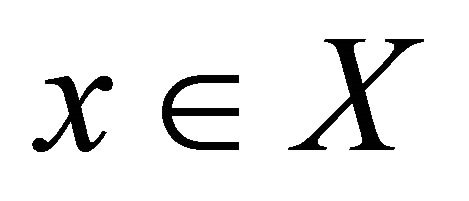 if
if 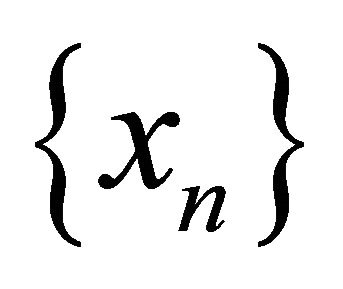 is eventually in every αδ-open set containing
is eventually in every αδ-open set containing .
.
Definition 3.2. A space 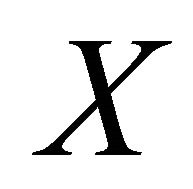 is said to be αδ-US if every sequence in
is said to be αδ-US if every sequence in , αδ-converges to a point of
, αδ-converges to a point of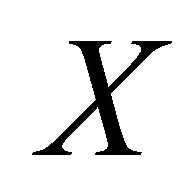 .
.
Definition 3.3. A space 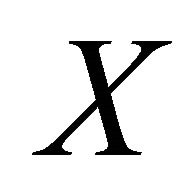 is said to be
is said to be
(a)  if each pair of distinct points
if each pair of distinct points 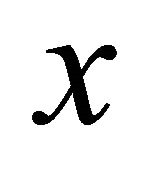 and
and 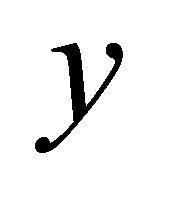 in
in 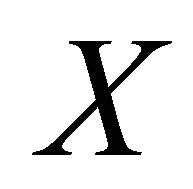 there exists an αδ-open set
there exists an αδ-open set 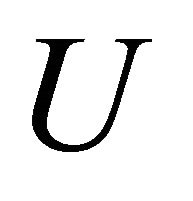 in
in 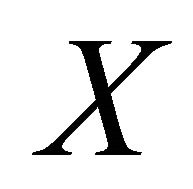 such that
such that 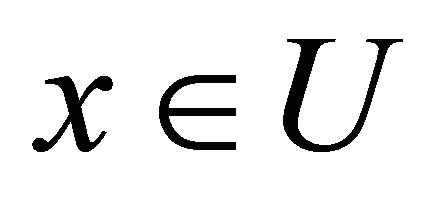 and
and  and a αδ-open set
and a αδ-open set 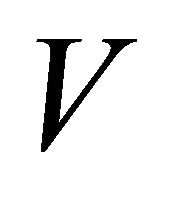 in
in 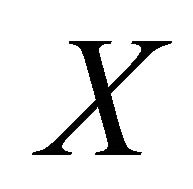 such that
such that 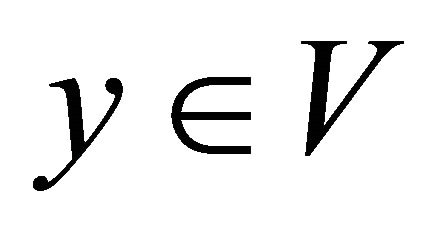 and
and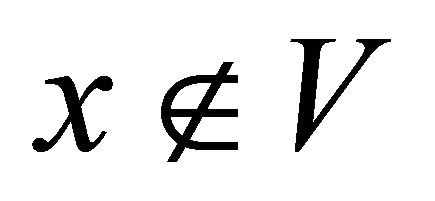 .
.
(b) 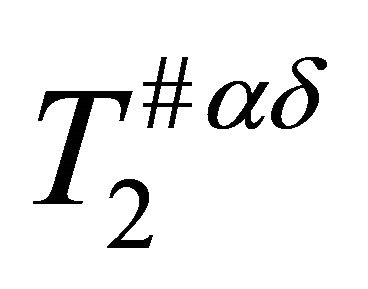 if for each pair of distinct points
if for each pair of distinct points 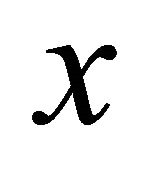 and
and 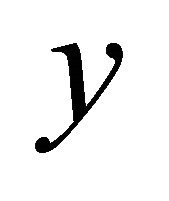 in
in 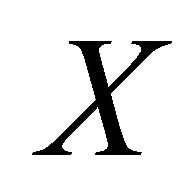 there exists an αδ-open sets
there exists an αδ-open sets 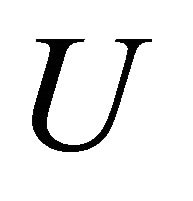 and
and 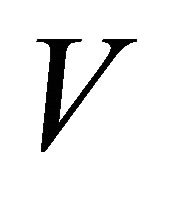 such that
such that  and
and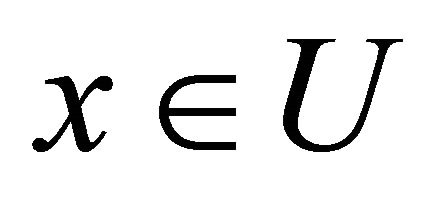 ,
,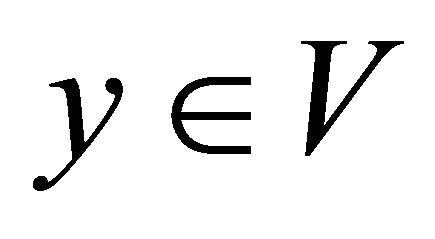 .
.
Theorem 3.4. Every αδ-US-space is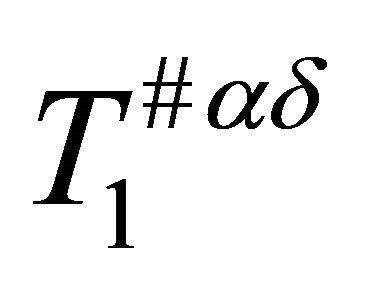 .
.
Proof. Let 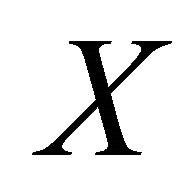 be an αδ-US-space and
be an αδ-US-space and 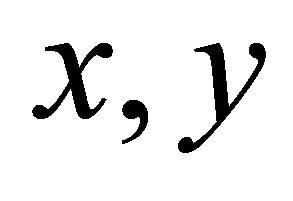 be two distinct points of
be two distinct points of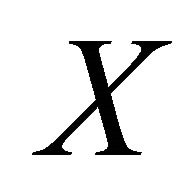 . Consider the sequence
. Consider the sequence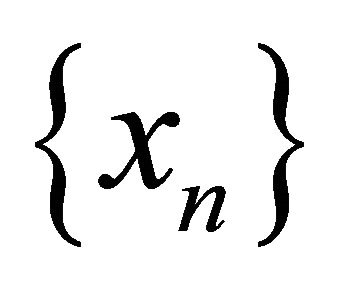 , where
, where 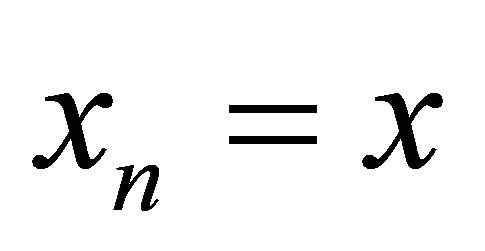 for any
for any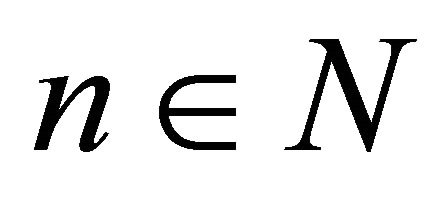 . Clearly
. Clearly  αδ-converges to
αδ-converges to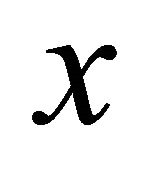 . Since
. Since 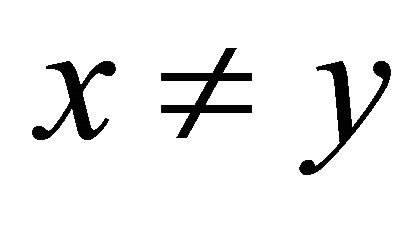 and
and 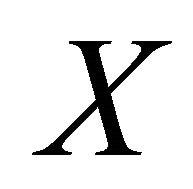 is αδ-US,
is αδ-US, 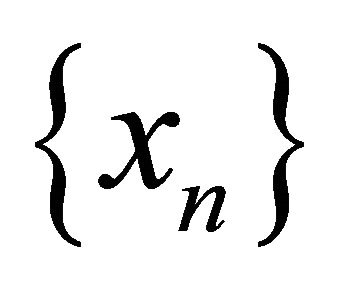 does not αδ-converges to
does not αδ-converges to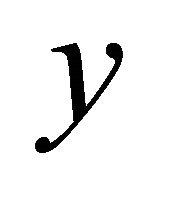 , i.e., there exists an αδ-open set
, i.e., there exists an αδ-open set 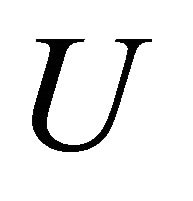 containing
containing 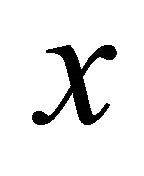 but not
but not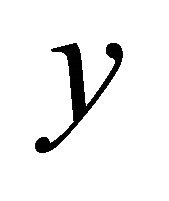 . Similarly, we obtain an αδ-open set
. Similarly, we obtain an αδ-open set  containing
containing 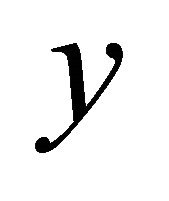 but not
but not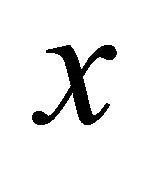 . Thus,
. Thus,  is
is .
.
Theorem 3.5. Every 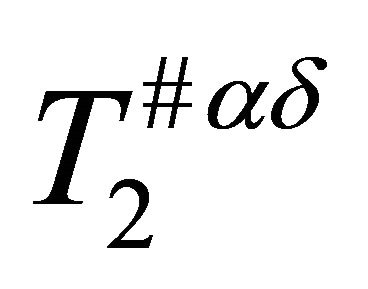 -space is αδ-US.
-space is αδ-US.
Proof. Let 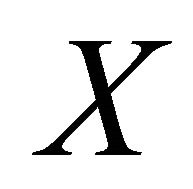 be a
be a 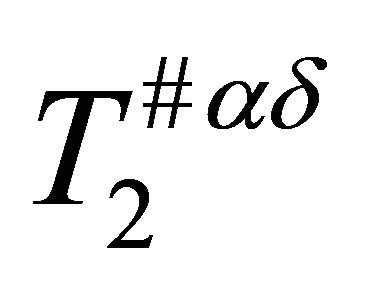 space and
space and 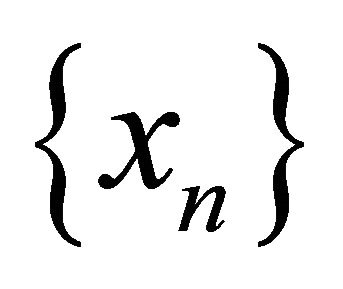 a sequence in
a sequence in . Assume that
. Assume that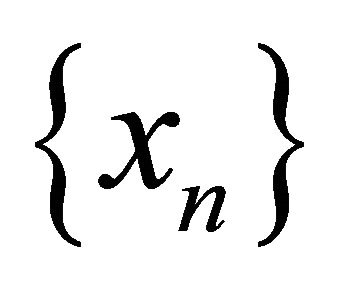 αδ-converges to two distinct points
αδ-converges to two distinct points 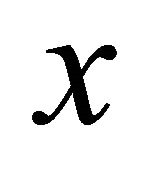 and
and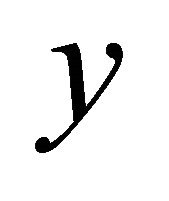 . Then
. Then 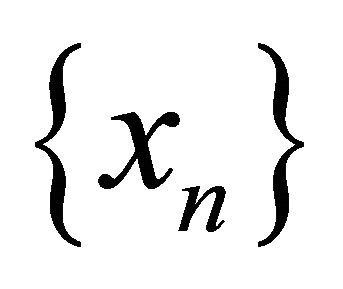 is eventually in every
is eventually in every  then
then 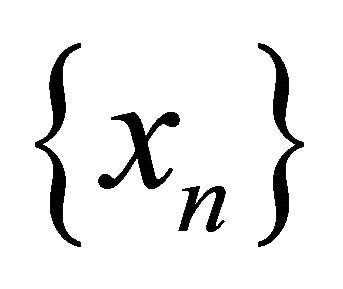 is eventually in two disjoint αδ-open sets. This is a contradiction. Therefore,
is eventually in two disjoint αδ-open sets. This is a contradiction. Therefore, 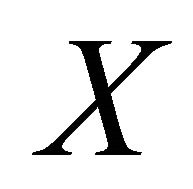 is αδ-US.
is αδ-US.
Definition 3.6. A subset A of a space  is said to be
is said to be
(a) Sequentially αδ-closed if every sequence in A αδ-converges to a point in A(b) Sequentially αδO-compact if every sequence in A has a subsequence which αδ-converges to a point in A.
Theorem 3.7. A space is αδ-US if and only if the diagonal set Δ is a sequentially αδ-closed subset of the product space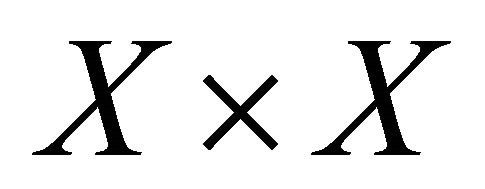 .
.
Proof. Suppose that 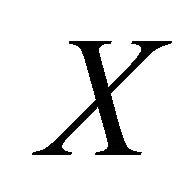 is an αδ-US space and
is an αδ-US space and
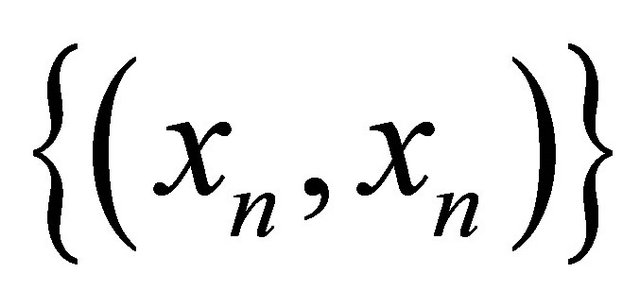 is a sequence in the diagonal Δ. It follows that
is a sequence in the diagonal Δ. It follows that 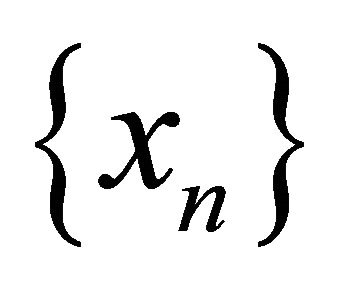 is a sequence in
is a sequence in . Since
. Since 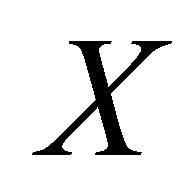 is αδ-US, the sequence
is αδ-US, the sequence αδ-converges to
αδ-converges to 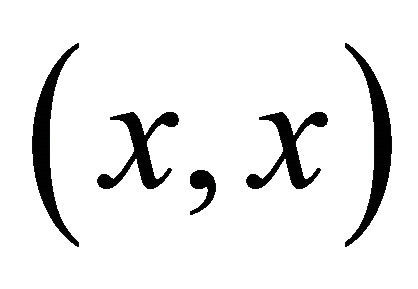 which clearly belongs to Δ. Therefore, Δ is a sequentially
which clearly belongs to Δ. Therefore, Δ is a sequentially 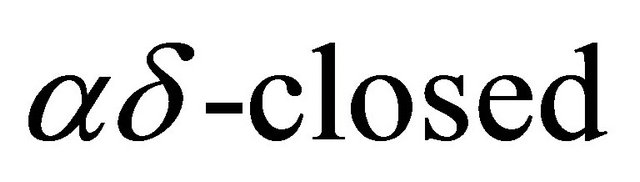 subset of
subset of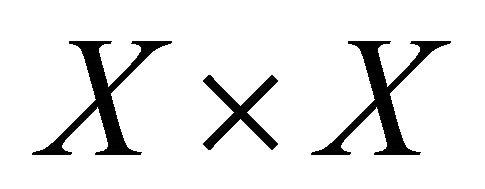 . Conversely, suppose that the diagonal Δ is a sequentially αδ-closed subset of
. Conversely, suppose that the diagonal Δ is a sequentially αδ-closed subset of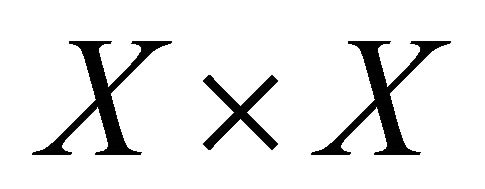 . Assume that a sequence
. Assume that a sequence 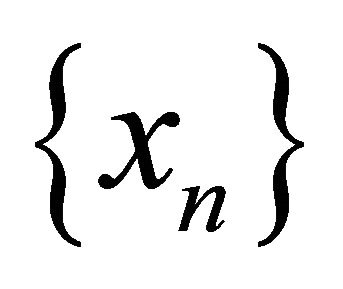 is αδ-converging to x and
is αδ-converging to x and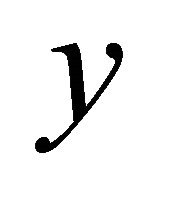 . Then it follows that
. Then it follows that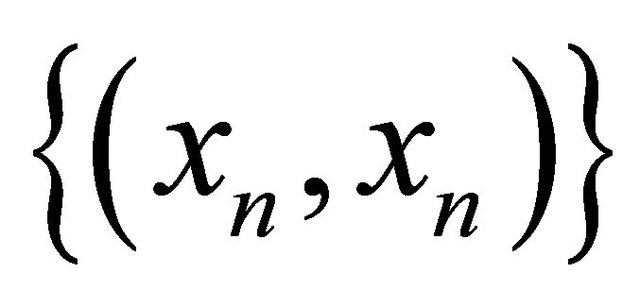 αδ-converges to
αδ-converges to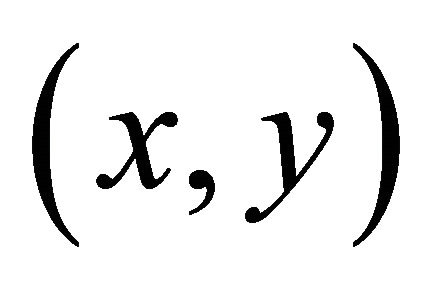 . By hypothesis, since Δ is sequentially αδ- closed, we have
. By hypothesis, since Δ is sequentially αδ- closed, we have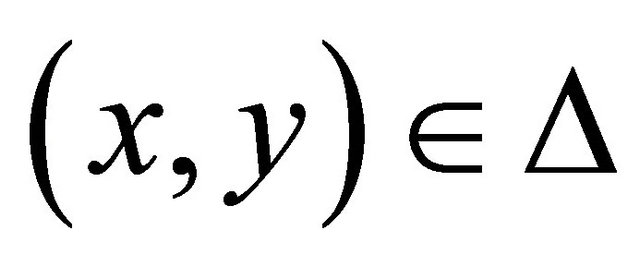 . Thus
. Thus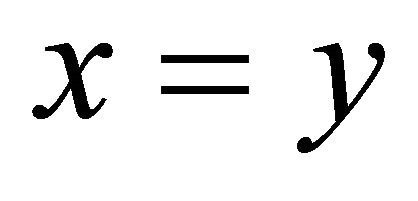 . Therefore,
. Therefore, 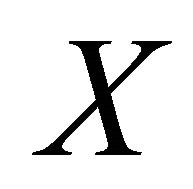 is αδ-US.
is αδ-US.
Theorem 3.8. If a space 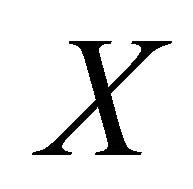 is αδ-US and a subset M of X is sequentially
is αδ-US and a subset M of X is sequentially 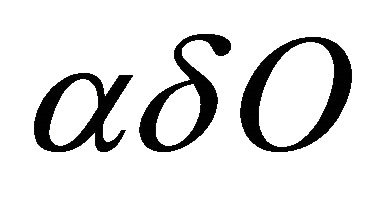 -compact, then M is sequentially αδ-closed.
-compact, then M is sequentially αδ-closed.
Proof. Assume that  is any sequence in
is any sequence in 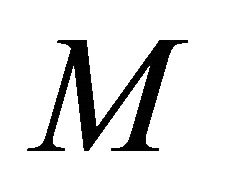 which αδ-converges to a point
which αδ-converges to a point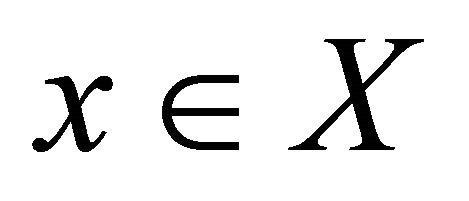 . Since M is sequentially αδO-compact, there exists a subsequence
. Since M is sequentially αδO-compact, there exists a subsequence 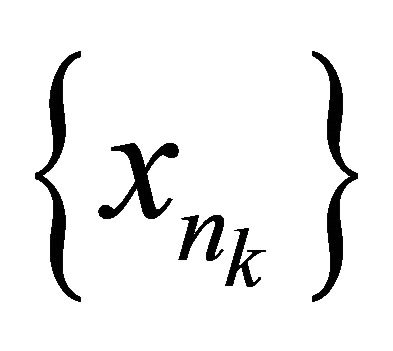 of
of αδ-converges to
αδ-converges to . Since
. Since 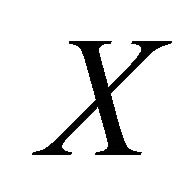 is αδ-US, we have
is αδ-US, we have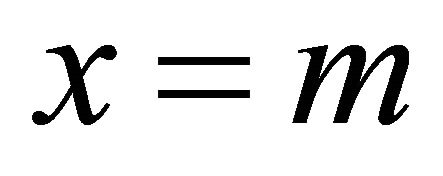 . This shows that M is sequentially αδ-closed.
. This shows that M is sequentially αδ-closed.
Theorem 3.9. The product space of an arbitrary family of αδ-US topological space is an αδ-US topological space.
Proof. Let 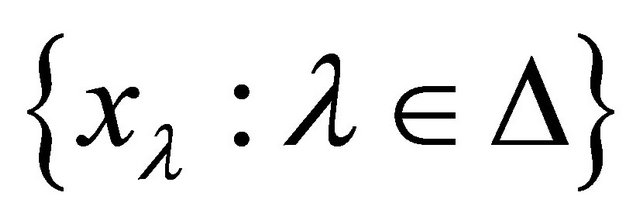 be a family of αδ-US topological spaces with the index set Δ. The product space of
be a family of αδ-US topological spaces with the index set Δ. The product space of  is denoted by
is denoted by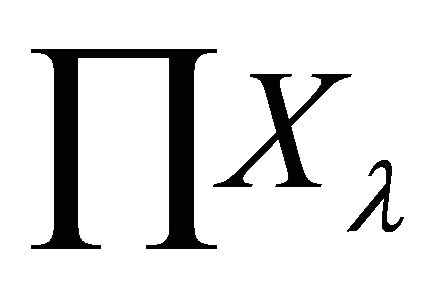 . Let
. Let 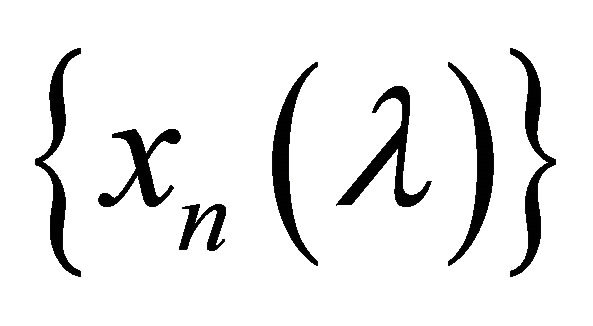 be a sequence in
be a sequence in . Suppose that
. Suppose that
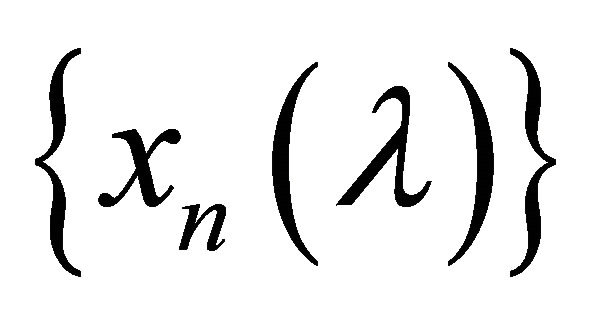 αδ-converges to two distinct points x and y in
αδ-converges to two distinct points x and y in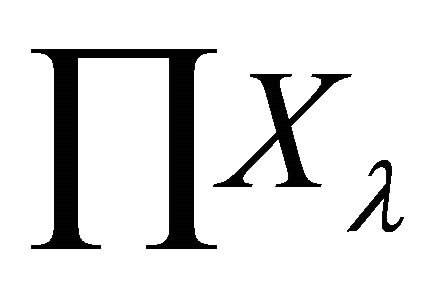 . Then there exists a
. Then there exists a 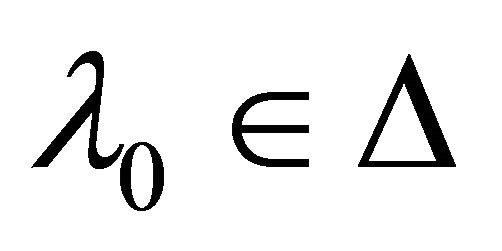 such that
such that
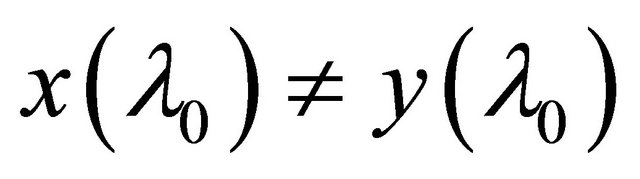 . Then
. Then  is a sequence in
is a sequence in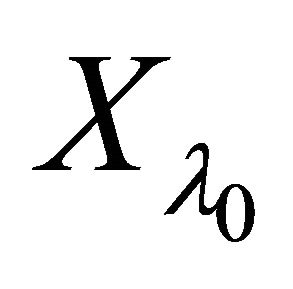 .
.
Let  be any αδ-open in
be any αδ-open in 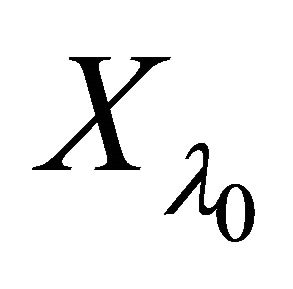 containing
containing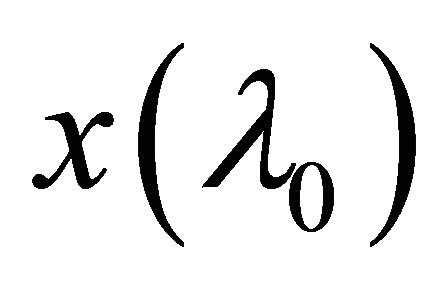 .
.
Then 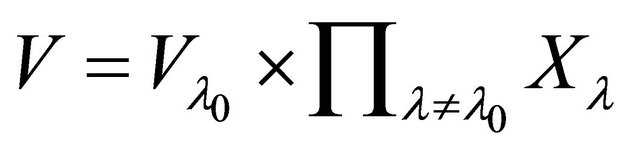 is a αδ-open set of
is a αδ-open set of 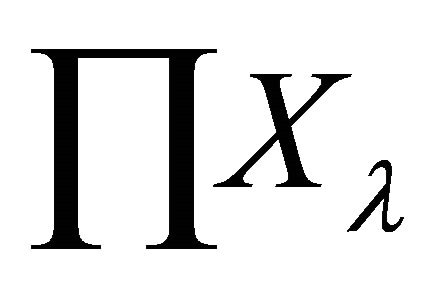
containing x. Therefore,  is eventually in
is eventually in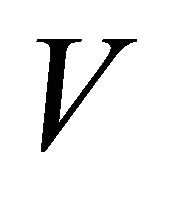 . Thus
. Thus 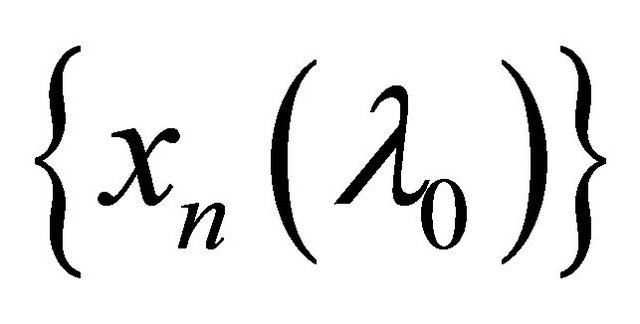 is eventually in
is eventually in 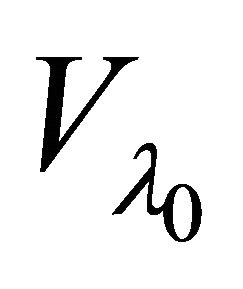 and it αδ-converges to
and it αδ-converges to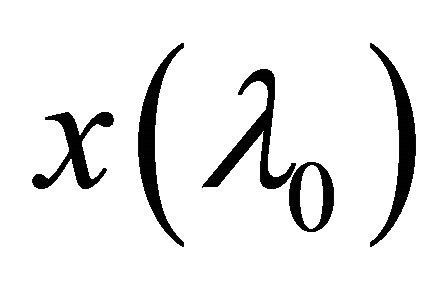 . Similarly, the sequence
. Similarly, the sequence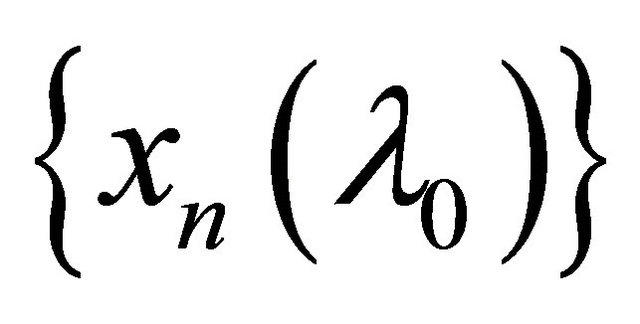 αδ- converges to
αδ- converges to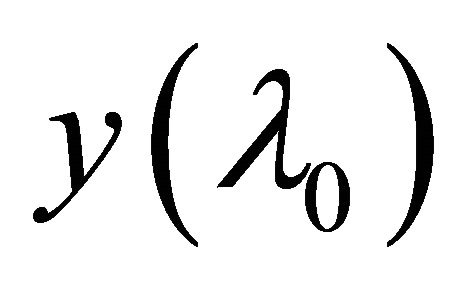 . This is a contradiction as
. This is a contradiction as 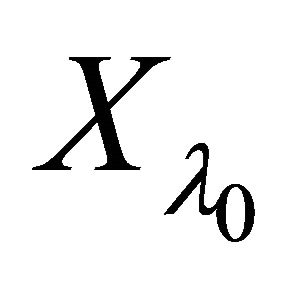 is a
is a
αδ-US space. Therefore, the product space 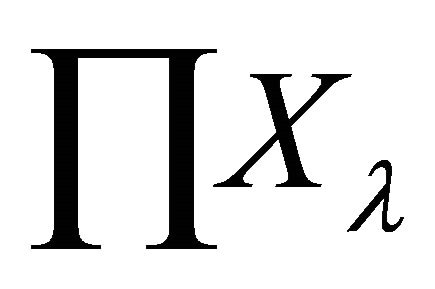 is
is
αδ-US.
4. Sequentially αδO-Compact Preserving Functions
Definition 4.1. A function 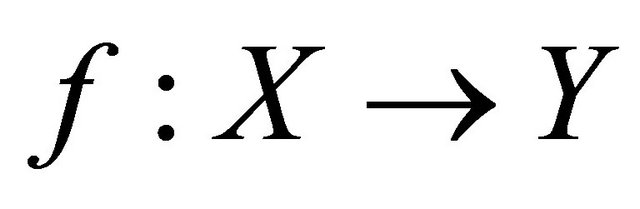 is said to be
is said to be
(a) Sequentially-αδ-continuous at 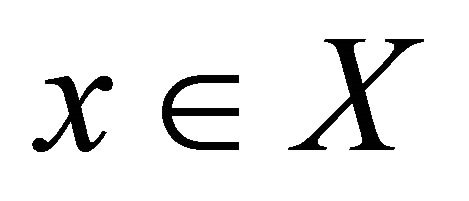 if the sequence
if the sequence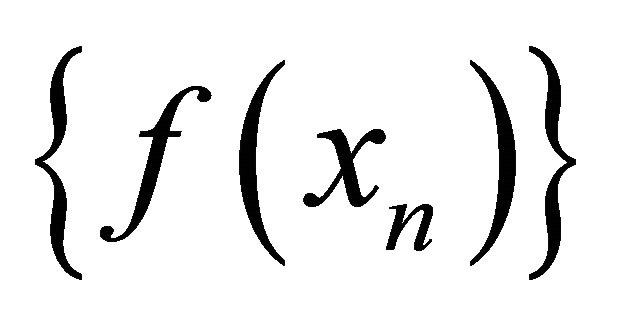 αδ-converges to
αδ-converges to 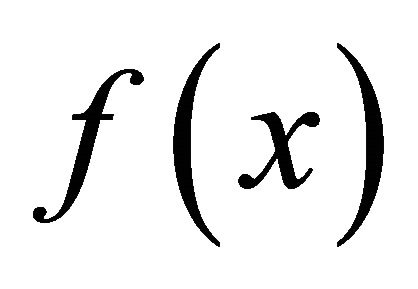 whenever a sequence
whenever a sequence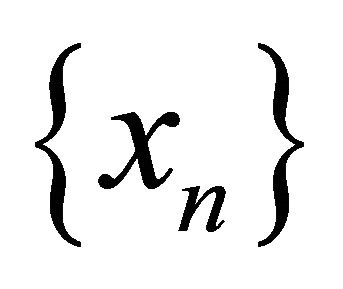 αδ-converges to
αδ-converges to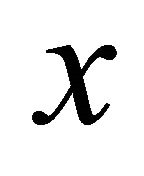 . If
. If 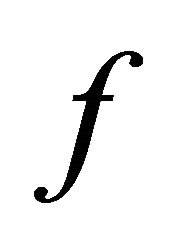 is sequentially αδ-continuous at each
is sequentially αδ-continuous at each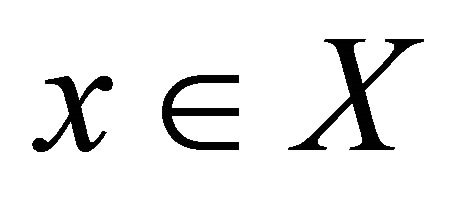 , then it is said to be sequentially αδ-continuous.
, then it is said to be sequentially αδ-continuous.
(b) Sequentially-Nearly-αδ-continuous, if for each sequence 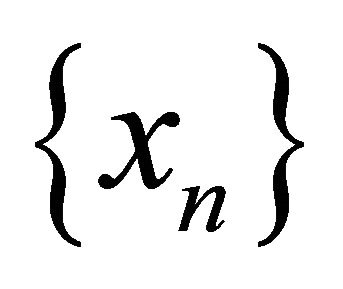 in
in 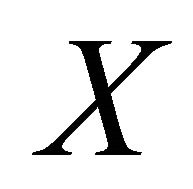 that αδ-converges to
that αδ-converges to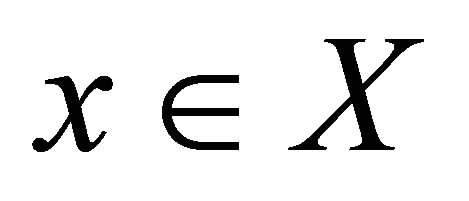 , there exists subsequence
, there exists subsequence 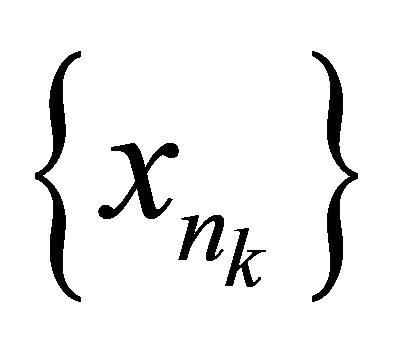 of
of 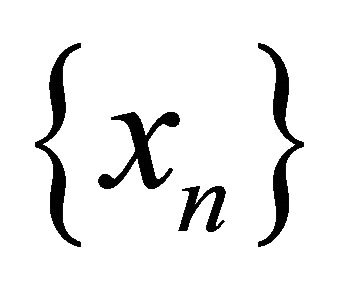 such that the sequence
such that the sequence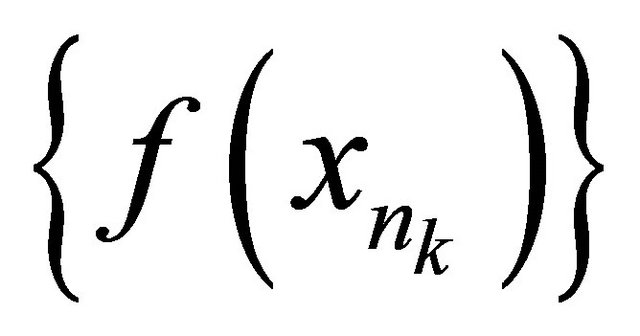 αδ-converges to
αδ-converges to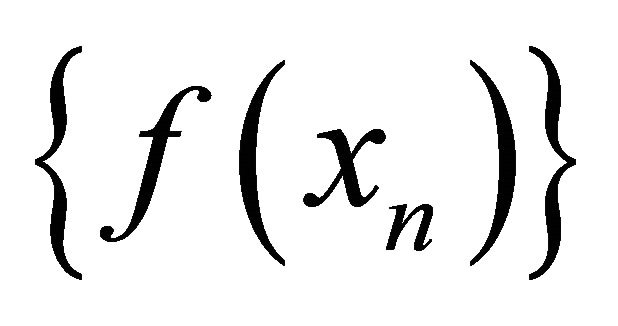 .
.
(c) Sequentially-Sub-αδ-continuous if for each point 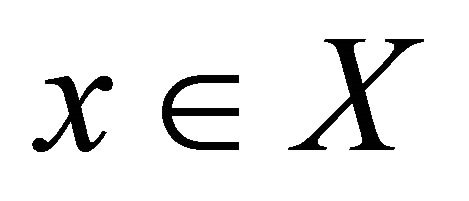 and each sequence
and each sequence 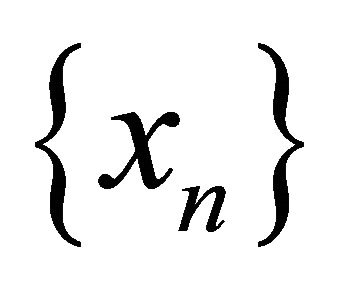 in αδ-converging tothere exists a subsequence
in αδ-converging tothere exists a subsequence  of
of 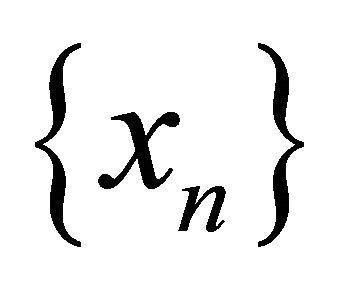 and a point
and a point
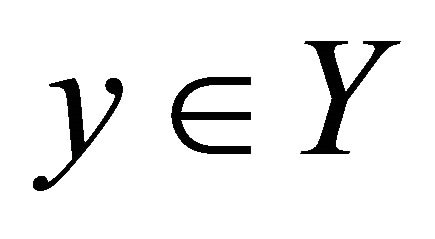 such that the sequence
such that the sequence αδ-converges to
αδ-converges to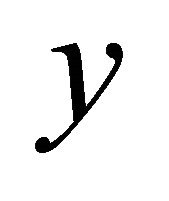 .
.
(d) Sequentially, αδO-compact preserving if the image 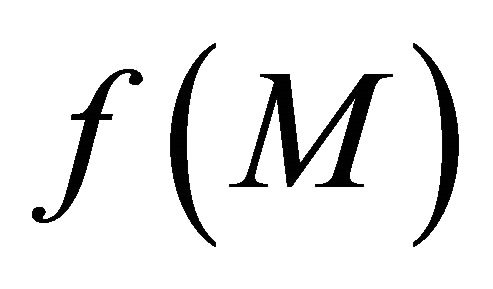 of every sequentially αδO-compact set
of every sequentially αδO-compact set 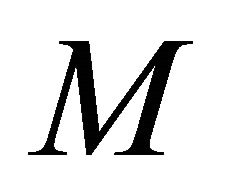 of
of  is a sequentially αδO-compact subset of
is a sequentially αδO-compact subset of .
.
Theorem 4.2. Let 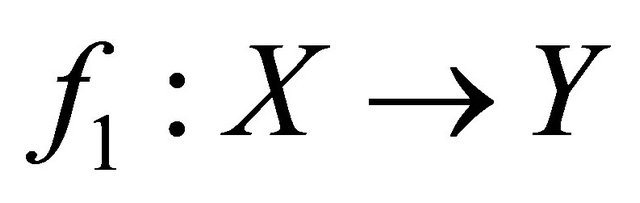 and
and  be two sequentially αδ-continuous functions. If
be two sequentially αδ-continuous functions. If  is αδ-US, then the set
is αδ-US, then the set  is sequentially αδ-closed.
is sequentially αδ-closed.
Proof. Suppose that  is αδ-US and
is αδ-US and 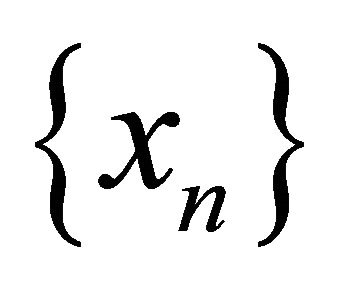 is any sequence in E that
is any sequence in E that 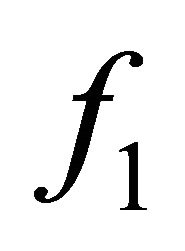 -converges to
-converges to . Since
. Since  and
and 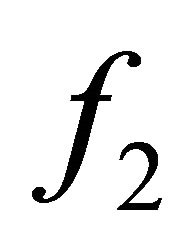 are sequentially αδ-continuous functions, the sequence
are sequentially αδ-continuous functions, the sequence 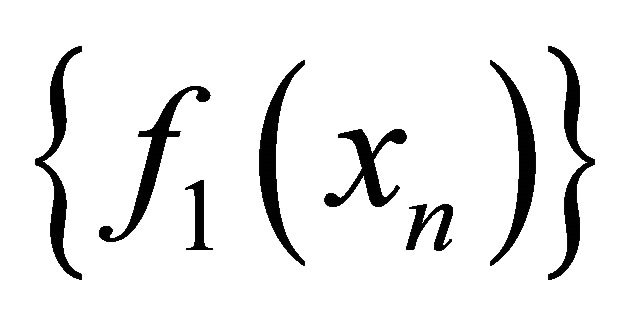 (respectively,
(respectively,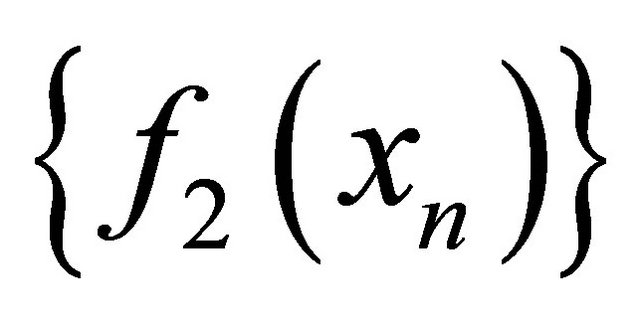 ) converges to
) converges to  (respectively,
(respectively,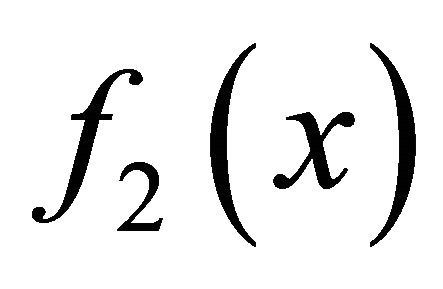 ). Since
). Since 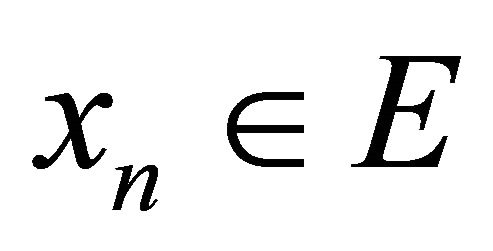 for each
for each 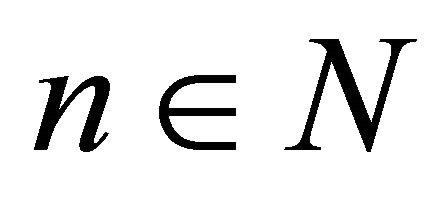 and
and  is αδ-US,
is αδ-US, 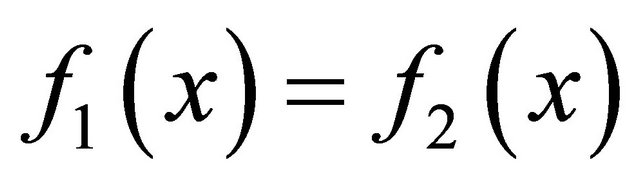 and hence
and hence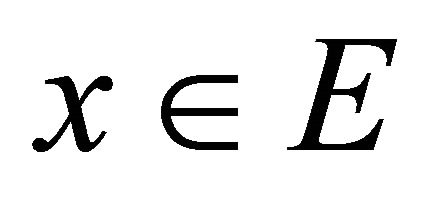 . This shows that
. This shows that 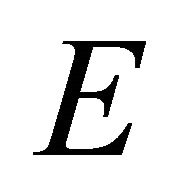 is sequentially αδ- closed.
is sequentially αδ- closed.
Lemma 4.3. Every function  is sequentially sub αδ-US αδ-US continuous if
is sequentially sub αδ-US αδ-US continuous if  is sequentially αδO-compact.
is sequentially αδO-compact.
Proof. Let 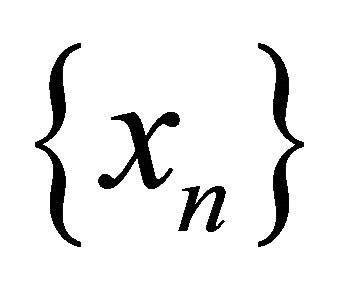 be a sequence in
be a sequence in 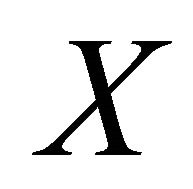 that αδ-US converges to
that αδ-US converges to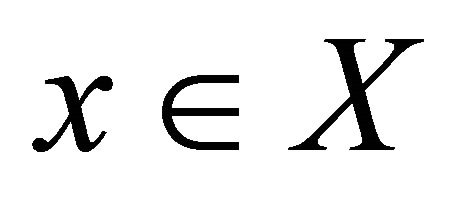 . It follows that
. It follows that 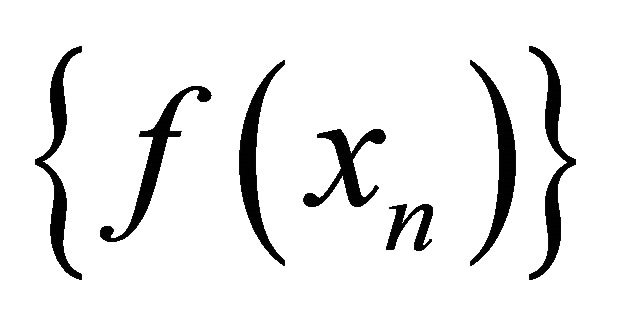 is a sequence in
is a sequence in . Since
. Since  is sequentially αδO-compactthere exists a subsequence
is sequentially αδO-compactthere exists a subsequence  of
of  that
that
αδ-converges to a point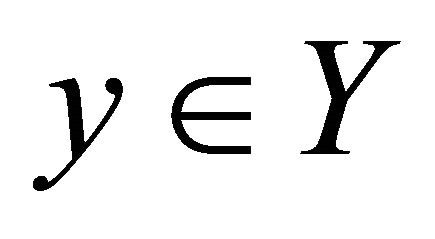 . Therefore
. Therefore 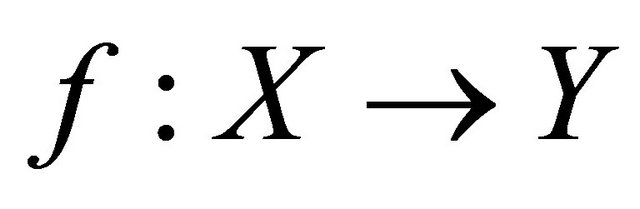 is sequentially sub αδ-continuous.
is sequentially sub αδ-continuous.
Theorem 4.4. Every sequentially nearly αδ-continuous function is sequentially αδO-compact preserving.
Proof. Let 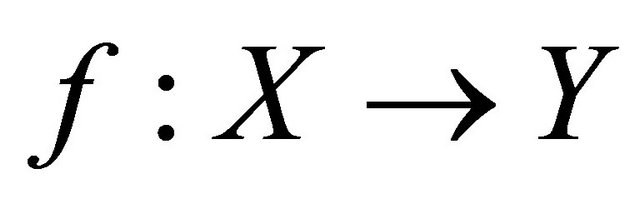 be a sequentially nearly αδ- continuous function and
be a sequentially nearly αδ- continuous function and 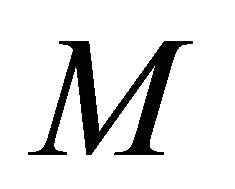 be any sequentially αδOcompact subset of
be any sequentially αδOcompact subset of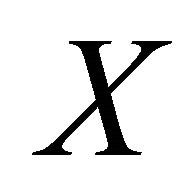 . We will show that
. We will show that 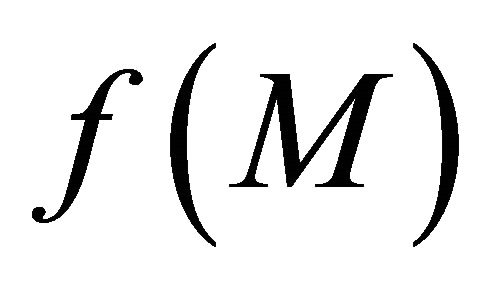 is a sequentially αδO-compact subset of
is a sequentially αδO-compact subset of . So, assume that
. So, assume that 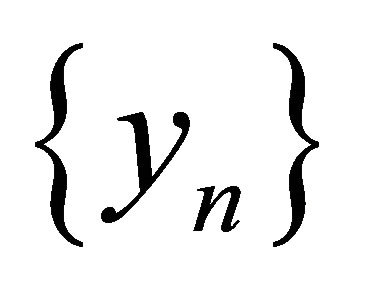 is any sequence in
is any sequence in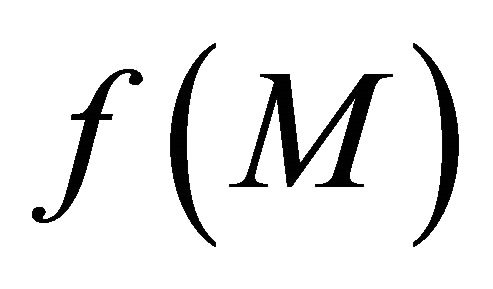 . Then for each
. Then for each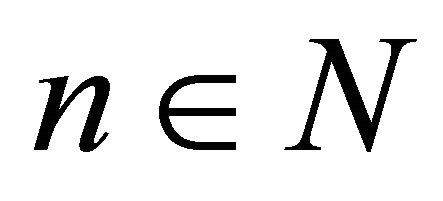 , there exists a point
, there exists a point 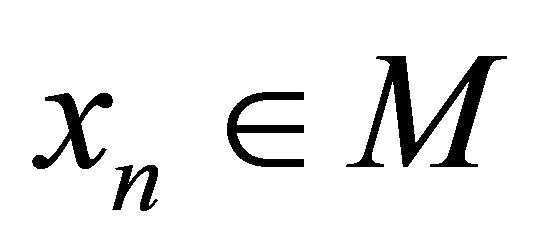 such that
such that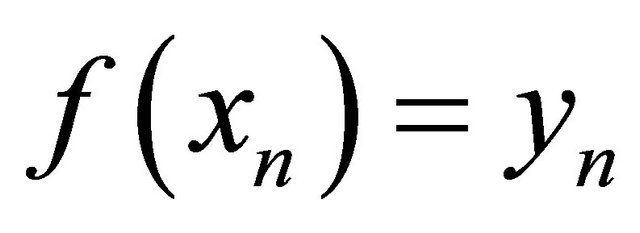 . Now
. Now 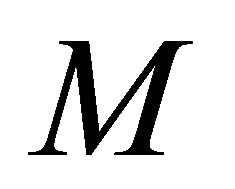 is sequentially αδO-compact, so there exists a subsequence
is sequentially αδO-compact, so there exists a subsequence  of
of 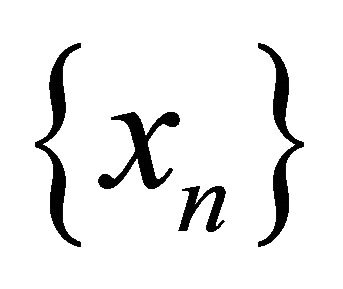 that αδ-converges to a point
that αδ-converges to a point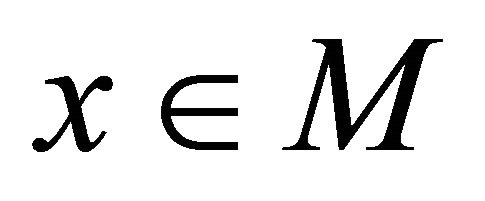 . Since
. Since 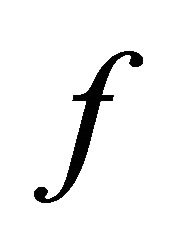 is sequentially nearly αδ-continuous, there exists a subsequence
is sequentially nearly αδ-continuous, there exists a subsequence
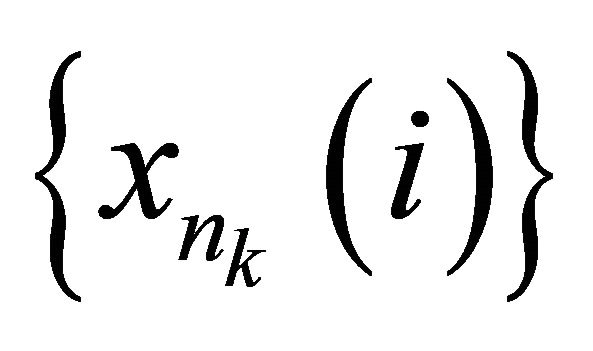 of
of 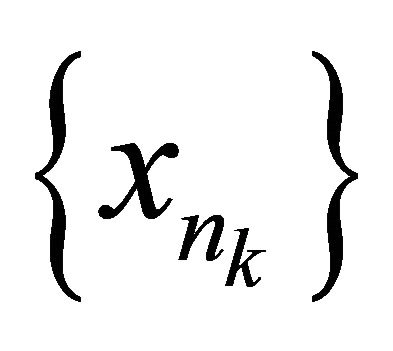 such that
such that αδ-converges to
αδ-converges to . Therefore, there exists a subsequence
. Therefore, there exists a subsequence  of
of 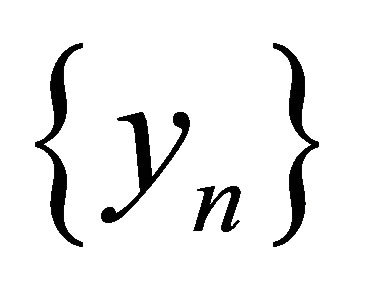 that αδ-converges to
that αδ-converges to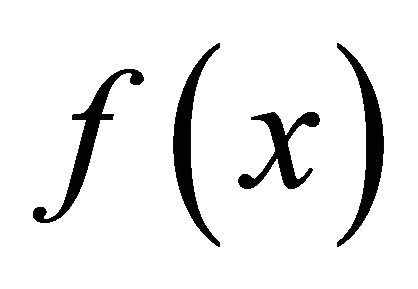 . This implies that
. This implies that 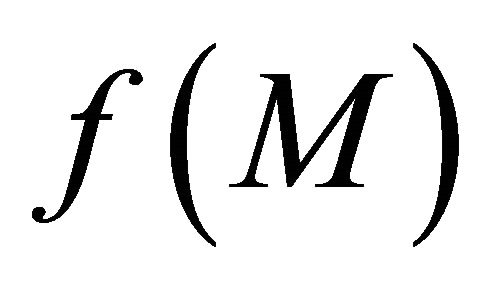 is a sequentially αδO-compact set of
is a sequentially αδO-compact set of .
.
Theorem 4.5. Every sequentially αδO-compact preserving function is sequentially sub-αδ-continuous.
Proof. Suppose that  is a sequentially
is a sequentially  -compact preserving function. Let
-compact preserving function. Let 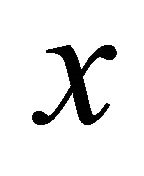 be any point of
be any point of 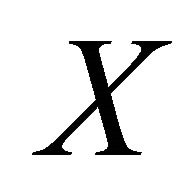 and
and  a sequence that αδ-converges to
a sequence that αδ-converges to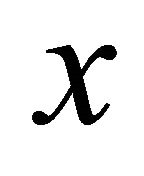 . We denote the set
. We denote the set 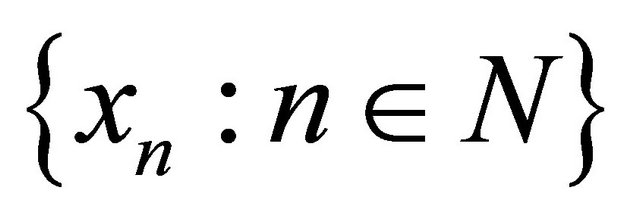 by
by  and put
and put . Since
. Since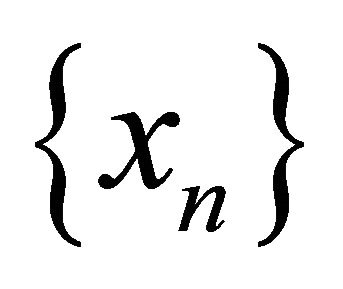 αδ-converges to
αδ-converges to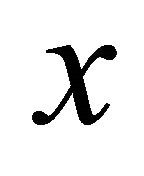 ,
, 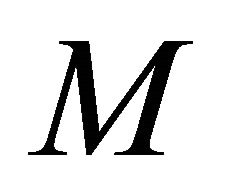 is sequentially αδO-compact. By hypothesis,
is sequentially αδO-compact. By hypothesis, 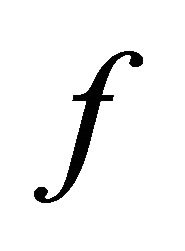 is sequentially αδO-compact subset of
is sequentially αδO-compact subset of . Now in
. Now in 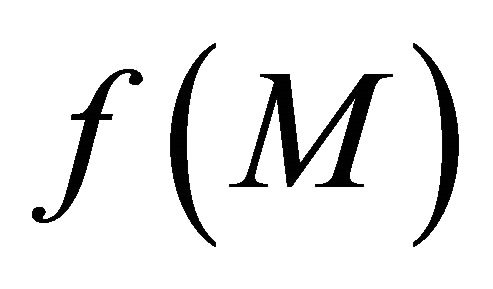
there exists a subsequence 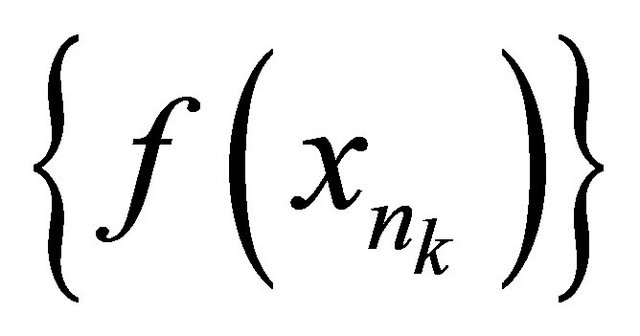 of
of 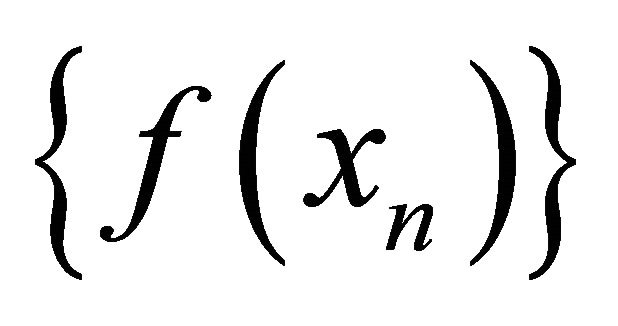 that
that
αδ-converges to a point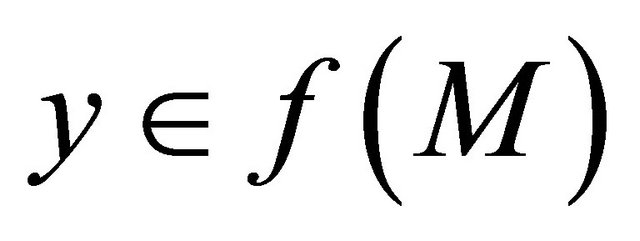 . This implies that
. This implies that 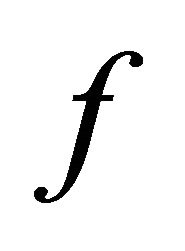 sequentially sub-αδ-continuous.
sequentially sub-αδ-continuous.
Theorem 4.6. A function 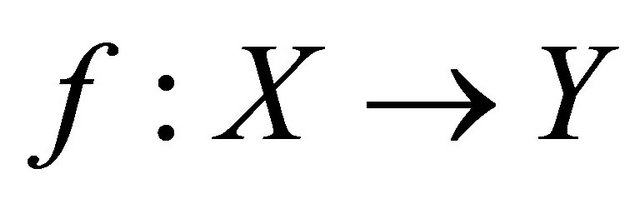 is sequentially
is sequentially  -compact preserving if and only if
-compact preserving if and only if
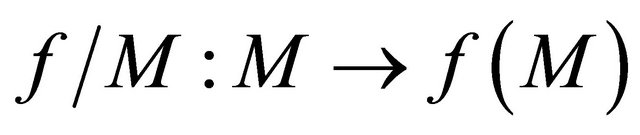 is sequentially sub-αδ-continuous for each sequentially αδO-compact set
is sequentially sub-αδ-continuous for each sequentially αδO-compact set 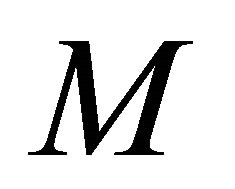 of
of .
.
Proof. Necessity: Suppose that  is a sequentially αδO-compact preserving function. Then
is a sequentially αδO-compact preserving function. Then 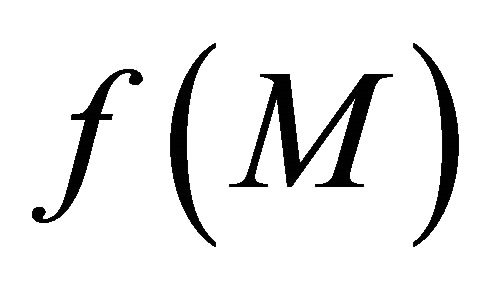 is sequentially αδO-compact in
is sequentially αδO-compact in  for each sequentially αδO-compact subset
for each sequentially αδO-compact subset 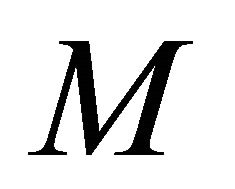 of
of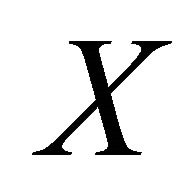 . Therefore, by Theorem 3.5
. Therefore, by Theorem 3.5 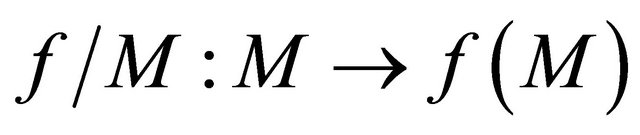 is sequentially sub-αδ-continuous.
is sequentially sub-αδ-continuous.
Sufficiency: Let 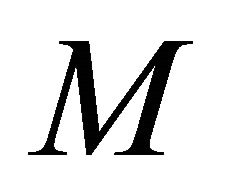 be any sequentially αδO-compact set of
be any sequentially αδO-compact set of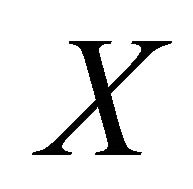 . We will show that
. We will show that  is sequentially αδO-compact subset of
is sequentially αδO-compact subset of . Let
. Let 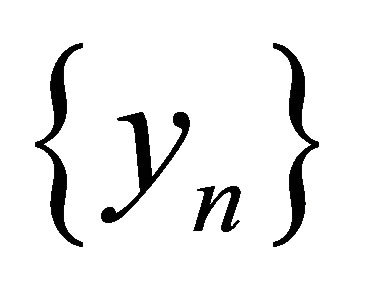 be any sequence in
be any sequence in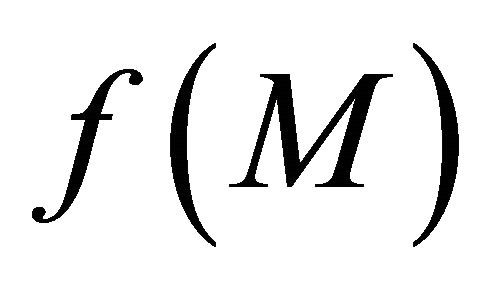 . Then for each
. Then for each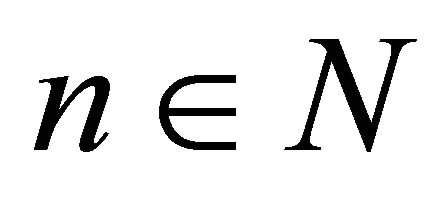 , there exists a point
, there exists a point 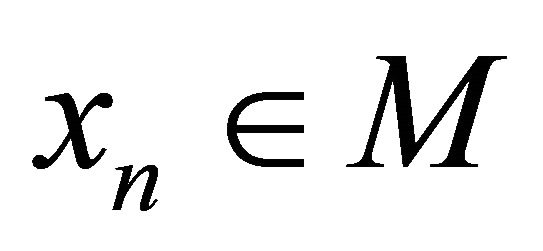 such that
such that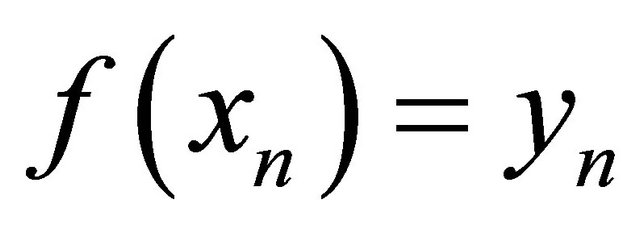 . Since
. Since 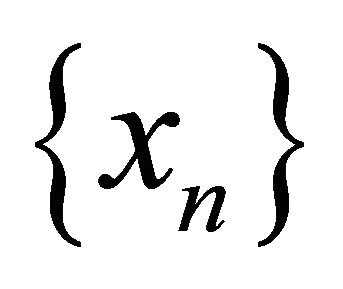 is a sequence in the sequentially αδO-compact set
is a sequence in the sequentially αδO-compact set 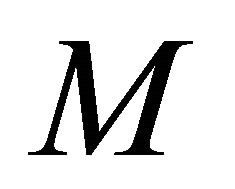 there exists a subsequence
there exists a subsequence 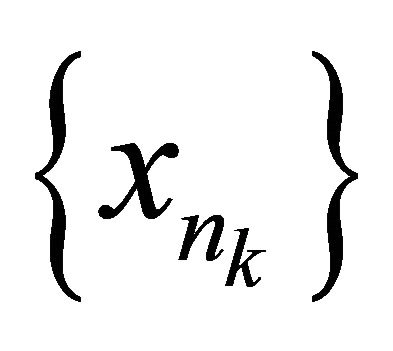 of
of 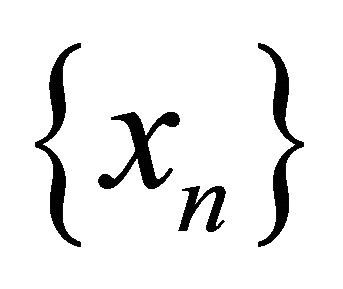 that αδ-converges to a point in
that αδ-converges to a point in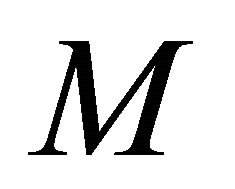 . By hypothesis
. By hypothesis
 is sequentially sub-αδ-continuous, hence there exists a subsequence
is sequentially sub-αδ-continuous, hence there exists a subsequence 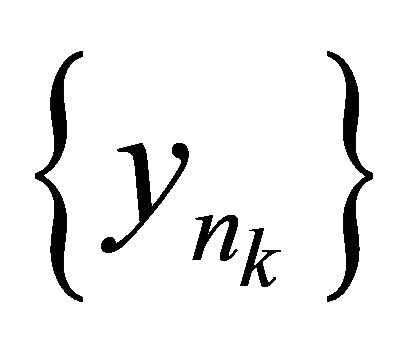 of
of  that αδ-converges to y
that αδ-converges to y  f(M). This implies that f(M) is sequentially αδO-compact in
f(M). This implies that f(M) is sequentially αδO-compact in .
.
Corollary 4.7. If a function 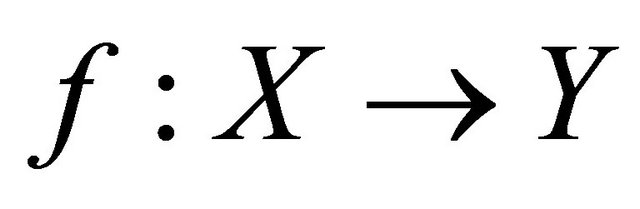 is sequentially sub-αδ-continuous and
is sequentially sub-αδ-continuous and 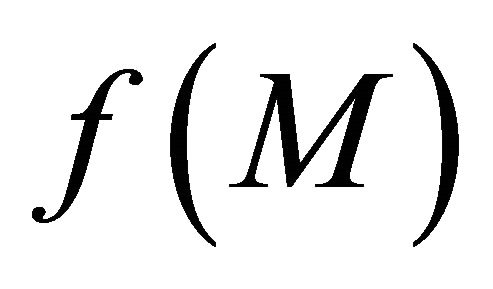 is sequentially αδ-closed in
is sequentially αδ-closed in  for each sequentially αδO-compact set M of
for each sequentially αδO-compact set M of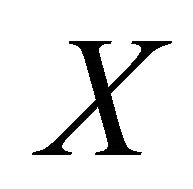 , then f is sequentially αδO-compact preserving.
, then f is sequentially αδO-compact preserving.
Proof. It will be sufficient to show that
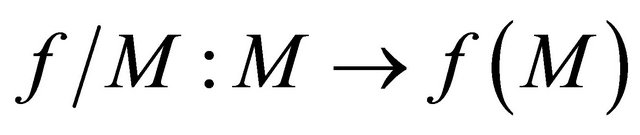 is sequentially sub-αδ-continuous for each sequentially αδO-compact set
is sequentially sub-αδ-continuous for each sequentially αδO-compact set 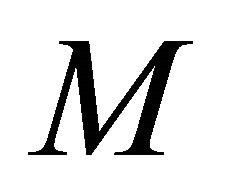 of
of  and by Lemma 3.3. We have already done. So, let
and by Lemma 3.3. We have already done. So, let 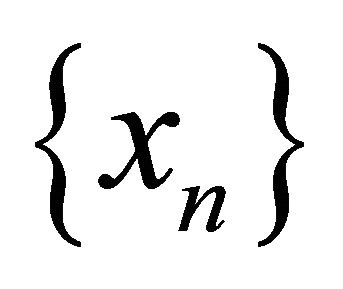 be any sequence in
be any sequence in 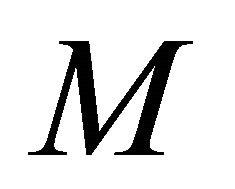 that αδ-converges to a point
that αδ-converges to a point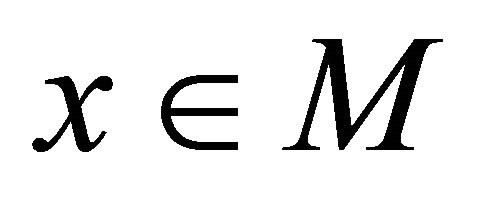 . Then, since
. Then, since  is sequentially sub-αδ-continuous there exists a subsequence
is sequentially sub-αδ-continuous there exists a subsequence 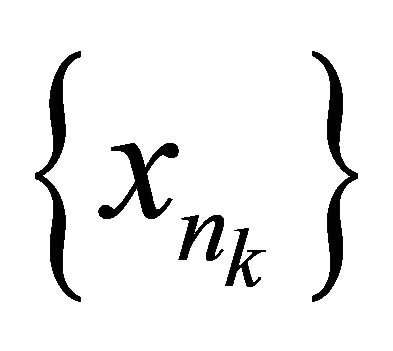 of
of 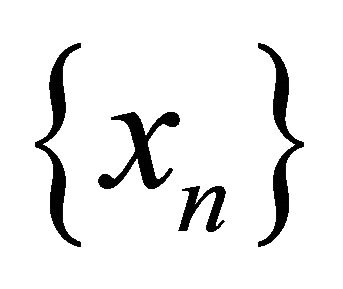 and a point
and a point 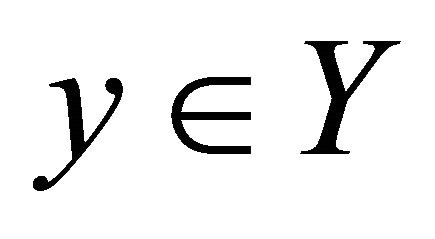 such that
such that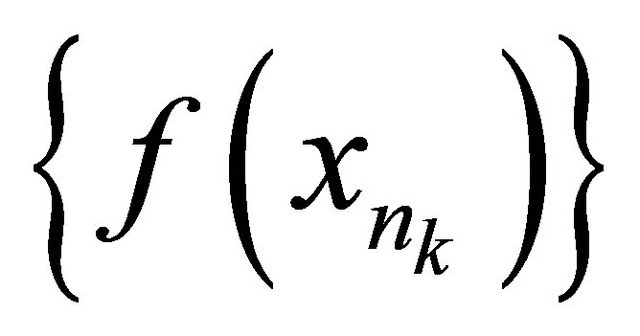 αδ-converges to y.
αδ-converges to y.
Since 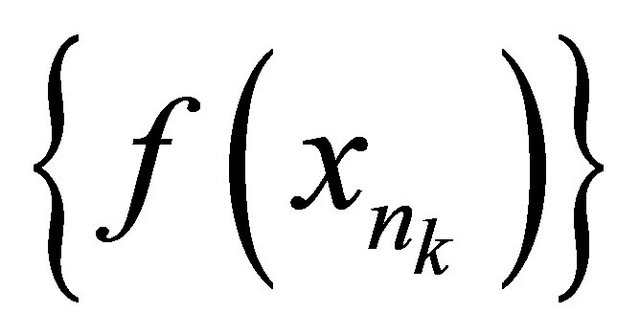 is a sequence in the sequentially αδclosed set
is a sequence in the sequentially αδclosed set  of
of , we obtain
, we obtain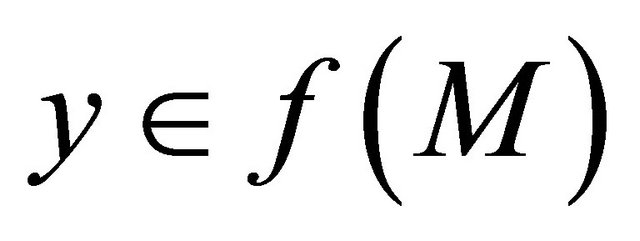 . This implies that
. This implies that 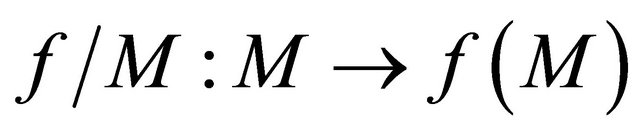 is sequentially sub αδ-continuous.
is sequentially sub αδ-continuous.
5. Slightly αδ-Continuous Functions
Definition 5.1. A function  is said to be slightly αδ-continuous if for each
is said to be slightly αδ-continuous if for each 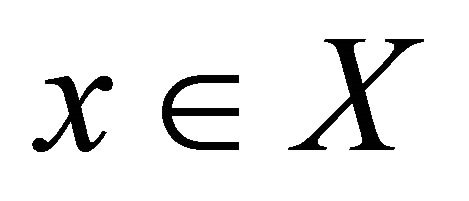 and for each
and for each
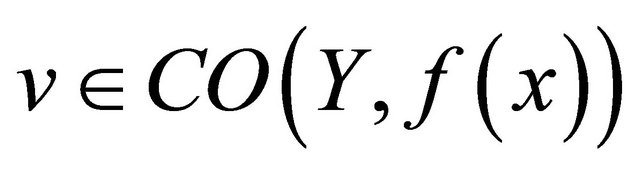 , there exists
, there exists 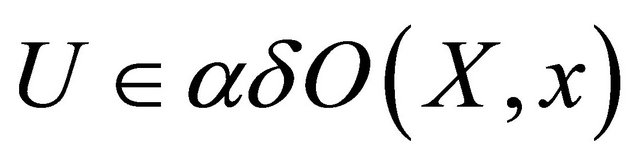 such that
such that , where
, where  is the family of clopen sets containing f(x) in a space
is the family of clopen sets containing f(x) in a space .
.
Definition 5.2. Let 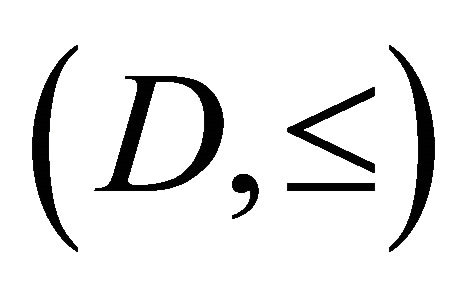 be a directed set
be a directed set  net
net 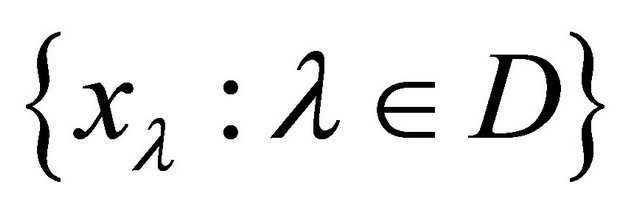 in
in  is said to be αδ-convergent to a point
is said to be αδ-convergent to a point 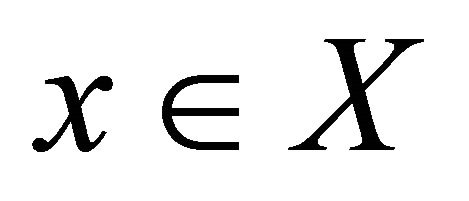 if
if 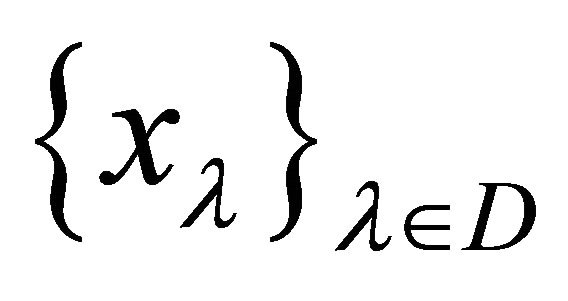 is eventually in each
is eventually in each 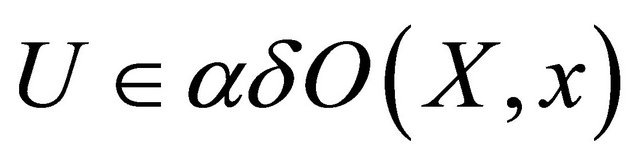 .
.
Theorem 5.3. For a function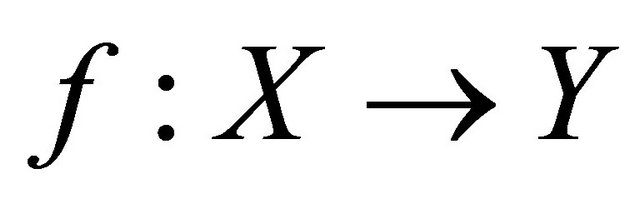 , the following are equivalent:
, the following are equivalent:
(a) 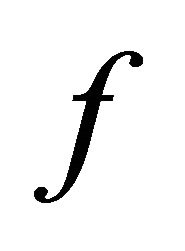 is slightly αδ-continuous.
is slightly αδ-continuous.
(b) 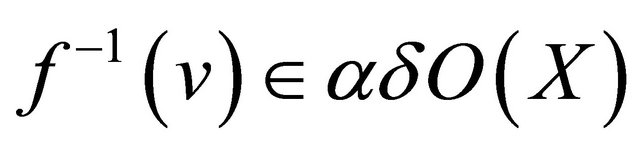 for each
for each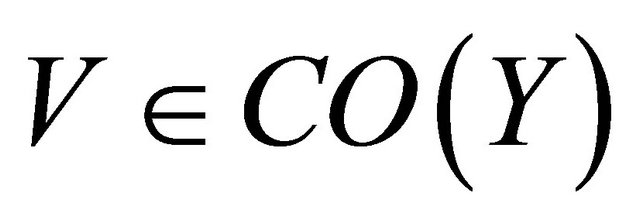 .
.
(c) 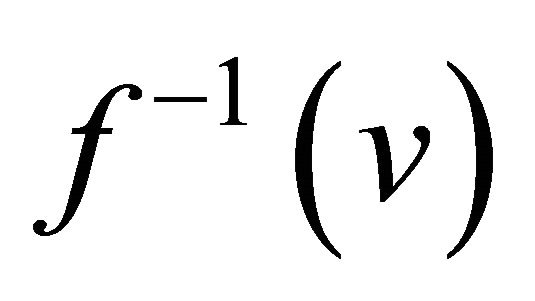 is αδ-cl-open for each
is αδ-cl-open for each 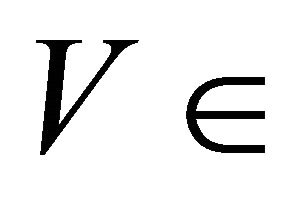 CO(Y).
CO(Y).
(d) for each 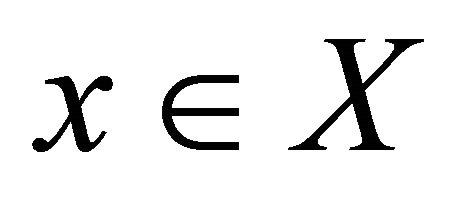 and for each net
and for each net 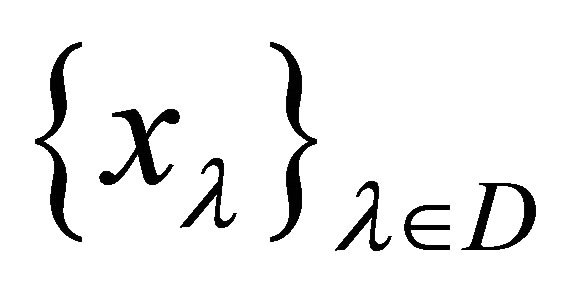 in
in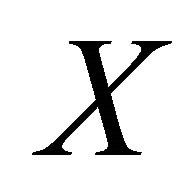 .
.
Proof.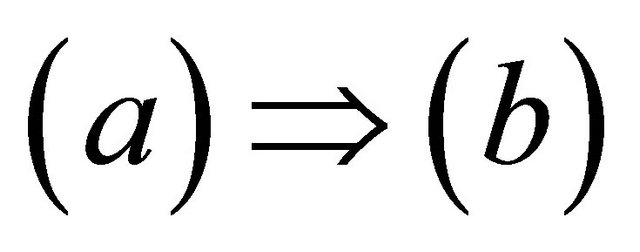 . Let
. Let 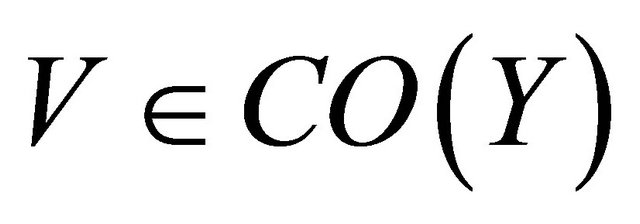 and let
and let 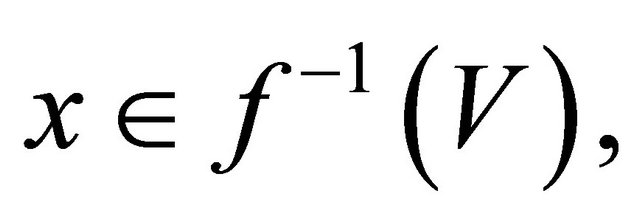 then
then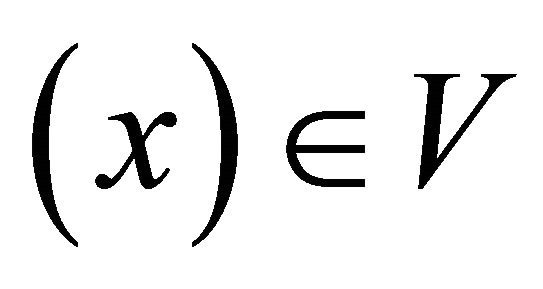 . Since
. Since 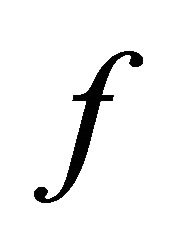 is slightly αδ-continuous, there is a
is slightly αδ-continuous, there is a  such that
such that
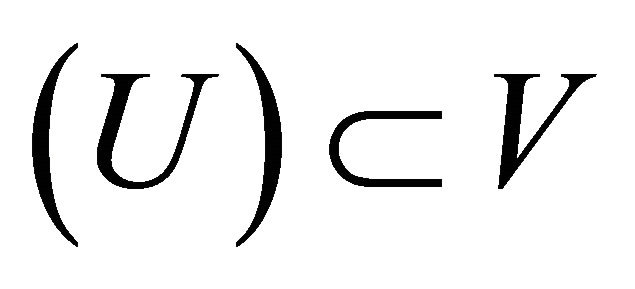 . Thus
. Thus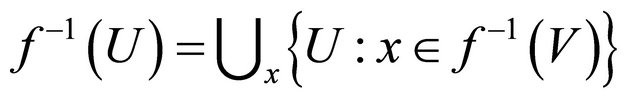 , that is
, that is
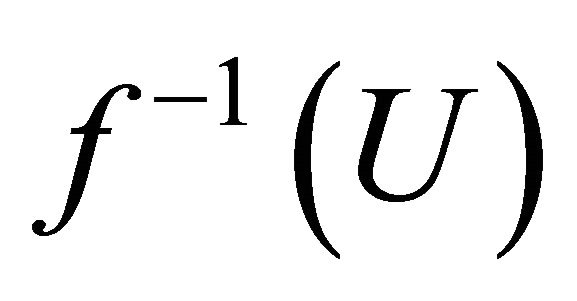 is a union of αδ-open sets. Hence
is a union of αδ-open sets. Hence 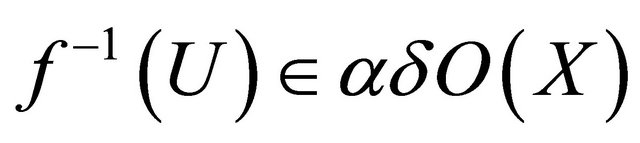 .
.
 . Let
. Let , then
, then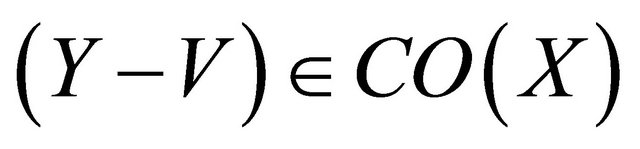 .
.
By hypothesis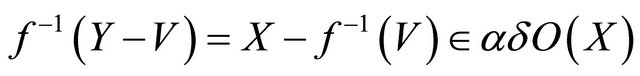 .
.
Thus 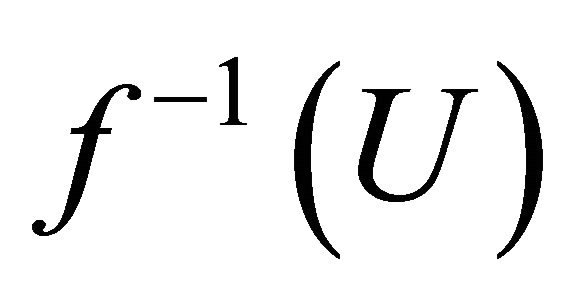 is αδ-closed.
is αδ-closed.
 . Let
. Let 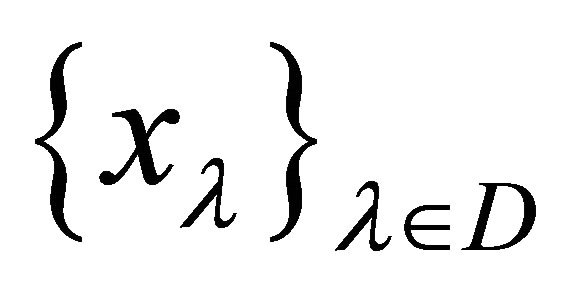 be a net in
be a net in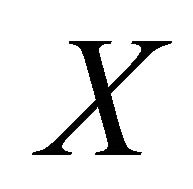 αδ-converging to
αδ-converging to 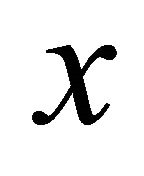 and let
and let . There is thus a
. There is thus a
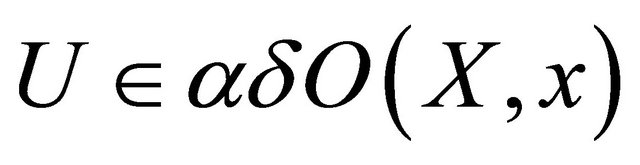 such that
such that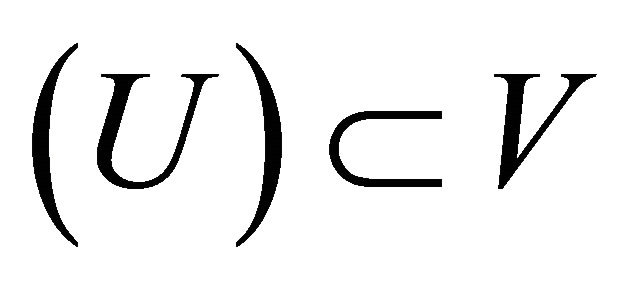 . There is thus a
. There is thus a  such that
such that 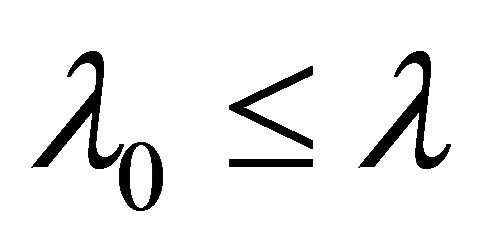 implies
implies 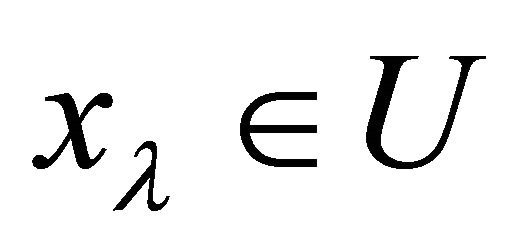 since
since
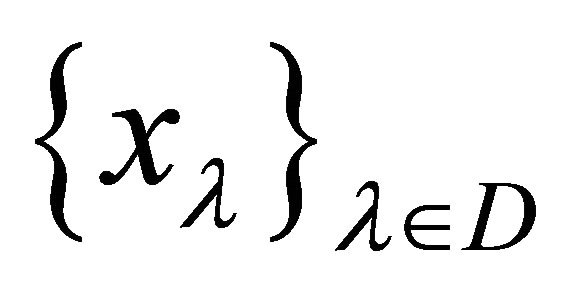 is αδ-convergent to
is αδ-convergent to . Thus
. Thus
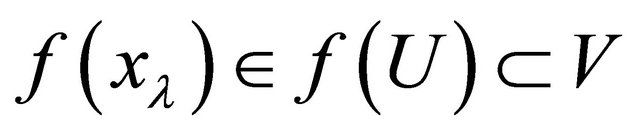 for all
for all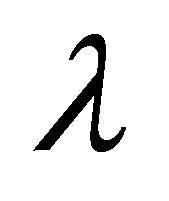 . Thus
. Thus 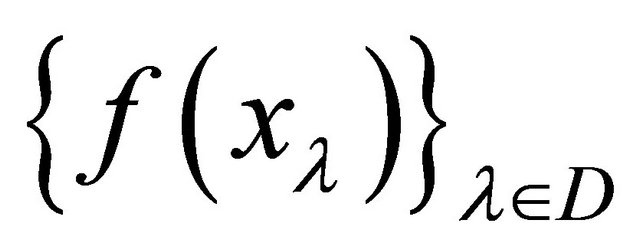 is αδ- convergent to
is αδ- convergent to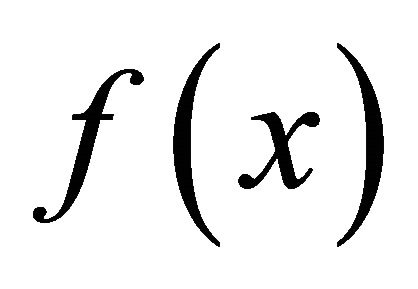 .
.
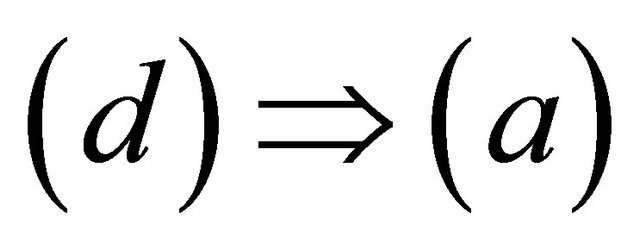 Suppose that
Suppose that  is not slightly αδ-continuous at a point
is not slightly αδ-continuous at a point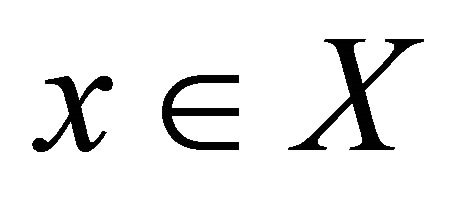 , then there exists a
, then there exists a
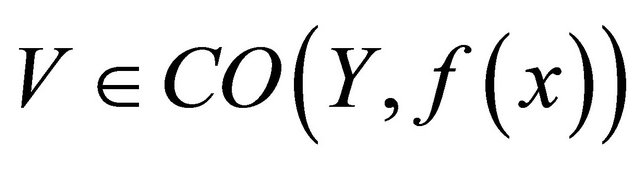 such that
such that 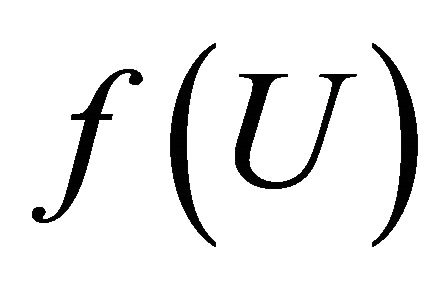 does not contained in
does not contained in  for each
for each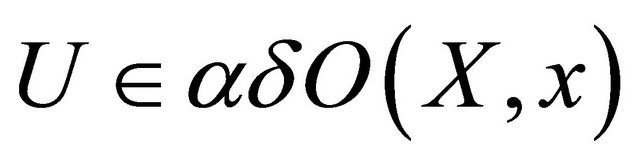 . So
. So  and thus
and thus 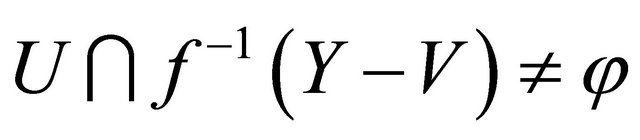 for each
for each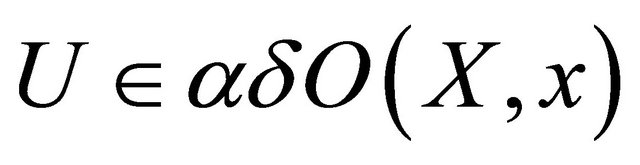 , since
, since 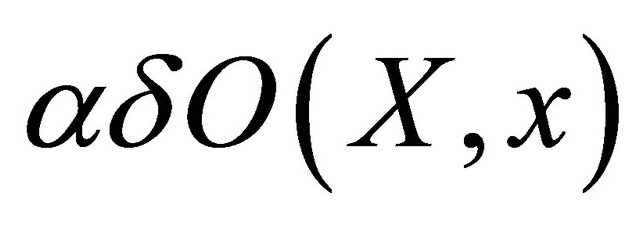 is directed by set inclusion
is directed by set inclusion , there exists a selection function
, there exists a selection function 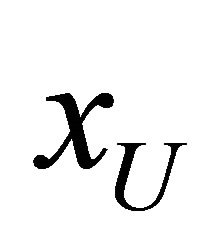 from
from  into
into 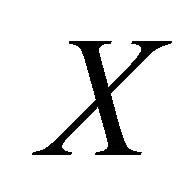 for each
for each . Thus
. Thus 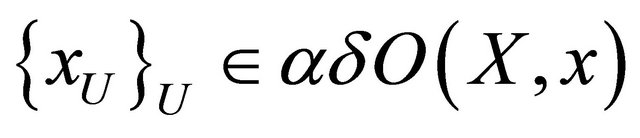 is a net in
is a net in  αδ-converging to
αδ-converging to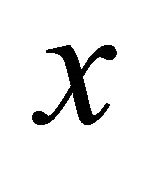 . Since
. Since  and so
and so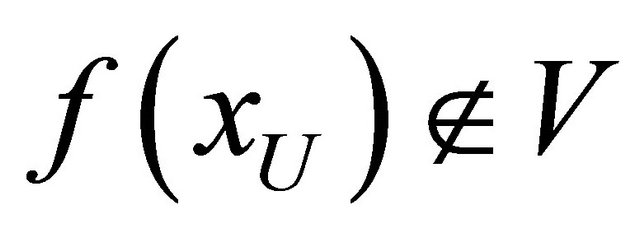 , for each
, for each ,
,
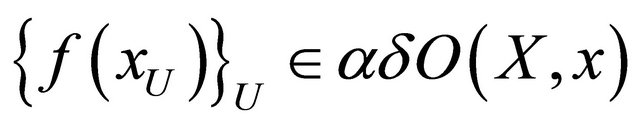 is not eventually in
is not eventually in
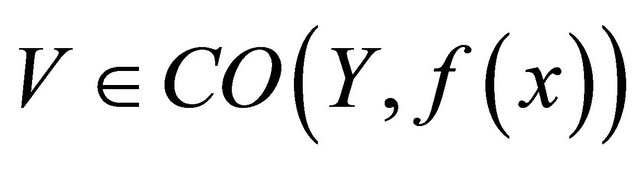 , which is a contradiction. Hence
, which is a contradiction. Hence  holds.
holds.
Theorem 5.4. If 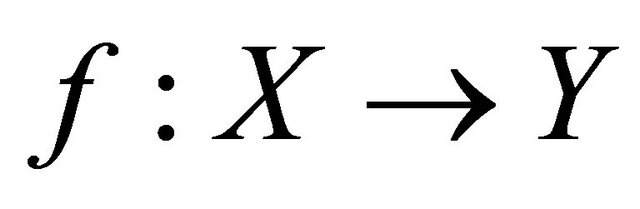 is slightly αδ-continuous and
is slightly αδ-continuous and 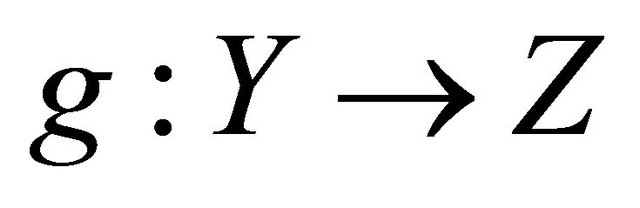 is slightly continuous, then their composition
is slightly continuous, then their composition 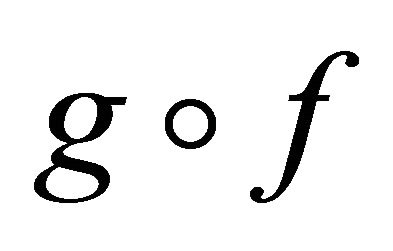 is slightly αδ-continuous.
is slightly αδ-continuous.
Proof. Let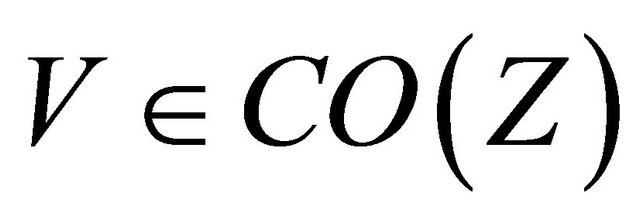 , then
, then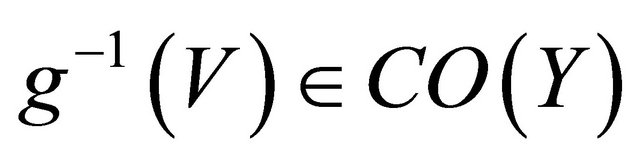 . Since
. Since 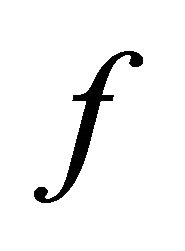 is slightly αδ-continuous,
is slightly αδ-continuous,
 . Thus
. Thus 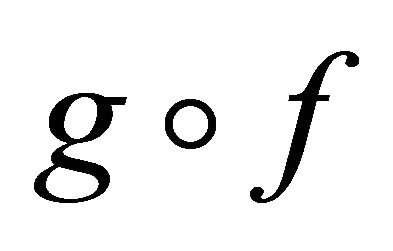 is Slightly αδ-continuous.
is Slightly αδ-continuous.
Theorem 5.5. The following are equivalent for a function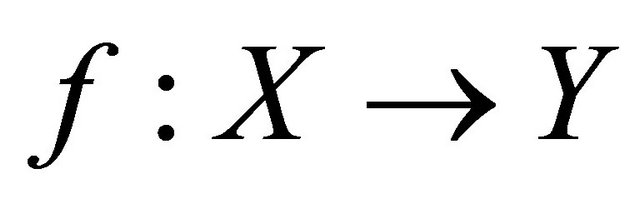 :
:
(a)  is slightly αδ-continuous(b) for each
is slightly αδ-continuous(b) for each 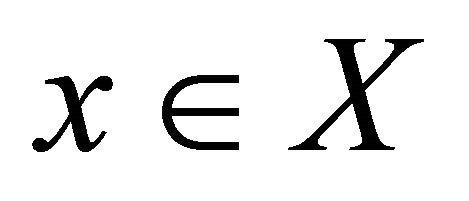 and for each
and for each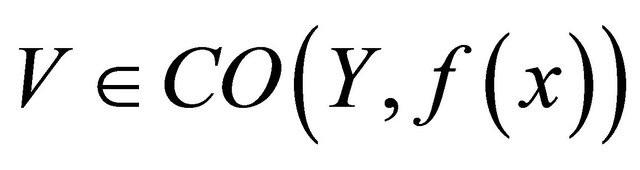 there exists αδ-cl-open set
there exists αδ-cl-open set 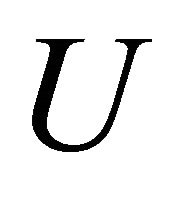 such that
such that (c) for each closed set
(c) for each closed set  of
of ,
, 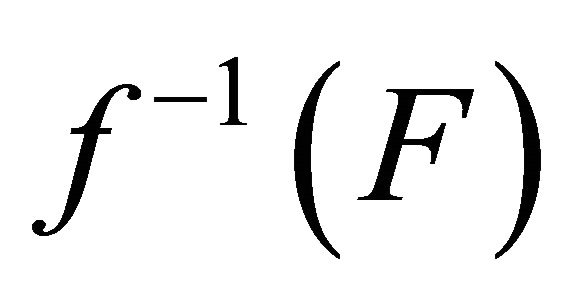 is αδ- closed(d)
is αδ- closed(d)  for each
for each  and
and
(e) 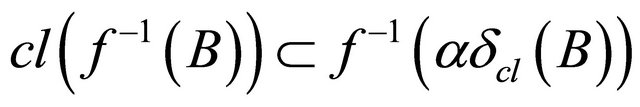 for each
for each .
.
Proof.  Let
Let 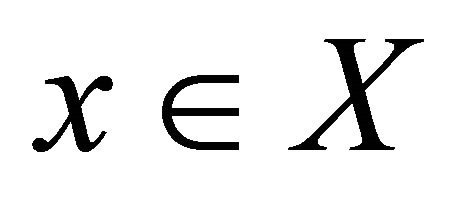 and
and
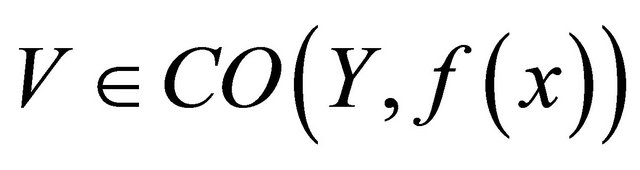 by Theorem 4.3.
by Theorem 4.3.  is clopen.
is clopen.
Put , then
, then  and
and .
.
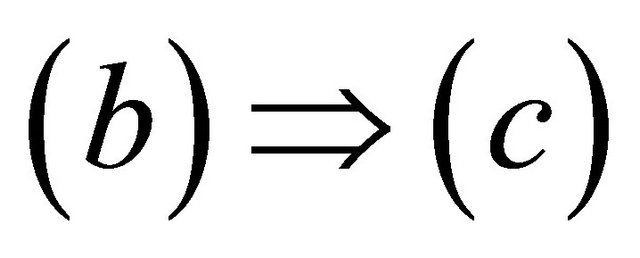 is obvious.
is obvious.
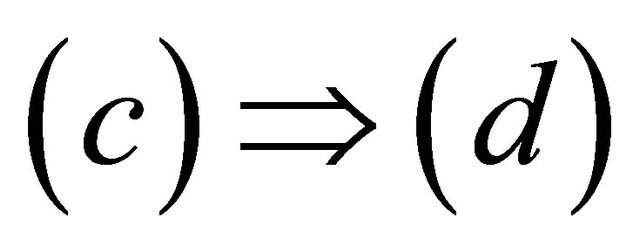 since
since  is the smallest αδclosed set containing
is the smallest αδclosed set containing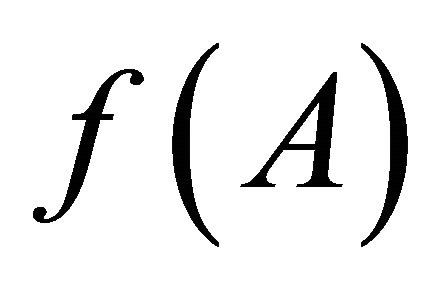 , hence by
, hence by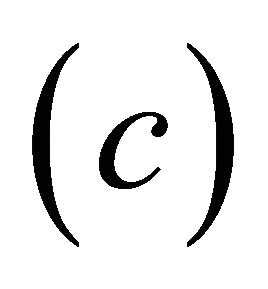 , we have
, we have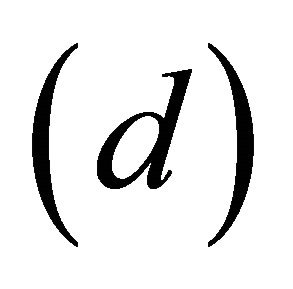 .
.
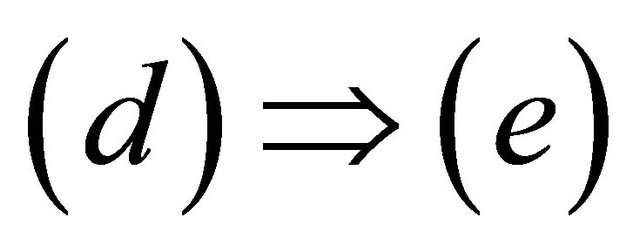 for each
for each ,
,
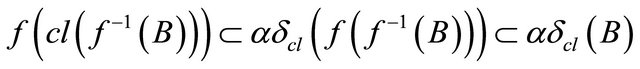 . Hence
. Hence
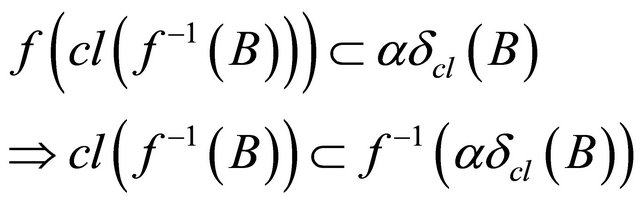 .
.
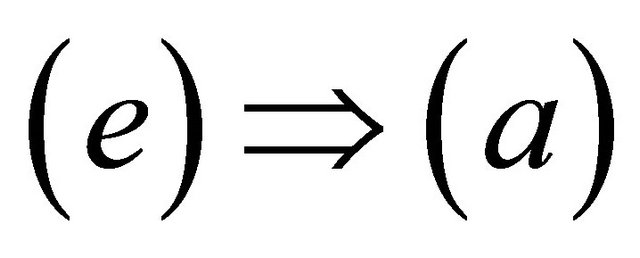 Let
Let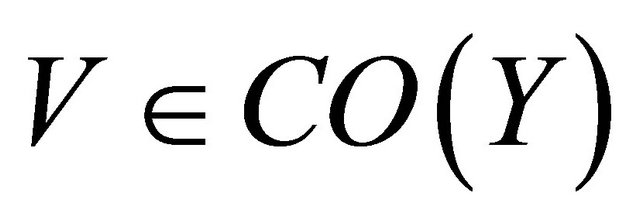 . then
. then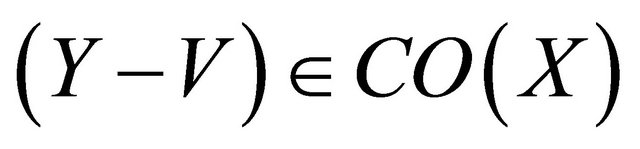 , by
, by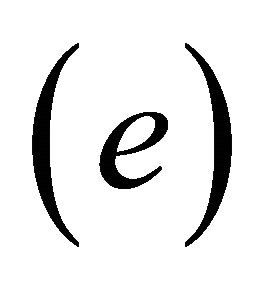 , we have
, we have
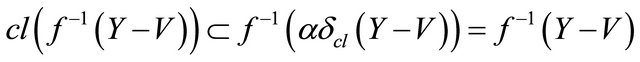 , since every closed set is αδ-closed, thus
, since every closed set is αδ-closed, thus
 is closed and thus αδ-closed, thus
is closed and thus αδ-closed, thus 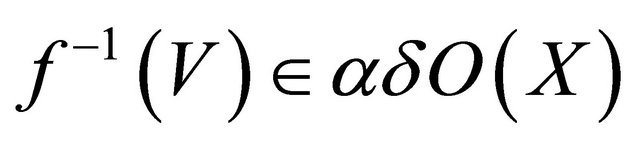 and
and 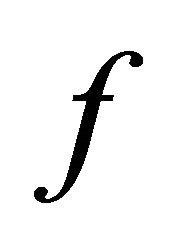 is slightly αδ-continuous.
is slightly αδ-continuous.
Theorem 5.6. If 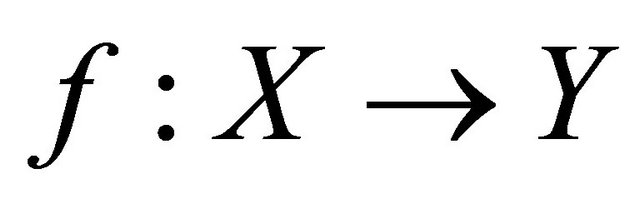 is a slightly αδ-continuous injection and
is a slightly αδ-continuous injection and  is clopen
is clopen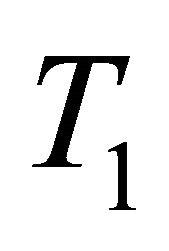 , then
, then 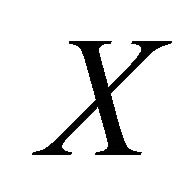 is
is 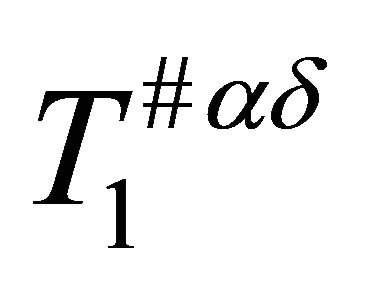 .
.
Proof. Suppose that  is clopen
is clopen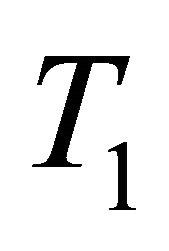 . For any distinct points
. For any distinct points  and
and 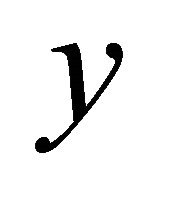 in
in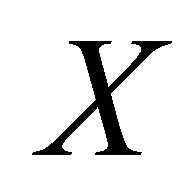 , there exist
, there exist 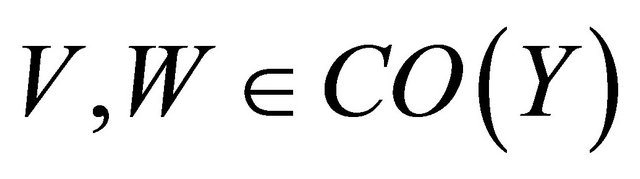 such that
such that 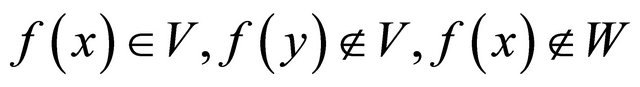 and
and 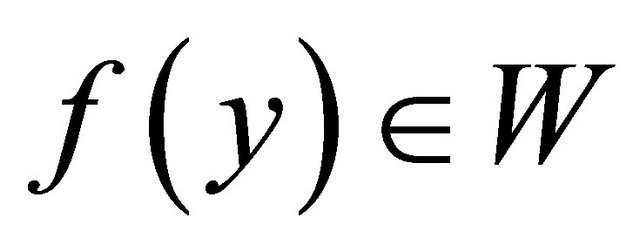 . Since
. Since 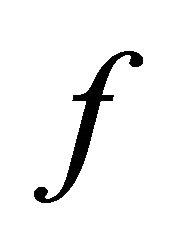 is slightly αδ-continuous,
is slightly αδ-continuous,
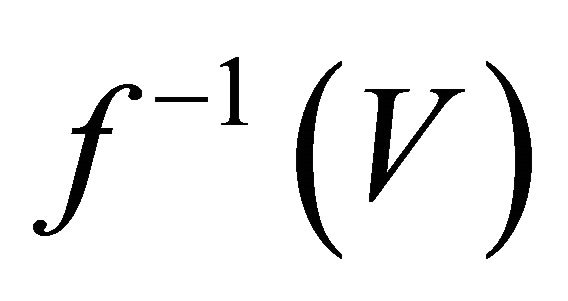 and
and 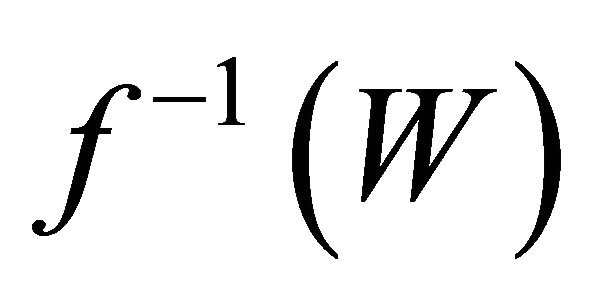 are αδ-open subsets of
are αδ-open subsets of 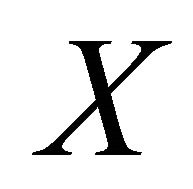 such that
such that 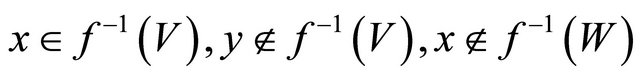 and
and  . This shows that
. This shows that 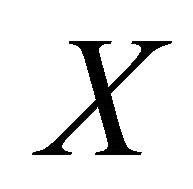 is
is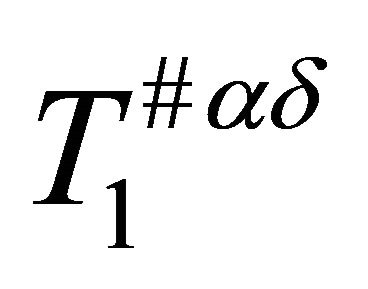 .
.
Theorem 5.7. If 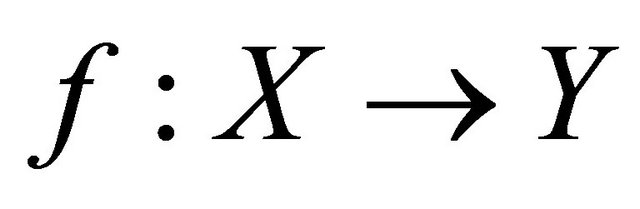 is a slightly αδ-continuous surjection and
is a slightly αδ-continuous surjection and  is clopen
is clopen , then
, then 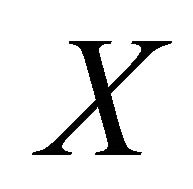 is
is 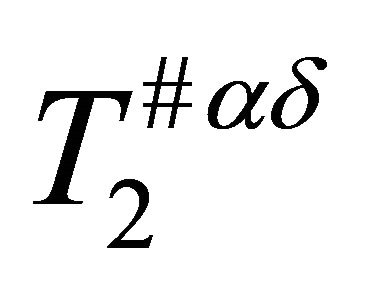 .
.
Proof. For any pair of distinct points 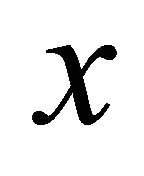 and
and 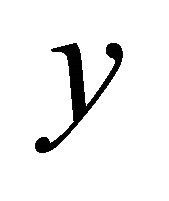 in
in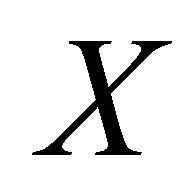 , there exist disjoint clopen sets U and
, there exist disjoint clopen sets U and 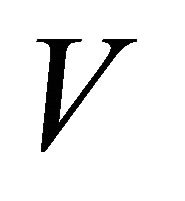 in
in  such that
such that 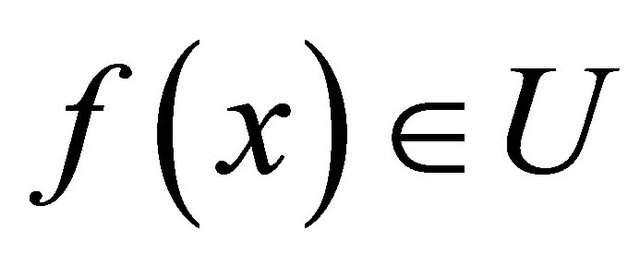 and
and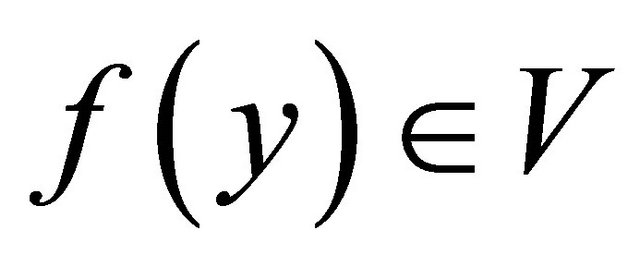 . Since f is slightly αδ-continuous,
. Since f is slightly αδ-continuous, 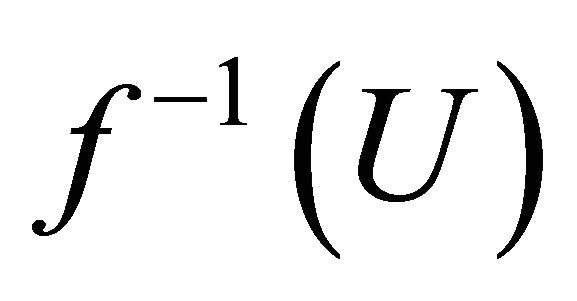 and
and 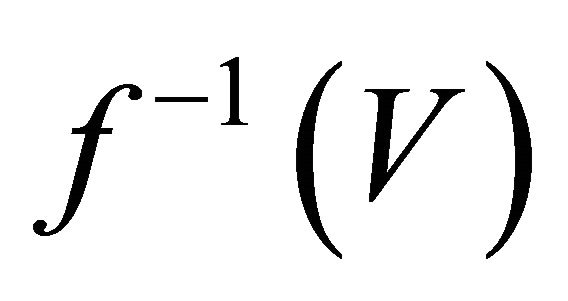 are αδ-open in
are αδ-open in  containing
containing  and
and 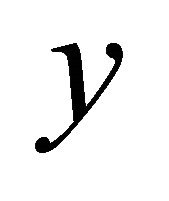 respectively. Therefore
respectively. Therefore
 because
because . This shows that
. This shows that  is
is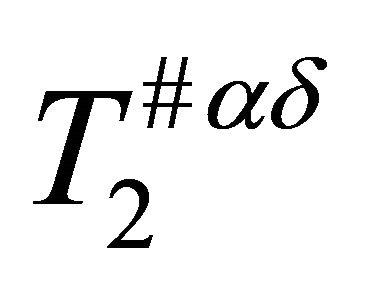 .
.
Definition 5.8. A space is called αδ-regular if for each αδ-closed set  and each point
and each point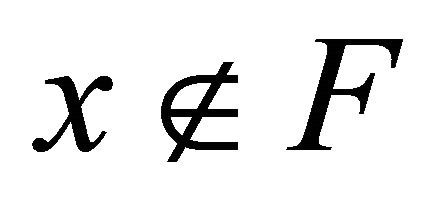 , there exist disjoint open sets
, there exist disjoint open sets  and
and 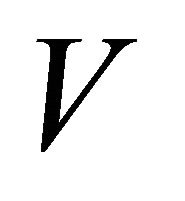 such that
such that  and
and 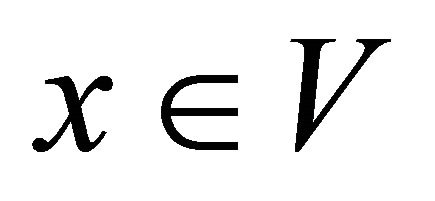 .
.
Definition 5.9. A space is said to be αδ-normal if for every pair of disjoint αδ-closed subsets  and
and 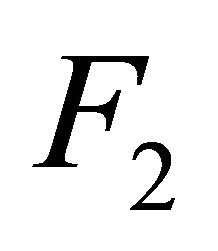 of
of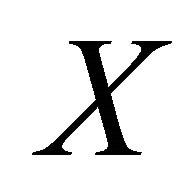 , there exist disjoint open sets
, there exist disjoint open sets 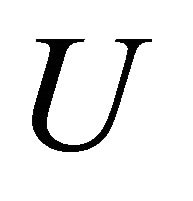 and
and  such that
such that  and
and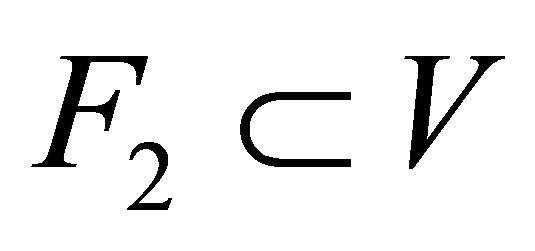 .
.
Theorem 5.10. If f is slightly αδ-continuous injective open function from an αδ-regular space 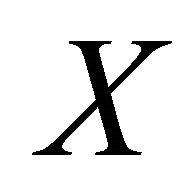 onto a space then
onto a space then  is clopen regular.
is clopen regular.
Proof. Let F be clopen set in  and be
and be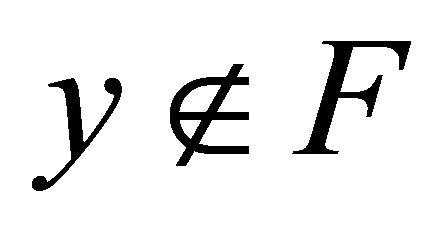 , take
, take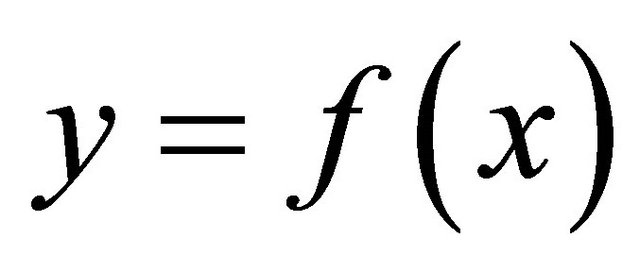 . Since f is slightly αδ-continuous,
. Since f is slightly αδ-continuous, 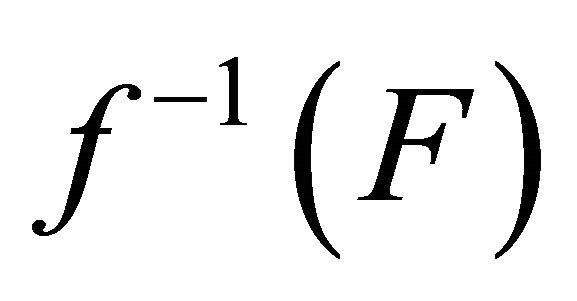 is a αδ-closed set, take
is a αδ-closed set, take , we have
, we have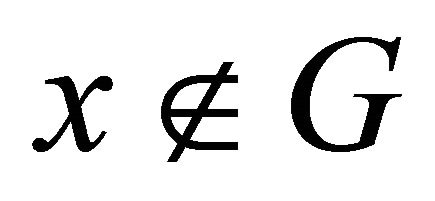 . Since
. Since 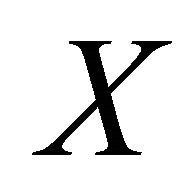 is αδ-regular, there exist disjoint open sets
is αδ-regular, there exist disjoint open sets 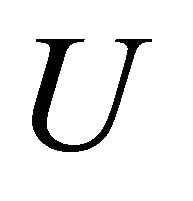 and
and 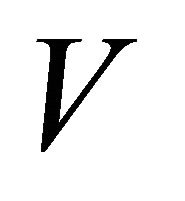 such that
such that  and
and . We obtain that
. We obtain that 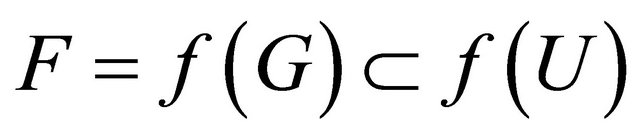 and
and 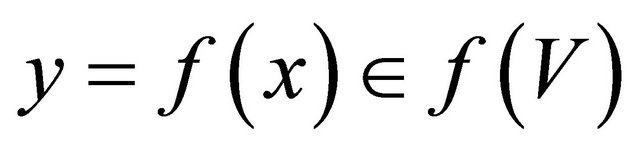 such that f(U) and f(V) are disjoint open sets. This shows that
such that f(U) and f(V) are disjoint open sets. This shows that  is clopen regular.
is clopen regular.
Theorem 5.11. If 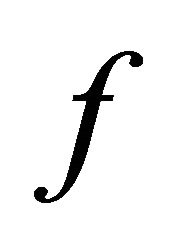 is slightly αδ-continuous injective open function from a αδ-normal space
is slightly αδ-continuous injective open function from a αδ-normal space 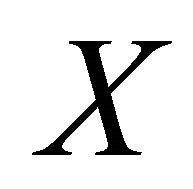 onto a space
onto a space , then
, then  is cl-open normal.
is cl-open normal.
Proof. Let  and
and 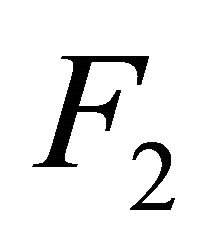 be disjoint cl-open subsets of
be disjoint cl-open subsets of  Since
Since 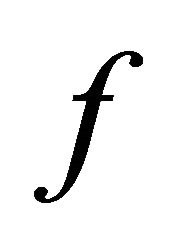 is slightly αδ-continuous,
is slightly αδ-continuous, 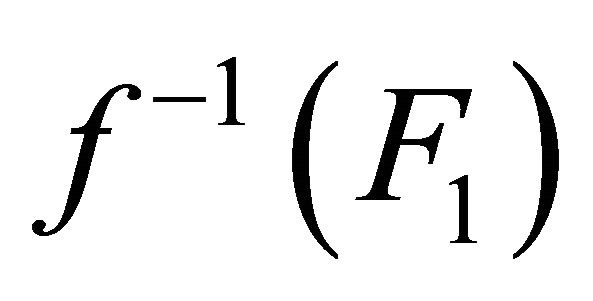 and
and
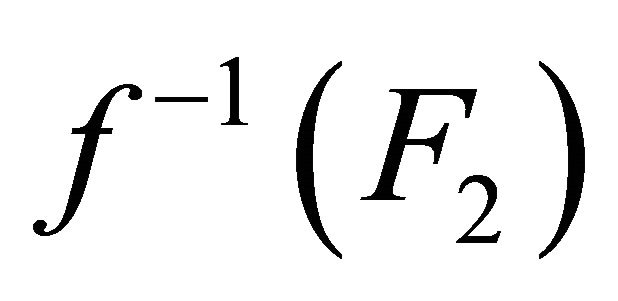 are αδ-closed sets. Take
are αδ-closed sets. Take  and
and
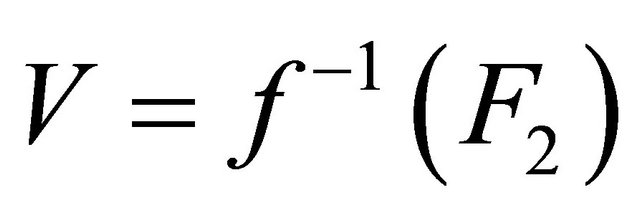 . We have
. We have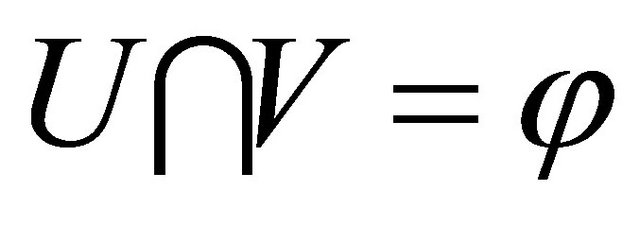 . Since
. Since 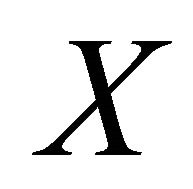 is αδ- regular, there exist disjoint open sets A and B such that
is αδ- regular, there exist disjoint open sets A and B such that 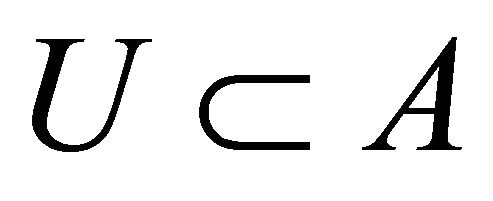 and
and . We obtain that
. We obtain that 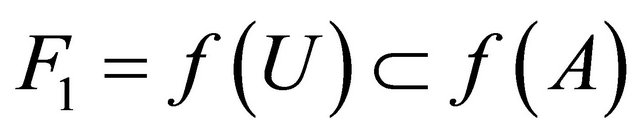 and
and 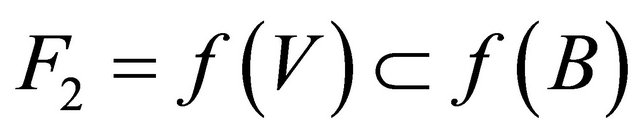 such that
such that  and
and  are disjoint open sets. Thus, Y is clopen normal.
are disjoint open sets. Thus, Y is clopen normal.
REFERENCES
- A. Wilansky, “Between T1 and T2,” American Mathematical Monthly, Vol. 74, No. 3, 1967, pp. 261-266.
- R. Devi, V. Kokilavani and P. Basker, “On Strongly-αδ- Super-Irresolute Functions in Topological Spaces,” International Journal of Computer Applications, Vol. 40, No. 17, 2012, pp. 38-42.
- V. Kokilavani and P. Basker, “On
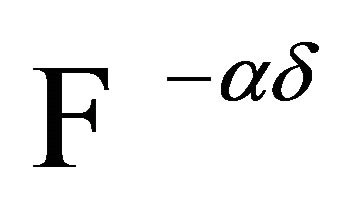 Continuous Multifunctions,” International Journal of Computer Applications, Vol. 41, No. 2, 2012, pp. 0975-8887.
Continuous Multifunctions,” International Journal of Computer Applications, Vol. 41, No. 2, 2012, pp. 0975-8887. - E. Ekici and M. Caldas, “Slightly—Continuous Functions,” Boletim da Sociedade Paranaense de Matemática, Vol. 35, No. 22, 2004, pp. 63-74.
- N. V. Velicko, “H-Closed Topological Spaces,” Transactions of American Mathematical Society, Vol. 78, 1968, pp. 103-118.
- V. Kokilavani and P. Basker, “On Some New Applications in
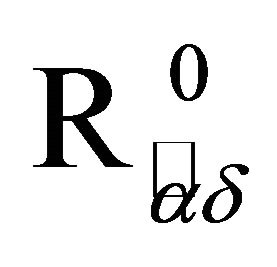 and
and 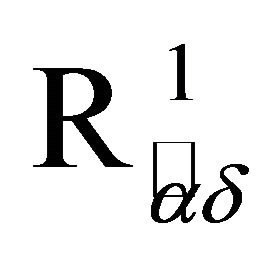 Spaces via αδ-Open Sets,” Elixir Applied Mathematics, Vol. 45, 2012, pp. 7817-7821.
Spaces via αδ-Open Sets,” Elixir Applied Mathematics, Vol. 45, 2012, pp. 7817-7821. - V. Kokilavani and P. Basker, “The αδ-Kernel and αδ-Closure via αδ-Open Sets in Topological Spaces,” International Journal of Mathematical Archive, Vol. 3, No. 4, 2012, pp. 1665-1668.
- V. Kokilavani and P. Basker, “
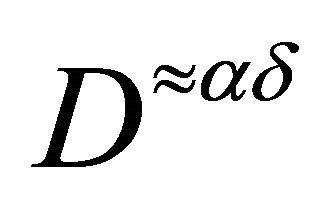 -Sets and Associated Separation Axioms in Topological Spaces,” Elixir Discrete Mathematics, Vol. 46, 2012, pp. 8207-8210.
-Sets and Associated Separation Axioms in Topological Spaces,” Elixir Discrete Mathematics, Vol. 46, 2012, pp. 8207-8210.
NOTES
*Corresponding author.

