ABSTRACT

In the paper, a auxiliary equation expansion method and its algorithm is proposed by studying a second order nonlinear ordinary differential equation with a four-degree term. The method is applied to the generalized Benney-Luke (GBL) equation with any order. As a result, some new exact traveling wave solutions are obtained which singular solutions, triangular periodic wave solutions and jacobian elliptic function solutions. This algorithm can also be applied to other nonlinear wave equations in mathematical physics.

1. Introduction

Nonlinear phenomena that appear in many areas of scientific fields such as solid state physics, plasma physics, fluid dynamics, mathematical biology and chemical kinetics can be modeled by partial differential equation. A broad class of analytical solutions methods and numerical solutions methods were used in handle these problems. The investigation of exact traveling wave solution to nonlinear equations plays an important role in the study of nonlinear physical phenomena. Various methods for seeking traveling wave solutions to nonlinear partial differential equations are proposed such as inverse scattering transform method [1], BÄacklund and Darboux transform [2-6], Hirota method [7], Lie group method [8,9] and so on.

In the paper, we shall consider the following generalized Benney-Luke (GBL) equation [10]:

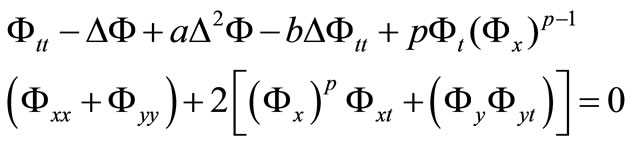(1.1)

The paper is organized as follows. In Section 2, we present the auxiliary equation method and its algorithm. In Section 3, we present some exact traveling wave solutions of system (1.1). Finally some conclusion are given.

2. The Auxiliary Equation Algorithm

We outline our auxiliary equation algorithm:

Step I. For a given nonlinear wave equation with one physical field; in three variables

(2.1)

We seek its special solution, traveling wave solution, in the form of

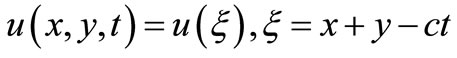(2.2)

where is constant. Substitution (2.2) into (2.1) gives rise to a nonlinear ordinary differential equation

(2.3)

Step II. To seek the traveling wave solution of (2.3), we assume that (2.3) has the solution in the form of

(2.4)

with the new variable satisfying:

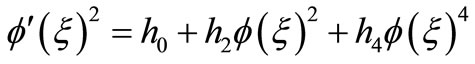(2.5)

are constants and is the integer to be determined later.

Step III. Determined the parameter. Substituing Equation (2.4) along with Equation (2.5) into Equation (2.3) and balancing the highest derivative term with the nonlinear terms in the Equation (2.3), we then obtain the value of.

Step IV. Determine the parameters

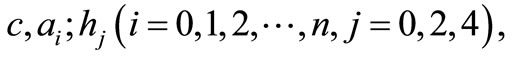
Substitution Equation (2.4) along with Equation (2.5) into Equation (2.3) and setting the coefficients of all powers to zero, we will obtain a system of nonlinear algebraic equations (NAEs) with respect to the parameters

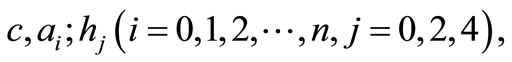
By solving the NAEs if available, we can determine those parameters explicitly.

3. Exact Traveling Wave Solutions for the Generalized Benney-Luke (GBL) Equation with Any Order

By considering that the traveling wave solutions of (1.1) propagate in the direction of the positive x-axis, i.e. 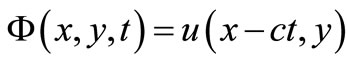Ref. [10] gave the following traveling equation:

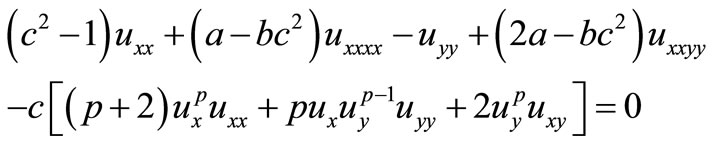(3.1)

In this paper, we will study the traveling wave solutions of (1.1) with the form:

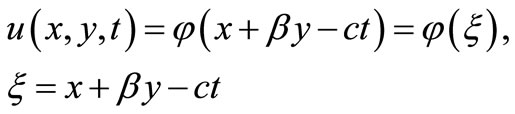
where c is the wave speed. Substituting it into (1.1) and noting (3.1), we have

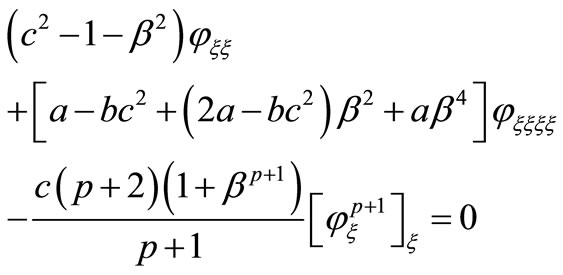(3.2)

Integrating (3.2) once with respect to and taking the integral constant as zero, we obtain

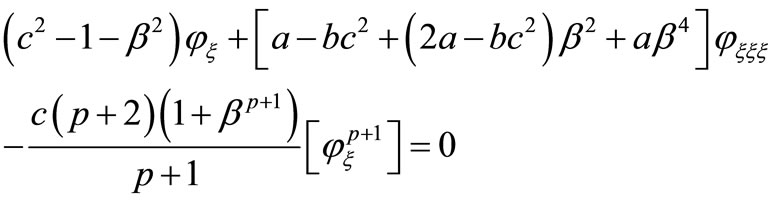(3.3)

Letting

(3.4)

and writing

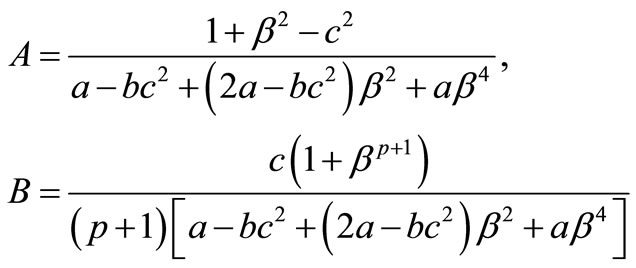
then from (3.4), we have that

(3.5)

Let

We have

(3.6)

We expand the solution of Equation (3.6) in form of Equation (2.4). Substitution Equation (2.4) along with Equation (2.5) and balancing the highest order derivative term.

with nonlinear term 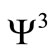in Equation (3.6) gives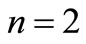. Hence, we have

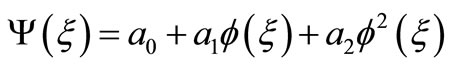(3.7)

where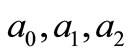are constant to be determined later; 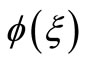satifiyed Equation (2.5).

We can get the following equation by Step IV

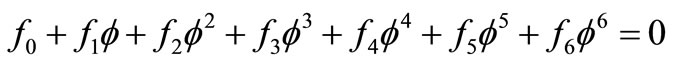(3.8)

If, we can get the following solution:

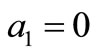
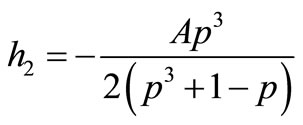
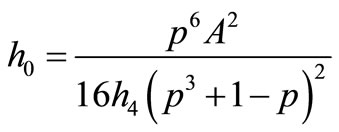
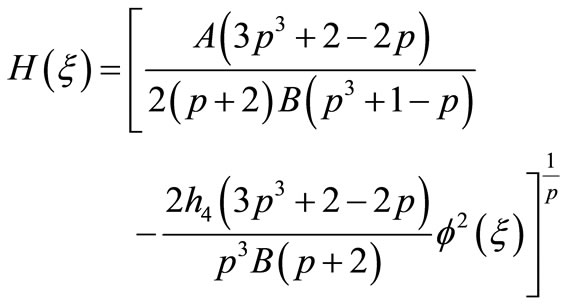(3.9)

where

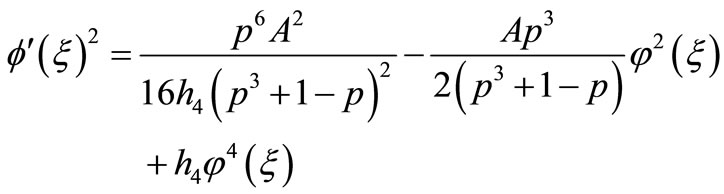(3.10)

Th 3.1. Suppose that

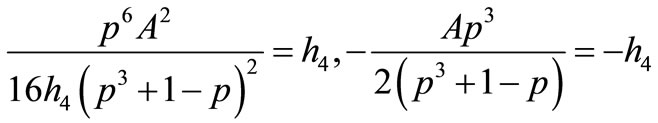
If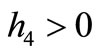, that Equation (1.1) has a kink profile solution

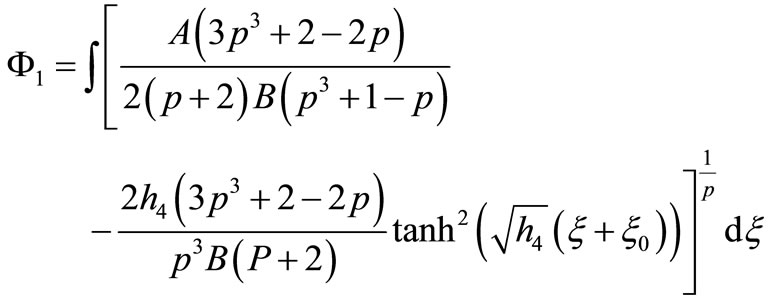
Th 3.2. 1) If

that Equation (1.1) has two Jacobian elliptic function solutions

2) If

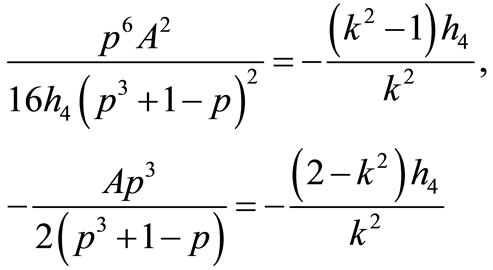
that Equation (1.1) has a Jacobian elliptic function solution

3) If

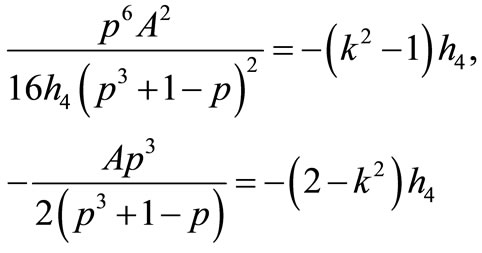
that Equation (1.1) has a Jacobian elliptic function solution

4) If

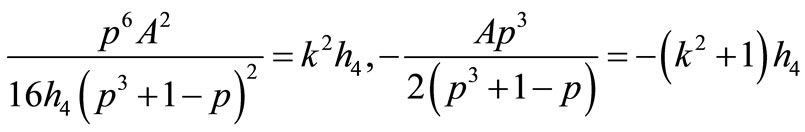
that Equation (1.1) has two Jacobian elliptic function solutions

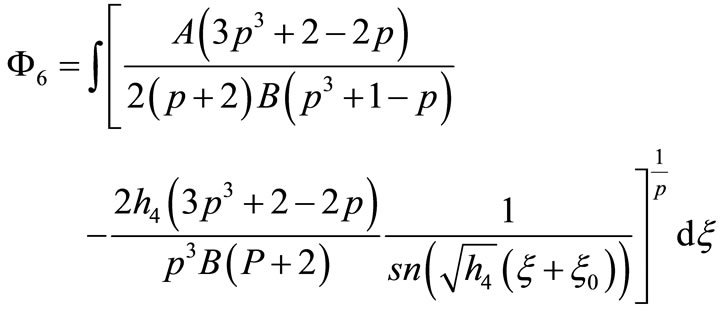
5) If

that Equation (1.1) has a Jacobian elliptic function solution

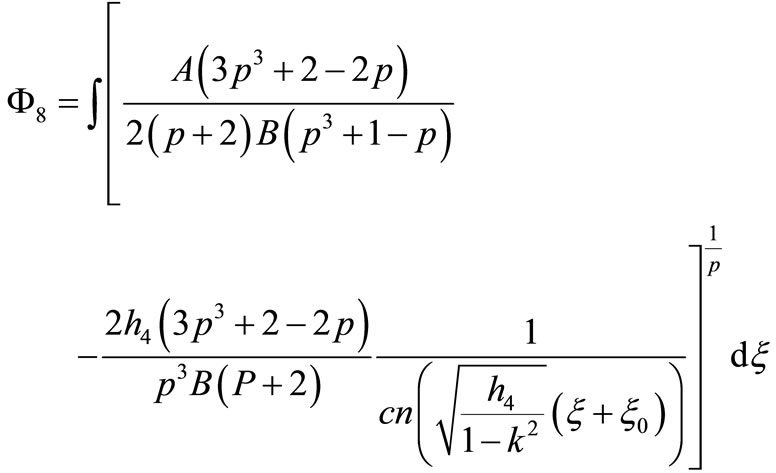
6) If

that Equation (1.1) has a Jacobian elliptic function solution

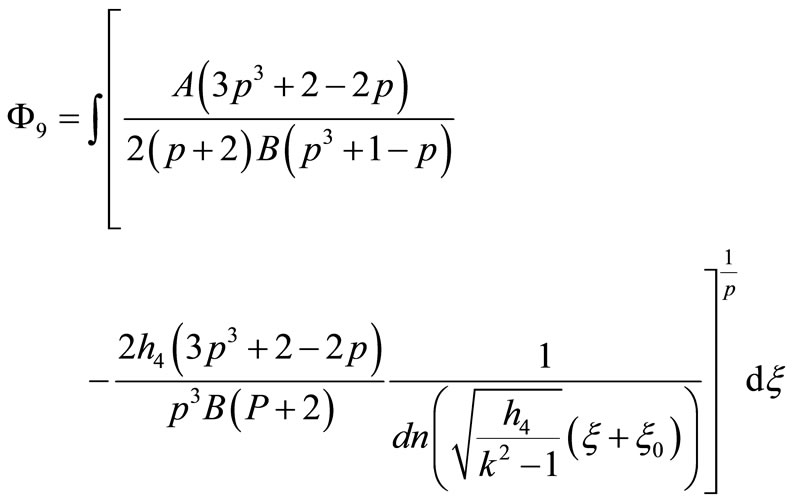
7) If

that Equation (1.1) has a Jacobian elliptic function solution

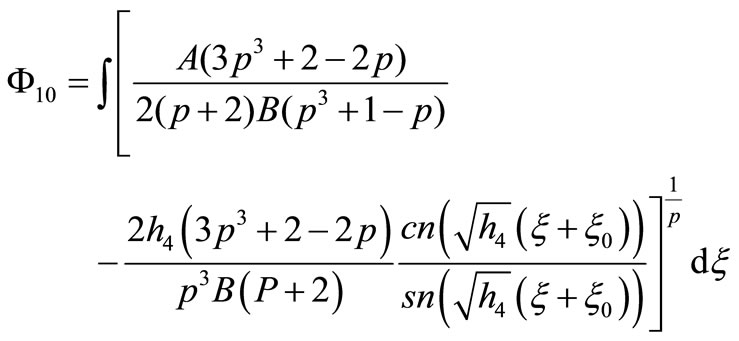
8) If

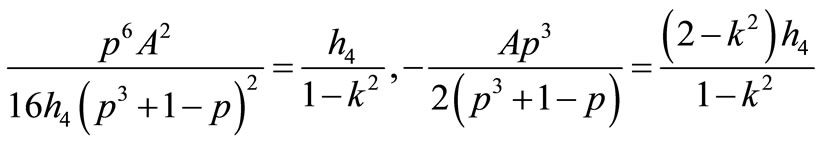
that Equation (1.1) has a Jacobian elliptic function solution

9) If

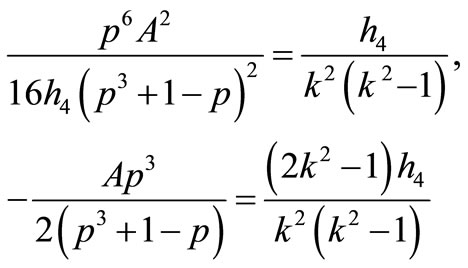
that Equation (1.1) has a Jacobian elliptic function solution

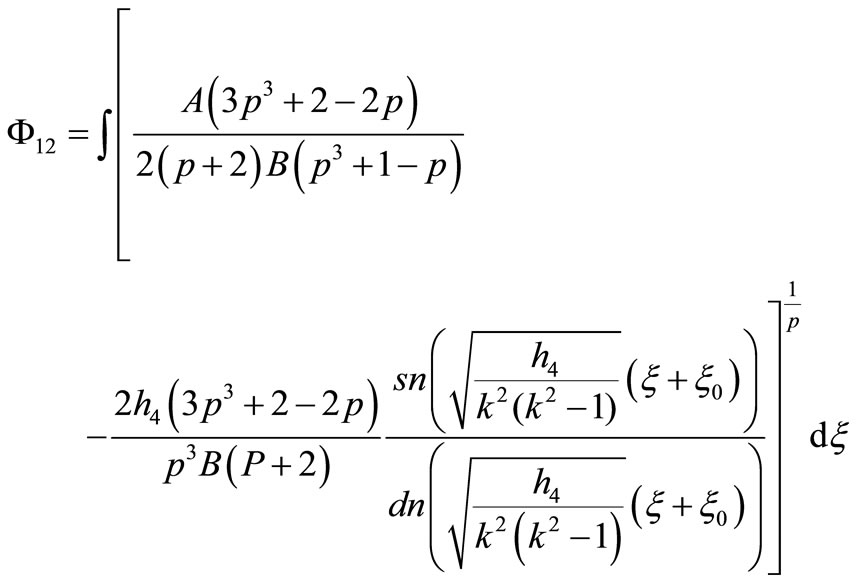
10) If

that Equation (1.1) has a Jacobian elliptic function solution

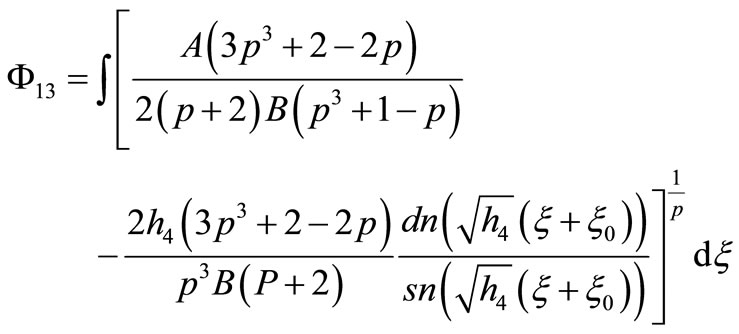
11) If

that Equation (1.1) has four Jacobian elliptic function solutions

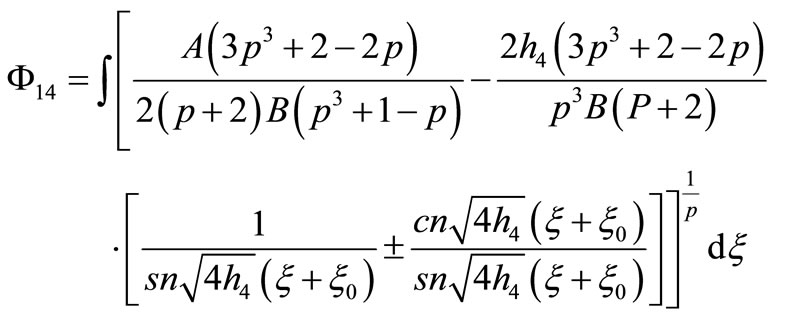
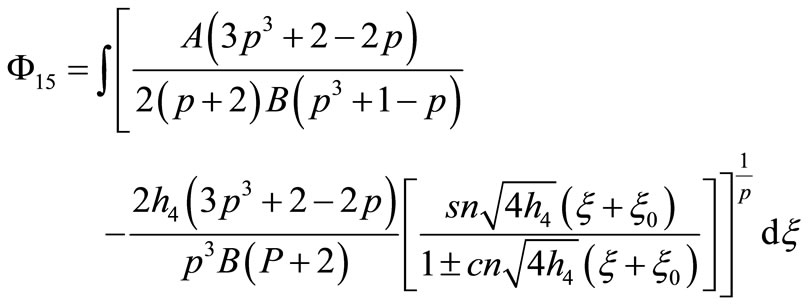
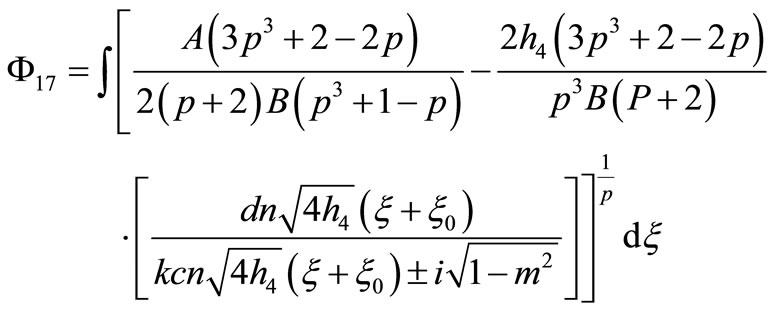
12) If

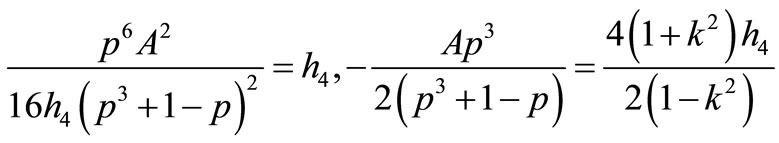
that Equation (1.1) has a Jacobian elliptic function solution

13) If

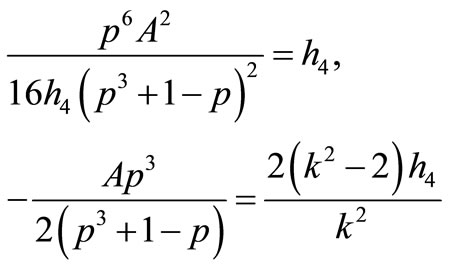
that Equation (1.1) has three Jacobian elliptic function solutions

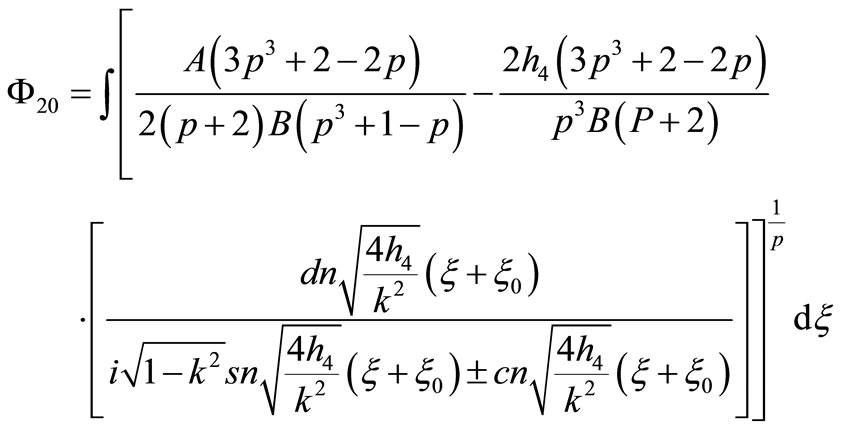
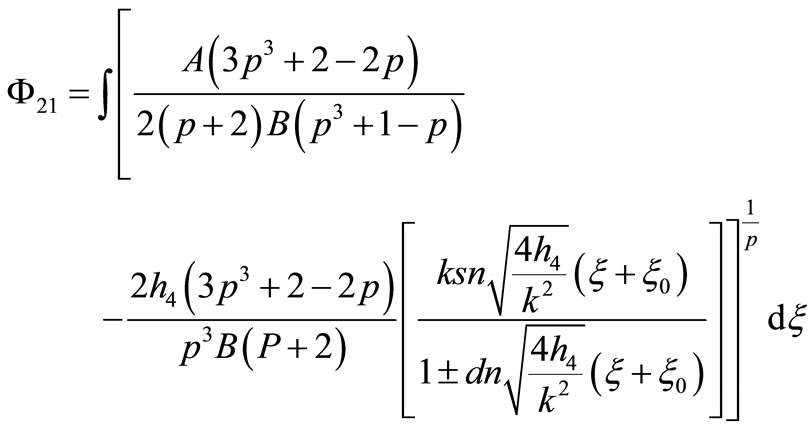
14) If

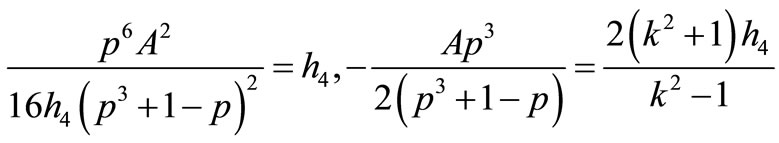
that Equation (1.1) has a Jacobian elliptic function solution

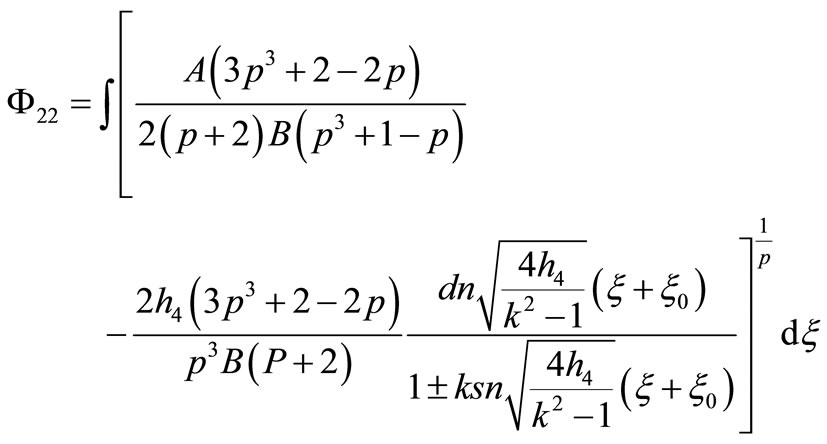
15) If

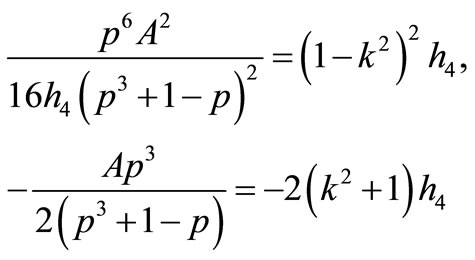
that Equation (1.1) has a Jacobian elliptic function solution

16) If

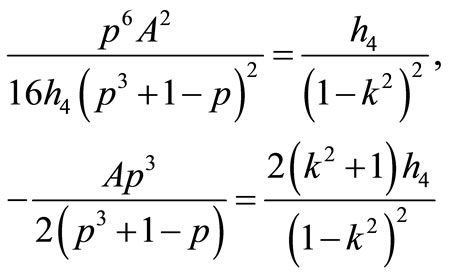
that Equation (1.1) has a Jacobian elliptic function solution

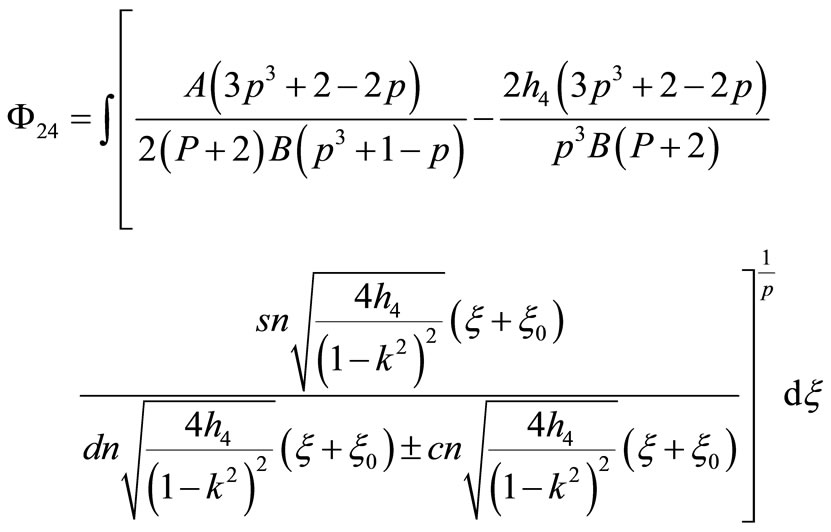
17) If

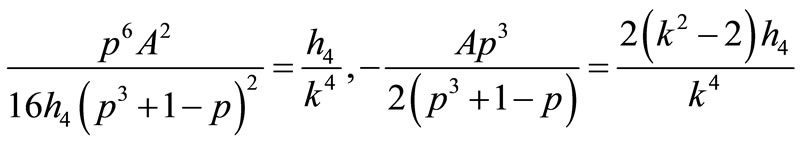
that Equation (1.1) has a Jacobian elliptic function solution

4. Conclusion

In the paper, we apply the auxiliary equation method to study Equation (1.1), and get some new conclusions. Some new exact traveling wave solution of Equation (1.1) are obtain which include new singular solution, triangular periodic wave solutions and Jacobian elliptic function solutions. These solutions may be useful for describing certain nonlinear physical phenomena of Equation (1.1). The method which we have propose in this paper is standard, direct and computerized method ,which allow us to do complicated and tedious algebraic calculation.It is shown that the algorithm can be also applied to other nonlinear wave equations such as generalized BBM equation,

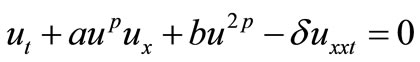
and generalized Klein-Gordon equation:

REFERENCES