Applied Mathematics
Vol. 3 No. 3 (2012) , Article ID: 18084 , 6 pages DOI:10.4236/am.2012.33031
The Response of Viscously Damped Euler-Bernoulli Beam to Uniform Partially Distributed Moving Loads
Department of Pure and Applied Mathematics, Ladoke Akintola University of Technology, Ogbomoso, Nigeria
Email: foakinpelu@yahoo.co.uk
Received July 21, 2011; revised February 14, 2012; accepted February 21, 2012
Keywords: Viscously Damped; Euler-Bernoulli Beam; Uniform Partially Distributed and Moving Loads
ABSTRACT
The paper investigates the response of non-initially stressed Euler-Bernoulli beam to uniform partially distributed moving loads. The governing partial differential equations were analyzed for both moving force and moving mass problem in order to determine the behaviour of the system under consideration. The analytical method in terms of series solution and numerical method were used for the governing equation. The effect of various beam observed that the response amplitude due to the moving force is greater than that due to moving mass. It was also found that the response amplitude of the moving force problem with non-initial stress increase as mass of the mass of the load M increases.
1. Introduction
In the recent years all branches of transport have experienced great advances characterized by increasing higher speeds and weight of vehicles. As a result, structures and media over or in which the vehicles move have been subjected to vibrations and dynamic stresses far larger than ever before. Many scholars have studied vibration of elastic and inelastic structures under the action of moving loads for many years, and effort are still being made to carry out investigation dealing with various aspect of the problem [1-15]. The structures on which these moving loads are usually modeled are by elastic beams, plates or shells. The problem of elastic beam under the action of the moving loads was considered by Willis [2]. He made the assumption that the mass of the beams is smaller than that of the load and obtained an approximate solution of the problem. Yoshida [3] studied the vibration of a beam subjected to moving concentrated moving using finite element method. A simply supported to a constant moving force at uniform speed was considered by Krylov [4] who used the method of expansion of the associated Eigen modes. He assumed the mass of the load to be smaller than that of the beam. Bolotin [5] carried out a dynamic analysis of the problem involving a concentrated mass traversing a simply supported beam at constant speed. His approach involves using Galerkin’s method. The response of finite simply supported EulerBernoulli beam to a unit force moving at a uniform velocity was investigated by steel [8] The effects of this moving force on beams with and without an elastic foundation were analysed. In all the studies discussed above it was only the force effects of the moving loads are taken into consideration. The moving load problem involving both the inertia effect as well as the force effects were not considered for several years. This type of dynamical problem was first considered by Saller [6], later by Jeffcott [7] whose iterative method became divergent in some cases. Recently, Esmailzadeh and Gorashi [9] worked on the vibration analysis of beams traversed by uniform partially distributed moving masses using analytical-numerical method. They discovered that the inertia effect of the distributed moving mass is of importance in the dynamic behaviour of the structure. The critical speeds of the moving load were also calculated for the mid span of the beam. The length of the distributed moving mass was also found to affect the dynamic response.
This paper deals with the response of non-initially stresses Euler-Bernoulli beam with an attached mass to uniform partially distributed moving loads. The main objectives of this paper are
1) To present the analysis of the dynamic response of a non-initially stressed finite elastic Euler-Bernoulli beam with an attached mass at the end x = L, but arbitrary supported at the end x = 0, to uniform partially distributed moving load.
2) To present a very simple and practical analyticalnumerical technique for determine the response of beams with non-classical boundary conditions carrying mass.
2. Mathematical Model
With reference to Figure 1, it is assumed that a uniform simply supported Euler-Bernoulli beam of finite length L, having an attached mass at x = L acted upon initially at time t = 0, by mass M, over fixed length of the beam with a specified constant velocity v. The load is in contact with the beam throughout the motion.
3. The Governing Equations
The governing equations describing the vibration behaviour of a uniform non-initially stressed Euler-Bernoulli with an attached mass at the end x = L but traversed by a concentrated moving loads are
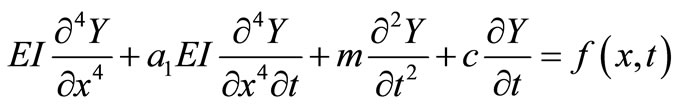 (1)
(1)
where, E the is the modulus of elasticity, I is the second moment of area of the beam’s cross-sectional, m is the mass per unit length of the beam, 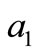 is the damping constant,
is the damping constant, 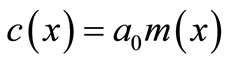 , Y is the deflection of the beam, x is the spatial coordinate, t is the time and f(x, t) is the applied force (i.e. the resultant concentrated force caused by the moving mass).
, Y is the deflection of the beam, x is the spatial coordinate, t is the time and f(x, t) is the applied force (i.e. the resultant concentrated force caused by the moving mass).
The applied force per unit length F(x, t) is the uniform partially distributed moving load which is defined as
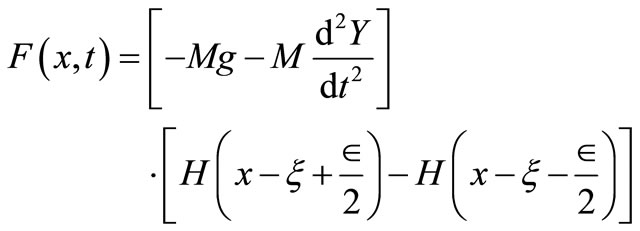 (2)
(2)
M: is the mass of the load.
g: is the acceleration due to gravity.
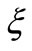 : is the fixed length of load.
: is the fixed length of load.
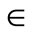 : is the length of the beam.
: is the length of the beam.
The differential operator 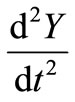 is defined as
is defined as
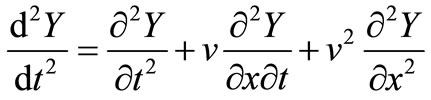 (3)
(3)
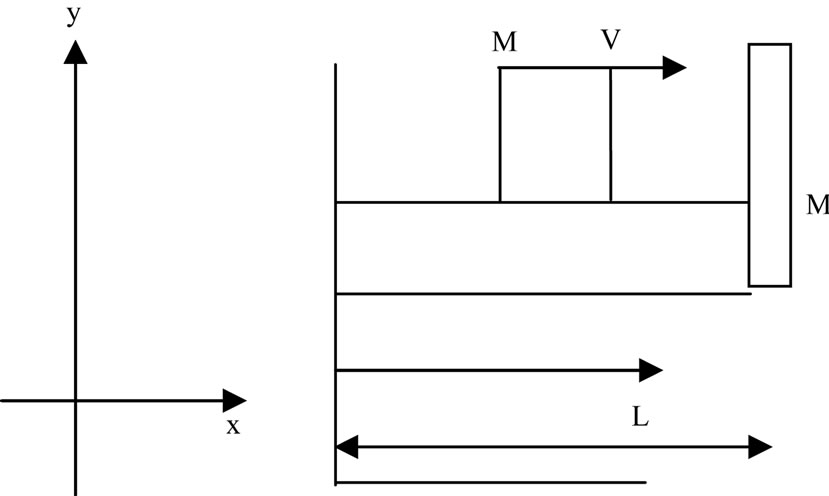
Figure 1. The mathematical model of the problem.
H(x) is function such that
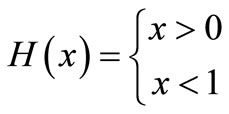 (4)
(4)
Hence the governing equations describing the vibration behaviour of a uniform non-initially stressed EulerBernoulli beam with an attached mass at the end x = L becomes
 (5)
(5)
Subject to the following boundary conditions
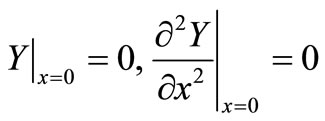 (6)
(6)
 (7)
(7)
The corresponding initial conditions are
 (8)
(8)
4. Solution to the Initial-Boundary Value Problem
We assumed a solution in the form of a series
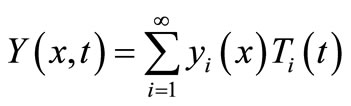 (9)
(9)
where 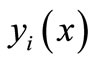 are the known Eigen functions of the beam.
are the known Eigen functions of the beam.
The Eigen functions satisfying the following equation
 (10)
(10)
 (11)
(11)
where 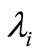 are natural frequencies.
are natural frequencies.
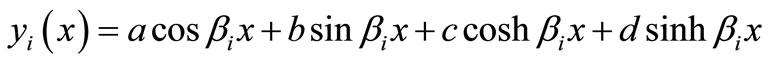 (12)
(12)
is the solution to Equation (10) and a, b, c, d are constants coefficients and 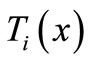 are functions of time to be determined We further assumed
are functions of time to be determined We further assumed
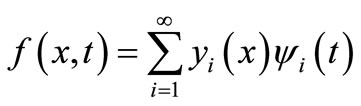 (13)
(13)
Substituting Equation (9) into Equation (5), we have
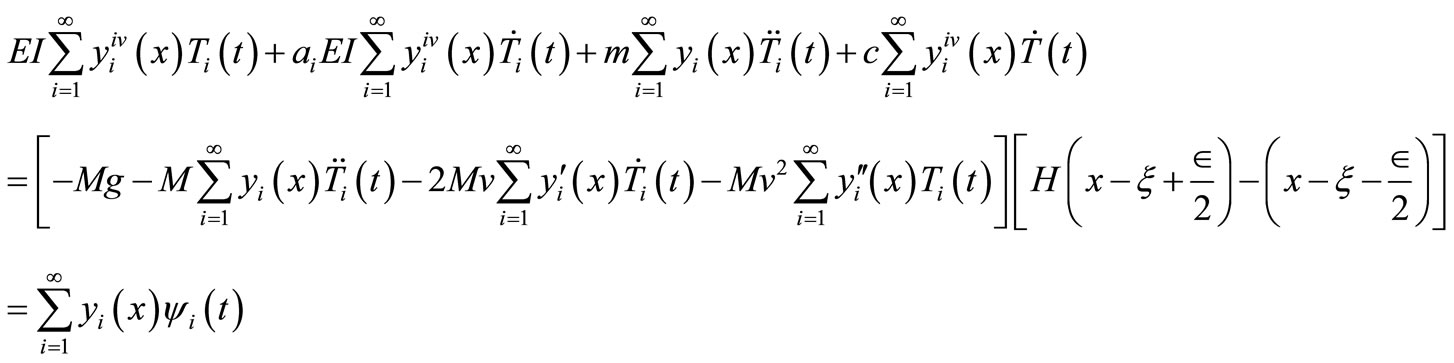 (14)
(14)
Multiply both sides of the R. H. S. of Equation (14) by  and taking the definite integrals of both sides along the length
and taking the definite integrals of both sides along the length  of the beam with respect to x, we have
of the beam with respect to x, we have
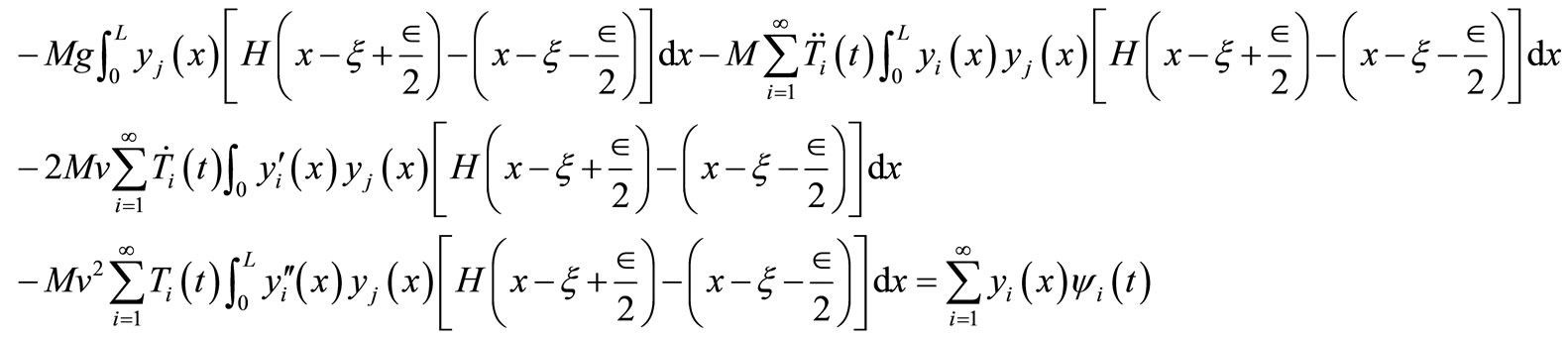 (15)
(15)
Evaluation the first definite integral in Equation (15) by carrying out integration by part with respect to  using the following two properties of singularity function [ ]
using the following two properties of singularity function [ ]
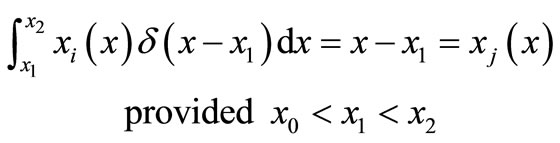 (16)
(16)
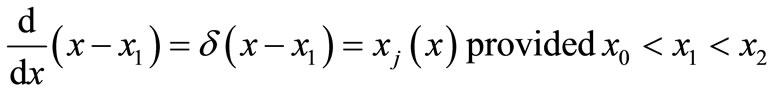 (17)
(17)
Similar arguments to second, third to fifth definite integral in (15) hence evaluating the integrals using Taylor’s series expansion and applying orthogonality properties of the characteristics function  the R. H. S. of (15), we finally obtain
the R. H. S. of (15), we finally obtain
 (18)
(18)
Substituting Equation (18) into the R. H. S. of Equation (14) we have
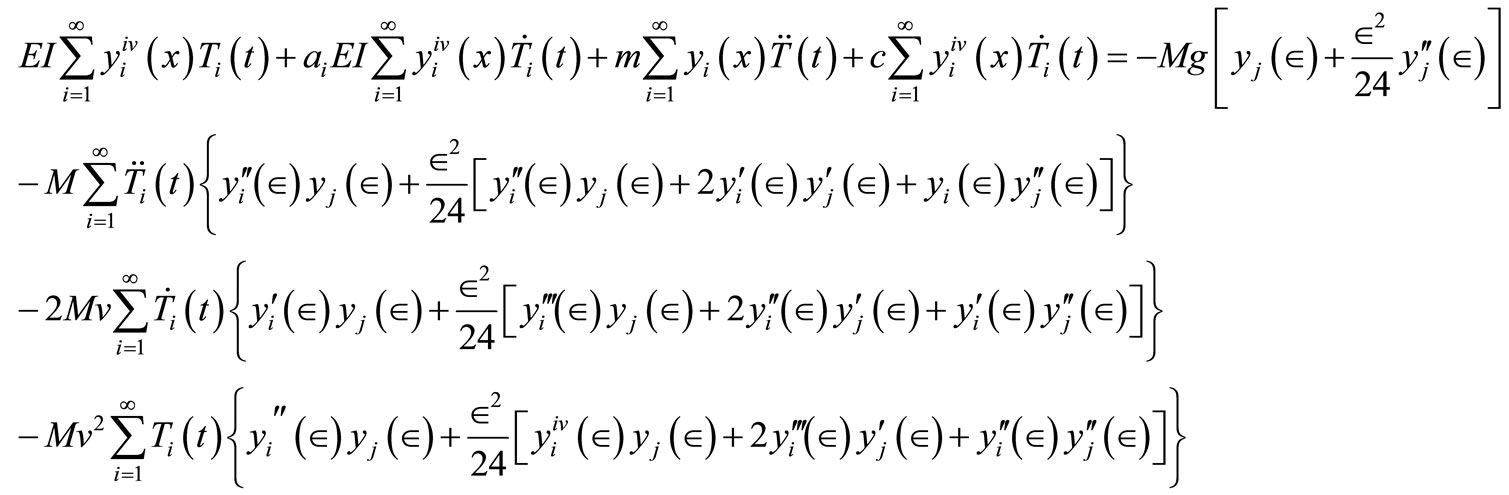 (19)
(19)
Considering Equations (10) and (11), then Equation (19) becomes
 (20)
(20)
The Equation (20) must be satisfied for arbitrary 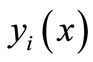 and this possible only when the expression in the curl bracket is equal to zero. Hence
and this possible only when the expression in the curl bracket is equal to zero. Hence
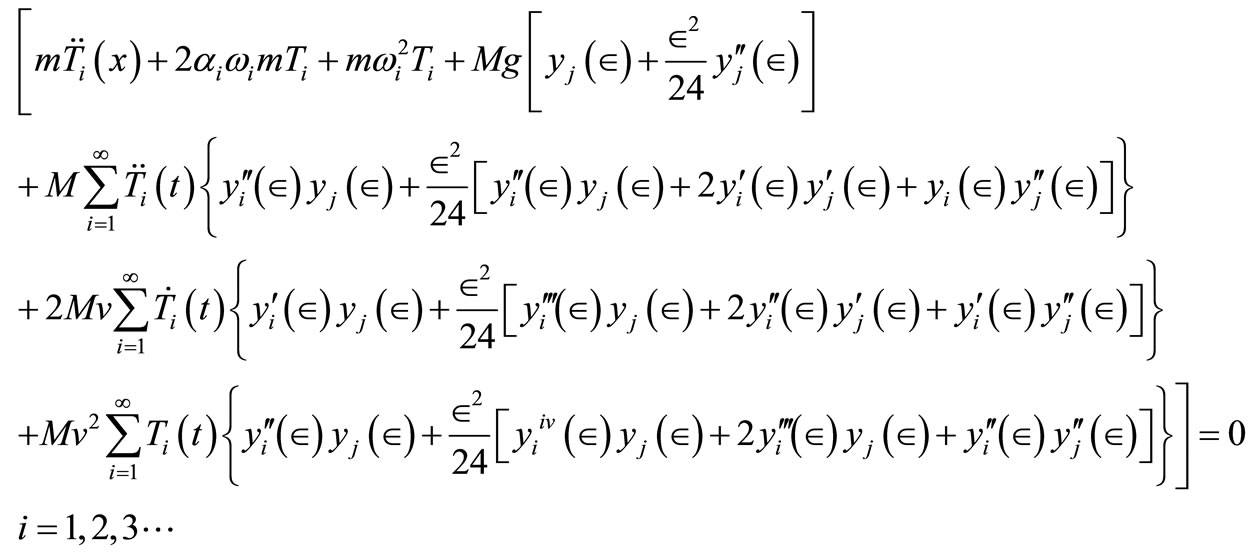 (21)
(21)
The system of Equation (21) is a set of coupled ordinary second order differential equations and it is easily observed that a numerical approach is required to solve it.
5. Simply Supported Non-Initially Euler-Bernoulli Beam
The Eigen functions
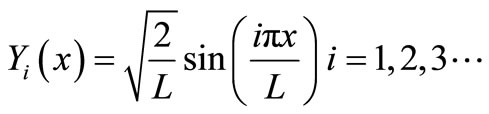 (22)
(22)
We obtain the set of exact governing differential equation for the vibration of the beam by employing Equation (22) and evaluating the exact values of the integral in Equation (15) and we finally obtain
 (23)
(23)
Note for the case i = j we replace the expression involving 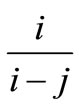 by
by 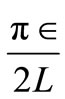
To solve Equation (23) recourse can be made to a numerical method, but two interesting cases are to be tackled.
5.1. The Moving Forces Non-Initially Stressed Euler-Bernoulli Beam
A moving force problem is one in which the inertia effects of the moving load are neglected and only the force effects are retained. In other words by neglecting all the terms on the R. H. S. of Equation (23) except the first term.
5.2. The Moving Mass Non-Initially Stressed Euler-Bernoulli Beam
This is the case in which both the inertia effect as well as the force effect are taken into consideration. The entire Equation (23) is the moving mass problem To obtain results given in this paper, an approximate central difference formulas have been made used of, for the derivatives in Equation (23) for both cases [5.1 and 5.2]. Thus, for N modal shapes, Equation (23) are transformed to a set of N linear algebraic equations, which are to be solved for each interval of time. Regarding the definition of approximation involved, in order to ensure the stability and convergence of the solution, sufficiently small time steps have been utilized.
Computer programe was developed and the following numerical data which are the same as those in reference [ ] were used for the purpose of comparison
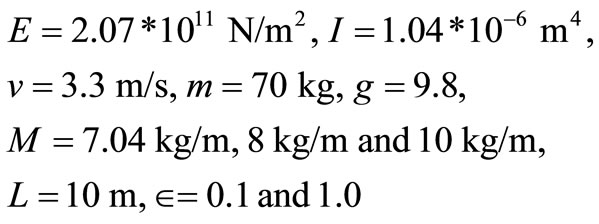
Hence we have the graphs of results. See Figures 2-5.
5.3. Numerical Simulation
The displacement profiles of the beam are display graphically to demonstrate the effect of the mass, the angular frequency and the viscous damping magnification factor.
5.4. Discussion of Result and Conclusion
From the response profile of the beam it was observed that the beam has more than one mode of vibration with
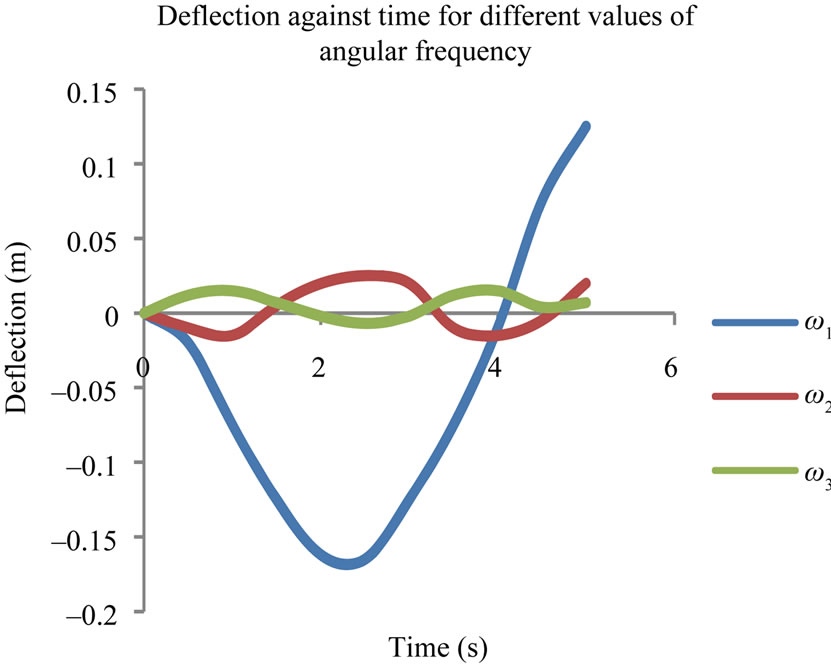
Figure 2. Deflection against time for different values of damped coefficient.

Figure 3. Deflection against time for 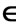 = 0.1 with different values of mass.
= 0.1 with different values of mass.
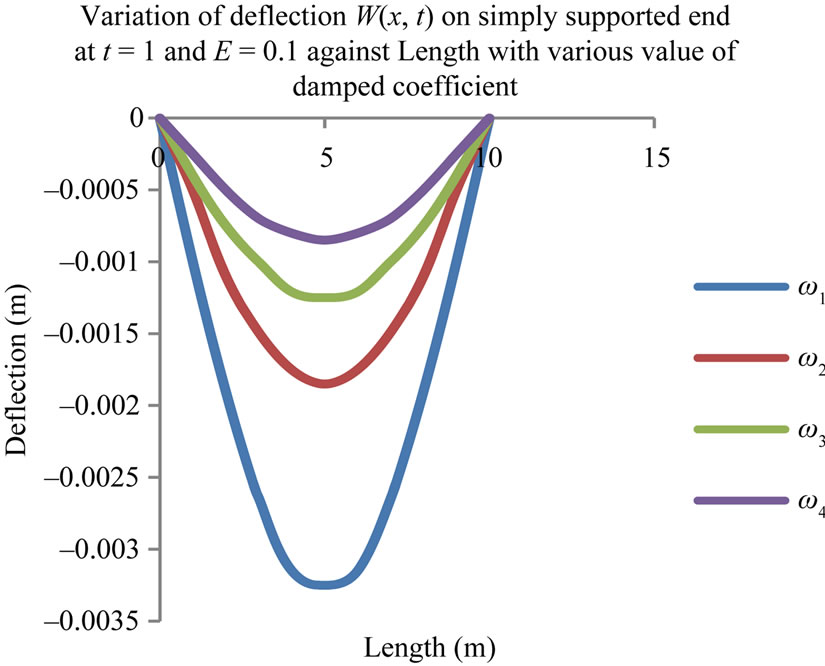
Figure 4. Deflection against length for different values of damped coefficient.

Figure 5. Magnification factor against frequency ratio for different values of damped coefficient.
each mode having a different natural frequency. The amplitude increases with increase in viscous damping. Also it was observed from Figure 5 that as the mass of the load increase the amplitude is also increases and the value of the magnification factor occurs for a value 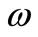 less than one for
less than one for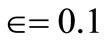 .
.
REFERENCES
- A. O. Cifuentes and S. Lalapet, “A General Method to Determine the Dynamic Response of a Plate to a Moving Mass,” Computers and Structures, Vol. 42, No. 1, 1992, pp 31-36. doi:10.1016/0045-7949(92)90533-6
- R. Willis, “Preliminary Essay to the Appendix B: Experiment for Determining the Effects Produced by Causing Weight to Travel over Bus with Difference Velocities,” 1951.
- D. M. Yoshida, “Finite Element Analysis of Beams with Moving Loads,” Publication of Internal Association Bridge and Structured Engineering, Vol. 31, No. 1, 1971, pp. 179-195.
- A. N. Krylov, Mathematical Collection of Paper of the Academy of Sciences, Vol. 61, Petersburg, 1995.
- E. Esmailzadeh and M. Gorashi, “Vibrations Analysis of the Beams Traversed by Uniform Partially Distributed Moving Masses,” Journal of Sound and Vibration, Vol. 184, No. 5, 1995, pp. 9-17. doi:10.1006/jsvi.1995.0301
- J. J. Kalker, “Discretely Supported Rails Subjected to Transient Loads,” Vehicle System Dynamics, Vol. 25, No. 1, 1996, pp 71-88. doi:10.1080/00423119608968958
- H. H. Jeffcott, “On the Vibrations of the Beams under the Action of Moving Loads,” Philosophical Magazine, Series 7, Vol. 48, 2000, pp. 66-67.
- H. P. Lee, “Dynamic Response of a Beam with Intermediate Point Constraints Subject to a Moving Load,” Journal of Sound and Vibration, Vol. 1, No. 71, 1994, pp. 361-368. doi:10.1006/jsvi.1994.1126
- E. Esmailzadeh and M. Gorashi, “Vibrations Analysis of the Beams Traversed by Moving Masses,” Proceedings of the International Conference on Engineering Application of Mechanics, Tehran, Vol. 2, 9-12 June 1992, pp. 232- 238.
- S. Timoshenko, “On the Transverse Vibration of Bars of Uniform Cross Section,” Philosophical Magazine, Series 6, Vol. 43, 2000, pp. 125-131. doi:10.1080/14786442208633855
- L. Fryba, “Vibration of Solids and Structures under Moving Loads,” Groningen, Noordhoff International Publishing, Groningen, Vol. 1-2, No. 1-5, 1972, pp. 452-457.
- J. A. Gbadeyan and S. T. Oni, “Dynamic Behaviour of Beams on Rectangular Plate under Moving Load,” Journal of Sound and Vibration, Vol. 182, No. 5, 1995, pp. 677-695. doi:10.1006/jsvi.1995.0226
- Y. H. Lin, “Vibrations Analysis of the Beams Traversed by Uniform Partially Distributed Moving Masses,” Journal of Sound and Vibration, Vol. 199, No. 4, 1995, pp. 697-700. doi:10.1006/jsvi.1995.0675
- I. A. Adetunde, F. O. Akinpelu and J. A. Gbadeyan, “Dynamics Analysis of Non-Prestressed Rayleigh Beams Carrying an Attached Mass and Traversed by Uniform Partially Distributed Moving Load,” Journal of Engineering and Applied Sciences, Vol. 2, No. 2, 2007, pp. 445-455.
- I. A. Adetunde, F. O. Akinpelu and J. A. Gbadeyan, “The Response of Initially Stressed Euler-Bernoulli Beams with an Attached Mass to Uniform Partially Distributed Moving Loads,” Journal of Engineering and Applied Sciences, Vol. 2, No. 3, 2007, pp. 488-493.

