Advances in Bioscience and Biotechnology
Vol.07 No.03(2016), Article ID:64283,10 pages
10.4236/abb.2016.73011
An Optimization Study of α-Amylase Production by Aspergillus niger ATCC 16404 Grown on Orange Waste Powder
Djekrif-Dakhmouche Scheherazed1*, Bennamoun Leila1, Ait Kaki Amel1, Labani Kenza1, Nouadri Tahar1, Gheribi-Aoulmi Zoubida2, Meraihi Zahia1
1Research lab in enzymatic engineering, Dept of Biology, Mentouri University, Constantine, Algeria
2Department of Mathematics, Mentouri University, Constantine, Algeria

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 August 2014; accepted 5 March 2016; published 8 March 2016
ABSTRACT
In this work, sequential optimization strategy, based on statistical designs, was employed to enhance the production of α-amylase by Aspergillus niger ATCC 16404. This statistical study consists of optimizing the factors that influence the production of a-amylase of A. niger ATCC 16404. Indeed, another statistical study has allowed the selection of 5 factors (pH, starch, yeast extract, “corn steep liquor”, CaCl2 and salts) affecting both the development of mould (biomass) and that of the enzyme production. The central composite design allows the determination of the optimum of these selected factors and a quadratic model explains the factor reaction. Thus, the “ridge analysis” method, has led to maximizing the experimental reaction. The results indicate that the production rate of a-amylase is maximized in the presence of starch at 8.97 g/l, yeast extract at 2.86 g/l, CaCl2 at 1.224 g/l, salts (composed of 25% FeSO4, 7H2O, 25% MnSO4 and 50% MgCl2, 6H2O): FeSO4, 7H2O, MnSO4 0.1518 g/l and MgCl2, 6H2O at 0.3036 g/l. As for the pH, it is maintained at the rate of 5.68.
Keywords:
a-Amylase, Aspergillus niger, Optimization, Central Composite Design, Ridge Regression

1. Introduction
α-amylase (E.C 3.2.1.1) is an extracellular enzyme which is widespread among higher plants, animals and microorganisms. It catalyses the hydrolysis of α-D-(1, 4) glycosidic linkages in starch components and related carbohydrates. It can be obtained from several sources, such as plants, animals and microorganisms. The major advantage of using microorganisms for the production of amylase is the economical bulk production capacity and the fact that microbes are easy to manipulate to obtain enzymes of desired characteristics. α-Amylase has been derived from several fungi, yeasts and bacteria. This enzyme holds the maximum market share of the enzyme sales with major applications in the starch industry, baking industry, analytical chemistry, automatic dishwashing detergents, desizing fabrics, medicine, and paper industry [1] .
The optimal design of the culture medium is a very important aspect in the development of fermentation processes. The conventional method for medium optimization involves changing one parameter at a time while keeping all others constant. This method may be very expensive and time-consuming. In addition, it fails to determine the combined effect of different factors [2] [3] .
Statistical experimental designs have been used to address these problems, such as the response surface methodology (RSM). In the present investigation, optimizing critical factors for α-amylase production was performed using RSM with CCD of Box-Wilson. Knowing that Djekrif-Dakhmouche [4] adapted, in a previous research work, the Plackett and Burman design [5] for the selection of the factors which affect the production of α-amylase of Aspergillus niger ATCC16404 such pH, starch, yeast extract, “corn steep liquor”, CaCl2 and salts. This study enabled the selection of the most significant factors for enzymatic production including pH, starch, yeast extract, CaCl2 and Salts [4] . Central composite design of Box and Wilson [6] was employed to find out the optimal levels of these factors selected. Furthermore, we know that in addition to the environmental conditions of fermentation, the production of extra cellular enzyme is highly dependent on the origin of the fungal strain [7] [8] .
Indeed, the central composite design of Box and Wilson (1951) has already been used in previous studies: the optimization of pectinase by Pseudozyma sp. SPJ [9] , Optimization of fermentation medium for xylanase- producing strain Xw 2 [10] , the optimization of the production of the caroténoïdes of Rhodotorula glutinis DBVPG 3853 [11] , the optimization of the production of a-amylase by Aspergillus flavus [12] , the optimization of the production of milk clotting enzymes by Bacillus subtilis [13] .
Using multiple linear regressions and analyses variance, the model is determined in the form of second-degree polynomials, starting from the most significant factors.
As for the reaction surface line, it permits to catch a glimpse of the operational optimal zone. Furthermore, the use of the “ridge analysis” method is necessary to specify the maximum if it lies at the edge of the experimental field.
2. Material and Methods
2.1. Mould
The strain of Aspergillus niger ATCC 16404 is offered by the institute Louis Pasteur, Paris, France.
2.2. Culture media
The strain was mainted at 0˚C - 4˚C on CYA medium (Czapec-yeast extract-agar).
The inoculum was prepared on 250 ml flasks with 40 ml PDA medium. After 72 h incubation at 35˚C, 50 ml distilled water was added. Spores were suspended under agitation with a magnetic stirrer [14] .
The basic medium is prepared starting from the powder of orange scrap (mesocarpe and endocarpe) of waste resulting from the UNAJUC Ramdhan Djamel, wilaya of Skikda. The powder is obtained after drying of waste to the free air, then crushed, filtered (sieve AFNOR, opening 0.250 mm) and preserved in box hermetically closed: 20 g of this powder is added to 100 ml of distilled water, mixed well, and then centrifuged at 6000 g for 20 min. The supernatant is used as basic medium after its dilution with the phosphate buffer 0.1 M pH 5.
The composition of the medium of production varies according to the experimental plan (Table 1).
2.3. Fermentation
The medium production is made of the basic medium supplemented according to the experimental design (Table 1 and Table 2). In 250 ml Erlenmeyer flask containing 50 ml of the medium production, sterilised at 110˚C for 15 min. An inoculum from Aspergillus niger ATCC16404 of 5 × 106 spores per flask was used. Cultures
Table 1. Experimental matrix of the central composite design for the study of five factors.
a = 2.378.
Table 2. Relationship between the coded levels and the real levels of the factors used in the central composite design.
were shaken in an orbital incubator at 200 rpm and 30˚C for a period of 72 hours. The filtrate is used to measure out the activity of α-amylase.
2.4. Enzyme Assay
For determination of α-Amylasic activity, 0.5 ml of culture filtrate (suitably diluted, if necessary) are added to 0.5 ml of soluble starch 1% w/v in the 0.1 M pH 5 phosphate buffer. This mixture is incubated at 40˚C during 30 minutes. The reaction is stopped using 2.4, dinitrosalicylic acid. One unit of α-amylase activity was defined as the amount of enzyme that produced reducing sugar equivalent to 1 µmoles of maltose per min under the conditions described above [15] .
2.5. Statistical Methods
In order to precisely determine the previously selected factors optima (pH, starch, yeast extract, CaCl2, FeSO4, MnSO4 and MgCl2) in the production of a-amylase of A. niger, we have applied the central composite design of Box and Wilson (1951). This framework allows the determination of a quadratic polynomial where each factor is analysed at least on 3 levels [6] [16] .
The experimental framework used in our work, which corresponds to 5 factors is shown in Table 1. It is constituted of three parts:
1) 32 points of co-ordinates (−1, +1) which form a complete factorial design 2K (K in our study is equal to 5)
2) 10 stars with 2 levels +a and −a corresponding to the factorial design 25: −2.378 and +2.378.
3) 5 repetitions of the central point (level 0).
This framework makes it possible to study each factor at 5 levels (Table 2), and to obtain the second degree equation the derivatives of which, compared to 0, make it possible to determine the extremums coded co-ordin- ates which will be, then, converted into actual values [8] [13] . The relationship between the coded levels and the real levels of the factors used in a central composite design is also displayed in Table 2.
Starch: 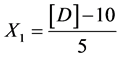
Yeast Extract: 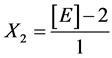
CaCl2: 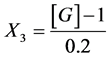
Salts: 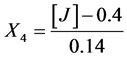
FeSO4∙7H2O (25%) = MnSO4 (25%) = 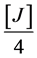
MgCl2∙6H2O (50%) = 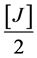
pH: 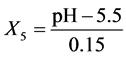
X1, X2, X 3, X4 and X5 are the coded factors of the central composite design according to the transformation:

y: is the value on level 0 of the studied factor
Z: is the step.
The reaction of the explained factor is adjusted by a quadratic model of the type:
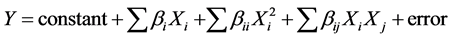
where, bi represent the linear coefficients of the explanatory factors, the bii quadratic effects and the bij the interactions of order 2 of the considered factors.
The derivatives compared to 0 of this equation provide the coded co-ordinates of the stable point. The reactions surface lines, considering the explicative factors two by two and the reaction may be very useful to visualize the factors influence and to determine the optimal conditions.
The statistical processing of the resulting data, the surfaces line of the reactions and that of the graphs have been carried out using the software STATISTICA 5.
3. Results and Discussion
The statistical processing of the centred composite design used in our study leads to the results indicated in Table 3. The Student T test is used as a criterion to evaluate the significance of the regression coefficients of the linear quadratic effects and that of the interaction of the associated quadratic model [11] .
The correlation and determination coefficients are shown in Table 3. The correlation coefficients high values R = 0.969, on one hand, and the determination coefficients R2 (0.938) (R2 is a global measure for the model quality), on the other hand, show that the selected model is representative of the production of α-amylase [13] .
The 0.938 value of R2 means that 94% of the α-amylase production variation may be explained by the five factors.
Moreover, Table 4 of the variance analysis (ANOVA) provides Fisher’s test of which the value (Fobs) is 19.754 for the α-amylase production, and is, thus, higher than the value found on Fisher’s table at the threshold α = 0.05 (F20, 26  1.82). The suggested model is very plausible.
1.82). The suggested model is very plausible.
3.1. The Evaluation of the X 0 Stationary Point
The extremums coded co-ordinates (stationary point coordinates) and the actual values are reported on Table 5. By substituting such values in the model equation, the a-amylase production rate at this stationary point is, then, deduced.
The reactions surfaces analysis shows that factors (starch; yeast extract), (starch; CaCl2), (starch; pH) and (yeast extract; pH) are most influential to increase the reaction.
It seems that factors (starch; salts), (yeast extract; CaCl2), (CaCl2; salts), (CaCl2; pH), (yeast extract; salts), (salts; pH) are not very positively influential (Figure 1). Hence, it seems to us imperative to break up the reaction Y in its canonical form to easily determine the stationary point’s nature.
To improve interpretation, the reaction equation is reduced to its canonical form

The WI’s represent the canonical components and the canonical coefficients revealing in this way that the obtained stationary point is, in fact, a “saddle” point.
The use of the “ridge analysis” method has enabled us to determine the optimal reactions (Figure 2) according to the R ray for various spheres centered in (0, 0), the central point of our experimental device.
Figure 3, representing the x1∙∙∙x5 curves line according to R, makes it possible to determine “the maximum absolute ridge”. Thus, at the periphery of our experimental area, the optimal values of the XI coded factors are: 0.206, 0.86, 1.12, 1.48 and 1.19, which correspond to the real optimal values (Table 6). The optimal value of the reaction at this point is equal to 1267.5 IU.
Table 3. Coefficient of regression of the equations representing the production of α-amylase.
Variable: α-amylase activity, Number of test: 47; Correlation Coefficient R = 0.969, Determination Coefficient of R2 = 0.938, Squared error of estimate = 74.392.
Table 4. Analysis of variance of the equations representing the production of a-amylase by Aspergillus niger ATCC 16404.
Table 5. a-amylase coordinates and production rate at the X0 stationary point.
Figure1. Response surface plot for the production of α-amylase by Aspergillus niger ATCC16406. (a) Effect of yeast extract and Salts, (b) Effect of starch and salts, (c) Effect of CaCl2 and pH, (d) Effect of yeast extract and CaCl2, (e) Effect of CaCl2 and salts, (f) Effect of salts and pH.
Figure 2. Optimal reactions determined by ridge analysis.
Figure 3. Plot of x1, ∙∙∙, x5 as a function of R for absolute maximum ridge.
Table 6. Optimal solutions of the coded co-ordinates and the corresponding actual values.
This study has made it possible to define the optimal value of the pH (5.68) for the production of a-amylase of A. niger. This value is close to 5.5 - 6, which is brought by the bibliography for a-amylase of A. niger and A. oryzae [17] [18] .
The starch optimal value is 8.97 g/l, which corroborates the value found by Spencer-Martin [19] for the production of yeast Lipomyces kononenkoaeau a-amylase. However, other studies advocate different values: 4 g/l for Schwanniomyces castelii a-amylase [20] , 10 g/l for B amyloliquefacians a-amylase [21] and Pseudomonas sp a-amylase IMD. 355 [22] ; 20 g/l for a-amylase of B. thermooleovorans [23] , 50 g/l for the same Halomonas meridiana enzyme [24] . Concerning the yeast extract, we have noticed a wide range in the bibliography: 1 g/l [25] , 3 g/l [26] , 5 g/l [22] , 10 g/l [21] . The same applies to CaCl2, 0.12 g/l [25] , 1 g/l [26] . A similar observation is made for salts concentration: FeSO4 (0.1 g/l) [27] , MnSO4 (0.1 g/l) [27] or 0.4 g/l [21] , MgCl2 (0.2 g/l) [28] . These differences are explained by the diversity of the medium constitution used for each case and also by the corresponding micro-organism. Nevertheless, the concentrations dealt with in this study fits well the range indicated in the bibliography.
3.2. Model Validation
The study of the α-amylase production by Aspergillus niger ATCC16404 was performed on the optimized medium in shake Erlenmeyer flasks. The maximum production of α-amylase using a statistical model is 1345, 16 IU ± 150 IU. This is obviously in close agreement with the model prediction which is 1267.5 U IU. After optimization, the α-amylase production has doubled (Table 6).
4. Conclusions
What emerges from this study is that orange waste constitutes a suitable fermentation medium for the growth of Aspergillus niger ATCC 16404 and for the α-amylase production.
The previously selected factors optimum is determined by the central composite design of which the results are as follows: starch 8.97 g/l; yeast extract 2.68 g/l; CaCl2 1.224 g/l; FeSO4 0.1518 g/l; MnSO4 0.1518 g/l; MgCl2, 0.3036 g/l, and pH = 5.68.
The optimal reactions have allowed us to get an acid a-amylase (as an instance) of 1267.5 IU, i.e. an increase twice that in the initial activity (658.40 IU, Table 5).
Cite this paper
Djekrif-DakhmoucheScheherazed,BennamounLeila,Ait KakiAmel,LabaniKenza,NouadriTahar,Gheribi-AoulmiZoubida,MeraihiZahia, (2016) An Optimization Study of α-Amylase Production by Aspergillus niger ATCC 16404 Grown on Orange Waste Powder. Advances in Bioscience and Biotechnology,07,123-132. doi: 10.4236/abb.2016.73011
References
- 1. de Souza, P.M. and de Oliveira e Magalhães, P. (2010) Application of Microbial α-Amylase in Industry—A Review. Brazilian Journal of Microbiology, 41, 850-861.
- 2. Lee, H., Song, M.H. and Wang, S. (2003) Optimizing Bioconversion of Deproteinated Cheese Whey to Mycelia of Ganoderma lucidum. Process Biochemistry, 38, 1685-1693.
http://dx.doi.org/10.1016/S0032-9592(02)00259-5 - 3. Zhang, T., Wen, S. and Tan, T. (2007) Optimization of the Medium for Glutathione Production in Saccharomyces cerevisiae. Process Biochemistry, 42, 454-458.
http://dx.doi.org/10.1016/j.procbio.2006.09.003 - 4. Djekrif-Dakhmouche, S., Gheribi-Aoulmi, Z., Meraihi, Z. and Bennamoun, L. (2006) Application of a Statistical Design to the Optimization of Culture Medium for α-Amylase Production by Aspergillus niger ATCC 16404 Grown on Orange Waste Powder. Journal of Food and Engineering, 73, 190-197.
http://dx.doi.org/10.1016/j.jfoodeng.2005.01.021 - 5. Plackett, R.L. and Burman, J.P. (1946) The Design of Optimum Multifactorial Experiment. Biometrica, 33, 305-325.
http://dx.doi.org/10.1093/biomet/33.4.305 - 6. Box, G.E.P. and Wilson, K.B. (1951) On the Experimental Attainment of Optimum Condition. Journal of the Royale Statistical Society, XIII, 1-49.
- 7. Botton, B., Breton, A., Fevra, M., Gauthier, S., Guy, P., Larpent, J.P., Reymond, P., Sanglier, J.J., Vayssier, Y. and Veau, P. (1990) Moisissures utiles et nuisibles. Importance industrielle. Masson, Paris, 41-220.
- 8. Gregory, D.F., Rambouts, P. and Buxton, F.P. (1993) Cloning and Characterization of PEPC, a Gene Encoding a Serine Protease from Aspergillus niger. Gene, 25, 57-64.
- 9. Sharma, S., Sharma, J. and Mandhan, R.P. (2014) Lucrative Pectinase Production by Novel Strain Pseudozyma sp. SPJ with Statistical Optimization Techniques Using Agro-Industrial Residues. Frontiers in Biology, 9, 317-323.
http://dx.doi.org/10.1007/s11515-014-1316-0 - 10. Ye, B.Y., Xue, T., Ye, S.C., Xu, S.Y., Li, W.Y., Lu, J.H., Wei, F., He, W.J. and Chen, Y.Q. (2013) Optimization of Fermentation Medium for Xylanase-Producing Strain Xw2. Frontiers in Biology, 8, 611-617.
http://dx.doi.org/10.1007/s11515-013-0282-2 - 11. Buzzini, P. (2000) An Optimization Study of Carotenoid Production by Rhodotorula glutinis DBVPG 3853 from Substrates Containing Concentrated Rectified Grape Must as the Sole Carbohydrate Source. Journal of Industrial Microbiology and Biotechnology, 24, 41-45.
http://dx.doi.org/10.1038/sj.jim.2900765 - 12. Viswanathan, P. and Surlikar, N.R. (2001) Production of Alpha-Amylase with Aspergillus flavus on Amaranthus Grains by Solid-State Fermentation. Journal of Basic Microbiology, 41, 57-64.
http://dx.doi.org/10.1002/1521-4028(200103)41:1<57::AID-JOBM57>3.0.CO;2-S - 13. Wu, F.-C., Chang, C.-W. and Shih, I.-L. (2013) Optimization of the Production and Characterization of Milk Clotting Enzymes by Bacillus subtilis Natto. SpringerPlus, 2, 33.
http://dx.doi.org/10.1186/2193-1801-2-33 - 14. Solis-Pereira, S., Ernesto, F.T., Gustavo, V.G. and Mariano, G. (1993) Effects of Different Carbon Sources on the Synthesis of Pectinase by Aspergillus niger in Submerged and Solid State Fermentations. Applied Microbiology and Biotechnology, 39, 36-41.
http://dx.doi.org/10.1007/BF00166845 - 15. Bernfeld, P. (1955) Amylase α and β. Methods in Enzymology, 1, 149-158.
http://dx.doi.org/10.1016/0076-6879(55)01021-5 - 16. Larpent-Gourgand, M. and Sanglier, J.J. (1992) Biotechnologies. Principes et méthodes. Biosciences et techniques. Doin éditeurs, Paris, 72-323.
- 17. Murado, M.A., Gonzalez, M.P., Torrado, A. and Pastrana, L.M. (1997) Amylase Production by Solid State Culture of Aspergillus oryzae on Polyurethane Foams. Some Mechanistic Approaches from an Empirical Model. Process Biochemistry, 32, 35-42.
http://dx.doi.org/10.1016/S0032-9592(96)00044-1 - 18. Khan, J.A. and Yadav, S.K. (2011) Production of Alpha Amylases by Aspergillus niger Using Cheaper Substrates Employing Solid State Fermentation. International Journal of Plant, Animal and Environmental Sciences, 1, 100-108.
- 19. Spencer, M. and Van Uden, N. (1979) Extracellular Amylolytic System of the Yeast Lipomyces kononenkoae. European Journal of Applied Microbiology and Biotechnology, 6, 241-250.
http://dx.doi.org/10.1007/BF00508096 - 20. Oteng-Gyang, K., Mouli, G. and Galzy, P. (1980) Effect of Medium Composition on Excretion and Biosynthesis of the Amylases of Schwanniomyces castelii. European Journal of Applied Microbiology and Biotechnology, 9, 129-132.
http://dx.doi.org/10.1007/BF00503508 - 21. Mc Tigue, M.A., Kelly, C.T., Fogarty, W.M. and Doyle, E.M. (1994) Production Studies on the Alkaline Amylases of Three Alkalophilic Bacillus spp. Biotechnology Letters, 16, 569-574.
http://dx.doi.org/10.1007/BF00128602 - 22. Fogarty, W.M., Bourke, A.C., Kelly, C.T. and Doyle, E.M. (1994) A Constituve Maltotetraose—Producing Amylase from Pseudomonas sp IMD.353. Applied Microbiology and Biotechnology, 42, 198-203.
- 23. Malhotra, R., Noorwez, S.M. and Satyanarayana, T. (2000) Production and Partial Characterization of Thermostable and Calcium-Independent Alpha-Amylase of an Extreme Thermophyle Bacillus thermooleovorans NP54. Letters in Applied Microbiology, 31, 378-384.
http://dx.doi.org/10.1046/j.1472-765x.2000.00830.x - 24. Coronado, M., Vergas, C., Hofemeister, J., Ventosa, A. and Nieto, J.J. (2000) Production and Biochemical Characterization of an Alpha-Amylase from the Moderate Halophile Halomonas meridiana. FEMS Microbiology Letters, 183, 67-71.
- 25. Groom, C.A., Daugulis, A.J. and Bradley, W.N. (1988) Continious Alpha-Amylase Production Using Bacillus amyloliquefaciens Adsorbed on an Ion Exchange Resin. Applied Microbiology and Biotechnology, 28, 8-13.
http://dx.doi.org/10.1007/BF00250489 - 26. Mc Mahon, H.E.M., Kelly, C.T. and Fogarty, W.M. (1997) Effect of Growth Rate on α-Amylase Production by Streptomyces sp IMD 2679. Applied Microbiology and Biotechnology, 48, 504-509.
http://dx.doi.org/10.1007/s002530051087 - 27. Dercova, K., Augustin, J. and Krajcova, D. (1992) Cell Growth and α-Amylase Production, Characteristics of Bacillus substilis. Folia Microbiologica, 37, 17-23.
http://dx.doi.org/10.1007/BF02814574 - 28. Kelly, C.T., Collins, B., Fogarty, W.M. and Doyle, E.M. (1993) Mechanisms of Action on the α-Amylase of Micromonospora melanosporea. Applied Microbiology and Biotechnology, 39, 599-603.
http://dx.doi.org/10.1007/BF00205059
NOTES
*Corresponding author.






