Modern Economy
Vol.09 No.03(2018), Article ID:82884,7 pages
10.4236/me.2018.93025
Application of Hierarchical Model in Non-Life Insurance Actuarial Science
Guiming Miao
University of Kent, Kent, UK
Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 29, 2018; Accepted: March 5, 2018; Published: March 8, 2018
ABSTRACT
Loss data structures in non-life insurance businesses are increasingly complex, and the tendency of correlation and heterogeneity is gradually presented. Hierarchical model can breakthrough limitation that the traditional rate determination method only analyzes the loss data of the same insurance policy; meanwhile, the accuracy of complex structure data prediction is improved. This paper, using a hierarchical generalized linear model, studies the non-life rate determination of multi-year loss data and takes auto insurance data for empirical analysis. The research results show that GLMM’s fitting degree is greatly improved compared with GLM, considering the random effects. It can more effectively reflect different risk individual differences and also reveal the heterogeneity and correlation of risk individual loss during multiple insurance periods.
Keywords:
Hierarchical Model, Actuaries, Non-Life Insurance, Random Effect

1. Introduction
In the 1990s, as a new statistical analysis technique, layered model is widely used in the world. The hierarchical model determines the model parameters to set its own probability submodel, extending the standard linear model (Linear Models, LM), generalized linear models (Generalized Linear Moeels, GLM) and the nonlinear model (Non-linear Models). In the process of using the above model for statistical analysis, data must be observed from independent (random) variables in general. At the same time in some actuarial and statistical problems [1] , vertical data, spatial clustering data, and general clustering data are also needed. These data do not have the independence assumption, but have a certain level of hierarchy. According to the hierarchical structure difference of data, the data can be divided into different levels. Then the concept of hierarchical model is introduced.
Two of the core topics in non-life actuarial science are pricing and reserve assessment. For a property insurance company, its competitiveness and the company’s profitability are closely related to the rationality of pricing. In the 1990s, British actuaries introduced GLM in non-life insurance pricing. Since then, GLM has been widely used in non-life insurance pricing practices in many countries and made great achievements.
However, GLM still has inadequacies. For example, when some classification explanatory variables have less data at some level, the standard error of these horizontal parameter assessments will be enhanced. Moreover, the direct application of GLM also faces too many estimated parameters. In order to solve these problems, the actuary incorporates reliability theory into the GLM framework, and some statistical models and methods appeared [2] , including Hierarchical Generalized Linear Models (HGLM), Generalized Linear Mixed Models (GLMM) and so on.
The liability of the largest share of the balance sheet of the property insurance company is the claim reserve. The accurate assessment of the claim reserve is conducive to the correct judgment of the operating performance and solvency of the property insurance company. Therefore, the reasonable assessment of this liability is of great significance to the development of the property insurance company.
2. The Basic Theoretical Model of Non-Life Insurance Rate in the Framework of Layered Model
2.1. A Theoretical Introduction of the Model Based on GLMM Rate
Make the following assumptions: There are m risk individuals, using random variables to represent the number of claims or amounts incurred by the i-th risk individual in the year of the i-th policy. Use the GLMM framework to set the following three parts:
1) The setting of the random part: Under the premise of specifying the random effect , the observed variables of are independent of each other, and it is also consistent with the distribution of the exponential population (EDF). Then the probability density function can be recorded as:
(1)
is a natural parameter. and signify a known function. Scale parameter is .
2) System section Settings: The relationship between the mean of the response variable and the explanatory variable can be represented by a linear predictor. Let’s say the prediction is . Its design matrix of fixed effect is expressed as X. The design matrix of random effects is represented by Z. The estimated parameters of model fixed benefit are .
3) Setting of the join function: . This function is a monotone differentiable function. There’s a logarithmic bond, identity connecting and logit connections. Given , then can be used to represent mean conditions.
2.2. Theoretical Framework Based on HGLM Rate Setting Model
The four basic assumptions in this structure:
1) Independence: That is, under the conditions of the risk parameters, the following assumption is made. The claims (or amounts) of the number (or amounts) of individual risk individuals is non-interference.
2) Distribution: is in consistent with the exponential distribution. Then the probability density function is:
(2)
One of the known weights (constants) is , the natural and discrete parameters are respectively and , the given function is and .
3) Structuredness: There is a kind of change relation between and , and this relation can be connected by the join function. That is , or . The new variable produced by u through the strict monotonic function is the cumulative effect v, which could be written as = .
4) Distribution of risk parameters: In HGLM, is a random risk parameter, which can depict heterogeneity risk characteristics of different risk individual i. This assumption is subject to the distribution of EDF and can be written as:
(3)
Above, the super parameter is , and discrete parameter is and .
2.3. Compare GLM, GLMM and HGLM
We can see through the above that the connections and differences between models can be summarized as follows:
1) Structure of the model: GLM can get GLMM by extension and expansion. HGLM is a relatively general framework. The linear prediction of GLM introduces a stochastic effect based on the assumption of normal distribution [3] [4] , and gets GLMM. After removing the random effect, it can be reduced to GLM. However, HGLM assumes that the effect of stacking benefit is beyond the normal distribution. It can also show the inverse Gaussian distribution and Beta distribution, which can analyze non-life loss data accurately, especially is true in the non-life loss data for longitudinal data.
2) Theoretical Calculation: Compared to the other two models, GLM is relatively simple. In general, GLM use the construction of maximum natural functions to calculate the estimator parameters of MLE. The general calculation method is Fisher algorithm, Newton Raphson iterative algorithm and so on.
3. Empirical Analysis―Number of Claims Based on Auto Insurance Business
The data of this paper is from Sun Weiwei’s paper [5] , and has been sorted out in order to be compared easily. There are 40,000 policies (insured) in the data. The observation data of the number of claims for three consecutive policies years is used as the longitudinal data. And there are 120,000 records. The original sample data set variables respectively are: numclaims represent the number of claims; policyID represents the code for the policy; agecat represents the driver’s age classification variable: 1, 2, 4, 5, 6, 10 (Age is in an increasing order); valuecat represents the vehicle value classification variables: 2, 3, 4, 5, 6, 9; period represents the year of observation policy: 1, 2, 3.
3.1. Construct Model: The Fixed Effects Are Agecat and Valuecat. The Model Is Built According to the Distribution Characteristics of the Number of Claims
1) Model 1
Proposed a hypothesis: The number of claims is consistent with the Poisson distribution of the parameter . Ignoring the correlation between the heterogeneity of the number of claims made by the random benefit and the claim for three years, the model can be built as:
(4)
2) Model 2
It’s in the same form as model 1. But at the same time, the zero value problem of the number of claims is taken into account. Assume the number of claims is consistent with the zero expansion Poisson distribution (ZIP), then the model can be built as:
(5)
3) Model 3
Based on model 1, the problems that are ignored have been taken into account. Make assumptions under the GLMM framework: Random effects do not interfere with each other, and it is consistent with the normal distribution [6] [7] . The variance parameter in normal distribution is . Then the model can be built as:
(6)
4) Model 4
Make a further hypothesis: In the HGLM framework, the random effects of individual claim differences can be reflected. It also corresponds to the gamma distribution. Its obey parameters are and . Then the model can be built as:
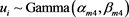 (7)
(7)
3.2. Parameter Estimation
In this study, the program package gamlss, lme44, glmmML, and hglm in R software is adopted. And model 1 uses maximum likelihood estimation. The calculation method is Fisher’s score iteration. The discrete parameter in the calculation is 1. In model 2, the estimation parameter method is the RS algorithm under the GAMLSS framework and calculates 12 iterations. Model 3 adopts Gauss-Hermitian integral method [8] [9] , and calculate the fixed effect parameter estimation. Model 4 adopts the method of the maximum h likelihood function. The estimated results are shown in Table 1.
3.3. Result Analysis
From the above empirical analysis, the parameters under different models differ greatly. Fundamentally, if random effects of three consecutive policy years are excluded, the GLM model should be built. The statistical quantity of AIC is
Table 1. Parameter estimation results of the model 1 - 3.
Note: Data is from calculation of R software. *, ** and *** represent a significant level of confidence of 5%, 1%, 0.1%.
169,100. But the AIC statistic under the ZIP distribution is 14,575.0. And the AIC statistic under GLMM integral method is 81,169. Therefore, the AIC statistic of this method is the lowest, which improved the goodness of fit of the model. If the AIC statistic is used as the standard to measure the model, then the GLMM model will be greatly improved.
In the use of R software, model 4 cannot converge after 10 iterations. Thus it is eliminated. The valuecat and agecat rate factors in the sample data are multi-level classification variables. Not including the base level, each observation unit must estimate 10 fixed effects in a given period of time [10] . At this point, the dimension of the estimated parameter will increase with the increase of sample size n. When solving the problem, the estimated parameters of exponential growth and a series of problems will generate.
4. Conclusion
Through this study we can see that the layered framework has a great advantage in the processing of non-life insurance rate. It can deal with the relevant data of the policy year in different risk individuals in the claims data of non-life insurance companies, analyze the relationship between individual loss data in the same risk, and be applied in practice to help actuaries handle complex insurance data. At the same time HGLM can process the data and longitudinal data of the layered structure, and provide enlightenment to actuaries and related personnel on non-life insurance data structure so that they can make scientific analysis and reasonable interpretation of the results. By analyzing a hierarchical generalized linear model, this paper studies the non-life rate determination of multi-year loss data and takes auto insurance data for empirical analysis.
Cite this paper
Miao, G.M. (2018) Application of Hierarchical Model in Non-Life Insurance Actuarial Science. Modern Economy, 9, 393-399. https://doi.org/10.4236/me.2018.93025
References
- 1. Duan, B.G. and Zhang, L.Z. (2013) The Research Evaluation of Layered Model in Non-Life Insurance Actuarial Science Application. Statistical Research, 30, 98-105.
- 2. Górecki, J., Hofert, M. and Holeňa, M. (2016) An Approach to Structure Determination and Estimation of Hierarchical Archimedean Copulas and Its Application to Bayesian Classification. Journal of Intelligent Information Systems, 46, 21-59. https://doi.org/10.1007/s10844-014-0350-3
- 3. Wang, J. (2015) Discussion on the Teaching Reform of “Non-Life Insurance Actuarial Science” Based on “Big Project View”—Take Jishou University for Example. The Weekly.
- 4. Sun, W.W. and Zhang, L.Z. (2016) The Calculation Example Analysis Based on HLM2 and Its Thinking in Chinese Non-Life Insurance Actuarial Calculation. Statistics and Decision, No. 22, 4-8.
- 5. Sun, W.W., Zhang, L.Z. and Hu, X. (2017) The Studies on the Actuarial Model of Non-Life Insurance Rate Based on the Generalized Linear Model. The Statistics and Information Forum, 32, 48-54.
- 6. Zheng, X.L. and Meng, S.W. (2016) A Bayesian Hierarchical Model with Spatial Effect and Its Application in Prediction of Claim Frequency. Mathematics in Practice & Theory.
- 7. Duan, B.G. (2014) The Application of Bayesian Nonlinear Hierarchical Model in the Assessment of Multiple Claims Reserve. Quantitative and Technical Economics, No. 3, 148-160.
- 8. Meng, S.W. and Qiu, Z.Z. (2016) Hybrid Effect Model and Its Application in Non-Life Insurance Rate Determination. Mathematical Statistics and Management, 35, 154-161.
- 9. Jiang, W. Xia, X.L. and Wu, H. (2015) Application Comparison of Distribution Fitting Model in the Actuarial Calculation of Social Health Insurance. Public Health and Preventive Medicine, 26, 34-38.
- 10. Li, H. and Duan, P.J. (2016) The Promotion of the Relationship between the Instantaneous Compensation of Death and the Present Value Model of Death Insurance Actuarial Calculation Based on the Age of the Score Age. Journal of Jiamusi University, 34, 144-146.


