Received 7 March 2015; accepted 30 March 2015; published 3 April 2015

ABSTRACT

This study applies a constructive research approach to develop a novel profit potential calculation method framework suitable for web manufacturing processes. The theoretical framework is the profit function, which is further developed to form the web profit model. The profit model is optimized with respect to technology and process related input parameters to form the profit potentials. Then, new concepts: profit potentials on different optimization levels of increasing complexity are presented. Application of the novel method is demonstrated with a short case example. The findings show that the created profit potential framework can be applied to web process profit potential analyses. In addition, applying this framework profit potentials for other processes, pro- ducts, and services can be defined in the future.

Keywords:

Profit, Potential, Calculation, Method, Web, Manufacturing

1. Introduction

The classical competitive firm is continuously searching for new ways to maximize profit. To describe profit potential, the discussion presented by Quest [1] [2] provides a good starting point. Quest advises that a different way of thinking is needed to unlock hidden potential: unrecorded and unnoticed losses.

Losses are important sources of potential. However, in addition to identified losses, there are also new possibilities to improve the current profit situation of a web production process. Possibilities consist of new technology, raw materials, products, and business ideas.

The effect of one single variable, for example a change in one production machine setting on the profit would be an interesting subject to study. However, it is even a more interesting research question to try to find out how to calculate the maximum profit achieved when many process and technology parameters are changed simultaneously and what would be the profit potential compared to the existing situation after the changes. To be able to carry out the research needed to solve this research question, first it is needed to define the profit potential. Then it should be defined which theories and methods are available to find out what type of research is needed to fill this gap between the existing knowledge and new knowledge.

In this study, profit potential is defined as follows: A profit potential is a gap between the profit produced applying the current technology settings, and the new technology settings, calculated over a certain time period.

This study can be condensed to the following research question:

RQ: How to calculate the web process profit potential when there is new process technology included in the calculation?

2. Literature Study

Several studies have been carried out to establish different factors limiting profit of a production unit. Some of these studies are considering directly the profit, but most are applying indirect measures.

The distance function representation of a production technology is introduced by Shephard [3] . Later on, Shephard’s theories are summarized and completed by Färe and Primont [4] , and discussed under profit maximizing behaviour by Coelli [5] .

Coelli et al. [6] apply a distance function based technique and presents the effect of unused capacity on the profit gap between the observed and the maximum profit when analyzing international airline companies. As a result, they present a new ray economic capacity measure, which involves short-run profit maximization, with the output mix held constant.

Pesonen [7] demonstrates a design to profit procedure. The essential elements of this procedure are product business case calculations and profit consciousness of employees.

The theory of constraints (TOC) is introduced by Goldratt and Cox [8] . They claim that every real system such as a profit-making enterprise must have at least one constraint that prevents it from making more profits.

Efficiency calculation methods are widely used in the paper industry. Kleef et al. [9] presents a financial model, which shows that for every 1% decrease in downtime, profits increase by 4.7%… 8.2%. In addition, they present a continuous process developed in downtime reduction. The main steps in this process are registration of failures, verification of downtime data, automatic analysis to create trend and prognosis graphs, and a structured approach to corrective action.

There are also other indirect measures and methods developed. Productivity (Boyd and McClelland [10] , Hannula [11] ), reliability (Virtanen [12] ), risk analysis (Henley and Kumamoto [13] , McCormick [14] ), cost function models (Fogelholm [15] , Fogelholm and Hämäläinen [16] ), energy saving potential analyses (Treppe, Dixit, and Kuitunen [17] ), and multi-objective optimization for process design (Linnala and Hämäläinen [18] ) are examples of such methods and studies. In addition, life cycle cost (LCC) and life cycle profit (LCP) analyses are widely applied to investment profitability calculations (Peltonen et al. [19] and Koskinen [20] ).

The existing methods and measures provide information, which can be successfully applied to web process improvements. Despite the fact, the existing methods are inadequate: they do not present how to calculate the web process profit potential when there is new process technology included in the calculation.

3. Research Process

To be able to answer to the previous mentioned research question, a constructive research approach, which is described in Kasanen et al. [21] , Lukka [22] , Labro and Tuomela [23] , is applied. In this work research steps are carried out as described in Figure 1.

4. Method Development

The profit function (see for example Fuss and McFadden [24] , Färe and Primont [4] , and Coelli [5] ) is the basis for the novel method development. Färe and Primont [4] present the following definition of the maximum profit function:

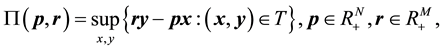(1)

where

p = input price vector,

r = output price vector,

x = input vectors,

y = output vectors,

and the technology is denoted by T. According to this definition, 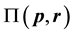may become +¥.

To define the simulation model for the web process profit the notations of Madetoja and Mäkelä [25] are applied. The submodels are denoted by 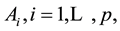and submodel number i takes input parameters x and outputs of previous submodels to produce new process quantity. An example of a submodel is the calculation of the annual saleable production, which uses momentary production, annual production time and total efficiency to obtain the annual production.

An abstract mathematical formulation for the ith step of the process line model can be given as follows: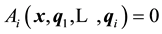. After the final step all process quantities are available and the annual profit for year t, denoted by П_t, can be calculated. It is defined as:

(2)

where

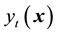= Web process saleable production (mass unit),

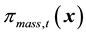= Profit per mass unit of product (currency unit/mass unit),

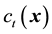= Cost components (currency unit),

which are all intermediate process quantities q_i.

To calculate the profit over Y years, the same chain of submodels is repeated for each year separately to obtain the values Π_t. Time value of future cash flows is given by the net present value function:

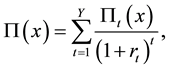(3)

where r_t is the interest rate at year t. Then, the problem of finding the optimal input parameters to maximize the profit of the current web process technology T can be formulated as the optimization problem:

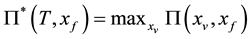(4)

subject to

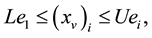
where (x_v)_i is value of the ith variable parameter and input value limiting matrices L and U are diagonal with lower and upper bound vectors l_v and u_v forming the diagonal entries. The ith entry of vector e_i is one while all others are zero. Since some of the variable input parameters x_v may be constant during the period of Y years, the maximization of Π cannot be performed separately for each year t. An example of x_v that is constant over inspection period is new technology component length. It can be optimized, but has the same value over the inspection period. Production speed, on the other hand, is marked with x_v,t, where t denotes that this variable can be optimized separately each year.

The maximization of the profit Π is divided on three levels of increasing complexity and different profit potential. The profit in the current situation (Base) is denoted by Π_c and the profit potential is the difference between the maximum profit in the new optimized situation and the current situation:

(5)

The subscript k above refers to the optimization level.

On the lowest level (k = 1) only the driving parameters without any modifications of the technology are optimized. This optimization problem is defined above with the function Π^*, where the variable parameters are controlled within lower and upper bounds. The profit potential is of the form:

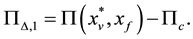(6)

The second optimization level (Fixed Invest) comprises an investment with fixed cost C. In this theoretical framework, this means a change in the value of some fixed parameter. The investment might require shutting down the current web process production and making some modifications. In order to evaluate the profit potential of the investment, it is needed to take into account the cost of the production shut down, denoted by S, and the residual value of the investment after the period of Y years, denoted by R. If r_t > 0, the value of R is discounted. These values depend on some fixed parameter(s) x_f and the profit in the current situation. Then, the optimization problem is the same as above except the term R-S-C is added to the profit. The profit potential is of the form:

(7)

On the third optimization level (Opti Invest), also the investment is optimized by changing the status of investment and technology related parameters from fixed to variable x_f −> x_v. Then the optimization problem involves parameters which influence also the technology investment costs, performance, and operating costs, and the profit potential has the form:

(8)

It is emphasized that on the third level the set of variable parameters is larger than on the previous two levels.

Case Example

Let there be a production line where the current profit П_c is calculated as follows:

(9)

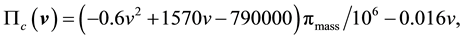
where

v = Production speed (m/min).

For the investment the profit is calculated as:

(10)

where

l = New technology component length (m),

π_mass = Profit per euros/ton (EUR/t) = 150 EUR/t (constant in this case example).

For the fixed investment, l = 0 and not changed during the optimization. On the first and second level the profit is optimized only with respect to v. On the third level l is changed during the optimization also and in addition to an effect on the production level, it has also an effect on the investment cost (C = C − l on the third level). The length l is limited in this case example and has a maximum value of 30 m. r_t has a value of 0 in this example. Table 1 presents the other input parameters:

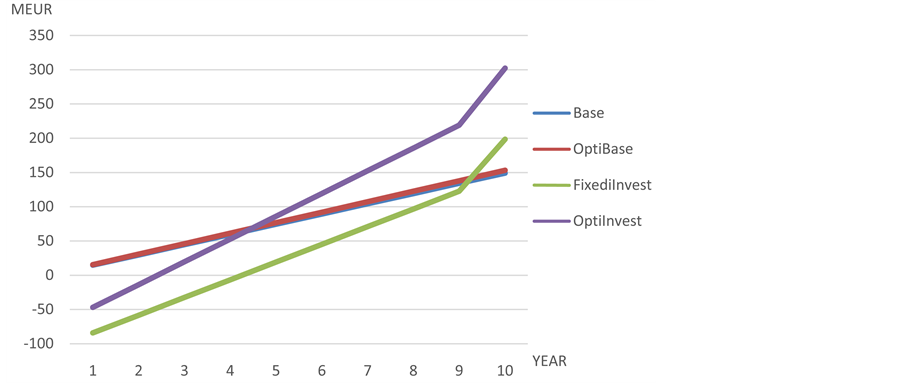
Calculation over a period of 10 years produces the following profit potentials (Table 2) and cumulative cash flows (Figure 2):

5. Discussion

5.1. Method Development

Applying a constructive research method, the research process was carried step by step starting from the profit function and ending to the profit potential definitions and a short case example. Constructive research method offers a straightforward procedure to carry out the research process. The advantage of this research method is to concentrate the focus on solving the problem. However, by focusing on one research path might lead to a minor ignorance of the other possible research paths which could bring other solutions to the problem.

The profit function is a general function and can be applied to different types of processes, products, or services. When the profit function definition is applied to form the web profit model including new process technology, the essential parameters and equations limiting the web production process are needed to be defined. This requires a deep understanding of the process. One should limit the amount of parameters to create a model that is fast to form and calculate. On the other hand, limiting the amount of parameters may lead to a model, where some sources of new potentials are not identified.

Calculating the different profit potentials on different optimization levels brings the different profit improvement potential options visible. Therefore a decision maker can choose between the improvement options. Depending on the company’s improvement targets and the ability of the company to invest in new technology it is possible to improve the existing production or to carry out a bigger profit improvement step by investing in new technology.

5.2. Results

In this study, a simple case example presents how production speed and new technology component length have an effect on production amount according to Equations (9) and (10). In addition, new technology length component has an effect on investment cost. Therefore both the production level achieved and the investment cost will change according to the new technology component length. As a result, assuming that the additional production can be sold to the market, an investment in the new optimized technology (Opti Invest) leads to the highest profit potential and cumulative cash flows over the calculation period (see Figure 2). Here, it is important to note that the new technology process investment is optimized to reach the highest profit potential. The new technology optimization leads to reduced investment costs, which is a significant improvement also.

Since the amount of parameters in this example is limited, there might be some other profit potentials found by adding more parameters and equations describing the process. This example presents also that the current process can be already tuned close to the maximum profit that can be achieved applying the current technology. The new technology can, especially when optimized, bring out significant possibilities to improve the profit.

5.3. Method Improvement Proposals

To improve the applicability of the method to web process profit improvement analyses, there should be more parameters and equations describing the process, prices, and investments modelled. In this way, the different subprocesses from raw materials to the end product can be included into calculation. This would lead to an improved understanding of where the most important profit potentials are.

To improve the accuracy and reliability of the method, there could be sensitivity and uncertainty analyses included in the calculation process. Then, sensitivity of profit potential to changes in parameters and inaccuracy of the parameter input values could be defined.

5.4. Application of the Method Framework to Other Processes, Products, and Services

This study presents a new method: a new framework for calculating web process profit potentials. In addition to the web process solution, the profit potential framework developed in this study can be applied to other types of processes, products, and services. Generally, a profit model and profit potentials of a production process, product, or service can be formed applying the same procedure as described in Chapter 4: Method development and following the case example. The steps are:

1) Form the profit model where the parameters affecting the profit, prices, costs, investments, production amount or rate, quality etc. are described by submodels.

2) Define and calculate the profit potentials on levels 1 - 3.

3) Describe the results by monetary profit potential values and by the Figures presenting the cash flows.

The most important phase is to produce submodels where the connections between the process, product, or service parameters and the profit and investment costs are described. Typically parameters can have connections to several cost components, production level and also to prices. Therefore depending on the model system simple or rather complex optimization problems aiming to one target, maximum profit and highest profit potential, can be formed and solved.

6. Conclusions

The target of this study was to develop a framework for web process profit potential calculation. Instead of finding out the improvement of indirect factors affecting the profit or applying multi-objective optimization of many targets, this study concentrated on finding the new further reaching boundaries to improve the profit by finding profit potentials directly related to changeable production process parameters.

The areas for further research can include the framework testing applying more web or other process, product, or service parameters, models, and data. In addition, applying sensitivity and uncertainty analyses would improve the accuracy of the method.

A common problem for decision makers is to find out where to put the efforts and which changes would lead to highest profit improvements. This study provides one solution to the problem: The new profit potential analysis is a tool for better and more effective decisions.

References