Modern Economy
Vol.06 No.02(2015), Article ID:53762,11 pages
10.4236/me.2015.62011
An Analysis of Regional Income Variation among the Five Regions of Oklahoma
Orley M. Amos Jr.1, Tim C. Ireland2
1Department of Economics and Legal Studies, Oklahoma State University, Stillwater, OK, USA
2Department of Management Science and Information Systems, Oklahoma State University, Stillwater, OK, USA
Email: orley.amos@okstate.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 January 2015; accepted 25 January 2015; published 3 February 2015
ABSTRACT
This paper investigates recent trends of per capita personal income in the state of Oklahoma to ascertain what if any long-run trends are exhibited. Standard theoretical analysis suggests that per capita incomes are expected to converge, especially across regions. However, recent research indicates that the national trend is one of the regional income divergences. The question posed by this paper is whether or not the per capita income in Oklahoma supports evidence of divergence. The data for 1969 to 2012 obtained from Department of Commerce, Bureau of Economic Analysis (BEA) are analyzed. These data are used to regionalize the state into five distinct county-based areas. Results suggest that Oklahoma exhibits a transitional pattern from convergence to divergence during the period of study. The three objectives of this study are: 1) a test of the growth pole cycle theory; 2) an extension of previous analysis of Oklahoma regional income variation; and 3) a preliminary test of the impact of the 2008 recession on regional income variation. After identification and analysis of the five substate regions, an overview of the growth pole cycle theory explaining the hypothesized pattern is provided, followed by an exposition of the analytical methodology. The analytical results are twofold, first, a baseline analysis regressing variation on per capita income and second, the inclusion of the unemployment rate.
Keywords:
Regional Income Inequality, Kuznet’s Inverted-U, Income Convergence

1. Introduction
This study investigates the variation of regional income within each of five multi-county regions that divide up the state of Oklahoma for the period 1969 to 2012. The objectives of this study are three-fold. First, it is as a test of the hypothesized pattern of long-term development implied by the growth pole cycle theory in Amos [1] [2] that regional income variation diverges after a period of convergence. Second, it is to build upon and enhance the substate analysis of regional income variation undertaken for the state of Oklahoma using data from 1969 to 2008 in Amos and Ireland [3] . And third, it is as a preliminary analysis of the potential impact of the 2008 housing and financial market disruption on long-term regional income variation.
The growth pole cycle theory and the implication for regional income variation have been subject to previous test, most recently in Amos [4] . Evidence suggests that regional income variation began diverging in the United State in the mid-1970s. However, individual states made the transition from convergence to divergence at different times, some early in the 1970s and other in later years, an expected result given that states progress at different rates. Evidence indicates that Oklahoma is among the lesser developed of the 50 states and thus its documented divergence within the latter portion of the time period of analysis provides not only a test of the hypothesis but also the contention that states develop differentially.
Previous analysis of regional income variation has been relegated to either the variation of regional income among states within the entire nation (Williamson [5] , Amos [6] ) or among counties within each state (Amos [4] [6] ). This study examines regional income variation within counties that comprise sub-regions in a state, in this case, Oklahoma. This adds a new level of analysis to the study of regional income variation by recognizing the hierarchical internal structure of a state that is likely to exhibit a regional income variation pattern apart from the state pattern.
The housing market collapse in 2008 and resulting financial and economic problems were quantitatively as severe and sustained as anything experienced in the United States since the 1930s Great Depression. The question posed by this study is whether it also qualitatively affected the long-term development process and the observed pattern of divergence. Previous work suggests that short-run economic instability can impact the measured variation of income among counties with states (Amos [7] ).
2. The Oklahoma Study Area
Oklahoma joined the United States in 1907 and as an agrarian, resource based economy, has generally lagged behind the development of most other states. In 2012, Oklahoma per capital income was about 93% of the U.S. average. Oklahoma typically ranks in the bottom 10% of states for most measures of economic progress and development, such as education and health care. Moreover, analysis of regional income variation in Amos [4] estimated that Oklahoma reached the transition from convergence to divergence in 1990, 15 years after the estimated turning point of 1975 initially identified in Amos [6] .
Like most states, Oklahoma can be separated into different substate regions, differentiated by culture, economy, resources, and production. The counties included in the five substate regions used in this analysis are:
Central: Canadian, Cleveland, Grady, Kingfisher, Lincoln, Logan, McClain, Oklahoma, Payne, Pottawatomie, and Seminole.
Northeast: Adair, Cherokee, Craig, Creek, Delaware, Mayes, Muskogee, Nowata, Okfuskee, Okmulgee, Osage, Ottawa, Pawnee, Rogers, Tulsa, Wagoner, and Washington.
Northwest: Alfalfa, Beaver, Blaine, Cimarron, Dewey, Ellis, Garfield, Grant, Harper, Kay, Major, Noble, Texas, Woods, and Woodward.
Southeast: Atoka, Bryan, Carter, Choctaw, Coal, Garvin, Haskell, Hughes, Johnston, Latimer, LeFlore, Love, McCurtain, McIntosh, Marshall, Murray, Pittsburg, Pontotoc, Pushmataha, and Sequoyah
Southwest: Beckham, Caddo, Comanche, Cotton, Custer, Greer, Harmon, Jackson, Jefferson, Kiowa, Roger Mills, Stephens, Tillman, and Washita.
The Central Region contains Oklahoma City, the largest metropolitan area in the state and the center of government. The Northeast Region contains the second largest city, Tulsa. The other three regions―Northwest, Southeast and Southwest―have resource and agrarian based economies. In 2012, per capita income for Oklahoma was $40,620. The two metropolitan―centric Central and Northeast Region’s per capita incomes were $42,411 and $42,011, respectively. The Northwest Region was the third most prosperous in 2012, coming in at $41,195. The Southwest Region lagged behind at $37,557 and the Southeast trailed all others at $33,197. The relative ranking of these five regions is generally consistent throughout the study period, 1969-2012. It is thus anticipated that the pattern of convergence to divergence would occur first in the Central and Northeast Regions, followed closely by the Northwest and later by the Southwest. The Southeast Region is then expected to exhibit the pattern after the other four, if at all.
3. State and Regional Trends
Per capita personal income (PCI) in Oklahoma, while trending higher, has historically fallen short of that for the United States. As shown in Table 1, Oklahoma PCI has been between 80% and 95% of the U.S. PCI. Oklahoma PCI in nominal terms rose from $3329 in 1969 to a level of $40,620 in 2012. In like fashion, the U.S. PCI grew to a value of $43,735 in 2012 from a starting level of $3930 in 1969. However, Oklahoma PCI was 85% of the U.S. average in 1969, rose to 95% in 1980, fell back to 81% by 2000, then increased once again to 93% in 2012. As a major petroleum producer, Oklahoma PCI relative to the national average appears driven largely by the boom and bust of the oil market. Relative gains were achieved from 1969 to 1980, driven by surging oil prices. The bust in the oil market then led to the relative decline in Oklahoma PCI up to 2000. Higher oil prices in the past decade have also corresponded with relative gains in Oklahoma PCI.
Table 2 presents annual growth rates by decade, in both nominal and real1 PCI for Oklahoma during the study period. For the overall period, 1969-2012, nominal PCI had an annual growth rate of 6%, with real PCI growing by just over 2%. The 1969-1980 period saw the biggest gains in both measures, over 10% for nominal PCI and 3% for real PCI. Both growth measures declined in subsequent decades. While nominal PCI exhibited the second highest annual growth rates in the 1980-1990 period at 5.38%, notably the inflation-adjusted real PCI had the lowest annual growth rate at 1.16%.
Regional diversity within Oklahoma is indicated by per capita income values for each of the five regions presented in Table 3. The Central and Northeast Regions, with the two largest urban areas (Oklahoma City and
Table 1. Income indicators.
Source: Calculated from Bureau of Economic Analysis, Department of Commerce, “Local Area Personal Income: Population and Per Capita Personal Income” CA1-3.
Table 2. Decade compound annual growth rates (%).
1Inflation adjusted real per capita personal income levels were calculated using the GDP implicit price deflator (2009 base year) provided by the Bureau of Economic Analysis. Source: Calculated from Bureau of Economic Analysis, Department of Commerce, “Local Area Personal Income: Population and Per Capita Personal Income” CA1-3.
Table 3. Oklahoma per capita incomes.
Source: Calculated from Bureau of Economic Analysis, Department of Commerce, “Local Area Personal Income: Population and Per Capita Personal Income” CA1-3.
Tulsa, respectively), take turns at the top of the five regions throughout the 1969 to 2012 study period. Central PCI increased from $3651 to $42,411 and the Northeast increased from $3456 to $42,011 during this time. While the Northeast Region was slightly higher in 1990 ($17,125 versus $16,924), the Central Region was the leader during the rest of the study period. The Northwest Region closely matched these other two regions, with the exception of 2000. Northwest PCI increased from $3371 to $41,195. The two remaining regions, Southwest and Southeast, consistently came in at the bottom of the five regions. Southwest PCI increased from $3221 to $37,557 and the Southeast Region increased from $2363 to $33,197.
Diversity is also evident from annual growth rates of PCI, by decade, presented in Table 4. Mirroring the state trend, all five regions had higher annual growth rates for the 1969 to 1980 period (between 9% and 10.4%), with subsequent decades coming in at lower rates. While the Central, Northeast and Southeast Regions followed the state trend of diminishing growth rates, the Northwest and Southwest Regions both saw lower growth rates in the 1990-2000 period than the 2000-2012 period. Notably, the Central Region, with the highest PCI had the lowest overall growth for the period (5.87%), while the Southeast Region with the lowest PCI also had the highest annual growth rate (6.34%).
4. Housing Market Collapse of 2008
The most severe economic and financial decline in the U.S. economy since the Great Depression of the 1930s is commonly attributed to the collapse of the housing market in 2007. According to the Bureau of Labor Statistics, the U.S. unemployment rate increased from about 5% in the first few months of 2008 to 10% in October 2009. And according to the National Bureau of Economic Research, while the contraction itself lasted 18 months, ending in June of 2009, the recovery lagged well behind that of other recessions occurring since the 1930s. As late as August 2014, 62 months into the expansion, the U.S. unemployment rate exceeded 6%. This study examines the possibility that the severity of this contraction affected the long-term regional income variation pattern.
5. Growth Pole Cycle Theory
Economic growth and development is not a smooth, continuous process, but is characterized by temporal surges and spatial imbalances. The growth pole cycle theory discussed in Amos [1] [2] [8] provides an explanation of this process by combining the temporal aspects of long waves or long cycles originally discussed by Kondratieff [9] [10] , Schumpeter [11] and van Duijn [12] , with the spatial dimension of Perroux’s [13] growth pole analysis examined by Lasuen [14] and Hansen [15] . The growth pole cycle theory indicates that the economy traverses an approximate 50-year “polarization phase” followed by about a 50-year “spread phase”. Similar to the growth pole theory, this process involves a fundamental spatial dimension, however, with the added temporal dimension of the long cycle process.
During the 50-year polarization phase, regional incomes diverge as economic activity, productive resources, and wealth are geographically concentrated. During the 50-year spread phase, regional incomes converge as economic activity spreads outward from the concentrated pole to the periphery. Kuznets [16] noted this pattern
Table 4. Oklahoma growth rates.
Source: Calculated from Bureau of Economic Analysis, Department of Commerce, “Local Area Personal Income: Population and Per Capita Personal Income” CA1-3.
as the inverted-U of income inequality, in which increases in income inequality (divergence) are followed by decreases (convergence). Williamson [5] adapted the Kuznet’s inverted-U hypothesis to regional income variation. The working proposition for both variations of the hypothesis has been that the inverted-U is a one-time phenomenon. The growth pole cycle theory implies that the divergence-convergence pattern is an ongoing process, with convergence subsequently followed by another period of divergence, in the same way that standard, short-run business cycles exhibit repeated periods of expansion and contraction. As such, inequality related to the process of development is characterized more by a mathematical sine curve than a simple inverted-U (Amos [1] ).
The pattern of regional income inequality implied by the growth pole cycle theory is illustrated in Figure 1 (Amos [4] ), which extends the basic Kuznet’s inverted-U to an additional period of divergence. The conventional pattern of convergence is indicated for segment I, points a to b. The transition to a new period of divergence is found in segment II, points b to c. The subsequent period of divergence is then in segment III, points c to d. Presumably there is then a transition to convergence once again in segment IV, points d to e.
The temporal dimension of this theory suggests that the Great Depression of the 1930s was a transition between the diverging polarization phase and the subsequent converging spread phrase. The spread phase, and convergence, then continued until the late 1970s or early 1980s, which marked the transition to a new diverging polarization phase. Evidence suggests that regional income variation is once again diverging (Amos [4] [17] ).
A key reason for periodic periods of divergence then convergence appears to be technological innovations that create major, society-wide structural changes. Previous development-inducing innovations include silicon- chip-based computers (the latter fourth of the 1900s), internal combustion powered automobiles (the latter fourth of the 1800s), and steam engine driven manufacturing and railroads (the latter fourth of the 1700s). In each case the production and subsequence diffusion of the technological innovation stimulates economic progress, benefiting some regions more so than others, but also through a process that crosses decades.
Because some regions benefit first, other regions clearly lag behind. In many cases, lagging regions benefit only when the divergence turns the corner to convergence. Throughout the 1900s, the state of Oklahoma typically lagged behind much of the rest of the country. Moreover, some regions within the state of Oklahoma tended to lag behind, not just the country, but also the average for the state.
This study investigates not just regional income variation within the state of Oklahoma in its entirety, but also how five distinctive regions of the state (Northeast, Southeast, Northwest, Southwest, and Central), exhibit patterns of regional income variation. That is, this study analyzes the variation of per capita income among the counties within each of the five regions.
Figure 1. Hypothesize regional income variation.
6. Methodology and Data
The key to this analysis is the measure of regional income variation initially specified in Williamson [5] and later estimated in Amos [4] [17] . It is calculated as:
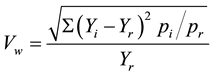
where 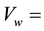 the weighted variation of regional income,
the weighted variation of regional income,  per capita personal income in county
per capita personal income in county  of region
of region  (or the state),
(or the state),  per capita personal income in region
per capita personal income in region  (or the state),
(or the state),  population in county
population in county  of region
of region 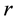 (or the state),
(or the state), 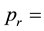 total population in the region
total population in the region 


Data used to estimate regional income variation are obtained from the Bureau of Economic Analysis. This data includes population and per capital income values for Oklahoma for each of the state’s 77 counties for the period 1969 to 2012. County data are then aggregated into population and per capital income values for each of the 5 multi-county regions to estimate regional income variation.
Unemployment data are obtained from the Bureau of Labor Statistics, once again for the state and each county. This data includes labor force and number unemployed for the period 1990 to 2012. Ideally unemployment data for the entire study period from 1969 to 2012 would be used in the study, but pre-1990 county numbers are not available. County data are also aggregated into labor force and number unemployed totals to estimate unemployment rates for each of the 5 multi-county regions.
6.1. Baseline Analysis
Data are used to estimate two sets of equations. The first set of baseline equations regress regional income variation against income and income-squared for the period 1969 to 2012. Two alternative regression models are estimated:


where: 

Equation (1) captures the general trend correlation between per capita income and regional income variation. Equation (2) enhances this general trend by allowing for the possibility of a nonlinear relationship between the variables. The following general statements can be made about convergence-divergence behavior, although other specific cases do exist. Convergence is indicated if 







This study hypothesizes that between 1969 and 2012 each of the five Oklahoma regions, moved through the convergence phase of segment I, the transition phase of segment II, and into the divergence phase of segment III of Figure 1. A key bit of analysis involves an estimate of when each region reached the minimum point of segment II. The quadratic Equation (2) is used to estimate the level of per capita income in which convergence gives way to divergence using the simple formula:
6.2. Unemployment Analysis
The second set of equations regresses regional income variation against income, income-squared, and the unemployment rate for the period 1990 to 2012:


where: 


This analysis investigates the role that the housing market induced economic decline might have played in the long-term pattern of regional income variation. The question posed by this study is whether economy-wide financial and economic problems disrupt this long-term trend.
7. Analysis
Figure 2 illustrates the pattern of regional income variation for each of the five regions and the state as a whole. The overall trend for the four-decade period exhibited by the six lines appears to be fairly horizontal, with a slight overall downward trend initially, but somewhat of an upturn in latter years. The Northeast Region, containing the Tulsa metropolitan area, effectively mirrors the trend for the state, tracing a slight upward trend since the mid-1990s. The Central Region, containing the Oklahoma City metropolitan area, also generally mirrors the state trend, with the exception of a state peak in the late 1970s not seen in the Central Region. It also traces a recent upward trend, also beginning in the mid-1990s.
The Southeast Region traces an inequality pattern that increases up to the early-1980s, declines until the early- 2000s then rises once again. The Southwest and Northwest Regions, although with a great deal of year-to-year fluctuations, exhibit general downward trends of reduced inequality until the mid-1990s.
Taken as a whole, the five regions do exhibit general convergence throughout most of the study period, with an apparent pattern of divergence beginning in the mid-1990s and early-2000s. One question that arises from
Figure 2. Regional income variation oklahoma and five regions: 1969-2012.
this analysis, is how Oklahoma and its component regions compare with the rest of the country. Previous analysis of all fifty states (Amos [4] [17] ), suggests that the general convergence trend ended in the mid-1970s and that divergence continued at least up to the 2000s in several states. Previous analysis also suggests that Oklahoma is one of several states that lagged behind the rest of the country.
As such, if Oklahoma “bottomed out”, making the transition from convergence to divergence post mid-1970s, it would not be expected to exhibit a clear-cut pattern of convergence or divergence in the time frame of this analysis. The fact that signs of divergence are indicated in the early-2000s, suggests that Oklahoma made the convergence to divergence transition in the mid- to late-1990s.
7.1. Baseline
As noted previously, convergence is indicated if 







Results of the estimation are summarized in Table 5. Estimating Equation (1) for the state suggests a possible pattern of convergence. The 


The focus of this analysis, however, is the differential patterns of income convergence or divergence that were experienced by the five regions of Oklahoma. Table 5 also presents estimates of Equations (1) and (2) for each region. Estimates of Equation (1) show negative values for the 

Further insight is garnered from estimates of Equation (2) for each of the five regions. All five regions mirror results for the state, with 



These regression results along with the graphical patterns in Figure 2 provide support for the growth pole cycle hypothesis of divergence after a period of convergence. The five regions individually appear to have moved from segment I, through segment II and into segment III of the augmented inverted-U curve in Figure 1. This raises the question: When did each region make the transition? Again using the simple formula 
The estimated turning points of per capita income for the state and the five regions are presented in Table 6. The estimated minimum value for the state using the coefficients for Equation (2) is $18,677. Per capita income for Oklahoma was $19,144 in 1995, suggesting that the state reached the transition turning point from convergence to divergence in the mid-1990s, about 20 years after that estimate for the country as a whole. The estimated value for the Central Region is $20,728. This value is consistent with the mid-1990s as well, with per capita income in 1996 at $21,113. Surprisingly the Central Region lagged behind the state, if only by a year, when it is expected to lead the state.
The Northeast Region is the only one reaching an estimated minimum value before the state, with a value of $13,874, consistent with an actual per capita income of $13,965 in 1986. Surprisingly, the least developed of the five regions, the Southeast Region, reached an estimated minimum value turning point only slightly after the Central Region. The $17,270 value is consistent with $17,691 actual per capita income in 1998.
The two remaining western regions, Northwest and Southwest, achieved minimum values of $30,441 and $20,391 respectively. Both values place these regions after the turn of the century―2006 with an actual per capita income of $31,337 for the Northwest and 2000 with an actual per capita income of $21,351 for the South-
Table 5. Baseline regression results 1969-2012.
a0.01 Significance Level; b0.05 Significance Level; c0.10 Significance Level; dSerial correlation correction with maximum likelihood estimator.
Table 6. Estimated per capita income minimum value turning points.
west.
This analysis of Equations (1) and (2) along with the graphical analysis indicates that the state of Oklahoma and its five regions have quite likely all experienced divergence of regional income variation, albeit decades after the estimated mid-1970s turning point for the country as a whole, a result that is not unexpected. These results also support the hypothesis that substate regions, like states, move through the augmented inverted-U, at different times. One unexpected result is that the lesser developed Southeast Region lagged behind the state and Central Region by only a few years, while the two western regions exhibited a greater lag.
7.2. Unemployment
The possible impact of short-run economic instability, such as that resulting from the 2007 housing market collapse, can be investigated with Equations (3) and (4), which add the unemployment rate to Equations (1) and (2), respectively. Expectations are that a higher unemployment rate would have a greater detrimental effect on those with lower incomes and thus increase income inequality. Because county unemployment data used to estimate unemployment rates for the five substate regions are only available from 1990, this analysis focused only on the period from 1990 to 2012. As with the previous analysis, equations are initially estimated using OLS, then re- estimated with a one period serial correlation correction when necessary. Results for the state and the five sub- state regions are presented in Table 7.
Table 7. Unemployment regression results 1990-2012.
a0.01 Significance Level; b0.05 Significance Level; c0.10 Significance Level; dSerial correlation correction with maximum likelihood estimator.
As might be expected with only a subset of the original data period, the overall convergence-divergence trend identified previous is not readily apparent. Linear results in Equation (1) for the state and each of the five regions indicate divergence, 


Estimation of Equations (3) and (4) generally indicates an overall negative relation between the unemployment rate and regional income variation. In all but the Southeast and Southwest Regions, the unemployment rate coefficient is negative and statistically significant at the 0.05 level or better. The two southern regions display positive signs in three of the four equations but none of the coefficients are statistically significant. R2s range from 0.3359 to 0.7957.
This analysis suggests that short-run instability does impact regional income variation. In particular, higher unemployment rates experienced after the 2007 housing market collapse has apparently disrupted the longer- term pattern of divergence, creating convergence and lesser income inequality. This result clearly warrants further study, especially with other states and a longer time period. It also raises the question of whether the unemployment rate variable, while on the surface an apparent detriment to those with lower incomes, might actually reflect a more fundamental process that differentially affected higher incomes during the 2007 downturn.
8. Summary and Conclusions
This analysis of the variation of county per capita income within the five substate regions of Oklahoma provides support for the hypothesized augmented inverted-U. The inverted-U pattern hypothesized by Kuznets [16] suggests that regional income variation converges after a period of divergence, with no indication of what if anything might occur after convergence. The growth pole cycle theory proposed by Amos [1] [2] implies that convergence is followed once again by divergence. Previous work (Amos [4] [17] ) identifies that divergence of per capita income variation at the state level begins in the mid-1970s, with some states, including Oklahoma, lagging behind others.
The graphical and regression analysis presented here is the first to investigate substate regional income variation. It supports previous results of differential lags in the per capita income divergence implied by the augmented inverted-U.
Moreover, inclusion of the unemployment rate in the regression analysis suggests a key role played by short-run economic instability in the longer-run development process. While the analysis period is necessarily shortened due to the lack of unemployment rate data, evidence suggests that further investigation into this relationship is warranted.
References
- Amos, O.M. (1990) Growth Pole Cycles: A Synthesis of Growth Pole and Long Wave Theories. Review of Regional Studies, 20, 37-48.
- Amos, O.M. (1995) Secular Seasons: Long Run Trends in Spatial-Temporal Socio-Economic Behavior. Papers in Regional Science, 74, 187-204. http://dx.doi.org/10.1111/j.1435-5597.1995.tb00636.x
- Amos, O.M. and Ireland, T.C. (2010) Oklahoma Per Capita Personal Income: Converging or Diverging Trends? The 47th Missouri Valley Economic Association Annual Meeting, St. Louis, 28-30 October 2010.
- Amos, O.M. (2014) Evidence of Increasing Regional Income Variation in the United States: 1969-2006. Modern Economy, 5, 520-532. http://dx.doi.org/10.4236/me.2014.55049
- Williamson, J.G. (1965) Regional Inequality and the Process of National Development: A Description of the Patterns. Economic Development and Cultural Change, 13, 3-47. http://dx.doi.org/10.1086/450136
- Amos, O.M. (1988) Unbalanced Regional Growth and Regional Income Inequality in the Latter Stages of Development. Regional Science and Urban Economics, 18, 549-566. http://dx.doi.org/10.1016/0166-0462(88)90026-9
- Amos, O.M. (2012) An Examination of Short-Run and Long-Run Factors Affecting Regional Income Inequality in the United States. 2012 Conference Proceedings, Mid-Continent Regional Science Association, Bloomington, 6-8 June 2012, 63-79.
- Amos, O.M. (1989) A Re-Evaluation of Long Cycle Theories: Development as the Satisfaction of Hierarchial Needs. Social Science Quarterly, 70, 341-355.
- Kondratieff, N.D. and Stolper, W.F. (1935) The Long Waves in Economic Life. The Review of Economics and Statistics, 17, 105-115. http://dx.doi.org/10.2307/1928486
- Kondratieff, N. (1984) The Long Wave Cycle (Translated by Guy Daniels). Richardson and Snyder, New York.
- Schumpeter, J.A. (1939) Business Cycles: A Theoretical, Historical, and Statistical Analysis of the Capitalistic Process (2 Volumes). McGraw-Hill, New York.
- van Duijn, J.J. (1983) The Long Wave in Economic Life. Allen & Unwin, London.
- Perroux, F. (1955) Note sur la notion de pole de croissance? Economic Appliqee, 307-320. (Translated as: Perroux, F. (1970) Note on the Concept of Growth Poles. In: McKee, D., Dean, R. and Leahy, W., Eds., Regional Economics: Theory and Practice, The Free Press, New York, 93-104.)
- Lasuen, J.R. (1969) On Growth Poles. Urban Studies, 6, 137-161. http://dx.doi.org/10.1080/00420986920080231
- Hansen, N.M. (1967) Development Pole Theory in a Regional Context. Kyklos, 20, 709-727. http://dx.doi.org/10.1111/j.1467-6435.1967.tb00871.x
- Kuznets, S. (1955) Economic Growth and Income Inequality. The American Economic Review, 45, 1-28.
- Amos, O.M. (1989) An Inquiry into the Causes of Increasing Regional Income Inequality in the United States. The Review of Regional Studies, 19, 1-12.




