Modern Economy
Vol.4 No.7(2013), Article ID:34271,5 pages DOI:10.4236/me.2013.47049
The Discrimination Method and Empirical Research of Individual Credit Risk Based on Bilateral Clustering*
School of Economics and Management, University of Electronic Science and Technology of China, Chengdu, China
Email: xcwdl@126.com
Copyright © 2013 Li Shuai et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 1, 2013; revised May 6, 2013; accepted June 6, 2013
Keywords: Individual credit risk; Bilateral clustering; ROC
ABSTRACT
Individual credit risk evaluation has played an extremely important role in the credit risk management of commercial banks. Firstly, through Logistic regression, this paper selects and determines the clustering factors. Then the bilateral clustering structure is proposed. Based on the clustering structure, we cluster to the test samples, and distinguish the individual credit risk as well. Finally, we use the ROC method to test the proposed model and Logistic regression model. The results of comparison show that the discrimination method of individual credit risk based on bilateral clustering can better identify the risk.
1. Introduction
The rapid development of Chinese economy led to rapid growth of the credit consumption and continuous growing of the personal credit scale. However, there is neither a scientific and practical system built for personal credit risk valuation, nor robust and reliable valuation models.
Personal credit risk valuation method mainly includes statistics, operation research, artificial intelligence method etc. Among them statistics method includes classification tree, cluster method, linear discriminant analysis etc. David D. (1941) pioneered in applying discriminant analysis in credit risk valuation system [1]; Zhang X., Zhu T. and Yu L. (2011) build credit critical value model based on real sample of some bank through Fisher discriminant analysis model [2]. Classification tree is a nonparametric identification technology, Makowski (1985) and Coffman (1986) applied this method in credit risk valuation area [3]. The application of cluster analysis in credit risk valuation is mainly to classify the sample, Tam et al. applied nearest neighbour analysis method in credit risk analysis, using mahalanobis distance to classify the sample, Lundy used cluster analysis to classify and make regression marking for consumer loans applicant according to their application data and age, occupation etc. [4] Regression analysis model includes linear regression, Logistic regression, Probit regression etc. Foreign scholars who did research in personal credit risk valuation using regression analysis method include, Fitzpatrick (1976), Lucas (1992) and Henley (1996) [5], etc. There are quite a few research at home in this area, Zheng Y. (2009) did application research in personal credit risk of some bank in Zhejiang Province using traditional probit model [6]; Yang Y. and Shi X. (2009) build bilateral clustering probability model based on artificial immune mechanism, and compared it with Logistic regression model [7]. Operation research method includes integer programming and linear programming; Freed (1981) used linear programming in personal credit risk classification [8]. The most popular artificial intelligence method is a neural network, Security Pacific Bank (SPB) applied neural network intelligence system in the credit valuation of small business loan [9]; Huang H. and Zhou Z. (2010) proposed improved LMBP algorithm to mend the defect of applying BP neural network model in personal credit valuation, and applied ILMBP model in credit risk valuation [10].
Cluster analysis can be applied even when no performance result is available, while Logistic is characterized as simple result, small burden, and propounding classification performance. In order to take advantage of both Logistic regression and cluster analysis, this paper firstly use Logistic regression to regress the element needed in cluster regression, determine the cluster element, so as to build the Bilateral Clustering Structure, and use the minimum distance to classify the sample data, then we get the default rate, finally, use ROC curve to test the model.
2. To Determine the Cluster Element
2.1. Cluster Element
In cluster analysis, it is very important to determine the cluster elements, which directly influence the accuracy and reliability of the classification result. This paper selects the original data from some Germany commercial bank. As is shown in the Table 1, there includes indexes of the original data [11].The left side of Table 1 are the indexes as follows: X1 Age, X2 Marriage, X3 Supporting family members, X4 Occupation, X5 Year of working , X6 Housing condition, X7 Year of live in current house, X8 Installment to deposable disposable income rate, X9 assets, X10 Current payment account status, X11 The rest plan for the installment, X12 Debt amount, X13 Saving account/bonds, X14 Loan Period, X15 Credit record, X16 Existing loan project number in this bank, X17 other note debtor/guarantor. While accordingly, the right side in
Table 1 are the definitions of the variables from the original data. Therefore, when we do cluster elements selection, the cluster elements will be picked from 17 indexes form Table1.
2.2. Pre-Process of the Sample Data
Table 1 indicates that, the indexes should be standardized: 1) For the discrete data, we use minimum max standardization methods to linear transform the original data, make them into the interval [0,1]; 2) Use scaling transformation to proceed the continuous data [11].
2.3. To Determine the Cluster Element
2.3.1. Collinearity Diagnostics of the Explanatory Variables
In order to make the parameter estimation more accurate, this paper use SPSS16.0 to diagnose the collinearity of the 17 variables, and then use the statistic TOL and VIF to diagnose the existence of collinearity between the explanatory variables. Table 2 lists the diagnose result of the former 9 variables: Generally, when TOL < 0.1 or VIF > 10, the variables have collinearity problem, table 2 shows that the TOL and VIF of variable X7 and X8 in
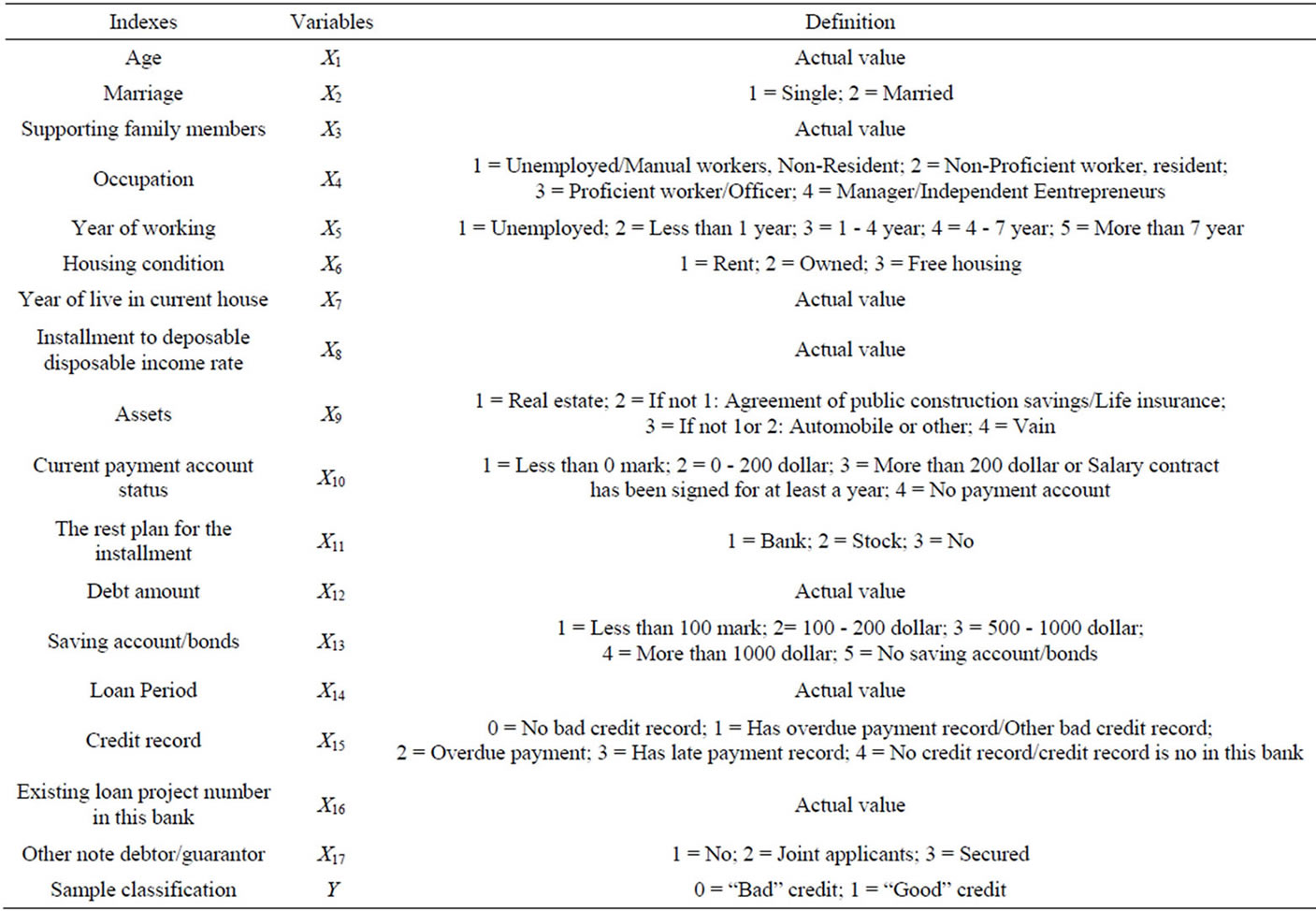
Table 1. The indexes and the definition of the variables from the original data.

Table 2. Collinearity diagnostics.
dicate collinearity between them.
2.3.2. Logistic Stepwise Regression
To avoid the adverse effect caused by the collinearity of variables, this paper adopts Logistics step wise regression, Table 3 is the result of the regression. As is shown in the Table 3, after 8 steps of screening, the model finally picked variables X14, X9, X10, X4, X3, X15, X16 and X11, that is loan period, supporting family members, current check account, year of working, credit records, loan project number in the current bank and the rest installment plan, the coefficient are 0.007, 0.044, −0.098, 0.064, 0.071, −0.066, 0.085, 0.030, The following model can be used to assess the Default status of the individuals:

2.3.3. To Determine the Cluster Elements
By using Logistic stepwise regression we selected 8 variables X14, X9, X10, X4, X3, X15, X16 and X11, Because Logistic regression is highly descriptive, this paper select the most descriptive variable from the above 8 variables as the cluster element of the sample data, screen according to the condition ROC > 0.5, according to table 4 shows, the cluster elements are X14, X9, X4 and X16, recorded as cluster element g1, cluster element g2, cluster element g3, and cluster element g4.
3. To Build the Bilateral Cluster
3.1. The Structure of the Bilateral Cluster
Through normalizing preprocessing, the sample client are randomly divided into 3 groups, the first group is 500 observed samples; the rest of the two group is divided from the remaining 500 data, as test samples. Figure 1 is the demonstration of the bilateral structure. As is shown in Figure 1, the observed samples are divided into default group and non-default group, also called normal client cluster, and default client cluster, so as to form the bilateral cluster. While the remained data, as the test data, also called the newly entered sample wl, which will be clustered to the default group and non-default group, thus forming a bilateral cluster structure.
Cluster analysis is based on the “distance” and “similarity coefficient”, while “distance” is commonly used to measure the similarity of samples. This paper according to the division of observed sample into normal and default client cluster, and based on the similarity between

Table 3. Logistic regression MLE.

Table 4. ROC value of the explanatory variables.
samples, use “distance” as the standard for clustering.
3.2. The Definition of Clustering Distance
Figure 1 not only shows us the structure of bilateral cluster, but also shows us how to definite the “distance”, in order to make the newly entered sample wl clustered to the default and non-default group. As is shown in the figure, supposing {ui, I = 1, 2, 3, ∙∙∙, n1} is the normal client cluster in the observed sample, among which ui is the normal client i, Uik (k = 1, 2, 3, 4) is the attribute value of the kth cluster element gk of client i in the observed sample normal client cluster; Similarly, supposing {vj, j = 1, 2, 3, ∙∙∙, n2} is the default client cluster in the observed sample, among which vj is the jth default client, and Vjk (k = 1, 2, 3, 4) is the attribute value of the kth cluster element gk of the ith client in the observed sample; {wl, l = 1, 2, 3, ∙∙∙, n3} is the test sample cluster, among the wl is the lth client in the observed sample to be tested, Wlk (k = 1, 2, 3, 4) is the attribute value of the cluster element gk of the lth client to be tested in the test sample.
This paper use Euclidean distance as the distance between the normal client ui and the default client vj in the observed sample:
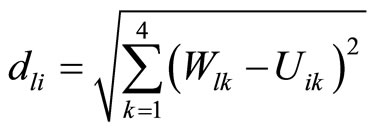 (1)
(1)
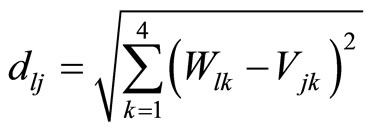 (2)
(2)
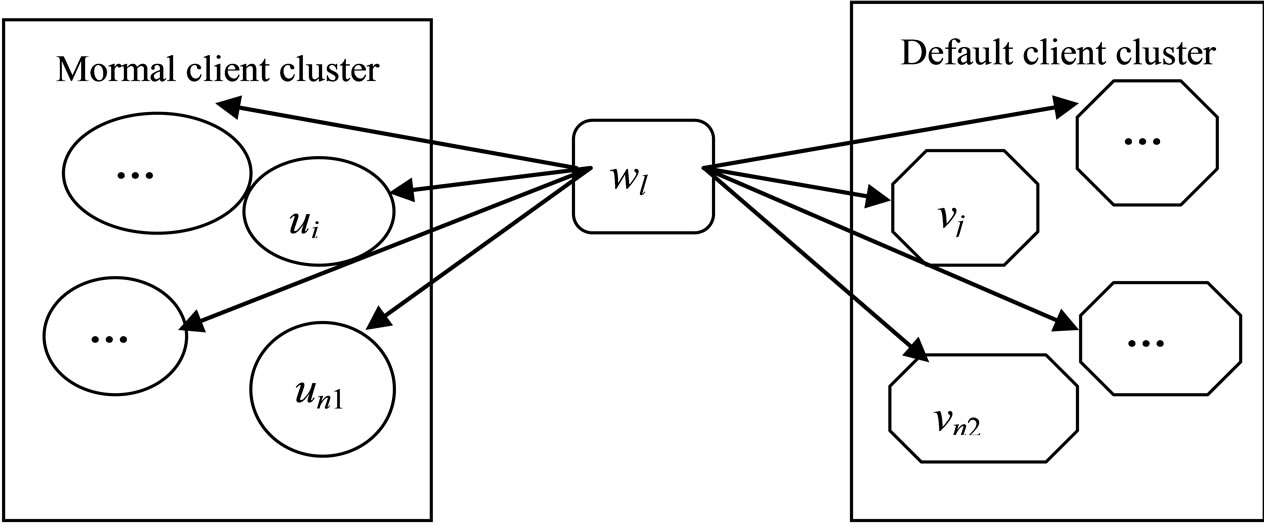
Figure 1. Demonstration of the bilateral cluster structure.
The algorithm of the cluster classification:
1) Select test sample wl, l = 1, 2, 3, ∙∙∙, n, stop while l > n;
2) Calculate the bilateral distance of observed sample wl 
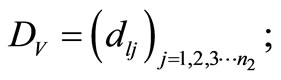
3) d1 = min(DU), d2 = min(DV), if d1 ≥ d2, then wl Î default client cluster ,n2 = n2 + 1; or d1 < d2, then wl Î normal client cluster, n1 = n1 + 1;
4) Repeat the above operation, until the termination conditions occur.
During formation of the normal and default client cluster, n1 represents the number of the normal clients, n2 represents the number of defaulted clients, and then we can estimate the default rate of the entire sample client cluster:
 (3).
(3).
4. Model Test
Ususally, ROC value and ROC curve is used to assess the test of the personal credit risk valuation model .
4.1. ROC Curve Test
Figure 2 shows that, after stepwise cluster, the space under the ROC curve grows with adding the test sample. According to the principle that the bigger the space under the ROC curve is indicates the better the discrimination ability the model has. Comparing to the original 500 observed data, after stepwise adding the remaining test data (each of them has 250 data), the discrimination ability gradually increases, which indicates that the cluster model is highly feasible.
4.2. To Compare the Discrimination Ability between Models
Using the same data, the comparison of the bilateral cluster model and the Logistic regression model is shown above (Table 5). Logistic regression used 1000 data, get the ROC value of the model is 0.692, while for bilateral cluster model, after adding the test sample a2 and clustering the ROC value of the model is 0.739 which is
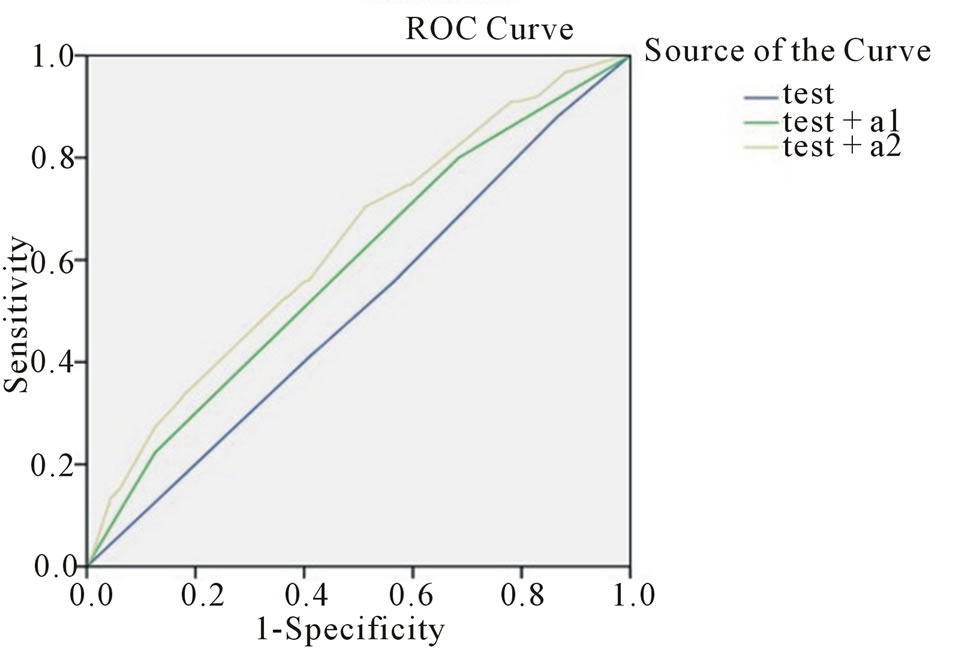
Figure 2. ROC curves of cluster model after twice adding test sample.
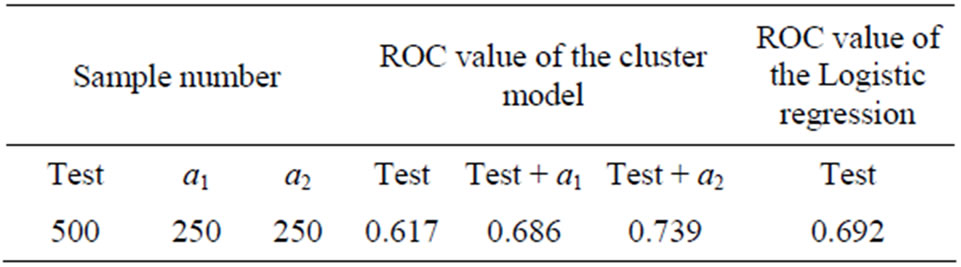
Table 5. Influence of the sample scale to the ROC value.
higher than the ROC value of the Logistic regression value 0.692, the result indicates that the cluster model can use less data to achieve higher efficiency.
5. Conclusion
This paper used the data from some Germany commercial bank, built the personal credit risk valuation model based on bilateral clustering, and conducted empirical research. The research result indicates that this method is unusually practicable and effective in the discrimination of personal credit risk, which overcome the defect of traditional personal credit risk valuation and obtains the quality of strong explanatory; The bilateral clustering reduced the complexity of common cluster analysis, and has the advantage of high accuracy and less data oriented, this is the main innovation of this paper. The method which discriminate the clustering result according to “similarity” is very subjective, so, further work can be done in the weight determination, which can be determined by the contribution of the cluster element, and then calculate the distance.
REFERENCES
- D. Durand, “Risk Elements in Consumer Installment Financing,” National Bureau of Economy Research, New York, 1941, pp. 189-201.
- X. L. Zhang, T. X. Zhu and L. X. Yu, “Research on the Personal Credit Risk Valuation of Commercial Bank Based on Discriminatory Analysis,” Industrial Technology Economics, Vol. 10, 2011, pp. 131-137.
- J. Y. Coffman, “The Proper Role of Tree Analysis in the Forecasting the Risk Behaviour of Borrowers,” MDS Reports, Management Decision Systems, Atlanta, 1986, pp. 47-59.
- E. Mays, “Credit Risk Modeling: Design and Application,” Fitzroy Dearborn Publishers, Chicago, 1998, pp. 190-200.
- D. B. Fitzpatrick, “An Analysis of Bank Credit Card Profit,” Journal of Bank Research, Vol. 7, 1976, pp. 199-205.
- Y. Zheng, “Application Research of Personal Credit Risk Based on Probit Model,” Shanghai Finance, Vol. 10, 2009, pp. 85-89.
- Y. Yang and X. H. Shi, “Personal Credit Risk Measurement: Bilateral Antibody Artificial Immune Probability Model,” Systems Engineering-Theory & Practice, Vol. 29, No. 12, 2009, pp. 89-92.
- N. Freed and F. Glover, “A Linear Programming Approach to the Discriminant Problem,” Decision Sciences, Vol. 12, No. 1, 1981, pp. 68-74. doi:10.1111/j.1540-5915.1981.tb00061.x
- D. West, “Neural Network Credit Scoring Models,” Computers & Operations Research, Vol. 27, No. 11-12, 2000, pp. 1131-1152. doi:10.1016/S0305-0548(99)00149-5
- H. Z. Huang, Z. F. Zhou and J. K. Yu, “ILMBP Neural Network Model and Its Application in Personal Credit Valuation,” Managerialist, Vol. 10, 2010.
- “Research of the Combination Forecast Method of Individual Credit Evaluation for Commercial Bank,” Harbin Industrial University Press, Harbin, 2011, pp. 44-45.
NOTES
*This research was be supported by National Natural Science Foundation of China (No. 70971015, 71271043); the special research Foundation of Ph.D program of China (20110185110021).

