Journal of Biophysical Chemistry
Vol.05 No.04(2014), Article ID:51403,8 pages
10.4236/jbpc.2014.54014
Consequences of Non-Uniformity in the Stoichiometry of Component Fractions within One and Two Loops Models of α-Helical Peptides
Walter F. Schmidt1*, Cathleen J. Hapeman1, James Wachira2, Clayton G. Thomas3
1United State Department of Agriculture, Agricultural Research Service, Beltsville, Maryland, USA
2Department of Biology, School of Computer, Mathematical, and Natural Sciences, Morgan State University, Baltimore, Maryland, USA
3Clarence M. Mitchell Jr. School of Engineering, Morgan State University, Baltimore, Maryland, USA
Email: *walter.schmidt@ars.usda.gov
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 September 2014; revised 7 October 2014; accepted 6 November 2014
ABSTRACT
A 3-D electrostatic density map generated using the Wavefront Topology System and Finite Element Method clearly demonstrates the non-uniformity and periodicity present in even a single loop of an α-helix. The four dihedral angles (N-C*-C-N, C*-C-N-C*, and C-N-C*-C) fully define a helical shape independent of its length: the three dihedral angles, φ = −33.5˚, ω = 177.3˚, and Ψ = −69.4˚, generate the precise (and identical) redundancy in a one loop (or longer) α-helical shape (pitch = 1.59 Å/residue; r = 2.25 Å). Nevertheless the pattern of dihedral angles within an 11 and a 22-peptide backbone atom sequence cannot be distributed evenly because the stoichiometry in fraction of four atoms never divides evenly into 11 or 22 backbone atoms. Thus, three sequential sets of 11 backbone atoms in an α-helix will have a discretely different chemical formula and correspondingly different combinations of molecular forces depending upon the assigned starting atom in an 11-step sequence. We propose that the unit cell of one loop of an α-helix occurs in the peptide backbone sequence C-(N-C*-C)3-N which contains an odd number of C* plus even number of amide groups. A two-loop pattern (C*-C-N)7-C* contains an even number of C* atoms plus an odd number of amide groups. Dividing the two-loop pattern into two equal lengths, one fraction will have an extra half amide (N-H) and the other fraction will have an extra half amide C=O, i.e., the stoichiometry of each half will be different. Also, since the length of N-C*-C-N, C*-C-N-C*, and C-N-C*-C are unequal, the summation of the number of each in any fraction of n loops of an α-helix in sequence will always have unequal length, depending upon the starting atom (N, C*, or C).
Keywords:
Pattern Recognition, α-Helix, Dihedral Angle Patterns, Peptide Backbone Sequence, Molecular Orbital Theory, Electrostatic Density Gradient, Wavefront Topology System, Finite Element Method

1. Introduction
A helix is a line composed of only two variables: pitch and diameter [1] . Analogous to a circumference, a loop of a helix is a measure of length, not area or volume. Wavefront Topology System and Finite Element Methods enable calculating a “scaffolding” of unit building blocks of equal unit size and volume along this linear structure, Figure 1(a) [2] [3] . In this model, the pitch, diameter, volume, and shape of such volume are inputs which can have virtually any value. Applied to a peptide structure, the unit shape and volume of the “scaffolding” can be matched to contain any repeating pattern of molecular structure. The unit cell is mathematically independent of the number unit cells. A very precise unit cell molecular model is required to detect both small localized variations in the uniformity of patterns within arrays of α-helical peptide structural data and to enable identifying sequence-related sequential changes, as in a gradual increase or decrease in diameter or pitch within/between α-helical sequences.
Macromolecular studies computationally identify extended α-helical regions of proteins [4] - [9] ; the average loop has a rise of 3.6 residues per helical turn. For three loops, the rise is 11/3 = 3.667; for two loops, the rise is 7/2 = 3.50. In the Wavefront Topology System, fractional changes in pitch and/or diameter of a peptide result in a mathematically precise and cumulative value for its length along the helical axis. The structure of n loops of an α-helix is assumed to be composed only of a whole number of precise unit cells.
Such a more precise model of the same helical shape contains eleven peptide backbone atoms in one loop of an α-helix [1] equal to eleven amino acid residues forming three loops. Modeling a single loop of an α-helix however requires assigning an exact stoichiometry to any one set of eleven sequential backbone atoms. We propose a model in which the eleven backbone atoms in a helix begin and end with an amide, i.e., three chiral center C* atoms and four amide groups, one before and after each C* atom. An amide group is 2/3 of an amino acid backbone, and thus the model retains both the 3.667 pitches and the whole number unit cell step of the three-loop helix model.
Specific atoms at specific sites in a helix enables an electrostatic density gradient map to be calculated (Figure 1(b)). The positions of C* atoms are redundant and the electrostatic density gradient for the amide groups repeats itself four times. The electrostatic density gradient is different inside versus outside the helix. In a helix starting from an amide atom type, the resulting eleven backbone atoms would have the same specific di-

Figure 1. Right-handed helical coil and electrostatic energy map of one loop of an α-helix. The mesh conforms to the orientation, length, radius, and pitch of the α-helix. The surface values were computed using coulomb potential.
ammeter and pitch; starting from the second amide group, the same specific diameter and pitch would result. Thus, data on the relative position of atoms in three loops of a helix contain not three full sets of data on an α-helix, but 22. Every set of eleven sequential data points results in a precise average pitch. The individual atom in a sequence at which the pitch begins to change, or sharply changes, becomes computationally accessible. Further, we propose a molecular level mechanism for the high degree of redundancy in the peptide α-helix structure in unit cell structure even shorter than a sequence of eleven backbone atoms.
2. Pattern Use in Eleven Atom Sequence
The stoichiometry of one loop of an eleven peptide backbone helix will always be different than the stoichiometry of a peptide. Since twelve atoms have the proper ratio of three atom types: N-C*-C, 11/12 of the same atom set requires one backbone atom is repeated once less than the other two. Beginning from the normal peptide sequence N-C*-C, the final C=O structure is missing. Ending with N-C*-C, the initial N-H structure is missing. Computationally, each of these sequences is complicated because the force field parameters for C=O and N-H are discretely different from each other and are actually not part of any redundant pattern. In both cases, one of the amide bonds is divided in half. Because an amide is dipolar, half of an amide is half of a dipole. Each eleven atoms sequence would not only begin with (or end with) half of a dipole: it would begin with (or end with) exactly the same positive (or negative) half of the dipole.
The 11/12 of four peptides that avoids dividing the dipolar properties of an amide is simply three C* atoms plus four amide groups. The pattern recognition model in effect begins at an amide C, observes the location of next eleven backbone atoms, then advances three atoms to the next amide C and observes the location of the next eleven atoms. The “cost” is that, on average, for every four times an amide site is sampled, a C* site will be sampled only three times.
A second more complicate model of an α-helix arises again from this stoichiometry. Because one loop of a helix has three C* atoms and four amide groups, the second and third loops together must have eight C* atoms and seven amide groups. In the second case, the number of amide bonds is odd and the number of C* atoms is even. Since 21 atoms equals exactly seven backbone atom, 22 atoms (two loops) has seven amino acids plus one extra C* atom. This structurally would be: C*-(N-C-C*)7. In each case redundancy in these patterns requires model identifying the specific (peptide backbone) atom at which an individual pattern begins. In neither of these cases does the pattern redundancy originate from the normally labeled sequence of peptides as N-C*-C. The stoichiometry of the second and third loops of a helix clearly depends upon from which backbone atom the counting of eleven backbone atoms begins. The patterns of redundancy in sequence clearly depend upon from which backbone atom the counting of backbone atoms begins.
Backbone Sequence Steps Forming an α-Helical Shape
Not only are eleven atom sequences repeating per one loop of a helix: patterns shorter than eleven atoms are repeating within one loop of helix. Identifying any uniform repeating pattern of atoms which generates one loop of a helix is complicated by the fact that the backbone contains eleven atoms, a prime number. Patterns that do not add up to the eleven atoms can only partially explain a helix. Six schemes of simple repeating peptide backbone sequence patterns are presented, Figure 2.
In Scheme I, four groups of backbone atoms, N-C*-C, yield a pattern of twelve atoms. This pattern does not include (nor depend upon) the side chain of the four amino acids. One atom less than twelve in this sequence has a different stoichiometry if an amide N is removed or if a carbonyl C is removed. Computationally, one cannot remove one atom from an N-C*-C pattern without altering the bond stretching, bending, torsional parameters concurrently assigned to that atom and its neighboring atom(s). Eleven atoms are composed of three atom types, namely N, C*, and C, and since 4 + 4 + 3 = 11, only one of the three atom types will occur thrice in the helix. In Scheme I, with twelve atoms, each is present as four of each. A single atom (N) at the beginning removed or a single atom (C) at the end removed gives rise to three amide N atoms or three amide C atoms, respectively. In both cases, four C* atoms would be present.
Mathematically, the best site at which to measure of an α-helix diameter and pitch is from its midpoint. The sites at which each half starts and ends are 180˚ from this midpoint. The midpoint of the twelve atoms is halfway step six and step seven. The center is intermediate between C and N in the central C-N bond. Since the length C2*-C and N-C3* are unequal, the midpoint between C2* to C3* actually is not the middle of the C-N bond. On
Figure 2. Three, four, and five step patterns in one single loop of an α-helix.
reducing the length of the backbone 1/12, the center of mass and/or distance along this C-N bond is shifted even further to left or right. Thus in Scheme I, the midpoint, diameter, and pitch of an α-helix can only be calculated using a complicated formula that approximates a physically-undetectable center.
In Scheme II, two sets of four atoms, C1*-C-N-C2* and C3*-C-N-C4*, connected with an amide bond C-N adds up to ten atoms. The center by mass of this pattern is near the middle of an amide C-N bond, except nearer to N because its mass is higher than C. Adding either an amide N or a carbonyl C atom to form in an eleven member backbone sequence increases the spatial asymmetry between the two halves. The stoichiometry (mole ratio of atom types) in each half of an α-helix is dissimilar. Discerning molecular forces due to common and dissimilar molecular structure in both halves is then computationally complicated and/or ambiguous.
In Schemes I and II, the initial N could be an 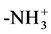 or an -NH2; the terminal C could be an -O− or an -OH. For internal consistency, N and C refer only to amide N and amide C. The pattern for an amine N and/or for a COO carbonyl group never repeats, i.e., they only occur once per peptide sequence.
or an -NH2; the terminal C could be an -O− or an -OH. For internal consistency, N and C refer only to amide N and amide C. The pattern for an amine N and/or for a COO carbonyl group never repeats, i.e., they only occur once per peptide sequence.
Scheme III is markedly different than the first two. Four full amide C-N groups occur evenly among only three C* atoms. C2* is centrally located at the central position 6 and two complete sets of amides occur to the right and to the left of C2*. A molecular length from C2* five atoms to the left (to C) can exactly equal the distance of five atoms to the right (to N). The same number of atoms [of the same bond type] repeats in sequence exactly; correspondingly the length and pitch can also repeat exactly. In the presence of this symmetry, identifying the discrete molecular sites most significant in peptide structure is possible.
The eleven member pattern, C C2* N, requires two end points and the middle of one loop to fully characterize its structure. Multiple patterns occur within the same shape, e.g., C C1* C2* C3* N and C1* C2* C3* . The major structural criteria for a self-con- sistent α-helical shape in Scheme III is that amide bonds on either side of the C* sites are consistently in the same proper alignment/orientation. The pattern has symmetry around C2* even though the direction, C N, remains unidirectional. The amide bonds are always in the same C-N sequence, independent of an individual site in the α-helix. The C1* C2* pattern therefore should not be presumed to be the same as C2* C1*. The pattern C1*-C-N-C2* is discrete from C1*-N-C-C2*. Beginning an α-helix from an amide instead of an amine, the first atom in the sequence becomes a C, not an N. The amide bond between any two C* atoms in backbone sequence retains the same order, i.e., C-N.
Scheme IV is a repeating pattern of four atoms, N N. In every helical structure with C* at its center, the same pattern repeats three times. The relative conformation of the amide N, i.e., N-H, sites before and after each C* site must be self-consistent among each of the three C* atoms or the structure cannot be uniform. Uniformity among the sets of these four atom patterns, each of which contain two N atoms, is essential, though also insufficient, for an eleven backbone helical shape to exist.
Scheme V is a repeating pattern of four atoms, C C. In every helical structure with C* at its center, the same pattern repeats three times. The relative conformation of the amide C, i.e., C=O sites before and after each C* site must be self-consistent among each of the three C* atoms for the structure to be uniform.
Scheme IV and V are actually variations on Scheme I. In Scheme IV, the N-C*-C pattern is extended one additional backbone N atom “up” the helical shape. In Scheme V, the N-C*-C pattern is extended one additional backbone C atom “down” the helical shape. Together, they approximate the pattern in Scheme VI.
Scheme VI is a repeating pattern of five atoms, Cn* . When Scheme VI is uniform for any C* atom, both the patterns, N N and C C, must be also be uniform. This five-step pattern, repeated once per C*, covers all eleven sites at least once and two amide C-N sites twice. The pattern of amide sites covered twice is redundant information, i.e., the orientation of the amide groups in both cases must be virtually indistinguishable. Scheme VI also enables identifying sites at which regularly repeating patterns begin to be disrupted.
In Scheme III and VI, the α-helix essentially begins at its middle and then ends five atoms later at both ends, and each concludes with C-N sites. Scheme VI correctly identifies that the amide containing N-C* must be self- consistent with the amide containing the C*-C site. The Scheme VI pattern is a more general and less specific than the Scheme III pattern.
None of data sets in Scheme VI, however, contain more than one C* components. Thus, correlations to C* sites are not specific to any particular site, and C2* cannot be identified as discrete from any other C* site. Scheme III does not require all three are equal. The dipolar forces for example could stepwise increase from C1* to C2* to C3*. Unless C1*-C-N-C2* and C2*-C-N-C3* patterns are correspondingly similar, the helix can neither be symmetrical, nor uniform.
3. Four-Atom Three-Bond Molecular Order Orbitals
Patterns at the molecular level order are atoms grouped together such as α-helices and β-sheets [10] . Patterns can be analyzed by Group Theory [11] . An important pattern is sets of atom by atom type. Peptide backbones return to the same atom type every fourth atom in sequence and three sets of four atoms are sufficient to fully parameterize the pattern of eleven atoms in an α-helix. An amide, O=C-N-H, has the pattern, O H. Structurally, this sequence is identical with C1* C2*, e.g., C1*-C-N-C2*. Because the distance of O H is about 20% shorter than the distance of C1* C2*, the six atom model of this planar surface is a trapezoid and not a square, Figure 3. The top right to the bottom left corners of this shape have a set dipolar charge: δ− for the O=C end and δ+ for the N-H end. Even if C1*, C2*, and C3* were chemically identical, this second diagonal would not equal a zero dipole: the C-N dipole component, δ− for C and δ+ for N, is always present.
Identifying the magnitude and absolute direction of the dipole is beyond the scope of this manuscript. Two sets of relative directions of dipolar forces align differently relative to the O=C-N-H dipole. Since the relative direction of these dipolar forces can be 180˚ from either other, the dipolar force in C2* C3* compared to C1* C2* need to be in the same relative direction, or symmetry would be broken.
The central site common to both vectors is about half way between C and N. However, the angle between O H and C1* C2* dipolar vectors is not 90˚, i.e., 60˚ or 120˚. Because two vectors are not 90˚ from each other, the vectors are not orthogonal. Thus, the dihedral angle C1*-C-N-C2* cannot be independent of the dihedral angle O=C-N-C2* which in turn cannot be independent of the dihedral angle O=C-N-H. Complete molecular information from dipolar forces within an amide group requires six atoms. Four atoms alone are insuffi-
Figure 3. Four possible dipole directions (C-C-N-C backbone versus O=C-N-H). The angles between the pairs of vectors are not 90˚ and therefore C-C-N-C vectors and O=C-N-H vectors cannot change independently. From C1* to C3*, the direction can be self-consistent or in the opposite direction.
cient to distinguish the pattern. Redundancy in the pattern of sets of four atoms can and does distinguish a pat- tern. Each different pattern of redundancy is composed of a different mix of molecular forces related to the dif- ferent stoichiometry in each individual pattern. Iteratively, self-consistency in the relative position of atoms in the amide group among the three sets of dihedral angles is sufficient to define a single uniform helical shape for the peptide backbone. Structurally different and/or non-uniform side chains at C* site can and will alter this specific helical shape.
Since the C1*-C-N-C2* distance is longer than for O=C-N-H, and the O=C distance is longer than for N-H, the amide shape “ribboning” the helix is trapezoidal, not rhombic. A rhombic shape would predict a C1*-C-N-C2* dihedral angle of 180˚. A trapezoidal shape explains the 177.3˚ dihedral angle molecular level “tilt” calculated in this study. A pattern of trapezoidal amide alternating tilt between +177.3˚ and −177.3˚ would average to a flat planar 180˚, e.g., in a β-sheet structure.
4. Two Loops α-Helical Structures
Two loops of a helix of polyglycine contain 22 backbone atoms. α-Helical parameters were generated in Hyper Chem [12] using seven glycine molecules as a standard peptide. The initial NH2 on Gly(1) was replaced by an amide group, and the COO site on Gly(7) was replaced with the amide O=C-N-H. The resulting structure was C- (Gly)7-N. This structure was energy minimized using a Polak-Ribiere gradient to a RMS (relative mean square) gradient of 0.001 kcal∙Å−1∙mol−1. All sets of backbone dihedral angles were recorded, and the average value for each set was calculated. Individual dihedral angles that deviated more than 2 standard deviations from their average value were not included. Each of the individual dihedral angles per atom type was replaced with the calculated average value, and the dihedral angles were concurrently optimized.
Using 180˚ as the initial value, the dihedral angle of C*-C-N-C* was the first to become constant, indicating the the initial planar structure bent 2.8˚ to 177.3˚, i.e., the N-H bent to a smaller radius than the amide. For C-N-C*-C, the best uniform dihedral angle was −69.4˚. The dihedral angle with the largest variability was for N-C*-C-N with the resulting best dihedral angle of −33.5˚. In this model, all the dihedral angles have equal weight in determining the α-helical structure, Figure 4(a). The N-C*-C-N sequence was found to be the most flexible, the C*-C-N-C* sequence the most rigid.

Figure 4. Simplified repeating patterns in α-helical peptide structures. Positions of backbone atoms in all four cases are identical.
The view from the z-axis of the C-(Gly)7 structure shows that redundancy does occur and does so over two loops, Figure 4(a). (One loop is shown in Figure 4(b).) The -(CH2)- groups are evenly spaced and repeat precisely seven times (360˚/7 = 51.43˚). The average of the two dihedral angles coming into and out of any one CH2 site C-N-C*-C (−69.4˚) and N-C*-C-N (−33.5˚) is also −51.45˚. Focusing on the anomeric pro-chiral pro-
ton in Gly, Figure 4(c), C-(AA)3-N, reveals that this hydrogen in N-C-C*-H is roughly coplanar with the amide bond. Unexpectedly, the relative positions of the three C* atoms are what defines the helical shape, Figure 4(d). The uniformity of circumference can be directly calculated from the pitch and from the triangulated points of central data point C2* (atom 6) and going through any C* atom with another C* before and after it. The uniformity of pitch can be calculated from the distance between atom 1 and atom 11 along the z-axis. In two loops of an α-helix, seven discretely different -CH2- sites enable generating a single or a narrow distribution of values for circumference and pitch.
In addition, the length L1 of C*-C-N-C* (3.80 Å) repeated uniformly seven times over 21 backbone atoms is 26.61 Å. The L2 of C-N-C*-C (2.98 Å) repeated uniformly seven times is 20.88 Å. The L3 of N-C*-C-N (2.83 Å) repeated uniformly seven times is 19.83 Å. The corresponding correction from 21 to 22 atoms is 28.14 Å, 22.22 Å, and 21.28 Å, respectively. Since 22/7 is effectively the value of π, Ln/π = dn, the diameter when the pitch equals zero. Thus, d1 = 7.26 Å, d2 = 7.07 Å, and d3 = 6.77 Å. The pattern of redundancy is due to L1 ≠ L2 ≠ L3 and d1 ≠ d2 ≠ d3, even though the dihedral angles are/can be identical. The patterns and the molecular forces concurrent with these patterns will add up differently depending upon which components are odd and which are even in number.
5. Biochemical Consequences
Two nano-scale models of morphological shape are a ribbon and a cylinder [13] [14] . Mathematically, an α-helix is a line, whereas the ribbon has an area and a cylinder has a volume. Structural information about periodicity, however, is not part of either of these models.
Neural networks using AA sequence data have been ineffectual in predicting α-helical domains in peptide structures [15] . Nevertheless, successful parameterizations of more complex molecular patterns which include helices have been reported [16] [17] . Redundancy and periodicity also occur in one or two loops of an α-helix. Structural information on unit cells smaller than a single amino acid is required to identify empirically the atom at which an α-helix starts and stops. The macromolecular pattern redundancy typically presumes helices start and stops at C* atoms. At the molecular level, amino acid residues start at an N-H and end at C=O. In a 32-atom helix, C1* to the final C=O is structurally different from N-H to C32*. In the more precise unit cell model, the 32-atom length is composed of the same component fractions only repeated a different number of times.
Ramachandran plots were used, for example, for repeating dipeptides to predict rings and ribbons of protein structure [15] and for polyglycine [18] . In both cases, the model works for large changes in structure. The dispersed distribution of data points in the plots is evidence that specific dihedral angles φ and Ψ are not necessarily uniform. A more precise model of an α-helix enables identifying which of these site on which macromolecular structures most closely match the more precise model.
Binding of cis-polyunsaturated fatty acids (PUFA) across helical transmembrane proteins roughly perpendicular to the helical structure has been proposed [19] . The more precise model presented enables proposing N-C*-C-N sites, i.e., (HN)-C*-C-(NH) sites on helix as specific binding sites to cis CH2-(H-C=C-H)-CH2 groups on the PUFA structure. In Figure 4(b), all NH sites structurally have a diameter smaller that the helix drawn through C* sites. Thus, these NH sites would not occur on the area of a ribbon parallel to outside of the helical surface.
6. Conclusions
A unit cell composed of 11 amino acids equaling three loops of a helix is a model from which diameter and pitch can be calculated. Wavefront Topology System and Finite Element Method enable calculating an α-helix of virtually any diameter and pitch with any desired precision. Since conditions could exist in which 11.26 amino acids can equal one loop, the diameter and pitch would be a precise number, and, in any predictive model, naming any fraction of an amino acid also requires assigning them to actual specific backbone atoms.
A unit cell composed of 11 backbone atoms equals one loop of a helix and is likewise a model from which diameter and pitch can be calculated. This affords the unit dimensions that are more precise by a factor of three. Thirty-two and 34 backbone atoms are structurally and computationally distinct from 33 backbone atoms in three loops of an α-helix.
The proposed model sequence (CN)-C1*-(CN)-C2*-(CN)-C3*-(CN) has an exact molecular structure centered around C2*. Although the length, stoichiometry, structure and conformation are all constant, the diameter and pitch do not actually need to be constant. The same helical structure can be compressed or stretched, each of which will change both diameter and pitch. In contrast with the present model, pitch and diameter are changed by altering the number and the identity of the atoms in the helix. Changing the stoichiometry in the length of a helix can preclude accurately adding components in the molecular forces assigned to the atoms of any precise helical structure.
In this model, because C1*, C2*, and C3* are on (or very close to) the same mathematically concise α-helical line, these atoms generate a helical structure. The diameter and pitch between C1* and C2* must be redundant with the diameter and pitch between C2* and C2* for the pitch and the diameter from C*1 to C*3 to be uniform. This uniformity allows for the repeated and reoccurring redundancy among other sets of distances and dihedral angles at other sites in the helix.
The distances and dihedral angles in Cn* and Cn+1*, Cn and Cn+1 , and Nn and Nn+1 in any redundant (helical) structure will be constant. Compression and stretching alter an α-helix shape changing both distances dihedral angles among different atom types unevenly. Nn and Nn+1 distances and dihedral angles appear to be sensitive markers of flexible and site-selective changes in helical structure.
References
- Schmidt, W.F. and Thomas, C.G. (2012) More Precise Model of α-Helix and Transmembrane α-Helical Peptide Backbone Structure. Journal of Biophysical Chemistry, 3, 295-303. http://dx.doi.org/10.4236/jbpc.2012.34036
- Thomas, C.G. (2013) The Wavefront Topology System and Finite Element Method Applied to Engineering Visualization. Morgan State University, Baltimore, 160 p.
- Meskers, A.J.H., Voigt, D. and Spronck, J.W. (2013) Relative Optical Wavefront Measurement in Displacement Measuring Interferometer Systems with Sub-nm Precision. Optics Express, 21, 1-12. http://dx.doi.org/10.1364/OE.21.017920
- Barlow, D.J. and Thornton, J.M. (1988) Helix Geometry in Proteins. Journal Molecular Biology, 201, 601-619.
- Harper, E.T. and Rose, G.D. (1993) Helix Stop Signals in Proteins and Peptides: The Capping Box. Biochemistry, 32, 7605-7609. http://dx.doi.org/10.1012/bi00081aoo1
- Kumar, S. and Bansal, M. (1998) Dissecting α-Helices: Position-Specific Analysis of Alpha-Helices in Globular Proteins. Proteins, 31, 460-476.
- Olivella, M. Deupi, X., Govaerts, C. and Pardo, L. (2002) Influence of the Environment in the Conformation of α-Helices Studied by Protein Database Search and Molecular Dynamics Simulations. Biophysical Journal, 82, 3207- 3213. http://dx.doi.org/10.1016/S0006-3495(02)75663-4
- Maiti, N.C., Apetri, M.M., Zagorski, M.G., Carey, P.R. and Anderson, V.E. (2004) Raman Spectroscopic Characterization of Secondary Structure in Natively Unfolded Proteins: α-Synuclein. Journal of American Chemical Society, 126, 2399-2408. http://dx.doi.org/10.1012/ja0356176
- Guo, Z., Kraka, E. and Cremer, D. (2013) Description of Local and Global Shape Properties of Protein Helices. Journal of Molecular Modeling, 19, 2901-2911. http://dx.doi.org/10.1007/s00894-013-1819-7.
- Eisenberg, D. (2003) The Discovery of the α-Helix and β-Sheet, the Principal Structural Features of Proteins. Proceedings of the National Academy of Sciences USA, 100, 11207-11210.
- Bishop, D.M. (1973) Group Theory and Chemistry. Dover Publications, New York, 300 p.
- Hypercube, Inc. (2007) HyperChem 8.0 for Windows Molecular Modeling Systems. Gainsville.
- Hayward, S., Leader, D.P., Al-Shubailly, F. and Milner-White, E.J. (2014) Rings and Ribbons in Protein Structures: Characterization Using Helical Parameters and Ramachandran Plots for Repeating Dipeptides. Proteins: Structure, Function, and Bioinformatics, 82, 230-239. http://dx.doi.org/10.1002/prot.24357
- Uesake, A., Ueda, M., Makino, A., Imai, T., Sugiyama, J. and Kimura, S. (2014) Morphology Control between Twisted Ribbon, Helical Ribbon, and Nanotube Self-Assembies with His-Containing Helical Peptides in Response to pH Change. Langmuir, 30, 1022-1028. http://dx.doi.org/10.1021/la404784e
- Hayward, S. and Collins, J.F. (1992) Limits on α-Helical Prediction with Neural Network Models. Proteins, 14, 372-381. http://dx.doi.org/10.1002/prot.340140306
- Albrecht, B., Grant, G.H., Sisu, C. and Richards, W.G. (2008) Classification of Proteins Based on Similarity of Two-Dimensional Maps. Biophysical Chemistry, 138, 11-22. http://dx.doi.org/10.1016/j.bpc.2008.08.004
- Cantoni, V., Ferone, A., Ozbudak, O. and Petrosino, A. (2013) Protein Motifs Retrieval by SS Terns Occurrences. Pattern Recognition Letters, 34, 559-563. http://dx.doi.org/10.1016/j.patrec.2012.12.003
- Ho, B.K. and Brasseur, R. (2005) The Ramachandran Plot of Glycine and Pre-Proline. BMC Structural Biology, 5, 14-29. http://dx.doi.org/10.1186/1472-6807-5-14
- Kachlishvili, K. and Brenna, J.T. (2013) Steric Effects in the Interaction between Transmembrane Proteins and Polyunsaturated Phospholipids. Journal of Biological Physics and Chemistry, 13, 36-44. http://dx.doi.org/10.4024/33KA12A.jbpc.13.01
NOTES

*Corresponding author.




