Wireless Engineering and Technology
Vol.07 No.02(2016), Article ID:65303,8 pages
10.4236/wet.2016.72006
Rain Attenuation in the Microwave-to-Terahertz Waveband
Seishiro Ishii1, Masahiro Kinugawa1, Shunichiro Wakiyama1, Shuji Sayama2, Toshihisa Kamei2
1Department of Information Networks, National Institute of Technology, Sendai College, Sendai, Japan
2Department of Communication Engineering, National Defense Academy, Yokosuka, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 February 2016; accepted 29 March 2016; published 1 April 2016
ABSTRACT
In recent years, there has been increased interest in the terahertz waveband for application to ultra-high-speed wireless communications and remote sensing systems. However, atmospheric pro- pagation at these wavelengths has a significant effect on the operational stability of systems using the terahertz waveband, so elucidating the effects of rain on propagation is a topic of high interest. We demonstrate various methods for calculating attenuation due to rain and evaluate these methods through comparison with calculated and experimental values. We find that in the 90 - 225 GHz microwave band, values calculated according to Mie scattering theory using the Best and P-S sleet raindrop size distributions best agree with experimental values. At 313 and 355 GHz terahertz-waveband frequencies, values calculated according to Mie scattering theory using the Weibull distribution and a prediction model following ITU-R recommendations best agree with experimental values. We furthermore find that attenuation due to rain increases in proportion to frequency for microwave-band frequencies below approximately 50 GHz, but that there is a peak at around 100 GHz, above which the degree of attenuation remains steady or decreases. Rain-indu- ced attenuation increases in proportion to the rainfall intensity.
Keywords:
Terahertz Wave, Microwave, Rain Attenuation, Weibull Distribution, ITU-R

1. Introduction
There is interest in ultra-high-speed wireless communications and remote sensing systems in the terahertz waveband [1] [2] . However, the features of atmospheric propagation in the microwave-to-terahertz frequency waveband during precipitation are affected in complex ways by the inherent properties of electromagnetic waves, absorption by atmospheric gases, and scattering due to particulates of clouds, rain, and snow. In terahertz bands above 300 GHz, in particular, it is easy to predict the effects of atmospheric gases and small-particle clouds, but rain attenuation due to raindrops with particle diameters that are relatively large relative to the wavelength have an especially strong effect and can significantly impact systems that employ atmospheric propagation in these bands.
Conventional methods of predicting rain attenuation in wavebands above the microwave band have been based on Mie scattering theory with various distributions of raindrop particle size [3] - [5] or with the International Telecommunications Union Radiocommunication Sector (ITU-R) recommendations, which provide a prediction model for rain attenuation between at wavelengths between 1 and 1000 GHz [6] . However, to the authors’ knowledge, no reports have been published on evaluating rain attenuation from the microwave through terahertz bands and comparing calculated values with actual measurements.
We verify the fitness of these methods by comparing between calculated and measured values for rain attenuation at rainfall intensities of up to 25 mm/hr at frequencies from 96 to 355 GHz. With the goal of applying these results to the wider wavebands used in the field of wireless communications, we furthermore evaluate changes in rain attenuation over wider ranges of frequency and rainfall intensity.
2. Calculated and Measured Values for Rain Attenuation
2.1. Calculation of Rain Attenuation
We applied Mie scattering theory with four types of raindrop size distribution as well as the predictive calculation method recommended by ITU-R for rain attenuation to calculate theoretical values for rain attenuation. Rainfall intensity was set at up to 25 mm/hr, and the following frequencies of 96, 140, 225, 313, and 355 GHz were used.
2.1.1. Calculations Based on Mie Scattering Theory
1) Calculation of rain attenuation
The rain attenuation coefficient A [dB], which represents attenuation due to raindrops after propagation over 1 km, can be calculated from the attenuation cross-section Qt, which is a function of particle diameter, D, the wavelength 𝜆, and the complex reflection coefficient of water droplets m and a raindrop size distribution N(D) as
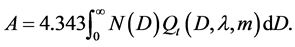 (1)
(1)
For this, the attenuation cross-section can be obtained by applying Mie scattering theory to attenuation due to spherical particles in plane-wave radiation. Here we use the formula of Hulst [7] for this:
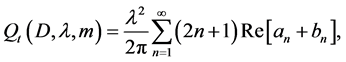 (2)
(2)
where an and bn are the Mie scattering coefficients [7] . These are complex amplitude coefficients that characterize the influence of the scattering fields created by multiple scattering within spheres, such as raindrops. We use the value given in Ray [8] for m, the complex reflection coefficient of water droplets.
2) Raindrop size distribution used in calculations
We used several raindrop size distributions for calculating rain attenuation by Mie scattering theory: the M-P, Best, P-S (hail, sleet, and snow), and Weibull distributions. These are shown in Equations (3)-(6), respectively.
The M-P distribution proposed in Marshall and Palmer [9] was found by fitting empirical data recorded in Ottawa, Canada, in 1946 with the filter-paper method. The fit of this distribution to the experimental dataset was not very good for drops with diameter less than 1 mm.
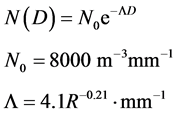 (3)
(3)
In this, D is the diameter in mm, and R is the precipitation rate in mm/hr.
In 1950, Best [10] proposed a drop-size distribution model based on analysis of a large amount of experimental data. The Best distribution is written as the following.
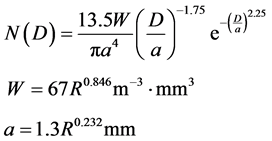 (4)
(4)
The P-S distribution was described by Litovinov in 1957 [11] and 1958 [12] as due to Polyakva and Shifrin, based on Russian data for hail, sleet, and snow. This model was also described by Krasyuk, Rozenberg and Chistyakov [13] in 1968 and by Rice and Peebles at the University of Tennessee [14] in 1975. It is a special case of the Gamma distribution proposed by Atlas and Ulbrich [15] in 1984.
 (5)
(5)
Here, 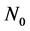 and
and 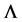 vary according to the rain type, as shown in Table 1.
vary according to the rain type, as shown in Table 1.
Sekine and Lind [16] proposed the Weibull distribution in 1982, using FOA data from the National Defence Research Institute of Sweden:
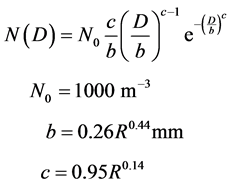 (6)
(6)
This distribution is still in use for microwave and terahertz applications [17] - [19] .
2.1.2. Predictions from ITU-R Recommendations
ITU-R P.838-3 [6] provides a prediction model for rain attenuation. In that model, the attenuation coefficient γR [dB/km] from rainfall intensity R is calculated from
 (7)
(7)
Here, the values of k and 𝛼 are determined for a given frequency f in the range 1 to 1000 GHz, and ITU-R P676-6 [20] gives values for these, reportedly found by fitting the attenuation amounts from scattering calculations to a power curve.
2.2. Experimental Values for Rain Attenuation
This section presents experimental values for rain attenuation at frequencies of 96, 140, 225, 313, and 355 GHz from previous reports.
2.2.1. Experimental Values for 96, 140, and 225 GHz
Experimental values for rain attenuation at 96, 140, and 225 GHz are taken from results by Nemarich et al. [21] ,
Table 1. Values for  and
and .
.
who performed measurements on 26 Jan 1983 at Camp Rilea, Oregon, USA. The measurements were performed. between transmitters and receivers placed 1.3 km apart on flat ground. The maximum rainfall was 10 mm/hr, with rain falling at a similar rate over a long period of time.
The average temperature during the experiment was 8.3˚C, average humidity was 95.7%, and absolute humidity was 1.4 g/m3. Variation in attenuation due to changes in absolute humidity was reportedly estimated to be less than 0.1 dB, so no correction for absolute humidity was performed. Figures 1(a)-(c) show the experimental values as triangles, and the dashed curves indicate regression curves for the experimental values found from fitting.
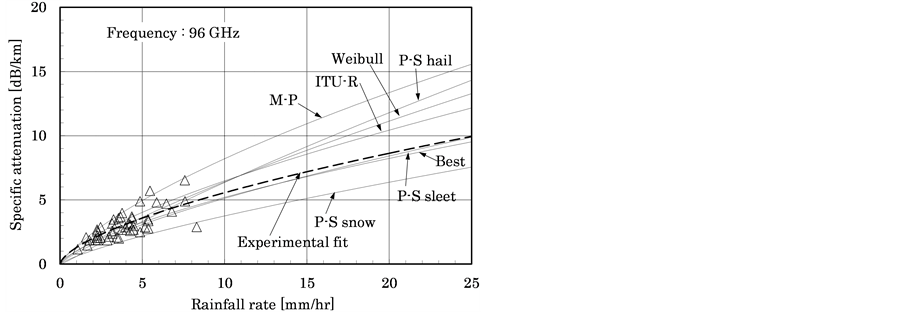
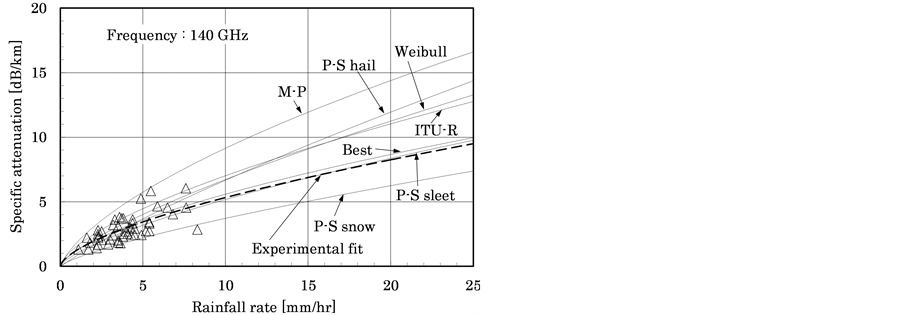
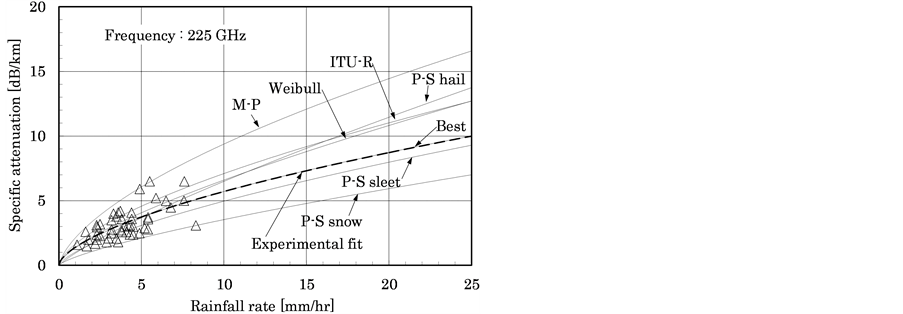
Figure 1. Comparisons between calculations and measure- ments at 96, 140 and 225 GHz.
2.2.2. Experimental Values for 313 and 355 GHz
1) 313 GHz
Experimental values for rain attenuation at 313 GHz are taken from the results of Babkin et al. [22] , who performed measurements in Central Europe between June and July 1969. Transmitters and receivers were placed 1.0 km apart on flat ground for the measurements. The maximum rainfall was 12 mm/hr. Figure 2(a) shows the experimentally obtained values as triangles, and the dashed curves indicate the regression curves fitted to those values. We evaluated rain attenuation at this frequency, with maximum rainfall intensity of 12 mm/hr, in [23] .
2) 355 GHz
Values for rain attenuation at 355 GHz are taken from the results of an experiment and evaluation performed by the authors between 10:00 and 16:00 on 28 Apr 2010 on the campus of the National Defense Academy in Yokosuka, Japan [24] . The maximum rainfall was 25 mm/hr, average temperature was 13.9˚C, average relative humidity was 89.2%, and atmospheric pressure varied between 991 and 994 hPa. Water vapor per unit volume was calculated as 11 g/m3, with the level of variation in attenuation due to atmospheric absorption below 0.5 dB/km, so experimental values were not corrected for absorption attenuation. Figure 2(b) shows the experimental values as triangles, and the dashed curves indicate regression curves fitted to those values.
3. Verification of Fit between Theoretical and Experimental Values
We verified the level of fit between theoretical and experimental values for the microwave-to-terahertz waveband. Verification was performed according to the root mean square error (RMSE) of regression curve values found by fitting calculated and experimental values for each frequency. Table 2 shows the results, with minimal RMSE values for each frequency underlined; the calculation method producing the minimal value is that with best fit to experimental values.
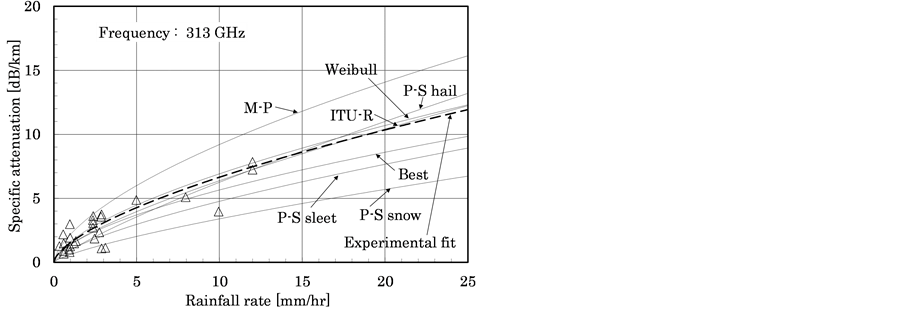
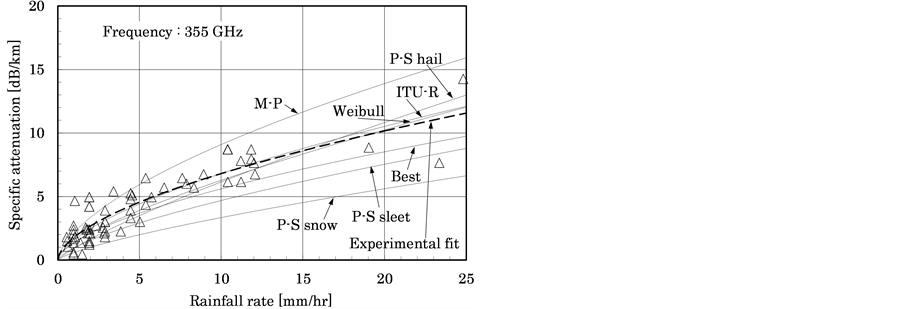
Figure 2. Comparisons between calculations and measurem- ents at 313 and 355 GHz.
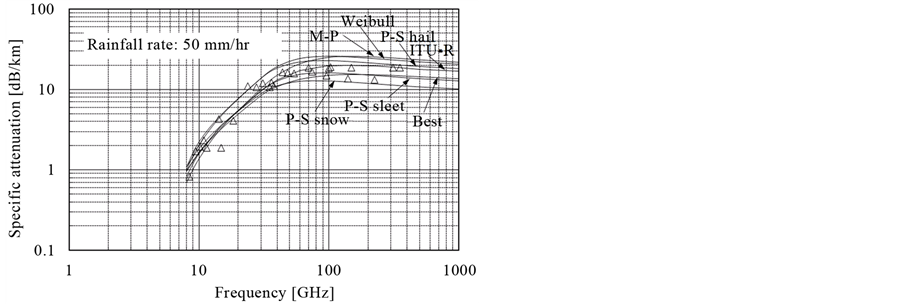
Figure 3. Rain attenuation from 8 GHz to 1000 GHz for various frequencies.
Table 2. Values of RMSE various frequency and calculation types.
The results suggest that rain attenuation in the 90 - 225 GHz waveband has best fit when using Mie scattering theory with the Best and P-S sleet distributions. At 313 and 355 GHz frequencies, good fit was obtained using Mie scattering theory with the Weibull distribution and by the prediction model according to ITU-R recommendations.
4. Influence of Frequency Characteristics and Effect of Rainfall Intensity on Rain Attenuation
In this section we compare calculated and measured values when holding rainfall intensity constant and varying frequency. We also demonstrate frequency characteristics when rainfall intensity is varied.
4.1. Frequency Characteristics
Figure 3 shows calculated and experimental values for rain attenuation at a rainfall intensity of 50 mm/hr when the frequency is varied between 8 and 1000 GHz. Values between 8.4 and 100 GHz are according to De Bettencourt [25] .
Here, we obtained a regression formula using experimental values from Nemarich [21] for 96, 140, and 225 GHz, from Babkin [22] for 313 GHz, and the authors [24] for 355 GHz, and calculated values for rain attenuation at a rainfall intensity of 50 mm/hr. The results suggest that rain attenuation increases in proportion to the frequency at microwave bands below 50 GHz, but peaks at around 100 GHz, and in higher wavebands remains largely constant or decreases.
4.2. Effects of Rainfall Intensity
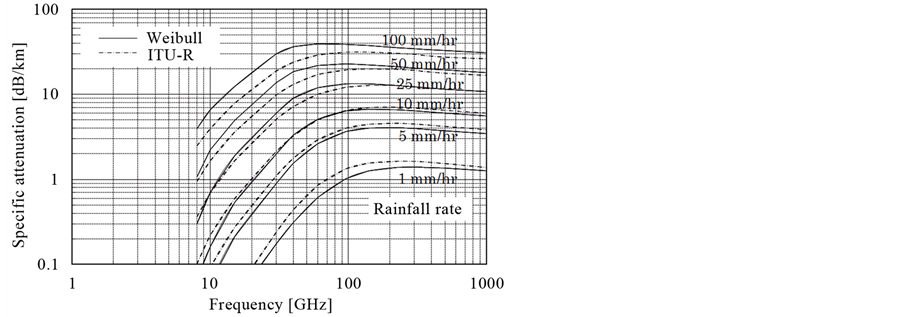
We calculated rain attenuation at frequencies between 8 and 1000 GHz, using the Weibull distribution and the ITU-R prediction model while varying rainfall intensity between 1 and 100 mm/hr. Figure 4 shows the results, and suggests that rain attenuation increases in proportion to rainfall intensity at all frequencies.
5. Conclusions
We verified fitness by comparing calculated and measured values for rain attenuation in the microwave-to-
Figure 4. Rain attenuation from 8 GHz to 1000 GHz for various rainfall rates.
terahertz frequency waveband. We found that in the 90 - 225 GHz microwave band, calculated values from Mie scattering theory using the Best and P-S sleet raindrop size distributions well agreed with experimental values. At 313 and 355 GHz terahertz-waveband frequencies, calculated values from Mie scattering theory using the Weibull distribution and a prediction model following ITU-R recommendations well agreed with experimental values.
We furthermore found that rain attenuation increased in proportion to frequency for microwave-band frequencies below approximately 50 GHz, but that there was a peak at around 100 GHz, above which attenuation remained steady or decreases. Rain attenuation increased in proportion to the rainfall intensity.
Cite this paper
Seishiro Ishii,Masahiro Kinugawa,Shunichiro Wakiyama,Shuji Sayama,Toshihisa Kamei, (2016) Rain Attenuation in the Microwave-to-Terahertz Waveband. Wireless Engineering and Technology,07,59-66. doi: 10.4236/wet.2016.72006
References
- 1. Akyildiz, J.A., Jornet, J.M. and Han, C. (2014) Terahertz Band Frontier for Wireless Communications. Physical Communication, 12, 14-32.
http://dx.doi.org/10.1016/j.phycom.2014.01.006 - 2. Fitch, M.J. and Osiander, R. (2004) Terahertz Waves for Communications and Sensing. Johns Hopkins APL Technical Digest, 25, 348-355.
- 3. Sekine, M. (1986) Rain Attenuation from Various Raindrop-Size Distributions. Transactions on IECE of Japan (Section E), 69, 711-712.
- 4. Sekine, M., Chen, C.D. and Musha, T. (1987) Rain Attenuation from Log-Normal and Weibull Rain-Drop Distributions. IEEE Transactions on Antennas Propagation, AP-35, 358-359.
http://dx.doi.org/10.1109/TAP.1987.1144099 - 5. Sekine, M. and Chen, C.D. (1989) Inversion Problem in Rain Attenuation Calculations. Proceedings of the 1989 URSI International Symposium on Electromagnetic Theory, Stockholm, 23-25.
- 6. International Telecommunication Union (2005) Specific Attenuation Model for Rain for Use in Prediction Methods. Recommendation ITU-R, P.838-3.
- 7. Hulst, H.C. (1957) Light Scattering by Small Particles. Wiley, New York.
- 8. Peter, S.R. (1972) Broadband Complex Refractive Indices of Ice and Water. Applied Optics, 11, 1836-1844.
http://dx.doi.org/10.1364/AO.11.001836 - 9. Marshall, J.S. and Palmer, W.M.K. (1948) The Distribution of Raindrops with Size. Journal of Meteorology, 5, 165-166.
http://dx.doi.org/10.1175/1520-0469(1948)005<0165:TDORWS>2.0.CO;2 - 10. Best, A.C. (1950) The Size Distribution of Raindrops. Quarterly Journal of the Royal Meteorological Society, 76, 16-36.
http://dx.doi.org/10.1002/qj.49707632704 - 11. Litovinov, I.V. (1957) On the Distribution Function of Particles of Rainfall. Izvestia AN SSSR, Geophysical Series, 838-839.
- 12. Litovinov, I.V. (1958) Size Distribution of Raindrops from Melting Hail. Izvestia, Geophysical Series, 903-912.
- 13. Krasyuk, N.P., Rozenberg, V.I. and Chistyakov, D.A. (1968) Attenuation and Scattering of Radar Signals by Radio with Shifrin and Marshall-Palmer Drop Size Distributions. Radio Engineering and Electronic Physics, 13, 1638-1640.
- 14. Rice, R.W. and Peebles, P.A. (1975) Investigation of Radar Rain Clutter Cancellation Using a Polarization Method. Final Technical Report, University of Tennessee, Knoxville.
- 15. Ulbrich, C.W. and Atlas, D. (1984) Assessment of the Contribution of Differential Polarization to Improve Rainfall Measurements. Radio Science, 19, 49-57.
http://dx.doi.org/10.1029/RS019i001p00049 - 16. Sekine, M. and Lind, G. (1982) Rain Attenuation of Centimeter, Millimeter and Submillimeter Radio Waves. Proceedings of the 12th European Microwave Conference, Helsinki, 584-589.
http://dx.doi.org/10.1109/euma.1982.333124 - 17. Sekine, M. and Chen, C.D. (1985) Rain Attenuation in Terrestrial and Satellite Communications Links. Proceedings of the 15th European Microwave Conference, Paris, 985-990.
http://dx.doi.org/10.1109/euma.1985.333606 - 18. Chen, C.D., Okamoto, Y. and Sekine, M. (1985) Cancellation of Radar Rain Clutter Using Circular Polarization. Transactions on IECE of Japan, E68, 620-624.
- 19. Sekine, M. (1986) The Relationship between Radar Reflectivity and Rainfall Rate. Transactions on IECE of Japan, E69, 581-582.
- 20. International Telecommunication Union (2005) Attenuation by Atmospheric Gases. Recommendation ITU-R, P.676-3.
- 21. Nemarich, J., Wellman, R.J. and Lacombe, J. (1988) Backscatter and Attenuation by Falling Snow and Rain at 96,140, and 225 GHz. IEEE Trans. Geoscience and Remote Sensing, GRS-26, 319-329.
- 22. Babkin, Y.S., Zimin, N.N., Izyumov, A.O., Iskhakov, I.A., Sokolov, A.V., Stroganov, L.I., et al. (1970) Measurement of Attenuation in Rain Over 1 km Path at a Wavelength of 0.96 mm. Radio Engineering and Electronic Physics, 15, 2164-2166.
http://dx.doi.org/10.1109/36.3034 - 23. Ishii, S., Sayama, S. and Mizutani, K. (2010) Rain Attenuation at Terahertz. Wireless Engineering and Technology, 1, 92-95.
http://dx.doi.org/10.4236/wet.2010.12014 - 24. Ishii, S., Sayama, S. and Kamei, T. (2011) Measurement of Rain Attenuation in Terahertz Wave Range. Wireless Engineering and Technology, 2,119-124.
http://dx.doi.org/10.4236/wet.2011.23017 - 25. De Bettencourt, J.T. (1974) Statistics of Millimeter Wave Rainfall Attenuation. Journal de Recherches Atmospheriques, 8, 98-112.