Wireless Engineering and Technology
Vol.2 No.2(2011), Article ID:4540,8 pages DOI:10.4236/wet.2011.22006
Bandwidth Enhancement and Size Reduction of Microstrip Patch Antenna by Magnetoinductive Waveguide Loading
![]()
Department of ETV and ECE, National Institute of Technical Teachers’ Training and Research, Chandigarh, India.
Email: shyampattnaik@yahoo.com, joshij11@rediffmail.com
Received January 11th, 2011; revised February 6th, 2011; accepted February 9th, 2011.
Keywords: Bandwidth enhancement, Magnetoinductive waveguide, Split squared ring resonator (SSRR), Negative permeability, Magnetic coupling, Dispersion relation
ABSTRACT
A planar magnetoinductive (MI) waveguide loaded rectangular microstrip patch antenna is presented and discussed. The MI waveguide consists of two planar metamaterial split squared ring resonators (SSRRs) placed in between two microstrip lines. The backward wave propagation takes place through this structure. The rectangular microstrip patch antenna is magnetically coupled to the MI waveguide. The unloaded rectangular microstrip patch antenna resonates at 37.10 GHz. When loaded with planar MI waveguide, its resonant frequency is reduced to 9.38 GHz with the bandwidth and gain of 44% and 4.16 dBi respectively. In loaded condition, the dimension of antenna is 12.50 mm x 3.70 mm (0.390 λ x 0.115 λ). The appreciable bandwidth is achieved in such a small size antenna. The pass band frequency of MI waveguide is predicted by using the theoretical model of dispersion equation. The effective medium theory is used to verify the metamaterial characteristics of SSRR. The simulated results and theoretical calculations are also presented. The results show that the proposed method can be used to design compact and high bandwidth microstrip patch antennas.
1. Introduction
In 1967, the Russian physicist Viktor Veselago presented the properties of artificial materials named as metamaterials. These materials possess negative permeability (μ) and negative permittivity (ε) that support the backward wave propagation of electromagnetic waves [1]. About 30 years later, in 1999 Pendry proposed an interesting subwavelength element termed as split ring resonator (SRR) to achieve negative permeability. Basically, SRR is a LC tank circuit having equivalent inductance “L” and the capacitance “C” between two concentric rings resonating at particular frequency [2]. Further, the negative permittivity of the wire array is experimentally verified and is presented in [3]. Metamaterials are the composite structures of periodically arranged SRRs and wires having negative refractive index hence, they are also called as negative index materials (NIM). The basic properties of metamaterials like effective permeability and permittivity are normally analyzed by using effective medium theory [4-7]. However, this approach does not discuss the internal modes of the structure. These modes are the short-wavelength eigen modes present in the microscopic nature of periodic metamaterial split ring resonator array. These eigen modes are referred as magnetoinductive waves which are the slow waves that only propagate within certain pass band along the periodically coupled array of small magnetic resonators that is SRRs and wires [8,9]. The SRR elements or unit cells in the array are magnetically coupled due to which the voltage get induced in the resonators to generate the magnetoinductive waves. Such waves exist in one, two, and in three dimensional patterns of array. Magnetoinductive waves permit the propagation of low frequency signals in the miniaturized structures hence; it is an interesting and promising phenomenon for microwave applications. By using this phenomenon, different components like magnetoinductive waveguide transducer, directional couplers, power dividers, splitters, tapers etc. have been proposed and fabricated [7-14].
Recently, metamaterial is used to load the microstrip patch antennas as superstrate and substrate to enhance the gain, bandwidth, directivity as well as to achieve miniaturization [6-7,15-18]. Pai Yen Chen and Andrea Alu (2010) proposed a dual band elliptical patch antenna partially loaded with negative permeability (μ) metamaterial and reported that such loading enhances the bandwidth and miniaturize the antenna [15]. J.G. Joshi et al. in 2010 presented a planar electrically small rectangular microstrip patch antenna loaded with metamaterial square split ring resonator (SRR) [6]. The modification of TM020 mode is reported by partially metamaterial loaded rectangular patch antenna [16]. Miniaturized circular microstrip patch antenna partially loaded with metamaterial has been reported in [17]. Le-Wei Li et al. proposed a novel rectangular microstrip patch antenna partially loaded with planar metamaterial patterned substrate [18]. The above cited evidences from the literature inspired the authors to propose a loading on microstrip patch antenna using planar MI waveguide.
E. Shamonina et al. investigated the phenomenon of magnetoinductive waves in one, two and three dimensional periodic structure of SRRs. In one dimensional axially arranged structure or lattice the wave propagation is forward whereas it is backward in planar orientation. In their work, the dispersion relations are also presented indicating the range of frequencies for which propagation is possible whereas other frequencies get stopped or rejected. The authors reported that the frequency range over which the effective permeability varies rapidly from high positive value to high negative value is the pass band of magnetoinductive waves [9-11]. Ilya V. Shadrivov et al. experimentally demonstrated the propagation of magnetoinductive electromagnetic waves in an array of SRRs operating at microwave frequencies. In this work, the transverse and longitudinal orientation of the SRRs array is used. The SRRs are excited by separate antennas in which the bandwidth changes dramatically as the coupling coefficient between the resonators is varied. In longitudinal array, the forward wave propagation takes place whereas the transverse geometry supports backward wave propagation [8]. Syms et al. examined the higher order interactions in MI waveguides [11] and theory of interaction between magnetoinductive and electromagnetic waves in SRRs and rods is illustrated by Syms et al. The coupling between neighbouring SRRs and propagation of electromagnetic waves with their related dispersion equation in stop and pass band in forward and backward wave propagation are also elaborated [12]. The theoretical model of dispersion relation and delay time of this device is also presented in [13,14]. Recently, J.G. Joshi et al. presented a compact and high gain rectangular microstrip patch antenna loaded with MI waveguide for public safety band applications. Labyrinth resonators are used to design this MI waveguide [7].
The objective of this paper is to present a squared split ring resonator (SSRR) based MI waveguide loading technique to load the rectangular microstrip patch antenna to enhance its bandwidth and to reduce the size. In the proposed work, rectangular microstrip patch antenna is loaded with planar MI waveguide consisting of metamaterial SSRRs. Initially, metamaterial characteristics of the SSRR unit cell are verified and it is found that the SSRR endows negative permeability (μ-negative). In loading condition, the rectangular microstrip patch is excited by coaxial feed. The MI waveguide is closely placed near to the rectangular microstirp patch. Due to magnetic coupling the electric field gets induced in MI waveguide and ultimately the SSRR elements get excited. This excitation makes the SSRRs to exhibit the metamaterial characteristics. After loading, the rectangular microstrip patch antenna shows reduction in its resonant frequency that is miniaturization is accomplished as well as the bandwidth is appreciably enhanced. In this paper, both effective medium theory as well as magnetoinductive wave analysis is used to validate the work.
The paper is structured into five sections. The sketch and detailed geometrical dimensions of the proposed planar MI waveguide loaded rectangular microstrip patch antenna with the design of metamaterial SSRR unit cell is presented in Section 2. In Section 3, the metamaterial properties of SSRR are verified using effective medium theory. The simulation results of unloaded and MI waveguide loaded rectangular microstrip patch antenna are also presented and analyzed in this section. In Section 4, the theoretical aspects related to dispersion relation and equivalent circuit analysis are discussed to validate the obtained results. Finally, the paper is concluded in Section 5.
2. Antenna Design
Figure 1 and Figure 2 respectively depicts the geometrical structure and cross sectional view of rectangular microstrip patch antenna loaded with planar MI waveguide. This antenna is an integrated structure of rectangular microstrip patch antenna loaded by planar magnetoinductive waveguide. The dimensions of rectangular microstrip patch antenna are; length Lr = 2.4 mm and width Wr = 2 mm respectively that is co-axially fed at the location x = –1.2 mm and y = 1.2 mm. The waveguide structure consists of two microstrip lines which are inductively coupled by means of two split squared ring resonator array for effective propagation of magnetoinductive waves. The position of SSRRs is parallel to microstrips along the waveguide line of symmetry. The distance between microstrip line and SSRR array is gm = 0.15 mm. The SSRRs are transversely oriented between the two
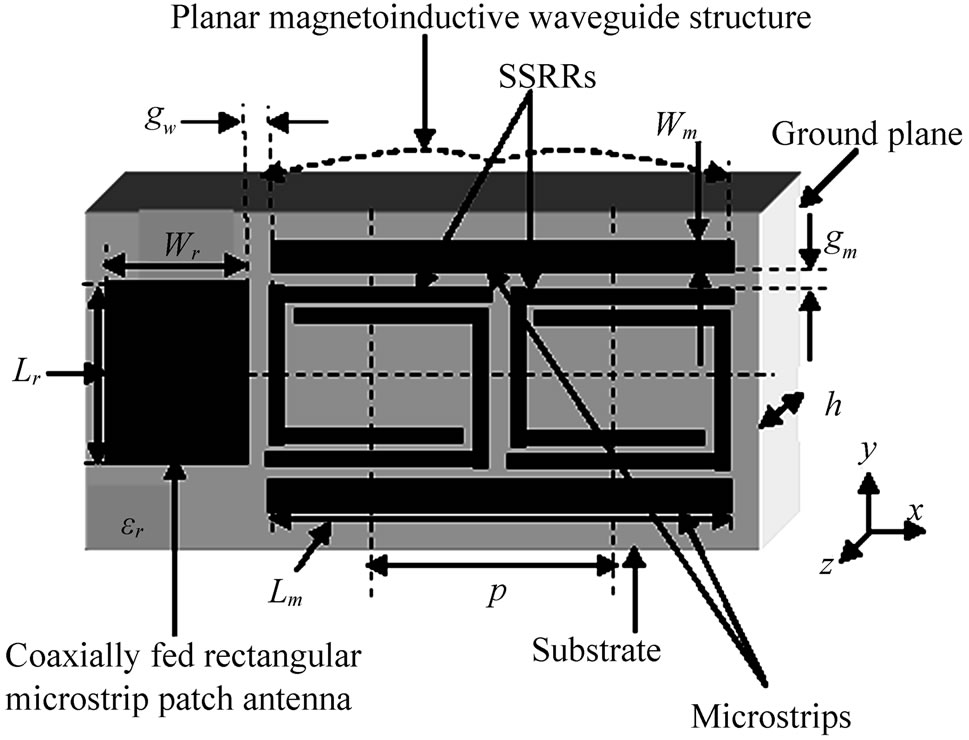
Figure 1. Sketch and geometrical structure of rectangular microstrip patch antenna loaded with magnetoinductive waveguide.
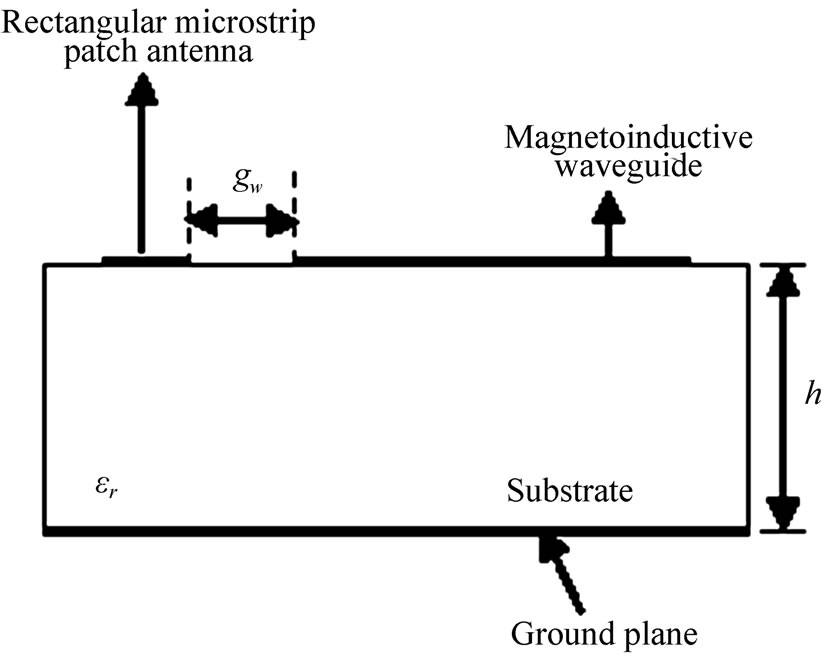
Figure 2. Cross sectional view of rectangular microstrip patch antenna loaded with magnetoinductive waveguide.
microstrip lines that constitute a finite length planar waveguide structure. The rectangular microstrip patch antenna is placed in the proximity to the waveguide at a distance gw = 0.25 mm. The length of microstrip lines is Lm = 10.25 mm and width Wm = 0.50 mm.
To realize the magnetoinductive waves, the ratio of resonant wavelength to the structure period should be of the order of 10 [8]. Hence, to satisfy this condition the period of this structure (p) is kept at 5.25 mm as shown in Figure 1. The total dimensions of the proposed antenna structure is 12.50 mm x 3.70 mm (0.390 λ x 0.115 λ), indicating a compact size antenna. Figure 3 shows the geometry of SSRR unit cell of the dimensions; length of outer strip l1 = 5 mm and the overlapping length of inner strip l2 = 4.6 mm. The gap at split of the strips (g), the separation between inner and outer strips (s) and width of the strips (w) are in the order of g = s = w = 0.2 mm.
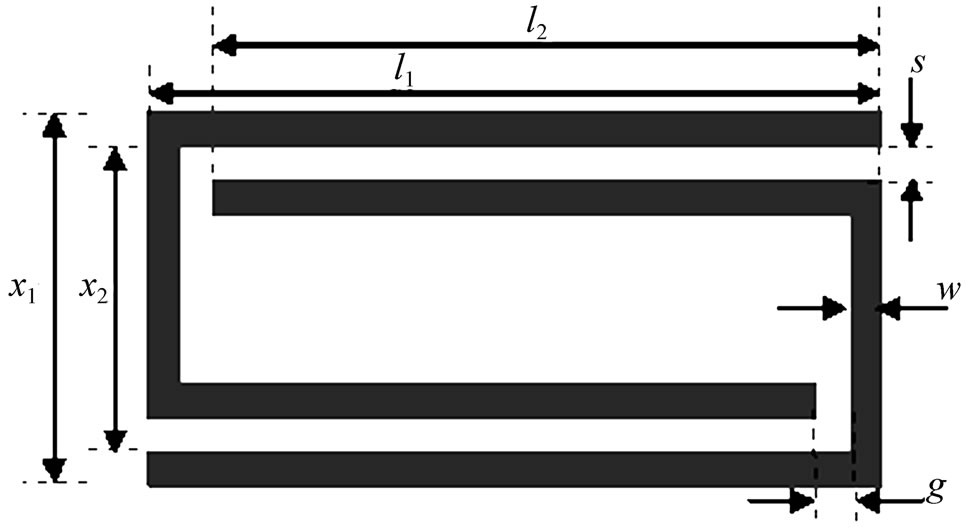
Figure 3. Geometrical structure of metamaterial split squared ring resonator (SSRR) unit cell.
The side length dimensions of the strips are; x1 = 2.4 mm and x2 = 2 mm respectively. The dimension of the SSRR at its resonant frequency 4.09 GHz is 0.033 λ x 0.068 λ. This antenna is designed and simulated on RT Duriod 5880 substrate of thickness h = 3.175 mm and dielectric constant εr = 2.2. In this work, method of moment based IE3D electromagnetic simulator of Zeland software incorporation, Fremont, USA is used to simulate the antenna.
3. Simulation and Verification of Metamaterial Characteristics
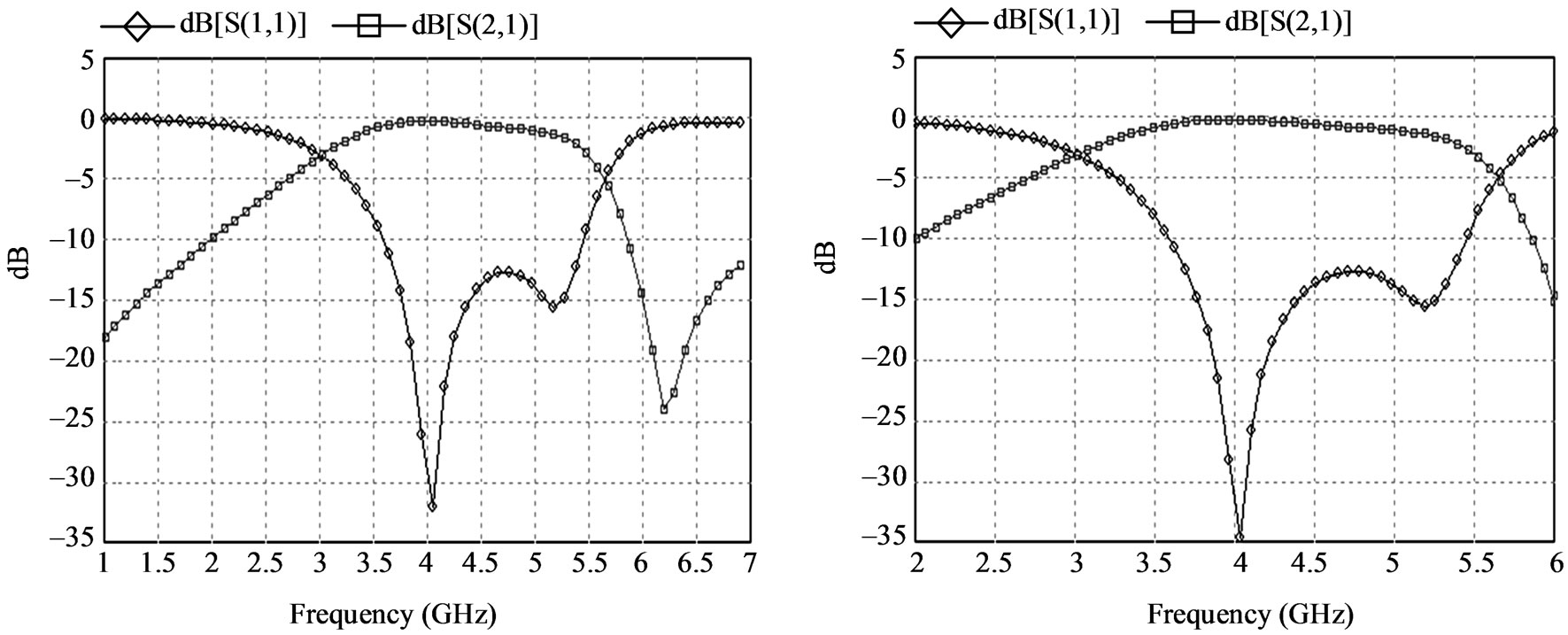
The SSRR and the designed antenna are simulated using IE3D of Zeland Software Incorporation. At the outset attempt is made to realize or verify the metamaterial characteristics of SSRR in the defined frequency band. Figure 4(a) and Figure 4(b) respectively shows simulated reflection coefficient (S11) and transmission coefficient (S21) characteristics of an isolated SSRR unit cell. Figure 4(b) shows the zoomed resonance behaviour of the SSRR unit cell in 2 GHz to 6 GHz frequency band and it resonates at 4.09 GHz. Figure 5 indicates the permeability characteristics (μ) of SSRR unit cell which exhibits the negative permeability (μr) in the frequency range 3.5 GHz to 5.5 GHz. Thus, the SSRR is single negative that is explicitly μ-negative (MNG) metamaterial.
The average cell size of SSRR unit cell is smaller than λg/4 which satisfies the condition of effective homogeneity [19]. Thus, the effective medium theory is applied to determine the permeability (μr) and permittivity (εr). The effective medium parameters are derived from the reflection and transmission coefficient parameters (S-parameters) using Nicolson-Ross-Weir (NRW) approach [4-7]. The expressions of Equations (1) and (2) are used to determine these effective medium parameters.
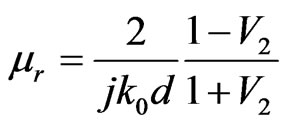 (1)
(1)
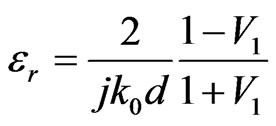 (2)
(2)
where k0 is wave number, d is the thickness of substrate, V1 and V2 are the composite terms to represent the addition and subtraction of S-parameters. In SSRR, the factor k0d = 0.266 which is  1 [4-7]. The values of V1 and V2 are estimated using Equations (3) and (4).
1 [4-7]. The values of V1 and V2 are estimated using Equations (3) and (4).
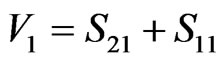 (3)
(3)
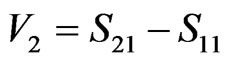 (4)
(4)
By using the obtained S-parameters, mathematical equations and MATLAB code the metamaterial characteristics have been verified [4-7].
From Figure 4(a) and Figure 4(b) a good matching is observed at 4.09 GHz. In the same frequency band as shown in Figure 5, the magnetic permeability of the SSRR is negative thus; the structure exhibits negative refractive index. Hence, the split squared ring resonators used in constituting the MI waveguide to load the rectangular microstrip patch antenna exhibits the metamaterial behaviour.
 (a) (b)
(a) (b)
Figure 4. (a) S-parameters (S11) and (S21) of metamaterial SSRR; (b) Zoom of S-parameters.
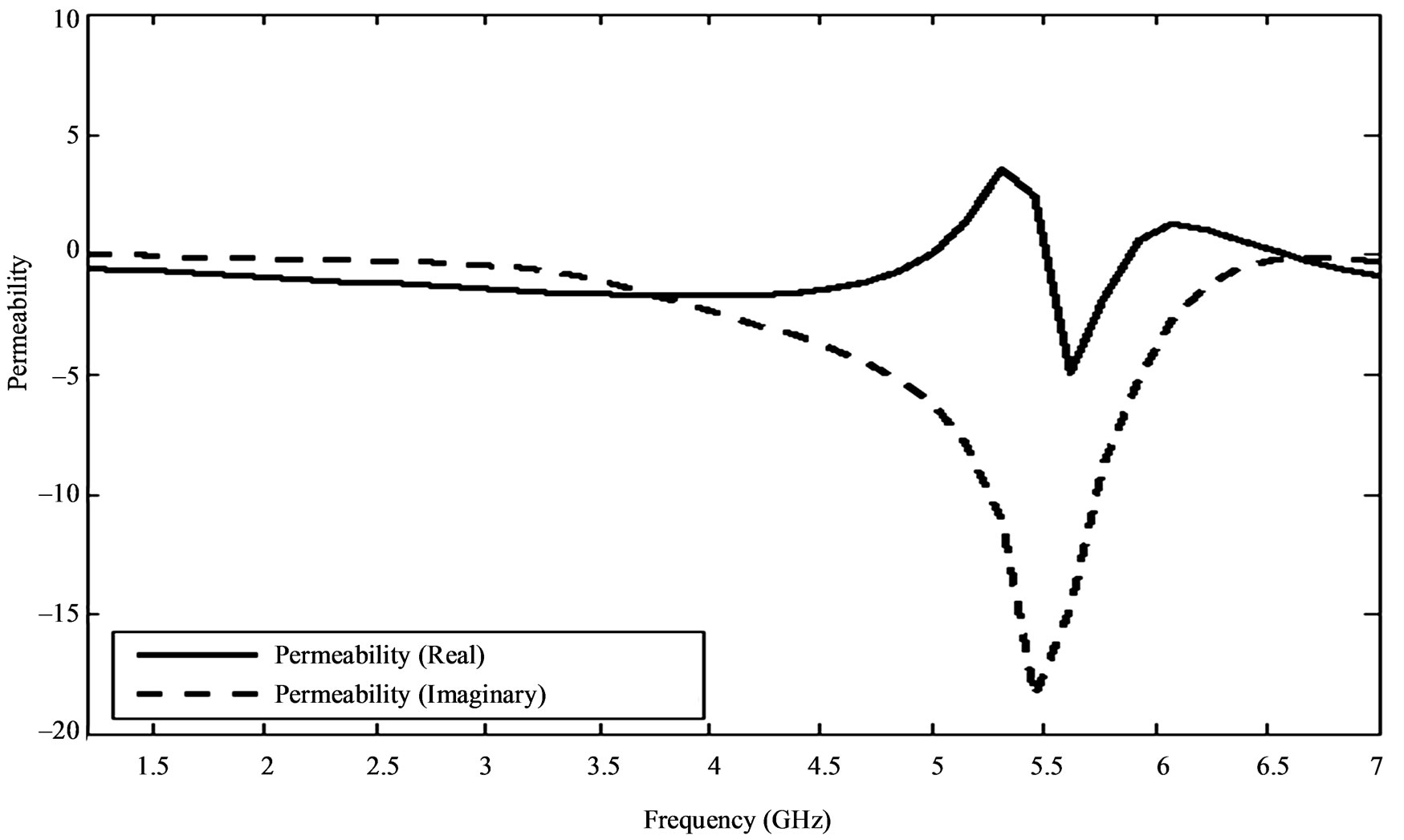
Figure 5. Permeability (μr) characteristic of SSRR.
Figure 6 which represents the return loss (S11) characteristics of the unloaded rectangular microstrip patch antenna resonates at frequency fr = 37.10 GHz with the bandwidth and gain of 15% and 0.5 dBi respectively. Hence, to decrease the resonant frequency and to increase the gain as well as bandwidth in the same dimensions of the rectangular microstrip patch antenna; it is loaded with planar MI waveguide. Figure 7 depicts the return loss characteristics (S11) of the rectangular microstrip patch antenna loaded with MI waveguide. The loaded antenna resonates at 9.38 GHz with the bandwidth of 44%. This is considerably a high bandwidth in such a compact size antenna. In the loaded antenna structure the spacing between neighbouring SSRRs is small consequently the mutual coupling is increased. In this antenna the directivity of 7.5 dBi is achieved. In general, for efficient radiation the electrical size of the antenna at resonant frequency 9.38 GHz should be equal to λ/2 that is 16 mm (at λ = 32 mm). In loaded condition the size of the proposed antenna is 12.50 mm x 3.70 mm (0.390 λ x 0.115 λ). The design of two long strips of the SSRR forms the two capacitors which cancel the electric dipoles associated with them at the resonance condition. Hence, in this antenna the cross-polarization gets reduced.
Figure 8(a) and Figure 8(b) respectively depicts the azimuth and elevation radiation patterns of the proposed magnetoinductive waveguide antenna showing the gain of 4.16 dBi. Figure 9 shows the current distribution of unloaded rectangular microstrip patch antenna at resonant frequency 37.10 GHz. Figure 10 represents the current distribution of loaded rectangular microstrip patch antenna loaded with MI waveguide at resonant frequency 9.38 GHz. Arrow shows the direction of current distribution.
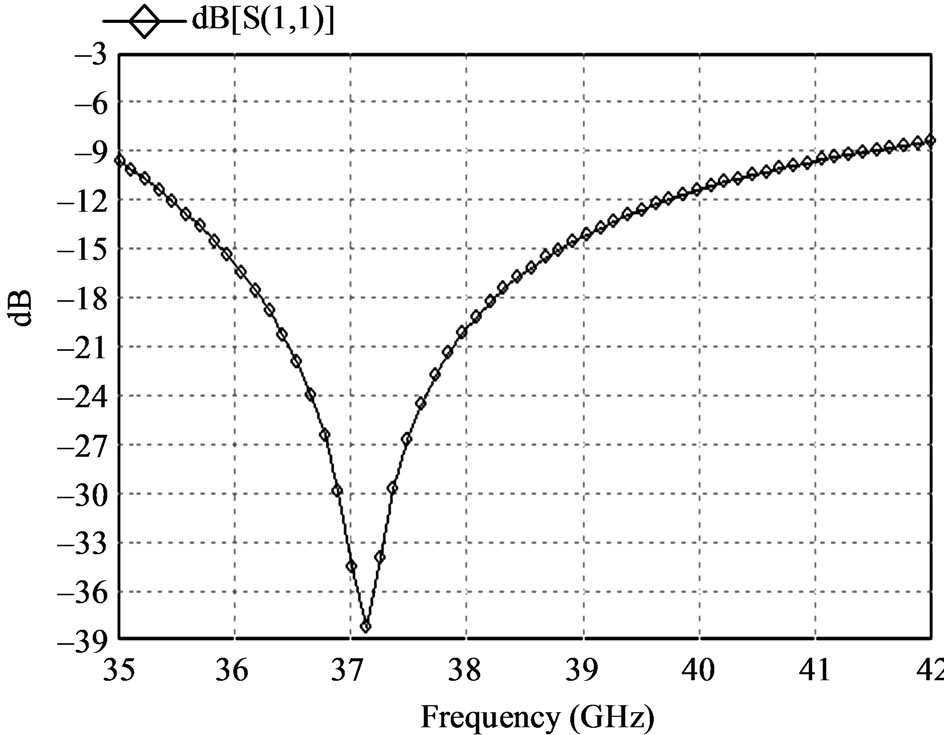
Figure 6. Return loss (S11) characteristics of unloaded rectangular microstrip patch antenna.

Figure 7. Return loss (S11) characteristics of rectangular microstrip patch antenna loaded with magnetoinductive waveguide.
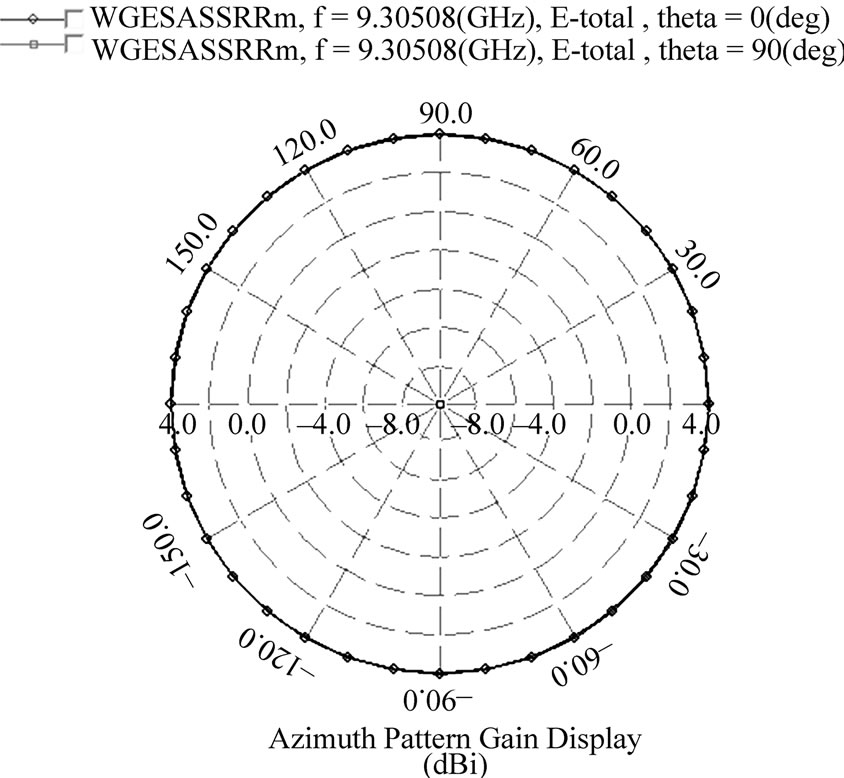 (a)
(a)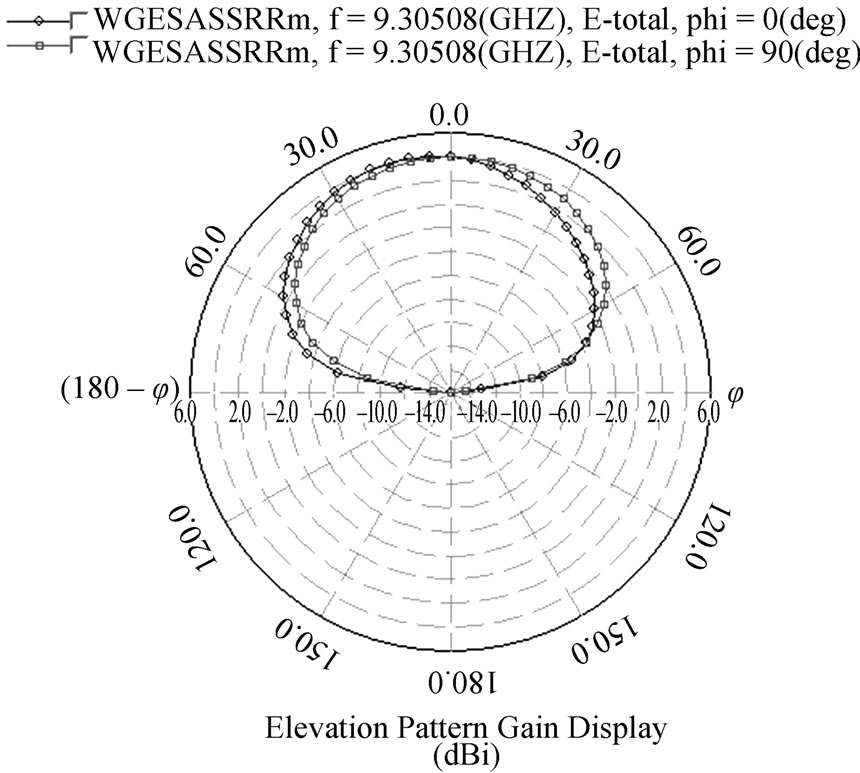 (b)
(b)
Figure 8. Radiation patterns of rectangular microstrip patch antenna loaded with magnetoinductive waveguide (a) azimuth (b) elevation.
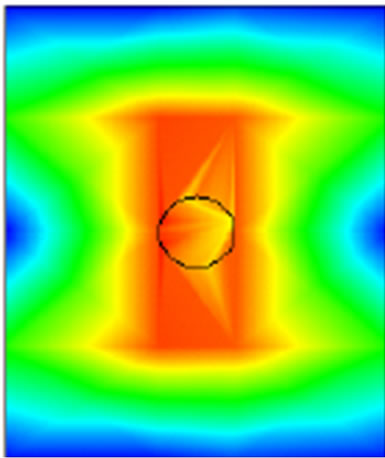
Figure 9. The simulated current distribution of unloaded rectangular microstrip patch antenna at 37.10 GHz.
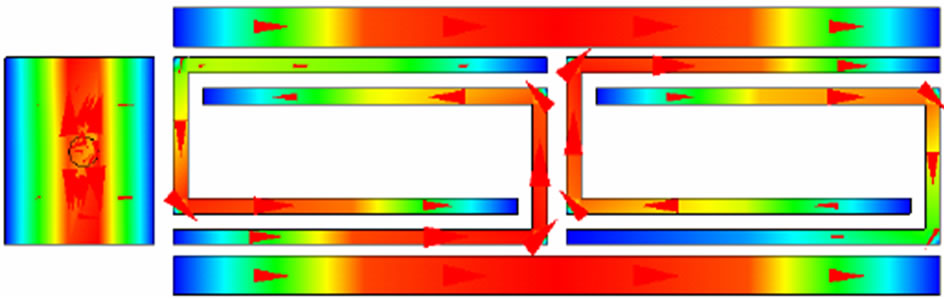
Figure 10. The simulated current distribution of MI waveguide loaded rectangular microstrip patch antenna at 9.38 GHz.
4. Theoretical Discussion
From Figure 1 it is seen that the rectangular microstrip patch antenna is positioned at the open end of MI waveguide structure. The electromagnetic waves radiated by the rectangular microstrip patch antenna at its resonant frequency are confined into the planar magnetoinductive waveguide through magnetic coupling. The magnetoinductive waves propagate through the SSRRs because they are mutually coupled in transverse geometry [7-14]. The MI waves are surface waves propagating on this planar substrate along the direction of an array. The electric field in first SSRR element is coupled to the second SSRR element by mutual induction and the process becomes persistent. The coupling coefficient strongly depends on spacing between SSRR elements of the array. In this structure, the interface or mutual induction between two resonators takes place and the excitation is transferred to the next resonator. This interface between the coupled SSRRs generates the strong mutual induction and the magnetoinductive approximation can be applied to this structure. Thus, the magnetic coupling between the elements causes the propagation of the magnetoinductive waves (MIWs) in metamaterial SSRRs comprising the array. As it is a planar transverse metamaterial based geometry, it supports the backward wave propagation hence the group and phase velocities are opposite in direction [7-14].
The dispersion relation of magnetoinductive waves propagating in the SSRR array of MI waveguide is expressed by Equation (5) [7-14].
 (5)
(5)
where M is the mutual inductance between adjacent SSRR, a is periodicity of the array, L is the inductance of resonant element, ω is angular frequency and k is the wave number. The resonant frequency (ω0) of an isolated SSRR unit cell is expressed by Equation (6) [7,13-14].
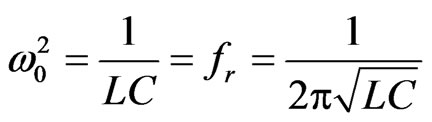 (6)
(6)
where L and C are the equivalent inductance and capacitance of SSRR respectively.
The inductance (L) is estimated by modifying the mathematical equations expressed in [20-21]. Equation (7) is used to calculate the value of “L”.
 (7)
(7)
where ρ is the filling ratio expressed as
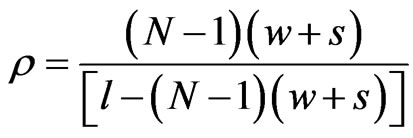 , L1avg is average length of the SSRR expressed by
, L1avg is average length of the SSRR expressed by , and N is number of rings.
, and N is number of rings.
The equivalent capacitance (C) of an isolated SSRR unit cell is calculated by dividing it into two sections as; the upper and lower two strips as fingers of an interdigital capacitor (CI) and secondly the parallel plate capacitance (Cs) between two inner strips. Therefore, the capacitance (C) is estimated using Equation (8).
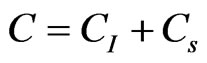 (8)
(8)
The inter-digital capacitance (CI) is calculated using Equation (9) [19].
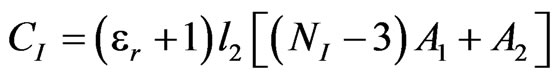 (pF) (9)
(pF) (9)
where NI is the number of fingers of inter-digital capacitor.
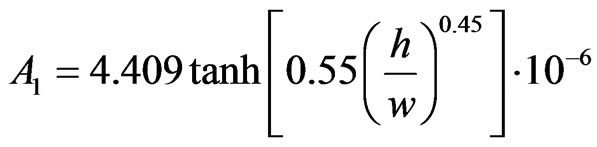 (pF/μm) (10)
(pF/μm) (10)
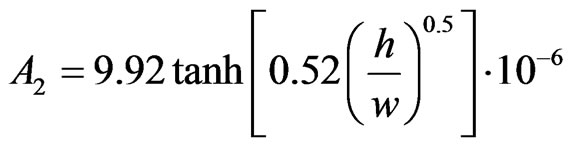 (pF/μm) (11)
(pF/μm) (11)
For calculations of A1 and A2 the dimensions of the SSRR are considered in μm.
Similarly, the parallel plate capacitance between two inner strips (Cs) is estimated using Equation (12) [22].
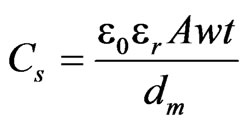 (12)
(12)
where ε0 is the permittivity of free space (8.854 x 10–12 F/m), A is modified factor (A = 60), t is the thickness of metal strips, and dm is the distance between two inner strips.
By using equivalent circuit theory and above mathematical equations, the estimated values of equivalent circuit elements are; inductance L = 7.45 nH and capacitance C = 0.211 pF respectively. Theoretically, from these values the resonant frequency (fr) of SSRR unit cell is found to be 4.03 GHz. The simulated resonant frequency of an isolated SSRR unit cell is fr = 4.09 GHz (Figure 4(b)) which is in good agreement with the theoretical results.
The mutual inductance M between two neighbouring SSRRs of the array is calculated using Equation (13) [21].
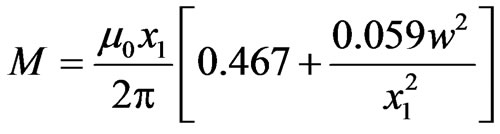 (13)
(13)
The estimated mutual inductance is M = –0.224 nH and the coupling coefficient of 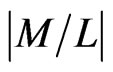 is 0.030. Here, the minus sign indicates the backward wave propagation in planar configuration of the SSRR array. Thus, from equation (5) the dispersion relation is negative indicating the propagation of backward wave in planar configuration causing to pass the lower resonant frequencies beyond which the propagation is not possible. The dispersion relation (5) is modified to determine pass band of MI waveguide and ultimately the resonant frequency of loaded antenna is expressed by Equation (14) beyond which there is no propagation.
is 0.030. Here, the minus sign indicates the backward wave propagation in planar configuration of the SSRR array. Thus, from equation (5) the dispersion relation is negative indicating the propagation of backward wave in planar configuration causing to pass the lower resonant frequencies beyond which the propagation is not possible. The dispersion relation (5) is modified to determine pass band of MI waveguide and ultimately the resonant frequency of loaded antenna is expressed by Equation (14) beyond which there is no propagation.
 (14)
(14)
Therefore, through the MI waveguide the propagation of resonant frequency 4.09 GHz at good matched condition in the pass band (3.5 GHz to 5.5 GHz) of MI waveguide takes place. In the same frequency band the effective permeability is negative which also validates the pass band of MI waveguide [9-11] beyond this band there is no propagation. Thus, the loaded rectangular microstrip patch antenna should resonate at 4.09 GHz by decreasing its resonant frequency 37.10 GHz in unloaded condition. But due to loading effect, there is magnetic coupling between rectangular microstrip patch antenna and planar MI waveguide that result to develop the mutual induction between these two elements. Due to this effect the pass band frequency of MI waveguide and ultimately the resonant frequency of loaded rectangular microstrip patch antenna is shifted to 9.38 GHz by a coupling coefficient of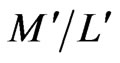 , where M' is the mutual inductance between the rectangular microstrip patch antenna and MI waveguide. L' is the inductance of rectangular microstrip patch antenna. Further, equation (10) is modified by incorporating the factor
, where M' is the mutual inductance between the rectangular microstrip patch antenna and MI waveguide. L' is the inductance of rectangular microstrip patch antenna. Further, equation (10) is modified by incorporating the factor 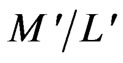 by considering the effect of magnetic coupling and expressed by Equation (15).
by considering the effect of magnetic coupling and expressed by Equation (15).
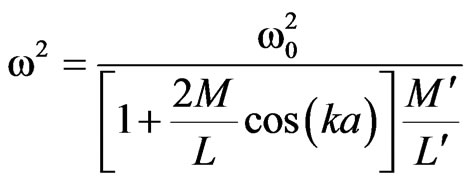 (15)
(15)
The mutual inductance M' is calculated by using Equation (16).
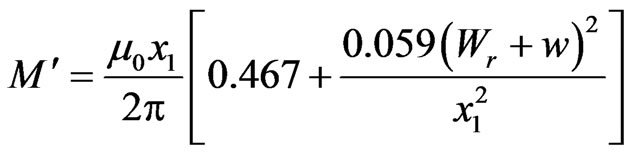 (16)
(16)
The inductance of rectangular microstrip patch antenna L' is computed by using its equivalent circuit and expressed by Equation (17) [23,24].
 (17)
(17)
where ωr = 2πfr; fr is the design frequency, and Cp is the parallel capacitance in the equivalent circuit given by Equation (18) [23,24].
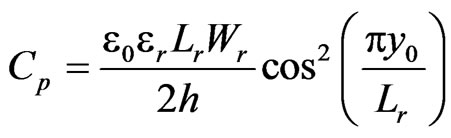 (18)
(18)
where y0 is the Y-coordinate of the feed point.
The estimated values of inductance L' and mutual inductance M' are 1.25 nH and 0.247 nH respectively. Therefore, in the loaded condition due to magnetic coupling effect the resonant frequency is shifted to 9.32 GHz which is closely matching with the simulated resonant frequency 9.38 GHz of the MI waveguide loaded rectangular microstrip patch antenna (Figure 7). Thus, due to MI waveguide loading resonant frequency of rectangular microstrip patch antenna is decreased to 9.38 GHz over the pass band of 8.85 GHz to 13 GHz at good matched condition.
5. Conclusions
This paper presents a new approach to enhance the bandwidth and reduce the size of microstrip patch antenna. The theoretical explanation using effective medium theory, dispersion relation and equivalent circuit agrees well with the simulated results. A good agreement is observed in terms of resonant frequency and bandwidth with the simulated results thus validating the approach. In future, the authors intend to carry out experimental measurements and to propose such approach in ISM band for wearable wireless devices.
6. Acknowledgements
The authors sincerely express their gratitude to the anonymous reviewers for their valuable comments. The support of Director, National Institute of Technical Teachers’ Training and Research (NITTTR), Chandigarh, India is thankfully acknowledged. J. G. Joshi is highly indebted to the Director, Directorate of Technical Education (M.S.), India and Principal, Government Polytechnic, Pune, India for sponsoring him to pursue the full time Ph.D. under AICTE sponsored Ph.D. QIP (POLY) Program.
REFERENCES
- V. G. Veselago, “The Electrodynamics of Substances with Simultaneously Negative Values of ε and μ,” Soviet Physics Uspekhi, vol. 10, no. 4, January-February 1968, pp. 509-514. doi:10.1070/PU1968v010n04ABEH003699
- J. B. Pendry, A. J. Holden, D. J. Robbins and W. J. Stewart, “Magnetism from Conductors and Enhanced Nonlinear Phenomena,” IEEE Transactions on Microwave Theory and Techniques, vol. 47, no. 11, 1999, pp. 2075- 2084. doi:10.1109/22.798002
- R. A. Shelby, D. R. Smith and S. Schults, “Experimental Verification of a Negative Index of Refraction,” Science, vol. 292, No. 5514, 2001, pp. 77-79. doi:10.1126/science.1058847
- D. R. Smith, D. C. Vier, T. Koschny and C. M. Soukoulis, “Electromagnetic Parameter Retrieval from Inhomogeneous Metamaterials,” Physical Review E, Vol. 71, 2005, Article ID 036617, pp. 1-10.
- R. W. Ziolkowski, “Design, Fabrication, and Testing of Double Negative Metamaterials,” IEEE Transactions on Antennas and Propagation, vol. 51, no. 7, 2003, pp. 1516-1529. doi:10.1109/TAP.2003.813622
- J. G. Joshi, S. S. Pattnaik, S. Devi and M. R. Lohokare, “Electrically Small Patch Antenna Loaded with Metamaterial,” IETE Journal of Research, vol. 56, no. 6, 2010, pp. 373-379.
- J. G. Joshi, S. S. Pattnaik, S. Devi and M. R. Lohokare, “Microstrip Patch Antenna Loaded with Magnetoinductive Waveguide,” Proceedings of 12th National Symposium on Antennas and Propagation, Cochin, 6-10 December 2010, pp. 101-105.
- I. V. Shadrivov, A. N. Reznik and Y. S. Kivshar, “Magnetoinductive Waves in Arrays of Split-Ring Resonators,” Physica B, Vol. 394, No. 2, 2007, pp. 180-183. doi:10.1016/j.physb.2006.12.038
- E. Shamonina, V. A. Kalinin, K. H. Ringhofer and L. Solymar, “Magneto-Inductive Waveguide,” Electronics Letters, vol. 38, no. 8, 2002, pp. 371-373. doi:10.1049/el:20020258
- R. R. A. Syms, E. Shamonina and L. Solymar, “Magnetoinductive Waveguide Devices,” IEE Proceedings on Microwave Antennas Propagation, vol. 153, no. 2, 2006, pp. 111-121. doi:10.1049/ip-map:20050119
- R. R. A. Syms, O. Sydoruk, E. Shamonina and L. Solymar, “Higher Order Interactions in Magneto-Inductive Waveguides,” Metamaterials, vol. 1, No. 1, 2007, pp. 44- 51. doi:10.1016/j.metmat.2007.02.005
- R. R. A. Syms, E. Shamonina, V. Kalinin and L. Solymar, “A Theory of Metamaterial Based on Periodically Loaded Transmission Lines: Interaction between Magnetoinductive and Electromagnetic Waves,” Journal of Applied Physics, vol. 97, 2005, pp. (064909)1-6.
- M. J. Freire, R. Marques, F. Medina, M. A. G. Laso and F. Martin, “Planar Magnetoinductive Wave Transducers: Theory and Applications,” Applied Physics Letters, vol. 85, no. 19, 2004, pp. 4439-4441. doi:10.1063/1.1814428
- R. Marques, F. Martin and M. Sorolla, “Metamaterials with Negative Parameters Theory, Design and Microwave Applications,” Wiley Interscience, John Wiley and Sons, Hoboken, 2008.
- P. Y. Chen and A. Alu, “Dual-Mode Miniaturized Elliptical Patch Antenna with μ-Negative Metamaterials,” IEEE Antennas and Wireless Propagation Letters, vol. 9, 2010, pp. 351-354.
- J. Xiong, H. Li, Y. Jin and S. He, “Modified TM020 Mode of a Rectangular Patch Antenna Partially Loaded with Metamaterial for Dual-Band Applications,” IEEE Antennas and Wireless Propagation Letters, vol. 8, 2009, pp. 1006-1009. doi:10.1109/LAWP.2009.2030771
- F. Bilotti, A. Alu and L. Vegni, “Design of Miniaturized Metamaterial Patch Antenna with μ-Negative Loading,” IEEE Transactions on Antennas and Propagation, vol. 56, no. 6, 2008, pp. 1640-1647. doi:10.1109/TAP.2008.923307
- L.-W. Li, Y.-N. Li and J. R. Mosig, “Design of a Novel Rectangular Patch Antenna with Planar Metamaterial Patterned Substrate,” Proceedings of International Workshop on Antenna Technology, Chiba, 4-6 March 2008, pp. 123-126.
- C. Caloz and T. Itoh, “Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications,” Wiley Interscience, John Wiley and Sons, Hoboken, 2006.
- F. Bilotti, A. Toscano, L. Vegni, K. Aydin, K. B. Alici and E. Ozbzy, “Equivalent-Circuit Models for the Design of Metamaterials Based on Artificial Magnetic Inclusions,” IEEE Transactions on Microwave Theory and Techniques, vol. 55, no. 12, 2007, pp. 2865-2873. doi:10.1109/TMTT.2007.909611
- S. S. Mohan, “Design, Modeling and Optimization of OnChip Inductor and Transformer Circuits,” Ph.D. Dissertation, Stanford University, Palo Alto, 1999.
- J. Wang, S. Qu, Z. Xu, H. Ma, Y. Yang and C. Gu, “A Controllable Magnetic Metamaterial: Split Ring Resonator with Rotated Inner Ring,” IEEE Transactions on Antennas and Propagation, vol. 56, no. 7, 2008, pp. 2018- 2022. doi:10.1109/TAP.2008.924728
- A. K. Gautam and B. R. Vishwakarma, “Frequency Agile Microstrip Antenna Using Symmetrically Loaded Tunnel Diodes,” Indian Journal of Radio and Space Physics, vol. 35, 2006, pp. 212-216.
- I. J. Bahal and P. Bhartia, “Microstrip Antennas,” Artech House, London, 1980.

