ABSTRACT

In order to harness wind energy with high coefficients, horizontal axis wind turbines (HAWT), like propeller-type wind turbines, have an advantage in terms of practical utilization because of their scale merit. However, large size and high tip-speed ratio are inherently related to material strength problems and low frequency noise emissions to the environment. In contrast to HAWT, we will discuss a flapping-type turbine driven at low speed. The flapping turbine works using lift force like the HAWT, but employs a new wind turbine concept in the present report. The concept involves the unique flapping motion of a wind blade mounted on a Chebyshev-dyad linkage by which the wing transforms wind energy into mechanical rotation. Both static and dynamic numerical estimates are developed to optimize all fundamental parameters of this linkage in order to obtain the desired torque. In this paper, the results of primitive optimization for determining the fundamental characteristics of motion and the trajectory of the wind turbine blade are demonstrated in order to obtain smooth rotation of the generator-driving shaft. It is also shown that the present turbine can be driven at low speed with a suitable energy conversion rate. Moreover, the practicality of operating slow flapping-type wind turbines is demonstrated, focusing on usage near residential areas or, e.g., on rooftops owing to lower noise. The feasibility of “figure eight” trajectory diversity is discussed along with geometrical parameters. Assuming one-blade motion with a variable trajectory for optimization, the smooth motion and required torque at slow rotation speeds are studied.

Keywords:

Chebyshev-Dyad, Flapping Turbine, VAWT, Link Mechanism

1. Introduction

To develop reliable wind power technology among the various renewable sources, a considerable amount of research has been conducted. Currently, it is possible to harness around 7.5 MW from a single unit whose size is larger than a Boeing 747 [1] . Conventional HAWT-like propeller-type wind turbines contribute to ecologically conscious profit. Alternatively, vertical axis wind turbines (VAWT) have been installed in urban areas. Various configurations and design techniques related to VAWT have been studied, from the micro scale up to 4 MW [2] [3] . Although they are economic and efficient, unexpected problems have arisen, such as the high avian mortality rate in onshore areas due to bird attacks [4] and noise annoyance problems such as sleep prevention and psychological distress affecting residents living near wind turbines [5] . In contrast to traditional HAWTs with large tip speed ratios, we attempt to develop a new concept regarding energy extraction, adopting a flapping mechanism with prospective use for wind energy in urban areas and tidal energy, which is progressing rapidly as “blue energy” [6] [7] . Comparing the present turbine with rotating wind turbines, the flapping wing of the former results in spatial motion that varies in both position and orientation, inducing a distinct aerodynamic flow mechanism [8] [9] . Because of the cyclic movement of the wind turbine, even though the wind flow is uniform, the relative velocity of the wind blade and flow direction varies during each cycle. At angles of attack beyond the stall condition, flow separation occurs around the airfoil, which may be a major factor in reducing the torque developed; in VAWT, a dynamic stall implies a defect of the power coefficient at low blade speed ratios (λ) for blade angles of attack of ±50˚ [10] .

In this paper, we advocate a third category of wind turbines―a flapping type. The flapping wind turbine is a relatively new concept. We propose a novel wind turbine moving along a unique trajectory fabricated with the Chebyshev-dyad linkage. The blade flaps are controlled through various geometrical parameters for a given attack angle and wind velocity; the wing then produces unsteady lift and drag forces to generate rotational torque. Whereas preceding research related to HAWT focused on relatively higher tip speed ratios for optimum driving conditions of about 3 to 4 [11] [12] , the present research mainly focused on a more environmentally friendly, slower type of flapping wind turbine that can be easily installed in or near residential areas.

In order to find a suitable flapping motion, we must optimize several geometric parameters. In the present research, a Chebyshev-dyad linkage is connected to a single blade composed of a NACA 0012 airfoil mounted vertical to the flow direction, as shown in Figure 1. Fundamentally, a Chebyshev-dyad linkage consists of a 3-bar linkage and an isosceles triad [13] . In the figure, a set of two linkages supports a single wing. A suitable combination of geometric parameters of these linkages provides reasonable stability in performance for numerous applications involving high operational speed and high load-bearing capabilities [14] [15] [16] . Generally, there are two types of path generation―a) point-to-point

path generation and b) continuous path generation. Point-to-point generation is concerned with a varying number of points on the path where the trajectory between these points is not important, whereas optimal synthesis methods are used for continuous path generation. In other words, the latter method focuses on minimizing constraints such as link-length ratios, transmission angles, and crank existence conditions [17] .

The aim of the present research is to design a prototype wind turbine by optimizing various parameters to obtain sufficient torque under smooth flapping movement at low speed, producing lower turbine noise and mechanical vibrations while reducing the avian mortality rate. The simplicity of these kinematic linkage pairs in a planar layout without gears makes the design simpler, utilizing the unique trajectory of the blade. A schematic view is shown in Figure 1. The blade is fastened onto a deltoid that rotates around axes A and B. A numerical simulation is conducted considering all of the variable parameters, and the trajectories are then examined in order to develop a smooth path. The generated torque is analyzed temporally for two different conditions. The first is static analysis, where stationary mechanical relations are considered at various points along the trajectory. The second is dynamic analysis, where the blade is set free to rotate owing to the development of the resultant force. As the present system uses a single-blade wind turbine, power production can be increased by extending the length and width of the blade. Therefore, the wind turbine generates sufficient torque by using a unique “figure eight” blade trajectory.

2. Chebyshev-Dyad Linkage Mechanism

2.1. Trajectory

As shown in Figure 2, wind force is converted into rotor motion through a Chebyshev-dyad linkage mechanism. This figure shows the linkage mechanism of the present system, including all variable parameters considered in this paper in the optimization. Here, the point K moves along a figure eight path. The cen-

ter of gravity of the wing was fixed at point K, i.e., it was fixed with ABK. The links AO and BC are connected with a deltoid, ABK, at points A and B, respectively. Points A, B, and C are free. The points O and C are the centers of revolution of links AO and BC, respectively. On rotating point A, point B moves in a rocking motion; path B and point K transform along path K as figure eight. In the succeeding section, the link length ratio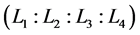, the blade mounting angle (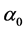) and geometric parameters of the shape of the deltoid (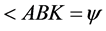) are discussed as design parameters. As we will discuss later, the orbital movement, path K, can accept a locus with wide variance if geometrical parameters and the angle of the wind direction (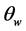) are considered.

In order to estimate the efficiency of the resultant torque for the assumed parameters, the inner product between the direction of force generated at the nodal point K and its trajectory direction is important, detailed in Figure 3. The product of force and the tangent vector of the trajectory may affect the work ability of the turbine. The force is calculated at 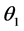according to the shaft rotation at one-degree intervals. The vector q is the resultant force (combining lift and drag forces) and p represents the segmental vector along the trajectory curves, which is calculated between the nodes on path K. These nodes are plotted at increments of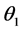. When the cosine value is close to unity, the turbine works at a desirable condition for obtaining a higher torque.

2.2. Geometrical Representation of Linkage Points

In this section, we describe the fundamental geometry for the reader’s convenience. According to the geometric relationship in Figure 2, the coordinates of points A, B, C, and K are expressed relative to the origin O as follows.

Coordinates of point A:

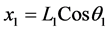(1)

(2)

Coordinates of point B:

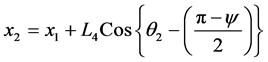(3)

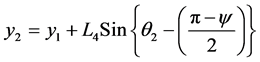(4)

where the angle 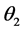is:

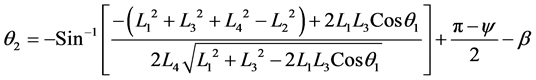(5)

Here, the angle 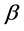is

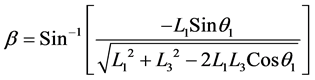(6)

The value of is discussed in the next section.

Point C is fixed at

. (7)

The locus of point K is calculated as

(8)

(9)

The angle of attack of the wing is determined using the following relation with

the mounting angle, and the wind angle,:

(10)

where, degrees was assumed in the simulation. The validation of this value is discussed in the succeeding section.

The fundamental specifications are listed in Table 1. NACA airfoil was selected because it shows good performance as a standard superior blade at moderate Reynolds numbers, and has been tested thoroughly [18] . Chord length c and wing span b were 0.2 m and 0.3 m, respectively, which were chosen for moderate model size.

2.3. Static Analysis

Let us consider the balances of forces and moments at each linkage as shown in Figure 4; the torque acting on the rotating disc is then determined using these relations. For this purpose, when, the following set of equilibrium equations from Equations (11) to (21) must be solved for links OA, BC, and deltoid ABK.

Balancing link OA,

(11)

(12)

(13)

For link BC,

(14)

(15)

(16)

Balancing the plate ABK,

(17)

(18)

(19)

(20)

(21)

The lift and Drag forces are

(22)

(23)

Here, and are drag and lift forces, which are determined by Equations (20) and (21). The coefficients and were obtained from experimental data for the NACA 0012 airfoil [19] . Figure 5 shows the coefficients of lift and drag of the NACA 0012 airfoil for angles of attack from 0˚ to 360˚ at a Reynolds number of around. The Reynolds number in the present system for the wind velocity of 10 m/s is, which is close to the value of considered in the literature [20] .

As the trajectory analysis describes in the following section, a large angle of attack inevitably appears in a certain region. In this case, the wing enters a stall but maintains a large lift coefficient. On the other hand, the drag coefficient also becomes large owing to the stall. By designing a suitable trajectory, we can obtain an effective driving force; this is discussed in the following direction.

Note that the thirteen equations from Equations (11) to (23) include thirteen variables, so the set of equations is closed. These can be solved analytically to determine the torque at any position (details in Appendix 1), as shown in Equation (24):

(24)

Figure 6 demonstrates the instantaneous static force calculated at nodal points along the orbit. The wind blows in the positive y-direction. In this figure, blue, red, and pink vectors represent drag, lift, and resultant forces, respectively. When, the wing is in the stalled state. The lift force is attributed to the leading-edge stall but still plays a major part in driving the turbine. The inner product in this state is still positive, although the drag force of the wind power acts to prevent regular rotation. When, the wing is still in a stalled state although it maintains large lift and drag forces. The inner product of the resultant force is still positive and the movement of the blade is in the clockwise direction. For, the inner product of the forces becomes negative and movement of the blades then flips the direction of motion into the anti-clockwise direction.

During this condition, the resultant force does not increase, so motion only eases on its track in the moving direction. Subsequently, forces cause acceleration and a gain in moment in the same direction as the continuous motion. When, the angle of attack acts in the negative direction with a negative cross product, which drives the blades in the anti-clockwise direction. In general, the movement of the trajectory is clockwise from θ₁ = 0˚ to 180˚, whe-

reas the remaining portion of movement is in the anti-clockwise direction depending upon the inner product of the forces.

2.4. Driving Simulation

The lift, drag, and torque of the system depend on the velocity of the wing relative to the free stream; hence, the relative velocity must be considered in the simulation. Through these simulations, we aim to design a suitable, relatively slow rated speed. Both static and dynamic numerical simulation has been conducted using MATLAB programming code.

In the previous section, we described the equations for static analysis. Here, we represent the equations for estimating the driving speed and describe modifications for the relative velocity when the turbine is in motion. In order to monitor the wing force, i.e., the lift and drag forces, a simulation model was developed to evaluate the forces produced at the node at any time step with the following assumptions:

・ The gravity force is not considered in the model.

・ The friction force in the mechanism is ignored.

・ The forces developed in the wind affect only the nodes without considering the moment.

・ The analysis model developed in the simulation is two-dimensional for all the cross-sectional views of the blade in its width direction.

The relative velocity is calculated with wing velocity as follows:

(25)

In the present system, the rotor speed is variable; therefore, the wing velocity should be calculated as indicated in the following equations:

(26)

(27)

Here, the number i represents the calculated nodal number. Using and, the relevant relative inlet angle of the flow is expressed as follows:

(28)

The temporal angle of attack is evaluated with the mounting angle and the inflow angle. The lift and drag forces are given by Equations (22) and (23) for relative velocity. The rotational angular velocity of the rotor is calculated by solving the following equation of motion with Euler’s explicit integration, where the calculation of the force and velocity acting on each nodal coordinate needs to be updated for each time step.

(29)

and

(30)

where I, r, and M are the moment of inertia of the rotating disk, its radius, and its mass, respectively, which are tentatively assumed the rotor of the generator. Here, we supposed that M = 5 kg and r = 0.05 m. The mass has a significant influence in the simulation where a more realistic approach for angular velocity development is considered. The calculation was started at and from the rest state, e.g.,. The increment angle was 0.01˚ in the simulation.

3. Results and Discussion

3.1. Torque Estimation by Static Analysis

3.1.1. Dependence of Deltoid Angle Ψ

Several geometrical parameters are considered, such as the deltoid angle, , mounting angle, , link ratio, , and the direction of the wind,. These parameters must be determined in order to achieve a conceptual design for the desired overall performance and effective movement about the wing trajectory. First, after the basic combination of these parameters provides fundamental specifications for the present flapping-type wind turbine step-by-step, optimal conditions must be determined in each case to accomplish the prototype design. Each parameter is interlinked with the others, and the variation of each parameter affects those of the others. Therefore, it is necessary to be cautious in order to obtain higher performance as well as a smooth trajectory for the movement, in which the basic trajectory and speed play important roles in stabilizing the system.

The advantage and uniqueness of the present system involve the wide variation of the orbit of the blade. The trajectory K is obtained with Equations (8) and (9). The variation of the trajectory depends on the deltoid angle, which is one of important geometric parameters. Figure 7 shows the variation of the trajectory for various values of. As shown in this figure, the path K seems to be a figure eight, and its slope changes with. In order to attain smooth motion,

care must be taken to avoid an abrupt change of the orbit. As shown in Figure 8, the locus is approximately symmetric at. Therefore, should be chosen between about 50˚ and 70˚, where the resulting contour of the trajectory is closer to the ordinal shape of the figure eight, for more favorable conditions.

To obtain the desired results in performance and higher values of torque, several values of were examined by computing the average torque, the trajectory, and cosγ. The variation of torque with is shown in Figure 8. The developed torque value changes with the internal angle of the coupler, and this determines the optimum condition required to achieve higher average torque by using a suitable trajectory.

The variation of generated torque in each case strongly depends on the trajectory. The maximum value of the average torque determines the optimum condition for the design. The maximum average torque of 0.037 N.m was achieved for Ψ = 80˚ at a wind velocity of 5 m/s, as shown in Figure 8.

Furthermore, the direction of the resultant force of the wing and the orbital direction are consistent in each phase; a cosine value close to unity determines

the characteristics favorable for the design condition. In order to confirm the optimum coupler angle, on viewing the relation between the trajectories, the average torque value and the cosine value determine the fundamental characteristics of the mechanism. Even though the higher value of torque and the cosine value obtained at Ψ = 80˚ appear to present a more favorable condition for design, the shape of the trajectory is that of a figure eight with two different sizes of curves, breaking the symmetry of the path. Because of this, the optimum value at Ψ = 70˚ develops a more symmetric trajectory shape of a figure eight with relatively high average torque in comparison with other cases.

3.1.2. Optimization of the Mounting Angle (α₀)

The mounting angle () is one of variable parameters that govern the performance of the wind turbine. As the angle of attack in Equation (10) is determined by the value of the mounting angle directly, the overall lift and drag forces developed vary with the mounting angle. Figure 10 shows the developed tangential force for different mounting angles at the joint of the wing blade and the linkage

for a wind velocity of 5 m/s. Maximum average force is developed at around 80˚, which is considered as the optimum condition for the design.

3.1.3. Optimization of the Link Length Ratio

1) Linear optimization

In this study, the link length of the dyad is an important variable parameter for transferring the generated resultant force from the wing to the shaft as torque. The trajectory and torque vary with even a small variation of the link length in the Chebyshev dyad mechanism. In other words, the length of each link and the position and distance of the frame support must be optimized for the best performance. The link lengths and, as listed in Table 1, are optimized based on the torque and the trajectory. In this section, the link length is assumed initially as 0.05 m based on the design of the prototype model for the experimental setup; on this basis, the other link length parameters are determined for the average value of the torque and the characteristic nature of the trajectory. Considering the example of varying the length of, the link length is 0.05 m, and are equal to 0.1 m, the coupler angle is 70˚, and the mounting angle is 80˚ for a wind velocity of 10 m/s; this gives various average torques, as shown in Figure 12. In addition, Figure 11 shows some higher values of the average torque for the case where link length is 0.1 m and 0.11 m in the range of 0.143 Nm and 0.149 Nm. In addition, the nature of the trajectory for each case is evidently different. Furthermore, the trajectory when link is 0.1 m develops a figure eight shape with more symmetrical loops in comparison to the case where is 0.11 m, which governs the parameter responsible for smoother rotation.

Figure 12 shows the different trajectories made by the wing blade in each complete period for different link lengths. The optimum design length is that of according to the Chebyshev-dyad criteria [12] ; this confirms that the optimum conditions in both cases must be the same. Both the torque value and the trajectory govern a significant parameter for the design of a link length parameter. As for the four link lengths, is assumed at the beginning of the design process, based on which, , and are determined by taking into

consideration better performance and higher coefficient values. Furthermore, the negative torque generated at the end of an azimuth angle signifies a change in the direction of motion of the wind blade, where inertia governs the continuation of the motion.

Subsequently, Figure 13 shows a summary plot of the torque value simulated for different L₂, L₃, and L₄ with individual variation to obtain the maximum torque as a linear change in the individual link lengths. Moreover, while considering the results of the torque value for optimization, the maximum torque was calculated for L₂ and L₃ lengths of 0.11 m and 0.09 m, respectively.

Furthermore, a higher value of torque is considered for optimizing the link length without accounting for the nature of its trajectory, leading to a higher torque. However, there might be a sharp bend in the trajectory motion owing to rapid change direction with an asymmetric trajectory as shown in Figure 14, developing instabilities in the system. The nature of the torque shows two peaks between which the torque value close to zero acts to obstruct the motion while gaining acceleration. Considering all these factors, the particular design condition is not the optimum and suitable for design consideration.

By considering static linear optimization, the optimized parameter determined up to now was the link length ratio of as, i.e., L₁ = 0.05 m and the rest of the link lengths equal to 0.1 m, the coupler angle equal to 70˚ and mounting angle equal to 80˚.

2) Optimization by changing parameters randomly

Instead of linear optimization, these parameters can be considered randomly to obtain a greater orbital direction component with the largest wing force with the average cosine value approaching unity, which is the optimal combination of parameters. For the optimal condition, the variable parameters obtained for the link length ratio must satisfy (i.e., , and), where is 40˚ and is 80˚. Figure 15 shows the resultant of the nodal vector force calculation with the pink arrow and lift and drag vector forces in red and blue, respectively, at a wind speed of 5 m/s. The movement of the trajectory by a blade for azimuth angles θ₁ = 0˚ to 90˚ and θ₁ = 270˚ to 360˚ has a greater travel distance compared to the remaining azimuth angles.

Figure 16 shows the direction of the resultant force on the wing, and the orbital direction is consistent with the number of phases, appearing suitable for wind turbine design. Subsequently, the track of the path followed by the blade attached to node K changes very rapidly when: a sharp turn of the blade occurs with a change in angle of attack from positive to negative through a flip. If such conditions exist, then the trajectory breaks down from the figure eight form and the stability of the system does not last for a longer period.

3.1.4. Static Optimum Condition

The static optimum condition for the various parameters before dynamic analysis calculation for the internal coupler angle equals 70˚, the mounting angle is 80˚, and the link length ratio determined from linear optimization is considered optimum at, i.e., L₁ = 0.05 m and the rest of the link lengths are equal to 0.1 m. Hence, Figure 17 shows the relationship of various torques developed under various wind velocities for this static optimum condition, which shows the large amount of torque achieved by increasing the velocity from 5 m/s to 10 m/s.

3.2. Dynamic Analysis

3.2.1. Dynamic Torque Analysis

Further dynamic analysis is conducted based on the optimum conditions obtained from static analysis to determine realistic results under various load conditions and wind speeds. The dynamic analysis gives the concept of performance and the characteristics of the new flapping-type wind turbine. In the relative wind velocity approach, the starting torque concept, extraction of a certain percentage of the developed torque after gaining some momentum, the mass of the rotating disc of radius 0.05 m, and angular velocity make the simulation model a conceptual design. Figure 18 shows the dynamic analysis of torque produced for 5 s at three different wind velocities of 5 m/s, 7 m/s, and 10 m/s. In each case,

80% of the generated torque is transformed to overcome the load, whereas any remaining torque is used for the development of motion.

3.2.2. Angular Velocity Analysis

Angular velocity varies depending on time owing to the acceleration of the system, which starts from the rest condition and attains the full-load operating condition. At the beginning of the motion, a no-load condition is assumed, and after the rotor has accelerated, the full-load operating condition is taken into account. Figure 19 shows the angular velocity curve for 30 s for three different wind conditions where the full-motion condition develops more rapidly for higher wind velocity compared to lower wind velocity. The nature of the curves shows higher gradients in the beginning because all the torque is considered as being used for the generation of motion. After the point marked by the arrows in the figure, separation of 80% of the developed torque is used to counterbalance the load generated for the generator and the remaining torque for the continuation of motion.

3.3. Comparison of Static and Dynamic Torques

The torque values obtained from both static and dynamic analysis are compared

for wind velocities of 5 m/s, 7 m/s, and 10 m/s for a full period (Figure 20). Indeed, as the dynamic torque varies over the time intervals from the starting condition, a comparison was performed for the data after the angular velocity reached at 20 s. Both curves show the same trendline, and eventually, the curve is smoother in the dynamic than in the static case, but the peak value of the static torque is greater than for the dynamic torque.

4. Conclusions

Aiming to operate wind turbines in multi-use zones such as neighboring residential areas and to reduce noise annoyance, we performed design and development of a small vertical axis flapping wind turbine using a Chebyshev-dyad linkage. In order to confirm the feasibility of this system, we considered both static and dynamic numerical analyses. Different variable parameters for the flapping-type wind turbine were also analyzed to determine the optimum parameters for better performance.

The optimal Chebyshev-dyad link length ratio () was determined to be with an internal coupler angle () equal to 70˚. The mounting angle () for the wind blade was considered as 80˚ in the design to attain higher torque with smooth flapping motion of the wind blade. The slow swinging vertical axis wind turbine utilizes both lift and drag forces to obtain smooth motion. Using a single wing blade unit (NACA 0012) and a Chebyshev- dyad mechanism with a unique trajectory makes this a novel design.

Considering the correlation of the inner product between the forces and the locus along the trajectory defines maximum forces along the slope of the trajectory to improve the characteristics of the wind turbine for different combinations of geometrical parameters. A simulation model was developed in order to quantify the force and the momentum in each phase of movement to improve the performance of the design. The torque developed from static analysis was compared with that from the dynamic analysis for verification of the simulation model, and the results showed good agreement. Although torque is generated within a cyclic rotation, it was found to vary owing to the variation of movement along a unique path with varying angles of attack; this makes the design more complicated when minimizing the fluctuations in each cycle. In future, authors would like to focus on experimental investigation for the present flapping wind turbine, which has a great influence to judge the turbine performance for practical utilization.

Cite this paper

Alam, M.S. and Hirahara, H. (2017) Numerical Performance Assessment of a Flapping-Type Vertical Axis Wind Turbine with Chebyshev-Dyad Linkage. Smart Grid and Renewable Energy, 8, 53-74. https://doi.org/10.4236/sgre.2017.82004

References

Appendix 1

Simplify all Equations (11)-(19), we get

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

By solving equations (36 & 39), we get

Therefore,

Finally, Torque value obtained as: