Smart Grid and Renewable Energy
Vol.1 No.1(2010), Article ID:1941,6 pages DOI:10.4236/sgre.2010.11001
Design of a Photo-Voltaic System to Enhance Network Dynamic Stability*
![]()
1Department of Electrical Engineering, Shanghai Jiao Tong University, Shanghai, China; 2the School of Electrical Engineering, Wuhan University, Wuhan, China; 3Power System Department, China Electrical Power Research Institute, Beijing, China; 4School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore; 5State Grid Operation Company Ltd, Beijing, China.
Email: liguojie2000@126.com, wangqi@epri.ac.cn, ESSCHOI@ntu.edu.sg
Received April 26th, 2010; revised May 6th, 2010; accepted May 7th, 2010.
Keywords: PV Damping System, Power Oscillations, Damping Ratio
ABSTRACT
Due to the increasing amount of photovoltaic (PV)-based power generation being connected to power systems, issues pertaining to the integration of the PV-based generators have attracted intense attention. In this connection, the design of a PV-based stabilizer for enhancing power system dynamic stability is examined. The damping action is achieved through the independent control of real power flow from the stabilizer and voltage at the point of common coupling between the stabilizer and grid system. The stabilizer system is designed based on classical frequency response technique. Robustness of the proposed control strategy in enhancing network dynamic stability is demonstrated through computer simulation.
1. Introduction
Due to the increasing energy consumption, diminishing fossil fuel-based energy reserve and the concern for the environment, development for renewable energy sources has progressed at ever greater pace in recent years. In this regard, harnessing the energy from the sun using photovoltaic (PV) system has received much support [1,2]. Normally, the PV generation system operates under the maximum power point tracking (MPPT) mode so as to extract the maximum amount of energy from the sun [3-8]. Unfortunately, thus far the relatively high cost of the PV generation system has acted as a barrier to large-scale application of the renewable technology. In order to enhance the attractiveness of PV system, one possible way would be to extent its functionality so that it can be used to serve additional utility functions.
In pursuing this possibility, one notes that a most fundamental challenge to power system control is to suppress undesirable system oscillations initiated (for example) due to some network switching actions. The scale of the oscillating power component is often small initially, compared to the level of the transferred power. However, if no appropriate control action is taken, the undamped oscillations can endanger the operation of the network. Networks which contain weakly coupled transmission links operating under heavy load transfer conditions are particularly prone to this type of problem [9-12]. In this regard, the proposed PV system to be considered in this paper is intended for providing the ability to enhance network dynamic stability. It will be shown through detailed analysis that the inverter within the PV-based stabilizer system can exercise independent real and reactive power flow controls which will lead to enhanced system damping.
The paper is organized in the following manner. In Section 2, a description of the PV damping system is given. The analysis of the PV damping action is described and the design of the control system shown in Section 3. Digital simulation results, based on PSCAD/EMTDC, are presented in Section 4 to illustrate the efficacy of the scheme.
2. Description of the PV Damping System
Similar in structure to the conventional photo-voltaic generator as described in e.g. [5,6], the main hardware components of the PV-based stabilizer system includes the PV panel, inverter system, filtering reactor, and stepup transformer for grid connection. The schematic of the PV-based grid-connected stabilizer system is shown in Figure 1. The PV panel converts the harnessed solar
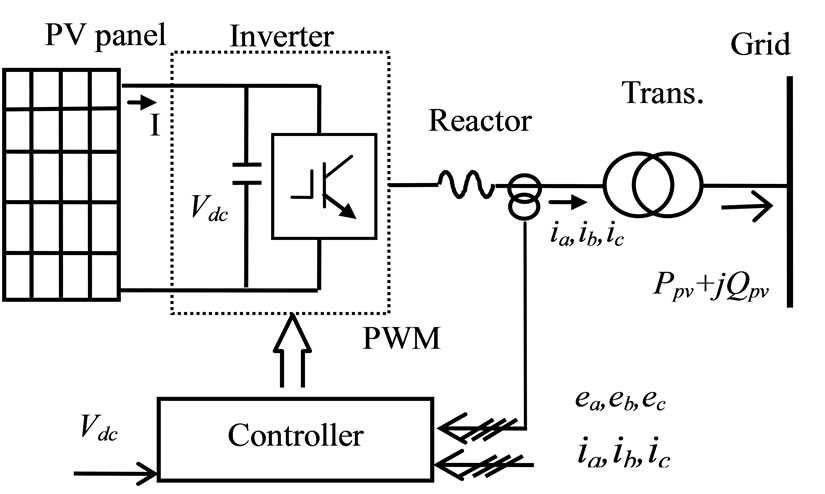
Figure 1. Schematic of the PV-based grid-connected stabilizer system
energy directly to electrical power and the outputs DC voltage Vdc is converted to AC voltage through the inverter system. The inverter system consists of fast switching IGBT, usually operating under PWM scheme. The switching pattern of the PWM is governed by a controller acting on the input three-phase AC voltages ea, eb, ec and currents ia, ib, ic, as shown in the figure.
The inverter of the PV damping system acts as a voltage source converter (VSC). As in a standard VSC, by adjusting its modulation index and the phase of the VSC terminal voltage with respect to the grid-side voltages, real and reactive power outputs of the VSC can be independently controlled [13,14].
The typical V/I characteristics of a solar cell and that relating its output power PPV with Vdc are as shown in Figure 2 [3,4,6]. The figure shows that there is a maximum output power (Ppvmax) operating point. Based on the PPV – Vdc characteristics, it will be necessary to operate the PV damper with its output voltage Vdc within the range Vm ~ Voc. In this way, Vdc will then undergo a much smaller change when the PV output power PPV changes. This is necessary as the PWM converter can only operate effectively within a limited Vdc range. The capacitor shown in Figure 1 and connected across the DC-link acts as an energy storage device so that the voltage Vdc can be maintained the range. Furthermore, when the PV damper acts to suppress network oscillations, the excursions in PPV would be equally likely to move to either side of its steady state value. Hence, it is proposed that the PV damper is to operate with its steady-state Vdc set to produce an output power Ppv0 = 0.5Ppvmax. In this manner, while Ppv0 is only at half of the maximum possible, this operating state is nevertheless accompanied by an attractive PPV swing range which can be used to advantage in enhancing network stability, as will be shown next.
3. Analysis of the PV Damping Action
The damping characteristics offered by the PV system can be illustrated using the classical lossless single-machineinfinite bus (SMIB) power system shown in Figure 3. The
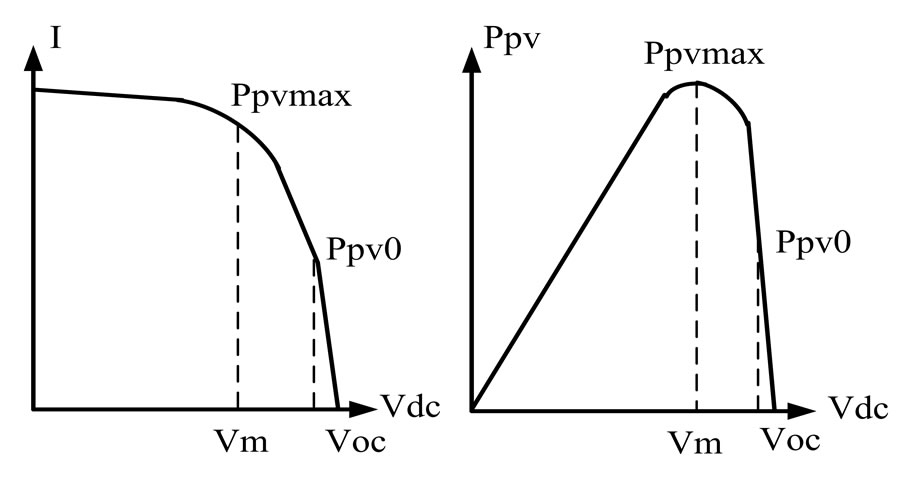
Figure 2. Typical PV current-voltage, voltage-power characteristics and the regulated operating range of the damping system
corresponding equivalent circuit is shown in Figure 4. The use of SMIB example is to facilitate analysis and to demonstrate the beneficial effects of the PV damping system, without having to resort to complicated mathematical analysis. Note that the PV is connected at an intermediate bus M, which divides the transmission link between the generator and the infinite bus into two sections. It is assumed that the PV-based stabilizer system contributes toward meeting only a small part of the load demand at the infinite bus. This is a realistic assumption as one would not expect the PV system is the major source to meet the power demand at the infinite bus. Instead, it will be more meaningful to examine how the PV system would enhance network stability, when the power system is subjected to small disturbances. The stabilization function is thus an additional benefit that can be extracted from the PV system.
In Figure 4, d denotes the rotor angle of the generator with respect to the infinite bus, and 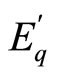 represents the generator EMF behind the machine transient d-axis reac tance xd’. Hence x1 would be the sum of xd’ and the line reactance between the generator terminal and bus M. φ is the phase difference between bus M voltage Vm and that of
represents the generator EMF behind the machine transient d-axis reac tance xd’. Hence x1 would be the sum of xd’ and the line reactance between the generator terminal and bus M. φ is the phase difference between bus M voltage Vm and that of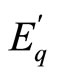 . Pe + j Qe, Ppv + j Qpv and Ps + j Qs are the respective real and reactive power flows at the generator, PV and infinite-bus terminals. The PV-based stabilizer is represented by the inverter which has the output voltage
. Pe + j Qe, Ppv + j Qpv and Ps + j Qs are the respective real and reactive power flows at the generator, PV and infinite-bus terminals. The PV-based stabilizer is represented by the inverter which has the output voltage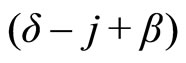
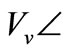 . Vs is the voltage of the infinite system bus.
. Vs is the voltage of the infinite system bus.
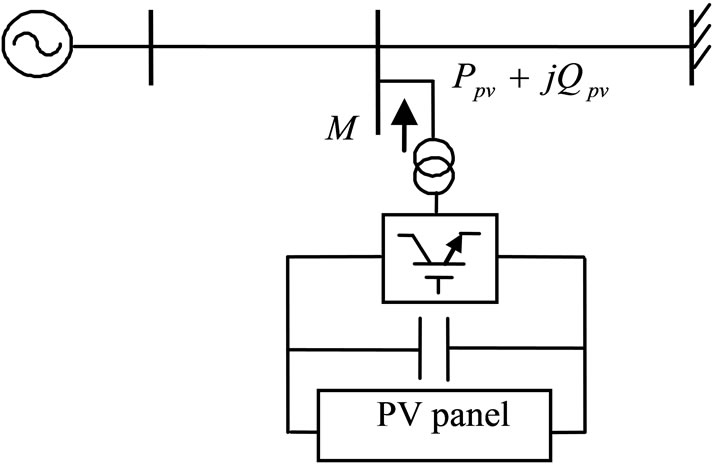
Figure 3. A SMIB system incorporated with a PV damping system
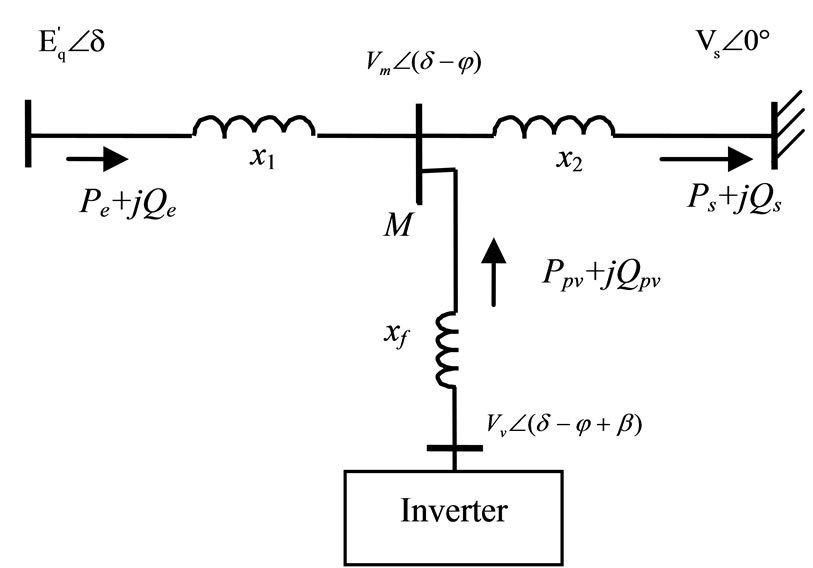
Figure 4. Equivalent circuit of the SMIB system with the PV-based stabilizer
A simplified 2nd-order linearized model of the power system is used in which the generator excitation and governor control actions are neglected [9], viz.:
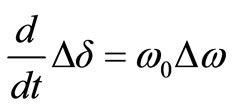 (1)
(1)
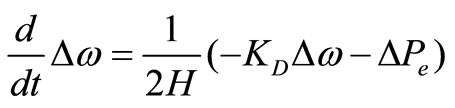 (2)
(2)
where 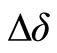 and
and 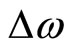 denote the generator rotor angle and speed deviations respectively, H is the generator inertia constant,
denote the generator rotor angle and speed deviations respectively, H is the generator inertia constant, 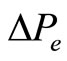 is the deviation of the generator electrical output power,
is the deviation of the generator electrical output power,  is the machine damping torque coefficient and w0 is the synchronous speed. From the network equation, Pe is given by
is the machine damping torque coefficient and w0 is the synchronous speed. From the network equation, Pe is given by
 (3)
(3)
Laplace transform (1) and (2) with the operator s, one obtains
 (4)
(4)
Also apply power balance at bus M,
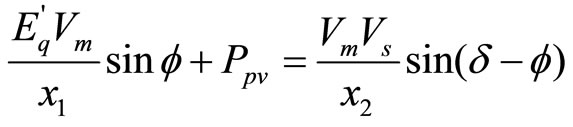 (5)
(5)
As the focus of the analysis is on the small-signal response of the power system, one could make use of the linearized version of (3) and (5) around the nominal operating point to obtain
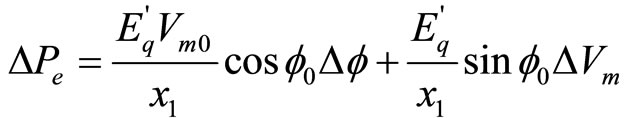 (6)
(6)
 (7)
(7)
Note that in (6) and (7), symbols with the subscript “0” denote the nominal operating states of the variables. From (6), 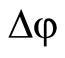 can be expressed in terms of
can be expressed in terms of 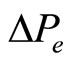 and
and![]() ,
,
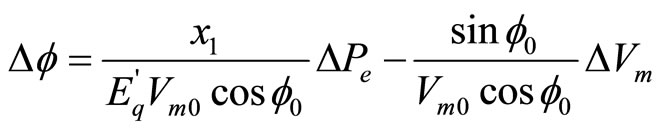 (8)
(8)
Substitute (8) into (7), (7) can be rewritten into the form
 (9)
(9)
where
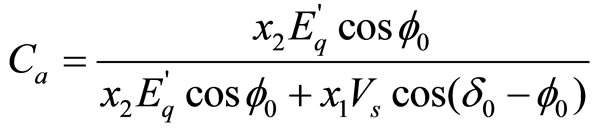 ,
,
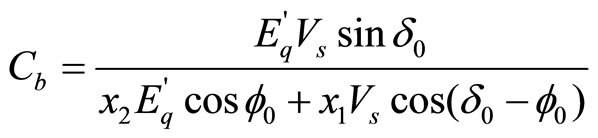 ,
,
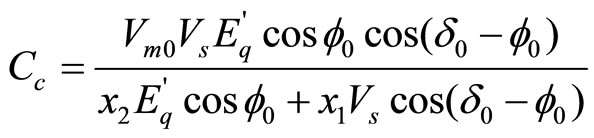 Equations (1),(2) and (9) can be represented by the block diagram shown in Figure 5. In adopting this model, Ca, Cb and Cc are constant for a given network condition. To improve on the overall dynamic performance of the power system, the next task is to design the PI feedback control systems to achieve specified objectives through the judicious selection of parameters k1-k4, as follows.
Equations (1),(2) and (9) can be represented by the block diagram shown in Figure 5. In adopting this model, Ca, Cb and Cc are constant for a given network condition. To improve on the overall dynamic performance of the power system, the next task is to design the PI feedback control systems to achieve specified objectives through the judicious selection of parameters k1-k4, as follows.
3.1 Design of the Vm Feedback Controller
In terms of design procedure, one should design the Vm feedback loop first because it corresponds to the case when Ppv = 0 (case of no solar power input). The design problem is therefore to determine the values of k2 and k4 shown in Figure 5 such that the closed-loop system is well-damped. Firstly examine the open loop transfer function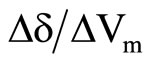 . The method is based on the wellknown frequency response technique. Consider the case when the Vm control loop in Figure 5 is opened, as shown in Figure 6.
. The method is based on the wellknown frequency response technique. Consider the case when the Vm control loop in Figure 5 is opened, as shown in Figure 6.
From Figure 6, the open loop transfer function of 
referring to ![]() is:
is:
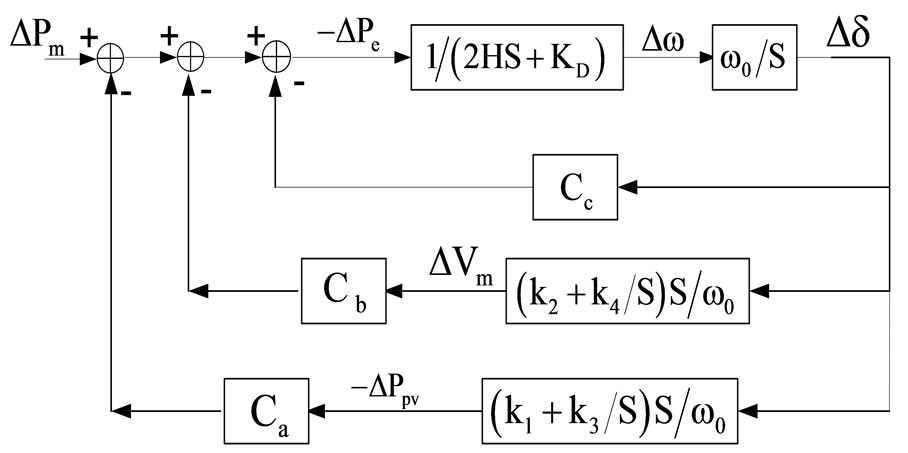
Figure 5. The block diagram of the power system model
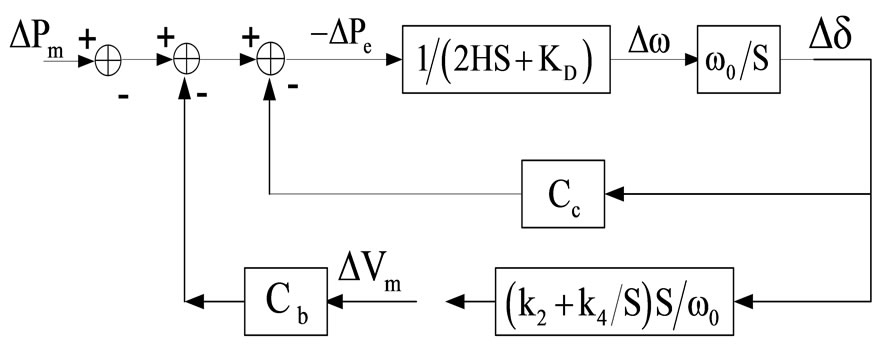
Figure 6. Open-loop transfer function 
 (10)
(10)
For convenience, denote  as G(s). According to the basic frequency response technique, after adding the Vm feedback controller, at the cross-over point
as G(s). According to the basic frequency response technique, after adding the Vm feedback controller, at the cross-over point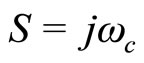 , the desired system open-loop gain should be
, the desired system open-loop gain should be 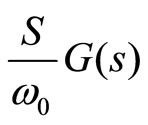
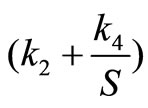
 and the phase angle should be (
and the phase angle should be (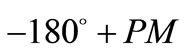 ),where PM is the desired phase margin at the cross-over point. Thus,
),where PM is the desired phase margin at the cross-over point. Thus,
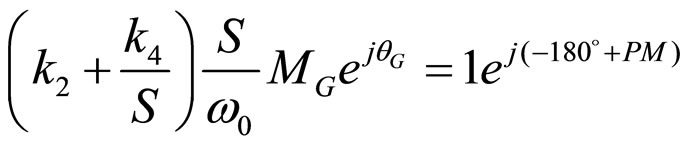 (11)
(11)
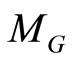 and
and 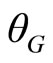 are the gain and phase angle of G(s) at the frequency
are the gain and phase angle of G(s) at the frequency . Therefore (11) can be written as
. Therefore (11) can be written as
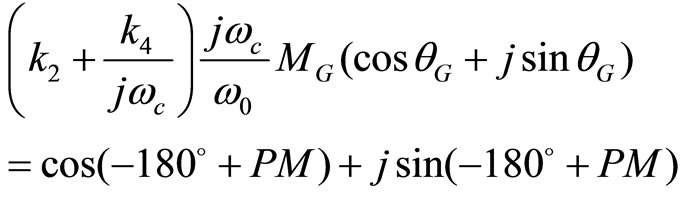
Separate the last equation into its real and imaginary parts, k2 and k4 can be derived
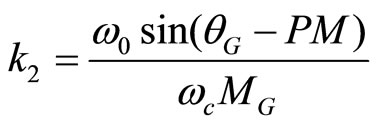 ,
,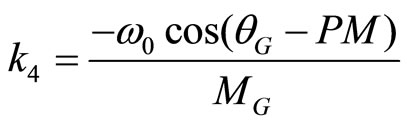 (12)
(12)
Generally, a good damping factor  of closed-loop system is 0.707, the necessary phase margin PM should be approximately 70°. To obtain the desired phase margin, it is usual to make the targeted phase margin a few degrees higher (say by 5°). This is because the Vm feedback control introduces an additional zero to the system. The zero will make the final cross-over frequency
of closed-loop system is 0.707, the necessary phase margin PM should be approximately 70°. To obtain the desired phase margin, it is usual to make the targeted phase margin a few degrees higher (say by 5°). This is because the Vm feedback control introduces an additional zero to the system. The zero will make the final cross-over frequency  slightly higher. The recommended PM is therefore 75°.
slightly higher. The recommended PM is therefore 75°.
Once knowing ,
,  and
and , (12) permits k2 and k4 to be readily determined.
, (12) permits k2 and k4 to be readily determined.
3.2 Design of Ppv Feedback Controller
Suppose the Vm feedback controller has already been designed and is in service. Consider the case when the Ppv control loop in Figure 5 is opened, as shown in Figure 7.
From Figure 7, the open loop transfer function of 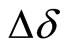 referring to
referring to  is:
is:
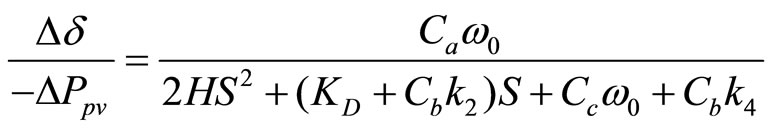 (13)
(13)
For convenience, denote 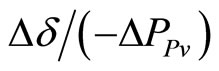 as G’(s). Using the same reasoning as before, after adding the Ppv feedback controller and at the cross-over point
as G’(s). Using the same reasoning as before, after adding the Ppv feedback controller and at the cross-over point , the desired system open-loop gain should be
, the desired system open-loop gain should be 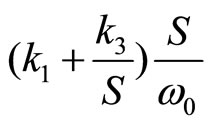
 and the phase angle should be (
and the phase angle should be (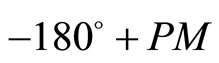 ) where PM is the desired phase margin at the cross-over point. Thus,
) where PM is the desired phase margin at the cross-over point. Thus,
 (14)
(14)
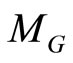 and
and 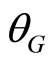 are the gain and phase angle of G’(s) at the point
are the gain and phase angle of G’(s) at the point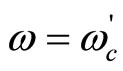 . Separate the above equation into its real and imaginary parts, k1 and k3 can be derived
. Separate the above equation into its real and imaginary parts, k1 and k3 can be derived
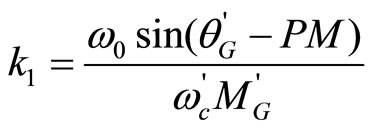 ,
, (15)
(15)
Based on similar design consideration as that in Subsection 3.1, with known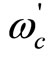 ,
, 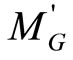 and
and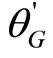 , (15) permits k1 and k3 to be evaluated.
, (15) permits k1 and k3 to be evaluated.
4. Illustrative Examples: Response under Small Disturbances
In order to assess the controller design shown in the previous section, simulation studies have been carried out.
Extensive study has been carried out using the SMIB example but in this paper, only the results of a small disturbance is simulated by introducing a 0.05 p.u. step increase of the input mechanical power of the generator at1s will be presented. The time response will be studied under two modes: 1) Mode 1 corresponds to the case with only Vm feedback control loop; 2) Mode 2 represents the case with both Vm and Ppv feedback control loops. The study will be carried out for the following operating con
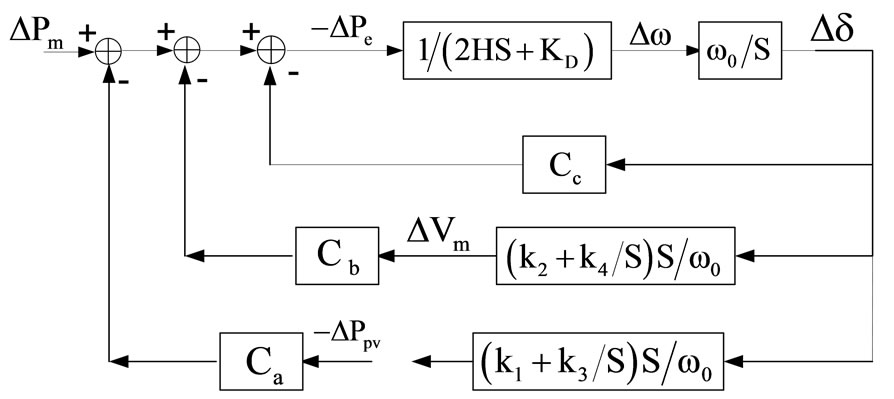
Figure 7. Open-loop transfer function , with Vm control loop closed
, with Vm control loop closed
 (a)
(a)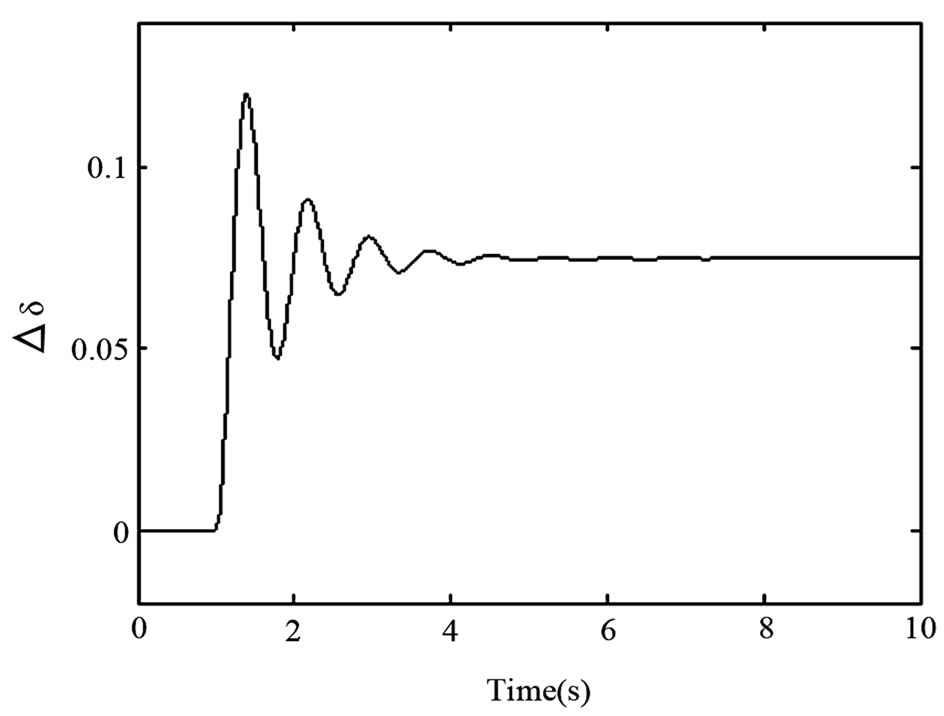 (b)
(b)
Figure 8. Power system response following a step change of the generator mechanical power with Vm feedback control
dition: Pe0 = 0.32 for all 2 modes. 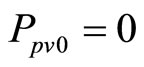 for mode 1 Ppv0 = 0.24 for Mode 2.
for mode 1 Ppv0 = 0.24 for Mode 2.
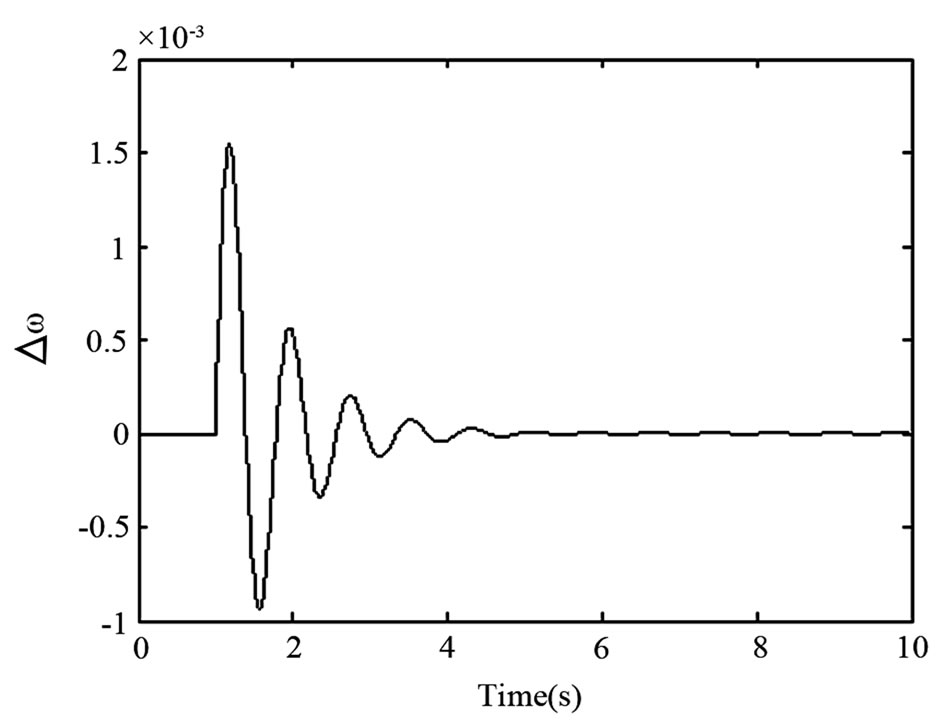
Time response plots of rotor speed variation ∆ω and angle variation ∆δ following the disturbance are as shown in Figures 8 and 9, corresponding to the system operating under Modes 1 and 2 respectively.
From the results of Figure 8, it is shown that the generator rotor oscillations following the power increase disturbance have been suppressed when only Vm is controlled under Mode 1, i.e. via the control scheme described in Section 3 via (9). This means that the system damping is effective even when there is no sunlight, and the PV system acts as a conventional STATCOM. Oscillations are damped out even more quickly and effectively when both Ppv and Vm are controlled through the feedback strategies described in Section 3 via (9) (Mode 2). Thus it confirms the PV damping system with the proposed control strategy is effective in suppressing power system
 (a)
(a)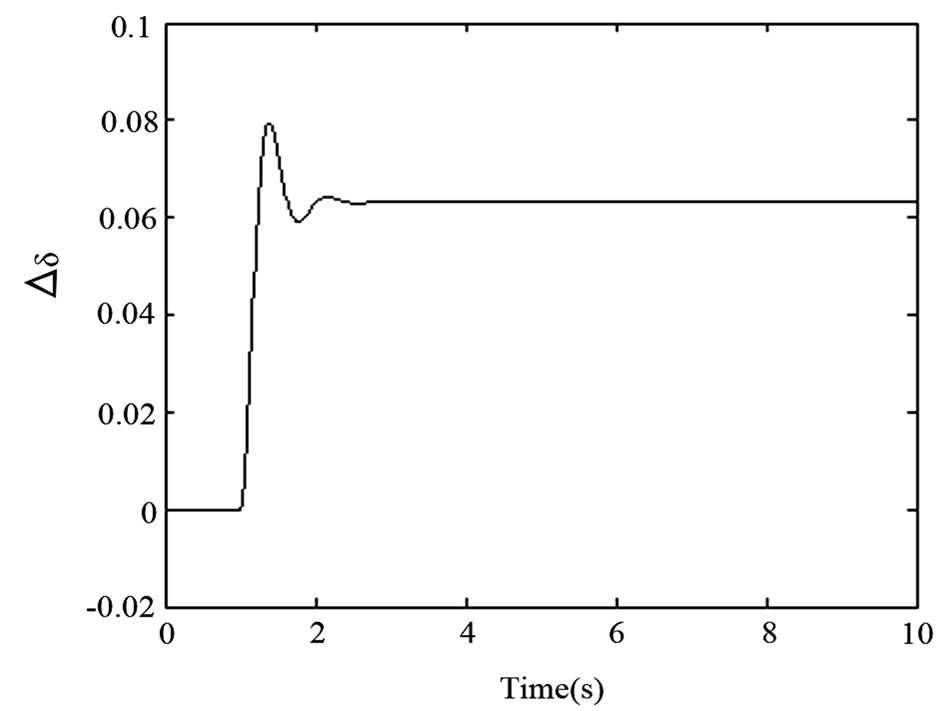 (b)
(b)
Figure 9. Power system response following a step change of the generator mechanical power with both Vm and Ppv feedback control
oscillations.
5. Conclusions
Unlike the conventional PV generation system which is only intended to harness energy from the sun, the proposed PV scheme has the added advantage for it is designed to provide damping control following disturbance. A theoretical analysis is provided in showing how improved damping is achieved. The proposed PV-based stabilizer system includes real power feedback and the voltage control strategy and is shown to be effective in enhancing network dynamic stability.
REFERENCES
- T. M. Razykov, “Photovoltaic Solar E1ectricity: State of the Art and Future Prospects,” Proceedings of 6th International Conference on Electrical Machines and Systems, Vol. 1, 9-11 November 2003, pp. 297-301.
- C. Rodriguez and G. A. J. Amaratunga, “Dynamic Maximum Power Injection Control of AC Photovoltaic Modules Using Current-Mode Control,” IEE Proceedings – Electric Power Applications, Vol. 153, No. 1, January 2006, pp. 83-87.
- M. W. Park and I. K. Yu, “A Novel Real-Time Simulation Technique of Photovoltaic Generation Systems Using RTDS,” IEEE Transactions on Energy Conversion, Vol. 19, No. 4, March 2004, pp. 164-169.
- L. Zhang, A. A. Amoudi and Y. F. Bai, “Real-Time Maximum Power Point Tracking for Grid-Connected Photovoltaic Systems,” Proceedings of IEE 8th International Conference on Power Electronics and Variable Speed Drives, 18-19 September 2000, pp. 124-129.
- U. Boke, “A Simple Model of Photovoltaic Module Electric Characteristics,” Proceedings of European Conference on Power Electronics and Applications, 2-5 September 2007, pp. 1-8.
- T. Shimizu, O. Hashimoto and G. Kimura, “A Novel High-Performance Utility-Interactive Photovoltaic Inverter System,” IEEE Transactions on Power Electronics, Vol. 18, No. 2, March 2003, pp. 704-711.
- P. Sanchis, J. López, A. Ursúa and L. Marroyo, “Electronic Controlled Device for the Analysis and Design of Photovoltaic Systems,” IEEE Power Electronics Letters, Vol. 3, No. 2, June 2005, pp. 57-62.
- T. Shimizu, M. Hirakata, T. Kamezawa et al., “Generation Control Circuit for Photovoltaic Modules,” IEEE Transactions on Power Electronics, Vol. 16, No. 3, May 2001, pp. 293-300.
- P. Kundur, “Power System Stability and Control,” McGrawHill, New York, 1994.
- M. Joorabian, M. Razzaz, M. Ebadi and M. Moghaddasian, “Employing Fuzzy Logic in Damping Power System Oscillations using SVC,” Proceedings of 2nd International Conference on Electrical Engineering, 25-26 March 2008, pp. 1-5.
- M. Sedighizadeh, M. S. Toulabi, A. Rezazadeh, M. Khatibi and B. Allahverdi-Charandabi, “Damping Improvement by SSSC and STATCOM in a Part of Iran Electrical Network,” Proceedings of 43rd International Universities Power Engineering Conference, 1-4 September 2008, pp. 1-5.
- G. J. Li, T. T. Lie, G. B. Shrestha and K. L. Lo, “Implementation of Coordinated Multiple FACTS Controllers for Damping Oscillations,” International Journal of Electrical Power and Energy Systems, Vol. 22, No. 2, February 2000, pp. 79-92.
- B. R. Andersen, L. Xu, P. J. Horton and P. Cartwright, “Topologies for VSC Transmission,” Power Engineering Journal, Vol. 16, June 2002, pp. 142-150.
- Y. Jiang-Hafner, H. Duchen, K. Linden, et al., “Improvement of Sub-Synchronous Torsional Damping Using VSC HVDC,” International Conference on Power System Technology 2002 Proceedings, Kunming, Vol. 2, October 2002, pp. 998-1003.
NOTES
*This work was supported in part by National Natural Science Foundation of China under Grant 50977050 and 50823001 and BP Alternative Energy Ltd.

