Energy and Power Engineering
Vol.08 No.07(2016), Article ID:70005,12 pages
10.4236/epe.2016.87026
A Statistical Analysis of Wind Speed and Power Density Based on Weibull and Rayleigh Models of Jumla, Nepal
Ayush Parajuli
Department of Mechanical Engineering, Pulchowk Campus, Tribhuwan University, Lalitpur, Nepal

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 July 2016; accepted 21 August 2016; published 24 August 2016
ABSTRACT
In the present study, wind speed data of Jumla, Nepal have been statistically analyzed. For this purpose, the daily averaged wind speed data for 10 year period (2004-2014: 2012 excluded) provided by Department of Hydrology and Meteorology (DHM) was analyzed to estimate wind power density. Wind speed as high as 18 m/s was recorded at height of 10 m. Annual mean wind speed was ascertained to be decreasing from 7.35 m/s in 2004 to 5.13 m/s in 2014 as a consequence of Global Climate Change. This is a subject of concern looking at government’s plan to harness wind energy. Monthly wind speed plot shows that the fastest wind speed is generally in month of June (Monsoon Season) and slowest in December/January (Winter Season). Results presented Weibull distribution to fit measured probability distribution better than the Rayleigh distribution for whole years in High altitude region of Nepal. Average value of wind power density based on mean and root mean cube seed approaches were 131.31 W/m2/year and 184.93 W/m2/year respectively indicating that Jumla stands in class III. Weibull distribution shows a good approximation for estimation of power density with maximum error of 3.68% when root mean cube speed is taken as reference.
Keywords:
Mean Wind Speed, Rayleigh Distribution, Weibull Distribution, Wind Power Density

1. Introduction
The world energy demand and consumption have increased seriously over last decades and most of this demand is met from fossil fuels. The use of fossil fuels and non-renewable form of energy has major impact on environment and our ecosystem through increasing pollution rate. In simple sense, energy and environment are major crisis of today. Many countries in the world are taking a step towards renewable form of energy to solve this challenge. Renewable energy sources like wind, solar, geothermal, hydro, biomass and ocean thermal energy have drawn attention from all over the world due to their almost inexhaustible and non-polluting characteristics. Wind energy being one of the important source for electricity production. It is vigorously pursued in many countries [1] .
Like other kind of energy, wind energy is ultimately a solar resource. Wind systems are created mainly due to two main causes: 1) temperature differences between the equator and the poles (the earth’s latitudes), 2) the rotation of the earth. Dry air in the vicinity of 30˚N and 30˚S flows towards the equator where it replaces rising hot air [2] . Wind is highly variable in space and time [3] . The energy potential of wind turbines can be calculated by toting up the energy corresponding to possible wind speeds in a certain period of time; so the probability distribution of different wind speeds of region is an important aspect in calculations. Thus, wind speed frequency distribution plays a critical role for predicting the energy output of a wind energy conversion system. During the last two decades, ample attentions were paid towards the development of a better statistical model for describing wind speed frequency distribution.
As seen from the literature, much concentration has been given to Weibull function because it is found to give fit to the observed wind speed data both at the surface [4] [5] and in the upper air [6] . Wentink compared the Weibull functions with other distributions like Plank’s frequency distribution, Rayleigh Distribution and Gamma distribution [7] . Fyrippis et al. have analysed wind data and calculated wind power density in Naxos Island Greece [8] . Weibull distribution was useful for them to distribute huge statistical data and present it as a continuous distribution for further analysis. They presented the site falls under class 7, indicating possibility of large scale electricity generation. Oner et al. have studied about Weibull distribution, Rayleigh distribution & normal distribution and used them to study potential turbine locations [9] . For similar analysis, Odo et al. [10] in Enugu, Nigeria; Ahmed et al. [11] in Halabja, Iraq; Islam et al. [12] in Kudat and Labuan, Malaysia; Safari et al. [13] in Rwanda; Oyedepo et al. [14] in south-east Nigeria; Abbas et al. [15] in Pakistan and many other researchers have used Weibull distribution & Rayleigh Distribution in different places for analysing wind speed data. Such work have been done whole over the world except for Nepal. Thus, we also use weibull and Rayleigh distribution among others to understand wind potential in high altitude region in Nepal.
Weibull distribution is a two parameter function, namely, shape factor k (dimensionless) and scale parameter c (dimensional). It is used in describing the wind speed frequency distribution. Several methods have been proposed to estimate Weibull parameters. Graphic method, maximum likelihood method and moment methods are commonly used to estimate Weibull parameters. The purposes of estimation are: a) To retrospectively characterize past conditions; b) to predict future power generation at one location; c) to predict power generation within a grid of turbines; d) to calibrate meteorological data.
Nepal is landlocked country with diversity in its climate from Himalayan region to Terai (Plain Lands) within short range of distance. Nepal’s total energy consumption in the fiscal year of 2008/09 was 400.5 million GJ. Traditional sources such as fuel wood, crop residues, and animal dung shared 87.1% of total energy consumption with commercial sources like petroleum products, coal and electricity, and other renewable energy sources contributing only 12.2% and 0.7% of the total energy consumption, respectively [16] . In context of Nepal, few researches regarding wind potential have been done. Studies made for the World Bank in 1977 indicate that the Khumbu area is a high potential area. The study by DANGRID, a Danish consulting firm, in 1992 reported a potential to generate 200 MW of electrical power with an annual energy production of 500 GWh from the wind resources along the 12 km valley between Kagbeni and Chusang in the Mustang district. The Kagbeni wind power project was one of the biggest projects with installed capacity of 20 kW built in 1987 under the support of the Danish Government. Although the government declared a plan to generate 20 MW electricity by wind energy in the Three Year Interim Plan (2007/08-2009/10), the lack of sufficient research data, and complicated geographical landscape of the country hindered its successful implementation [17] [18] . Ghimire et al. studied about wind energy resource assessment and feasibility study of wind farm in Mustang albeit predictive model of probability distributions were not applied. This article will look forward to provide information regarding theoretical wind harnessing potential in Himalayan region which is supposed to be region of high wind speed in Nepal and project to verify mostly accepted weibull probability distribution in Terrain of Nepal.
2. Materials and Methods
2.1. Site Location and Data Collection
Jumla is centre of Chandannath municipality in Jumla district and is located in Karnali zone of Nepal. The primary observation have shown that the region has wind potential. Since there was no similar study for this region, this study aimed to examine the wind energy potential of Jumla by finding Weibull and Rayleigh distribution parameters & determining the available power density. Besides applying mean wind speed, a root cube wind speed was applied to calculate the wind power and energy density. Since the wind power is proportional to cube of wind speed, it is a better representation of wind speed to be considered in calculations [19] . The average annual temperature in Jomsom is 13.5˚C. The rainfall here averages 766 mm. Department of Hydrology and Meteorology has setup a synoptic station in Jumla which is at 2300 m above sea level. Wind speed was measured at height of 10 m from ground level and average daily wind speed was available. Wind speed from 2004 to 2014 (2012 excluded) was used for analysis.
2.2. Vertical Extrapolation of Wind Speed
In real measurement, the wind speed tends to increase with height in most locations and depends mainly on atmospheric mixing and terrain roughness. Therefore, to calculate the total wind energy potential, the measured surface wind speed must be modified for an altitude different (40 m in this literature) from the normalized height (i.e. 10 m). For this reason the following equation was used: [1] [20]
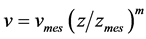 (1)
(1)
where, vmes is the wind speed at normalized height (m/s), zmes is the normalized height (m) and Z is the turbine height (m). The exponent m depends on factors as surface roughness and atmospheric stability. Numerically, it lies in the range of 0.05 - 0.5. Surface roughness (m) which is dependent on the terrain condition varies from 0.128 to 0.160 even in a very homogenous surface as flat or farm land. A typical value for surface roughness is 0.14 (for low roughness surface) and varies from less than 0.1 (for very flat land, water or ice surfaces) to more than 0.25 (for forest and woodlands). According to the literature, for neutral stable condition, m is approximately 0.143, which is commonly assumed to be constant in wind resource assessments. In this research, the surface roughness (m) is taken as 0.143 [19] .
2.3. Wind Speed Probability Distribution
To investigate the feasibility of the wind energy resource at any site, the best method is to calculate the wind power density based on the measured data of the meteorological station. Another method is to calculate the wind power density using frequency distribution functions like Weibull distribution, Rayleigh distribution, chi- squared distribution, generalized normal, log normal-distribution, three parameter log-normal, gamma distribution, inverse Gaussian distribution, kappa, wakeby, normal two variable distributions, normal square root of wind speed distribution, as well as hybrid distribution [19] [21] . Researches have shown that Weibull function fits the wind probability distribution more accurately compared to others [22] . Here the author uses Weibull and Rayleigh distribution to fit the time series data.
As wind speed changes regularly, frequency distribution of wind speed based on time series data can be calculated. Exact probability density function describing the speed data is difficult to find. Weibull distribution is a two parameter function characterized by scale parameter c (m/s) and shape parameter k (dimensionless). When Probability of occurrence of certain velocity is given by [11] [23] :
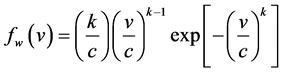 (2)
(2)
The corresponding weibull cumulative density function (CDF) is given by
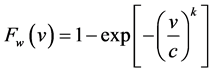 (3)
(3)
Rayleigh function is special case of Weibull function. When shape parameter k = 2, Weibull distribution becomes Rayleigh distribution.
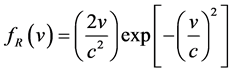 (4)
(4)
Shape parameter k and scale parameter c can be calculated using many methods as shown by previous researches. Graphical method (GM), Method of moments (MOM), Standard deviation method (STDM), Maximum likelihood method (MLM), Power density method (PDM), Modified maximum likelihood method (MMLM), Equivalent energy method (EEM) are widely used. In literature about wind energy, these methods are compared several times however results and recommendations of the previous studies are different from each other. For this reason, according to the results of the studies, it might be concluded that suitability of the method may vary with the sample data size, sample data distribution, sample data format and goodness of fit tests [24] . Research of Aazad et al. shows MOMs to be the most efficient method for determining the value of k and c to fit the Weibull distribution curves at any altitude [25] . This research proves to provide better information than others as 7 methods for parameter evaluation are compared at different altitudes. Researches must be conducted in terrains of Nepal because wind speed pattern shows different behaviour here. In absence of such studies, we choose work done by Azad et al. as our base, and choose MOMs to predict weibull parameters (k and c). Mean wind speed and variance of data shall be calculated beforehand then value of k & c can be as:
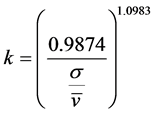 (5)
(5)
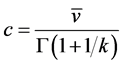 (6)
(6)
where Г is the gamma function.
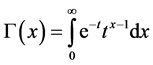 (7)
(7)
2.4. Evaluation of Weibull and Rayleigh Distributions
In order to check how accurately a theoretical probability density function fits with observation data, in this paper, four types of statistical errors are considered as judgement criterion. To evaluate the performance of considered distribution, the mean percentage error (MPE), mean absolute percentage error (MAPE), root mean square error (RMSE) parameter, and the chi-square test are performed [25] . MPE shows the average of percentage deviation between calculated value from weibull & Rayleigh distribution from the observed value whereas MAPE shows average absolute percentage deviation. Best results are obtained when these values are close to zero. The Chi-square goodness-of-fit test judges the adequacy of a given theoretical distribution to a data sample. The size of class intervals chosen in this study is 1 m/s [22] [26] .
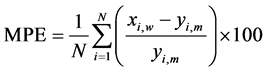 (8)
(8)
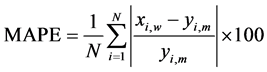 (9)
(9)
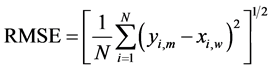 (10)
(10)
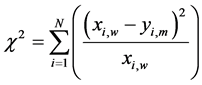 (11)
(11)
where N is number of observations, yi,m is frequency of observation or ith calculated value from measured data, xi,w is frequency of weibull or ith calculated value from the weibull distribution and same set of formulas can be used when subscript w is replaced by r representing Rayleigh distribution.
2.5. Wind Power Density (WPD)
Wind power density is measure of capacity of wind resources in specified site. Wind Power density can be measured based on many approaches [1] [19] [27] . It is well known that the power of wind that flows at (v) through a blade swept area (A = 1) increases as the cube of its velocity and is given by:
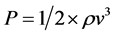 (12)
(12)
Many researches have used mean velocity to calculate wind power density. Mean power can be calculated by:
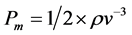 (13)
(13)
Because the wind power is proportional to cube of velocity, root mean cube of wind speed gives better result and is defined as [28] :
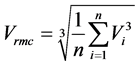 (14)
(14)
From Weibull distribution, power density can be calculated by:
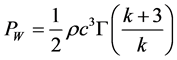 (15)
(15)
From Rayleigh distribution, power density can be calculated by:

where P represents Wind Power Density (W/m2) and ρ is density (kg/m3) at studied region. A typical value used in all the literature consulted is average air density 1.225 kg/m3 corresponding to standard conditions (sea level, 15˚C) [29] . However, air density is function of temperature T & Pressure P, both of which vary with altitude above z. The corresponding air density ρ could be evaluated using [8] :

where g is the gravitational acceleration (9.81 m/s2); T represents the average air temperature (K); To = 288 K (273 + 15); R is the gas constant (287 J/Kg/k) for air; and Г is vertical temperature gradient usually taken as 6.51 K/Km. Based on calculations, value of 1.231 was chosen as the air density.
However there is always an error in predicted value and measured value. Calculated wind power density by root mean cube speed or mean speed for the measured probability density distribution serves as reference power density (Pm). Power density predicted using Weibull and Rayleigh distribution (PW) & (PR) can be calculated using eqns. (15) & (16) respectively. Error in calculating the power density using distribution compared to measured value can be calculated as [15] :

2.6. Useful Wind Speeds
Knowing scale parameter (c) and shape parameter (k) of Weibull distribution function, average velocity can be predicted by Weibull and Rayleigh distribution [30] .


Similarly, most probable wind speed (Vmp) and maximum energy carrying wind speed (Vop) also can be calculated using following formulas [12] [30] :


Wind direction is important parameter for selection of wind turbines. For this purpose, a wind rose plot is needed which shows dominant wind direction. Wind rose can be done from 4 point, 8 point, 16 point and 32 points. To some users, the 8-point rose is sufficient for their needs. To another user, yet for same purpose, a 16-point rose is absolutely necessary [31] . Mainly two types of wind rose: wind frequency rose and wind speed rose can be drawn [32] . Unavailability of data on wind direction in stations of DHM barred us from plotting wind rose and thus is not presented in this article.
3. Results and Discussions
3.1. Monthly Mean Wind Speed and Seasonal Variations
Wind speeds are different as months and seasons vary. Figure 1 shows mean wind speed for different months in different sets of years. Average of 2 consecutive years for same month is taken as a data point and plotted in graph. Figure shows a similar trend for all five curves where wind speed increases from January and reaches its peak value in May/June. Then, wind speed decreases in July/August as these months are susceptible to heavy rainfall in Nepal. But, wind speed again rises in October & decreases gradually till December. July & October are two months when wind speed rises in Jumla region. The same scenario is experienced in whole Nepal. The maximum & minimum mean wind speed in different months belonged to July 2004/05 and December 2013/14. For better analysis, a single year was divided in two season as cold season (November-April) and Warm Season
(May-October). Table 1 shows yearly mean wind speed for cold season & warm season. 80% of years analyzed have high mean wind speed in warm season. Average mean wind speed in warm season & cold season for 10 years are 6.17 m/s and 5.76 m/s respectively. Results clearly shows that warmer season has higher mean wind speed compared to colder season. The pattern is different compared to other countries seasonal variation where wind speed will be greater in colder season. In Nepal, lower wind speed coupled with colder dense air will give similar power as in warmer season where wind speed is higher but air density will be lower. So, the power
Figure 1. Monthly mean wind speed in Jumla (2004-2014).
Table 1. Yearly mean wind speed for cold and warm seasons in Jumla.
available will be constant throughout.
Table 2 shows yearly mean wind speed and corresponding standard deviation. Maximum mean wind speed & minimum mean wind speed was calculated to be 7.35 m/s and 5.07 m/s respectively. Yearly mean wind speed for 2014 was almost same as for 2011. The general trend in yearly mean wind speed seems to be decreasing gradually from 2004 to 2014. Especially, mean wind speed in December/January seems to be sharply decreasing as year progresses which lead to decrease in yearly mean wind speed. In other words, drop of wind speed on cold season is more severe than warm season. Several Processes on local, regional and global scales are likely contributing to this decrease. Increasing forest density can’t alone explain this phenomenon described by Iacono [33] . On other hand, several researches have shown using both climate model simulations [34] and surface observations [35] [36] that the positions of the main storm tracks that cross North America, which are generally associated with the jet stream, have moved northwards. This may be impacting the wind speed pattern in nearby areas. Although, similar research is not found in sub-continent region, it can be predicted from their analysis, the global climate change has played a major role in this declining wind speed. The severe decrease of speed in cold season is also explained by increasing temperature in Mountainous region. The region which otherwise would be much colder, air with higher density would move to replace hotter air in lower belts. This pattern is affected.
3.2. Weibull and Rayleigh Distribution
The variation of wind speeds is often described using Weibull & Rayleigh density function. These are statistical tool which are widely accepted for evaluation of local wind probabilities and considered as a standard approach. Methods of Moments was used to calculate both weibull parameters. To calculate weibull parameters, yearly mean wind speed and standard deviation were calculate and shown in Table 2. Table 2 shows yearly weibull parameters and average weibull parameters for whole 10 years. It is seen from table that, while scale factor varies between 5.66 and 8.13, the shape factor ranges from 2.83 to 3.84. The 10 year average value of scale factor and shape factor are 6.69 and 3.03 m/s respectively. As it can be seen from Table 2, the highest and the lowest of k parameter belongs to 2004 & 2009 respectively. From the result, it is obvious that shape parameter has small variation compared to scale parameter. It has been found that for most wind conditions value of k varies from 1.5 to 3, whereas c ranges from 3 to 8 [37] . Value of c is within the range specified but value of k is offset for this location. k being shape parameter shows how peaked the wind distribution is. For this belt, the wind distribution is peaked compared to general trend. Ration of k/c is a crucial factor as this will determine peak frequency. The high value of k/c will be useful for predicting most probable speed with greater accuracy. Apart from that, methods used for parameter evaluation is also responsible for this difference. Ahmed [11] shows value of k varied between 2.3029 and 3.2592 when four different methods were compared. MOMs as shown a better predictor by researchers, we stick to this value.
Table 2. Yearly mean wind speed for cold and warm seasons in Jumla.
Table 3 shows characteristics wind speed predicted from Weibull model & Rayleigh model. The most probable wind speed, wind speed which is carrying the maximum energy, predicted mean speed and root mean cube speed were calculated. The Vmp for weibull ranged from 5.01 to 7.52 m/s with an average of 5.86 m/s whereas for Rayleigh ranged from 4 to 5.75 m/s with an average of 4.73 m/s. Also, the highest value of Vop was at 2004. Weibull predicted it to be 9.07 m/s whereas Rayleigh predicted it as 11.5 m/s. Mean speed predicted by weibull was same as predicted main speed because same equation (6, 19) are used to calculate value of shape factor and mean speed. Rayleigh model predicted mean wind speed with maximum deviation of 0.37 m/s with 80% of difference not over 0.1 m/s. Root mean cube speed was calculated with an average value of 6.7 m/s. Figure 2 shows histogram of the actual frequency distribution for all these years with the Weibull and Rayleigh function for fitting a wind data probability distribution. The difference between these two function is shape parameter k. Estimated average Weibull distribution shape parameter 3.03 which is different with Rayleigh distribution shape parameter 2. As it can be seen in figure, Weibull distribution fits the time series data more appropriately than Rayleigh distribution. Several statistical tools were used to analyze the error in fitting weibull and Rayleigh distribution. Table 4 shows evaluation of Weibull and Rayleigh distribution and MPE, MAPE, RMSE and Chi- Square goodness-of-fit were used to evaluate them. Table 4 shows χ2 is 0.03 for Weibull and 0.46 for Rayleigh. χ2 with lower value shows better goodness of fit. The MPE, MAPE & RMSE for Weibull distribution were 18%, 30% and 0.012 while these indices for Rayleigh distribution were 70%, 84% and 0.024 respectively. Literatures have found that the weibull model predict the actual value better than in comparison to the Rayleigh model which is supported by this study [8] [9] [12] [19] . Dhunny et al. [38] have analysed among 7 distribution to support Weibull distribution is better probability distribution.
3.3. Wind Power Density
The power density calculated from measured probability density distributions and those obtained from models are presented in Table 5. As it can be seen in Table 5, the average value of wind power calculated from mean wind speed was 131.31 W/m2/year. Extreme values of wind power calculate using root mean cube speed (for 2004 and 2011) were 306.36 and 109.29 W/m2/year with an average of 184.93 W/m2/year. The values of wind power which have been calculated by applying root mean cube speed approach were higher than that of arithmetic mean wind speed values. The wind power density calculated from root mean cube speed and predicted by weibull model are similar. Average wind power density predicted using Weibull and Rayleigh model are 183.28 and 244.82 W/m2/year. Table 5 clearly shows wind power estimated by Rayleigh model is higher than that predicted by Weibull model. Betz limit gives maximum efficiency of wind power conversion system (wind turbine) to be 0.593. Best wind turbine have efficiency of around 0.4. So, maximum power generation capability is 183.28 (0.4) W/m2.
Errors in calculating the power density using Weibull and Rayleigh models are presented in Table 6. Taking arithmetic mean wind speed as reference speed, maximum error of 45.36% in Weibull and 88.11% in Rayleigh distribution were estimated. When root mean cube speed was taken as reference, maximum error for Weibull of 3.86% with remaining of calculated errors below 0.9% and for Rayleigh of 43.52%. As was shown before, the weibull function describe the observed values of wind speed reasonably well, so it can be easily guessed that predicted and observed value of wind power density will be similar. This analogy shows root mean cube speed measures wind power density more accurately than arithmetic mean speed. Results of wind power density shows Jumla is in class 3 [39] . Class 1 are generally not suitable for wind turbine applications whereas class 2 areas are marginal. Areas which are classified as class 3 or greater are suitable for most wind turbine applications [40] . For initial years, Jumla was a class 6 region and the decreasing wind speed has put in class 3 today. It is a big
Table 3. Characteristics wind speed (m/s).
Table 4. Evaluation of Weibull and Rayleigh distribution.
Table 5. Wind power density (W/m2/year) of Jumla (2004-2014).
challenge to forecasting power density with similar trend of decreasing speed and if similar trend is seen, it may be class 2 region some years later which is a subject of concern for investors. Similarly, road transportation puts a question mark for such projects is Himalayan region.
Figure 2. Comparison of observed and predicted wind speed frequencies of Jumla.
Table 6. Error (%) values in calculating wind power density (2004-2014).
4. Conclusions
In the present study we discussed analysis whose objective was to investigate the potential of wind energy resource in Jumla. For this purpose, wind speed data of Jumla station (DHM) were analyzed over a 10 year period from 2004 to 2014 (2012 excluded). The probability density distributions and power density were derived from time series data. Weibull and Rayleigh probability density function have been fitted to the measured probability distributions. The wind power density has been evaluated. The most important outcomes of the study can be summarized as follows:
1) Jumla is shown to be a marginal site (Class III) for wind energy generation as the region possesses moderate wind characteristics. This is shown by average monthly & yearly wind speed along with wind power density. Himalayan region is supposed to have higher power generation capability in Nepal. Jumla, as one of perceived potential site, being a class III region shows Nepal has modest probability of wind energy generation capability in large scale.
2) There is a decreasing trend in yearly & monthly wind speed in Jumla which is a subject of concern. Decrease of wind speed is more than in warm season. We emphasize global climate change for this effect. This will be a subject of concern for Government while they’re focusing on diverse source of energy after fuel crisis in Nepal and looking forward for wind energy development.
3) Warm season has higher mean wind speed compared to cold season and this will make sure, energy generation during warm and cold season don’t have much difference as density varies with temperature.
4) The Weibull distribution is fitting the measured probability distribution better than Rayleigh distribution and supports the studies done in other parts of the world.
These results fulfill our four reasons of estimation of weibull parameter mentioned in introduction section. Meteorological data was calibrated to characterize the past data which was used to predict power generation capability. The results obtained are satisfying. Meanwhile, further investigations are to be done based on a more detailed and systematic analysis of wind speed patterns. Similarly, wind rose is not shown because of non- availability of information on wind direction from the station. Future works shall be guided in that path.
Acknowledgements
Supports by Department of Mechanical Engineering, Pulchowk Campus, Institute of Engineering, Tribhuwan University is gratefully acknowledged and also the author would like to thank Department of Hydrology and Meteorology, Government of Nepal for providing wind data of Jumla station.
Cite this paper
Ayush Parajuli, (2016) A Statistical Analysis of Wind Speed and Power Density Based on Weibull and Rayleigh Models of Jumla, Nepal. Energy and Power Engineering,08,271-282. doi: 10.4236/epe.2016.87026
References
- 1. Dhunny, A.Z., Lollchund, M.R., Boojhawon, R. and Rughooputh, S.D.D.V. (2014) Statistical Modelling of Wind Speed Data for Mauritius. International Journal of Renewable Energy Research, 4, 1056-1064.
- 2. Mohammadi, K. and Mostafaeipour, A. (2013) Using Different Methods for Comprehensive Study of Wind Turbine Utilization in Zarrineh, Iran. Energy Conversion and Management, 65, 463-470.
http://dx.doi.org/10.1016/j.enconman.2012.09.004 - 3. Elliott, D. and Holladay, C. (1987) Wind Energy Resource Atlas of the United States. NASA STI/Recon Technical Report N, 87, 24819.
- 4. Kaldellis, J.K. (1999) Wind Energy Management. Stomoullis, Athens.
- 5. Wang, X.L., Wan, H. and Swail, V.R. (2006) Observed Changes in Cyclone Activity in Canada and Their Relationships to Major Circulation Regimes. Journal of Climate, 19, 896-915.
http://dx.doi.org/10.1175/JCLI3664.1 - 6. Leibensperger, E.M., Mickley, L.J. and Jacob, D.J. (2008) Sensitivity of US Air Quality to Mid-Latitude Cyclone Frequency and Implications of 1980-2006 Climate Change. Atmospheric Chemistry and Physics, 8, 7075-7086.
http://dx.doi.org/10.5194/acpd-8-12253-2008 - 7. Yin, J.H. (2005) A Consistent Poleward Shift of the Storm Tracks in Simulations of 21st Century Climate. Geophysical Research Letters, 32, L18701.
http://dx.doi.org/10.1029/2005GL023684 - 8. Iacono, M.J. (2009) Why Is the Wind Speed Decreasing? Journal of Geophysical Research: Atmospheres, 114, 1-3.
- 9. Dore, A.J., Vieno, M., Fournier, N., Weston, K.J. and Sutton, M.A. (2006) Development of a New Wind-Rose for the British Isles Using Radiosonde Data, and Application to an Atmospheric Transport Model. Quarterly Journal of the Royal Meteorological Society, 132, 2769-2784.
http://dx.doi.org/10.1256/qj.05.198 - 10. Crutcher, H.L. (1957) On the Standard Vector-Deviation Wind Rose. Journal of Meteorology, 14, 28-33.
http://dx.doi.org/10.1175/0095-9634-14.1.28 - 11. Caretto, L. (2010) Use of Probability Distribution Functions for Wind. California State University Northridge, Calif.
- 12. Keyhani, A., Ghasemi-Varnamkhasti, M., Khanali, M. and Abbaszadeh, R. (2010) An Assessment of Wind Energy Potential as a Power Generation Source in the Capital of Iran, Tehran. Energy, 35, 188-201.
http://dx.doi.org/10.1016/j.energy.2009.09.009 - 13. Patel, M. (2005) Wind and Solar Power Systems: Design, Analysis, and Operation. CRC Press, Boca Raton.
http://dx.doi.org/10.1201/9781420039924 - 14. Carlin, P.W. (1997) Analytical Expressions for Maximum Wind Turbine Average Power in a Rayleigh Wind Regime. ASME Wind Energy Symposium, Reno, 6-9 January 1997, 1-9.
- 15. Chang, T.P. (2010) Wind Speed and Power Density Analyses Based on Mixture Weibull and Maximum Entropy Distributions. International Journal of Applied Science and Engineering Research, 8, 39-46.
- 16. Azad, A., Rasul, M. and Yusaf, T. (2014) Statistical Diagnosis of the Best Weibull Methods for Wind Power Assessment for Agricultural Applications. Energies, 7, 3056-3085.
http://dx.doi.org/10.3390/en7053056 - 17. Akdag, S.A. and Dinler, A. (2009) A New Method to Estimate Weibull Parameters for Wind Energy Applications. Energy Conversion and Management, 50, 1761-1766.
http://dx.doi.org/10.1016/j.enconman.2009.03.020 - 18. Weibull, W. (1951) A Statistical Distribution Function of Wide Applicability. Journal of Applied Mechanics, 103, 293-297.
- 19. Ouarda, T.B.M.J., Charron, C., Shin, J.-Y., Marpu, P.R., Al-Mandoos, A.H., Al-Tamimi, M.H., et al. (2015) Probability Distributions of Wind Speed in the UAE. Energy Conversion and Management, 93, 414-434.
http://dx.doi.org/10.1016/j.enconman.2015.01.036 - 20. Simiu, E. and Heckert, N.A. (1996) Extreme Wind Distribution Tails: A “Peaks over Threshold” Approach. 539-547.
- 21. Buenestado-Caballero, P., Jarauta-Bragulat, E. and Hervada-Sala, C. (2006) Weibull Parameters Distribution Fitting in the Surface Wind Layer. International Association for Mathematical Geology 11th International Congress, Liège, 3-8 September 2006, 6-9.
- 22. Pishgar-Komleh, S.H., Keyhani, A. and Sefeedpari, P. (2015) Wind Speed and Power Density Analysis Based on Weibull and Rayleigh Distributions (A Case Study: Firouzkooh County of Iran). Renewable and Sustainable Energy Reviews, 42, 313-322.
http://dx.doi.org/10.1016/j.rser.2014.10.028 - 23. Ghimire, M., Poudel, R.C., Bhattarai, N. and Luintel, M.C. (n.d.) Wind Energy Resource Assessment and Feasibility Study of Wind Farm in Mustang. Journal of Institute of Engineering, 8, 93-106.
http://dx.doi.org/10.3126/jie.v8i1-2.5099 - 24. Surendra, K.C., Khanal, S.K., Shrestha, P. and Lamsal, B. (2011) Current Status of Renewable Energy in Nepal: Opportunities and Challenges. Renewable and Sustainable Energy Reviews, 15, 4107-4117.
http://dx.doi.org/10.1016/j.rser.2011.07.022 - 25. WECS (2008) Energy Sector Synopsis Report.
- 26. Abbas, K., Alamgir, K., Ali, A., Khan, D. and Khalil, U. (2012) Statistical Analysis of Wind Speed Data in Pakistan. World Applied Sciences Journal, 18, 1533-1539.
- 27. Oyedepo, S.O., Adaramola, M.S. and Paul, S.S. (2012) Analysis of Wind Speed Data and Wind Energy Potential in Three Selected Locations in South-East Nigeria. International Journal of Energy and Environmental Engineering, 3, 7.
http://dx.doi.org/10.1186/2251-6832-3-7 - 28. Safari, B. and Gasore, J. (2010) A Statistical Investigation of Wind Characteristics and Wind Energy Potential Based on the Weibull and Rayleigh Models in Rwanda. Renewable Energy, 35, 2874-2880.
http://dx.doi.org/10.1016/j.renene.2010.04.032 - 29. Islam, M.R., Saidur, R. and Rahim, N.A. (2011) Assessment of Wind Energy Potentiality at Kudat and Labuan, Malaysia Using Weibull Distribution Function. Energy, 36, 985-992.
http://dx.doi.org/10.1016/j.energy.2010.12.011 - 30. Ahmed, S.A. (2013) Comparative Study of Four Methods for Estimating Weibull Parameters for Halabja, Iraq. International Journal of Physical Sciences, 8, 186-192.
- 31. Odo, F.C., Offiah, S.U. and Ugwuoke, P.E. (2012) Weibull Distribution-Based Model for Prediction of Wind Potential in Enugu, Nigeria. Advances in Applied Science Research, 3, 1202-1208.
- 32. Oner, Y., Ozcira, S., Bekiroglu, N. and Senol, I. (2013) A Comparative Analysis of Wind Power Density Prediction Methods for Çanakkale, Intepe Region, Turkey. Renewable and Sustainable Energy Reviews, 23, 491-502.
http://dx.doi.org/10.1016/j.rser.2013.01.052 - 33. Fyrippis, I., Axaopoulos, P.J. and Panayiotou, G. (2010) Wind Energy Potential Assessment in Naxos Island, Greece. Applied Energy, 87, 577-586.
http://dx.doi.org/10.1016/j.apenergy.2009.05.031 - 34. Rehman, S., Halawani, T.O. and Husain, T. (1994) Weibull Parameters for Wind Speed Distribution in Saudi Arabia. Solar Energy, 53, 473-479.
http://dx.doi.org/10.1016/0038-092X(94)90126-M - 35. Baynes, C. and Davenport, A. (1975) Some Statistical Models for Wind Climate Prediction. Preprints Fourth Conference Probability and Statistics in the Atmospheric Sciences, Tallahassee, 18-21 November 1975, 1-7.
- 36. Justus, C.G., Hargreaves, W.R. and Yalcin, A. (1976) Nationwide Assessment of Potential Output from Wind-Powered Generators. Journal of Applied Meteorology, 5, 673-678.
- 37. Wentink Jr., T.W. (1976) Study of Alaskan Wind Power and Its Possible Applications. Final Report, 1 May 1974-30 Jan 1976, Geophysical Institute, Alaska University, Fairbanks.
- 38. Hernandez-Escobedo, Q., Manzano-Agugliaro, F., Gazquez-Parra, J.A. and Zapata-Sierra, A. (2011) Is the Wind a Periodical Phenomenon? The Case of Mexico. Renewable and Sustainable Energy Reviews, 15, 721-728.
http://dx.doi.org/10.1016/j.rser.2010.09.023 - 39. Ramachandra, T. and Shruthi, B. (2005) Wind Energy Potential Mapping in Karnataka, India, Using GIS. Energy Conversion and Management, 46, 1561-1578.
http://dx.doi.org/10.1016/j.enconman.2004.07.009 - 40. Albuhairi, M.H. (2006) Assessment and Analysis of Wind Power Density in Taiz—Republic of Yemen. Assiut University Bulletin for Environmental Researches, 9, 13-21.




