Energy and Power Engineering
Vol.08 No.10(2016), Article ID:71902,13 pages
10.4236/epe.2016.810029
New Analytical Model for Optimal Placement of Wind Turbines in Power Network under Pool and Reserve Markets Conditions
Babak Safari Chabok1*, Ahmad Ashouri2, Majid Yekta Khalilsaraei3, Hossein Shahidi Moghadam4, Fariborz Ghasemi5
1Department of Power System Engineering, Tarbiat Modares University, Tehran, Iran
2Department of Electrical Engineering, Khodabandeh Branch, Islamic Azad University, Khodabandeh, Iran
3Department of Mechatronic Research Laboratory (MRL), Qazvin Branch, Islamic Azad University, Qazvin, Iran
4Department of Regional Electric Company, Guilan Branch, Rasht, Iran
5East Azerbaijan Science and Research Branch, Islamic Azad University, Tabriz, Iran

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 19, 2016; Accepted: July 10, 2016; Published: October 8, 2016
ABSTRACT
In this paper a new market based analytical model is proposed for optimal placement of Wind Turbines (WTs) in power systems. In addition to wind turbines, thermal units (THUs) and Pumped Storage Hydro Power Plants (PSHPPs) owners participate in power market. Objective function is defined as participants’ social welfare achieved from power pool and ancillary markets in yearly horizon. Wind turbines have been modeled by probability-generation tree scenarios based on statistical information. We concentrate on investment profits of WTs numbers and its generation capacity beside to PSHPPs and THUs power plants in power systems due to increase in high flexible tools for Independent system operator into the planning and operation planning time interval. For effectiveness evaluation of proposed model, simulation studies are applied on 14-Bus IEEE test power system.
Keywords:
Wind Turbine, Pumped Storage Hydro Power Plants (PSHPPs), Power Pool and Ancillary Market, Independent System Operator

1. Introduction
Optimal placement of distributed generations (DGs) has a great importance. In a power system, optimal placement of wind turbines at the presence of PHESS is of high importance for improving objectives such as maximizing profits of owners and investors of wind turbines and turning into a market with perfect competitive conditions, loss reduction to a considerable extent, increasing reliability levels of network, improving voltage profiles of network, etc. Distributed generation units of wind turbines can participate in energy sale or reserve market independently, or they can act in an integrated way with a company that has PHESS or traditional thermal units or both of them. One of very common techniques is using optimal placement of DGs in sub-transmission or distribution networks. Application of wind turbines as a type of DGs for generating energy has a high capital cost, but its operation cost is very low. In PHESS, electrical energy is converted to potential energy and is stored in the upper reservoir in the form of water, and during the peak load times the stored water flows back through turbine path and like a usual hydroelectric system the energy is again converted to electricity. Compromise between incentives for DG developers and distribution network operators (DNOs) is evaluated in [1] by using multi-objective OPF. Reconfiguration of the network is used in [2] in order to assess the maximum installed capacity of DGs in an optimal way. Authors in [3] proposed a hybrid optimization method for finding optimal locations and sizes of WTs, which reduces the annual loss amount to its minimum value. The proposed method combines genetic algorithm, gradient-based constrained nonlinear optimization and Monte-Carlo iterative simulations. A Tabu search method is proposed in [4] for determining optimal location and size of DGs. In [5] wind characteristics are analyzed using data collected wind speed for five weather stations in Lebanon and available for at least one year. The Weibull distribution is used to model the wind speed at these five locations in Lebanon. Shape parameters and scale were estimated using four methods, the variability of the method, the method of standard deviation, the method of power density and the Moroccan method. The purpose of this article is to compare the methods of assessment of wind energy potential, as well as evaluation of the power density at different altitudes. In [6] the simulation and evaluation of a renewable hybrid power plant for off-grid fully autonomous operation on an intermediate-sized island in the Aegean Sea has been presented. A stand-alone energy system including storage facilities is simulated, optimized and analyzed relying on real-case weather and demand data of a relatively large remote community. Optimization of the power plant structure shows that to ensure continuous off-grid energy generation, even under extreme conditions, the combination of more than one renewable technology is required. Recent trends of differing electricity market design and increasing amounts of variable renewable generation have allowed for pumped storage hydro to provide other services to support the power system, and earn additional revenue. While the market design topics have been evolving since their inception, there are still ways that the designs can be improved to better value all of the capabilities that pumped storage hydro has to offer, while still maintaining a fair and impartial perspective. In [7] some of the issues that may limit the ability to fully value pumped storage hydro plants in today’s markets has been presented and propose some solutions to those problems. It is essential that the safe operation guidelines of the hydropower plants be defined accurately, in advance. To achieve that, detailed numerical simulations should be done with reliable software. In some cases, even physical modeling may also be necessary. In the present study, water-hammer problems in [8] are investigated. Time-dependent flow conditions in the penstocks are simulated by the help of computer software. It solves nonlinear differential equations by using the method of characteristics that uses the principles of finite difference method. Firstly, hydraulic transients for various operational cases are investigated using some scenarios. The objectives of [9] [10] are to investigate the associated costs of stand-alone renewable hybrid power plants on a Greek island and compare them to the cost of the currently used fossil- fuel-based conventional plant. The plants examined here are designed to fully cover the electricity needs of the island. Islands may face numerous energy problems and rely heavily on foreign and environmentally-harmful fuels. It is shown that the relatively high cost of electricity of such a remote region can increase the competitiveness and promote the wider incorporation of technologies based on renewable energy sources that may, in other cases, seem economically inferior to business-as-usual energy solutions. In this paper, in order to avoid problems in coding and decoding of problem parameters in intelligent methods and also due to nonlinear equations of power balance in constraints of optimal power flow (OPF) equations based on energy and reserve market conditions, mixed Integer Nonlinear Programming (MINLP) analytic method is used for optimizing the problem of allocating optimal number, location and installation capacity of WTs from the viewpoint of the WTs investment owners and with regard to the presence of PHESS. For DG resources placement, mathematical formulation of the objective function of mentioned optimization problem should be defined in such a way that both owners of these resources with regard to installation-operation costs. In addition to the resulting income of circulating money in the market for investment and more active attendance in the electricity market are justified. Finally, the profits of the other partners of reserve and pool-based markets such as thermal and PHESS units are determined in an optimal way.
2. Mathematical Formulation of Proposed Model
2.1. Objective Function
The first term of objective function is as “Equation (1)”, 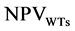 index will address the analysis of profitable investment for horizon of several years, which is carried out by owners and investors of WTs; owners net profit value (NPV) is defined as difference between obtained currents from electrical energy sale and investment cost of these DGs. The second term,
index will address the analysis of profitable investment for horizon of several years, which is carried out by owners and investors of WTs; owners net profit value (NPV) is defined as difference between obtained currents from electrical energy sale and investment cost of these DGs. The second term, 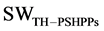 index, is social welfare of remaining market partners, i.e. owners of PHESS and thermal units, which models the obtained profit of presence of these resources in pool-based energy market by simultaneous clearing of energy and reserve during an annual horizon. Net profit value of xi-th owner of WT in the several year planning horizon
index, is social welfare of remaining market partners, i.e. owners of PHESS and thermal units, which models the obtained profit of presence of these resources in pool-based energy market by simultaneous clearing of energy and reserve during an annual horizon. Net profit value of xi-th owner of WT in the several year planning horizon 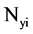 regarding optimal capacity allocation of this DG installed in an appropriate location in the network, is defined as “Equation (2)”. Index
regarding optimal capacity allocation of this DG installed in an appropriate location in the network, is defined as “Equation (2)”. Index
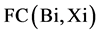 which is obtained by selling electrical energy to pool-based market under different levels of consumers load demands Li in yearly horizon, is calculated using “Equation (3)”. Where,
which is obtained by selling electrical energy to pool-based market under different levels of consumers load demands Li in yearly horizon, is calculated using “Equation (3)”. Where, 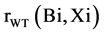 is investment profit rate and
is investment profit rate and 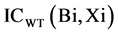 is capital cost of Xi-th owner of WT connected to bus Bi of power system, and
is capital cost of Xi-th owner of WT connected to bus Bi of power system, and  index is the number of years accounted for optimal placement of WTs in the planning horizon. Index
index is the number of years accounted for optimal placement of WTs in the planning horizon. Index 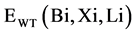 is wind energy sold by Xi-th owner of WT installed in bus Bi to pool-based market in electrical form in load demand level of Li.
is wind energy sold by Xi-th owner of WT installed in bus Bi to pool-based market in electrical form in load demand level of Li. 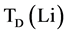 is time and
is time and  is market clearing price corresponding to load demand level of Li at the presence of DGs such as WTs in addition to the other energy generation resources including thermal and PHESS units, and
is market clearing price corresponding to load demand level of Li at the presence of DGs such as WTs in addition to the other energy generation resources including thermal and PHESS units, and 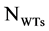 is the total number of identified and candidate buses for WTs installation. Therefore, investment net profit value of all developers of DGs such as WTs at the presence of PHESS is calculated based on Equation (4). During the solving process of proposed analytic model, NPV of owners of WTs will be assessed considering the installation location and amount of electrical energy generation amount in different levels of load demands with regard to the predicted velocity-power scenarios based on statistical data of climate patterns during the several years planning horizon. Prediction of daily or monthly velocity-power curve of wind energy for WTs developers during the annual planning horizon in different places affects the market clearing price and obtained income from energy sale to electricity market, and finally has impacts on NPV of WTs developers in various buses of the network. As a result, acceptance or rejection of proposals of present generators (manufacturers) in supply section of energy market is determined by independent system operator (ISO) based on OPF and considering supply conditions and different levels of load demand in pool-based market during yearly planning horizon, as “Equation (5)”. Since consumers load demands in different buses of inelastic network are assumed to take the energy price, therefore, social welfare can be attributed to sum profit of generations including PHESS and thermal units, where indexes
is the total number of identified and candidate buses for WTs installation. Therefore, investment net profit value of all developers of DGs such as WTs at the presence of PHESS is calculated based on Equation (4). During the solving process of proposed analytic model, NPV of owners of WTs will be assessed considering the installation location and amount of electrical energy generation amount in different levels of load demands with regard to the predicted velocity-power scenarios based on statistical data of climate patterns during the several years planning horizon. Prediction of daily or monthly velocity-power curve of wind energy for WTs developers during the annual planning horizon in different places affects the market clearing price and obtained income from energy sale to electricity market, and finally has impacts on NPV of WTs developers in various buses of the network. As a result, acceptance or rejection of proposals of present generators (manufacturers) in supply section of energy market is determined by independent system operator (ISO) based on OPF and considering supply conditions and different levels of load demand in pool-based market during yearly planning horizon, as “Equation (5)”. Since consumers load demands in different buses of inelastic network are assumed to take the energy price, therefore, social welfare can be attributed to sum profit of generations including PHESS and thermal units, where indexes  and
and  are profits of thermal and PHESS units respectively, obtained from energy sale to pool-based market in load level of Li. In next sections, the accurate modeling of WTs owners’ behaviors, PHESS and thermal units to attend the energy and reserve day- ahead pool-based market is presented assuming different load levels during an annual horizon.
are profits of thermal and PHESS units respectively, obtained from energy sale to pool-based market in load level of Li. In next sections, the accurate modeling of WTs owners’ behaviors, PHESS and thermal units to attend the energy and reserve day- ahead pool-based market is presented assuming different load levels during an annual horizon.
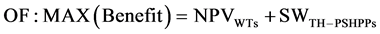 (1)
(1)
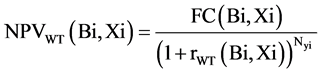 (2)
(2)
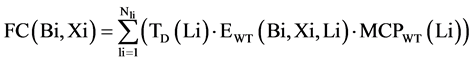 (3)
(3)
 (4)
(4)
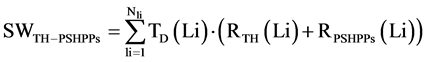 (5)
(5)
2.2. Analytical Algorithm for Optimal Placement of Wind Turbines
The algorithm procedure for optimal placement of WTs owners in power system is as Figure 1. First, one of candidate places is selected randomly with regard to predetermined probabilistic scenarios for wind turbine installation. Optimal power flow has been performed based on market conditions and if convergence condition is satisfied problem variable can be concluded and next wind turbine location and capacity is selected same as previous method. If convergence condition is not satisfied then algorithm from step 2 will be restarted.
3. Simulation Studies and Numerical Results
At last, in order to verify the effectiveness and validation of the proposed algorithm in finding optimal location and size of wind turbines in power systems, the algorithm is carried out on a 14-bus power network. Single-line diagram of this power system is shown in Figure 2.
As it is seen from the figure, generation part of the power system includes 4 thermal units respectively connected to Bus 2, Bus 3, Bus 5 and Bus 9, where all of them have permission of presence in energy and reserve market. Technical and economic data of the mentioned thermal units in terms of active and reactive power capacities and the way prices are proposed in the energy market and ancillary services are listed in Table 1.
Figure 1. New analytical model for optimal placement of WTs on power network.
Figure 2. Single-line diagram of the studied 14-bus network.
Table 1. Thermal unit owner information for power pool and reserve markets.
One PHESS unit connected to Bus 7 is available in the network, which has only permission of presence in the energy market from the operator. PHESS unit connected to Bus 7 in the 14-bus network under study has 4 turbo units, which have both pump and generator modes of operations. In generator mode, maximum capacity for generating active and reactive powers are 100 MW and 85 MVar, respectively, and minimum active and reactive powers injected to the network are 10 MW and 5 MVar, respectively. For operation in pump mode, the maximum consumption level of active and reactive powers are 80 MW and 55 MVar and its minimum is 10 Mw and 5 MVar, respectively. All technical and economic data of these PHESS systems including initial energy and min/max stored energy behind the upper reservoir, efficiency and fixed cost of operation of power plant are given in Table 2.
Table 2. Pump storage hydro power plant owner information for power pool markets.
In addition, there will be the possibility of presence and investment of two owners of WTs on predetermined buses Bus 7, Bus 12, Bus 13 and Bus 14, which are good choices to install these DG resources from the aspect of climate pattern studies. Owners and investors of WTs, considering possible scenarios of velocity-power and net profit value in circulation resulting from attending daily energy pool-based market during an annual horizon, are able to install a predetermined capacity and utilize it which in this study, these values for Bus 7, Bus 12, Bus 13 and Bus 14 are estimated 80, 100, 150 and 50 MW, respectively. Also, wind turbines as price taker resources for presence in power pool-based market during the annual horizon, benefit from incentive and penalty plans by ISO, respectively during excess and lower capacities of network requirements. As it can be seen from single-line diagram (SLD) of 14-bus studied power system, transmission network comprises 17 transmission lines: line 12, line 15, line 23, line 26, line 27, line 34, line 37, line 710, line 78, line 48, line 49, line 56, line 510, line 711, line 712, line 813 and line 914. Data related to admittance of transmission lines, Gij-jBij, and thermal limit capacity of transmission lines P line of 14-bus studied power system are shown in Table 3.
Demand of network consumers that is assumed to be constant power loads are located on buses Bus 5, Bus 7, Bus 9, Bus 10, Bus 11, Bus 12 and Bus 14 in the network. These consumers are modeled as inelastic and are presented in a unipolar pool-based market that only thermal generation resources compete for energy sale and determining market clearing price (MCP). Active and reactive power demand of these network buses is listed in Table 4 for three load levels of low, average and peak loads during an annual time horizon.
Here, thermal units propose their no-load synchronous capacity by a price equal to 10% of marginal cost of energy generation by that unit in order to present spinning reserve to deal with the uncertainty of network such as utilization of wind turbines installed by private owners, random load changes and sudden loss of units and lines, so certain criterion equal to 10% of total load demand is met. Then, the proposed analytic algorithm is used for wind turbine placement optimization problem at the presence of PHESS for a 14-bus power system. Based on network load demand situation at each level under pool-based market condition during the annual horizon, the proposed analytic algorithm chooses the whole cases of allocating size and placement capacity of these resources from the candidate places, iteratively, and carries out OPF on the transmission network by the aim of maximizing sum net profit value in circulation of
Table 3. Transmission lines information for power pool and reserve markets.
Table 4. Load demand information offers to power pool markets.
market partners including thermal and PHESS and WTs owners. Among the whole studied cases, the only case where WT placement problem at the presence of PHESS converges to an optimal solution is when two WTs are installed on Bus 7 and one bus is connected to Bus 13. It has to be noted that these two resources are modeled in placement problem by using probability tree scenarios in Table 5. Results of simulation studies for optimal placement of wind turbines during the annual horizon shows that for installation and investment, optimal capacity of WT 1 and WT 2 on Bus 7 and Bus 13 are obtained 80 MW and 66 MW respectively, which give net profit value in circulation equal to 38,056.33$ and 23,532.47$ for the owners. But dispatched active and reactive powers of thermal units according to the price-power proposals of piecewise linear curve and constant cost of PHESS are as follows.
The generated active and reactive powers and the sold spinning reserve to energy market and ancillary services of thermal units connected to Bus 2, Bus 3, Bus5 and Bus 9 during the annual horizon for three low, average and peak load levels are listed in Table 6. It is worth noting, however, after solving the placement problem by the proposed analytic algorithm based on iteration of market clearing price for each of load levels, Load-level 01, Load-level 02 and Load-level 03 are assessed as 5.20$, 5.33$ and
Table 5. Technical data of probabilistic generation capacity scenarios of owner of WT 1 connected to Bus 7 and WT 2 connected to Bus 13.
5.42$, respectively. As it can be seen in Table 7 from the simulation results, the PHESS installed on Bus 7 is used only for pump mode application with 3 units which has consumption equal to 375.45 MW. Under the assumed load demand conditions of pool-based market in different levels and configuration of remaining generation resources such as thermal units and wind turbines, considering the structure of transmission system it was expected that due to cheaper generation of these resources compared to PHESS, as long as capacity of these resources are not completely loaded, generation of hydroelectricity energy resource will not be used, and the numerical results are proofs for this claim. Based on optimal conditions of pool-based market’s supply and demand during the annual time horizon, OPF of system is carried out in three load demand levels and its results for magnitude and phase angle of bus voltages, active and reactive powers flowing through the lines are presented as follows. Numerical results of simulation for voltage magnitude and phase angle of network buses are given as Table 8.
Table 6. Dispatching active and reactive generation/spinning reserve by thermal units.
Table 7. Dispatching active and reactive generation by PSHPPi.
Table 8. Voltage magnitude and Phase angle results after wind turbins placement in 14-bus network.
The obtained numerical results for OPF in 14-bus power system show the fact that voltage static range is also accurately satisfied.
Similar to the previous studies, the positive direction for current flowing through the lines is assumed as from a bus with lower number toward a bus with higher number. Table 9 illustrates the active and reactive power flows in power system lines under a certain supply and demand condition for the day-ahead market during the annual time horizon.
Numerical results of the study show that allocation of optimal size and location of wind turbines in the network can lead to better OPF, in addition to increasing competition, and as a result, both technical and economical improvements in power system operations. According to the simulation results, social welfare level, i.e. total profit of market partners is optimally obtained as 150,900.64$.
4. Conclusion
In order to verify the effectiveness and application of the proposed iteration-based analytic algorithm for optimal placement of wind turbines at the presence of PHESS in addition to thermal units, simulation studies of 14-bus power system under pool-based power market with simultaneous clearing of energy and reserve during the annual time horizon, was performed. Behavior modeling of wind turbines based on generation capacity scenarios has been realized by applying probability tree structure. In addition, to study the loss values and active and reactive power flows through the lines for different
Table 9. Optimal power flow results after wind turbins placement in 14-bus test network.
load levels during a year, optimal power flow is used considering voltage constraints, thermal limit of lines and power plant constraints of generation resources present at the energy and reserve market under demand and supply conditions. The obtained numerical results from simulation studies can be categorized as follows: the main result achieved from the placement study of wind turbines at the presence of PHESS with the aim of maximizing investment profit of these resources and other partners under market conditions is obvious and clear that always when solution is converging to an optimum, a fixed installation place for wind turbine is considered on a bus where PHESS is installed, and overall, with regard to remaining optimal installation places, maximizing net profit value in circulation of all investor owners happens on these resources in the electrical energy sale market. The reason for this is providing high flexibility in system operation planning under pool-based market during the annual horizon; in such a way that PHESS by pumped operation in low load times of the network, will be able to prevent reduction of suboptimal load dispatching on some thermal units, or in some peak load times, working in its generation operation, avoid increase of suboptimal load dispatching on other resources present at pool-based market and in fact, it plays load adjustment role in the mentioned bus and network. For this purpose, analytic formulation of thermal and PHESS units considering the tree structure of power-velocity probabilistic scenarios under pool-based market conditions is included in this paper to accurately evaluate the effect of proposed model parameters on optimal placement of wind turbine and the required amount of spinning reserve. At last, simulation results show the fact that by allocating optimal number, place and capacity of wind turbines under pool- based conditions, in addition to maximizing the profit of investors on these resources and other present partners in the energy market during the annual horizon, simultaneously with modeling OPF with regard to demand side being inelastic, energy market will thrive more and as a result social welfare is increased and energy market will become closer to a perfect competitive market.
Cite this paper
Chabok, B.S., Ashouri, A., Khalilsaraei, M.Y., Moghadam, H.S. and Ghasemi, F. (2016) New Analytical Model for Optimal Placement of Wind Turbines in Power Network under Pool and Reserve Markets Conditions. Energy and Power Engineering, 8, 313-325. http://dx.doi.org/10.4236/epe.2016.810029
References
- 1. Atwa, Y.M. and El-Saadany, E.F. (2011) Probabilistic Approach for Optimal Allocation of Wind-Based Distributed Generation in Distribution Systems. IET Renewable Power Generation, 5, 79-88.
http://dx.doi.org/10.1049/iet-rpg.2009.0011 - 2. Albadi, M.H. and El-Saadany, E.F. (2010) Overview of Wind Power Intermittency Impacts on Power Systems. Electric Power Systems Research, 80, 627-632.
http://dx.doi.org/10.1016/j.epsr.2009.10.035 - 3. Zhang, N., Kang, C., Kirschen, D.S., Xi, W.M., Huang, J.H. and Zhang, Q. (2011) Thermal Generation Operating Cost Variations with Wind Power Integration. IEEE Power and Energy Society General Meeting, San Diego, 24-29 July 2011, 1-8.
http://dx.doi.org/10.1109/pes.2011.6039605 - 4. Caralis, G., Papantonis, D. and Zervos, A. (2012) The Role of Pumped Storage Systems towards the Large Scale Wind Integration in the Greek Power Supply System. Renewable and Sustainable Energy Reviews, 16, 2558-2565.
http://dx.doi.org/10.1016/j.rser.2012.01.068 - 5. Al Zohbi, G., Hendrick, P. and Bouillard, P. (2014) Evaluation du potentiel d’énergie éolienne au Liban. Revue des Energies Renouvelables, 17, 83-96.
- 6. Petrakopoulou, F., Robinson, A. and Loizidou, M. (2016) Simulation and Analysis of a Stand-Alone Solar-Wind and Pumped Storage Hydropower Plant. Energy, 96, 676-683.
http://dx.doi.org/10.1016/j.energy.2015.12.049 - 7. Ela, E., Kirby, B., Botterud, A. and Milostan, C. (2013) The Role of Pumped Storage Hydro Resources in Electricity Markets and System Operation. National Renewable Energy Laboratory, 1-9.
- 8. Ersin Dinçer, A. and Bozkus, Z. (2016) Investigation of Waterhammer Problems in Wind-Hydro Hybrid Power Plants. Arabian Journal for Science and Engineering, 41, 4787-4798.
http://dx.doi.org/10.1007/s13369-016-2142-2 - 9. Petrakopoulou, F. (2016) On the Economics of Stand-Alone Renewable Hybrid Power Plants in Remote Regions. Energy Conversion and Management, 118, 63-74.
http://dx.doi.org/10.1016/j.enconman.2016.03.070 - 10. Riva, R., Cacciola, S. and Luigi Bottasso, C., (2016) Periodic Stability Analysis of Wind Turbines Operating in Turbulent Wind Conditions. Wind Energy Society, 1, 177-203.
http://dx.doi.org/10.5194/wes-1-177-2016




