Energy and Power Engineering
Vol.08 No.01(2016), Article ID:63269,12 pages
10.4236/epe.2016.81001
Research on the Deformation of Turbine Blades at Machining
―Part 1. Properties of Materials and Features of Chips
Masu Yamada1, Keiji Sonoya2, Takahito Sobayashi3, Hiroshi Satoh4
1TBM Corporation, Nagano, Japan
2Department of Mechanical Systems, Yamanashi University, Kofu, Japan
3Nichia Tanko Co. Ltd., Tomioka, Japan
4Oridea Inc., Mishima, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 December 2015; accepted 26 January 2016; published 29 January 2016
ABSTRACT
Along with the recent expansion of demand for electricity, the production of steam turbine blades has increased, and various materials forged of 12Cr ferritic heat-resistant types of steel have become widely used for this purpose. Although this material seems to be an excellent choice as heat-resistant steel, it requires a post-correction process for deformation after machining and thus lowers productivity. Therefore, we started basic experimental research, and through a series of tests, we found that 12Cr steel is a sticky material; the residual stresses after machining concentrate in the vicinity of the surface; and this influences the deformation of blades.
Keywords:
Turbine Blade, Machining, Deformation, 12Cr Steel

1. Introduction
The production of steam turbine blades continues to increase along with the recent expansion of demand for electricity. As electric plants seek larger capacity and increased efficiency, the recent trend is to produce larger turbine blades that demand dimensional control with high accuracy. The materials typically used for turbine blades are chrome alloy steel, nickel alloy steel, and titanium, as well as austenitic stainless steel for special environments and 17-4PH steel with high strength. The contents of the additives vary slightly among turbine manufacturers. One material among them, the forged material 12Cr steel, which is a ferritic heat-resistant steel, began to be used as a turbine blades material [1] . Although considerable time has passed since the development of the fundamental technological background, there are a lot of complaints when this material is seen from the standpoints of forging suppliers and machining workers, who report that “care must be taken in the heat-treatment of removing stress after forging”, and “there is unexplained transforming behavior at machining”. Moreover, although there is some research on creep strength, etc., for this material as heat-resistant steel [2] [3] , there is little research on its characteristics upon machining. In terms of the amount of deformation at machining of the turbine blades, foregoing research does not exist at all.
Considering this current situation, we started research on the engineering issue: how can this machining deformation be brought as close as possible to zero? In a series of experimental research projects, first, we examined the cutting resistance and investigated how it is influenced by the number of teeth and the depth of the cut made by the tool [4] [5] . Next, we tried to acquire basic data that tend to be lacking, such as the tensile and compression test, and investigated the work-affected layers [6] . Consequentially, their thicknesses were obtained by the hardness method, and it was calculated that the values were larger than the ones seen in the reference. Moreover, we have not come to an understanding of the situation of the metallographic structure and residual stress.
As a result, we found that 12Cr steel is a sticky material; the residual stresses after machining concentrate in the neighborhood of the surface; and this influences the deformation of blades.
2. Experiments and Measurements
2.1. Material Properties and Blades Deformation State
Although it depends on the product shape after machining, these forged materials are delivered from turbine manufacturers via forging suppliers to us, as the fabricator, in the state of cutting stock of about 4 mm thickness remaining on both sides to be finished with two rounds of machining.
The machining is done using simultaneous NC milling for such materials, and the deformation correction of a deformed blade, which is discussed in this paper, is done using a press machine as shown in Figure 1(a) and Figure 1(b), respectively. Here, in Figure 1(a), when the amount of the deformation during machining increases, it is likely to end only in a rising vibration value or in an abnormal warning in the index table, or both at the same time. In this case, a worker is forced to do corrective work using a press, shown in Figure 1(b). There is a loss of productivity because this work must rely on the worker’s intuition and experience.
When restraint of the work materials on the milling bed during machining is relieved, and after supporting the root part of the blades that are the working reference of the machined blades and other parts are freed, the run-outs of the blade center have no fixed form, as well as magnitudes and directions. One sample in which all blades are distorted in the direction of the back is shown in Figure 2. This figure was obtained through data on blades for a 700 MW electric generating plant, 400 mm in length for 45 blades after finishing, and it is known that large deformations close to 1.5 mm developed for the tolerance of 0.2 mm. In the age of NC versatile

Figure 1. Cutting by simultaneous NC milling (a) and the stage of correcting deformation with a press (b).
machines, although the introduction of improved cutting methods have been anticipated some time, the fact is that, without this solution, most concerns have been concentrated on the corrective method.
As a sample of the chemical composition of 12Cr steel that contains 10% - 12% Cr, shown in Table 1, besides Cr, a small amount of Mo, W or V, and Nb, based on Fe, are added. These chemical compositions differ among turbine makers, and the hardness is also different, from an upper value of HV 380 to a lower value of HV 210. This creates the difficulty of maintaining accuracy in machining.
2.2. Cutting Test Using a Strip-Shaped Test Piece
First, we decided to investigate the amount of deformation in machining using a small, rectangular, strip-shaped test piece (TP) in this experiment. Then, after trying out various dimensions of rectangular plates, plates of 200 mm in length, 50 mm in width, and 10 mm thick were made of the same material as in Figure 1, and their direction was matched, rolling to the long sides. We selected this size using the following considerations: ease of treatment, and the dimensions are near the dimensional ratio of actual blade parts. In the cutting experiment, we tried to align the long side (X-axis, 200 mm) of the TP with the feed direction of milling, and eliminate the effect of the short side (Y-axis, 50 mm) as much as possible. Therefore, after cutting to a prescribed length from a long piece of material with a section 120 mm square, we divided this into four segments longitudinally, and
Figure 2. Example of blade transformation in milling.
Table 1. Chemical composition of tested 12% Cr steel.
divided one of them into four, and eventually obtained 16 strip-shaped TPs that can be secured as 10 mm thick, by using a hacksaw. These TPs were finished on both sides by machining and grinding on the test surface, and the surface roughness was finished to Ra = 1.2 µm.
In the experiment, after some trials, we executed the annealing to all TPs at 675˚C for one hour, the same conditions as with forged materials, and supplied it to the cutting tests. All tests were performed under the same conditions using a numerically controlled machining-center with a cutter diameter of 63 mm, with the cutting conditions of the cutting speed at 120 m/min., and feed rate 0.1 mm/edge. We assumed the depth of the cut and the number of cutting edges to be parameters to be machined, and the cutting fluid was dispersed during the machining process in the same way. The cutting resistance during machining was measured over the three directional elements of the X, Y, and Z axes at the same time with a fixed dynamometer from HK & Co., type 9257B.
When we measured the dimensions before and after machining of the TPs, we used a three-dimensional measuring instrument. In this case, as the measuring points, the inside span of 160 mm from both ends by 20 mm along the X-axis were the measurement section. Nine points were assumed by equally dividing at the pitch of 20 mm, and five points were taken at the pitch of 10 mm along the Y-axis, leaving 5 mm at both ends. Thus 45 points were measured in total. Furthermore, one of the 20 mm edges, regarded as the root part of the actual blades, was made the reference plane for the measurement.
2.3. Measurement of Deformation Stress
We felt there was insufficient data regarding tensile stresses and compression stresses for basic material data concerning 12Cr steel, and no information was found on the residual stresses in the work-affected layer, which is thought to contribute greatly to machining deformation. We thus decided to include these matters in our investigation.
First, tensile stress was tested using a JIS14 test piece made of the same material as the strip-shaped test piece using the Shimadzu AG-300kNXplus as the testing equipment. Next, for the compression test, we assumed 80 kN, which was 80% of the maximum capacity, as the target, because the limitation of the test equipment (Shimadzu AG-IS 100kN) is 100 kN. We decided the dimensions (diameter: d, height: h) of the test piece to be h = 1.5 d, referring to the document [7] . After the above preparation, we obtained a test piece 3 mm in diameter and 4.5 mm in height. In the test to see the diameter change in the columnar test piece, before adding the load, both edges’ surface roughness was finished to Ra = 0.4 - 1.6 µm, and a lubricant was spread between the TP and the vertical compression jig to avoid lateral side bulging of the TP. To transform it as if it were columnar, PTFE sheets of 0.1 mm thickness were inserted. In addition, we implemented a residual stress measurement on the surface of the strip-shaped TP after cutting had been done, using Rapid X-Ray Stress Analyzer PSPC-MSF by Rigaku Corp.
2.4. Investigation of Work-Affected Layer
We investigated the work-affected layer, which is one of the essential items in this paper, through both sides of thickness and metallographic structure by using the hardness method to measurement of the former, and electron beam backscatter diffraction (EBSD) for observation of the latter.
In the hardness method, in the example shown in Figure 3, the hardness of each 10 µm was measured from the machined surface of the TP sequentially with the Vickers hardness meter, and the thickness of the work- affected layer after machining was examined by changing the depth of the cut from 0.25 to 1.0 mm in four stages. The point at which the fluctuation of hardness, which seemed to be a feature of 12Cr steel, disappeared and turned uniform was made at the boundary of the work-affected layer and the substratum of the material.
After having ground the fragment edge, which had been made by a wire cut about 10 mm square and 2 mm thick, we observed its crystalline texture whiles canning using electron microscopy (Carl Zeiss, ULTRA Plus) and got the EBSD pattern.
3. Test Outcomes and Reviews
3.1. Cutting Resistance and Deformation State
In the investigation of cutting using strip-shaped TPs by changing the depth of the cut from 0.25 mm to 1.0 mm in four stages, we observed the cutting resistance, and obtained the data in Figure 4. The fact that the values of
Figure 3. Change in Vicker’s hardness between the work affected layer and the substratum.
Figure 4. Relations between depth of the cut and component forces in each direction.
the Y-axis are small, about half compared to those of the X- and Z-axis, seems to be explained by the fact that the diameter of the cutter, 63 mm, is larger than the width of the TP, 50 mm, and there is little cutting participation in the direction of width.
The amount of deformation of the strip-shaped TP for the cutting conditions (cutting speed 120 m/min., feed rate 0.1 mm/edge) is shown in Figure 5. When material that was annealed after machining was assumed to be ⓐ and the deformed shape after milling to be ⓑ, the net deformation was obtained by deriving ⓑ from ⓐ. Though this is a sample, almost all TPs showed the same tendency, and it has understood the deformation of machined side curve into concave in the direction of long side (in this experiment, five TPs of 200 mm length showed 40.6 µm of maximum deflection near to the center) and convex in the direction of short side (similarly, 10.6 µm for 50 mm width) as if a saddle. It is suggested, from above facts, to present a complex deformation, because the real turbine blades are the overall finished goods and also having three-dimensional torsion.
3.2. Measurement of Deforming Stress
1) Tensile stress: A stress-strain diagram obtained in the test is shown in Figure 6. It is known from this
Figure 5. Deformation measurement with 3-D measuring instruments for one of the test pieces.
Figure 6. Diagram of tensile stress-strain.
diagram that 12Cr steel does not show a plain yield point as a soft iron-like material, and looks like nonferrous metals, presenting a large load capacity. In maximum tensile stress, the differences in the values among three TPs are small, at 1006 MPa. From the inclination from the point that designates 0.2% of plastic strain to the maximum load point, it is proved that there is a relation between the true stress, 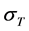 , and the strain,
, and the strain,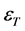 :
:
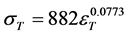 (1)
(1)
2) Compression stress: The result of the compression stress test is shown in Figure 7. It may be said that on examination, the columnar TP did not bulge, and the influence of friction is hardly seen between the TP and the compression jig. As the maximum compression stress obtained, 1290 MPa, we arrived at an empirical relation between the stress, 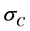 , and the strain,
, and the strain,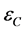 :
:
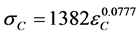 (2)
(2)
3) Residual stress: Measurements were obtained of the residual stress of the strip-shaped TP machined while changing the depth of the cut under the conditions (cutting speed 120 m/min., feed rate 0.1 mm/edge) in the work- affected layer. The depth for measurement, calculated from the profile measurement using the surface-roughness measuring instrument after shaving by adjusting the electrolytic grinding time, is based on values roughly converted numerically.
The results for residual stress obtained by changing the depth of the cut from 0.5 to 1.0 mm are shown in Figure 8. In both figures, it was understood that considerably large stresses remain concentrated within a shallow range in the vicinity of the machined surface.
Figure 7. Diagram of compressive stress-strain.
Figure 8. Residual stress measured from the surface in direction of depth.
3.3. Thickness of the Affected Layer and Metallography
The thickness of the work-affected layer obtained by the hardness method, along with the predicted values [8] , is shown in Figure 9. When the depth of the cut approaches 1.0 mm, the thickness of 12Cr steel has been known to exceed 400 µm, and the predicted value approaches 300 µm. The calculation method is described below.
Thinking about internal stress when the force of the cutting edge acts concentrically on the surface of a semi- infinite solid, and when there is an indexed relation of 




where 




Figure 9. Thickness of the affected layer measured by hardness change and empirical relation.

As for






When we calculate predictive values using Equation (6), the normal force that acts on the surface to be machined is already obtained from the load in the vertical (Z-axis) direction in Figure 4, and the yield stress 
4. Investigation of Chips
4.1. Features of Chips
The chips obtained from a 12Cr stainless steel rod under cutting conditions (cutting speed 120 m/min., feed rate 0.1 mm, edge rake angle 16˚) was observed with a microscope to present a chip called flow type. The chips observed by changing the depth of the cut in four stages, from 0.25 to 1.0 mm, are shown in Figure 11. Consequentially, these chips are known to have flaked off after plastic deformations of the parent material, and remarkable shearing deformation is recognized regardless of the dimension of the depth of cut. From this fact, the hardness is expected to rise (the hardness of the chips is described in Section 4.3).
Figure 10. Metallographic structure obtained by the electron backscatter diffraction method.
4.2. Conditions Obtained by Sudden Cut-Stop Method
A conspicuous symptom at the front of the edge is obtained by a sudden cut-stop method for the column of 12Cr steel under the same cutting conditions as in the previous section. An example of observations using a microscope, shown in Figure 12, was taken from a wire-cut fragment. The boundary of the shearing deformation of chips and the plastic strain area of the substratum become like a circular arc; it is known that this material has strong stickiness. The pitch of the measuring point was too large, and thus it was not possible to look for the expected work-affected (hardened) layer.
4.3. Hardness of the Chips
Concerning the part of the chip shown in Figure 12, although this is not separate from the parent metal, the color aspect is different from the parent metal, and a change in the metallographic structure is expected. The hardness, HV, of the chip part is high: impressions of the indenter of a Vickers hardness meter of 100 µm are seen on the photo. Hardness rises roughly to HV = 415 - 440 by 40 to 50 percent, compared to that of the parent metal, which is HV = 290 - 300. On the other hand, the hardness of the chips cut off by milling never rises this high. Their median of hardness, HV = 330, is shown in Figure 13, and is not more than 10 percent higher at most. This fact is thought to be due to the following. The stress generated by continuous lathe turning is larger than the stress of intermittent cutting of a multi-edge tool regarding the degree of work hardening.
Figure 11. Microphotograph of chips obtained by changing the depth of cut.
Figure 12. Aspect of the work piece near the blade edge made by the sudden cut-stop method.
Figure 13. Hardness of chips made by milling with a 1 mm depth of cut.
5. Conclusions
We examined the machining characteristics of 12Cr steel from various viewpoints, and obtained the following findings:
1) In one-side machining by milling in which feed direction coincides with the long side, the machined surface deforms into concave shape on the long side and convex shape on the short side, and comes to resemble a saddle.
2) From tensile and compression tests using a rod-type test piece, the allowable tensile stress and the allowable compressive stress are 1000 MPa and 1200 MPa, and the relations





3) The thickness of the work-affected layer obtained after milling on the strip-shaped TP increases with the depth of the cut, and the predicted value estimated from the literature approaches 300 µm; that obtained from experiment using the hardness method exceeds 400 µm.
4) Comparatively large stress remains in the surface neighborhood (100 µm or less of the affected layer), and it is understood that these values increase as the depth of the cut decreases.
5) It is understood that the work-affected layer is made of a refined crystal of 1.5 µm-level thickness right under the machined surface, and some plastic flow follows this.
Acknowledgements
The authors would like to thank all those who contributed to our paper. They are S. Yonekubo, K. Kamijo, and Y. Nagasu of the Industrial Technology Center of Nagano Prefecture, for acquiring the test data; Y. Watanabe and I. Masuda, graduates of Yamanashi University, for executing the tests; and K. Hosoi of TBM Corp., for arranging the figures. Their assistance is much appreciated.
Cite this paper
MasuYamada,KeijiSonoya,TakahitoSobayashi,HiroshiSatoh, (2016) Research on the Deformation of Turbine Blades at Machining. Energy and Power Engineering,08,1-12. doi: 10.4236/epe.2016.81001
References
- 1. Ohta, S. (1998) Ferritic Heat-Resisting Steels. Chijin, Shokan. (In Japanese)
- 2. Yamada, M., Watanabe, O., Yoshioka, Y. and Miyazaki, M. (1990) Development of Advanced 12Cr Steel Rotor Forgings. ISIJ, 76, 1084-1091. (In Japanese)
- 3. Uchida, H., Shinya, T. and Tsuchiya, T. (1996) Relationship between Creep Deformation Behavior and Structural Change in High Strength 12Cr Steel. ISIJ, 82, 249-254. (In Japanese)
- 4. Yamada, M., Watanabe, Y., Fujinuma, R., Sonoya, K. and Satoh, H. (2014) Study on Optimal Machining of Turbine Blades. 2014 IEEE 8th International Power Engineering and Optimization Conference (PEOCO), 24-25 March 2014, Langkawi Island, 641-646.
http://dx.doi.org/10.1109/peoco.2014.6814506 - 5. Yamada, M., Watanabe, Y. and Sonoya, K. (2014) Experimental Research on the Deformation at Turbine Blades Cutting. The Japan Society of Mechanical Engineers, 31-32. (In Japanese)
- 6. Yamada, M., Sonoya, K. and Sobayashi, T. (2015) Research on the Deformation at Turbine Blades Cutting. Japan Society of Mechanical Engineers, Kanto Branch, No. 10504, 2 p. (In Japanese)
- 7. JSTP (2006) Handbook of Plastic Working. JSTP, Corona, 237. (In Japanese)
- 8. Okushima, K. and Itano, Y. (1968) Study on the Generating Process of Machined Surface. Transactions of the Japan Society of Mechanical Engineers, 34, 971-978. (In Japanese)
http://dx.doi.org/10.1299/kikai1938.34.971















