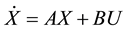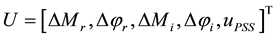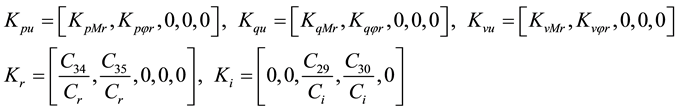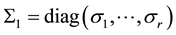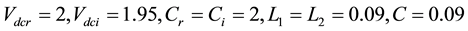Energy and Power Engineering
Vol.06 No.12(2014), Article ID:50884,17 pages
10.4236/epe.2014.612035
Damping Controller Based Quantum Particle Swarm Optimization for VSC HVDC to Improve Power System Stability
Naser Taheri1, Ahmad Hashemi2, Kowsar Kiani3
1Islamic Azad University, Quchan Branch, Quchan, Iran
2SAMA Technical and Vocational Training College, Islamic Azad University, Kermanshah Branch, Kermanshah, Iran
3Department of Electrical Engineering, Semnan University, Semnan, Iran
Email: n.taheri.1362@gmail.com, ahmad.hashemi.v@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 August 2014; revised 18 September 2014; accepted 26 September 2014
ABSTRACT
The use of the supplementary controllers of a High Voltage Direct Current (HVDC) based on Voltage Source Converter (VSC) to damp low Frequency oscillations in a weakly connected system is surveyed. Also, singular value decomposition (SVD)-based approach is used to analyze and assess the controllability of the poorly damped electromechanical modes by VSC-HVDC different control channels. The problem of supplementary damping controller based VSC-HVDC system is formulated as an optimization problem according to the time domain-based objective function which is solved using quantum-behaved particle swarm optimization (QPSO). Individual designs of the HVDC controllers using QPSO method are evaluated. The effectiveness of the proposed controllers on damping low frequency oscillations is checked through eigenvalue analysis and non-linear time simulation under various disturbance conditions over a wide range of loading.
Keywords:
VSC-HVDC, Power System Stability, Quantum Particle Swarm Optimization, Supplemetary Damping Controller

1. Introduction
Large interconnected AC systems have many well-known advantages. However, larger interconnected AC systems also increase the system complexity from the operation point of view, and might adversely decrease the system reliability [1] -[3] . Steady state stability, lack of reactive power supply, voltage stability, electromechanical oscillations and transient stability are common problems that can happen in expanded power systems and transmit a large amount of power over long distance transmission lines [3] [4] . Increasing power system complexity gives rise to low frequency oscillations in the range of 0.2 - 3.0 Hz. If not well damped, these oscillations may keep growing in magnitude until loss of synchronism results [5] . In order to damp these power system oscillations and increase system oscillations stability, the installation of power system stabilizer (PSS) is both economical and effective [5] [6] . However, PSSs may adversely affect voltage profile, result in leading power factor, and may not be able to suppress oscillations resulting from severe disturbances, especially those three-phase faults which may occur at the generator terminals [6] . Flexible AC transmission systems devices, such as Static VAR Compensators (SVC), Thyristor Control Series Compensators (TCSC), Static Synchronous Compensators (ST-ATCOM), and Unified Power Flow Controller (UPFC), are one of the recent propositions to alleviate such situations by controlling the power flow along the transmission lines and improving power oscillations damping [6] [7] . Recently High Voltage Direct Current (HVDC) systems have greatly increased. They interconnect large power systems offering numerous technical and economic advantages. This interest results from practical characteristics and performance that include for example, nonsynchronous interconnection, control of power flow and modulation to increase stability limits [8] . It is well known that HVDC may improve the transient and dynamic performance of the interconnected AC/DC system due to its fast electronic control of power flow also transient stability of the AC systems in a composite AC-DC system can be improved by taking advantage of the fast controllability of HVDC converters [6] - [10] . The conventional HVDC has several limitations and undesirable characteristics including being physically large and requiring the AC network with sufficient short-circuit ratio [11] - [13] . The Voltage Source Converter based on HVDC (VSC HVDC), which uses modern semiconductors with self-commuted ability, overcomes the disadvantages of conventional HVDC and is therefore more suitable for a weak AC network or a passive network without any power sources [13] . The control of the voltage magnitude and the phase angle of the VSCs make the use of separate control for active and reactive power possible. The active power loop can be set to control either the active power or the dc-side voltage [14] [15] . A traditional lead-lag damping controller structure is preferred by the power system utilities because of the ease of on-line tuning and also lack of assurance of the stability by some adaptive or variable structure methods [7] [16] [17] . Having several local optimum parameters for a lead-lag controller, using of traditional optimization approach is not suitable for such a problem. Thus, the heuristic methods as solution for finding global optimization are developed [18] - [20] . Particle swarm optimization (PSO) is a novel population based on metaheuristic, which utilizes the swarm intelligence generated by the cooperation and competition between the particle in a swarm and has emerged as a useful tool for engineering optimization [21] . This new approach features many advantages; it is simple, flexible, and fast and can be coded in few lines. Also, its storage requirement is minimal. However, the main disadvantage is that the PSO algorithm is not guaranteed to be globally convergent. In order to overcome this drawback and improve optimization synthesis, in this paper, a quantum-behaved PSO technique is proposed for optimal tuning of HVDC based damping controller for enhancing of power systems low frequency oscillations damping. In this paper a novel approach is presented to model parallel AC/DC power system namely Phillips-Heffron model based d-q algorithm in order to study dynamical stability of system. In addition, a block diagram representation is formed to analyze the system stability characteristics. Also, singular value decomposition (SVD) is used to choose damping control signal which has most effect on damping the electromechanical (EM) mode oscillations. A very powerful tool commonly used for this purpose is Popov-Belevitch-Hautus (PBH), which can be used to evaluate the EM mode controllability of the PSS and the different VSC HVDC controllers. A single machine infinite bus (SMIB) system equipped with a PSS and a VSC HVDC controller is used in this study. The problem of damping controllers design is formulated as an optimization problem to be solved using QPSO. The aim of the optimization is to search for the optimum controller parameter settings that maximize the minimum damping ratio of the system.
2. Problem Statement
Figure 1 shows a SMIB system equipped with a VSC HVDC. As it can be seen the infinite bus is supplied by HVAC parallel connected with a VSC HVDC power transmission system. The VSC HVDC consists of two coupling transformer, two three-phase IGBT based voltage source converters (VSCs). These two converters are connected either back-to-back or joined by a DC cable, depending on the application.
The AC side of each converter is connected to the line through a coupling transformer. The first voltage
Figure 1. A SMIB system Equationuipped with a VSC HVDC.
source converter behaves as a rectifier. It regulates the DC link voltage and maintains the magnitude of the voltage at the connected terminal. The second voltage source converter acts as a controlled voltage source, which controls power flow in VSC HVDC feeder. The four input control signals to the VSC HVDC are
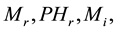
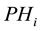 where
where
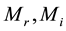 are the amplitude modulation ratio and
are the amplitude modulation ratio and
 are phase angle of the control signals of each VSC respectively.
are phase angle of the control signals of each VSC respectively.
2.1. Power System Nonlinear Model
By applying Park’s transformation and neglecting the resistance and transients of the coupling transformers, the VSC HVDC can be modeled:
 (1)
(1)
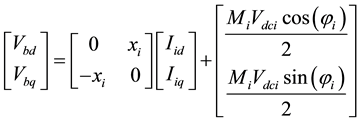 (2)
(2)
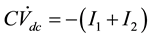 (3)
(3)
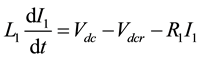 (4)
(4)
 (5)
(5)
where
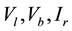 and
and
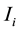 are the middle bus voltage, infinite bus voltage, flowed current to rectifier and inverter respectively.
are the middle bus voltage, infinite bus voltage, flowed current to rectifier and inverter respectively.
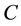 And
And
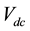 are the DC link capacitance and voltage, respectively.
are the DC link capacitance and voltage, respectively.
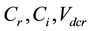 and
and
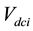 are the DC capacitances and voltages of rectifier and inverter respectively.
are the DC capacitances and voltages of rectifier and inverter respectively.
The non-linear model of the SMIB system of Figure 1 is:
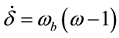



where:



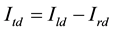


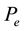

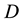
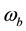


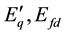



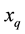

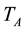
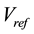
Also, from Figure 1 we have:


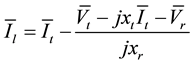
where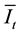
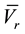
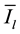
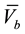

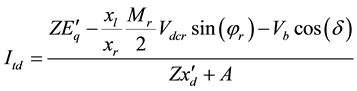
And for inverter side:


2.2. Power System Linearized Model
By linearizing Equations (1)-(7) (13)-(16):




where:
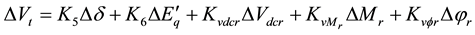
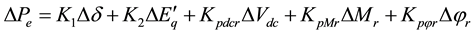
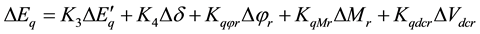

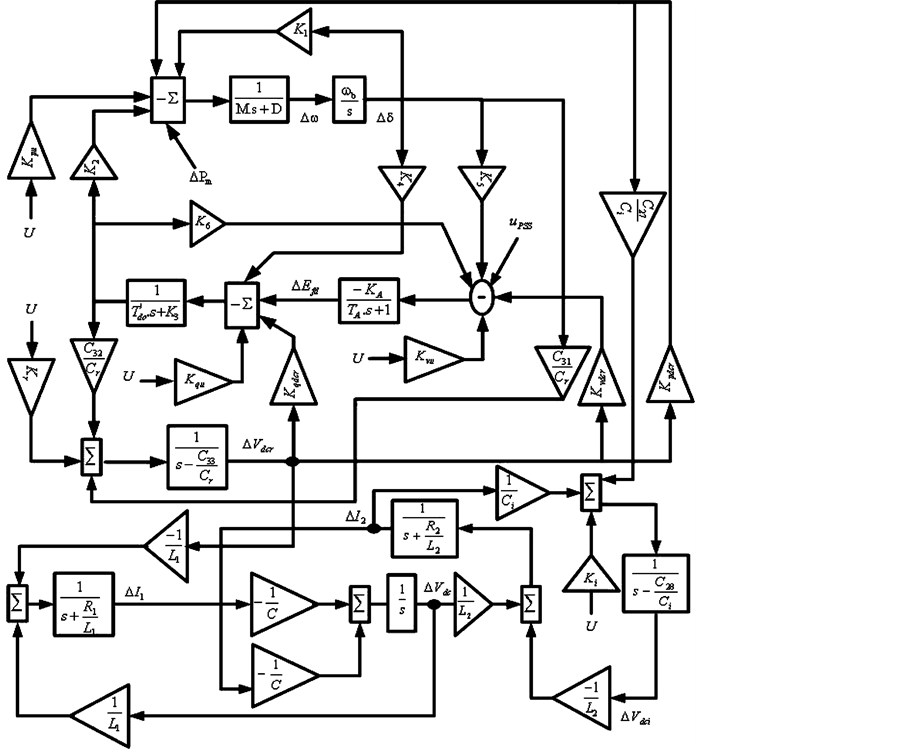
Substitute Equations (21)-(23) in (17)-(20) we can obtain the state variable of the power system installed with the VSC HVDC to be (state space model):
and

where



Figure 2. VSC HVDC block diagram based Equation (25).
It can be seen that the configuration of the Phillips-Heffron model is exactly the same as that installed with SVC, TCSC, TCPS, UPFC and STATCOM. Also from Equation (25) it can be seen that there five choice of input control signals of the VSC HVDC to superimpose on the damping function of the VSC HVDC
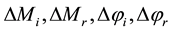

3. PSO versus QPSO
In a PSO system [21] -[23] , multiple candidate solutions coexist and cooperate simultaneously. Each solution candidate, called a “particle”, flies in the problem space (similar to the search process for food of a bird swarm) looking for the optimal position. A particle with time adjusts its position to its own experience, while adjusting to the experience of neighboring particles. If a particle discovers a promising new solution, all the other particles will move closer to it, exploring the region more thoroughly in the process.
PSO starts [22] with a population of random solutions “particles” in a D-dimension space. The ith particle is represented by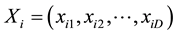
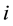
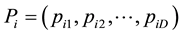
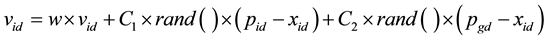

where,


PSO algorithm is as follow:
Step 1: Initialize an array of particles with random positions and their associated velocities to satisfy the inequality constraints.
Step 2: Check for the satisfaction of the equality constraints and modify the solution if required.
Step 3: Evaluate the fitness function of each particle.
Step 4: Compare the current value of the fitness function with the particles’ previous best value (pbest). If the current fitness value is less, then assign the current fitness value to pbest and assign the current coordinates (positions) to pbest.
Step 5: Determine the current global minimum fitness value among the current positions.
Step 6: Compare the current global minimum with the previous global minimum (gbest). If the current global minimum is better than gbest, then assign the current global minimum to gbest and assign the current coordinates (positions) to gbest.
Step 7: Change the velocities according to Equation (26).
Step 8: Move each particle to the new position according to Equation (27) and return to Step 2.
Step 9: Repeat Step 2 - 8 until a stopping criterion is satisfied or the maximum number of iterations is reached.
The main disadvantage is that the PSO algorithm is not guaranteed to be global convergent [24] . The dynamic behavior of the particle is widely divergent forming that of that the particle in the PSO systems in that the exact values of

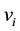
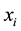


where




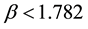

The procedure for implementing the QPSO is given by the following steps [23] [24] :
Step 1: Initialization of swarm positions: Initialize a population (array) of particles with random positions in the n-dimensional problem space using a uniform probability distribution function.
Step 2: Evaluation of particle’s fitness: Evaluate the fitness value of each particle.
Step 3: Comparison to pbest (personal best): Compare each particle’s fitness with the particle’s pbest. If the current value is better than pbest, then set the pbest value equal to the current value and the pbest location equal to the current location in n-dimensional space.
Step 4: Comparison to gbest (global best): Compare the fitness with the population’s overall previous best. If the current value is better than gbest, then reset gbest to the current particle’s array index and value.
Step 5: Updating of global point: Calculate the Mbest using Equation (29).
Step 6: Updating of particles’ position: Change the position of the particles according to Equation (28), where c1 and c2 are two random numbers generated using a uniform probability distribution in the range [0, 1].
Step 7: Repeating the evolutionary cycle: Loop to Step 2 until a stop criterion is met, usually a sufficiently good
3.1. PSS and VSC-HVDC Damping Controller
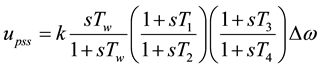
The VSC-HVDC damping controllers are of the structure shown in Figure 3 which

VSC-HVDC Controller Design Using QPSO
To obtain optimal parameters, this paper employs QPSO [24] to enhance optimization synthesis and find the global optimum value of fitness function. The objective function (which must be minimized) is defined as follows [25] :

where
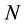

Typical ranges of the optimized parameters are [0.01 - 100] for

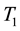
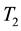


3.2. Controllability Measurement Based on SVD
Controllability shows how the state variables describing the behavior of a system can be influenced by its inputs.
Figure 3. VSC HVDC with lead-lag controller.
More accurately, the dynamical system
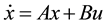



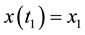
In damping of power oscillations, it is necessary to determine controllability for specific eigenvalues (electromechanical mode). A very powerful tool commonly used for this purpose is Popov-Belevitch-Hautus (PBH) test which is described as below. It includes in evaluating the rank of matrices:

which
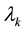
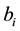



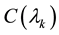
If

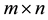
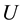
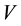
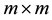
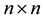

where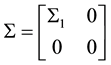
With

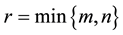


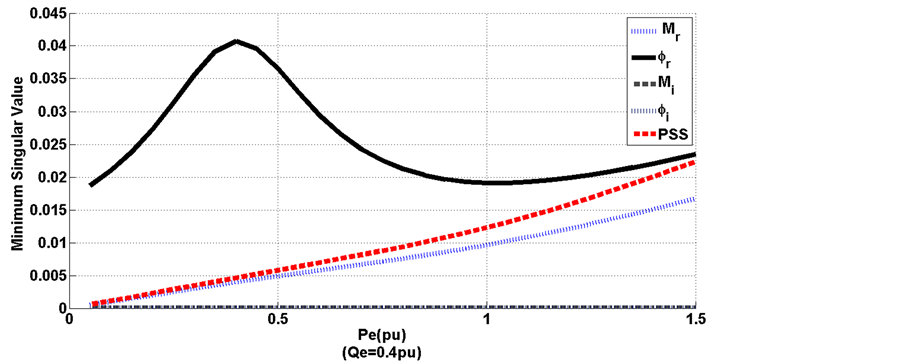
The minimum singular value


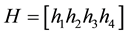
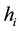
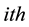
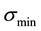


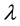
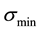

4. Simulation Results
Power system information is given in Appendix A. Constant coefficients in modeling are calculated according information which given in appendix B. In this paper, we consider
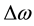

4.1. Controllability Measure by Using PBH Test
SVD based on PBH is employed to measure the controllability of the electromechanical mode (EM) mode from each of the five inputs: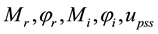

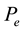



・ EM mode controllability via

・ The capabilities of


・ All control signals have low EM mode controllability in low load condition except
According to what said above, to design supplementary controller based VSC-HVDC, applying damping signal to

4.2. Using QPSO to Obtain Parameters of Supplementary Controllers
The QPSO algorithm is used to obtain the optimal parameter settings of each of the supplementary controllers so
Figure 4. Minimum singular value for different value for Qe.
that the objective function is optimized. The final parameters are given in Table 1.
These supplementary controllers are used by VSC-HVDC system in different loading condition (Table 2). According results which are obtained from SVD analysis, it is obvious that best input for applying damping signal is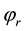

Table 1. Parameters of supplementary controller designed by QPSO.
Table 2. Synchronous machine condition.
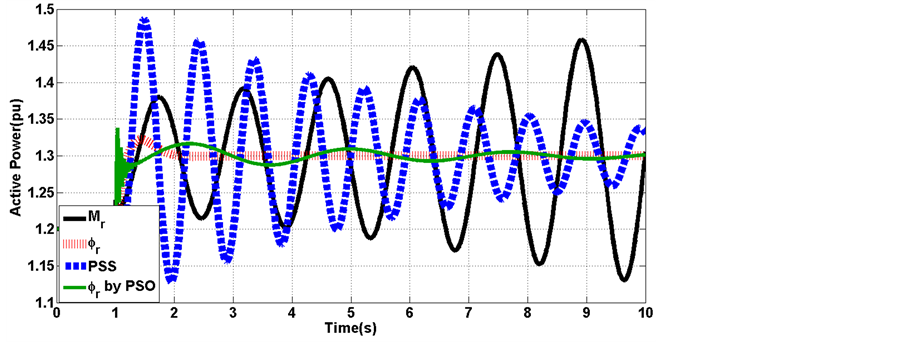
Figure 5. Active power
Figure 6. Active power
Parameters of PSO based damping controller are as:







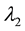




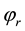
5. Conclusion
In this paper, SVD has been employed to evaluate the electromechanical mode controllability to PSS and the four VSC HVDC control signals. It has been shown that the electromechanical mode is most powerfully controlled via a wide range of loading conditions. Also, the quantum-behaved particle swarm optimization algorithm has been successfully applied to the robust design of VSC HVDC based damping controllers. The effectiveness of the proposed VSC HVDC controllers for improving transient stability performance of a power system are demonstrated by a weakly connected power system subjected to different severe disturbances. The
Figure 7. Active power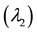
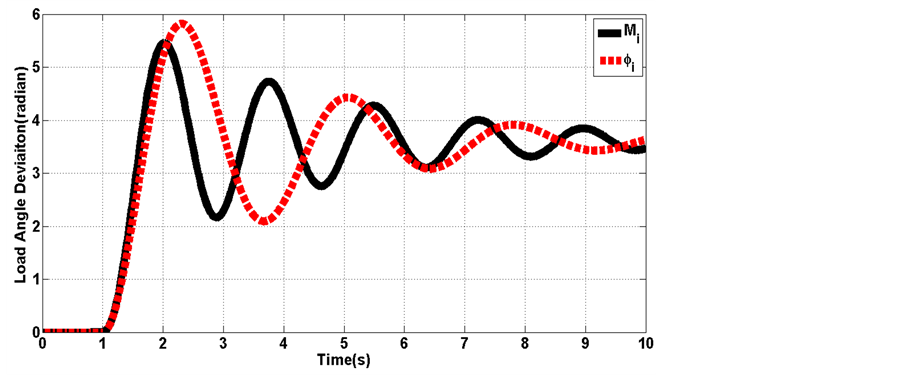
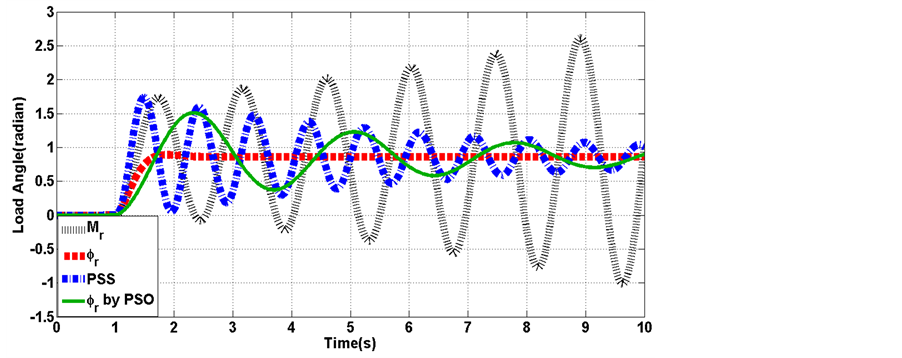
Figure 8. Load angle deviation
Figure 9. Load angle deviation
Figure 10. Load angle deviation
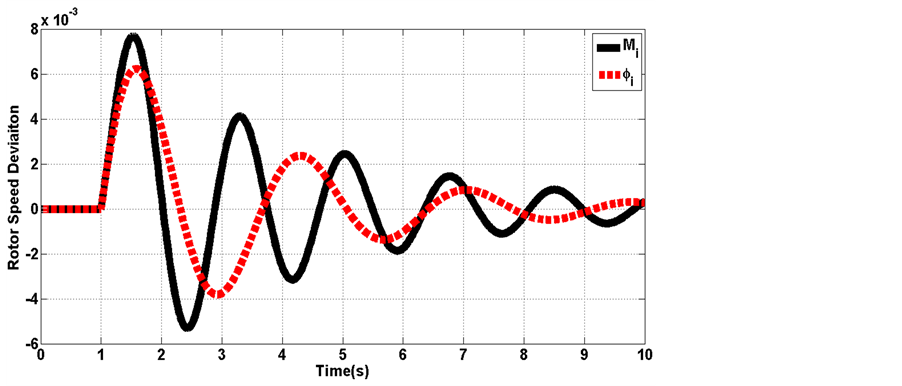
Figure 11. Rotor speed deviation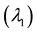
Figure 12. Rotor speed deviation
Figure 13. Rotor speed deviation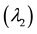
Figure 14. Active power
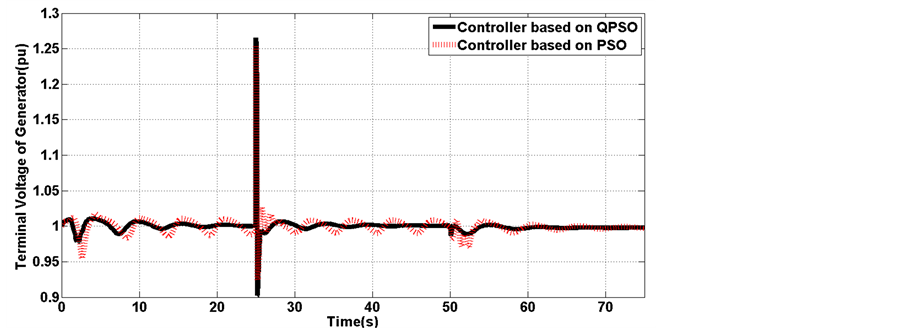
Figure 15. Terminal voltage of generator
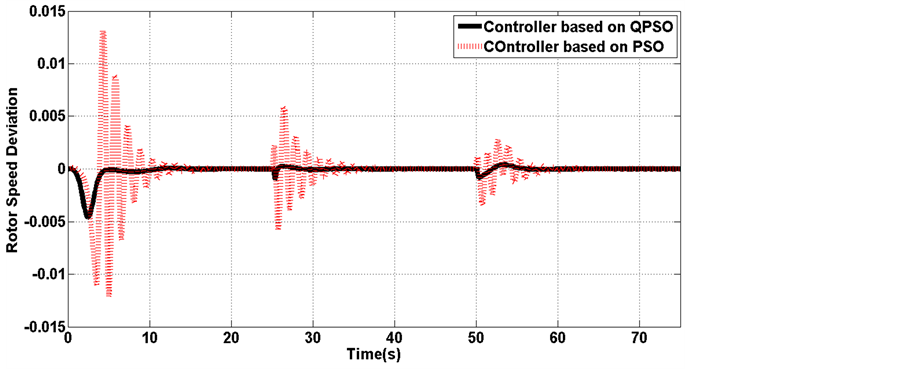
Figure 16. Rotor speed deviation
Figure 17. Active power
Figure 18. Terminal voltage of generator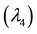
Figure 19. Rotor speed deviation
non-linear time-domain simulation results show the effectiveness of the proposed controller and their ability to provide good damping of low frequency oscillations.
References
- Hsu, Y.-Y. and Wang, L. (1988) Damping of a Parallel Ac-Dc Power System Using Pid Power System Stabilizers and Rectifier Current Regulators. IEEE Transactions on Energy Conversion, 3, 540-547. http://dx.doi.org/10.1109/60.8065
- Flourentzou, N., Agelidis, V.G. and Demetriades, G.D. (2009) VSC-Based HVDC Power Transmission Systems: An Overview. IEEE Transactions on Power Electron, 24, 592-602. http://dx.doi.org/10.1109/TPEL.2008.2008441
- Zhang, L., Harnefors, L. and Peter, H. (2011) Interconnection of Two Very Weak AC Systems by VSC-HVDC Links Using Power-Synchronization Control. IEEE Transactions on Power Systems, 26, 344-355.
- Licéaga-Castro, E., Licéaga-Castro, J. and Ugalde-Loo, C.E. (2005) Beyond the Existence of Diagonal Controllers: From the Relative Gain Array to the Multivariable Structure Function. Proceedings of the 44th IEEE Conference on Decision and Control and 2005 European Control Conference, 7150-7156.
- Shayeghi, H., Shayanfar, H.A., Jalilzadeh, S. and Safari, A. (2009) A PSO Based Unified Power Flow Controller for Damping of Power System Oscillations. Energy Conversion and Management, 50, 2583-2592. http://dx.doi.org/10.1016/j.enconman.2009.06.009
- Banaei, M. and Taheri, N. (2001) An Adaptive Neural Damping Controller for HVDC Transmission Systems. European Transactions on Electrical Power, 21, 910-923. http://dx.doi.org/10.1002/etep.485
- Shayeghi, H., Safari, A. and Shayanfar, H.A. (2010) PSS and TCSC Damping Controller Coordinated Design Using PSO in Multi-Machine Power System. Energy Conversion and Management, 51, 2930-2937. http://dx.doi.org/10.1016/j.enconman.2010.06.034
- Latorre, H.F. and Ghandhari, M. (2011) Improvement of Power System Stability by Using a VSC-HVDC. Electrical Power and Energy Systems, 33, 332-339. http://dx.doi.org/10.1016/j.ijepes.2010.08.030
- Bahrman, M.P. and Johnson, B.K. (2007) The ABCs of HVDC Transmission Technologies. IEEE Power & Energy, 5, 34-35, 44.
- Kundur, P. (1994) Power System Stability and Control. McGraw-Hill, New York.
- Guo, C.Y. and Zhao, C.Y. (2010) Supply of an Entirely Passive AC Network through a Double-Infeed HVDC System. IEEE Transactions on Power Electronics, 25, 2835-2841. http://dx.doi.org/10.1109/TPEL.2010.2050214
- Han, B.M., Baek, S.T., Bae, B.Y. and Choi, J.Y. (2006) Back-to-Back HVDC System Using a 36-Step Voltage Source Converter. IEE Proceedings-Generation, Transmission and Distribution, 153, 677-683. http://dx.doi.org/10.1049/ip-gtd:20060053
- Tang, X. and Lu, D. (2014) Enhancement of Voltage Quality in a Passive Network Supplied by a VSC-HVDC Transmission under Disturbances. International Journal of Electrical Power & Energy Systems, 54, 45-54. http://dx.doi.org/10.1016/j.ijepes.2013.06.030
- Du, C.Q., Bollen, M.H.J., Agneholm, E. and Sannino, A. (2007) A New Control Strategy of a VSC-HVDC System for High-Quality Supply of Industrial Plants. IEEE Transactions on Power Delivery, 22, 2386-2394. http://dx.doi.org/10.1109/TPWRD.2007.899622
- Du, C., Agneholm, E. and Olsson, G. (2008) Comparison of Different Frequency Controllers for a VSC-HVDC Supplied System. IEEE Transactions on Power Delivery, 23, 2224-2232. http://dx.doi.org/10.1109/TPWRD.2008.921130
- Panda, S. and Prasad Padhy, N. (2008) Comparison of Particle Swarm Optimization and Genetic Algorithm for FACTS Based Controller Design. Applied Soft Computing, 8, 1418-1427. http://dx.doi.org/10.1016/j.asoc.2007.10.009
- Shayeghi, H., Shayanfar, H.A., Jalilzadeh, S. and Safari, A. (2009) A PSO Based Unified Power Flow Controller for Damping of Power System Oscillations. Energy Conversion and Management, 50, 2583-2592. http://dx.doi.org/10.1016/j.enconman.2009.06.009
- Panda, S., Swain, S.C., Rautray, P.K., Malik, R. and Panda, G. (2010) Design and Analysis of SSSC-Based Supplementary Damping Controller. Simulation Modelling Practice and Theory, 18, 1199-1213. http://dx.doi.org/10.1016/j.simpat.2010.04.007
- Panda, S. (2011) Differential Evolution Algorithm for SSSC-Based Damping Controller Design Considering Time Delay. Journal of the Franklin Institute, 348, 1903-1926. http://dx.doi.org/10.1016/j.jfranklin.2011.05.011
- Panda, S. (2009) Multi-Objective Non-Dominated Shorting Genetic Algorithm-II for Excitation and TCSC-Based Controller Design. Journal of Electrical Engineering, 60, 87-94.
- Shayeghi, H., Jalili, A. and Shayanfar, H.A. (2008) Multi-Stage Fuzzy Load Frequency Control Using PSO. Energy Conversion and Management, 49, 2570-2580. http://dx.doi.org/10.1016/j.enconman.2008.05.015
- Awami, A., Abdel-Magid, Y. and Abido, M.A. (2007) A Particle-Swarm-Based Approach of Power System Stability Enhancement with Unified Power Flow Controller. International Journal of Electrical Power & Energy Systems, 29, 251-259. http://dx.doi.org/10.1016/j.ijepes.2006.07.006
- Shayeghi, H., Shayanfar, H.A., Jalilzadeh, S. and Safari, A. (2010) Tuning of Damping Controller for UPFC Using Quantum Particle Swarm Optimizer. Energy Conversion and Management, 51, 2299-2306. http://dx.doi.org/10.1016/j.enconman.2010.04.002
- Coelho, L.S. (2008) A Quantum Particle Swarm Optimizer with Chaotic Mutation Operator. Chaos, Solitons & Fractals, 37, 1409-1418. http://dx.doi.org/10.1016/j.chaos.2006.10.028
- Shayeghi, H., Shayanfar, H.A. and Jalili, A. (2006) Multi Stage Fuzzy PID Power System Automatic Generation Controller in Deregulated Environments. Energy Conversion and Management, 47, 2829-2845. http://dx.doi.org/10.1016/j.enconman.2006.03.031
- Skogestad, S. and Postlethwaite, I. (2007) Multivariable Feedback Control―Analysis and Design. John Wiley & Sons, Chichester.
Appendix
The test system parameters are (all in pu):
Machine and Exciter:
Transmission line and transformer reactance:
VSC HVDC:
Coefficients are:

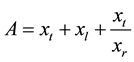

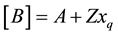
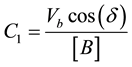
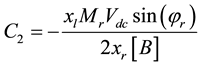
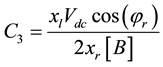


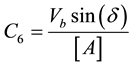



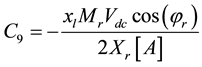

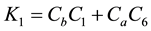
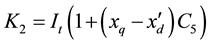
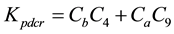
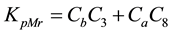

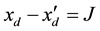
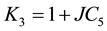





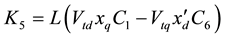

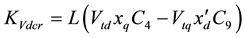
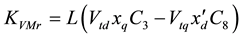


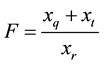

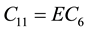

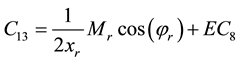


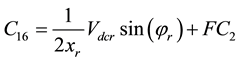
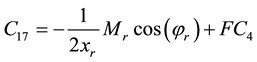
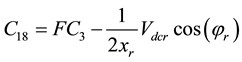
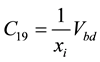




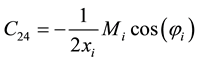
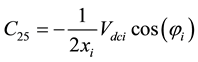
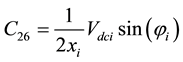
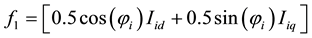
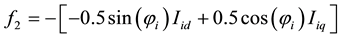
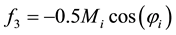


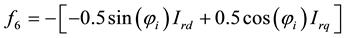




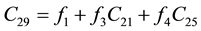


 ,
,
 ,
,
 ,
,