Communications and Network
Vol.6 No.3(2014), Article
ID:48556,10
pages
DOI:10.4236/cn.2014.63017
Stochastic Modeling and Power Control of Time-Varying Wireless Communication Networks
Mohammed M. Olama1, Seddik M. Djouadi2, Charalambos D. Charalambous3
1Computational Sciences and Engineering Division, Oak Ridge National Laboratory, Oak Ridge, USA
2Department of Electrical Engineering and Computer Science, University of Tennessee, Knoxville, USA
3Department of Electrical and Computer Engineering, University of Cyprus, Nicosia, Cyprus
Email: olamahussemm@ornl.gov, djouadi@eecs.utk.edu, chadcha@ucy.ac.cy
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Figure 2. Received signal estimates RMSE for 100 runs using the EM algorithm combined with the Kalman filter.
ABSTRACT
Wireless networks are characterized by nodes mobility, which makes the propagation environment time-varying and subject to fading. As a consequence, the statistical characteristics of the received signal vary continuously, giving rise to a Doppler power spectral density (DPSD) that varies from one observation instant to the next. This paper is concerned with dynamical modeling of time-varying wireless fading channels, their estimation and parameter identification, and optimal power control from received signal measurement data. The wireless channel is characterized using a stochastic state-space form and derived by approximating the time-varying DPSD of the channel. The expected maximization and Kalman filter are employed to recursively identify and estimate the channel parameters and states, respectively, from online received signal strength measured data. Moreover, we investigate a centralized optimal power control algorithm based on predictable strategies and employing the estimated channel parameters and states. The proposed models together with the estimation and power control algorithms are tested using experimental measurement data and the results are presented.
Keywords:Wireless Networks, Time-Varying Wireless Fading Channel, Impulse Response, Doppler Power Spectral Density, Stochastic State-Space Model, Stochastic Modeling, Optimal Power Control, Expectation Maximization, Kalman Filter

1. Introduction
Time varying (TV) wireless channel models capture both the space and time variations of wireless systems, which are due to the relative mobility of the receiver, transmitter and/or scatterers [1] -[4] . The majority of research papers in this field such as in [5] -[7] use time-invariant (static) models for wireless channels. In these models, the speeds of mobile nodes are assumed to be constant and the statistical characteristics of the received signal are assumed to be fixed in time. But in reality, the propagation environment varies continuously due to mobility of the nodes causing network topology to dynamically change, the angle of arrival of the wave upon the receiver can vary continuously, and objects or scatters move in between the transmitter and the receiver resulting in appearance or disappearance of existing paths from one instant to the next. As a result, the current models that assume fixed statistics can no longer capture and track complex time variations in the propagation environment. These time variations compel us to introduce more advanced dynamical models based on stochastic state-space representation, in order to capture higher order dynamics of the wireless channel. In time-invariant models, channel parameters are random but do not depend on time, and remain constant throughout the observation and estimation phase. This contrasts with TV models, where the channel dynamics become stochastic processes [1] - [4] . This paper focuses on the development of stochastic short-term fading channel models based on system identification algorithms using received signal measurement data to extract various channel parameters and apply an optimal power control scheme.
In [4] , the TV channel parameters are estimated from approximating the Doppler power spectral density (DPSD) of the wireless fading channel. However, in reality one does not have access to the TV DPSD at all times during the estimation process. Since these models are based on state-space forms, we propose to estimate the channel parameters as well as the inphase and quadrature components directly from received signal measurements, which are usually available or easy to obtain in any wireless network. A filter-based expectation maximization (EM) algorithm [8] and Kalman filter [9] are employed in estimating the channel parameters as well as the inphase and quadrature components, respectively. These recursive filters use only the first and second order statistics and therefore can be implemented online. These algorithms have been recently utilized in [1] and [2] to estimate the wireless channel parameters and states, and therefore the formulations of these algorithms are not presented in this paper. The proposed models and estimation algorithms are tested using received signal strength measurement data and the results are presented.
The developed stochastic channel models from received signal strength measurements are useful in most wireless applications. In this paper, these models are used to develop an optimal power control algorithm (PCA). Power control (PC) is important to improve performance of wireless communication systems. The benefits of power minimization are not just increased battery life, but also increased overall network capacity. The power allocation problem has been studied extensively as an eigenvalue problem for non-negative matrices [10] [11] , resulting in iterative PCAs that converge each user’s power to the minimum power [12] [13] , and as optimization-based approaches [14] . Much of this previous work deals with static time-invariant channel models.
The proposed PCA is based on predictable power control strategies (PPCS) that were first introduced in [4] . PPCS basically means updating the transmitted powers at discrete times and maintaining them fixed until the next power update begins. The PPCS mechanism is proven to be effectively applicable to such dynamical models for an optimal PC. The outage probability (OP) is used as a performance measure. Since few TV dynamical channel models have so far been investigated with the application of any PCA, the suggested dynamical models and PCA thus provide a far more realistic and efficient optimal control of wireless networks.
The remainder of this paper is organized as follows. In Section 2, stochastic modeling and online estimation of TV wireless fading communication channels are presented. Section 3 introduces an optimal PCA based on predictable strategies and employing the estimated channel parameters and states. Section 4 presents numerical results that validate the proposed models together with the estimation and power control algorithms. Finally, Section 5 provides concluding remarks.
2. Stochastic Modeling and Estimation of Time-Varying Wireless Channels
The general TV model of a wireless channel is typically represented by the following multipath band-pass impulse response [6]
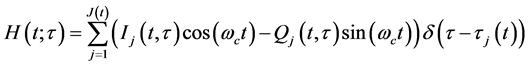 (1)
(1)
where 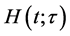 is the band-pass response of the channel at time
is the band-pass response of the channel at time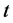 , due to an impulse applied at time
, due to an impulse applied at time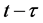 ,
, 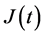 is the random number of multipath components,
is the random number of multipath components, 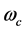 is the carrier frequency,
is the carrier frequency, 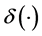 is the Dirac delta function, and the set
is the Dirac delta function, and the set  describes the random TV inphase component, quadrature component, and arrival time of the different paths, respectively. Let
describes the random TV inphase component, quadrature component, and arrival time of the different paths, respectively. Let 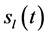 be the low-pass equivalent representation of the transmitted signal, then the band-pass representation of the received signal is given by
be the low-pass equivalent representation of the transmitted signal, then the band-pass representation of the received signal is given by
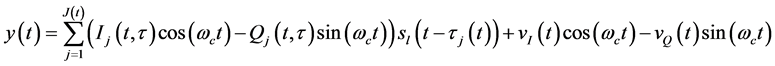 (2)
(2)
where 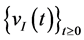 and
and  are two independent and identically distributed (iid) white Gaussian noise processes.
are two independent and identically distributed (iid) white Gaussian noise processes.
It is shown in [4] and [15] that the DPSD of a wireless fading channel, denoted by , can be approximated by an even, stable, rational, and factorizable transfer function,
, can be approximated by an even, stable, rational, and factorizable transfer function, 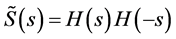 , where
, where 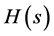 is given by
is given by
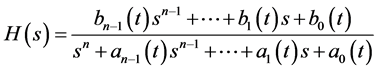 (3)
(3)
Consequently, the inphase and quadrature components can be realized using the following stochastic statespace representation [16]
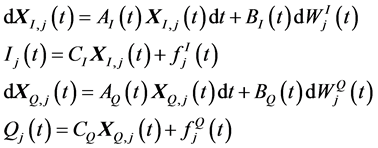 (4)
(4)
where
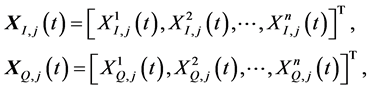
 (5)
(5)
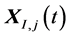 and
and  are the state vectors corresponding to the inphase and quadrature components, respectively.
are the state vectors corresponding to the inphase and quadrature components, respectively.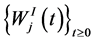 ,
,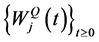 are independent standard Brownian motions, which correspond to the inphase and quadrature components of the
are independent standard Brownian motions, which correspond to the inphase and quadrature components of the 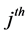 path respectively,
path respectively, 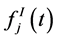 and
and  are arbitrary functions representing the presence or absence of line-of-sight (LOS) of the inphase and quadrature components for the
are arbitrary functions representing the presence or absence of line-of-sight (LOS) of the inphase and quadrature components for the 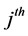 path respectively, and
path respectively, and 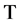 denotes matrix or vector transpose. Without loss of generality, we consider the case of flat fading, in which the fading channel has purely a multiplicative effect on the signal and the multipath components are not resolvable, and, thus, can be considered as a single path [6] . We also consider the non-lineof-sight (NLOS) case, i.e.,
denotes matrix or vector transpose. Without loss of generality, we consider the case of flat fading, in which the fading channel has purely a multiplicative effect on the signal and the multipath components are not resolvable, and, thus, can be considered as a single path [6] . We also consider the non-lineof-sight (NLOS) case, i.e.,  , which represents an environment with large obstructions. The time-varying state space model described in (4) has a solution given by
, which represents an environment with large obstructions. The time-varying state space model described in (4) has a solution given by
 (6)
(6)
where 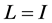 or
or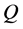 ,
,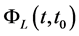 is the state transition matrix associated to
is the state transition matrix associated to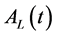 , and
, and 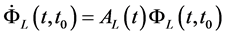 . Therefore, the mean of
. Therefore, the mean of 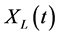 is
is
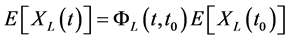 (7)
(7)
and the covariance matrix of 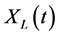 is
is
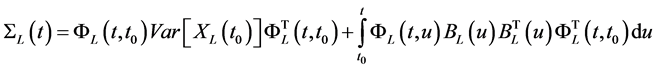 (8)
(8)
For the time-invariant case,  , then (6), (7), and (8) simplify to
, then (6), (7), and (8) simplify to
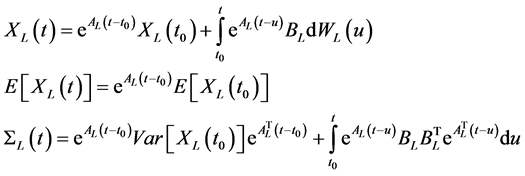 (9)
(9)
It can be observed in (7) and (8) that the mean and variance of the inphase and quadrature components are functions of time. Thus, the statistics of the inphase and quadrature components, and therefore the statistics of the channel, are times varying.
Similarly, following the state space representation in (4) and the received signal in (2), the fading channel can be represented using general stochastic state-space representation of the form
 (10)
(10)
where
 (11)
(11)
In this case, 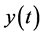 represents the received signal measurements,
represents the received signal measurements,  is the state variable of the inphase and quadrature components, and
is the state variable of the inphase and quadrature components, and  is the measurement Gaussian noise.
is the measurement Gaussian noise.
In [4] and [15] , the channel parameters  are obtained from approximating the DPSD. However, in reality one does not have access to the DPSD at all times during the estimation process. Therefore, we propose estimating the channel parameters as well asinphase and quadrature components directly from received signal measurements, which are usually available or easy to obtain in any wireless network. A filter-based expectation maximization (EM) algorithm combined with the Kalman filter is employed to estimate the channel model parameters and states in (10). These filters use only the first and second order statistics and are also recursive, and therefore can be implemented online. These algorithms have been recently utilized in [1] and [2] to estimate wireless channel parameters and states, and therefore the formulations of these algorithms are not presented in this paper. Experimental results demonstrating the applicability of these algorithms in conjunction with the proposed stochastic wireless models are discussed in Section 4. In the next section, we introduce an important application based on the developed models; that is stochastic PC in wireless networks.
are obtained from approximating the DPSD. However, in reality one does not have access to the DPSD at all times during the estimation process. Therefore, we propose estimating the channel parameters as well asinphase and quadrature components directly from received signal measurements, which are usually available or easy to obtain in any wireless network. A filter-based expectation maximization (EM) algorithm combined with the Kalman filter is employed to estimate the channel model parameters and states in (10). These filters use only the first and second order statistics and are also recursive, and therefore can be implemented online. These algorithms have been recently utilized in [1] and [2] to estimate wireless channel parameters and states, and therefore the formulations of these algorithms are not presented in this paper. Experimental results demonstrating the applicability of these algorithms in conjunction with the proposed stochastic wireless models are discussed in Section 4. In the next section, we introduce an important application based on the developed models; that is stochastic PC in wireless networks.
3. Optimal Power Control Based on the Stochastic Wireless Channel Models
In this section, an optimal PCA is investigated based on the estimated wireless channel models. Since the channel model parameters are estimated from received signal measurements, PC can be performed solely from having these measurements. The aim of the PCA described here is to minimize the total transmitted power of all users while maintaining acceptable quality-of-service (QoS) for each user. The measure of QoS is defined by the signal-to-interference ratio (SIR) for each link to be larger than a target SIR.
By generalizing the wireless channel model in (10), the state-space representation of a wireless network with  transmitters and
transmitters and  receivers can be described as
receivers can be described as
 (12)
(12)
where 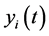 is the received signal at the
is the received signal at the 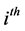 receiver at time
receiver at time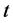 ,
,  is the states of the channel between transmitter
is the states of the channel between transmitter 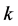 and the receiver assigned to transmitter
and the receiver assigned to transmitter ,
, 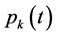 is the transmitted power of transmitter
is the transmitted power of transmitter  at time
at time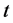 , which acts as a scaling on the information signal
, which acts as a scaling on the information signal ,
, 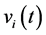 is the channel disturbance or noise at receiver
is the channel disturbance or noise at receiver , and
, and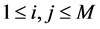 .
.
Consider the wireless network described in (12), the centralized PC problem for TV channels over a time interval 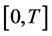 can be stated as follows [4]
can be stated as follows [4]
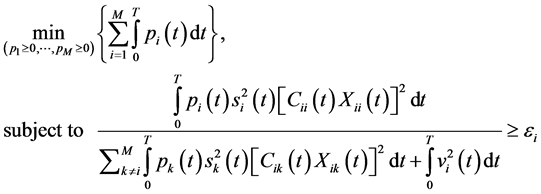 (13)
(13)
where  is the target SIR at receiver
is the target SIR at receiver 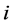 and
and . A solution to (13) is presented by first introducing the communication meaning of predictable power control strategies (PPCS). In wireless cellular networks, it is practical to observe and estimate channels at the base stations and then send the information back to the mobiles to adjust their power signals
. A solution to (13) is presented by first introducing the communication meaning of predictable power control strategies (PPCS). In wireless cellular networks, it is practical to observe and estimate channels at the base stations and then send the information back to the mobiles to adjust their power signals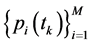 . Since channels experience delays, and power control is not feasible continuously in time but only at discrete time instants, the concept of predictable strategies is introduced [4] . Consider a set of discrete time strategies
. Since channels experience delays, and power control is not feasible continuously in time but only at discrete time instants, the concept of predictable strategies is introduced [4] . Consider a set of discrete time strategies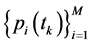 ,
,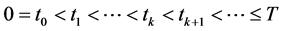 . At time
. At time , the base stations estimate the channel information
, the base stations estimate the channel information 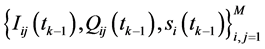 as illustrated in Section 2. Using the concept of predictable strategy, the base stations determine the control strategy
as illustrated in Section 2. Using the concept of predictable strategy, the base stations determine the control strategy 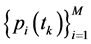 for the next time instant
for the next time instant . The latter is communicated back to the mobiles, which hold these values during the time interval
. The latter is communicated back to the mobiles, which hold these values during the time interval . At time
. At time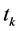 , a new set of channel information
, a new set of channel information 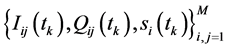 is estimated at base stations and the time
is estimated at base stations and the time  control strategies
control strategies 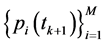 are computed and communicated back to the mobiles which hold them constant during the time interval
are computed and communicated back to the mobiles which hold them constant during the time interval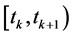 . Such decision strategies are called predictable. Using the concept of PPCS over any time interval
. Such decision strategies are called predictable. Using the concept of PPCS over any time interval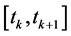 , Expression (13) is equivalent to
, Expression (13) is equivalent to
 (14)
(14)
where
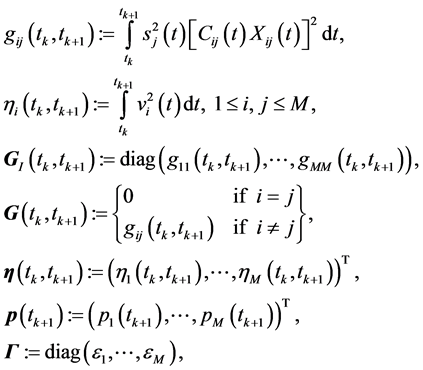 (15)
(15)
and 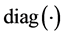 denotes a diagonal matrix with its argument as diagonal entries. The optimization in (14) is a linear programming problem in
denotes a diagonal matrix with its argument as diagonal entries. The optimization in (14) is a linear programming problem in 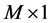 vector of unknowns
vector of unknowns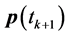 . Here
. Here 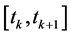 is a time interval such that the channel model does not change significantly, i.e.,
is a time interval such that the channel model does not change significantly, i.e., 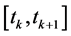 should be smaller than the coherence time of the channel. Throughout this section, we assume that the PC problem is feasible, i.e., there exists a power vector
should be smaller than the coherence time of the channel. Throughout this section, we assume that the PC problem is feasible, i.e., there exists a power vector 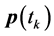 that satisfies the inequality in (14) for all
that satisfies the inequality in (14) for all 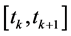 in
in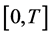 .
.
In the next section, a numerical example is presented to determine the performance of the proposed PCA under the estimated wireless channel models.
4. Numerical Results
In this section, two numerical examples are presented. In Example 1, the EM algorithm combined with Kalman filtering is performed to estimate the channel parameters as well as inphase and quadrature components from received signal measurements. In Example 2, the performance of the proposed PCA based on the estimated channel models in Example 1 is determined and compared with fixed transmitted powers.
4.1. Example 1: Wireless Channel Estimation
In this numerical example, a  order channel model as described in (10) and (11) is considered. Therefore, the system parameters
order channel model as described in (10) and (11) is considered. Therefore, the system parameters 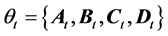 can be represented as
can be represented as
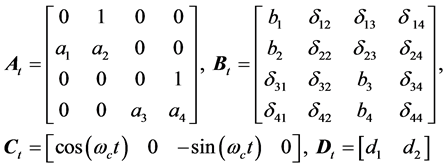 (16)
(16)
Experimental data for a cellular network is provided by the Canadian Communication Research Center (CRC) and include measurement samples for the inphase and quadrature components and received signal strength.
As previously mentioned, the estimation of a flat fading wireless channel from received signal measurement data is considered. In particular, the estimation includes the channel parameters, inphase and quadrature components, and the received signal, which are then compared to the ones obtained from the provided measurement data. It is also assumed that the received signal measurement data are corrupted by white Gaussian noise sequences.
Figure 1 shows the measured and estimated inphase and quadrature components as well as the received signal using the EM algorithm together with the Kalman filter for 400 sampled data taken from the measurements of one channel chosen at random. At a certain time instant, the system parameters are estimated as
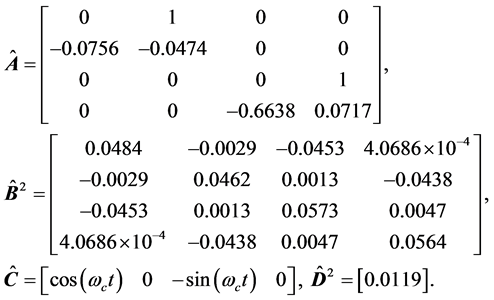 (17)
(17)
From Figure 1, it can be observed that the inphase and quadrature components of the wireless fading channel as well as the received signal have been estimated with very high accuracy. It can also be noticed that the estimation error decreases as the number of samples increases; this is because the algorithm is recursive and the channel parameters converge to the actual values as more samples are being estimated. Figure 2 shows the received signal estimates root mean square error (RMSE) for 100 runs. It can be noticed that it takes just few iterations (less than 15) for the filter to converge, and the steady state performance of the proposed channel estimation algorithm is excellent. Since we consider  order channel model, the computational cost of the proposed estimation algorithm is moderate and can be implemented in real time. Moreover, the filters of the expectation step are recursive and decoupled and hence are easy to implement in parallel on a multi-processor system [17] .
order channel model, the computational cost of the proposed estimation algorithm is moderate and can be implemented in real time. Moreover, the filters of the expectation step are recursive and decoupled and hence are easy to implement in parallel on a multi-processor system [17] .
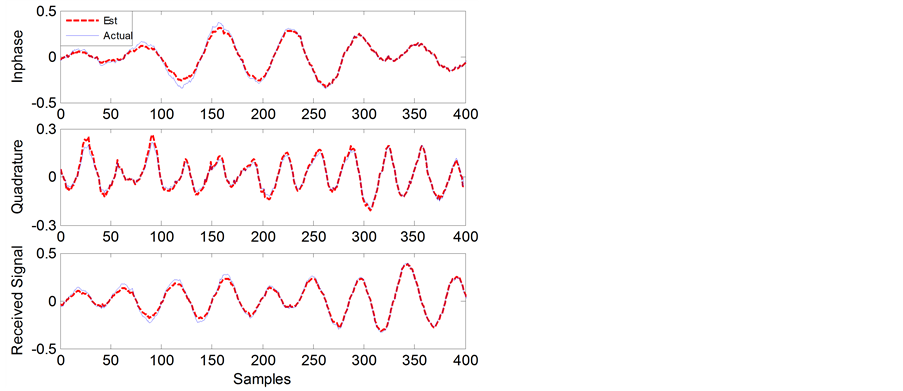
Figure 1. The measured and estimated inphase and quadrature components, and received signal for the  order channel model in Example 1, using the EM algorithm combined with the Kalman filter.
order channel model in Example 1, using the EM algorithm combined with the Kalman filter.
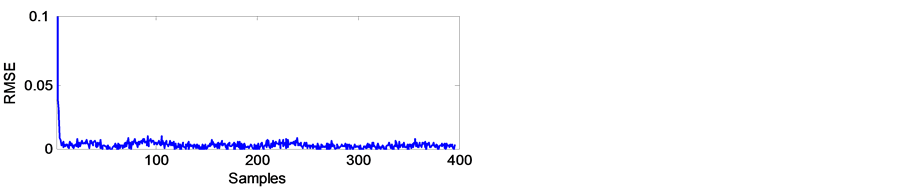
Figure 2. Received signal estimates RMSE for 100 runs using the EM algorithm combined with the Kalman filter.
4.2. Example 2: Optimal Power Control
In this numerical example, the received signal measurement data for 24 users are collected experimentally. They represent flat Rayleigh fading environment where the signal envelope at the receivers exhibit Rayleigh distributed density. The channel model parameters as well as the inphase and quadrature components for all users are estimated online from the measurement data using the EM algorithm together with the Kalman filter as illustrated in Example 1. The PCA described in (14) is performed using the estimated channel parameters and states. The outage probability (OP) is used as a performance measure for the PCA. A link with a received SIR,  , less than or equal to a target SIR,
, less than or equal to a target SIR, 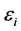 , is considered a communication failure. The OP,
, is considered a communication failure. The OP, 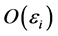 , is expressed as
, is expressed as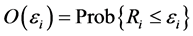 , where
, where 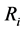 is the received SIR at receiver
is the received SIR at receiver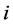 .
.
It is assumed that the targets SIR, 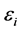 for all users are the same, and varied from 5 dB to 25 dB with step 5 dB. For each value of
for all users are the same, and varied from 5 dB to 25 dB with step 5 dB. For each value of  the OP is computed every 15 millisecond, i.e.,
the OP is computed every 15 millisecond, i.e.,  millisecond. The simulation is performed for 4.5 seconds, i.e.,
millisecond. The simulation is performed for 4.5 seconds, i.e., 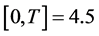 seconds. The OP is computed using Monte-Carlo simulations. The performance of the proposed PCA is compared with the one of constant transmitted powers (CTP).
seconds. The OP is computed using Monte-Carlo simulations. The performance of the proposed PCA is compared with the one of constant transmitted powers (CTP).
The OP for both the CTP and the proposed PCA based on PPCS are demonstrated in Figure 3(a) and Figure 3(b), respectively. Figure 3 shows how the OP changes with respect to target SIR and time. As the target SIR increases the OP increases. This is obvious since we expect more users to fail. The OP also changes as a function of time, since users move in different directions and velocities while gathering the measurements.
 (a)
(a)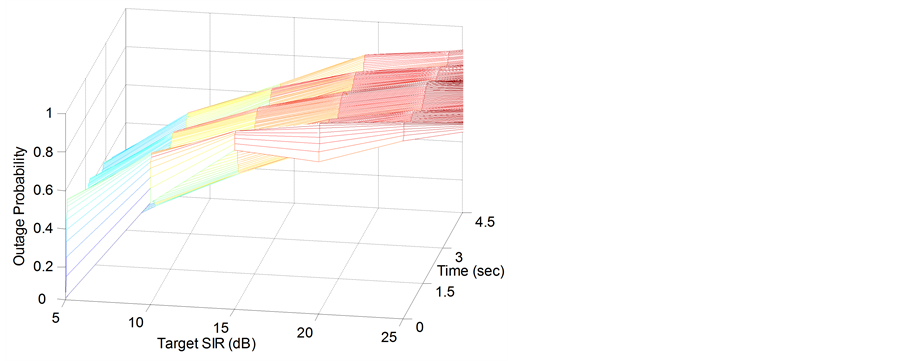 (b)
(b)
Figure 3. The outage probability for the dynamical flat Rayleigh wireless network in Example 2. (a) Using CTP; (b) Using PC based on PPCS.

Figure 4. Average outage probability of the PC case based on PPCS and the CTP case in Example 2. Performance comparison.
The average OP versus target SIR for both cases over the whole simulation time (4.5 seconds) is demonstrated in Figure 4, which shows that the performance of the proposed PCA based on PPCS is on average much better than that of the CTP. For example, at 10 dB target SIR, the OP is reduced from 0.51 for the CTP algorithm to 0.37 for the PCA; this represents an improvement of over 27%.
5. Conclusion
This paper describes a general scheme for extracting mathematical wireless channel models from noisy received signal measurements, and performing power control based on the estimated channel parameters. The channel models are represented in stochastic state-space form. The proposed estimation algorithm consists of filtering based on the Kalman filter to remove noise from data, and identification based on the EM algorithm to determine the parameters of the model which best describe the measurements. Numerical results indicate that the measured data can be regenerated through a simple 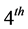 order discrete-time stochastic state-space model. Moreover, a stochastic PCA based on the estimated parameters and channel states is investigated. Numerical results indicate that there is potentially large gain to be achieved by using the proposed PCA, which can be used as long as the channel model does not change significantly; that is
order discrete-time stochastic state-space model. Moreover, a stochastic PCA based on the estimated parameters and channel states is investigated. Numerical results indicate that there is potentially large gain to be achieved by using the proposed PCA, which can be used as long as the channel model does not change significantly; that is 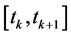 is a subset of the coherence time of the channel.
is a subset of the coherence time of the channel.
Acknowledgements
This paper has been authored by employees of UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy. This work was also supported in part by NSF grant CMMI-1334094.
References
- Olama, M.M., Djouadi, S.M. and Charalambous, C.D. (2009) Stochastic Differential Equations for Mod-
eling, Estimation and Identification of Mobile-to-Mobile Communication Channels. IEEE Transactions
on Wireless Communications, 8, 1754-1763. http://dx.doi.org/10.1109/TWC.2009.071068 - Olama, M.M., Li, Y., Djouadi, S.M. and Charalambous, C.D. (2007) Time-Varying Wireless Channel Modeling, Estimation, Identification, and Power Control from Measurements. Proceedings of the American Control Conference (ACC’07), New York, 9-13 July 2007, 3100-3105.
- Olama, M.M., Djouadi, S.M. and Charalambous, C.D. (2006) Stochastic Power Control for Time-Varying Long-Term Fading Wireless Networks. EURASIP Journal on Applied Signal Processing, 2006, Article ID: 89864.
- Charalambous, C.D., Djouadi, S.M. and Denic, S.Z. (2005) Stochastic Power Control for Wireless Networks via SDE’s: Probabilistic QoS Measures. IEEE Transactions on Information Theory, 51, 4396-4401. http://dx.doi.org/10.1109/TIT.2005.858984
- Jakes, W. (1974) Microwave Mobile Communications. IEEE Inc., New York.
- Proakis, J.G. (2000) Digital Communications. 4th Edition, McGraw Hill, New York.
- Rappaport, T.S. (2002) Wireless Communications: Principles and Practice. 2nd Edition, Prentice Hall, Upper Saddle River.
- Charalambous, C.D. and Logothetis, A. (2000) Maximum-Likelihood Parameter Estimation from Incomplete Data via the Sensitivity Equations: The Continuous-Time Case. IEEE Transactions on Automatic Control, 45, 928-934. http://dx.doi.org/10.1109/9.855553
- Bishop, G. and Welch, G. (2001) An Introduction to the Kalman Filters. University of North Carolina, North Carolina.
- Zander, J. (1992) Performance of Optimum Transmitter Power Control in Cellular Radio Systems. IEEE Transactions on Vehicular Technology, 41, 57-62. http://dx.doi.org/10.1109/25.120145
- Aein, J. (1973) Power Balancing in Systems Employing Frequency Reuse. COMSAT Technical Review, 3, 277-299.
- Bambos, N. and Kandukuri, S. (2002) Power-Controlled Multiple Access Schemes for Next-Generation Wireless Packet Networks. IEEE Wireless Communications, 9, 58-64.
http://dx.doi.org/10.1109/MWC.2002.1016712 - Foschini, G.J. and Miljanic, Z. (1993) A Simple Distributed Autonomous Power Control Algorithm and Its Convergence. IEEE Transactions on Vehicular Technology, 42, 641-646.
http://dx.doi.org/10.1109/25.260747 - Kandukuri, S. and Boyd, S. (2002) Optimal Power Control in Interference-Limited Fading Wireless Channels with Outage-Probability Specifications. IEEE Transactions on Wireless Communications, 1, 46-55. http://dx.doi.org/10.1109/7693.975444
- Olama, M.M., Djouadi, S.M. and Charalambous, C.D. (2006) Stochastic Channel Modeling for Ad-Hoc Wireless Networks. Proceedings of the American Control Conference, Minneapolis, 14-16 June 2006, 6075-6080.
- Oksendal, B. (1998) Stochastic Differential Equations: An Introduction with Applications. Springer, Berlin. http://dx.doi.org/10.1007/978-3-662-03620-4
- Elliott, R.J. and Krishnamurthy, V. (1999) New Finite-Dimensional Filters for Parameter Estimation of Discrete-Time Linear Guassian Models. IEEE Transactions on Automatic Control, 44, 938-951. http://dx.doi.org/10.1109/9.763210

