Communications and Network
Vol. 4 No. 1 (2012) , Article ID: 17488 , 7 pages DOI:10.4236/cn.2012.41001
Energy Efficient Non-Cooperative Methods for Resource Allocation in Cognitive Radio Networks
1University of Florence, Florence, Italy
2CNIT, Florence Research Unit, Florence, Italy
Email: renato.pucci@unifi.it
Received November 4, 2011; revised December 13, 2011; accepted January 9, 2012
Keywords: Cognitive Radio Networks; Resource Allocation
ABSTRACT
In a cognitive radio network wherein primary and secondary users coexist, an efficient power allocation method represents one of the most important key aspects. This paper provides a novel approach based on a game theory framework to solve this problem in a distributed and fair way. Formulated as an optimization problem, the resource allocation problem between secondary users and primary users can be modeled and investigated with the Game Theory, and in particular S-Modular Games, since they provide useful tools for the definition of multi objective distributed algorithms in the context of radio communications. This paper provides also a performance comparison among the proposed game and two other algorithms, frequently used in this context: Simulated Annealing and Water Filling.
1. Introduction
Cognitive Radio represents a promising paradigm aimed to optimize the radio spectrum efficiency. In a cognitive radio network, two kind of users can exist: primary (noncognitive) users and secondary (cognitive) users. Even though primary and secondary users coexist within the same network and sharing the same frequency bands, primary users may be unaware of the presence of secondary users. Contrary to primary users, secondary users are smart, since they are intelligent and interact with selfish network users, choosing best operating parameters on the base of the sensed spectrum. Due to the natural radio environment changes, spectrum sharing schemes change frequently, accordingly with the users allocated resource. In this scenario, a game theoretic framework allows to study, model and analyze cognitive radio networks in a distributed way. Such attractive feature allows to achieve the flexibility and the efficient adaptation to the operative environment that were previously mentioned. Due to the players behavior, noncooperative game theory is closely connected to mini/max optimization and typically results in the study of various equilibria, most notably the Nash equilibrium [1]. Developed cognitive radio strategy has been formulated according the mathematical discipline of Game Theory, with particular reference to S-Modular Games [2].
Non-cooperative games have been proposed for spectrum sharing in [3], which reports a detailed survey on game theoretic approaches for dynamic spectrum sharing in cognitive radio networks, by in-depth theoretic analysis and an overview of the most recent practical implementations. In [4], the authors investigate the issue about the spectrum sharing between a decentralized cognitive network and a primary system, comparing a suboptimal distributed non-cooperative game theoretic power control algorithm with the optimal solution power control algorithm and the power control algorithm proposed in [5]. Besides the above referred papers, in [6] and [7] it is also discussed the power control problem in spectrum sharing model. In [8,9] authors proposed different game-theoretic approaches to maximize energy efficiency of the users within wireless networks, making the utility functions being inversely proportional to the transmit power.
This paper extends the above described results providing a distributed game-theoretic approach to obtain a quasi-optimal power allocation method that maximize the energy efficiency of each user, within the coexistence of primary and secondary users. The proposed method take into account throughput fairness among secondary users.
The paper is organized as follows: in Section 2 the proposed system model and applicative scenario are presented. The game description and the NE existence and uniqueness is discussed in Section 3, while in Section 4 the Water-Filling algorithm and a his energy efficient modified version is reported. In 5 the results from computer simulation are commented. Finally some conclusions are expressed in Section 6.
2. System Model
In this work we consider a Cognitive Radio context inspired by a tactical/military scenario where a primary system (owner of the spectrum rights) coexisting with one or more secondary systems and sharing the same frequency band. This kind of situation is very interesting and, at the same time, very frequent, i.e. during coalition deployment of forces or in case of coexistence of humanitarian and military convoys, especially when mobility is taken into account. It is to be noted that such kind of context is a suggested scenario by EDA and NATO [10] to provide a better reuse of the frequency resource among several nations (coexistence of networks) and give a great help to accommodate dynamism of the operational deployments. Note that, considering a primary system in the network, the proposed scheme includes the possibility to existence of more than one primary user.
In the proposed system, each user is characterized by a dedicated sender and receiver, thus each communicating couple consists of a transmitter site 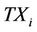 and a receiver site
and a receiver site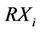 , as shown in Figure 1. In the most general context, in this work we consider the transmitters and the receivers positions completely independent the ones from the others. Moreover, we use a discrete-time model, based on iterations (which we ahead refer as
, as shown in Figure 1. In the most general context, in this work we consider the transmitters and the receivers positions completely independent the ones from the others. Moreover, we use a discrete-time model, based on iterations (which we ahead refer as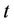 ). Indeed, for every single iteration, all users act only once and until
). Indeed, for every single iteration, all users act only once and until

Figure 1. Scenario with one primary users pair (represented by circles) and 5 secondary users pairs; shaded colors represent the path loss component of the channel.
the next iteration they can’t do anything else. Each user broadcast a pilot signals at the first iteration of the algorithm in order estimate the channel gain coefficients, that are assumed not changing during the execution of the algorithm.
Since in the above described scenario primary users may be unaware of the presence of secondary users, in the proposed system there can’t be a “direct” cooperation among primary and secondary users. However, by definition, primary users should not undergo a degradation of the required QoS due to the presence of secondary users. For this reason, we propose the following the solution: the primary AP selects and broadcasts periodically on the shared channel a reasonable interference cap on the total interference it willing to tolerate. Together with the interference cap, the value of the total interference received by the primary receiver is transmitted. Thanks to this solution, we introduce a sort of “indirect” unaware cooperation among the two kind of users. The direct result of the introduction of a chosen interference cap is a limitation of the total transmit power of the secondary users on the shared channel. Thanks to the introduction of the interference cap, for the simplicity of exposition, hereinafter we will consider only one primary transmitter-receiver pair, since the proposed scheme can be easily extended to include more than one primary user.
Viewed from the perspective of secondary users, each of them will choose the more suitable transmission power in order to achieve the best transmission quality, respecting the interference cap (broadcasted by primary AP) and ensuring low interference to other secondary users. Due to the consistent decisions made by primary and secondary users, game theory represents an inbred framework to study, analyze and predict the behavior of this system. For simplicity of exposition, we will consider a fixed primary interference cap and therefore a fixed maximum transmission power for the secondary users; this assumption can be made without altering the validity of the system, since variations of this value are relatively slow compared with the time of convergence of the algorithm. In case of wireless networks with high primary mobility and/or more strict delay needs, a delay efficient approach should be followed, see [11].
3. The Proposed Game
3.1. Game Description
The non-cooperative game proposed in this paper can be modeled as game with 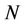 secondary users, namely the players of the game, operating on one radio resource. This game can be easily extended considering
secondary users, namely the players of the game, operating on one radio resource. This game can be easily extended considering 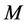 radio resources (i.e. subcarriers of the same multi-carrier channel or different channels) following the approach proposed in [12], where subcarrier allocation is based on the normalized channel gain. Formally, the proposed noncooperative game can be modeled as follows:
radio resources (i.e. subcarriers of the same multi-carrier channel or different channels) following the approach proposed in [12], where subcarrier allocation is based on the normalized channel gain. Formally, the proposed noncooperative game can be modeled as follows:
• Set of Players: 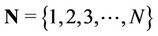 where
where 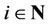 is the
is the 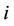 -th secondary user.
-th secondary user.
• Set of Strategies: .
.
• Utility function: 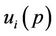 where
where  is the
is the  -th secondary user.
-th secondary user.
Following the approach proposed by [8,13], we take into account the energy efficiency problem at the physical layer, considering an utility function expressed in bit/Joule as performance measure of the model. Each player tries to maximize the following utility function:
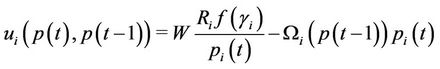 (1)
(1)
where 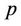 is the complete set of strategies of all secondary users,
is the complete set of strategies of all secondary users,  is the ratio between the number of information bits per packet and the number of bits per packet,
is the ratio between the number of information bits per packet and the number of bits per packet, 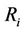 is the transmission rate of the
is the transmission rate of the 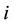 th user in bits/sec,
th user in bits/sec, 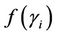 is the is the efficiency function (depending on the considered modulation), that represents a stochastic modeling of the number of bits that are successfully received for each unit of energy drained from the battery for the transmission.
is the is the efficiency function (depending on the considered modulation), that represents a stochastic modeling of the number of bits that are successfully received for each unit of energy drained from the battery for the transmission.
Thanks to the efficiency function, the utility function each user tries to maximize is related to its instantaneous signal to noise plus interference ratio (SINR), defined as:
 (2)
(2)
where with the notation 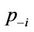 we refer to all components of
we refer to all components of 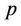 not belonging to user
not belonging to user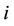 ,
,  is the power allocated from the secondary transmitter
is the power allocated from the secondary transmitter 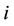 (
(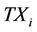 ),
), is the path gain from
is the path gain from 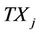 to
to ,
, 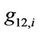 is the interference channel from the primary to the secondary receiver
is the interference channel from the primary to the secondary receiver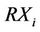 ,
, 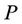 is the primary transmitted power, while
is the primary transmitted power, while 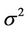 is the AWGN component at
is the AWGN component at .
.
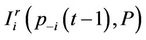 represents the total interference received by the
represents the total interference received by the 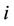 th user and it can be wrote as:
th user and it can be wrote as:
 (3)
(3)
The path gain can be written as [14]:
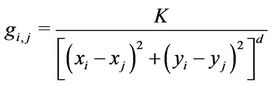 (4)
(4)
where 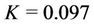 and
and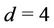 .
.
The adopted channel model is composed by a small scale fading and a path-loss component. In particular, the path-loss model is the Okomura-Hata model, while the small scale fading is modeled as a Rayleigh process.
Since the above defined utility function depends on the path gains, each secondary user need to know it. In order to solve this problem that could have a strong impact on the signalling process, we assume that each receiver periodically send out a beacon, thanks to which transmitters can measure path gains.
In order to make the NE of the game as efficient as possible (moving it to the Pareto Optimum), we consider the adaptive pricing function  that generates pricing values basing on the interference generated by network users. Thus, users that cause high interference transmitting at high power will obtain high value of pricing, due to the fact that
that generates pricing values basing on the interference generated by network users. Thus, users that cause high interference transmitting at high power will obtain high value of pricing, due to the fact that 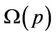 is strictly increasing with
is strictly increasing with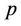 . The pricing function is written as follows:
. The pricing function is written as follows:
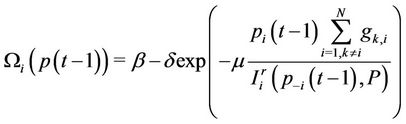 (5)
(5)
where:
• 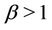 is the maximum pricing value•
is the maximum pricing value• 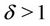 is the price weight of the generated interference•
is the price weight of the generated interference•  is the sensitivity of the users to interference.
is the sensitivity of the users to interference.
These three parameters are very useful to adapt the pricing function to the considered wireless network requirements; i.e. we can make the algorithm converge faster decreasing the value of 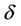 or force all secondary users to transmit at lower power levels increasing their sensitivity to the interference [13].
or force all secondary users to transmit at lower power levels increasing their sensitivity to the interference [13].
3.2. Existence and Uniqueness of NE
A Nash Equilibrium [15] offers a stable outcome and it can be guaranteed to exist, under certain conditions, but does not necessarily mean the best payoff for all the players involved, especially in presence of pricing techniques. In the literature there are lots of mathematical methods to demonstrate the existence and uniqueness of NE, like graphical [13,16], quasi-concavity curve [17] and super-modularity [8,18].
Supermodular Games are an interesting class of games that exhibits strategic complementarity. There are several compelling reasons like existence of pure strategy Nash equilibrium, dominance resolvability, identical bounds on joint strategy space etc. that make them a strong candidate for resource allocation modeling. Supermodular games are based on the concept of “supermodularity”, which is used in the social sciences to analyze how one agent’s decision affects the incentives of others.
S-Games are normal form games 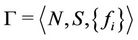 where
where 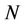 is the set of users,
is the set of users, 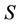 the strategy space,
the strategy space, 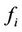 the set of utility functions and
the set of utility functions and  these conditions are satified:
these conditions are satified:
1) The strategy space 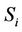 of user
of user 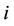 is a complete lattice.
is a complete lattice.
2) 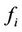 is supermodular in
is supermodular in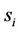 .
.
3)  presents increasing differences in
presents increasing differences in .
.
The proposed utility function in Equation (1) can be easily demonstrated to be supermodular, since:
1) The strategy space P is a complete lattice;
2)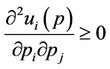 (6)
(6)
for all 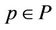 and
and .
.
3) The utility function has the increasing difference property.
For the details of proofs we refer to [8], under the proposed conditions. Uniqueness of the NE can be also demonstrated following the same approach, since we use a Best Response rule. Even if our proposed pricing function is more complicated, in comparison with the above-cited work, the demonstration procedure does not change. Indeed, the pricing function 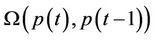 can be considered linear in
can be considered linear in , since the coefficient of
, since the coefficient of 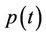 at time
at time 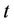 is a constant.
is a constant.
4. Energy Efficient Iterative Water-Filling Algorithm
Water filling is a frequently used algorithm in power allocation methods. This algorithm starts from the idea that a vase can be filled by a quantity of water equal to the empty volume of the vase. It is well-known in the literature that power allocation in parallel uncoupled channels can follow the water filling principle in order to maximize data-rate. A channel can be filled by an amount of power depending on the existing noise level. A multiuser scenario cannot be modeled as the parallel uncoupled channels case, but it has to be modeled following the approach of an interference channels.
On the base of these considerations, an iterative water filling procedure can be obtained; each user updates its transmission power level as follows:
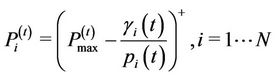 (7)
(7)
where  is the power level assigned at the user
is the power level assigned at the user  in the iteration
in the iteration 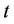 and
and 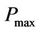 is maximum power that can be transmitted in the channel (the water level). Because of
is maximum power that can be transmitted in the channel (the water level). Because of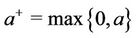 , if
, if , then
, then  is assigned to the user
is assigned to the user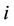 .
.
Iterative Water-Filling gets excellent performances in presence of low interference environments and/or limited number of users. However for increasing values of interference, the algorithm get worst; indeed, users experimenting the best channel conditions will transmit at high power levels, while users experimenting bad channel conditions (i.e. being the receiver close to another transmitter) will receive high interference values and then they will be inactivated. For this reason, EEIWF turns out to be unfair.
For a fixed target data-rate, we can identify a minimum target value for the SINR. In this case, Iterative Water-Filling is energy inefficient, due to the fact that the algorithm tries to maximize the total transmission power, achieving SINR values that are greater than the target value. For this reason, we propose the following energy efficient modified version of the algorithm, called Energy Efficient Iterative Water-Filling (EEIWF). For each iteration, 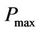 is updated as follows:
is updated as follows:
• If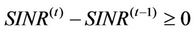 ,
, 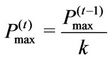
• If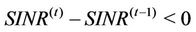 ,
, 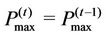
where 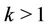 represents the reduction factor and it controls the convergence speed of the algorithm. Note that for
represents the reduction factor and it controls the convergence speed of the algorithm. Note that for 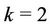 the algorithm becomes the bisection method.
the algorithm becomes the bisection method.
Such approach allows us to maintain the fixed datarate, using the lowest total transmission power level, taking into account its trend in Figure 2.
In the case of 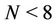 number of user, the SINR trend for decreasing values of
number of user, the SINR trend for decreasing values of 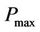 is a monotonous decreasing function. Otherwise, when
is a monotonous decreasing function. Otherwise, when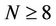 , a reduction of
, a reduction of 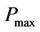 should also improve SINR final value.
should also improve SINR final value.
5. Simulation Results
In this paragraph we show the results of the simulations that we run in order to verify the behavior of a cognitive network based on the our proposed game-theoretical framework. In the subsection 5.1 the convergence of the algorithm is shown, while in subsection 5.2 a comparison between proposed game and heuristic power allocations will be presented.
5.1. Convergence of the Algorithm
The operating context is a terrain square area of 1 km edge, with a suburban path-loss profile. Primary transmitter and receiver positions are fixed; secondary transmitters are independently located in the area, while the secondary receivers positions are placed randomly in a 200 m diameter circle around the respective transmitters. Each secondary user transmits isotropically with 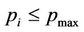 , where
, where 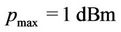 on the base of a fixed interference cap. Moreover, we consider a noise power
on the base of a fixed interference cap. Moreover, we consider a noise power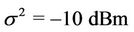 , frequency
, frequency ,
, 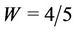 , a common rate
, a common rate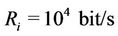 ,
, 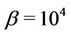 ,
, 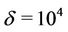 and
and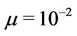 .
.
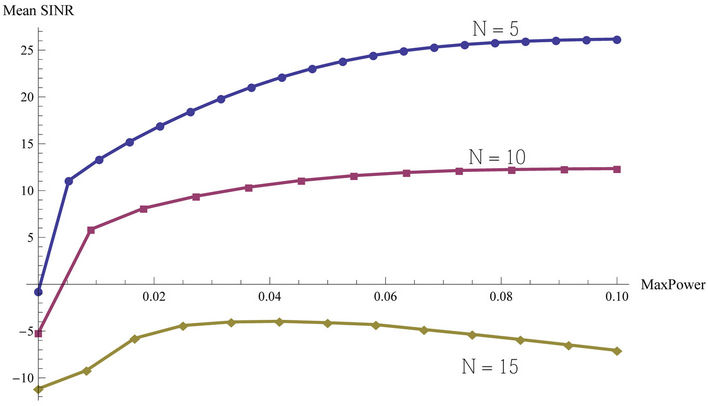
Figure 2. SINR trends for increasing values of maximum transmission power for different number of users.
Results of a simulation with a primary user and  secondary users show a fast convergence of the transmitted power levels and SINR experimented by secondary users. For increasing numbers of secondary users in the networks, the algorithm still maintains a very short time of convergence, see Figure 3; in the particular case of very bad location of secondary users (i.e. users concentrated in a small area), a possible growth of the time convergence may be avoided decreasing the value of
secondary users show a fast convergence of the transmitted power levels and SINR experimented by secondary users. For increasing numbers of secondary users in the networks, the algorithm still maintains a very short time of convergence, see Figure 3; in the particular case of very bad location of secondary users (i.e. users concentrated in a small area), a possible growth of the time convergence may be avoided decreasing the value of  parameter.
parameter.
5.2. Performance Comparison
In order to obtain a qualitative evaluation of the proposed game, we decide to compare its performance with both EEIWF and an optimal centralized heuristic power allocation system, like Simulated Annealing (SA) [19]. The mean value of the SINR (experimented by secondary users) has been chosen as the performance index for the three optimization methods. We run the simulations for

Figure 3. SINR convergence in a 15-user simulation with .
.
increasing number of secondary users, while all the other parameters of the system remain the same of the previous shown configuration. The simulation results illustrated in Figure 4 show clearly that the SA and the proposed game have quite the same performance, since the maximum difference between the mean value of the SINR obtained by the SA and the game is . On the other hand, Water-Filling obtains lower mean SINR levels and performance worsens for increasing number of users in the network.
. On the other hand, Water-Filling obtains lower mean SINR levels and performance worsens for increasing number of users in the network.
In addition to the SINR, the energy efficiency of the three considered methods is an another important key feature that we need to investigate. If the SINR performance are quite the same for the proposed game and the SA, on the contrary we can observe a great difference in terms of power allocations. Indeed, Figure 5 shows that, for a 15-user simulation, SA allocation uses approximately 80% of power more than game allocation. For what concern the EEIWF, while some users are switched off, the others transmit at highest levels, compared with the other two proposed allocations. In Figure 5 the power allocation of the proposed game is shown in purple, in yellow is reported the additional power allocated by SA (with respect to game) and in blue the excess additional power allocated by EEIWF (with respect to SA).
6. Concluding Remarks
In this paper we provide an energy efficient game theoretic framework to solve the resource allocation problem in a cognitive network, wherein primary and secondary users coexist. The power allocation problem is solved thanks to the application of S-Modular Games. Transmission power of secondary users is upper bounded by the interference cap, defined as the total interference

Figure 4. Trends of SINR mean values for increasing number of secondary users in the network; SA in red, Game in blue, EEIWF in green.
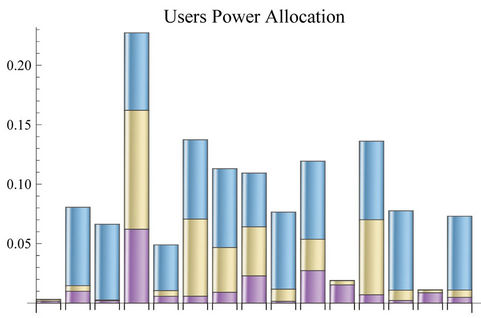
Figure 5. Example of power allocation for a 15 users network; SA in yellow, Game in purple, Water-Filling in blue.
that primary users willing to tolerate, without loosing their required QoS. Moreover, secondary users are discouraged to transmit at high power levels, since they are charged on the base of the interference they generate, thanks to the introduction of a pricing function inside of the utility function. Tuning utility function parameters, the proposed game is able to adapt his performance (in terms of time of convergence) to every kind of network configuration. Indeed, simulation results show a fast convergence of the algorithm for any number of considered users in the cognitive network.
In this work, a performance comparison among the proposed game, an optimal centralized resource allocation method (Simulated Annealing) and an Energy Efficient version of the Water Filling is also included. Simulation results show clearly that game theory obtains better performance than water filling and the proposed game converges to the same SINR values obtained from the heuristic optimization method. However, unlike these, the proposed game results to be the most energy efficient, also for a large number of considered users. Further investigations will be made in order to quantify and analyze the signaling process among secondary users.
7. Acknowledgements
The work presented in this paper is part of the CORASMA project (COgnitive RAdio for dynamic Spectrum MAnagement) promoted the European Defense Agency.
We would like to thank Pierpaolo Piunti for the contribution in Water-Filling algorithm.
REFERENCES
- L. S. Ronga and E. Del Re, “S-Modular Games for Distributed Power Allocation in Cognitive Radio Systems,” Proceedings of the PIMRC 2009, Tokyo, 13-16 September 2009.
- D. M. Topkis, “Equilibrium Points in Nonzero-Sum N- Person Submodular Games,” SIAM Journal on Control and Optimization, vol. 17, No. 5, 1979, pp. 773-778. doi:10.1137/0317054
- B. Wang, Y. Wu and K. J. R. Liu, “Game Theory for Cognitive Radio Networks: An Overview,” Computer Networks, vol. 54, No. 14, 2010, pp. 2537-2561. doi:10.1016/j.comnet.2010.04.004
- R. Luo and Z. Yan, “Power Allocation Using Non-Cooperative Game Theoretic Analysis in Cognitive Radio Networks,” Proceedings of WiCOM, Chengdu, 23-25 September, 2010.
- D. Li, X. Dai and H. Zhang, “Game Theoretic Analysis of Joint Rate and Power Allocation in Cognitive Radio Networks,” International Journal of Communications, Network and System Sciences, Vol. 1, 2009, pp. 1-89. doi:10.4236/ijcns.2009.21001
- G. Bansal, Md. J. Hossian and V. K. Bhargava, “Adaptive Power Loading for OFDM-Based Cognitive Radio Systems,” IEEE Conference on Communications, Glasgow, 24-28 June 2007, pp. 5137-5142. doi:10.1109/ICC.2007.849
- J. Huang, R. Berry and M. L. Honig, “Auction-Based Spectrum Sharing,” ACM/Springer Mobile Networks, 2010.
- C. U. Saraydar, N. B. Mandayam and D. Goodman, “Efficient Power Control via Pricing in Wireless Data Networks,” IEEE Transaction on Communications, Vol. 50, No. 2, 2002, pp. 291-303. doi:10.1109/26.983324
- R. D. Yates, “A Framework for Uplink Power Control in Cellular Radio Systems,” IEEE Journal on Selected Area of Communications, Vol. 13, No. 7, 1995, pp. 1341-1347. doi:10.1109/49.414651
- NATO IST-077 (RTG-035), “Final Technical Activity Report of IST077-RTG035,” Cognitive Radio in NATO, NATO, 2011.
- F. Meshkati, H. V. Poor and S. C. Schwartz, “Energy Efficiency-Delay Tradeoffs in CDMA Networks: A Game Theoretic Approach,” IEEE Transactions on Information Theory, Vol. 55, No. 7, 2009, pp. 3220-3228. doi:10.1109/TIT.2009.2021374
- D. Wu, D. Yu and Y. Cai, ‘Subcarrier and Power Allocation in Uplink OFDMA Systems Based on Game Theory,” Proceedings of IEEE International Conference Neural Networks & Signal Processing, Zhenjiang, 7-11 June 2008.
- C. K. Tan, M. L. Sim and T. C. Chuah, “Fair Power Control for Wireless Ad Hoc Networks Using Game Theory with Pricing Scheme,” IET Communications, Vol. 4, No. 3, 2008, pp. 322-333.
- H. Arslan, “Cognitive Radio, Software Defined Radio, and Adaptive Wireless Systems,” Springer, Berlin, 2007. doi:10.1007/978-1-4020-5542-3
- D. Fudenberg and J. Tirole, “Game Theory,” MIT press, Cambridge, 1991.
- F. Nan, M. Siun-Chuon and N. B. Mandayam, “Pricing and Power Control for Joint Network-Centric and UserCentric Radio Resource Management,” IEEE Transactions on Communications, Vol. 52, No. 9, 2004, pp. 1547- 1557. doi:10.1109/TCOMM.2004.833191
- H. Zhu, Z. Ji and K. J. R. Liu, “Fair Multiuser Channel Allocation for OFDMA Networks Using Nash Bargaing Solutions and Coalitions,” IEEE Transactions on Communications, Vol. 53, No. 8, 2005, pp. 1366-1376. doi:10.1109/TCOMM.2005.852826
- H. Jianwei, R. A. Berry and M. L. Honig, “Game Theoretic Model for Radio Resource Management in HIPERLAN Type 2 Networks,” IEEE Journal in Selected Areas in Communications, Vol. 24, No. 6, 2006, pp. 1074-1084.
- S. Kirkpatrick, et al., “Optimization by Simulated Annealing,” Science, New Series, Vol. 220, No. 4598, 1983, pp. 671-680.

