Communications and Network
Vol.3 No.4(2011), Article ID:8471,15 pages DOI:10.4236/cn.2011.34022
Sequential Tests for the Detection of Voice Activity and the Recognition of Cyber Exploits*
Department of Electrical Engineering, University of Colorado Denver, Denver, USA
E-mail: {ehababdalla.etellisi, Titsa.Papantoni}@ucdenver.edu
Received September 5, 2011; revised October 1, 2011; accepted October 19, 2011
Keywords: Voice Activity Detection, Sequential Detection of Change Test, Cyber Exploits
Abstract
We consider the problem of automated voice activity detection (VAD), in the presence of noise. To attain this objective, we introduce a Sequential Detection of Change Test (SDCT), designed at the independent mixture of Laplacian and Gaussian distributions. We analyze and numerically evaluate the proposed test for various noisy environments. In addition, we address the problem of effectively recognizing the possible presence of cyber exploits in the voice transmission channel. We then introduce another sequential test, designed to detect rapidly and accurately the presence of such exploits, named Cyber Attacks Sequential Detection of Change Test (CA-SDCT). We analyze and numerically evaluate the latter test. Experimental results and comparisons with other proposed methods are also presented.
1. Introduction
Voice Activity Detection (VAD) is deployed extensively, including the Global System for Mobile Communications (GSM), as well as several satellite and radar military and civilian applications, (see in Figure 1). Thus, VAD is an important component of most systems that incorporate digital voice transmissions. During real time voice transmission, periods of voice activity are followed by silence, where both voice and silence periods are imbedded in background noise. Since voice is generally transmitted through fixed bandwidth links, the transmission of the silence periods induces severe bandwidth waste. Voice Activity Detection (VAD) allows for the compression of the silence periods and may result in up to 30 to 40 percent of bandwidth savings.
To detect voice activity versus silence periods, the starting and ending points of continuous speech activity must be detected. Several research efforts have been invested in this area [1-3]. In this paper, we propose a novel VAD algorithm, named Voice Activity Detection using a Sequential Detection of Change Test (SDCTVAD). The algorithm is designed at an independent mixture of Laplacian and Gaussian distributions; it is tracking effectively the boundary points between continuous voice activity and silence time periods, where during silence there is only noise, while during speech there is speech plus noise. The noise and noisy speech are modeled by a “Gaussian” versus “Laplacian plus independent Gaussian” distributions. Results are included for the cases where the SDCT-VAD is applied to detect voice activity, in both the presence and the absence of noise. The algorithm is also tested within a realtime scenario, to exhibit its robustness and low complexity properties.
Figure 1. VAD integrated in a telecommunication system.
Considering the possibility of cyber exploits during voice transmission, we also present a novel cyber attacksequential detection of change Test (CA-SDCT). The CA-SDCT algorithm is deployed during voice activity periods, as detected by the SDCT-VAD algorithm. The proposed CA-SDCA algorithm is designed at the Additive White Gaussian Noise (AWGN) cyber attack model and is fully analysed and numerically evaluated in various environments.
The paper is organized as follows: In Section 2, the SDCT-VAD algorithm is presented. In Section 3, the CA-SDCT algorithm is developed. In Section 4, experimental results are included. In Section 5, we draw some conclusions.
2. Voice Activity Detection Algorithm
The general operation flowchart of the VAD algorithm is depicted by Figure 2. The problem to be solved here is the effective distinction between active and inactive voice periods. However, the variety of both the active voice and the ambient noise make this problem quite complicated in real life.
As shown in Figure 2, first the speech signal is generated and is then corrupted by Additive White Gaussian Noise (AWGN). The AWGN affects the shapes of both the active voice and silence periods. The SDCT-VAD is then applied to detect voice activity periods. As will be further discussed in Section 3, the SDCT-VAD operates on various Signal-to-Noise Ratios (SNRs).
2.1. Speech and Noise Probability Distributions
Throughout this section, we consider two distinct probability density functions (pdfs) which represent the voice and noise amplitude distributions of the proposed model. The two distributions for speech and noise are assumed to be “Laplacian” and “Gaussian”, respectively, as in [4], where different speech distribution models are shown in Figure 3.
Figures 4-5 show noiseless and noisy actual speech signals, respectively.
To decrease algorithmic design complexity, we assume statistical independence between successive voice periods, as well as between signal and noise. We then derive the noisy speech distribution via the convolution of the Laplacian and Gaussian densities. Assuming that the corrupting noise is AWGN, the noisy speech signal is represented below,
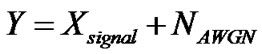 (1)
(1)
where 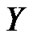 denotes the noisy speech,
denotes the noisy speech, 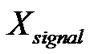 stands for the clean speech and
stands for the clean speech and 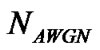 represents the noise, and
represents the noise, and
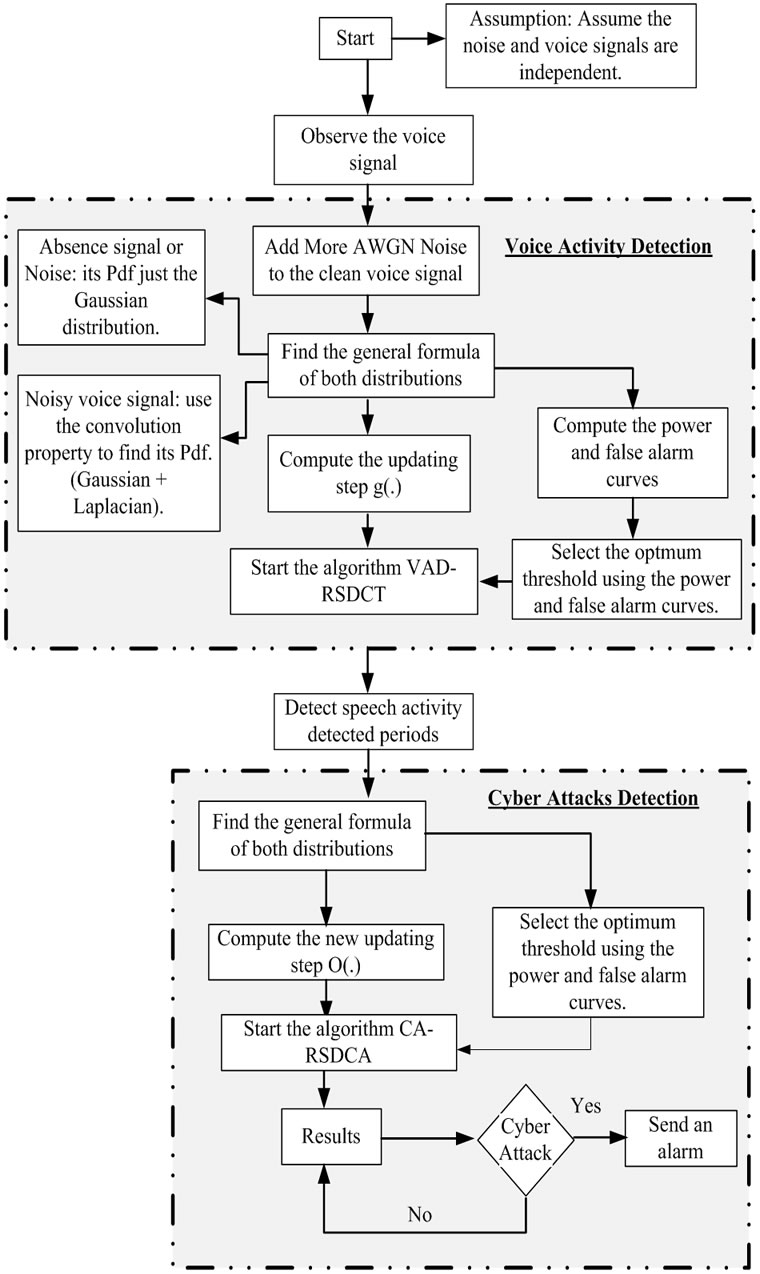
Figure 2. The general operation flowchart of the VAD algorithm.
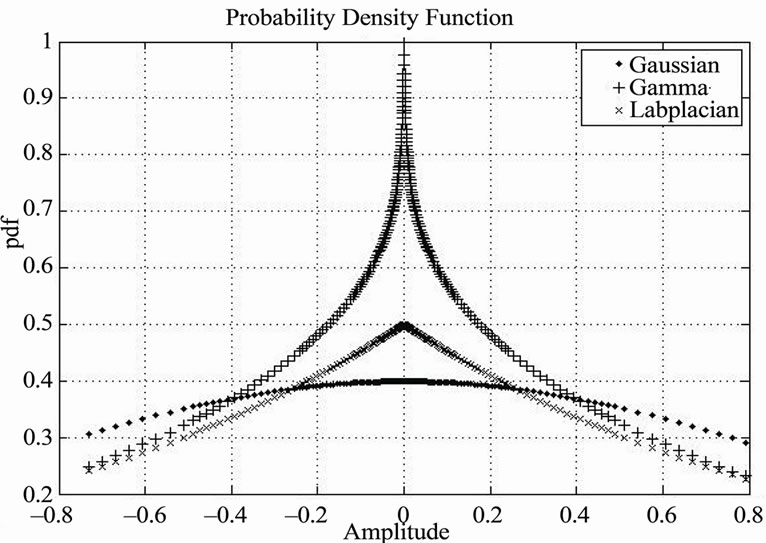
Figure 3. Distributions voice signals.
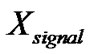 and
and 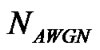 are statistically mutually independent.
are statistically mutually independent.
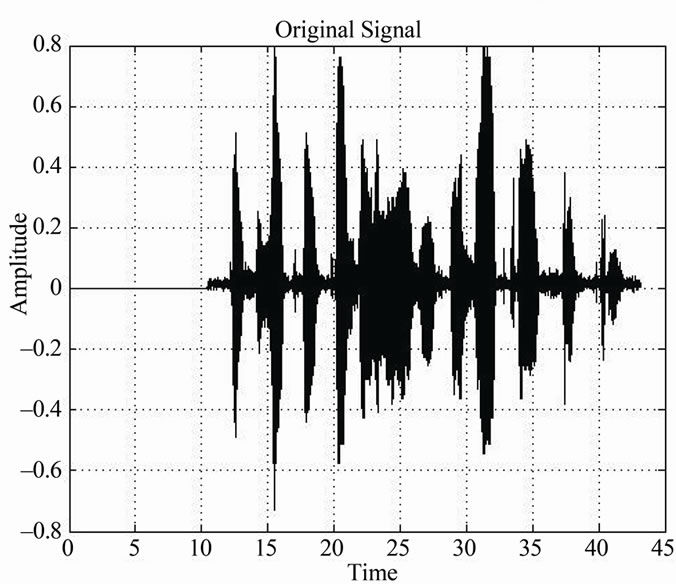
Figure 4. Actual noiseless voice signal “silence + active voice”.
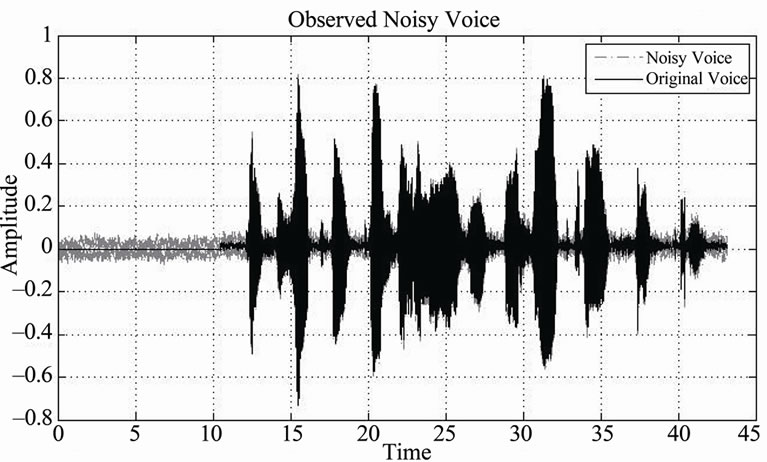
Figure 5. Actual voice “noisy voice signal”.
2.2. The Sequential Test for the Detection of Change
The sequential test for the detection of change, in its general form, was introduced and analyzed in [5-10]. It is assumed that an automated system will be monitoring the signal activity to decide when the voice is active versus not, whose design is based on the detection of change in the data generating stochastic process. The automated system will be implemented via the deployment of the SDCT-VAD algorithm which will be tracking voice to silence and silence to voice shifts, where voice and silence are modeled by two distinct stochastic processes. Below, we first present the general model considered in references [5-10].
Let 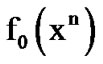 and
and 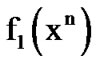 denote the n-dimensional density functions of two well known, distinct, mutually independent discrete-time stochastic processes at the vector point
denote the n-dimensional density functions of two well known, distinct, mutually independent discrete-time stochastic processes at the vector point 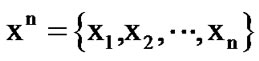 . Let it be known that the active process is initially generated by the density function
. Let it be known that the active process is initially generated by the density function 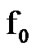 [8]. For the problem addressed, it is assumed that
[8]. For the problem addressed, it is assumed that 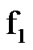 represents the noisy voice process, while
represents the noisy voice process, while 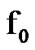 represents the AWGN noisy silence. Given the finite sequence
represents the AWGN noisy silence. Given the finite sequence 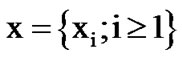 and the density functions
and the density functions 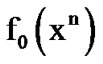 and
and  , the objective is to detect a possible
, the objective is to detect a possible 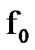 to
to 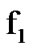 change as reliably and as quickly as possible. To detect a possible such change, select some positive threshold
change as reliably and as quickly as possible. To detect a possible such change, select some positive threshold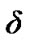 . Then, observe data points sequentially and decide that the
. Then, observe data points sequentially and decide that the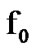 to
to 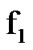 change has occurred the first time
change has occurred the first time 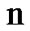 such that
such that 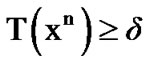 , where
, where
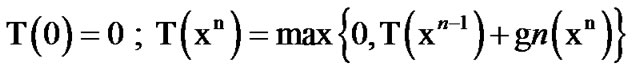 (2)
(2)
Where
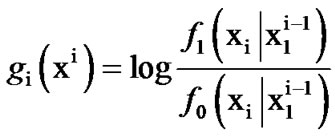
The above algorithm operates sequentially via the use of two thresholds, 0 and 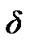 , where 0 represents a reflecting barrier and
, where 0 represents a reflecting barrier and 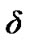 represents an absorbing or decision barrier [8].
represents an absorbing or decision barrier [8].
When the two stochastic processes represented by the density functions 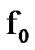 and
and 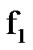 are memoryless, then the conditioning in the log likelihood in (2) drops and the algorithmic operations are memoryless as well. A symmetric algorithm that detects a shift from
are memoryless, then the conditioning in the log likelihood in (2) drops and the algorithmic operations are memoryless as well. A symmetric algorithm that detects a shift from 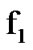 to
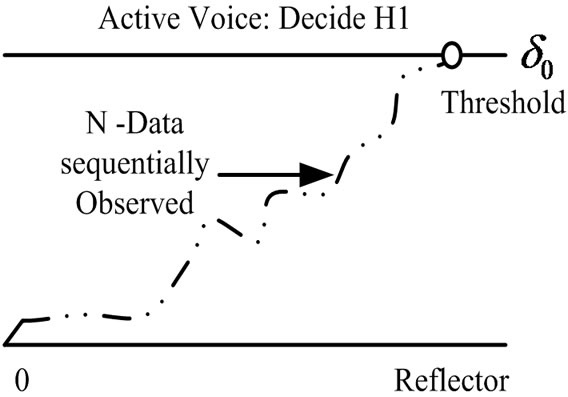
to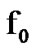 , instead, can be easily derived. In Figure 6, the timeevolution of both algorithms is depicted.
, instead, can be easily derived. In Figure 6, the timeevolution of both algorithms is depicted.
 (a)
(a)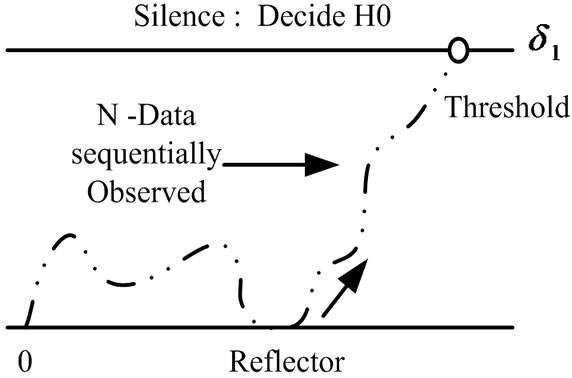 (b)
(b)
Figure 6. Making the final decision in the first crossing to the threshold, Detecting change (a) from 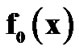 to
to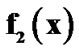 , (b) from
, (b) from 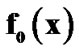 to
to 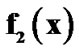 .
.
2.3. The SDCT-VAD Using Laplacian and Gaussian Distributions
Let 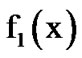 and
and 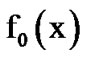 represent the density functions of a single datum x from noisy voice versus just noise, respectively. Let it be desirable to detect a possible change from
represent the density functions of a single datum x from noisy voice versus just noise, respectively. Let it be desirable to detect a possible change from 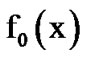 to
to 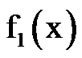 , where
, where 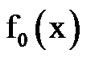 is Gaussian and
is Gaussian and 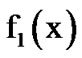 is Laplacian plus Gaussian. The assumption here is that the observed voice process is stationary, memoryless and Laplacian, while the noise process is independent from the voice process and AWGN. Then,
is Laplacian plus Gaussian. The assumption here is that the observed voice process is stationary, memoryless and Laplacian, while the noise process is independent from the voice process and AWGN. Then,
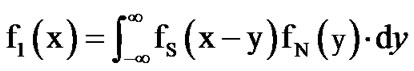 (3)
(3)
where  is the Laplacian distribution that represents the voice speech, and
is the Laplacian distribution that represents the voice speech, and 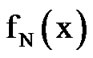 is the Gaussian distribution representing the AWGN.
is the Gaussian distribution representing the AWGN.
 (4)
(4)
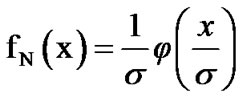 (5)
(5)
where 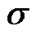 denotes the standard deviation of the Gaussian distribution. We now derive the expression
denotes the standard deviation of the Gaussian distribution. We now derive the expression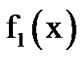 :
:
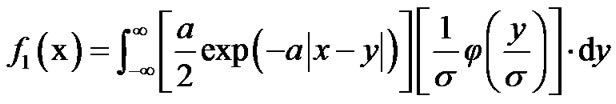
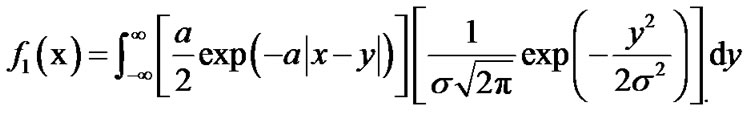
Alternatively, the distribution  can be expressed as follows,
can be expressed as follows,
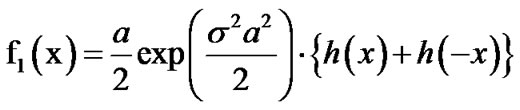 (6)
(6)
where
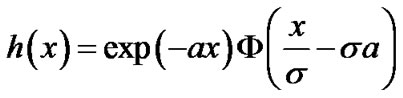
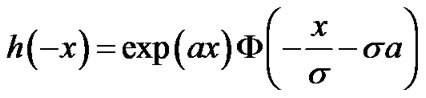
We then compute the log likelihood ratio updating step in the sequential test:
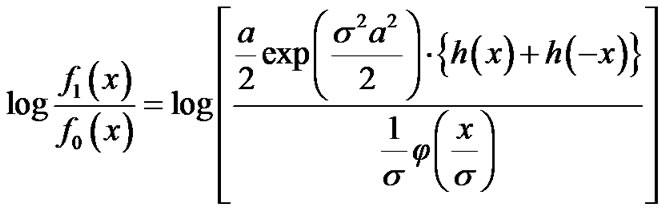

The algorithmic updating step can be written as:
 (7)
(7)
where
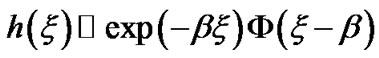
The algorithmic step may be subsequently modified as follows
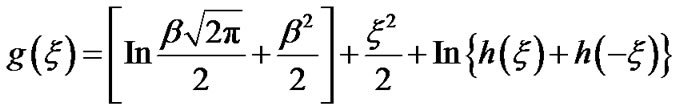 (8)
(8)
where
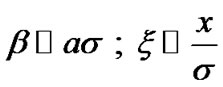
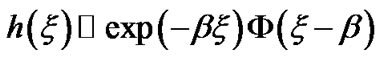
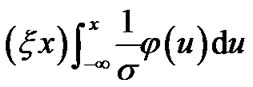
and
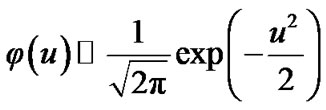
and where the Signal to Noise Ratio (SNR) is:
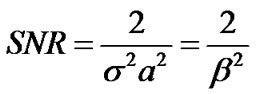
From the last equation, it can be recognized that the Signal-to-Noise Ratio (SNR) is a function of both the Laplacian constant 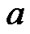 and the standard deviation
and the standard deviation 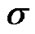 of the noise. To develop a robust method for tracking the noise and speech signals, in Section 2.4, we will test the use of different SNRs in the design of the algorithm. In Figure 7, we plot the SNR as a function of a, for various values of the standard deviation s of the noise.
of the noise. To develop a robust method for tracking the noise and speech signals, in Section 2.4, we will test the use of different SNRs in the design of the algorithm. In Figure 7, we plot the SNR as a function of a, for various values of the standard deviation s of the noise.
Let us now select some positive threshold d and define:
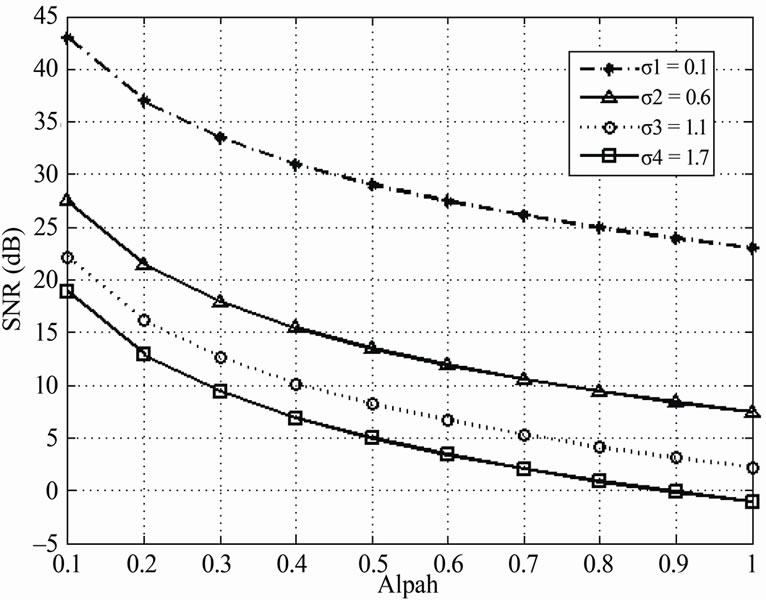
Figure 7. Signal-to-Noise Ratio (SNR).
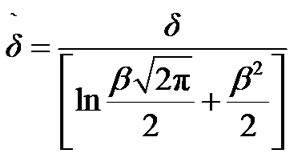
We may then modify the algorithm in (2), as manifested by the distributions derived in this section, via scaling, resulting in the following operation: Observe data sequentially and decide that the change from noise to voice activity has occurred the first time instant n such that 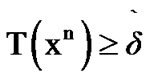 , where
, where
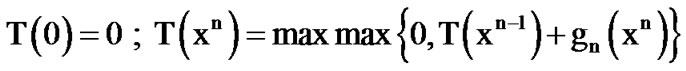
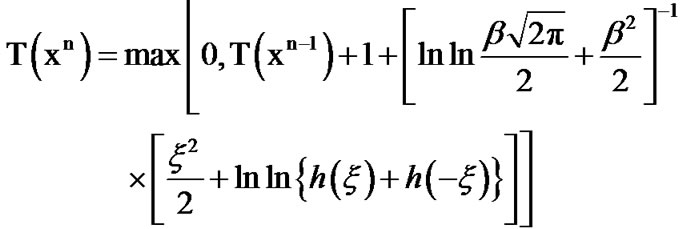 (10)
(10)
We note that the algorithm in (10) detects change from silence to active voice. The algorithm that detects change from active voice to silence, instead, is similarly derived, where its recursively derived algorithmic values are given by the expression in (12) below and where its decision threshold is generally different than that of the algorithm in (10).
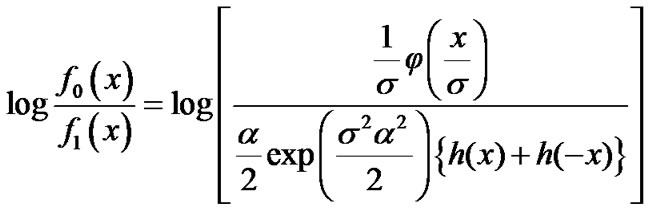 (11)
(11)
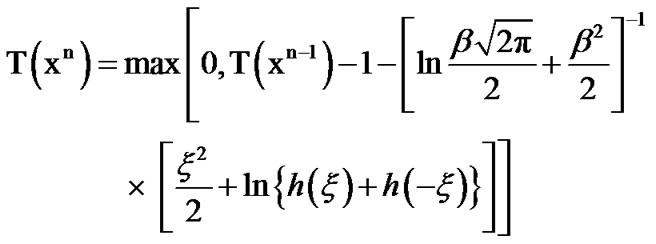 (12)
(12)
2.4. Power and False Alarm Curves for Threshold Values Selections
In this section, we present algorithmic performance criteria and their use in the selection of the decision thresholds. We specifically evaluate power and false alarm curves induced by the two algorithms in Section 2.3 for several given decision thresholds. We then compare such curves for different threshold values, to subsequently decide on the values of the operational algorithmic thresholds. Let us define• 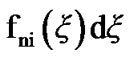 : The probability that at time n the algorithm has not crossed the threshold,
: The probability that at time n the algorithm has not crossed the threshold,  and its value lies in
and its value lies in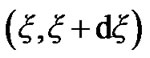 , given that the acting pdf is fi; where, the recursive expression below can be derived,
, given that the acting pdf is fi; where, the recursive expression below can be derived,
 (13)
(13)
• The probabilities 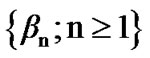 represent a power set• The probabilities
represent a power set• The probabilities 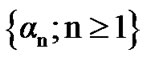 represent a false alarm set.
represent a false alarm set.
The main objective here is to find the threshold  that induces low false alarm and high power for small sample sizes. To compute the power and false alarm curves, as induced by the probability sequences
that induces low false alarm and high power for small sample sizes. To compute the power and false alarm curves, as induced by the probability sequences 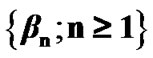 and
and , respectively, we need to analyse the characteristics of the updating step shown in Equation (8). This process is explained in the Appendix, where the expressions for the computation of the sequences
, respectively, we need to analyse the characteristics of the updating step shown in Equation (8). This process is explained in the Appendix, where the expressions for the computation of the sequences 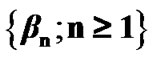 and
and  are also derived.
are also derived.
Given threshold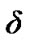 , the silence mode to active voice mode change detecting algorithm is basically characterized by two time curves: the power and false alarm curves, denoted respectively
, the silence mode to active voice mode change detecting algorithm is basically characterized by two time curves: the power and false alarm curves, denoted respectively 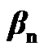 and
and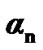 , respectively, where n denotes time instant and where,
, respectively, where n denotes time instant and where,
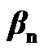 : The probability that the silence to active voice mode change detecting algorithm crosses its threshold before or at time n, given that the operation mode is active voice mode throughout [6].
: The probability that the silence to active voice mode change detecting algorithm crosses its threshold before or at time n, given that the operation mode is active voice mode throughout [6].
 : The probability that the silence to active voice mode detecting algorithm crosses its threshold before or at time n, given that the operational mode is silence mode throughout [6].
: The probability that the silence to active voice mode detecting algorithm crosses its threshold before or at time n, given that the operational mode is silence mode throughout [6].
When the algorithm that monitors change from mode silence to mode voice is considered, the threshold 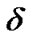 may be selected based on the following principle: At given time n , have the powers induced by the parallel algorithms be above a predetermined lower bound, while the false alarm induced by each algorithm remains below a predetermined upper bound. The threshold for the algorithm that monitors change from voice to silence, instead, is selected similarly.
may be selected based on the following principle: At given time n , have the powers induced by the parallel algorithms be above a predetermined lower bound, while the false alarm induced by each algorithm remains below a predetermined upper bound. The threshold for the algorithm that monitors change from voice to silence, instead, is selected similarly.
In Figure 8, we depict the 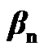 and
and 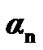 representative
representative
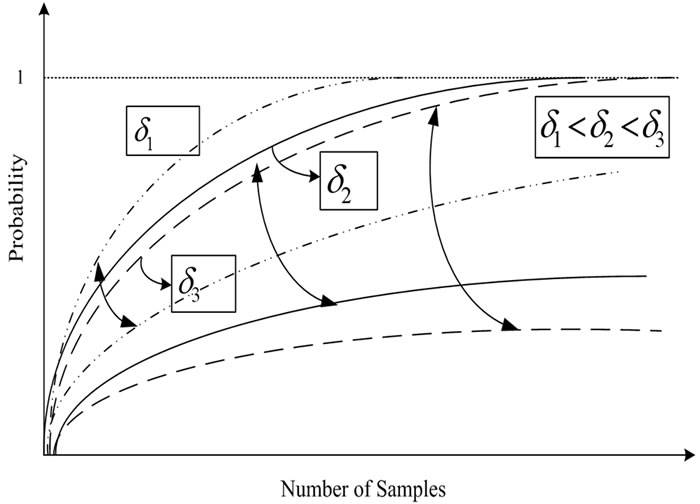
Figure 8. Power and false alarm curves vs different thresholds.
curves, to observe and discuss qualitative characteristics. We plot these curves for two different threshold values. From the figure, we note that as the value of the decision threshold increases, the false alarm curve decreases, but so does the power curve. The threshold selection for the silence to active voice change monitoring algorithm may be based on a required lower bound for the power and a required upper bound for the false alarm, at a given time instant n. A similar criterion may be adopted in the threshold selection for the active voice to silence monitoring algorithm.
3. An Algorithm for Detecting Cyber Attacks during Speech Activity
In this section, we consider the case where the voice transmission channel may be vulnerable to cyber exploits. We then focus on developing an automated system that, in concurrence with voice activity detection, also detects cyber exploit activities. We thus develop a Cyber AttackSequential Detection of Change Test (CA-SDCT), designed to detect cyber attacks during voice activity periods, as the latter are detected by the SDCT-VAD algorithm in Section 2. The block diagram of the overall system is depicted in Figure 2, Section 2. As shown in Figure 2, first the speech signal is generated and is then corrupted by additive white Gaussian noise (AWGN). The SDCT-VAD is then deployed to distinguish between voice activity and silence periods. We finally wish to detect possible cyber attacks during voice activity periods.
As in Section 2.2, let 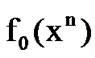 and
and 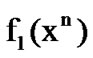 denote the n-dimensional density functions of two well known, distinct, mutually independent discrete-time stochastic processes at the vector point
denote the n-dimensional density functions of two well known, distinct, mutually independent discrete-time stochastic processes at the vector point . For the problem addressed here,
. For the problem addressed here, 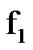 represents the process of cyber exploits superimposed on noisy voice activity, while
represents the process of cyber exploits superimposed on noisy voice activity, while  represents the noisy voice activity process in the absence of cyber attacks. Given the infinite sequence
represents the noisy voice activity process in the absence of cyber attacks. Given the infinite sequence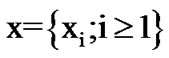 , let the n-dimensional density functions be denoted
, let the n-dimensional density functions be denoted 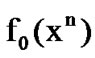 and
and . The objective is to detect a possible
. The objective is to detect a possible 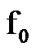 to
to 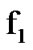 change as reliably and as quickly as possible, utilizing the observed data sequences. The sequential operation of the two algorithms is depicted in Figure 9.
change as reliably and as quickly as possible, utilizing the observed data sequences. The sequential operation of the two algorithms is depicted in Figure 9.
As in Section 2.2, we first select some positive threshold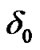 . Subsequently, we observe noisy voice data sequentially, during voice activity periods detected by the SDCT-VAD, and decide that the
. Subsequently, we observe noisy voice data sequentially, during voice activity periods detected by the SDCT-VAD, and decide that the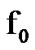 to
to  change has occurred, the first time
change has occurred, the first time 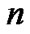 such that
such that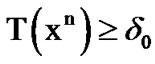 , where
, where
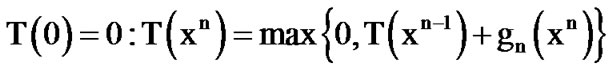 (14)
(14)
where
 (a)
(a)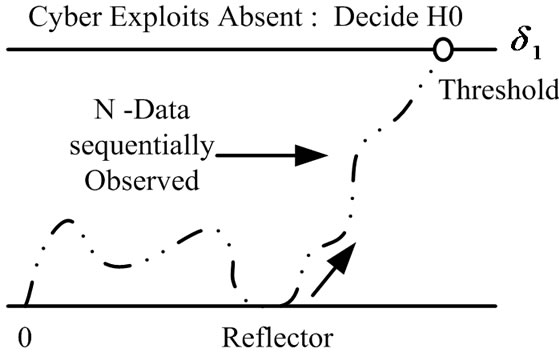 (b)
(b)
Figure 9. Making the final decision in the first crossing to the threshold. (a) Cyber Exploits Present, denoted H1; (b) Cyber Exploits Absent, denoted H0.
A similar algorithm may be devised for the detection of shifts from  to
to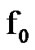 , instead.
, instead.
We model the presence of cyber exploits by Additive White Gaussian Noise (AWGN) that is superimposed on the transmission channel AWGN, resulting in relatively excessive cumulative white noise. When the two stochastic processes represented by the density functions 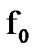 and
and 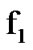 are memoryless, the conditioning in the log likelihood in (14) drops and the algorithmic operations are memoryless as well. As directly deduced from Section 2.3, in the present case we have:
are memoryless, the conditioning in the log likelihood in (14) drops and the algorithmic operations are memoryless as well. As directly deduced from Section 2.3, in the present case we have:
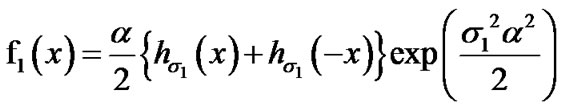 (15)
(15)
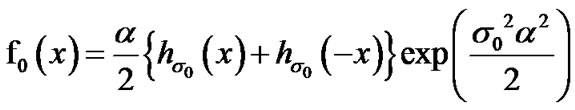 (16)
(16)
where,
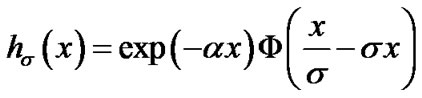
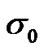 : Standard deviation of the transmission noise, in the absence of cyber exploits.
: Standard deviation of the transmission noise, in the absence of cyber exploits.
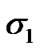 : Standard deviation of the cumulative noise when cyber exploits are added to the transmission noise.
: Standard deviation of the cumulative noise when cyber exploits are added to the transmission noise.
Then,
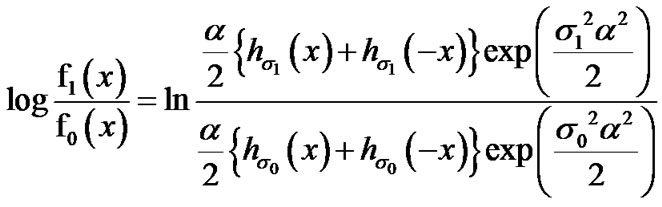
or,
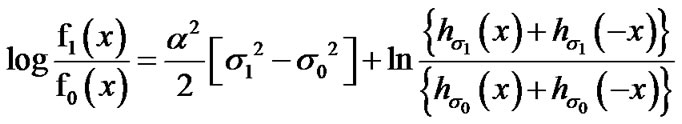 (17)
(17)
The implementation of the cyber exploits detection algorithm is then as follows:
During voice activity periods, as detected by the SDCTVAD algorithm, observe data sequentially and decide that the change from absence to presence of cyber exploits has occurred, the first time instant n such that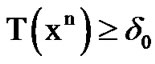 , where Equation (18).
, where Equation (18).
We note that the algorithm in (18) detects a 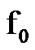 to
to  change. The algorithm that detects a
change. The algorithm that detects a 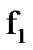 to
to 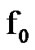 change, instead (from presence to absence of cyber exploits), is similarly derived, where its recursively derived algorithmic values are given by the expression in (19) below and where its decision threshold,
change, instead (from presence to absence of cyber exploits), is similarly derived, where its recursively derived algorithmic values are given by the expression in (19) below and where its decision threshold, 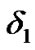 is generally different than that of the algorithm in (18), as shown in Figure 9.
is generally different than that of the algorithm in (18), as shown in Figure 9.
4. Experimental Results
4.1. Testing the SDCT-VAD
In this section, we state the steps involved in the numerical evaluation of the SDCT-VAD algorithm. First, we select the pertinent involved parameters and deploy the resulting SDCT-VAD algorithm, to detect any voice activity in the communication link. Then, the SDCTVAD is evaluated in various noisy environments. In our simplified model, the silence plus noise mode of operation is assumed to be represented by a Gaussian distribution, while the noisy voice signal is represented by a mixture of Laplacian and Gaussian distributions, as shown in Figure 10. The pertinent parameters to be chosen in the SDCT-VAD design are the Laplacian parameter, the standard deviation of the Gaussian noise and the two algorithmic thresholds: A threshold 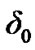 used by the algorithm in (10); for the detection of change from noise to noisy voice activity, and a threshold
used by the algorithm in (10); for the detection of change from noise to noisy voice activity, and a threshold 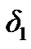 used by the algorithm in (12); for the detection of change from noisy active voice to just noise. We used the power and false alarm curves discussed in Section 2.4, to decide on the values of these two thresholds. In particular, we selected the (
used by the algorithm in (12); for the detection of change from noisy active voice to just noise. We used the power and false alarm curves discussed in Section 2.4, to decide on the values of these two thresholds. In particular, we selected the (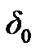 ,
,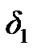 ,
,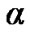 ,
, ) values (0.3, 0.05, 0.98, 0.0523).
) values (0.3, 0.05, 0.98, 0.0523).
We used the design parameter values (0.3, 0.05, 0.98, 0.0523) and tested the robustness of the resulting SDCT-VAD algorithm in the presence of various noisy environments. Various noises were mixed with the clean speech signals. Six different noises were used in our evaluations, including white noise, wind, computer fan, babble, flowing traffic and train passing. Figure 11 exhibits the various noise types, while Figures 12 and 13 show the effect of such noises when superimposed on the original noisy speech signal in Figure 10.
For comparison, the same voice and noise environments are also tested by the approach presented in [2] and the G.729 VAD algorithm in [11]. The results are summarized in Tables 1 and 3. The noise data are obtained from http://www.freesound.org/index.php and are added to the clean speech signal at SNRs varying from 5 dB to 25 dB.
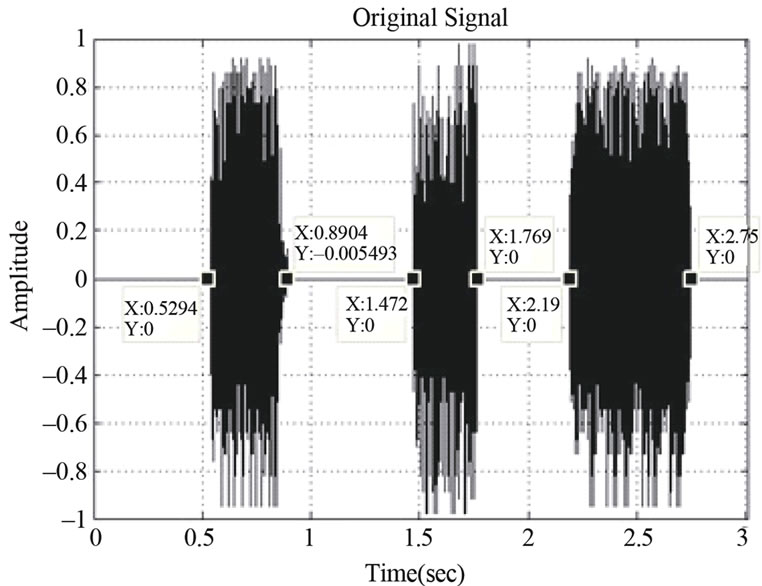
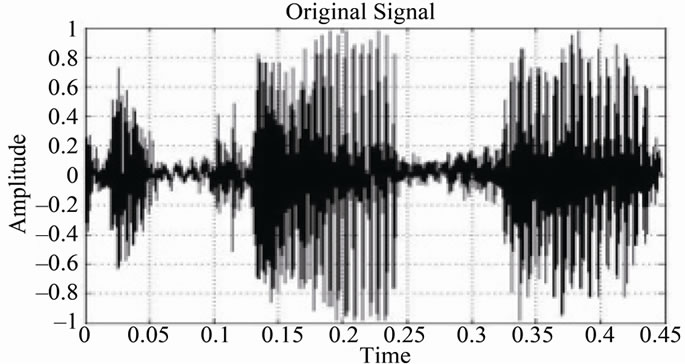
Figure 10. Original voice signal.
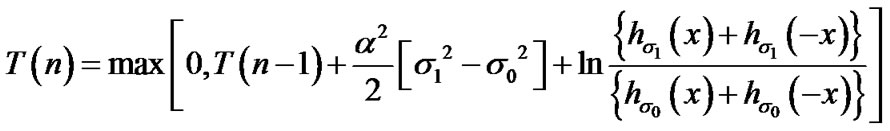 (18)
(18)
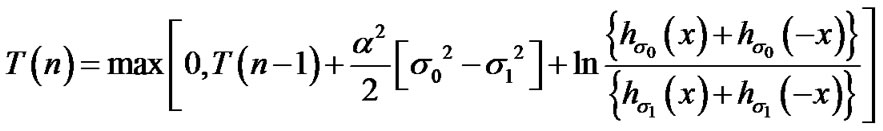 (19)
(19)
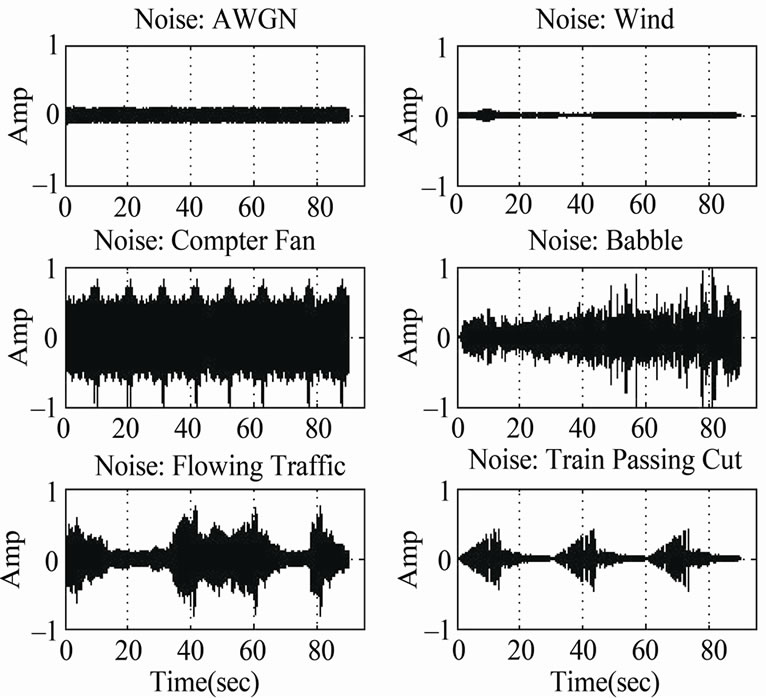
Figure 11. Various noisy environments.
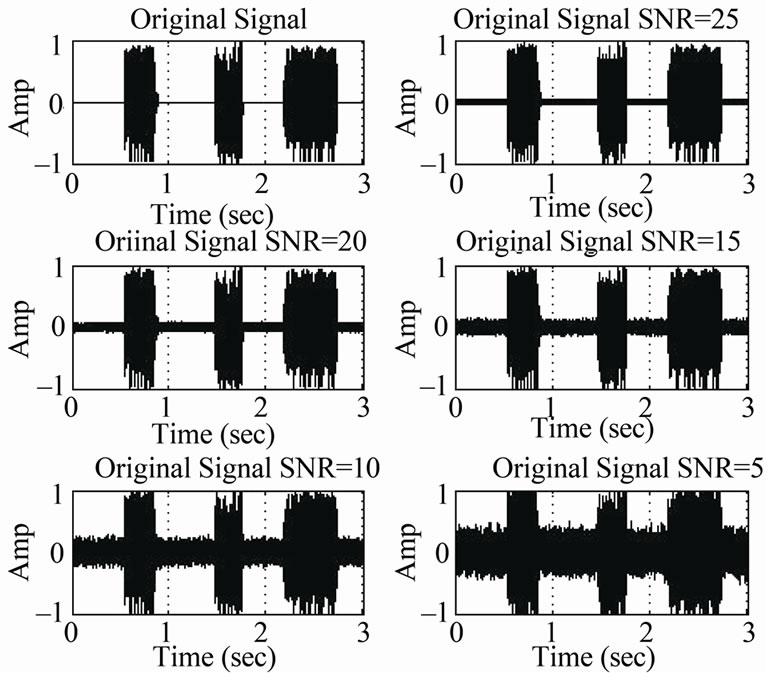
Figure 12. Original signal corrupted by AWGN “SNR = 25, 20, 15, 10 and 5 dB”.
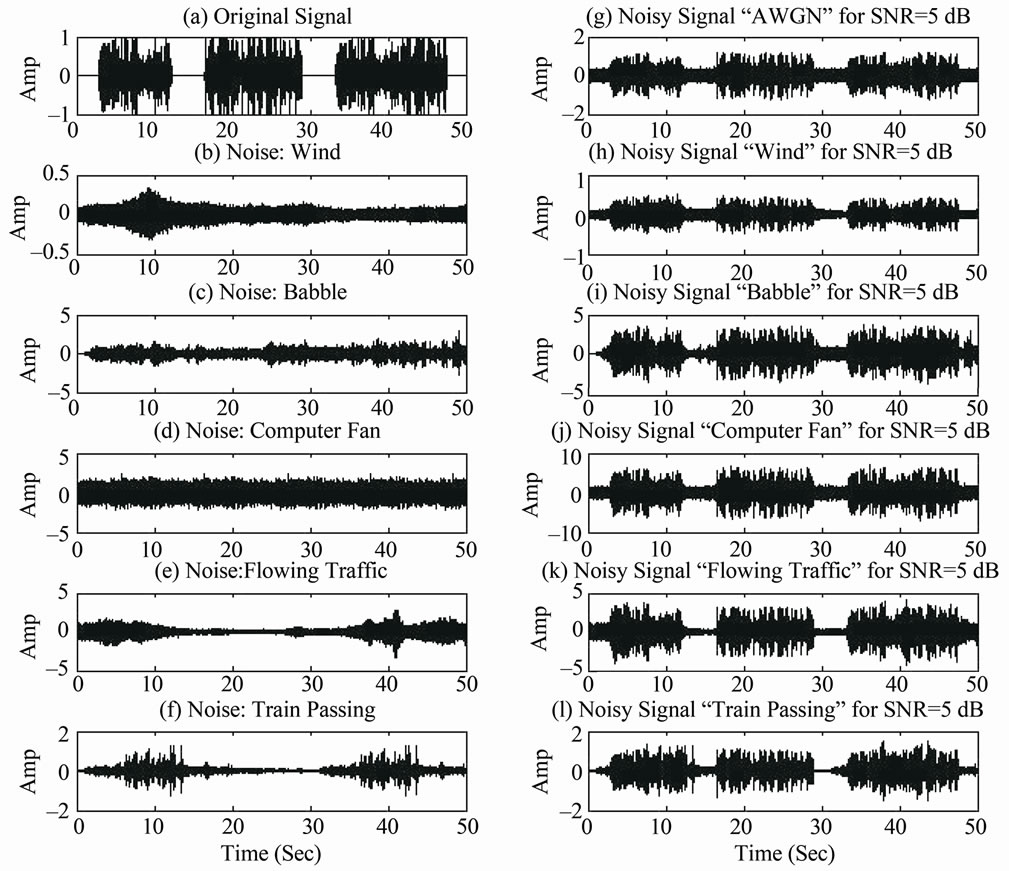
Figure 13. Results of adding noise to the original speech signal (5 dB SNR). (a) Clean speech; (b) Wind noise; (c) Babble noise; (d) Computer fan noise; (e) Flowing traffic; (f) Train passing noise; (g) Noisy signal “noise: AWGN”; (h) Noisy signal “noise: wind”; (j) Noisy signal “noise: computer fan”; (k) Noisy signal “noise: flowing traffic”; (l) Noisy signal “noise: train passing cut”.
To empirically evaluate the SDCT-VAD algorithm, many audio messages were used, with different lengths, (3 sec and 50 sec), with both male and female speakers and with different SNRs, (5 dB - 25 dB). The effect of these SNRs on the audio messages is exhibited in Figure 12, where Figure 10 exhibits the original speech signal.
To empirically evaluate the SDCT-VAD algorithm, many audio messages were used, with different lengths, (3 sec and 50 sec), with both male and female speakers and with different SNRs, (5 dB - 25 dB). The effect of these SNRs on the audio messages is exhibited in Figure 12, where Figure 10 exhibits the original speech signal.
Figures 14 and 15 below show results for the SDCTVAD algorithm with operating parameters as those stated in this Section, when the SNR is 25 dB and 5 dB, respectively.
The accuracy of the results depends on the level of the SNRs and the type of the noise environment, as shown in Tables 1 and 2.

Figure 14. SDCT-VAD results “original voice signal corrupted by AWGN (SNR = 25 dB)”.

Figure 15. SDCT-VAD results “original voice signal corrupted by AWGN (SNR = 5 dB)”.
The efficiency of the SDCT-VAD algorithm was evaluated for various noisy voice signals. In the first experiment, we tested the efficiency of the proposed method using the same audio recording discussed above, tracing the speed and the accuracy of the algorithm in detecting the silence mode to active mode change and vice verse.
To comparatively evaluate the performance of the proposed SDCT-VAD algorithm, we compared its induced results with those of the manual segmentation. Figure 10 exhibits the “hand-marked” results of manual segmentation. Figures 14 and 15 exhibit the automated segmentation induced by the SDCT-VAD proposed algorithm. We evaluated the algorithmic probability of error (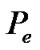 ), using the formula below:
), using the formula below:

(20)
AV: Active Voice;
AVSP: Active Voice Starting Point;
AVEP: Active Voice Ending Point;
N: Number of Active Voice Regions.
The performance of the SDCA-VAD is evaluated in terms of probability of false and correct decisions, where 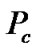 is the probability of correct speech classification and where
is the probability of correct speech classification and where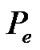 , is the probability of false speech classification, computed as in (20).
, is the probability of false speech classification, computed as in (20).
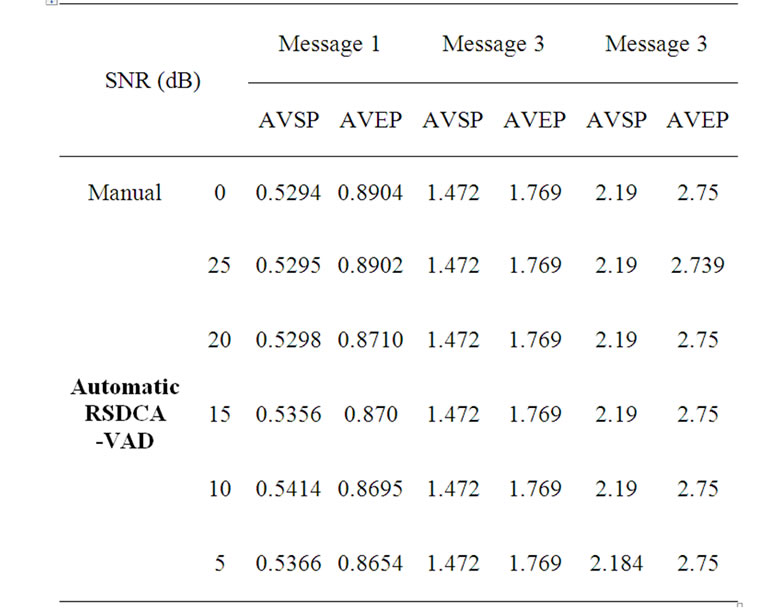
Table 1. Comparing the starting and ending detection time instances of the noisy active voice messages using the manual and proposed method.
To compute  we start with known voice activity and the starting and ending points of voice activity marked. We then superimpose AWGN voice contamination with various SNRs (25, 20, 15, 10 and 5 dB) and deploy the corresponding SDCT-VAD for various noisy environments, as shown in Figures 11-13. Results comparing the SDCT-VAD with the manual approach are shown in Table 1.
we start with known voice activity and the starting and ending points of voice activity marked. We then superimpose AWGN voice contamination with various SNRs (25, 20, 15, 10 and 5 dB) and deploy the corresponding SDCT-VAD for various noisy environments, as shown in Figures 11-13. Results comparing the SDCT-VAD with the manual approach are shown in Table 1.
In Figures 16 and 17 we plot the  and
and  results included in Table 2.
results included in Table 2.
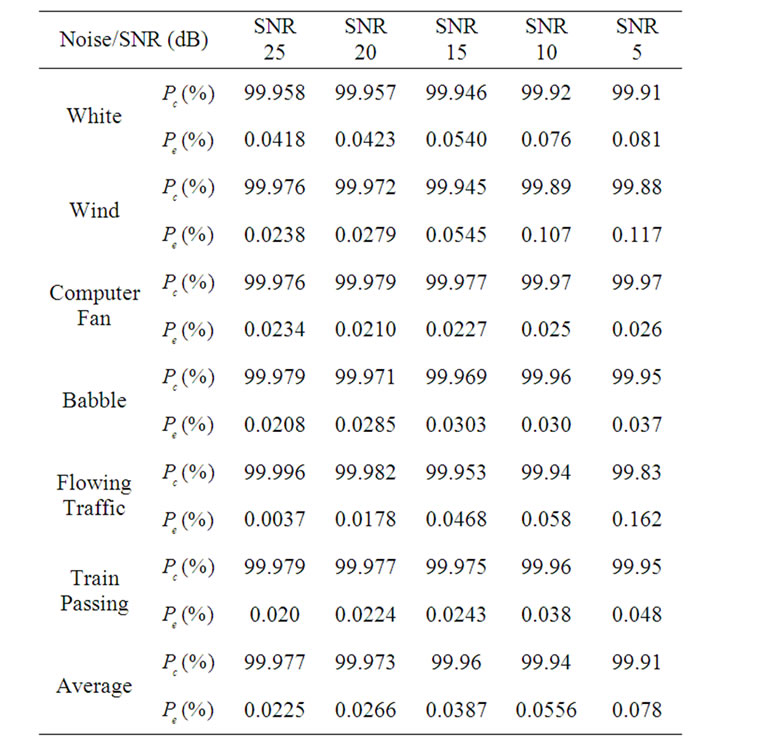
Table 2.  and
and  of the proposed RSDCA-VAD for various environmental conditions.
of the proposed RSDCA-VAD for various environmental conditions.
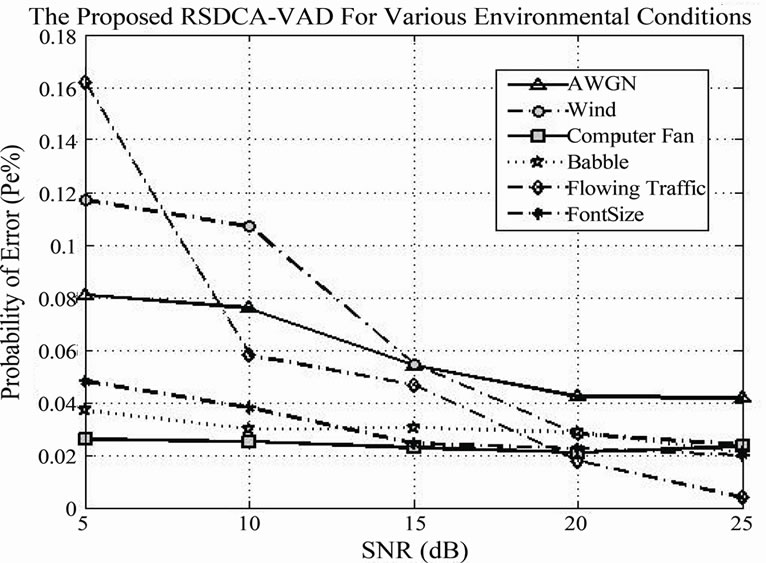
Figure 16. 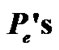 of the proposed RSDCA-VAD in various environmental conditions.
of the proposed RSDCA-VAD in various environmental conditions.
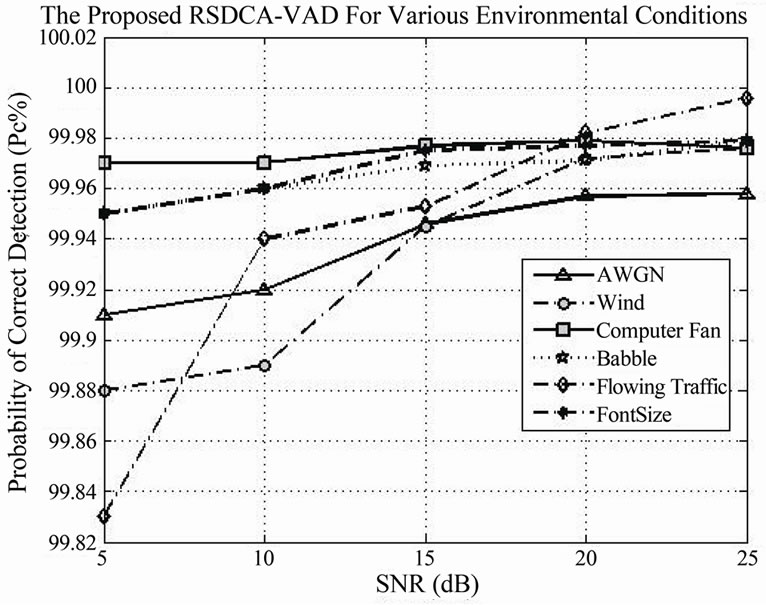
Figure 17. 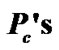 of the proposed RSDCA-VAD in various environmental conditions.
of the proposed RSDCA-VAD in various environmental conditions.
To further validate the effectiveness of the proposed SDCT-VAD, we compared its probabilities of correct speech activity detection with those of other approaches. Table 3 shows a comparison between the SDCT-VAD and two different VAD approaches: the G.729 in [11] and the proposed method in [2].
The clean speech signal that has length of 50 sec, 60.05% speech and 39.95% silence, was used to evaluate the proposed algorithm against various environmental conditions and to compare it with the ITU standard G729 Annex B [11] and the proposed in [2] approaches.
From Table 3, it can be recognized that even with environmental challenging conditions, the proposed SDCTVAD outperformed the G729B VAD and the method in [2].
4.2. Testing the CA-SDCT
As stated in Section 3, to detect shifts from absence to presence of cyber exploits and vice versa using the CA-SDCT algorithm, two algorithmic decision thresholds are needed: A threshold 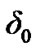 used by the algorithm in (18); for the detection of change from Cyber exploits absent to Cyber exploits present, and a threshold
used by the algorithm in (18); for the detection of change from Cyber exploits absent to Cyber exploits present, and a threshold 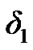 used by the algorithm in (19); for the detection of change from Cyber exploits present to Cyber exploits absent. It is assumed that the cyber attack is represented by AWGN. We tested the original signal and its noisy versions, as those exhibited in Figure 18. Using the power and false alarm curves, as with the SDCT-VAD algorithm, we selected the pertinent thresholds. In particular, we selected the (
used by the algorithm in (19); for the detection of change from Cyber exploits present to Cyber exploits absent. It is assumed that the cyber attack is represented by AWGN. We tested the original signal and its noisy versions, as those exhibited in Figure 18. Using the power and false alarm curves, as with the SDCT-VAD algorithm, we selected the pertinent thresholds. In particular, we selected the (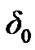 ,
,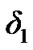 ,
,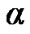 ,
,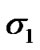 ) design values (0.07, 0.01, 0.98, 0.0773), while we tested the s2 values (0.0798, 0.0849, 0.1034), to evaluate the robustness of the resulting CA-SDCT algorithm.
) design values (0.07, 0.01, 0.98, 0.0773), while we tested the s2 values (0.0798, 0.0849, 0.1034), to evaluate the robustness of the resulting CA-SDCT algorithm.
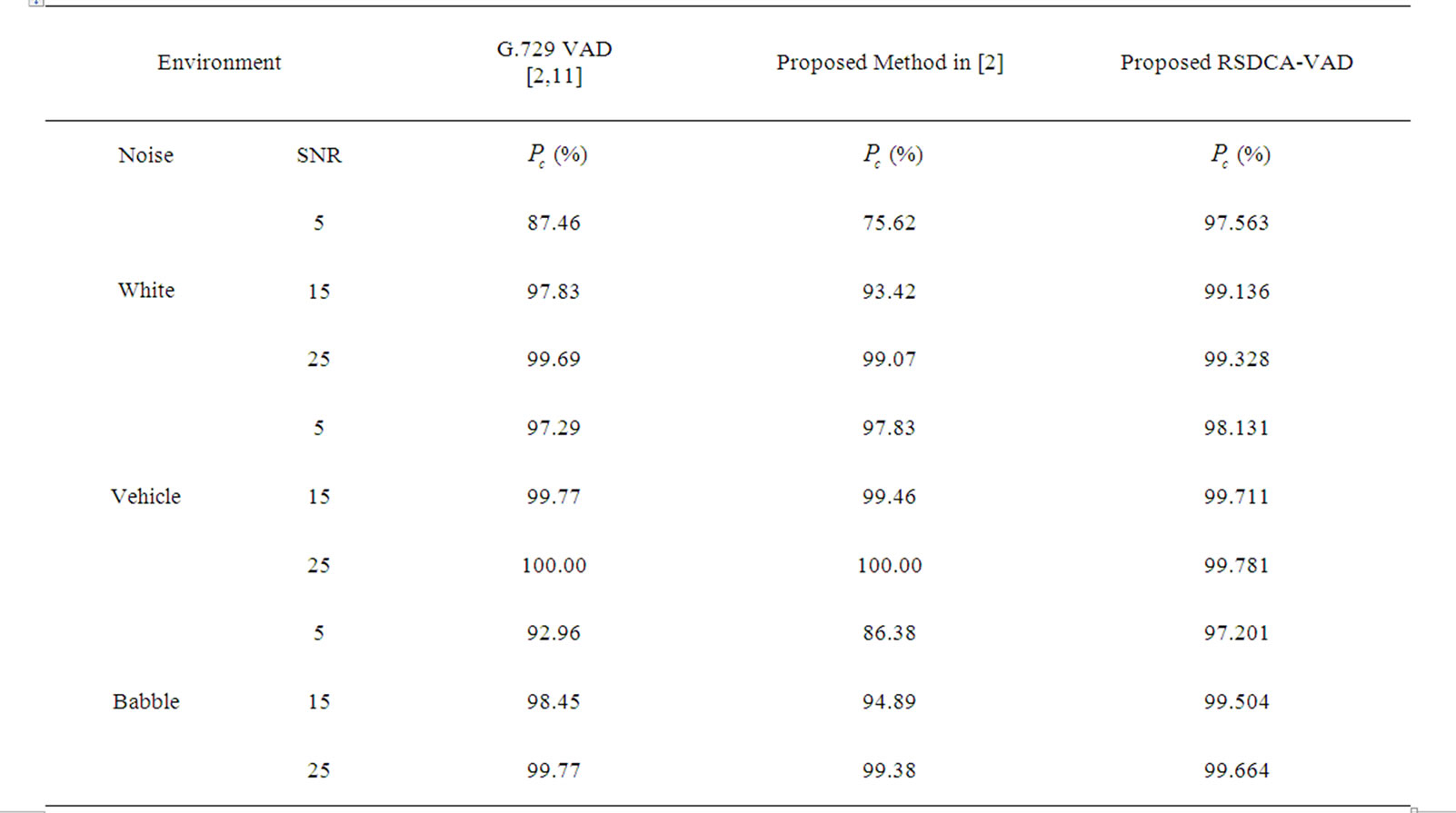
Table 3.  of the proposed RSDCT-VAD, and different VAD approaches for various environmental conditions.
of the proposed RSDCT-VAD, and different VAD approaches for various environmental conditions.
 (a)
(a)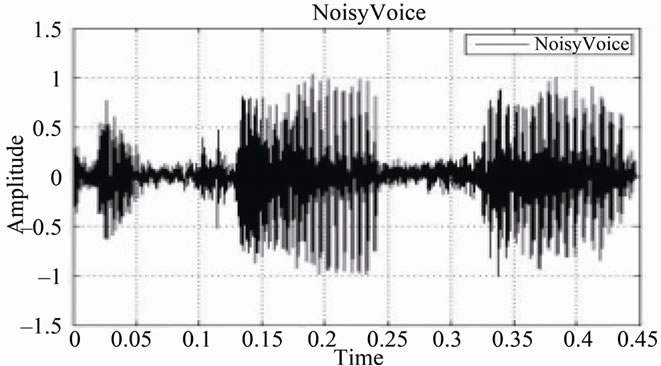 (b)
(b) (c)
(c)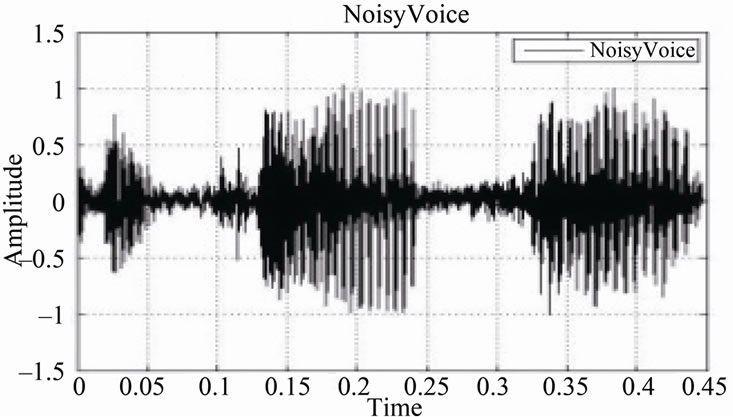 (d)
(d)
Figure 18. (a) Original signal; (b) Noisy signal with SNR = 15 dB; (c) Noisy signal with SNR = 10 dB; (d) Noisy signal with SNR = 5 dB.
 (a)
(a)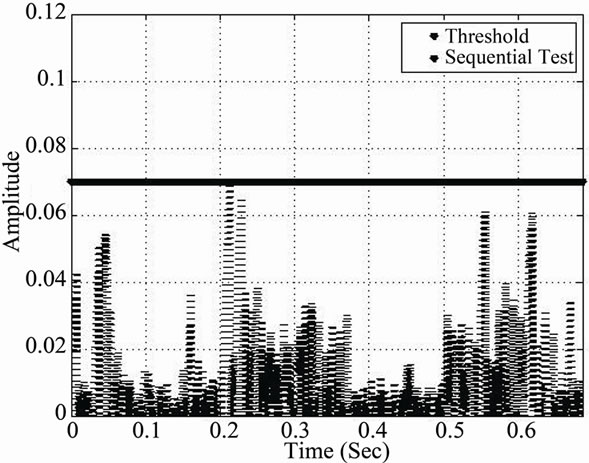 (b)
(b)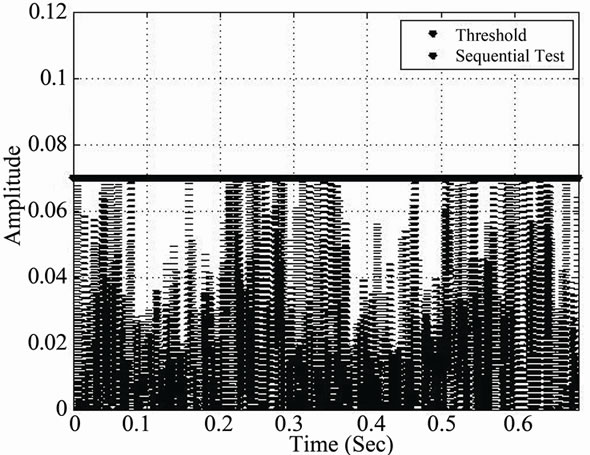 (c)
(c)
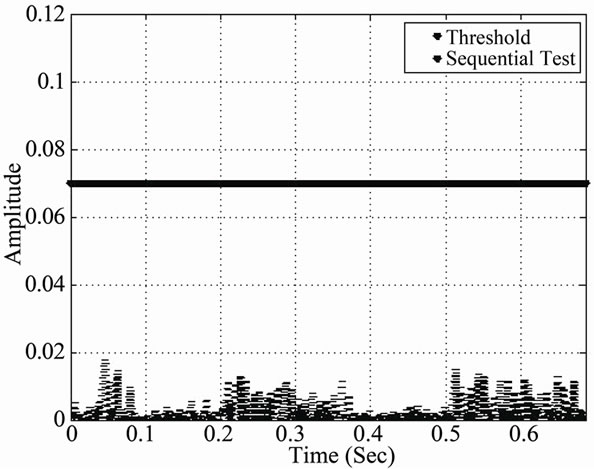
Figure 19. Cyber detection during speech activity detected periods using the CA-SDCT. (a) Sequential test: SNR = 15; (b) Sequential test: SNR = 10; (c) Sequential test: SNR = 5.
 (a)
(a)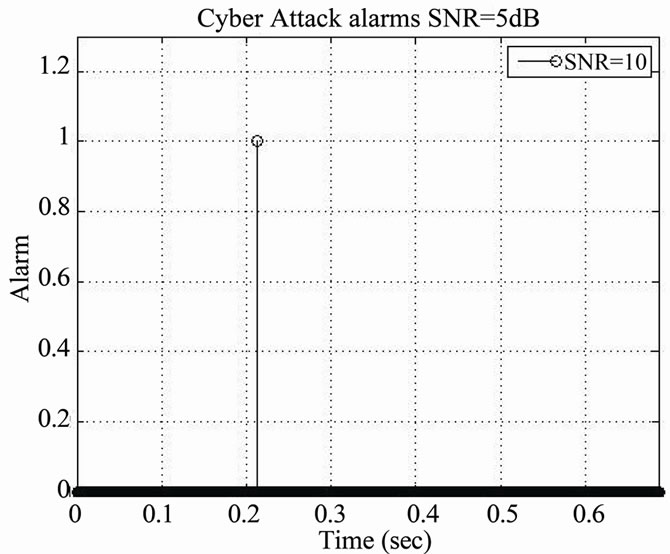 (b)
(b) (c)
(c)
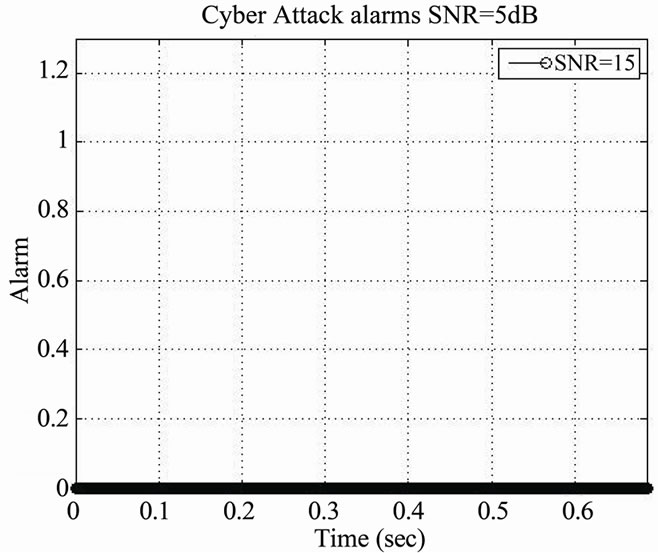
Figure 20. Cyber detection during speech activity detected periods using RSDA-CA. (a) Alarms SNR = 15; (b) Alarms SNR = 10; (c) Alarms SNR = 5.
From Figure 19, parts (a), (b) and (c), we may observe the evolution of the deployed CA-SDCT algorithm for different SNR values, where the latter values reflect the cumulative effect of normal channel noise and cyber noise. Each time the threshold is crossed, an alarm is activated.
Figure 20 shows alarm activation scenarios regarding cyber attacks, where in (a) no alarm is activated, where in (b) one alarm is activated and where in (c) several alarms are activated.
5. Conclusions
A novel voice activity detection (VAD) approach was presented. The approach uses the Sequential Detection of Change Algorithm (SDCT-VAD), designed at the Laplacian-Gaussian distributions additive mixture. We analysed and evaluated the robust sequential algorithm in the presence of Additive White Gaussian Noise. Several different speech messages were chosen for the effectiveness evaluation of the SDCT-VAD, regarding its accurate detection of changes from voice activity to silence and vice versa. The experimental results have shown that the algorithm is effective in various noisy environments and outperforms other existing voice activity detection methods.
A novel cyber attack-sequential detection of change algorithm (CA-SDCA) was also presented, deployed to detect cyber attacks during speech activity periods. The proposed algorithm is preceded by the Voice Activity Detection algorithm—Sequential Detection of Change Test (SDCT-VAD). We considered the case where voice messages are transmitted through the communications system, while a cyber attack may occur at any point in time. The proposed algorithm was analyzed and evaluated. The latter algorithm detects cyber attacks effectively; during speech activity periods detected-by the SDCT-VAD algorithm. We modeled the cyber attacks by Additive White Gaussian Noise. The experimental results have shown how the algorithm can be implemented with effective detection results, in a variety of different environments.
6. References
[1] J.-W. Shin, H.-J. Kwon, S.-H. Jin and N. S. Kim, “Voice Activity Detection Based on Conditional MAP Criterion,” IEEE Signal Processing Letters, Vol. 15, 2008, pp. 257-260.
[2] J. Sohn, N.-S. Kim and W.-Y. Sung, “A Statistical Model-Based Voice Activity Detection,” IEEE Signal Processing Letters, Vol. 6, No. 1, 1999, pp. 1-3.
[3] J.-W. Shin, J.-H. Chang, H.-S. Yun and N.-S. Kim, “Voice Activity Detection Based on Generalized Gamm Distribution,” Vol. 1, 2005, pp. 781-784.
[4] S. Gazor and W. Zhang, “Speech Probability Distribution,” IEEE Signal Processing, Vol. 10, No. 7, 2003, pp. 204-207. doi:10.1109/LSP.2003.813679
[5] R. K. Bansal and P. Papantoni-Kazakos, “An Algorithm for Detecting a Change in a Stochastic Process,” IEEE Transaction on Information Theory, Vol. IT-32, No. 2, 1986, pp. 227-235.
[6] A. T. Burrell and P. Papantoni-Kazakos, “Extended Sequential Algorithms for Detecting Changes in Acting Stochastic Processes,” IEEE Transaction on Systems, Man, and Cybernetics, Vol. 28, No. 5, 1998, pp. 703-710. doi:10.1109/3468.709621
[7] A. T. Burrell and P. Papantoni-Kazakos, “Detecting Software Faults in Distributed Systems,” IEEE 2009 World Congress on Computer Science and Information Engineering, Vol. 7, 2009, pp. 300-304.
[8] P. Papantoni-Kazakos, “Algorithms for-Monitoring Changes in Quality of Communication Links,” IEEE Transaction on Communication, Vol. COM-27, 1979, pp. 682-692.
[9] D. Kazakos and P. Papantoni-Kazakos, “Detection and Estimation,” Computer Science Press, New York, 1990.
[10] P. Papantoni-Kazakos, “Algorithms for Monitoring Changes in Quality of Communication Links,” IEEE Transactions on Communication, Vol. COM-27, 1979, pp. 656-659.
[11] A. Benyassine, E. Shlomot, H.-Y. Su, D. Massaloux, C. Lamblin and J.-P. Petit, “ITU-T Recommendation G.729 Annex B: A Silence Compression Scheme for Use with G.729 Optimized for V.70 Digital Simultaneous Voice and Data Applications,” Communications Magazine, IEEE, Vol. 35, No. 9, 1996, pp. 64-73.
Appendix
From expression (8), in Section 2.3, we have:
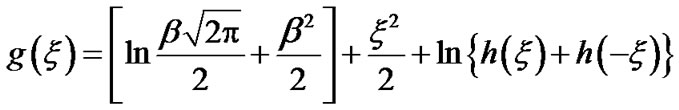
In Figure A below, we plot g(x) as a function of x. Let 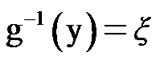 mean that x is such that,
mean that x is such that,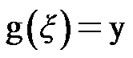 . Then,
. Then,
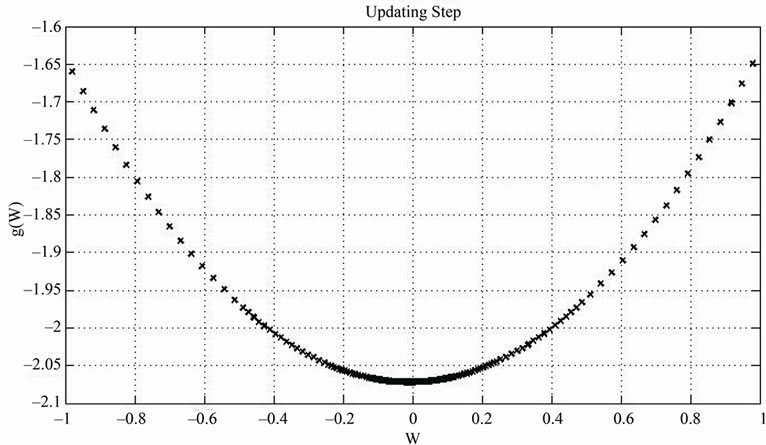
Figure A. Evaluate the whole updating step algorithm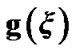 .
.
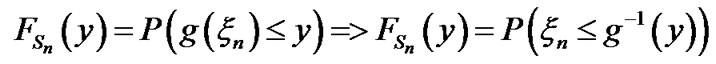
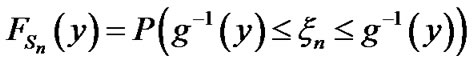
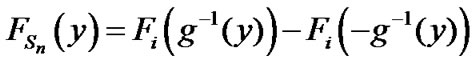
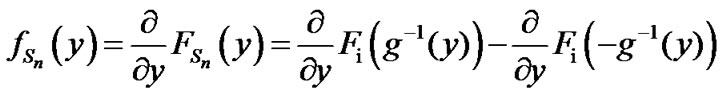
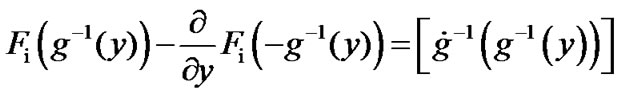
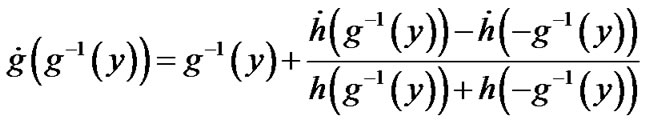
where

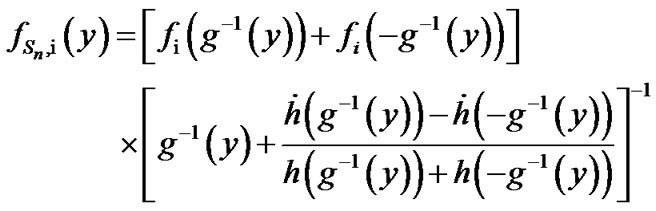
From Figure A, it can be concluded that,
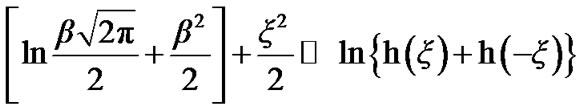
and then,
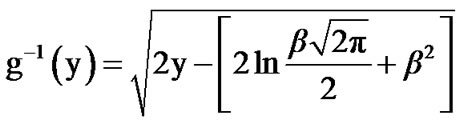
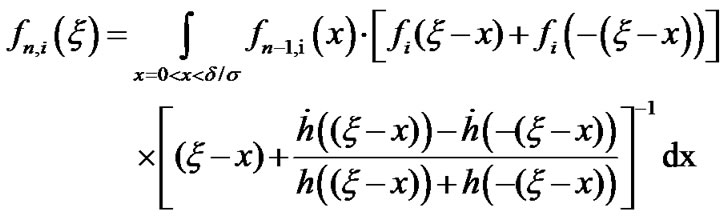
The following recursive expressions are used for the computation of the power curves:
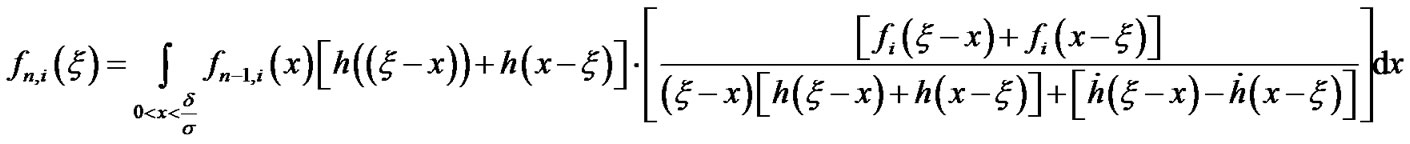
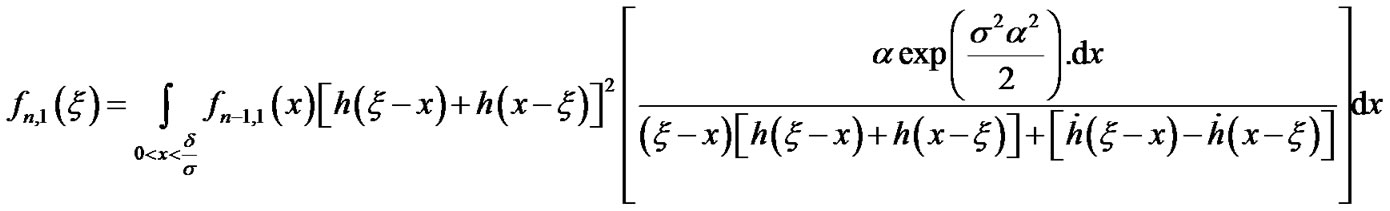
The following expressions are used for the computation of the false alarm curves:
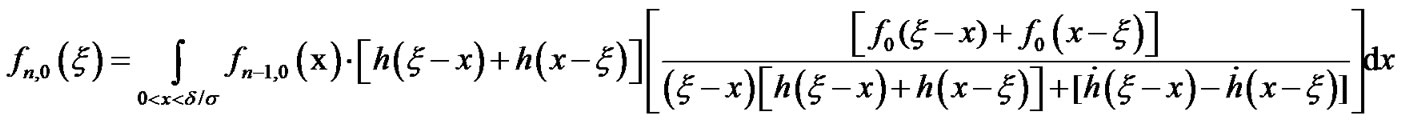
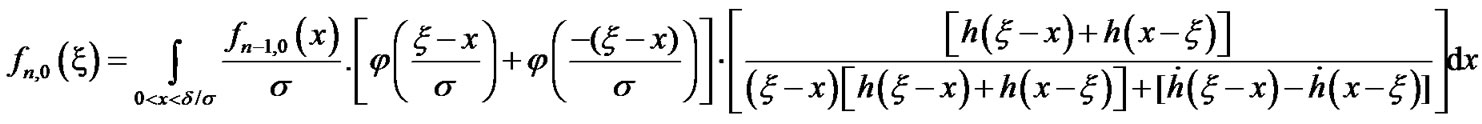
where
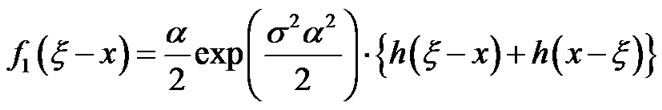
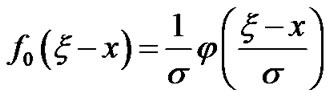
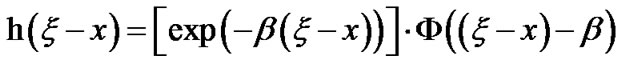
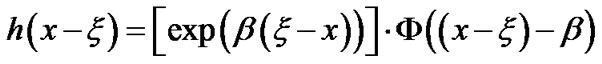
Then, 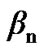 and
and 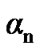 can be expressed as follows:
can be expressed as follows:
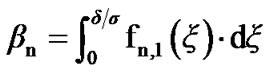 ;
;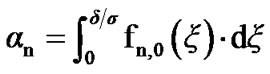
NOTES
*Partially supported by the US Air Force Office of Scientific Research under contract AFOSR FA9550-05-1-0388.

