Communications and Network
Vol.3 No.1(2011), Article ID:3984,7 pages DOI:10.4236/cn.2011.31001
Fast Sparse Multipath Channel Estimation with Smooth L0 Algorithm for Broadband Wireless Communication Systems
1Department of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu, China
2Department of Electrical and Communication Engineering, Graduate School of Engineering, Tohoku University, Sendai, Japan
3Key Laboratory of Universal Wireless Communications, Ministry of Education, Beijing University of Posts and Telecommunications, Beijing, China
4School of Software, Tsinghua University, Beijing, China
E-mail: gui@mobile.ecei.tohoku.ac.jp
Received November 29, 2010; revised December 14, 2010; accepted December 18, 2010
Keywords: Smooth L0 algorithm, restricted isometry property, sparse channel estimation, compressed sensing
Abstract
Broadband wireless channels are often time dispersive and become strongly frequency selective in delay spread domain. Commonly, these channels are composed of a few dominant coefficients and a large part of coefficients are approximately zero or under noise floor. To exploit sparsity of multi-path channels (MPCs), there are various methods have been proposed. They are, namely, greedy algorithms, iterative algorithms, and convex program. The former two algorithms are easy to be implemented but not stable; on the other hand, the last method is stable but difficult to be implemented as practical channel estimation problems because of computational complexity. In this paper, we introduce a novel channel estimation strategy using smooth L0 (SL0) algorithm which combines stable and low complexity. Computer simulations confirm the effectiveness of the introduced algorithm. We also give various simulations to verify the sensing training signal method.
1. Introduction
Coherent detection in broadband wireless communication systems often requires accurate channel state information (CSI) at a receiver. The study of channel estimation for the purposes of channel equalization has a long history. In many previous studies, they assume that the channel impulse responses (CIRs) in time domain are distributed densely. Under this assumption, it is necessary to use a redundant training sequence to probe the CSI. In addition, the linear channel estimation methods, such as least square (LS) algorithm and minimum mean square error (MMSE), always lead to lower spectral efficiency due to utilizing more training source in transmitted data block. It is very interesting to develop an effective channel estimation method to save training sequence and to improve spectral efficiency.
Recently, the compressive sensing (CS) has been developed as a novel technique. It is regarded as an efficient signal acquisition framework for signals characterized as sparse or compressible in time or frequency domain. One of applications of the CS technique is on compressive channel estimation. If the channel impulse response follows sparse distribution, we can apply the CS technique. As a result, the training sequence can be reduced compared with the linear estimation methods. Recent channel measurements show that the sparse or approximate sparse distribution assumption is reasonable [1,2]. In other words, the wireless channels in real propagation environments are characterized as sparse or sparse clustered; these sparse or clustered channels are frequently termed as a sparse multi-path channel (SMPC). An example of SMPC impulse response channel is shown in Figure 1. Recently, the study on SMPC has drawn a lot of attentions and concerning results can be found in literature [3-5]. Correspondingly, sparse channel estimation technique has also received considerable interest for its advantages in high bit rate transmissions over multipath channel [6].
Exploiting the sparse property of SMPC, orthogonal matching pursuit (OMP) algorithm [7,8] and convex program algorithm [9] have been proposed. OMP algorithm is fast and easy to be implemented. However, the stability of OMP for sparse signal recovery has not been well understood yet. To mitigate the unstability, Needell and Tropp have presented a compressive sampling matching pursuit (CoSaMP) algorithm for sparse signal recovery in [10]. After that, Gui et al. [11] have introduced the algorithm to SPMC channel estimation and acquired robust channel estimator [12]. However, as the increasing of number of channel dominant taps, accurate channel estimator is hard to obtain due to unavoidable correlation between columns of the training sequence, thus the instability of the CoSaMP algorithm easily leads to weak channel estimation. Convex program method can resolve the instability of Greedy algorithm. Convex program algorithm, such as Dantzig Selector (DS) [13], is based on linear programming. The main advantage of convex program method is its stability and high estimation accuracy. The convex problem method can work correctly as long as the RIC conditions of training sequences are satisfied. However, this method is computationally complex and difficult to be implemented in real applications [14].
In this paper, we introduce a novel SMPC estimation method using smooth L0 (SL0) algorithm [15]. It has both the advantages of the greedy algorithm and the
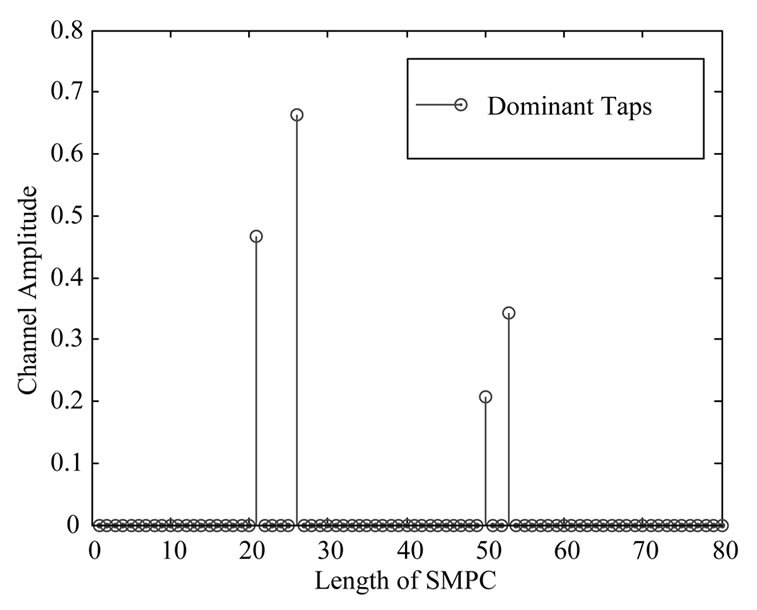
Figure 1. An example of SMPC where the channel sampling length is 80 while its number of dominant taps is 4.
convex program. In other words, SL0 algorithm combines low computational complexity and robustness on practical channel estimation, especially in high signal-noise-ratio (SNR) environment. The study in [15] focused on mathematical description on SL0 algorithm for sparse or approximate sparse signal recovery problem. The perfect CSI was assumed while practical channel estimation has not considered. In this paper, we introduce the SL0 algorithm to deal with the practical sparse channel estimation problems that via exploiting channel sparsity.
The rest of the paper is organized as follows. Sparse multipath channel model is presented in Section 2. Section 3 will describe the existing SL0 algorithm and propose a CS-based SMPC estimation method by using the SL0 algorithm. In Section 4, we compare the performance of the proposed method with the existing methods by simulations. Finally, conclusions are drawn in Section 5.
2. Sparse Multipath Channel Model
At first, the symbols used in this paper are described as follows. The superscript H stands for Hermite transposition Bolded capital letters denote a matrix where bolded lowercase letters represent a vector. Notation  stands for the absolute value. Norm operator
stands for the absolute value. Norm operator 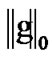 denotes
denotes  vector norm, i.e., the number of non-zero entries of the vector;
vector norm, i.e., the number of non-zero entries of the vector; 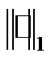 denotes
denotes  vector norm, which is the sum of the absolute values of the vector entries.
vector norm, which is the sum of the absolute values of the vector entries. 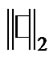 denotes L2 norm.
denotes L2 norm. 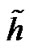 and
and 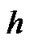 indicate estimate channel vector and actual channel vector, respectively.
indicate estimate channel vector and actual channel vector, respectively.
We consider single-antenna broadband communication systems, which are often equivalent to frequencyselective baseband channel model. Hence, the transmitted and received signal are related by
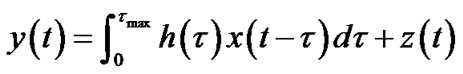 , (1)
, (1)
where 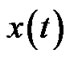 and
and  denotes the transmitted and received waveforms, respectively, and
denotes the transmitted and received waveforms, respectively, and  is defined as the maximum possible dominant taps delay spread introduced by the channel. And
is defined as the maximum possible dominant taps delay spread introduced by the channel. And 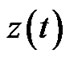 is a zero-mean, circularly symmetric, complex additive white Gaussian noise (AWGN). The equivalent baseband transmitted
is a zero-mean, circularly symmetric, complex additive white Gaussian noise (AWGN). The equivalent baseband transmitted  and received signals
and received signals 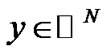 is given by
is given by
 , (2)
, (2)
where 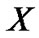 is a complex training signal with Toeplitz structure of
is a complex training signal with Toeplitz structure of  dimensions.
dimensions.  s the
s the  complex additive white Gaussian noise (AWGN) with zero mean and variance
complex additive white Gaussian noise (AWGN) with zero mean and variance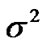 .
.  is an
is an 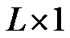 unknown deterministic channel vector which is given by
unknown deterministic channel vector which is given by
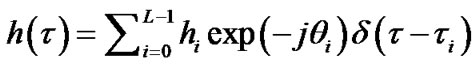 , (3)
, (3)
where 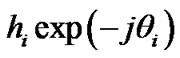 are complex channel coefficients and
are complex channel coefficients and 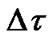 is a sampling rate and hence
is a sampling rate and hence 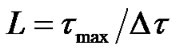 is defined as the channel length.
is defined as the channel length. 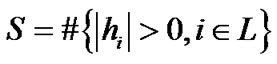 denotes the number of dominant taps of the SMPC where
denotes the number of dominant taps of the SMPC where . Suppose that there are S dominant channel taps distributed uniform randomly over the channel. Hence, accurate estimate the dominant coefficients in the channel is necessary for signal detection and demodulation at the receiver.
. Suppose that there are S dominant channel taps distributed uniform randomly over the channel. Hence, accurate estimate the dominant coefficients in the channel is necessary for signal detection and demodulation at the receiver.
3. CS-Based Sparse Channel Estimation
3.1. Review of Compressed Sensing
Compressed sensing (CS) [16,17] has attracted great attentions in sparse channel estimation. We review the CS theorem on channel estimation by two aspects: 1) sparse approximation, 2) incoherence property of training sequence (sensing matrix). We rewrite the above system model (2) as
 . (4)
. (4)
3.1.1. Sparse Representation
Consider a signal vector  that can be represented in an arbitrary basis,
that can be represented in an arbitrary basis,  , with the weighting coefficients
, with the weighting coefficients . Stacking the coefficients into a vector,
. Stacking the coefficients into a vector, , the relationship with
, the relationship with  is obviously through the transform
is obviously through the transform , where
, where  is a full rank
is a full rank 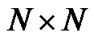 matrix. Let us take an example of sparse channel estimation problem in the time-frequency domain. Commonly, we sample
matrix. Let us take an example of sparse channel estimation problem in the time-frequency domain. Commonly, we sample  example from a finite length, discrete channel vector that one could represent as discrete sinusoids in a limited bandwidth. The matrix
example from a finite length, discrete channel vector that one could represent as discrete sinusoids in a limited bandwidth. The matrix 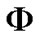 (sometimes is termed as dictionary) would then be the discrete Fourier transform (DFT) matrix.
(sometimes is termed as dictionary) would then be the discrete Fourier transform (DFT) matrix.
In CS one is particularly interested in any basis that allows a sparse representation of received signal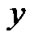 , i.e., a basis
, i.e., a basis 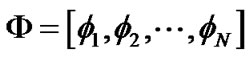 such that most coefficients
such that most coefficients  are zero. Obviously if one knows
are zero. Obviously if one knows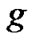 , one could always choose some basis for which
, one could always choose some basis for which  for some
for some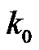 ; then all
; then all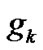 ,
,  , would be zero. This trivial case is not of interest; instead one is interested in a predetermined basis that will render a sparse or approximately sparse representation of any
, would be zero. This trivial case is not of interest; instead one is interested in a predetermined basis that will render a sparse or approximately sparse representation of any 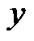 that belongs to some class of signals. In (4),
that belongs to some class of signals. In (4),  denotes random measurement matrix for reconstruct sparse signal. In the following section, we will discuss the restricted isometry property of measurement matrix
denotes random measurement matrix for reconstruct sparse signal. In the following section, we will discuss the restricted isometry property of measurement matrix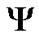 .
.
3.1.2. Restricted Isometry Property
In the theory of CS, restricted isometry property (RIP) has become a standard tool for studying how efficiently a sensing matrix acquires information about sparse and compressible signals. If the sensing matrix with small restricted isometry constants (RIC), many proposed CS algorithms can reconstruct unknown sparse signal successfully. Let’s give an example in the sparse channel estimation. We can utilize a small number of training sequence robust capture all the information in a sparse channel. Furthermore, we estimate the sparse channel from these training sequence using efficient CS algorithms. We give a definition of restricted isometry property (RIP) [18] on sensing matrix.
Definition 1 (RIP [18]). For each integer 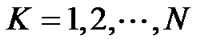 , define the restricted isometry constant (RIC) for all
, define the restricted isometry constant (RIC) for all  of a sensing matrix
of a sensing matrix 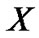 as the smallest number such that
as the smallest number such that
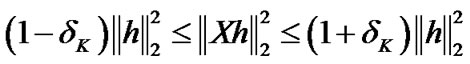 , (5)
, (5)
holds for all 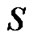 -sparse signal vector
-sparse signal vector . Due to simplify, we termed as
. Due to simplify, we termed as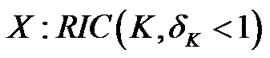 .
.
3.2. Sparse Channel Estimator
In this paper, we consider the complex Rayleigh probability density distribution for practical channel impulse response, which is defined as
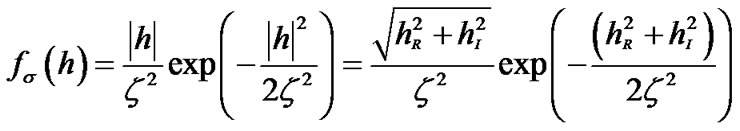 (6)
(6)
where ,
,  and
and  represent the amplitude, real and imaginary parts of channel vector
represent the amplitude, real and imaginary parts of channel vector . From above (6), we can find the complex channel amplitude
. From above (6), we can find the complex channel amplitude
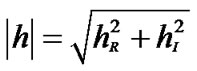 where its real part
where its real part  and imaginary part
and imaginary part 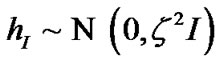 are two independent normal distributions, where
are two independent normal distributions, where 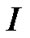 represents identity matrix which decided by channel length. On CS-based channel estimation, the optimal sparse estimators are given by [16]
represents identity matrix which decided by channel length. On CS-based channel estimation, the optimal sparse estimators are given by [16]
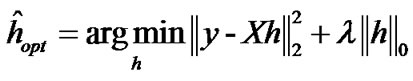 . (7)
. (7)
However, direct compute the 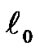 -norm is a high computational cost problem [16] and hence the optimal channel estimator cannot obtain. Fortunately, there have lot of sparse approximation methods (e.g., Lasso [16] and CoSaMP [19]) to obtain sub-optimal channel estimators. In this part, we introduce a fast algorithm for CS-based sparse channel estimation. At first, we define
-norm is a high computational cost problem [16] and hence the optimal channel estimator cannot obtain. Fortunately, there have lot of sparse approximation methods (e.g., Lasso [16] and CoSaMP [19]) to obtain sub-optimal channel estimators. In this part, we introduce a fast algorithm for CS-based sparse channel estimation. At first, we define  -th (
-th ( ) taps of channel satisfies the follow function
) taps of channel satisfies the follow function
 , (8)
, (8)
as a sparse measure function which related as channel variance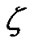 . And the approximate
. And the approximate 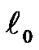 norm function is given by
norm function is given by
 . (9)
. (9)
That is to say,
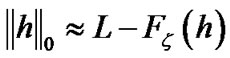 . (10)
. (10)
The channel variance  specifies a tradeoff between accuracy and smoothness of the sparse channel estimation: the smaller
specifies a tradeoff between accuracy and smoothness of the sparse channel estimation: the smaller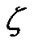 , the better estimation performance, and vice verse. From (5), minimization of the
, the better estimation performance, and vice verse. From (5), minimization of the  norm is equivalent to maximization of
norm is equivalent to maximization of 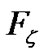 for sufficiently small
for sufficiently small 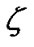 are described by following theorem [15].
are described by following theorem [15].
Theorem 1 Sparse channel approximation problem:
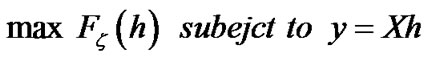 (11)
(11)
where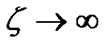 , is the minimum
, is the minimum  norm channel estimator that is,
norm channel estimator that is, 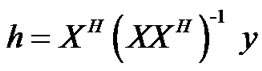 and
and , is the minimum
, is the minimum 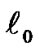 norm estimator of system model
norm estimator of system model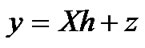 .
.
Based on the above Theorem 1, on sparse channel estimation with SL0 algorithm [15], the detail of channel estimation steps is given as follows.
CS-based sparse channel estimation
Input: Training sequence , received signal vector
, received signal vector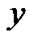 , decreasing channel variance
, decreasing channel variance . Choose the initial channel estimator
. Choose the initial channel estimator  by LS.
by LS.
Output: Sparse channel estimator 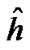
for 
1) Find the support set of dominant taps with function 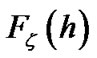
Initialization 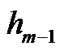
for j = 1, ,K
,K
• Let
• 
• 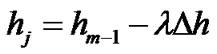 (where
(where 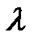 is small step length)
is small step length)
• Compute 
End 2) 
end
3.3. Lower Bound of Channel Estimators
To evaluate the MSE performance of channel estimators, it is very meaningful compare their achievements with theoretical performance bound in practical broadband communication systems, then they are approximate optimal and further improvements in these systems are impossible. This motivates the development of lower bounds on the MSE of estimators in the sparse channel estimation. Since the channel vector to be estimated is deterministic, and then we can give a lower bound as for the baseline of MSE. Suppose we know the location set 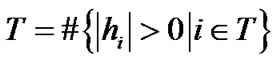 of dominant channel taps. Thus, the oracle estimator given by
of dominant channel taps. Thus, the oracle estimator given by
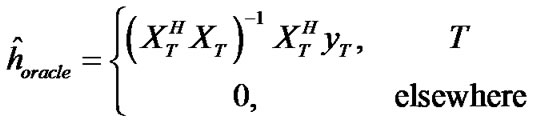 , (12)
, (12)
where  is the partial training signal constructed from columns of training signal
is the partial training signal constructed from columns of training signal 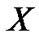 corresponding to the dominant taps of SMPC vector
corresponding to the dominant taps of SMPC vector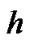 . Hence, the reference lower bound (RLB) of sparse channel estimator are given by
. Hence, the reference lower bound (RLB) of sparse channel estimator are given by
 . (13)
. (13)
4. Simulation Results and Discussions
The parameters used in the simulation are listed in Table 1. To illustrate the performance of proposed method with SL0 algorithm, Figure 2 shows the mean square error (MSE) of dominant taps by employing LS, Lasso, SL0. The estimation error using mean square error (MSE) evaluation criterion can be defined as:
 . (14)
. (14)
4.1. CDF Versus MSE
To compare the MSE performance of estimation methods, the cumulative density function (CDF) is compared in Figures 2, 3. It can be clearly observed that the CDF curve of the proposed method by using SL0 algorithm is very close to the LASSO and better than the performance
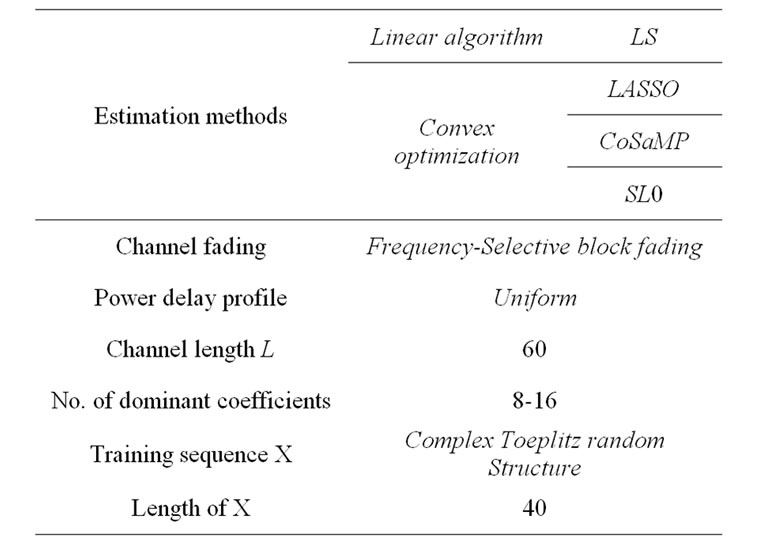
Table 1. Simulation condition.
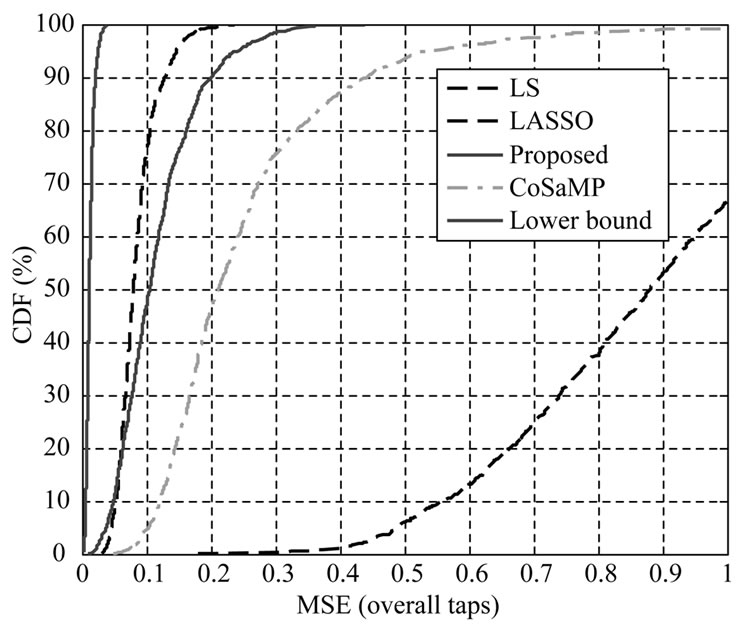
Figure 2. MSE of the overall coefficients at SNR = 10 dB.
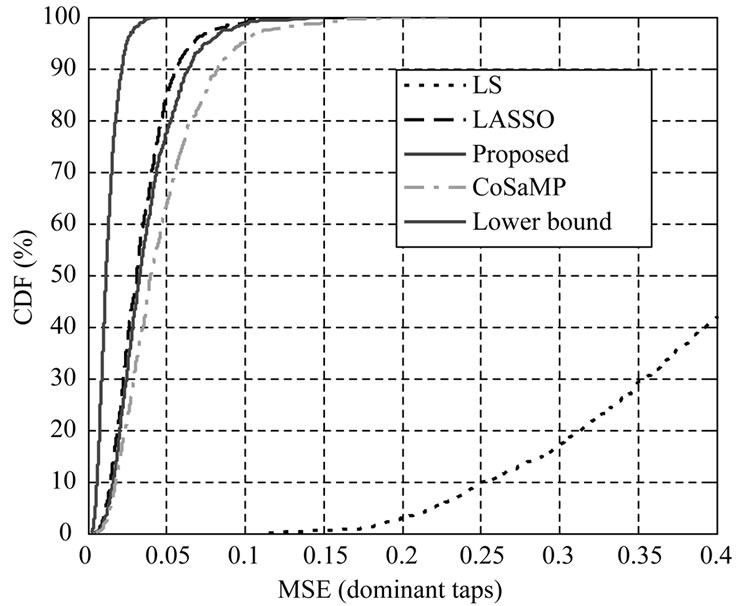
Figure 3. MSE of the dominant coefficients at SNR = 10 dB.
of other estimation methods when comparing with estimation performance on either taps or dominant taps.
4.2. MSE Versus SNR
As is shown in Figure 4, the proposed estimation method has a better MSE performance than LASSO and CoSaMP. It was worth noting that LS-based linear estimation has a bad MSE performance which invariant with SNR due to undetermined system, that is to say, the length of training sequence shorter than estimation channel length. Hence, the MSE performance of LSbased channel estimators is invariant whatever the SNR changes.
4.3. Computational Complexity
To study the computational complexity (CC) of the introduced algorithm, we have evaluated the CPU time in second to complete the channel estimation for SNR = 10 dB. It is worth mentioning that although the CPU time is not an exact measure of complexity, it can give us a rough estimation of computational complexity. Our simulations are performance in MATLAB 2007 environment using a 2.40 GHz Intel Core-2 processor with 2GB of memory and under Microsoft XP 2003 operating system.
The comparison of computational complexity between LS, LASSO, CoSaMP and SL0 algorithms is shown in Figure 5. It is seen that the computing time of proposed method is close to 0.02 second, while the computing time of the LASSO algorithm is more than 0.4 seconds. As for the CoSaMP algorithm, the compute complexity is increasing as the number of dominant taps increasing. Thus,
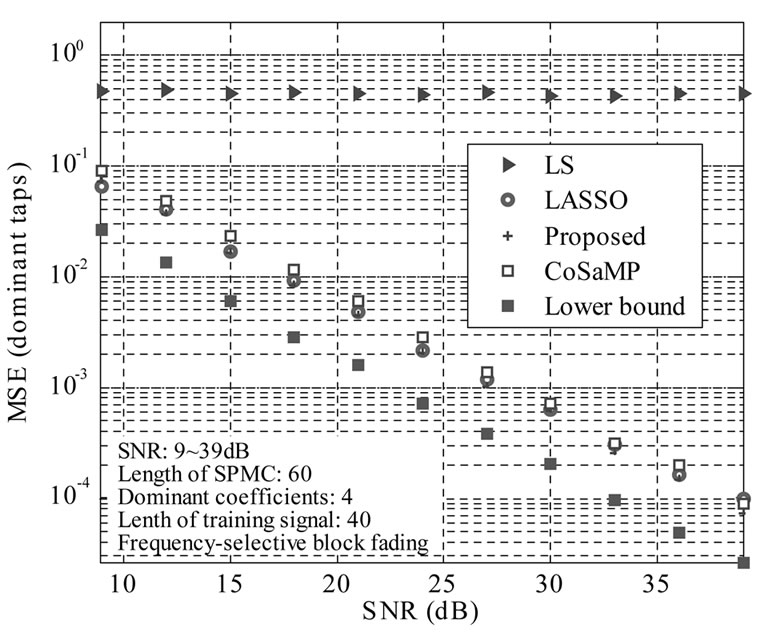
Figure 4. MSE versus SNR.

Figure 5. Compute complexity with different number of domiant taps.
CS-based sparse channel estimation with SL0 algorithm is lower complexity method and hence easy implement at receiver on practical communications system.
5. Conclusion
In this paper, we have proposed a novel sparse channel estimation method with SL0 algorithm which combines stable and fast. Thus this method has both advantages of the greedy algorithm and convex program algorithm. It has been shown that, when compared with the existing algorithms, our introduced method is both bandwidth and computationally efficient. In our future work, we will continue introduce the algorithm to sparse channel estimation problem in the multiple antennas systems and cooperative networks.
6. Acknowledgement
This work is supported in part by the National Natural Science Foundation of China under grant 60772146, the National High Technology Research and Development Program of China (863 Program) under grant 2008 AA12Z306, the Key Project of Chinese Ministry of Education under grant 109139 as well as Open Research Foundation of Chongqing Key Laboratory of Signal and Information Processing (CQKLS & IP), Chongqing University of Posts and Telecommunications (CQUPT). And the first author is special supported in part by China Scholarship of China Scholarship Council (CSC) under grant No. 2009607029 and the Outstanding Doctor Candidate Training Fund of University of Electronic Science and Technology of China (UESTC). And he is also supported in part by Tohoku University Global COE program “Global Education and Research Center for Earth and Planetary Dynamics”.
7. References
[1] Z. Yan, M. Herdin, A. M. Sayeed and E. Bonek, “Experimental Study of MIMO Channel Statistics and Capacity via the Virtual Channel Representation,” February 2007. http://dune.ece.wisc.edu/pdfs/zhoumeas.pdf.
[2] J. Kivinen, P. Suvikunnas, L. Vuokko and P. Vainikainen, “Experimental Investigations of MIMO Propagation Channels,” Antennas and Propagation Society International Symposium, IEEE, 2002.
[3] W. F. Schreiber, “Advanced Television Systems for Terres-Trial Broadcasting: Some Problems and Some Proposed Solutions,” IEEE Proceedings, vol. 83, No. 6, June 1995, pp. 958-981. doi:10.1109/5.387095
[4] R. Steele, “Mobile Radio Communications,” IEEE Press, New York, 1992.
[5] M. Kocic, D. Brady and M. Stojanovic, “Sparse Equalization for Real Time Digital Underwater Acoustic Communications,” OCEANS’95 MTS/IEEE Challenges of Our Changing Global Environment Conference Proceedings, San Diego, Vol. 3, October 1995, pp. 1417-1422. doi:10. 1109/OCEANS.1995.528671
[6] C. Carbonelli, S. Vedantam and U. Mitra, “Sparse Channel Estimation with Zero Tap Detection,” IEEE Transactions on Wireless Communications, vol. 6, No. 5, May 2007, pp. 1743-1753. doi:10.1109/TWC.2007.360376
[7] Z. G. Karabulut and A. Yongacoglu, “Sparse Channel Estimation Using Orthogonal Matching Pursuit Algorithm,” 2004 IEEE 60th Vehicular Technology Conference, vol. 60, No. 6, 2004, pp. 3880-3884. doi:10.1109/ VETECF.2004.1404804
[8] J. A. Tropp and A. C. Gilbert, “Signal Recovery from Random Measurements via Orthogonal Matching Pursuit,” IEEE Transaction on Information Theory, vol. 53, No. 12, 2007, pp. 4655-4666. doi:10.1109/TIT.2007.909 108
[9] U. W. Bajwa, J. Haupt, G. Raz and R. Nowak, “Compressed Channel Sensing,” 42nd Annual Conference on Information Sciences and Systems, CISS’08, Princeton, 19-21March 2008. doi:10.1109/CISS.2008.4558485
[10] D. Needell and J. A. Tropp, “CoSaMP: Iterative Signal Recovery from Incomplete and Inaccurate Samples,” Applied and Computational Harmonic Analysis, vol. 26, No. 3, 2008, pp. 301-321. doi:10.1016/j.acha.2008.07.002
[11] G. Gui, Q. Wan, W. Peng and F. Adachi, “Sparse Multipath Channel Estimation Using Compressive Sampling Matching Pursuit Algorithm,” IEEE VTS APWCS 2010, 19-22 May 2010.
[12] E. J. Candès, “The Restricted Isometry Property and Its Implications for Compressed Sensing,” Compte Rendus de l’Academie des Sciences, vol. 346, No. 9-10, May 2008, pp. 589-592. doi:10.1016/j.crma.2008.03.014
[13] E. Candès and T. Tao, “The Dantzig Selector: Statistical Estimation When p is Much Larger than n,” Annals of Statistics, vol. 35, No. 6, 2007, pp. 2313-2351. doi:10. 1214/009053607000000532
[14] N. H. Nguyen and T. D. Tran, “The Stability of Regularized Orthogonal Matching Pursuit Algorithm,” http:// www.dsp.ece.rice.edu/cs/Stability_of_ROMP.pdf.
[15] H. Mohimani, M. Babaie-Zadeh and C. Jutten, “Complex-Valued Sparse Representation Based on Smoothed L0 Norm,” Proceedings of ICASSP2008, Las Vegas, April 2008, pp. 3881-3884.
[16] E. Candès, J. Romberg and T. Tao, “Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information,” IEEE Transaction on Information Theory, vol. 52, No. 2, February 2006, pp. 489-509. doi:10.1109/TIT.2005.862083
[17] D. L. Donoho, “Compressed Sensing,” IEEE Transaction on Information Theory, vol. 52, No. 4, April 2006, pp. 1289-1306. doi:10.1109/TIT.2006.871582
[18] E. J. Candès, “The Restricted Isometry Property and Its Implications for Compressed Sensing,” Comptes Rendus Mathematique, vol. 346, No. 9-10, May 2008, pp. 589- 592. doi:10.1016/j.crma.2008.03.014
[19] D. Needell and J. A. Tropp, “CoSaMP: Iterative Signal Recovery from Incomplete and Inaccurate Samples,” Applied and Computational Harmonic Analysis, Vol. 26, No. 3, May 2009, pp. 301-321. doi:10.1016/j.acha.2008.07. 002

