Advances in Pure Mathematics
Vol.09 No.03(2019), Article ID:91519,23 pages
10.4236/apm.2019.93010
Deconvolution of the Error Associated with Random Sampling
Peter L. Irwin*, Yiping He, Chin-Yi Chen
Molecular Characterization of Foodborne Pathogens, United States Department of Agriculture, Wyndmoor, PA, USA

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 11, 2019; Accepted: March 26, 2019; Published: March 29, 2019
ABSTRACT
In this work empirical models describing sampling error ( ) are reported based upon analytical findings elicited from 3 common probability density functions (PDF): the Gaussian, representing any real-valued, randomly changing variable x of mean and standard deviation ; the Poisson, representing counting data: i.e., any integral-valued entity’s count of x (cells, clumps of cells or colony forming units, molecules, mutations, etc.) per tested volume, area, length of time, etc. with population mean of and ; binomial data representing the number of successful occurrences of something ( ) out of n observations or sub-samplings. These data were generated in such a way as to simulate what should be observed in practice but avoid other forms of experimental error. Based upon analyses of 104 measurements, we show that the average ( ) is proportional to ( ; Gaussian) or (Poisson & binomial). The average proportionality constants associated with these disparate populations were also nearly identical ( ; ±s). However, since for any Poisson process, . In a similar vein, we have empirically demonstrated that binomial-associated were also proportional to . Furthermore, we established that, when all were plotted against either or , there was only one relationship with a slope = A (0.767 ± 0.0990) and a near-zero intercept. This latter finding also argues that all , regardless of parent PDF, are proportional to which is the coefficient of variation for a population of sample means ( ). Lastly, we establish that the proportionality constant A is equivalent to the coefficient of variation associated with ( ) measurement and, therefore, . These results are noteworthy inasmuch as they provide a straightforward empirical link between stochastic sampling error and the aforementioned . Finally, we demonstrate that all attendant empirical measures of are reasonably small (e.g., ) when an environmental microbiome was well-sampled: n = 16 - 18 observations with isolates per observation. These colony counting results were supported by the fact that the two major isolates’ relative abundance was reproducible in the four most probable composition observations from one common population.
Keywords:
Stochastic Sampling Error, Modeling, Most Probable Composition, Quantitative Metagenomics, Food-Borne Bacteria

1. Introduction
There are various analytical procedures for enumerating organisms in environmental samples which diverge in their experimental approach yet are mathematically inter-related. Thus, if V represents the sample volume and the volume occupied by a test entity of interest (e.g., colony forming units or CFUs), the probability that one particular will not contain this entity at concentration [1] is
;
i.e., ―maximum possible number of entities in V and ~the actual number of objects present.
Assuming that many aliquots have been combined to generate V, the probability that no organism will be contained in V is [1]
therefore
.
Since
then, if ,
For (e.g., E. coli [2] has a ),
therefore
. (1)
In certain circumstances it is only possible to determine an organism’s by diluting the sample to such an extent that only a fraction of the n “technical” replicates tested are positive ( ) for the presence of the entity, or microbe, in question [3] [4]. This technique is referred to as the “dilution method” [1] since it involves diluting a test sample’s content to extinction ( ). This enumeration protocol is also known as the most probable number (MPN) method and entails sampling from a liquid source, making serial dilutions from this, distributing an aliquot of each of these dilutions into separate receptacles, incubating these under suitable growth conditions, and observing if any growth has occurred based upon some organism-specific detection method [5] [6]. The MPN enumeration procedure is particularly useful when sampling from environmental sources, such as foods, since damaged cells frequently recover in liquid media [7].
For example, were one to obtain a food sample containing ~14 CFU of a particular organism per 50 g, the cells would typically be washed from the food matrix, concentrated to a few mL (e.g., via centrifugation), and brought up to some appropriate volume (say 40 mL = Vsample) with media [5]. From this, eight 4 mL (V) samples could be randomly selected and distributed into 8 separate receptacles (n = 8 with a dilution factor of 1; i.e., undiluted). Of the remaining 8 mL, 4 could be further diluted with 36 mL (40 mL total) liquid media, mixed and distributed into another set of 8 containers. This set of dilutions has a dilution factor of 0.1 relative to the original. With the remaining 8 mL from the 0.1 dilution, 4 mL could be diluted again with 36 mL media, mixed and distributed into yet another eight 4 mL replicates (dilution factor = 0.01). After incubation the most likely number (Equation (2), below) of positive occurrences (e.g., presence of a specific gene [5] ) observed would be = 6, 1, and 0 (out of n = 8 observations per dilution) for dilution factors of 1, 0.1, and 0.01, respectively, and the calculated MPN (±s) per 50 g sample would = 13.8 ± 5.56. Note the relatively large error term. For a 4-fold proportional (200 g, 160 mL Vsample) experiment with n = 32, the calculated MPN is 13.8 ± 2.78 per 50 g sample.
For MPN-based organism detection and subsequent enumeration, the number of positive occurrences of growth in any jth experiment out of n observations = (θ = either 1 [presence] or 0 [absence]) can be estimated as
(2)
whereupon is integral (=ROUND( , 0) in Excel). The probability of observing successes out of n Bernoulli trials [8] each of volume V from a population of entities per V is
which is also known as the binomial PDF. Since = the population average (real) [9] number of positive responses out of n tests ( ), the above can be also written as
. (3)
The multiple dilution MPN calculation itself is determined by finding the value of at the maximum in the product of the from all dilutions ( ) and is easily achieved by adding the scaled sum of all dilutions’ values to an initial guess for (i.e.,
for any particular
ℓth one-to-ten dilution and m iterations; λ is a monotonically changing, with m, scaling function) then solving for the MPN recursively [1] [4] [5] [10] which minimizes the summation.
At the limit n → ∞, Equation (3) simplifies to what is known as the Poisson PDF
. (4)
Under these circumstances, x is the observed and is the population average number of counts in/on the tested volume, surface, chosen time period, etc. This PDF is applicable to all analytical systems involving, essentially, the counting of objects. However this PDF is applied, the most conspicuous aspect [11] [12] of any Poisson process is that the variance ( or second moment)
equals the population mean ( or first moment)
.
The last probability density function utilized in this stochastic sampling exercise is also related to , Equation (3). This is the Gaussian PDF which we use to quantitatively examine the effects of n and (fixed ) on the variability of sample means ( ) which have been created by randomly sampling from a population of real-valued variables (x; e.g., doubling time [13] ) which are normally distributed as
; (5)
in this relationship the Area term (~ ; for large K) is the approximate area under the fitting function f (frequently taken to be 1 since is often = 1 and is always ~1). There are several derivations of PG but none are as persuasive as the fact that this PDF is simple and has been experimentally shown to be the most likely probability distribution associated with most experimental observations [9] [12].
The original purpose of our sampling-related investigations [7] was to estimate a nominal value for n needed to achieve accurate most probable foodborne bacterial isolate enumeration, combined with 16S rDNA-based identification, for quantitative metagenomic purposes. The relationships were developed by examining the results of 6 × 6 colony counting (Poisson PDF) of highly diluted bacteria [14] [15] as a function of n and as well as by generating counts (x) derived from to simulate what occurred in the lab [15] [16] but which avoided other forms of experimentally based error [5]. We were able to establish that where is the number of observations necessary to accurately enumerate a population average of 1 count per volume tested. Based mainly on colony counting experience we estimate is somewhere in the range n ~ 20 - 30 observations.
Herein we model stochastic sampling errors associated with all the aforementioned PDFs and empirically demonstrate that the resultant mathematical models are, in part, a consequence of the “central limit theorem” [17] (CLT). In general, the CLT states that a distribution of sample means ( ), regardless of parent PDF, approaches a normal distribution analytically equivalent to , Equation (5), with , , and with the term = (= ) as the number of separate n-samplings increases. We also have elaborated on empirical findings developed previously [5] [15] [16] for predicting errors associated with the random sampling of microorganisms as well as comparing the internal variations associated with the three different sampling error data types derived from the Gaussian, binomial (MPN), and Poisson relationships. Thus, new results have been created using the aforementioned probability distributions, Equations (2), (4), and (5), and have been highly replicated since each “experiment”, comprising n (= 3, 6, 9, 12, or 24) observations, were repeated 100 times.
2. Materials and Methods
2.1. Poisson-Based Data: Equation (4), Figure 1
All counting data were created by multiplying Equation (4) by 360 in order to produce a large number of integral-valued repeats (=ROUND ( , 0)) for any particular count x: e.g., for particle per test volume, area, length of time, etc., there would be, most probably, 132 repeats of x = 0, 132 repeats of x = 1, 66 repeats of x = 2, 22 repeats of x = 3, 6 repeats of x = 4 and 1 repeat of x = 5 entities per test. From this pool of 360 counts for each μ, an n number of x values were randomly selected based upon random number tables created with Mathematica.
(6)
Figure 1. (A) relationship of average ( ) for Poisson-based data using Equation (7) (P-I: black symbols and curves) or Equation (8) (P-II: red symbols and curves) as a function of n (= 3, 6, 9, 12, 24) and various values for μ (= 1, 2, 4, 8, 16). Gauss-Newton least squares minimization-based curve-fitting [18] of data was performed [19] to fit to the equation (averages for a are provided ± s; averaged across 5× μ). (B) Non-linear relationship of individual values from (A) for P-I- and II-based data as a function of μ whereupon curve-fitting of data was also performed using the algebraic form (values for A and a are provided ± ASE). (C) and (D) Present linearized forms ( in (C) and in (D)) of data reported in Figure 1(A) and Figure 1(B) based upon all values of a = −1/2. Slopes of the lines in Figure 1(C) and Figure 1(D) are equivalent to and A, respectively.
which generates n random numbers between 1 and 360. Thus, 100 such random number sets were utilized for the twenty-five n (= 3, 6, 9, 12, 24) × μ (= 1, 2, 4, 8, 16) combinations. Briefly, each procedure involved arranging the aforementioned 360 x values (one set for each μ) in one column of a spreadsheet followed by filling in n adjacent columns with formulae which refer to the calculated x values but where each row’s reference number was taken from the Mathematica-generated random number, Equation (6), next in sequence. MPN- and Gaussian-based data arrays were treated in an identical fashion. The formula (P-I: normalized deviations of from ) for calculating our empirical measure of Poisson stochastic sampling error (Δ) was
(7)
whereupon the term is the experimental standard deviation ( or “=STDEV.S ( )” in Excel) for each j th
( ; J = 100) experiment and i th ( ) x. The average across
100× experiments, regardless of formulation, were symbolized as (= or “=AVERAGE ( )”). A second form for the Poisson-based measure of Δ was also calculated (P-II: normalized deviations of from known μ) from these same data
. (8)
Here the is the observed arithmetic mean for each j th counting experiment.
2.2. MPN Experiments: Equation (1), Figure 2
All MPN data were created by multiplying Equation (1) by 360 to produce the number (“=ROUND ( , 0)”) of positive responses (θ = 1) for any particular level of (=μ); e.g., for entity per volume tested there would be 34 repeats of θ = 1 and 326 repeats of θ = 0. From such a column of 360 θ values (one column for each μ), n were randomly selected based upon Mathematica tables, Equation (6), and treated similar to the Poisson data above. Thus, for each combination of n (= 3, 6, 9, 12, or 24) × μ (= 0.1, 0.2, 0.4, 0.8, 1.6), 100
Figure 2. (A) Relationship of average ( ) for MPN-based data using Equation (9) as a function of n (= 3, 6, 9, 12, or 24) and variable μ (= 0.1, 0.2, 0.4, 0.8, 1.6). Gauss-Newton least squares minimization-based curve-fitting [18] of data was performed [19] to fit the algebraic form (averages for a are provided ± s; averaged across 5 × μ) to these results. (B) Relationship of individual values from (A) for MPN-based data as a function of μ where curve-fitting of data was performed also to the algebraic form (values for A and a are provided ± ASE). (C) and (D) Represent linearized forms ( in (C) and in (D) of data reported in Figure 2(A) and Figure 2(B) based upon the assumption that a = −1/2. Slopes of the lines in Figure 2(C) and Figure 2(D) are equivalent to and A, respectively.
random n-selections were performed. The formula for calculating our empirical measure of MPN sampling error was
; (9)
where θ = either a “1” (a positive occurrence) or a “0” (a negative occurrence). As before, the average across J = 100 experiments (each of n observations) = . The MPN value for and provides the average MPN or CFU per sample; a rearrangement of Equation (2).
2.3. Gaussian-Based Data: Equation (5), Figure 3
All Gaussian PDF data were produced by multiplying Equation (5) ( ) by 360 producing an integral number of observations (“=ROUND ( , 0)”) for each value of x as a function of μ (fixed at 20) and σ (= 1, 1.5, 2, 3, 4). For instance, for σ = 1 there would be 2 repeats of x = 17, 19 repeats of x = 18, 87 repeats of x = 19, 144 repeats of x = 20, 87 repeats of x = 21, 19 repeats of x = 22, and 2 repeats of x = 23. From this column of 360 values of x, n (= 3, 6, 9, 12, or
Figure 3. (A) Relationship of average ( ) for Gaussian-based data using Equation (10) as a function of n with variable σ (=1, 1.5, 2, 3, 4; μ = 20). Gauss-Newton least squares minimization-based curve-fitting [18] of data was performed [19] to fit the equation (averages for a are provide ± s; averaged across 5× σ) to these results. (B) and (D) Relationship of individual values from (A) and (C) for Gaussian-based data as a function of μ-normalized standard deviations ( ). Linear regression-based fitting of data was performed to the algebraic form . Figure 3(C): linearized forms ( ) of data reported in Figure 3(A) based on a = −1/2. Slopes of the lines in Figure 3(C) are equivalent to and plotted in Figure 3(D).
24) were randomly selected based upon Equation (6) and treated identically to the Poisson and MPN data sets. Thus, for each combination of n × σ 100× n-based selections were performed. The formula for calculating our empirical measure of Gaussian sampling error, similar to Equation (7), was
. (10)
As usual, the average across J = 100 such sets of experiments each of n observations = .
2.4. Other Calculations
All curve-fitting was based upon a modified Gauss-Newton algorithm by least squares [18] minimization performed on a Microsoft Excel spreadsheet: [19] some of these results were fit to the algebraic form . However, certain MPN data ( and ) were also fit to a Gaussian (Equation (5): or ) with used as one of the parameters to be iteratively resolved (i.e., deconvolved). Where appropriate, confidence limits (CL) have been calculated using an approach applicable to any hypothetical fitting function : rows of the observed X-Y data sets with up to P (typically ≤ 3) fitting parameters ( ). In this procedure we use the propagation of error method [9] [20] for estimating the standard error associated with each ( ; illustrated below for P = 2 fitting parameters) data point
where, for any particular fitting parameter , = “asymptotic standard error” [19] (ASE; = residual sum of squares ÷ [K − P]), and the terms symbolize . The above equation simplifies to
.
In all the above relationships Z is the partial first derivative matrix of with respect to the parameters and (i.e., a 2-parameter fit) such that
,
is the transpose of Z, (K row vectors), and is the variance-covariance matrix [21]. CL were not used for all results since they might have muddled analytical aspects of the compositions.
2.5. Microbiome Sampling Data
For the food microbiome sampling experiment ~25 g of commercial, pre-thawed (~15 min at room temperature), frozen vegetables were washed with a volume of phosphate buffered saline (PBS; 10 mM Na2HPO4 + 2 mM NaH2PO4 + 137 mM NaCl; pH 7.4 ± 0.2; Boston BioProducts, 159 Chestnut Street, Ashland, MA 01721) equivalent to double the mass of the sample. In order to assist in the detachment of plant tissue-bound cells, 0.075% [w/v] Tween-20 (Sigma-Aldrich, 3050 Spruce St., St. Louis, MO 63103) was added to the PBS and filter sterilized. All washing was performed in sanitized plastic zip-lock bags wherein the formerly frozen vegetables and buffer wash were gently agitated at 80 rpm for approximately 20 min and immediately passed through a 40 μm nylon filter (BD Falcon; Becton Dickinson Biosciences, Bedford, MA) to remove large particles.
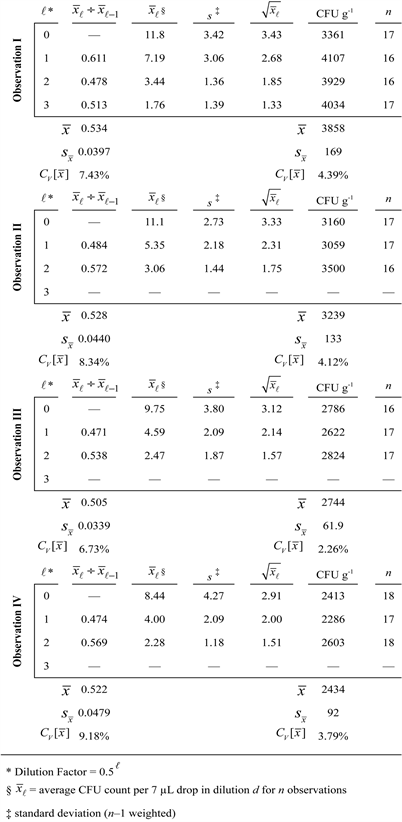
Directly sampled washes (5 mL Control = Observation I [cultured at 30˚C] and III [cultured at 37˚C]) as well as hollow fiber microfilter-concentrated (each 5 mL sample was diluted to ~100 mL PBS + Tween, concentrated, then washed with another 100 mL buffer, and eluted with ~5 mLs PBS + Tween = Observation II [cultured at 30˚C] and IV [cultured at 37˚C]) samples were collected and enumerated using the 6 × 6 drop plate method [14] but using 1:2 serial dilutions for colony selection on Brain Heart Infusion agar (BHI + 2% [w/v] agar). Briefly, this drop plate method involved loading 400 μL of each wash (either control or concentrated samples brought back to the control sample’s original volume = 5 mL) filtrate into the first well (row A) of a 96-well microtiter plate. Two-fold serial dilutions were made by transferring 200 μL (multichannel pipette, Rainin, Emeryville, CA) from the first row (row A; dilution 0) into 200 μL of diluent (PBS) in the 2nd row (row B; dilution 1), mixing 10 times while continuously stirring, and repeating the process until five 1:2 dilutions were produced; pipette tips were changed between dilutions. Based on a previous analysis of 6 × 6 drop plate sampling error [15] , we sampled n = 16 - 18 seven μL volumes from each of the 6 dilutions (dilutions 0 - 5; overall dilution factors of 0.50 = 1 to 0.55 = 0.03125) and drop-plated these onto BHI agar media using a multichannel pipette. After plating, the droplets were allowed to dry, inverted and then incubated at two temperatures (either 30˚C or 37˚C; 3 plates for each temperature and treatment combination). Colonies were counted after 16 - 24 hours. Colony collection for our 16S rDNA bacterial identification protocol [7] involved selecting all colonies from dilution 2 (0.52 = 0.25 dilution; = 2.79 ± 1.52 colonies per drop; ± s; the fact that = 1.67 ~ s might argue for an appropriately sampled population).
Each colony (n total) was carefully removed from the agar plate’s surface using a Rainin L20 tip, dispersed into 200 μL BHI in a 96-well plate and incubated at 30˚C for 16 - 24 hours. These cultures were restreaked onto solid media and incubated at 30˚C overnight. One colony from each of the original n plates was selected, suspended into 25 μL of Ultra PrepMan (Applied Biosystems, Foster City, CA) in a PCR tube and heated in a thermocycler at 99˚C for 15 min. Upon cooling, samples were centrifuged 10 min. to separate the DNA solution from the cell debris. A sample of supernatant was transferred to a new tube for the DNA amplification step (end-point PCR). Once the 16S rRNA “gene” amplification, sequencing reactions (EubA and EubB primers) and Sanger sequencing were performed, DNA sequences were edited, and contigs assembled using Sequencher software as explained in detail previously [7].
3. Results and Discussion
Figure 1 shows results related to averages of 100 × values ( ) derived from Equations (7) (P-I, black data) or (8) (P-II, red data) as a function of n (Figure 1(A)) and μ (Figure 1(B)). The least squares curve-fitting results show that the Figure 1(A) data follow the general form whereupon (averaged across 5 n-based fits) = −0.556 ± 0.00986 (black data sets; ±s) or (red data). These findings suggest that changes as the inverse square root of n for all values of μ. Figure 1(C) displays these same results on a linearized scale (X-axis = ) whereupon the slopes . Figure 1(B) illustrates that the values derived from Figure 1(A) non-linear regression change as the inverse square root of μ: i.e., where a = −0.547 ± 0.0179 (black data) or −0.503 ± 0.0374 (red data); a ± ASE. Figure 1(D) shows Figure 1(B) results plotted on an appropriately linearized scale (X-axis = ) as indicated by the above analysis whereupon the slope . Combining results from Figure 1(A) and Figure 1(B) we see that . The average value for A was 0.804 ± 0.0460 (P-I & P-II curve-fitting results ±s).
Figure 2 displays MPN-based enumeration data, Equation (9), manipulated in a similar fashion as that of the above Poisson-based results with a nearly identical result. The least squares curve-fitting shows that the data in Figure 2(A) once again follow the general form with = −0.554 ± 0.0499 (±s) which is the average a from 5× μ-based data sets. Figure 2(C) shows these same findings graphed on a linearized scale ( ) whereupon the slopes = . Figure 2(B) also shows that the values, derived from Figure 2(A) non-linear regression, change as the inverse square root of μ: where a = −0.515 ± 0.0910 (±ASE). As previously observed, when these results are presented on a linearized scale ( ; Figure 2(D)) the slope is equivalent to the parameter A. Combining fitting results from Figure 2(A) and Figure 2(B) we again note that (A = 0.807 ± 0.139; ± ASE).
Completely homologous relationships to the Poisson and MPN findings were also noted with Gaussian-based data (Figure 3) whereupon the least squares curve-fitting in Figure 3(A) shows that these data obey, again, the general form whereupon = −0.561 ± 0.0276 (±s; averaged across all σ since μ was fixed). Figure 3(C) has these same findings plotted on a linear scale ( ) where the slopes = . Figure 3(B) and Figure 3(D) also show that the values derived from Figure 3(A) and Figure 3(C) non-linear regression change linearly with : i.e., (A = 0.725 ± 0.0977; ± ASE). All Gaussian-based data fitting results combined indicate that whereupon is the coefficient of variation for a population of means associated with x.
3.1. Equivalence of Sampling Errors Associated with Any PDF
The counting results alluded to above (P-I, P-II, & MPN) are similar to those observed previously: [5] [15] [16] i.e., stochastic sampling errors associated with microbiological colony counting and MPN data are proportional to the inverse square root of n × μ. Also, the Poisson population-based results compare favorably with those obtained from actual colony counting experiments [14]. Thus, for all Poisson-based data (Figure 1)
(11)
because . We have simplified the expression by utilizing the term [22] (= ) which can be derived using the propagation of errors method [20]. Such nomenclature exemplifies the utilization of , as an approximation for , associated with a population of sample means ( ) of mean and standard deviation . However, for MPN results, does as an approximation? This question is addressed in detail (Figures 4-6).
Figure 4. (A) & (C) Frequency of observing each set of MPN-based calculated number of entities per sample tested ( ; μ = 0.8 for (A) & (B); μ = 0.4 for (C) & (D) fit to Equation (5) (i.e., as a function of ). (B) and (D) shows that (i.e., for MPN, ) for all modeled n-samplings. Error bars are = t0.05 × the experimental (overall) .
Figure 5. (A) & (B) Frequency of observing each set of MPN-based number of positive counts tested: μ = 0.8 and n = 3, 6, 9, 12, 24; (A) data points [red] = frequency of observed , (B) data points [blue] = calculated frequency of using Mathematica from , Equation (3), fit to a Gaussian probability distribution: e.g., , Equation (5). (C) Demonstrates that . Linear fit showing slope (A) and intercept (I) ± ASE. The non-linear fits were . Best fit curves shown ± P = 0.05 CL.
Figure 6. Demonstration that . All data are plotted ± P = 0.001 CL. (A) is related to P-I data (A = 0.741 ± 0.0203; ± ASE). (B) is related to P-II data (A = 0.827 ± 0.0133). (C) is related to MPN data (A = 0.861 ± 0.0273). (D) is related to Gaussian data (A = 0.637 ± 0.0280). All data are merged in (E): slope of this relationship which involves all three PDFs is 0.767 ± 0.0990.
In Figure 4(A) and Figure 4(C), we have examined some of our MPN data (μ = 0.8 per sample in Figure 4(A) and μ = 0.4 per sample in Figure 4(C) at the various levels of n-sampling) by converting the total number of positive occurrences ( ) in n observations to the most probable number of entities in the hypothetical sampled aliquot ( ) and curve-fit the frequency of occurrence of each to Gaussian PDFs (Equation (5); ). From these curve fits we extracted the parameters and . In Figure 4(B) and Figure 4(D) we show that the average (i.e., ) and, therefore, . This finding indicates that Equation (11) can be applied to both Poisson and MPN results as a reasonable approximation. We have confirmed the MPN results in Figure 2 and Figure 4 by showing that the frequency distribution of which we have observed in these experiments closely follows Equation (3) (compare Figure 5(A) with Figure 5(B)) whereupon we establish that , the standard deviation associated with the distribution of via the Gaussian approximation, was proportional to (Figure 5(C)) for both observed (red data) and calculated (blue data) with a proportionality constant numerically similar to A (=0.735 ± 0.0543; ±ASE) alluded to above.
The equality in Equation (11) is also visually confirmed by the results shown in Figure 6 where one can see that all values of closely follow the linear expression (for or ; A = 0.781 ± 0.0107; ±ASE) showing that
.
Since the combined data in Figure 6 are linear with a near-zero intercept (−0.0168 ± 0.00443), then
therefore cross-multiplying gives
and dividing both sides by produces the equality
.
All sampling error-related findings are summarized in Figure 7.
3.2. Demonstration That
Lastly, all these assertions are substantiated by the observation (Figure 8) that the standard deviations associated with all our sampling error measurements ( ) change linearly as a function of the 4 (P-I, P-II, MPN, Gaussian) sets of data with an average slope (i.e., average of the 4 values = 0.716 ± 0.0739) equivalent to the various values for A in Figures 1-3, Figure 5 and Figure 6. In fact, the slope in Figure 8 defines the coefficient of variation in ( ) and, if equal to A, then
(12)
where X = either or . Since in Figure 8 and in Figure 6 are linear functions with a near zero intercept then, assuming Equation (12) is true,
.
Substituting with
Figure 7. Summary of curve-fitting results associated with each PDF and method for calculating empirical stochastic sampling error ( ). Each constant of proportionality A is presented ± ASE. For binomial data (MPN) (the population average number of entities in V) and (the population average number of positive responses out of n observations).
and therefore
The above equality establishes that the coefficient of variation associated with ( ) is equivalent to the proportionality constant A seen in Figures 1-3 and Figure 6. Thus sampling errors can be estimated from the relationship whereupon for all PDFs we have tested.
3.3. Minimized Errors Associated with a Well-Sampled Food Microbiome via Most Probable Composition [7]
Based upon these results, the estimation of (i.e., ) should be germane in determining if data have been appropriately sampled. Figure 9 illustrates that all stochastic errors associated with native aerobic bacteria surviving
Figure 8. (A)-(D): Dependency of the standard deviation (plotted ± P = 0.05 confidence limits) derived from each experimental array ( ; ) on their averages ( ): Figure 8(A) = P-I data (Spearman’s coefficient of rank correlation: [22] ; ); Figure 8(B) = P-II data ( ; ); Figure 8(C) = MPN data ( ; ); Figure 8(D) = Gaussian data ( ; ). The average slopes associated with these 4 relationship = 0.716 ± 0.0739 (± s). All points (25× per set) from (A) through (D) are combined in the bottom-most figure ( ; ± ASE). The value is equivalent to an experimental coefficient of variation for .
on commercially available, frozen vegetables were sufficiently sampled using an n = 16 - 18 inasmuch as the -values associated with the normalized colony counts (CFU g−1 averaged across all dilutions = ÷ 0.007 mL per drop ÷ dilution factor × 57.2 mL total original sample volume ÷ 28.6 g total frozen vegetable mass) were appropriately small (ranging between ca. 2% to 4%). In a
Figure 9. Estimation of the stochastic sampling errors ( ~ calculated dilution factors; ; for all counts~4% across all dilutions ℓ) associated with a well-sampled [15] (n = 16 - 18) Poisson population (native bacteria on frozen vegetables: 28.6 grams rinsed with 57.2 mL PBS + Tween 20). All the colonies in ℓ = 2 (Control & grown at 30˚C = 55 colonies; Hollow Fiber Concentrated & grown at 30˚C = 49 colonies; Control & grown at 37˚C = 41 colonies; Hollow Fiber Concentrated & grown at 37˚C = 41 colonies) were collected and identified using 16S rDNA Sanger sequencing (EubA and EubB primers) as described previously [7]. Bacterial compositions were nearly identical for all samplings and treatment combinations.
similar vein, it is pertinent that the observed (s) and calculated ( ) standard deviations associated with the counts per drop were equivalent since the average deviation ( ) from ideality varied only 15.7% ± 3.54% ( ). Lastly it is also significant that the dilution factors calculated from the ratios of average plate counts ( ) were very close to ½ (average 0.523 ± 0.0172) which also argues for a minimized .
Across the 4 observational sets (I, II, III, and IV) depicted in Figure 9, the total number of collected colonies (from ) was 55 (n = 16), 49 (n = 16), 42 (n = 17), and 41 (n = 18), respectively. Bacteria identifications for each of these colonies were based upon rDNA sequence matching 1200 - 1400 basepair contigs searching against NCBI’s GenBank database. The rRNA “gene” sequencing results for the 2 major isolates (making up 88.3% ± 3.28% of the total sampled colonies) show that the 4 sets of observed bacterial compositions were nearly identical (43.6% ± 8.05% Luconostoc and 44.6% ± 13.3% Lactococcus; ±s) [23]. The remainder of the colonies was mainly Acinetobacter (3.74% ± 3.34%) and Streptococcus (4.17% ± 2.75%) with small amounts of diverse isolates (e.g., Staphylococcus, Arthrobacter, Sphingobacterium, Enterococcus, Kocuria, Raoultella, and Bacillus: averaging 1.49% ± 1.09% each). Such variability is expected for the relatively rare isolates (≤4%) due to errors associated with random sampling. The two major species sampled were relatively repeatable because of their abundance, adequate sampling, and very little treatment effect. The minor constituents would have to have been sampled 2.77 ± 0.647-fold more (n > 44) for an equivalent accuracy to the Luconostoc and Lactococcus fractions since the requisite number of samplings for the low count fractions, above, is proportional to the inverse cube root [5] [16] of the number of counts per sampled volume (~ ).
4. Summary
We have performed analyses associated with empirical stochastic sampling errors linked to data generated from 3 common probability density functions. We have used these to describe the limiting behavior of by generating models which suggest a generalized, and facile, mathematical solution. Based upon all our experiments, the common algebraic solution, regardless of parent distribution, is that experimental sampling errors are proportional to . This generalized relationship is intuitively reasonable inasmuch as this is the for any population of sample means ( ) and describes how closely values approach μ as n increases. The proportionality constant for all these findings was found to be mathematically related to or , which is the coefficient of variation associated with the error measurement itself. Lastly, using estimates of these sampling-associated errors ( ), we show that when a test microbiome was sufficiently sampled, several measures of stochastic sampling error were reasonably small for both counting and DNA sequence-based results.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Irwin, P.L., He, Y. and Chen, C.-Y. (2019) Deconvolution of the Error Associated with Random Sampling. Advances in Pure Mathematics, 9, 205-227. https://doi.org/10.4236/apm.2019.93010
References
- 1. Halvorson, H.O. and Ziegler, N.R. (1933) Application of Statistics to Problems in Bacteriology. I. A Means of Determining Bacterial Population by the Dilution Method. Journal of Bacteriology, 25, 101-121.
- 2. Kubitschek, H.E. (1990) Cell Volume Increase in Escherichia coli after Shifts to Richer Media. Journal of Bacteriology, 172, 94-101. https://doi.org/10.1128/jb.172.1.94-101.1990
- 3. Barkworth, H. and Irwin, J.O. (1938) Distribution of Coliform Organisms in Milk and the Accuracy of the Presumptive Coliform Test. Journal of Hygiene, 38, 446-457. https://doi.org/10.1017/S0022172400011311
- 4. Best, D.J. (1990) Optimal Determination of Most Probable Numbers. International Journal of Food Microbiology, 11, 159-166. https://doi.org/10.1016/0168-1605(90)90051-6
- 5. Irwin, P., Reed, S., Nguyen, L., Brewster, J. and He, Y. (2013) Non-Stochastic Sampling Error in Quantal Analyses for Campylobacter Species on Poultry Products. Analytical and Bioanalytical Chemistry, 405, 2353-2369. https://doi.org/10.1007/s00216-012-6659-2
- 6. Irwin, P., Gehring, A., Tu, S.-I., Brewster, J., Fanelli, J. and Ehrenfeld, E. (2000) Minimum Detectable Level of Salmonellae Using a Binomial-Based Ice Nucleation Detection Assay. Journal of AOAC International, 83, 1087-1095.
- 7. Irwin, P.L., Nguyen, L.-H.T., Chen, C.-Y. and Paoli, G. (2008) Binding of Nontarget Microorganisms from Food Washes to Anti-Salmonella and anti-E. coli O157 Immunomagnetic Beads: Most Probable Composition of Background Eubacteria. Analytical and Bioanalytical Chemistry, 391, 525-536. https://doi.org/10.1007/s00216-008-1959-2
- 8. de St. Groth, S.F. (1982) The Evaluation of Limiting Dilution Assays. Journal of Immunological Methods, 49, R11-R23. https://doi.org/10.1016/0022-1759(82)90269-1
- 9. Bevington, P.R. and Robinson, D.K. (1992) Data Reduction and Error Analysis for the Physical Sciences. McGraw-Hill, Boston, 17-23 and 41-43.
- 10. Irwin, P., Fortis, L. and Tu, S.-I. (2001) A Simple Maximum Probability Resolution Algorithm for Most Probable Number Analysis Using Microsoft Excel. Journal of Rapid Methods and Automation in Microbiology, 9, 33-51. https://doi.org/10.1111/j.1745-4581.2001.tb00226.x
- 11. Gosset, W.S. (1907) “Student” on the Error of Counting with a Haemocytometer. Biometrika, 5, 351-360. https://doi.org/10.1093/biomet/5.3.351
- 12. Fisher, R.A. (1922) On the Mathematical Foundations of Theoretical Statistics. Philosophical Transactions of the Royal Society, London, Series A, 222, 309-368. https://doi.org/10.1098/rsta.1922.0009
- 13. Irwin, P.L., Nguyen, L.-H.T., Paoli, G.C. and Chen, C.-Y. (2010) Evidence for a Bimodal Distribution of Escherichia coli Doubling Times below a Threshold Initial Cell Concentration. BMC Microbiology, 10, 207.
- 14. Chen, C.-Y., Nace, G.W. and Irwin, P.L. (2003) A 6×6 Drop Plate Method for Simultaneous Colony Counting and MPN Enumeration of Campylobacter jejuni, Listeria monocytogenes, and Escherichia coli. Journal of Microbiological Methods, 55, 475-479. https://doi.org/10.1016/S0167-7012(03)00194-5
- 15. Irwin, P.L., Nguyen, L.-H.T. and Chen, C.-Y. (2008) Binding of Nontarget Microorganisms from Food Washes to Anti-Salmonella and Anti-E. coli O157 Immunomagnetic Beads: Minimizing the Errors of Random Sampling in Extreme Dilute Systems. Analytical and Bioanalytical Chemistry, 391, 515-524. https://doi.org/10.1007/s00216-008-1961-8
- 16. Irwin, P.L., Nguyen, L.-H.T. and Chen, C.-Y. (2010) The Relationship between Purely Stochastic Sampling Error and the Number of Technical Replicates Used to Estimate Concentration at an Extreme Dilution. Analytical and Bioanalytical Chemistry, 398, 895-903. https://doi.org/10.1007/s00216-010-3967-2
- 17. Trotter, H.F. (1959) An Elementary Proof of the Central Limit Theorem. Archiv der Mathematik, 10, 226-234. https://doi.org/10.1007/BF01240790
- 18. Hartley, H.O. (1961) The Modified Gauss-Newton Method for Fitting of Non-Linear Regression Functions by Least Squares. Technometrics, 3, 269-280. https://doi.org/10.1080/00401706.1961.10489945
- 19. Irwin, P.L., Damert, W.C. and Doner, L.W. (1994) Curve Fitting in Nuclear Magnetic Resonance Spectroscopy: Illustrative Examples Using a Spreadsheet and Microcomputer. Concepts in Magnetic Resonance, 6, 57-67. https://doi.org/10.1002/cmr.1820060105
- 20. Beers, Y. (1957) Introduction to the Theory of Error. Addison-Wesley Publishing Company, Inc., Reading, 29-30.
- 21. Salter, C. (2000) Error Analysis Using the Variance-Covariance Matrix. Journal of Chemical Education, 77, 1239-1243. https://doi.org/10.1021/ed077p1239
- 22. Steel, R.G.D. and Torrie, J.H.D. (1960) Principles and Procedures of Statistics. McGraw-Hill, New York, 409.
- 23. Irwin, P., Capobianco, J., Nguyen, L., He, Y., Gehring, M., Gehring, A. and Chen, C.-Y. (2019) Bacterial Cell Recovery after Hollow Fiber Microfiltration Sample Concentration and Washing: Most Probable Bacterial Composition in Frozen Vegetables.
Definitions
Indices = i ( ) observations per experiment; j ( ) experiments with n observations each; k ( ) rows of X-Y values; ( ) dilutions; m ( ) iterations; p ( ) parameters
= j th experimental measure of sampling error out of J = 100 experiments: Equations (7)-(10).
= average sampling error in J = 100 observations of
A = proportionality constant associated with curve-fitting to n, μ (or σ)
= standard deviation associated with measurement; for this work there are 25 ( or for the Gaussian populations) such for each PDF type (2 types of Poisson, MPN or binomial, Gaussian)
= for either Poisson PDF or MPN assays ( ), the population average number of biological entities, or other analytes, per test; for Gaussian PDF, the population’s average of any real-valued, randomly changing variable
V = the sample volume to be tested
= volume of the biological entity, or other analyte, being tested
= concentration of the biological entity (count ÷ V) or other analyte
= population average number of positive growth responses (MPN) out of n observations;
= the standard deviation associated with the probability density of ; the Gaussian approximations for are plotted in Figure 5(C) as a function of Gaussian best fits for
= probability that will NOT contain the biological entity, or other analyte, being tested
= probability that will contain the biological entity, or other analyte, being tested; ; Equation (1)
=
= for Poisson populations, the i th observation’s number of counts per tested volume, surface area, etc. for each j th experiment; for Gaussian populations, any real-valued, randomly changing variable
=
= j th experiment’s number of positive growth responses out of n observations; where θ = 1 (positive) or 0 (negative)
= j th experiment’s number of positive counts in V volume; ; the x-bar symbol is used here because this relations contains a parameter, , which is the result of a summation across all ; it just isn’t normalized to n
n = number of technical replicates in each j th experiment; for MPN, number of observations each of volume V; for Poisson populations we have found [15] that the minimal number of replicates per assay was where is the number of replicates necessary to enumerate a population with μ = 1
= population standard deviation associated with μ
= standard deviation of a population of sample means ( ); the formula for the statistic can be derived from the propagation of errors method [20] without covariance
since
and
.
= any jth experiment’s estimation of population standard deviation
= estimation of from a limited number of ;
= coefficient of variation for a population of means; estimated as
= coefficient of variation for any set of observations x; estimated as
= if the vs. intercept ~ 0
CLT = central limit theorem: the mean ( ) of a population of observed means ( ) will be approximately equal to the mean of the sampled population (μ) and the standard deviation of this population of means will be approximately equal to ; Equation (5) with , , and
PDF = probability density function or probability distribution function
= binomial PDF: Equation (3)
= Poisson PDF: Equation (4)
= Gaussian PDF: Equation (5)
CL = confidence limit = t-statistic × =
ASE = asymptotic standard error [19] ; for any fitting parameter ,
; = residual sum of squares ÷ (K − M) where M =
the number of fitting parameters ( )
= kth row standard error of fitting function fk;
= partial first derivative matrix of with respect to associated fitting parameters
= transposition of
= for