ABSTRACT

The concept of quasi-periodic property of a function has been introduced by Harald Bohr in 1921 and it roughly means that the function comes (quasi)-periodically as close as we want on every vertical line to the value taken by it at any point belonging to that line and a bounded domain $\Omega$ . He proved that the functions defined by ordinary Dirichlet series are quasi-periodic in their half plane of uniform convergence. We realized that the existence of the domain $\Omega$ is not necessary and that the quasi-periodicity is related to the denseness property of those functions which we have studied in a previous paper. Hence, the purpose of our research was to prove these two facts. We succeeded to fulfill this task and more. Namely, we dealt with the quasi-periodicity of general Dirichlet series by using geometric tools perfected by us in a series of previous projects. The concept has been applied to the whole complex plane (not only to the half plane of uniform convergence) for series which can be continued to meromorphic functions in that plane. The question arise: in what conditions such a continuation is possible? There are known examples of Dirichlet series which cannot be continued across the convergence line, yet there are no simple conditions under which such a continuation is possible. We succeeded to find a very natural one.

Keywords:

Dirichlet Functions, Analytic Continuation, Fundamental Domains, Quasi-periodic Functions

1. Introduction

The theory of Dirichlet series started at the end of the 19-th Century with works of celebrated mathematicians as Hadamard, Landau, Bohr etc. These series are natural generalizations of the Riemann Zeta series. From the beginning questions were asked of what are those Dirichlet series which can be continued as meromorphic functions in the whole complex plane and satisfy there similar properties with those of the Riemann Zeta function, as for example a Riemann type of functional equation, similar display of non trivial zeros (the famous Riemann Hypothesis) etc. We devoted a lot of studies to these questions by using geometric methods. We perfected an idea of Speiser (1934) of studying the pre-image of the real axis by functions obtained as meromorphic continuations to the whole complex plane of general Dirichlet series. The key result was a way to identify the fundamental domains of these functions. These are domains represented conformally (hence injectively) by the functions onto the whole complex plane with some slits.

As Ahlfors [1] noticed, this is the most natural way to proceed when studying different classes of functions. The results are promising and there are a lot of followers mainly in the field of Blaschke products but also in that of Dirichlet functions.

By a general Dirichlet series we understand an expression of the form

${\zeta }_{A,\Lambda }\left(s\right)={\displaystyle \sum _{n=1}^{\infty }}{a}_n{\text{e}}^{-{\lambda }_{n}s},$ (1)

where $A=\left(a_n\right)$ is an arbitrary sequence of complex numbers and ${\lambda }_1<{\lambda }_2<\cdots$ is an increasing sequence $\Lambda$ of non negative numbers with $\underset{n\to \infty }{\lim }{\lambda }_n=\infty$ . There is no loss of generality by considering only normalized series (1) in which $a_1=1$ and ${\lambda }_1=0$ . It is known [2] that if the series (1) converges for $s=s_0={\sigma }_0+i{t}_0$ , then it converges for every s with $\mathrm{Re}s>{\sigma }_0$ . The number ${\sigma }_c=\inf \left\{\sigma |{\zeta }_{A,\Lambda }\left(\sigma \right)\text{converges}\right\}$ , when it exists, is called the abscissa of convergence of the series (1). When the series does not converge for any $s\in ℂ$ we denote ${\sigma }_c=+\infty$ and if it converges for every s we put ${\sigma }_c=-\infty$ . The line $\mathrm{Re}s={\sigma }_c$ is called the line of convergence of (1), although there are examples of Dirichlet series (see [2] ) which do not converge for any s with $\mathrm{Re}s={\sigma }_c$ . Other series converge for all the points of that line, or only for some points.

When (1) does not converge for $s=0$ , then (see [2] )1

${\sigma }_c=\underset{n\to \infty }{\lim \sup }\frac{1}{{\lambda }_n}\log \left|{\displaystyle \sum _{k=1}^n}{a}_k\right|\ge 0.$ (2)

If (1) converges for $s=0$ , then

${\sigma }_c=\underset{n\to \infty }{\lim \sup }\frac{1}{{\lambda }_{n+1}}\log \left|{\zeta }_{A,\Lambda }\left(0\right)-{\displaystyle \sum _{k=1}^n}{a}_k\right|\le 0.$ (3)

The abscissa ${\sigma }_a$ of absolute convergence of the series (1) is defined in an analogous way and it is obvious that $-\infty \le {\sigma }_c\le {\sigma }_a\le +\infty$ . For the Riemann Zeta function ${\sigma }_c={\sigma }_a=1$ , while for the alternate Zeta function ${\sigma }_c=0$ and ${\sigma }_a=1$ . When ${\sigma }_c<+\infty$ then ${\zeta }_{A\mathrm{,}\Lambda }\left(s\right)$ converges uniformly on compact sets of the half plane $\mathrm{Re}s>{\sigma }_c$ and ${\zeta }_{A\mathrm{,}\Lambda }\left(s\right)$ is an analytic function in that half plane and sometimes it can be continued analytically to the whole complex plane except possibly for some poles. We will deal with this problem in Section 3. We keep the notation ${\zeta }_{A\mathrm{,}\Lambda }\left(s\right)$ for this extended function and we call it Dirichlet function. Since $a_1=1$ and ${\lambda }_1=0$ in the series (1) we have that $\underset{\sigma \to +\infty }{\lim }{\zeta }_{A,\Lambda }\left(\sigma +it\right)=1$ and it can be easily seen [3] that this limit is uniform with respect to t. In other words, for every $\epsilon >0$ there is ${\sigma }_{\epsilon }$ such that for $\sigma >{\sigma }_{\epsilon }$ we have $\left|{\zeta }_{A,\Lambda }\left(\sigma +it\right)-1\right|<\epsilon$ for every real t, hence ${\zeta }_{A\mathrm{,}\Lambda }\left(s\right)$ maps the half plane $\mathrm{Re}\left(s\right)>{\sigma }_{\epsilon }$ into the disc $\left|z-1\right|<\epsilon$ .

This fact suggests that the series (1) converges uniformly on that half plane. Harald Bohr defined the abscissa of uniform convergence of (1) as being the infimum ${\sigma }_u$ of the abscisas $\sigma$ such that (1) converges uniformly for $\mathrm{Re}\left(s\right)>\sigma$ . It has been found that ${\sigma }_c\ge {\sigma }_u\ge {\sigma }_a$ and every value between ${\sigma }_c$ and ${\sigma }_a$ can be taken by ${\sigma }_u$ for particular series (1).

Studying Dirichlet L-functions $f\left(s\right)$ generated by ordinary Dirichlet series (the case where ${\lambda }_n=\log n$ ) Harald Bohr (see [4] ) discovered that they display on vertical lines a quasi-periodic behavior, namely for every bounded domain $\Omega$ of uniform convergence of the series and for every $\epsilon >0$ there is a sequence $\left({\tau }_n\right)$ ,

$\begin{array}{l}\cdots <{\tau }_{-2}<{\tau }_{-1}<0<{\tau }_1<{\tau }_2<\cdots \\ \underset{n\to \pm \infty }{\lim \inf }\left({\tau }_{n+1}-{\tau }_n\right)>0,\\ \underset{n\to \pm \infty }{\lim \sup }\frac{{\tau }_n}{n}<\infty \end{array}$ (4)

such that for every $s\in \Omega$ we have $\left|f\left(s+i{\tau }_n\right)-f\left(s\right)\right|<\epsilon$ .

This roughly means that the function comes (quasi)-periodically on a vertical line as close as we want to the value of it at any point of $\Omega$ belonging to that line.

We study in this paper the quasi-periodic property of functions defined by general Dirichlet series and show that this is a geometric property of the image by ${\zeta }_{A\mathrm{,}\Lambda }\left(s\right)$ of vertical lines related to the fundamental domains of these functions. These fundamental domains are obtained as shown in [3] and [5] .

2. The Quasi-Periodicity on Vertical Lines of General Dirichlet Series

Let us give first to the concept of quasi-periodicity a slightly different definition. We will say that $f\left(s\right)$ is quasi-periodic on a line $\mathrm{Re}s={\sigma }_0$ if for every $\epsilon >0$ and for every $s={\sigma }_0+it$ a sequence (4) exists such that $\left|f\left(s+i{\tau }_n\right)-f\left(s\right)\right|<\epsilon$ . We notice that this definition is no more attached to bounded domains, hence it appears less restrictive than that given by Bohr, yet the inequality refers only to the points of a given vertical line and not to the points of any vertical line intersecting the domain $\Omega$ , which is a restriction. This new definition serves better the purpose of studying the denseness properties of Dirichlet functions.

Theorem 1 If ${\lambda }_n$ with $n=2,3,\cdots$ are linearly independent in the field of rational numbers then the series (1) is quasi-periodic on every vertical line of the half plane $Res>{\sigma }_u$ .

Proof Let s be arbitrary with $\mathrm{Re}s={\sigma }_0>{\sigma }_u$ and divide ${\zeta }_{A\mathrm{,}\Lambda }\left(s\right)$ and ${\zeta }_{A\mathrm{,}\Lambda }\left(s+i\tau \right)$ into the sum $A_n$ of the first n terms and the rest $R_n$ . Since the series converges uniformly on $\mathrm{Re}s={\sigma }_0$ , when $\epsilon >0$ is given, there is a rank n such that $\left|R_n\left(s\right)\right|<\frac{\epsilon }{3}$ and $\left|R_n\left(s+i\tau \right)\right|<\frac{\epsilon }{3}$ for every real number $\tau$ . On the other hand

$\left|A_n\left(s+i\tau \right)-A_n\left(s\right)\right|=\left|{\displaystyle \sum _{k=1}^n}{a}_k{\text{e}}^{-{\lambda }_{k}s}\left({\text{e}}^{-i{\lambda }_k\tau }-1\right)\right|$ (5)

By Diophantine approximation, a sequence (4) exists such that for every ${\tau }_m$ of that sequence ${\text{e}}^{-i{\lambda }_k{\tau }_m}$ is as close to 1 on the unit circle as we whish. Since the set $\left\{a_k{\text{e}}^{-{\lambda }_{k}s}\right\}$ is bounded, we have $\left|A_n\left(s+i\tau \right)-A_n\left(s\right)\right|<\frac{\epsilon }{3}$ for every $\tau ={\tau }_m$ and then $\left|{\zeta }_{A,\Lambda }\left(s+i\tau \right)-{\zeta }_{A,\Lambda }\left(s\right)\right|<\epsilon$ for every $\tau ={\tau }_m$ , which proves the theorem.

Remark For ordinary Dirichlet series we have ${\lambda }_n=\log n$ , for $n=2,3,\cdots$ and these are linearly independent in the field of rational numbers, therefore these series are quasi-periodic on every vertical line from the half plane of convergence.

It is known (see [5] ) that for every series (1) which can be continued analytically to a the whole complex plane except possibly for a simple pole at $s=1$ , the complex plane is divided into infinitely many horizontal strips $S_k\mathrm{,}k\in \mathbb{Z}$ bounded by components of the pre-image of the real axis which are mapped bijectively by ${\zeta }_{A\mathrm{,}\Lambda }\left(s\right)$ onto the interval $\left(\mathrm{1,}\infty \right)$ . These are unbounded curves ${{\Gamma }^{\prime }}_k$ such that for $\sigma +it\in {{\Gamma }^{\prime }}_k$ we have $\underset{\sigma \to +\infty }{\lim }{\zeta }_{A,\Lambda }\left(\sigma +it\right)=1$ and no ${{\Gamma }^{\prime }}_k$ can be contained in a right half plane. If $S_k$ , $k\ne 0$ contains $j_k$ zeros of ${\zeta }_{A\mathrm{,}\Lambda }\left(s\right)$ counted with multiplicities, then it will contain $j_k-1$ zeros of ${{\zeta }^{\prime }}_{A\mathrm{,}\Lambda }\left(s\right)$ . The strip $S_0$ can contain infinitely many zeros of such a function. Every strip $S_k\mathrm{,}k\ne 0$ containing $j_k$ zeros counted with multiplicities can be divided into 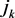unbounded subsets whose interiors 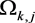are fundamental domains of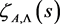, i.e. they are mapped conformally by onto the whole complex plane with some slits. The strip can contain infinitely many fundamental domains.

Every fundamental domain contains either a simple zero or no zero and in this last case a double zero belongs to the boundary of two adjacent fundamental domains. The zeros of are all simple zeros (see [6] ) and are all located on the boundaries of the fundamental domains.

Figure 1 illustrates the pre-image of the real axis for t between −20 and 20 by two Dirichlet L-functions defined by Dirichlet characters modulo 13 studied in [3] , the first one by a complex character and the second by a real one. On both

of them the strips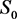, 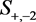and 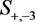can be seen, as well as the zeros belonging to these strips. For any Dirichlet function 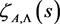every vertical line which does not pass through the pole is divided by the boundaries of the fundamental domains 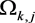into finite intervals which are mapped bijectively by 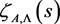onto Jordan arcs.

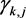The image of the whole line by 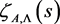is therefore the union of infinitely many Jordan arcs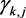. If two domains 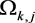are adjacent, then the ends of the corresponding 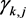which are images of the same point of the vertical line will obviously coincide. Moreover, different arcs can have some other common points.

The image of an interval determined by is a bounded curve starting and ending on and having a finite number of intersections with the real axis and also a finite number of self intersection points. These last points represent the intersections of different arcs as well as points corresponding to zeros of. At the points which are zeros of the corresponding arcs are tangent to each other (see [7] ).

When the analytic continuation to the whole complex plane of the series (1) is possible the arcs are defined for any vertical line, not only for the lines included in the half plane of convergence of this series. Then, expressing the quasi-periodic property in terms of these arcs, we can extend this concept to any vertical line. The extension can be performed by noticing that if is quasi-periodic on a vertical line from the half plane of uniform convergence of (1) then for every and every s with there is a sequence (4) such that

(6)

for small enough where is any term of the sequence (4). This means that to every term of this sequence corresponds an arc such that a point on that arc is located at a distance less than of for small enough. Then we can say that is quasi-periodic on the arbitrary line (not necessarily belonging to the half plane of uniform convergence of this series) if for every s with and every there are infinitely many fundamental domains of such that the inequality (6) is satisfied for some t with.

3. Analytic Continuation of General Dirichlet Series

It is known that some functions defined by Dirichlet series cannot be extended across the line since all the points of the abscissa of convergence are singular points. Examples of such series can be easily found as seen in [8] and [3] . On the other hand all the Dirichlet L-functions are analytic continuations to the whole complex plane, except for some poles of particular Dirichlet series. These continuations have been performed by using the Riemann technique of contour integration. In that follow, we will show that a similar technique is applicable also to general Dirichlet series.

We recall that the Gamma function can be expressed as

(7)

and this is a meromorphic function in the complex plane.

On replacing x by in (7), we obtain

which multiplied by and added gives

(8)

Here we have denoted by the sequence and we have interchanged the integration and the summation, which is allowed, since the integrals of the terms are absolutely convergent at both ends. We notice that Hardy and Riesz [2] have found (in Theorem 11) a similar formula to (8) in the case of a Dirichlet series convergent for, yet they did not use it to extend the function across the imaginary axis.

For the Riemann Zeta function we have (see [1] ) and after summation under integral in (8) one obtains

(9)

Riemann has shown that the integral from (9) is equivalent to a contour integral of on a curve C formed with a part of a circle of radius r centered at the origin and two half lines parallel to the real axis ( [1] , p. 216). The integrand is well defined on the respective curve and as the integral approaches that in (9). We cannot do the same thing with (8) as long as we don't make sure that the circle is in the half plane of convergence of. There is however a way to circumvent this difficulty by noticing that:

Theorem 2 If the series (1) has a finite abscissa of convergence, then the abscissa of convergence of is 0.

Proof Suppose that. Then

and the abscissa of convergence of is

If, then the abscissa of convergence of, which should be also less than or equal to zero, is given by the formula

Consequently, the half plane of convergence of is the right half plane.

Once we know this half plane of convergence, we can try to use the Riemann technique, but taking care to choose the integration curve in the right half plane. Fortunately such a choice is possible and we can prove:

Theorem 3 If has only isolated singularities on the imaginary axis, then the series (1) can be continued across the line to a meromorphic function in the whole complex plane.

Proof Let us form a contour with a half circle, where

and the half lines with, respectively with, as seen in Figure 2.

Since the singularities of are isolated, we can chose r such that the half circle does not contain anyone of them. We study the line integral. Let us notice first that is unambiguously defined as. The integrand is a continuous function on and therefore it is bounded on, since is a compact set. If is the blue contour, the red one and the green contour, then

as both of these integrals are obviously equal to, therefore the integral on does not really depend on r.

We can take r such that no singular point of except possible the origin exits on the interval of the imaginary axis between and. Now, we can let and show that the integral on tends to zero. Indeed, with we have and, thus

Since the function under the integral is bounded between and, the integral is finite and the whole expression tends to zero as, now, we can use the argument from [1] , page 214 to infer that (8) is equivalent to

(10)

The right hand side in (10) is defined for every complex value s and represents a meromorphic function in the whole complex plane.

4. Quasi-Periodicity and Denseness Property

The connection between the quasi-periodic property and the denseness property of the image of vertical lines by Dirichlet functions appears clearly when we interpret the first one in terms of the arcs. Indeed, we can prove the following:

Theorem 4 The necessary and sufficient condition for to be quasi-periodic on the line is that for for every and every point s on that line infinitely many fundamental domains exist such that the corresponding arcs intersect the disc.

Proof The condition is necessary, since if for every and every s on the line a sequence (4) exists with the property that, then the number of domains containing points must be infinite. Indeed, the inequality implies that every can contain only a finite number of points. Then there must be infinitely many arcs intersecting the disc. Vice versa, if infinitely many such arcs exist, then choosing a point belonging to that disc on each one of them, the sequence satisfies obviously the conditions (4).

Hence, if is quasi-periodic on the line then any small neighborhood V of every point with intersects infinitely many arcs, therefore the image of is dense in (at least a part of) V. Indeed, there is an arc passing through and as close as we want of this arc pass infinitely many arcs, which are parts of the image of the same line and every one of these arcs has the same property, hence the denseness of the image of in the part of V around this arc is obvious. Then we can say that the quasi-periodic property of on the line implies the denseness in itself of the image of that line by. Indeed, every point of is either an intersection point with another arc or a tangent point with such an arc or a limit point of arcs in the sense that there is a sequence of such arcs whose distance to that point tends to zero.

No two arcs and can overlap partially. Indeed, in the contrary case, we would have that the conformal mapping of onto given by, where, maps an interval of onto another interval of the same line, which would be possible only if were a linear transformation and this is not the case. Hence the image of the line by cannot have arcs towards which no other arcs accumulate. Its closure is necessarily a two dimensional set whose boundary is formed by arcs or limit points of such arcs.

In order to study the image of vertical lines by the series (1) the condition that the exponents are linearly independent in the field of rational numbers has been assumed in [9] . As we suppose that, we cannot use the results in [9] for the series (1), yet we can study the series and translate the results obtained to. By [9] , under the condition of linear independence of the exponents of, the closure of the image by of the line, where is greater than the abscissa of absolute convergence of the series (1) (which is obviously the same as that of) is either a ring domain or a disc, according to the case where the sequence has a leading (vorhanden) term or not. Consequently, under the same condition, this image by will be a ring domain, respectively a disc. We say that the numericseries has the leading term if. The previous numbers R and r are respectively and, where.

The results of Bohr are in agreement with the fact that the function (1) tends uniformly with respect to t to 1 as. Indeed, for, where is big enough, if there is a leading term of the series then the image by of the line is included in the ring domain and it is a dense set in this domain. Here we have denoted by the sequence. As gets smaller, some other term can become leading term and then the image by of the line will be included in the ring domain. If no leading term appears, then the respective ring domain will evolve into a disc. At the limit, as we have and the image of the line is a dense set either in the whole complex plane or outside of an open disc. Hence we can state:

Theorem 5 For any Dirichlet function the image of the line, is a dense set in either a ring domain or a disc according to the fact that has a leading term or not. When we have and these domains become the exterior of an open disc or respectively the whole complex plane.

For the Riemann series, the term is leading term for as long as. Let us denote by the solution of the equation

. By inspecting a table of values of we noticed that, hence for the image by of the line is included in the disc and it is a dense set in this disc. For, if we denote then this image is included in the ring domain.

5. Conclusion

A Dirichlet function is defined by an arbitrary sequence of complex numbers (the coefficients) and a sequence of increasing positive numbers (the exponents), otherwise also arbitrary. It is intriguing how two such arbitrariness can involve a strong property as that of quasi-periodicity. We have shown that this is in fact a geometric property related to the fundamental domains of the respective function. The domains are infinite strips which are mapped conformally by the function onto the whole complex plane with some slits. A vertical line intersects all those strips and the values of the function on each one of the segments obtained come quasi-periodically close to every given value on that line as illustrated in Figure 3 and Figure 4. The Diophantian approximation plays here

the same role as in the denseness property and this is the reason why the two properties come simultaneously. We brought in this paper some light into these two complex phenomena.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Cite this paper

Ghisa, D. and Horvat-Marc, A. (2018) Geometric Aspects of Quasi-Periodic Property of Dirichlet Functions. Advances in Pure Mathematics, 8, 699-710. https://doi.org/10.4236/apm.2018.88042

References

NOTES

¹We followed the tradition of this monograph by using the notation “log” for the principal branch of the multivalued function logarithm. Obviously, when the argument is positive, it simply means natural logarithm.