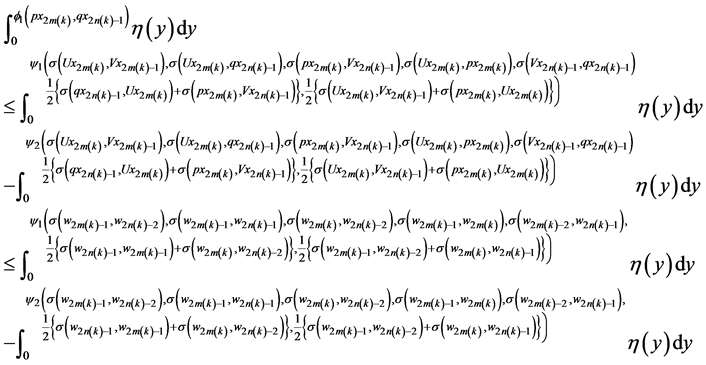Advances in Pure Mathematics
Vol.07 No.06(2017), Article ID:76781,10 pages
10.4236/apm.2017.76020
Common Fixed Point Theorems in Metric Space by Altering Distance Function
Vishnu Narayan Mishra1,2*, Balaji Raghunath Wadkar3, Ramakant Bhardwaj4, Idrees A. Khan5, Basant Singh3
1Applied Mathematics & Humanities Department, S.V. National Institute of Technology, Gujarat, India
2Department of Mathematics, Indira Gandhi National Tribal University, Madhya Pradesh, India
3Department of Mathematics, AISECT University, Bhopal, India
4Department of Mathematics, TIT Group of Institutes, Anand Nagar, India
5Department of Mathematics, Integral University, Lucknow, India
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 4, 2017; Accepted: June 6, 2017; Published: June 9, 2017
ABSTRACT
In the present paper, we prove two theorems. In first theorem, we prove fixed point result for self-maps in the metric space under contractive condition of integral type by altering distance. In second result, we prove a unique common fixed point theorem by considering four sub compatible maps under a contractive condition of integral type.
Keywords:
Altering Distance Function, Sub Compatible

1. Introduction and preliminaries
In [1] , Khan introduced and proved fixed point results by the altering distance in metric space. Aliouche [2] proved common fixed point results in symmetric space for weakly compatible mappings under contractive condition of integral type. In [3] , Babu generalized and proved fixed point results using control function. Later Bouhadjera and Godet [4] generalized concept of pair sub compatible maps and proved fixed point results. Also Chaudhari [5] [6] , Chugh & Kumar [7] , Naidu [8] , Sastry et al. [9] generalized and proved some fixed point results. Recently in [10] [11] , Hosseni used contractive rule of integral type by altering distance and generalized common fixed point results. Many authors proved fixed point results with different techniques in different spaces (see [12] - [17] ). In [18] [19] [20] [21] , Wadkar et al. proved fixed point theorems using the concept of soft metric space. In the present paper, we prove two theorems on fixed point under contraction rule of integral type in metric space by altering distance function, first for self map and second for a pair of sub compatible maps. Our results are motivated by V. R. Hosseni, Neda Hosseni.
Definition 1.1: A function
is an altering distance functions if
is continuous with monotone increasing in all variables and
if
The collection of all altering distance is denoted by
.
Now let us define a function
by
for
, clearly
if and only if
.
Examples of
are
for
, (1)
(2)
Definition 1.2: The maps
of metric space
are called as sub compatible if and only if the sequence
in E such that
and which satisfies
Example 1.3: Let
we define p & q with metric
as follows
&
(3)
Let us define the sequence
in E as
, for
then
(4)
and
(5)
(6)
Thus, we have
. (7)
Hence maps p and q are sub-compatible.
On the other hand, we have
if and only if
,
and
Then
but
, hence p and q are not OWC (Oscillatory weakly commuting).
2. Main Result
Theorem 2.1: Let us consider the mappings
of complete metric space
be such that for all
(8)
where
with
,
and Lebesgue-integr- able mapping
, which is positive, sum able, and for each
, then there exist a unique common fixed point in E for U and V.
Proof: Consider arbitrary point
of E, for
we have
and
.
Let
(9)
Substituting
and
in Equation (8), then for all
we have
Using Equation (9) for all
we get
(10)
As
implies that
, so we have
(11)
Now by monotone increase of
in all variables and using the property that
whenever
, we get a contradiction i.e.
not greater than
. Hence we have
, for
(12)
Substituting
in Equation (8) we have
(13)
By using (12) we consider
(14)
From (10) and (12) we obtain
(15)
From (8) & (11) for all
, we have
then
Taking summation in above equation we obtain
,
which implies
as
. (16)
Now from (13) sequence
is convergent and as
,
We know that
is continuous and from Equation (14) we obtain
which implies that
, i.e. as
(17)
We now show that the sequence
is a Cauchy sequence in E. Keeping in mind Equation (15) it is require to show that
is a Cauchy sequence. If
is not a Cauchy sequence of natural number
such that
,
(18)
Hence using (16)
Taking
in the inequality above & by result of Equation (15), we arrive at
. (19)
For all
(20)
Also for
. (21)
Making
in (18) & (19) respectively by using (15) & (17) we have
and
Therefore,
, for
(22)
Taking
in the above two inequalities and using (15) & (17) we obtain
. (23)
Putting
in (8), for all
, we obtain
Now in above inequality if we take
and by using results of (15), (20) & (21) we get
Then
This is due to monotone increasing fact of
in its variable and by using property of
that
if and only if
.
From the above inequality we get a contradiction. So that
. This establishes convergent sequence in
.
Let
as
. (24)
Substituting
in (8) for all
Taking limit n tends to infinity in the above inequality and using continuity of
and
and Equations (15), (22) we get
If
then monotone increasing
and
are monotone increasing and
if and only if
, we obtain
This contradiction, hence we obtain
(25)
In similar way we prove that
Hence
(26)
Hence (25) & (26) shows that z is a common fixed point of U and V.
Theorem 2.2: Let
be a complete metric space and p, q, U and V be four mappings from E to itself such that
(27)
for all
, where
,
, for
.
i: One of the four mappings p, q, U and V is continuous.
ii: (p, U) & (q, V) are sub compatible.
iii: The pairs
and
.
iv: Where
is Lebesgue-integrable mappings, which is sum able, non negative and such that for each
.
Then p, q, U and V have a unique common fixed point in E.
Proof: Consider arbitrary point
, we construct the sequence
and
in E such that
and
,
Let
, Substitution
and
in (27) we have
If
then
and
(28)
Thus we arrive at a contradiction. Hence
, similarly by substituting
in (27) we can prove that,
, for
. Thus
, for
. Hence the sequence
is sequence of positive real numbers, which is decreasing and converges to
.
Let
. Taking
in (27) we have
(29)
In view of (29), to prove sequence
is a Cauchy sequence it is sufficient to prove the subsequence
of sequence
is a Cauchy sequence. If
is not a Cauchy sequence there exist
& sequence of natural numbers
&
which are monotone increasing such that
.
(30)
Then from (29) we have
(31)
Taking
and using (29) we have
(32)
Taking
using (29) & (30) in
(33)
We get
(34)
Letting
and from Equations (29) & (30) in
We get
(35)
Putting
in (27), for all
we obtain
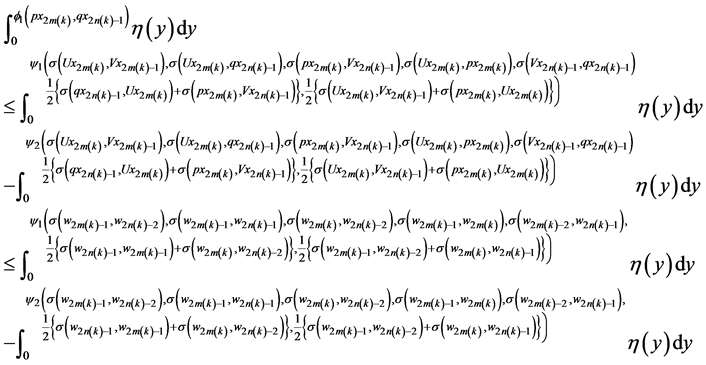
Taking
& using (29), (30), (32), (33) & (35) we get
This is contradiction. Hence
is a Cauchy sequence and is convergent. Since E is complete there exist
such that as
we have
.
Case I: Assume that U is continuous then
,
Since (p, U) is sub compatible, we have
Step I: Substituting
in (27), we have
It is contradiction if
. Hence
Step II: Substituting
in (27) and taking limit as n tends to infinity we get
.
Step III: We know that
then there exist
such that
. Substituting
in (27) we get
. Hence
and
, which gives
.
Step IV: Substituting
in (27) we have
so that
. Hence p, q, U & V have a common fixed point z in E.
Case II: Assume that U is continuous then
. Similarly we can prove that z is common fixed point of p, q, U & V. When q or V is continuous, then the uniqueness of common fixed point follows easily from (27).
Example: Let
with the usual metric
. Define
such that
,
,
,
.
Let
,
then
For all
, it follows that the condition (27).
Let
be a sequence in E such that
&
for some z in E. Then z = 0,
. Hence
is sub compatible. We have common fixed point in E.
3. Conclusion
In this paper, we proved the fixed point theorem for four sub compatible maps under a contractive condition of integral type. These results can be extended to any directions and can also be extended to fixed point theory of non-expansive multi-valued mappings.
Acknowledgements
The authors would like to give their sincere thanks to the editor and the anonymous referees for their valuable comments and useful suggestions in improving the article.
Cite this paper
Mishra, V.N., Wadkar, B.R., Bhardwaj, R., Khan, I.A. and Singh, B. (2017) Common Fixed Point Theorems in Metric Space by Altering Distance Function. Advances in Pure Mathematics, 7, 335-344. https://doi.org/10.4236/apm.2017.76020
References
- 1. Khan, M.S., Swaleh, M. and Sessa, S. (1984) Fixed Point Theorems by Altering Distances between Two Points. Bulletin of the Australian Mathematical Society, 30, 1-9.
- 2. Aliouche (2006) A Common Fixed Point Theorem for Weakly Compatible Mappings in Symmetric Spaces Satisfying a Contractive Condition of Integral Type. Journal of Mathematical Analysis and Applications, 322, 796-802.
- 3. Babu, G.V.R. (2004) Generalization of Fixed Point Theorems Relating to the Diameter of Orbits by Using a Control Function. Tamkang Journal of Mathematics, 63, 159-168.
- 4. Bouhadjera, H. and Godet, C. (2009) The Common Fixed Point Theorem for a Pair of Sub Compatible Maps. http://hal.archives-ouvertes.fr/hal-00356516v2
- 5. Choudhury, B.S. (2005) A Common Unique Fixed Point Result in Metric Spaces Involving Generalized Altering Distances. Mathematical Communications, 14, 105-110.
- 6. Choudhury, B.S. and Dutta, P.N. (2000) A Unified Fixed Point Result in Metric Spaces Involving a Two Variable Function. Filomat, 14, 43-48.
- 7. Chugh, R. and Kumar, S. (2001) Common Fixed Points for Weakly Compatible Maps. Proceedings of the Indian Academy of Sciences—Mathematical Sciences, 111, 241-247.
- 8. Naidu, S.V.R. (2001) Fixed Point Theorem by Altering Distances. Adv. Math. Sci. Appl., 11, 1-6.
- 9. Sastry, K.P.R., Naidu, S.V.R., Babu, G.V.R. and Naidu, G.A. (2000) The Generalization of Common Fixed Point Theorems for Weakly Commuting Maps by Altering Distances. Tamkang Journal of Mathematics, 31, 243-250.
- 10. Hosseni, V.R. and Hossseni, N. (2012) Common Fixed Point Theorems for Maps Altering Distance under Contractive Condition of Integral Type for Pairs of Sub Compatible Maps. International Journal of Math Analysis, 6, 1123-1130.
- 11. Hosseni, V.R. and Hossseni, N. (2010) Common Fixed Point Theorems by Altering Distance Involving under Contractive Condition of Integral Type. International Mathematical Forum, 5, 1951-1957.
- 12. Wadkar, B.R., Bhardwaj, R.K. and Singh, B. (2014) A Common Fixed Point Theorem in Dislocated Metric Space. International Journal of Engineering Research and Development, 10, 14-17.
- 13. Mishra, L.N., Mishra, V.N., Khatri, K. and Deepmala (2014) On the Trigonometric Approximation of Signals Belonging to Generalized Weighted Lipschitz W(Lr, ξ(t))(r ≥ 1)-class by matrix (C1⋅Np) Operator of Conjugate Series of Its Fourier Series. Applied Mathematics and Computation, 237, 252-263. https://doi.org/10.1016/j.amc.2014.03.085
- 14. Mishra, V.N., Khatri, K. and Mishra, L.N. (2013) Using Linear Operator to Appro-ximate Signal of Lip(α, p), (p ≥ 1)-Class. Filomat, 27, 355-365.https://doi.org/10.2298/FIL1302353M
- 15. Mishra, L.N., Tiwari, S.K., Mishra, V.N. and Khan, I.A. (2015) Unique Fixed Point Theorems for Generalized Contractive Mappings in Partial Metric Spaces. Journal of Function Spaces, 2015, Article ID: 960-827.
- 16. Mishra, L.N., Tiwari, S.K. and Mishra, V.N. (2015) Fixed Point Theorems for Gene-ralized Weakly S-Contractive Mappings in Partial Metric Spaces. Journal of Applied Analysis and Computation, 5, 600-612.
- 17. Deepmala and Pathak, H.K. (2013) A Study on Some Problems on Existence of Solutions for Nonlinear Functional-Integral Equations. Acta Mathematica Scientia, 33, 1305-1313. https://doi.org/10.1016/S0252-9602(13)60083-1
- 18. Wadkar, B.R., Bhardwaj, R. and Singh, B. (2017) Fixed Point Theorems in Dislocated Metric Space. Global Journal of Pure and Applied Mathematics, 13, 2089-2110.
- 19. Wadkar, B.R., Bhardwaj, R., Mishra, V.N. and Singh, B. (2017) Coupled Fixed Point Theorems in Soft Metric and b-Soft Metric Space. Ser. A: Appl. Math. Inform. and Mech., 9, 59-73.
- 20. Wadkar, B.R., Bhardwaj, R., Singh, B. and Mishra, V.N. (2017) Coupled Fixed Point Theorems with Monotone Property in Soft Metric and Soft b-Metric Space. International Journal of Mathematical Analysis, 11, 363-375. http://dx.doi.org/10.12988/7222
- 21. Wadkar, B.R., Bhardwaj, R., Mishra, V.N. and Singh, B. (2016) Fixed Point Results Related to Soft Sets. Australian Journal of Basic and Applied Sciences, 10, 128-137.