ABSTRACT

Without the successful work of Professor Kakutani on representing a unit vector space as a dense vector sub-lattice of 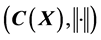in 1941, where X is a compact Hausdorff space and C(X) is the space of real continuous functions on X. Professor M. H. Stone would not begin to work on “The generalized Weierstrass approximation theorem” and published the paper in 1948. Latter, we call this theorem as “Stone-Weierstrass theorem” which provided the sufficient and necessary conditions for a vector sub-lattice V to be dense in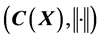. From the theorem, it is not clear and easy to see whether 1) “the vector sub-lattice V of C(X) contains constant functions” is or is not a necessary condition; 2) Is there any clear example of a vector sub-lattice V which is dense in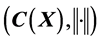, but V does not contain constant functions. This implies that we do need some different version of “Stone-Weierstrass theorem” so that we will be able to understand the “Stone-Weierstrass theorem” clearly and apply it to more places where they need this wonderful theorem.

Keywords:

Compact Hausdorff Space, Vector Sub-Lattice, Vector Sub-Algebra, Stone-Weierstrass Theorem

1. Introduction

Throughout this paper, [T]^<ω denotes the collection of all finite subsets of the given set T, “nhood” represents the word “neighborhood”, C(Z) (or C(X)) is the space of real (or bounded real) continuous functions on compact Hausdorff space Z (or X), and ||×|| is the supremum norm; i.e.,. For the other terminologies in Functional Analysis or General Topology which are not explicitly defined in this paper, the readers will be referred to the References [1] [2] .

Works on the sufficient and necessary conditions for a vector sub-lattice or vector sub-algebra V to be dense in 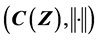were initiated in 1941 when Professor Kakutani tried to represent an order unit space V as a dense vector sub-lattice of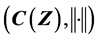. It seemed that at that time Professor Kakutani did not know the sufficient and necessary conditions for a vector sub-lattice V to be dense in. But it is clear that Professor Kakutani knew that a vector sub-lattice V is dense in 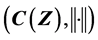if 1) V separates points of Z; and 2) V contains constant functions. In 1948, when Professor M. H. Stone published the “Generalized Weierstrass approximation theorem”, as I know, he did give honor and credit to Professor Kakutani for the work in inspiring the paper M. H. Stone published in 1948. In my personal opinion, a) V separates points of Z and b) V contains constant functions are sufficient conditions for a vector sub-lattice V to be dense in. It seemed that it first appeared in Professor Kakutani’s paper in1941. So, we should call this theorem as “Kakutani’s theorem”. Therefore, we will cite the Theorem 3.4 as Kakutani’s Theorem in Section 3 and prove it with the results either in Section 2 or in a Theorem of Section 4.

2. A Characterization of Compact Sets

Due to the lack of original document in proving X in Section 3 is compact by Professor Kakutani. We insert this section as Section 2 to develop some necessary results for proving that X is a compact Haudorff space. Let A be a family of continuous functions on a topological space Y. A net 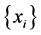in Y is called an A-net if 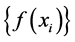converges for all f in A.

Proposition 2.1 Let 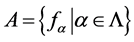be a family of continuous functions f_α on Y into Hausdorff spaces Y_α such that the topology on Y is the weak topology induced by A. E, F two subspaces of Y such that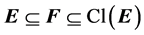, where Cl(E) is the closure of E in Y. Then the following are equivalent: 1) Every A-net in E has a cluster point in F. 2) Every A-net in F converges in F.

Proof. Let 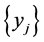be an A-net in F. For each y_j, pick a net in E converging to y_j. For each f_α in A, converges to a point z_α in Y_α and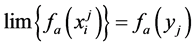, for each open nhood 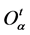of z_α, there is an in E such that. Thus for any and = { is an open nhood of z_α, α is in H}, there is an in E such that is in for each α in H. Direct, is an open nhood of z_α, by setting that iff and for each α in H₂. Then is an A-net in E. (1) implies that has a cluster point x in F. Since Y_α is Hausdorff and converges for each α in Λ, thus converges to for each α in Λ. This implies that for each α in Λ. Thus converges to x in F. (2) implying (1) is obvious.

Theorem 2.2 Let A be a family of continuous functions on a topological space Y. Then Y is compact iff 1) f(Y) is contained in a compact subset C_f for each f in A, and 2) every A-net has a cluster point in Y.

Proof. Let be an ultranet in Y. For each f in A, is an ultranet in C_f, hence converges in C_f; i.e., is an A-net. (2) implies that has a cluster point x in Y. Since is an ultranet, converges to x. Thus, Y is compact. The converse is obvious.

Corollary 2.3 Let A be a family of continuous functions on Y into Hausdorff spaces such that the topology on Y is the weak topology induced by A. E a subspaces of Y then Cl(E) is compact iff 1) is compact for each f in A, and 2) every A-net in E converges in Cl(E).

3. Kakutani Theorem

Definition 3.1 An element e in a vector lattice V is called an order unit if for every v in V, there is a r > 0 such that |v| ≤ re.

Definition 3.2 A topological vector lattice V is called an order unit space if V contains an order unit e such that the topology on V is equivalent to the topology induced

by the unit norm for every v in V.

Let L be the collection of all real continuous lattice homomorphisms t on the order unit space. Equip L with the weak topology induced by V. Then V is a space of real continuous functions on L. From now on, we regard every v in V as a real continuous function on L defined by for all t in L. It is obvious that:

1) V separates points of L: Since for any two different points s and t in L, s and t are two different real continuous lattice homomorphisms on, thus there is a v in V such that; i.e.. This implies that V separates points of L.

2) L is a Hausdorff space : Since the topology on L is the weak topology induced by V, V is a set of real continuous functions on L and V separates point of L, therefore, L is a Hausdorff space. Let, then X is a Hausdorff space. I believe that Professor Kakutani had proved that X is compact. We have no document available to see his proof. Let’s prove it by Corollary 2.3 in this paper as the following:

Theorem 3.3 X is a compact Hausdorff space.

Proof. By the setting, , then X is closed; i.e.,. Let’s prove that X satisfies (1) and (2) in Corollary 2.3: 1) For each v in V, there is a n in ℕ such that, thus; i.e.. So, is compact. 2) Let be a V-net in X. Let r be the function from V to ℝ defined by, it can be readily proved that r is a real lattice homomorphism on V such that; i.e. r is in X and converges to r. By Corollary 2.3 is compact.

Next, we will use the result of Stone-Weierstrass theorem (Theorem 4.1) to prove that V is dense in.

Kakutani’s Theorem

Theorem 3.4 Let V be a vector sub-lattice of C(X) such that 1) V separates points of X, and 2) V contains constant functions, then V is dense in.

Proof. We are going to show that for any f in C(X), any x, y in X and any ε > 0, there is a g in V such that and: For any x and y in X, since V separates points of X, pick a k in V such that. Then and has a unique pair of solutions for α and β. Since V contains constant function, let, then g is in V such that and. By the Stone-Weierstrass theorem, V is dense in.

Notes:

1) A lot of textbooks of Functional Analysis listed The above theorem as the “Stone- Weierstrass Theorem”. I strongly disagree on it.

2) In my opinion, the above Theorem 3.4 should be named as Kakutan’s theorem. Because Professor Kakutani used the result of this theorem to represent an order unit space as a dense subspace of, where X is compact Hausdorff space.

4. A New Version of Stone-Weierstrass Theorem for

Due to that the closure of a sub-algebra is a vector sub-lattice of C(X) (by Lemma 44.3 in the Reference [1] , p. 291), therefore, the sufficient and necessary conditions for a vector sub-lattice V of C(X) to be dense in are also the sufficient and necessary conditions for a vector sub-algebra of C(X) to be dense in. Let’s cite “The generalized Wierstrass approximation theorem” in the Reference ( [3] , p, 170) as the Theorem 4.1 in the following:

Theorem 4.1. Stone-Weierstrass Theorem

Let Z be a compact Hausdorff space. A vector sub-lattice or a sub-algebra V of C(Z) is dense in iff 1) V separates points of Z, and 2) for any f in C(Z), any x, y in Z, and any ε with 0 < ε < 1, there is a g in V such that and.

Theorem 4.2. New Version of Stone-Weierstrass

Theorem

Let Z be a compact Hausdorff space. A vector sub-lattice or sub-algebra V of C(Z) is dense in iff 1) V separates points of Z, and 2) for any x in Z, and any ε with 0 < ε < 1, there is a g in V such that.

To show the equivalence between Theorem 4.1 and Theorem 4.2, it is enough to show the equivalence between the following statements (A) and (B):

(A) for any f in C(Z), any x, y in Z and any ε with 0 < ε < 1, there is a g in V such that and.

(B) for any x in Z and any ε with 0 < ε < 1, there is a g in V such that.

Proof. (A) Þ (B): Let h₁ be the function in C(Z) such that for all x in Z. Then for each x in Z and any ε with 0 < ε < 1, there is a k_x in V such that; i.e. for any e with 0 < e < 1,. For each x in Z, let. Then. Since Z is compact, there exist in Z such that. Let . Then g is in V and for all x in Z,. Thus.

(B) Þ (A): Let. For every ε > 0 and any two points x, y in Z, let k be in V such that. Without loss of generality, assume that there exist α, β in ℝ, such that and. Pick r, s in V such that and. Let and . Then g is in V satisfying that

, and

.

Theorem 4.3. Theorem 4.1 and Theorem 4.2 are equivalent.

Remark 4.4:

1) If the vector sub-lattice or sub-algebra V in the Theorem 3.4 contains constant functions, (without using Theorem 4.1) then let g be the function such that for all x in Z, it is clear that the condition 2) in Theorem 4.2 is satisfied, thus by Theorem 4,2, the vector sub-lattice or sub-algebra V in Theorem 3.4 is dense in.

2) It is also clear to get an example of a vector sub-lattice V that is dense in, but V does not contain constant functions. See the example in the following:

Example. For each, let, if x = t;, if;, if;, otherwise. Let, if;, if;, otherwise. Let, if;, if;, otherwise. Let V be the vector sub-lattice of generated by. Then V does not contain constant functions, and V is dense in, by Theorem 4.2.

5. Conclusions

1) The Stone-Weierstrass Theorem is a great and wonderful theorem. We provided new version of Stone-Weierstrass Theorem, simply trying to understand the theorem better and trying to obtain more applications to where it should be.

2) It must be a tough work for getting sufficient and necessary conditions for a vector sub-lattice V to be dense in. It is not surprised for a mathematician to spend three years or more to get it. Recently, I heard that some publishers or editors of mathematical journals claimed that they could publish more than 50, 60, 80 or 90 multi- authors’ papers in a year. Is it possible? Do you believe it? Any comments or information are welcome.

Cite this paper

Wu, H.J. (2016) New Stone-Weierstrass Theorem. Advances in Pure Mathematics, 6, 943-947. http://dx.doi.org/10.4236/apm.2016.613071

References