Received 26 December 2015; accepted 11 June 2016; published 14 June 2016

ABSTRACT

In this paper, we study about trigonometry in finite field, we know that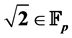, the field with p elements, where p is a prime number if and only if p = 8k + 1 or p = 8k − 1. Let F and K be two fields, we say that F is an extension of K, if K ⊆ F or there exists a monomorphism f: K ® F. Recall that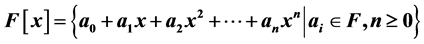, F[x] is the ring of polynomial over F. If 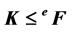(means that F is an extension of K), an element 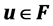is algebraic over K if there exists 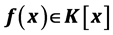such that f(u) = 0 (see [1] - [4] ). The algebraic closure of K in F is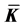, which is the set of all algebraic elements in F over K.

Keywords:

Trigonometry, Finite Field, Primitive, Root of Unity

1. Introduction

In this paper, we study about trigonometry in finite field, we know that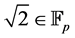, the field with p elements, where p is a prime number if and only if p = 8k + 1 or p = 8k − 1. More generally, what can be said about

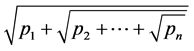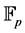in where 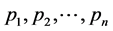are prime numbers. To attempt to answer the question, for which p, 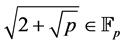, we are naturally led to use the formula, 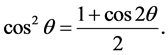Indeed, if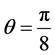, we have 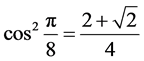and so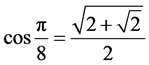, we can choose θ, a suitable 16th root of unity, such that. The crucial observation is that this formula makes sense any algebraic closure of if.

Let F and K be two fields, we say that F is an extension of K if or there exists a monomorphism. Recall that, is the ring of polynomial over F. If (means that F is an extension of K), an element is algebraic over K if there exists such that. The algebraic closure of K in F is, which is the set of all algebraic elements in F over K.

Definition. Let p be a prime number, and let k be an integer such that. Then we can define the set

.

Note that symbol “|” is divisor or divides such that means a divides b and means a does not divide b.

Remark. 1) Recall that θ is a primitive kth root of unity if but, for all (see [2] [4] ). The two make the assumption because if, then there are no primitive kth root of unity in.

2) We can define, in this set, i is a fixed square root of −1. We know that. In particular, we have and.

Theorem 1. If K is a field with 9 elements and if 𝔽 is a finite extension of K, then the mapping defined by is an automorphism of 𝔽 which fixes exactly the elements of K.

Proof. It is obviously that λ is onto and one to one (see [5] [6] ).

Theorem 2. Let θ be a primitive kth root of unity. Then if and only if.

Proof: Assume. If, then. Since the order of the multiplicative group of is p − 1. If, then the irreducible polynomial of θ over is. Hence and so.

Conversely, let. If then, since the multiplicative group of is cyclic of order p − 1, contains a primitive kth root of unity. Therefore contains all primitive kth root of unity and so. Hence. If then hence, so.

Corollary 3. If p ≠ 2 and θ is a primitive kth root of unity, then if and only if.

Remark. We observe that since membership of in depends only on p and k, we have that either or.

Lemma 4. Let θ be a primitive kth root of unity in, the algebraic closure of the rationales Q. Let, the subring of generated by the integers Z and θ, and let P be a prime ideal of R containing of, where (p, k) = 1, where (,) denotes the highest common factor. Let S be the valuation ring of con-

taining the ring, and let M be the maximal ideal of S. Then is a primitive kth root of unity in the field of.

Proof. The formal derivative of is relatively prime to and so has no repeated roots in. On the other hand, and so, over:. It follows that is a primitive root of unity in.

Remark. For the basic properties of valuation rings, the reader can consult. In particular, it is worth recalling that each valuation ring is integrally closed in its quotient field K, and so, if, , then (see [7] - [9] ). Moreover, each valuation ring is a local ring which means that for each, as well. Expression obtained for the real and imaginary parts of the roots of unity over complex number is meaningful in A/M.

2. Some Properties

Corollary 5. Let (q, 10) = 1. Then were n is the number of 2’s occurring under the root signs (excluding the 2 in the denominator!).

Proof. Define, , and for each n ≥ 2:,. Let,. Now is a primitive 5th root of unity viewed as an element of the complex number. Thus is a 5th primitive root of unity in provided p ≠ 5. Moreover, it is easy to check that

and so is a primitive root of 1.

Remark. If in corollary 5 we take, , we obtain a special case of the quadratic reciprocity law, namely: or

Corollary 6. Assume (2, q) = 1. Then where n is the number of 2’s occurring under root signs.

Proof. Let, and for each n ≥ 2 Let, where at each stage we make a specific choice of square root.

As before letting and we have is a primitive root of unity.

Corollary 7. Let (6, q) = 1. Then, where n is the number of 2’s under the square root signs.

Proof. Let and for each n ≥ 2 Let. Then with the same notation as above we have is a primitive root of unity.

Remark. If n = 0 and q = p above we have which is again a particular case of the quadratic reciprocity Law.

Corollary 8. Let (q, 34) = 1. Then

The Formula in corollary 8 is quite complicated and one is naturally interested to know whether already some subformula of this formula is an element of. Suppose that, then.

Indeed set where θ is a primitive 17^th root of unity in. Since we see and. On the other hand one checks easily that, hence. We climb that also is a square in. To show this consider and. Then. Moreover we have. Thus. Since

we see that both. Hence too. Since or we see that or. Since we see that both element and belong to. Combining corollary 8 with the considerations above, we obtain.

Corollary 9. Suppose that (q, 34) = 1, Then and both belong to if.

Remark ( [10] [11] ). One could use the formula given in the table at the end of this note to deduce corollary 9,

more easily. Indeed, for example, from c₁ and c₄ in we deduce that, similarly. From this follows that and.

Theorem 10. Suppose (34, q) = 1, Then if and only if.

Proof. If then also and. Indeed

if either and or with r even. In the first case and therefore, too. On the other hand p, when r is even, is congruent to one of the elements ±1, ±4, ±2, ±8. On the other hand, in the notation as above, we have if

and only if. If or we see that and. Hence . So.

We want to prove that then. It is enough to exclude possibilities. Suppose that, Then. Thus iff that this is contradiction.

Corollary 11. Assume (34, q) = 1. If, then if and only if and or and.

Therefore the inclusion depends only on q(mod 136). we now focus attention on

where θ is a primitive kth root of unity in. Note that if, which

has been dealt with is lemma 4 from now on we assume.

Definition. Let, we shall abbreviate s(θ) to s. The reader should beware that “is” is not necessarily the third person singular of the present tense of the verb to be!

Theorem 12. Let θ be a primitive kth root of unity. Then iff one of the following holds :

(i) where [,] denotes the least common multiple.

(ii) k has the form 8m + 4 and

(iii) k has the form 8m + 4 and

Proof. Assume. Then and set so that θ = c + is. For case (i), Let. Then and by corollary 3:. Therefore and so. Hence and thus.

Case (ii), Let and. Then too, and thus. Therefore. On the other hand Since and so, with, implies that.

Case (iii), , and is belong to. In this case and so. Now whence. But and so Therefore Hence and so

. Therefore. So and thus k is even and. There- fore, and. It is easily seen that these three condition are

equivalent to k = 8m + 4 and for some m.

Corollary 13. For any k, either or.

Proof. As depends only on q and k and not particular primitive root chosen, finally, we determine how many distinct values of and there are as θ varies over the primitive kth root of unity.

3. Conclusion

We conclude that in the field of real numbers, trigonometric ratios are defined as defined in finite fields. As well as relations between trigonometric ratios hold in the field of real numbers, finite fields are also established under the circumstances.

Cite this paper

Amiri Naser,Hasani Fysal, (2016) Some New Results about Trigonometry in Finite Fields. Advances in Pure Mathematics,06,493-497. doi: 10.4236/apm.2016.67035

References

NOTES

^*Corresponding author.