Advances in Pure Mathematics
Vol.06 No.08(2016), Article ID:67947,6 pages
10.4236/apm.2016.68039
Tensor Product of 2-Frames in 2-Hilbert Spaces
G. Upender Reddy
Department of Mathematics, University College of Science & Informatics, Mahatma Gandhi University, Nalgonda, India

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 October 2015; accepted 2 July 2016; published 5 July 2016
ABSTRACT
2-frames in 2-Hilbert spaces are studied and some results on it are presented. The tensor product of 2-frames in 2-Hilbert spaces is introduced. It is shown that the tensor product of two 2-frames is a 2-frame for the tensor product of Hilbert spaces. Some results on tensor product of 2-frames are established.
Keywords:
Tensor Product, 2-Inner Product Spaces, Frames, 2-Frames

1. Introduction
The concept of frames in Hilbert spaces has been introduced by Duffin and Schaefer in 1952 to study some deep problems in nonharmonic Fourier series. D. Han and D.R. Larson [1] have developed a number of basic aspects of operator-theoretic approach to frame theory in Hilbert space. Peter G. Casazza [2] presented a tutorial on frame theory and he suggested the major directions of research in frame theory.
The concept of linear 2-normed spaces has been investigated by S. Gahler in 1965 [3] and has been developed extensively in different subjects by many authors. A concept which is related to a 2-normed space is 2-inner product space which has been intensively studied by many mathematicians in the last three decades. The concept of 2-frames for 2-inner product spaces was introduced by Ali Akbar Arefijammaal and Ghadir Sadeghi [4] and described some fundamental properties of them. Y. J. Cho, S. S. Dragomir, A. White and S. S. Kim [5] are presented some inequalities in 2-inner product spaces. Some results on 2-inner product spaces are described by H. Mazaherl and R. Kazemi [6] . The tensor product of frames in tensor product of Hilbert spaces is introduced by G. Upender Reddy and N. Gopal Reddy [7] and some results on tensor frame operator are presented.
In this paper, 2-frames in 2-Hilbert spaces are studied and some results on it are presented. The tensor product of 2-frames in 2-Hilbert spaces is introduced. It is shown that the tensor product of two 2-frames is a 2-frame for the tensor product of Hilbert spaces. Some results on tensor product of 2-frames are established.
2. Preliminaries
The following definitions from [2] [5] are useful in our discussion.
Definition 2.1. A sequence 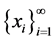 of vectors in a Hilbert space X is called a frame if there exist constants 0
of vectors in a Hilbert space X is called a frame if there exist constants 0
< A ≤ B <µ such that
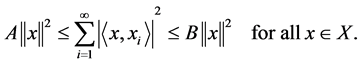
The above inequality is called the frame inequality. The numbers A and B are called lower and upper frame bounds respectively.
Definition 2.2. A synthesis operator T: l2 ®X is defined as  where
where 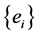 is an orthonormal basis for l2.
is an orthonormal basis for l2.
Definition 2.3. Let 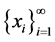 be a frame for X and
be a frame for X and  be an orthonormal basis for l2. Then, the analysis operator T*: X ® l2 is the adjoint of synthesis operator T and is defined as
be an orthonormal basis for l2. Then, the analysis operator T*: X ® l2 is the adjoint of synthesis operator T and is defined as 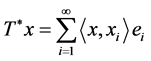 for all x Î X.
for all x Î X.
Definition 2.4. Let  be a frame for the Hilbert space H. A frame operator
be a frame for the Hilbert space H. A frame operator 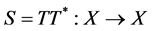 is defined as
is defined as 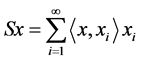 for all x Î X.
for all x Î X.
Here we give the basic definitions of 2-normed spaces and 2-inner product spaces from [3] [6] .
Definition 2.5. X be a real linear space of dimension greater than 1 and let 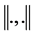 be a real-valued function on X × X satisfying the following conditions.
be a real-valued function on X × X satisfying the following conditions.
a) 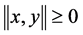 and
and 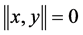 if and only if x and y are linearly dependent vectors.
if and only if x and y are linearly dependent vectors.
b)  for all
for all 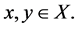
c) 

d) 
Then 

Definition 2.6. Let X be a linear space of dimension greater than 1 over the field K (=R or C). Suppose that 
a) 

b)
c)
d)
e)
Then 

If 


Let 


Using the above properties, we can prove the Cauchy-Schwartz inequality
A 2-inner product space X is called a 2-Hilbert space if it is complete.
3. 2-Frames
The definition of 2-frame from [1] as follows.
Definition 3.1 Let 




The above inequality is called the 2-frame inequality. The numbers A and B are called the lower and upper 2-frame bounds respectively.
The following proposition [1] shows that in the standard 2-inner product spaces every frame is a 2-frame.
Proposition 3.2. Let 

Proof: Suppose that 
Then
Similarly we can prove that

Suppose 







A sequence 


Definition 3.3. Let 


Definition 3.4. Let 


Definition 3.5. Let 


Theorem 3.6. Suppose that 



Proof: Since 


Theorem 3.7. Suppose that 

Proof: Since 

Since 

Therefore, the above Equation (1) is true for
By using the fact that T is co-isometry, we have
Which shows that 
4. Tensor Product of 2-Frames
Let H1 and H2 be 2-Hilbert spaces with inner products



for all 



where





The following definition is the extension of (3.1) to the sequence
Definition 4.1. Let 






The numbers A and B are called lower and upper frame bounds of the tensor product of 2-frame, respectively.
Theorem 4.2. Let 





Proof. Suppose that 


On using (2) and (3) the above equation becomes
This gives
That is
Therefore
where 

Which shows that 





Conversely, assume that 










and

multiplying the Equations (4) and (5) we get
Which shows that 

Hence we can have the following remark.
Remark 4.3. If the sequences








Theorem 4.4. If







Proof. For
Hence
The following two theorems are the extension of 3.6 and 3.7 to the sequence 
Theorem 4.5. Assume that 





Theorem 4.6. Suppose that 




Acknowledgements
The research of the author is partially supported by the UGC (India) [Letter No. F.20-4(1)/2012(BSR)].
Cite this paper
G. Upender Reddy, (2016) Tensor Product of 2-Frames in 2-Hilbert Spaces. Advances in Pure Mathematics,06,517-522. doi: 10.4236/apm.2016.68039
References
- 1. Han, D. and Larson, D.R. (2000) Frames, Bases and Group Representations. Memoirs of the AMS.
- 2. Casazza, P.G. (2000) The Art of Frame Theory. Taiwanese Journal of Mathematics, 4, 129-201.
- 3. Gahler, S. (1965) Lineare 2-Normierte Raume. Mathematische Nachrichten, 28, 1-43.
http://dx.doi.org/10.1002/mana.19640280102 - 4. Arefijammaal, A.A. and Sadeghi, G. (2013) Frames in 2-Inner Product Spaces. International Journal of Mathematical Sciences and Informatics, 8, 123-130.
- 5. Cho, Y.J., Dragomir, S.S., White, A. and Kim, S.S. (1999) Some Inequalities in 2-Inner Product Spaces. Demonstratio Mathematica, 32, 485-493.
- 6. Mazaherl, H. and Kazemi, R. (2007) Some Results on 2-Inner Product Spaces. Novi Sad Journal of Mathematics, 37, 35-40.
- 7. Reddy, G.U., Reddy, N.G. and Reddy, B.K. (2009) Frame Operator and Hilbert-Schmidt Operator in Tensor Product of Hilbert Spaces. Journal of Dynamical Systems & Geometric Theories, 7, 61-70.


























