Received 2 October 2015; accepted 6 November 2015; published 9 November 2015

ABSTRACT

In this paper, M is a smooth manifold of finite dimension n, A is a local algebra and M^A is the associated Weil bundle. We study Poisson vector fields on M^A and we prove that all globally hamiltonian vector fields on M^A are Poisson vector fields.

Keywords:

Weil Algebra, Weil Bundle, Poisson Manifold, Lie Derivative, Poisson 2-Form

1. Introduction

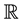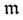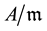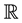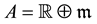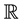A Weil algebra or local algebra (in the sense of André Weil) [1] , is a finite dimensional, associative, commutative and unitary algebra A over in which there exists a unique maximum ideal of codimension 1. In his case, the factor space is one-dimensional and is identified with the algebra of real numbers. Thus and is identified with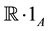, where 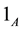is the unit of A.

In what follows we denote by A a Weil algebra, M a smooth manifold, 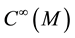the algebra of smooth functions on M.

A near point of 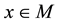of kind A is a homomorphism of algebras

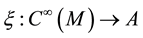
such that for any,.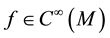

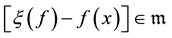We denote by 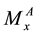the set of near points of x of kind A and 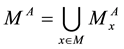the set of near points on M of

kind A. The set is a smooth manifold of dimension and called manifold of infinitely near points on M of kind A [1] - [3] , or simply the Weil bundle [4] [5] .

If is a smooth function, then the map

is differentiable of class [4] [6] . The set, of smooth functions on with values on A, is a commutative algebra over A with unit and the map

is an injective homomorphism of algebras. Then, we have:

We denote, the set of vector fields on and the set of A-linear maps

such that

Thus [4] ,

If

is a vector field on M, then there exists one and only one A-linear derivation

called prolongation of the vector field [4] [6] , such that

Let be the -module of Kälher differentials of and

the canonical derivation which the image of generates the -module i.e. for ,

with for any [7] et [8] .

We denote, the -module of Kälher differentials of which are A-linear. In this case, for, we denote, the class of in.

The map

is a derivation and there exists a unique A-linear derivation

such that

for any [9] . Moreover the map

is an injective homomorphism of -modules. Thus, the pair satisfies the following universal property: for every -module E and every A-derivation

there exists a unique -linear map

such that

In other words, there exists a unique which makes the following diagram commutative

This fact implies the existence of a natural isomorphism of -modules

In particular, if, we have

For any, denotes the - module of skew-symmetric multilinear forms of degree p from into and

the exterior -algebra of called algebra of Kähler forms on.

If then η is of the form with. Thus,

the -module is generated by elements of the form

with.

Let

be the -skew-symmetric multilinear map such that

for any and, where

is a unique -linear map such that [8] . Then,

is a unique -skew-symmetric multilinear map such that

We denote

the unique -skew-symmetric multilinear map such that

i.e. induces a derivation

of degree −1 [9] .

We recall that a Poisson structure on a smooth manifold M is due to the existence of a bracket on such that the pair is a real Lie algebra such that, for any the map

is a derivation of commutative algebra i.e.

for. In this case we say that is a Poisson algebra and M is a Poisson manifold [10] [11] .

The manifold M is a Poisson manifold if and only if there exists a skew-symmetric 2-form

such that for any f and g in,

defines a structure of Lie algebra over [8] . In this case, we say that is the Poisson 2-form of the Poisson manifold M and we denote the Poisson manifold of Poisson 2-form.

2. Poisson 2-Form on Weil Bundles

When is a Poisson manifold, the map

such that for any, is a derivation. Thus, there exists a derivation

such that

Let

be a unique -linear map such that

Let us consider the canonical isomorphism

and let

be the map.

Proposition 1. [9] If is a Poisson manifold, then the map,

such that for any

is a skew-symmetric 2-form on such that

for any x and y in. Moreover, is a Poisson manifold.

Theorem 2. [9] The manifold is a Poisson manifold if and only if there exists a skew-symmetric 2-form

such that for any and in,

defines a structure of A-Lie algebra over. Moreover, for any f and g in,

In this case, we will say that is the Poisson 2-form of the A-Poisson manifold and we denote the A-Poisson manifold of Poisson 2-form [9] .

3. Poisson Vector Field on Weil Bundles

Proposition 3. For any and for any, we have

Proof. If, then there exists, such that . Thus,

3.1. Lie Derivative

The Lie derivative with respect to is the derivation of degree 0

Proposition 4. For any, lthe map

is a unique A-linear derivation such that

for any.

Proof. For any, we have

A vector field on a Poisson manifold is called Poisson vector field if the Lie derivative of with respect to vanishes i.e.. A vector field

on a A-Poisson manifold of Poisson 2-form will be said Poisson vector field if.

Proposition 5. If is a Poisson manifold, then a vector field

is a Poisson vector field if and only if

is a Poisson vector field.

Proof. indeed, for any,

Thus, if and only if.

Proposition 6. Let be a A-Poisson manifold. Then, all globally hamiltonian vector fields are Poisson vector fields.

Proof. Let X be a globally hamiltonian vector field, then there exists such that i.e. X is the interior derivation of the Poisson A-algebra [6] . For any and,

Thus, all globally hamiltonian vector fields are Poisson vector fields.

When is a symplectic manifold, then is a symplectic A-manifold [6] [12] . For

, we denote the unique vector field on, considered as a derivation of into, such that

where

denotes the operator of cohomology associated with the representation

When is a symplectic A-manifold, then for any,

Therefore, all globally hamiltonian vector fields are Poisson vector fields.

Proposition 7. For any and for any Poisson vector field Y, we have

Proof.

Thus,

3.2. Example

When is a Liouville form, where is a local system of coordinates in the cotangent bundle of M, then (,) is a symplectic manifold on [7] . Let be the unique differential A-form of degree −1 on such that

Thus,

Therefore, (,) is a symplectic A-manifold.

For, let be the globally hamiltonian vector field

As [13]

we have

As

and

As,

Thus,

where. An integral curve of is a solution the following system of ordinary equation

When is a local system of coordinates corresponding at a chart U of M,

Thus,

where for. For,

As

we have

Cite this paper

Norbert Mahoungou Moukala,Basile Guy Richard Bossoto, (2015) Poisson Vector Fields on Weil Bundles. Advances in Pure Mathematics,05,757-766. doi: 10.4236/apm.2015.513069

References