Received 12 June 2015; accepted 4 December 2015; published 7 December 2015

ABSTRACT

This paper is concerned with nonlinear fractional differential equations with the Caputo fractional derivatives in Banach spaces. Local existence results are obtained for initial value problems with initial conditions at inner points for the cases that the nonlinear parts are Lipschitz and non-Lip- schitz, respectively. Hausdorff measure of non-compactness and Darbo-Sadovskii fixed point theorem are employed to deal with the non-Lipschitz case. The results obtained in this paper extend the classical Peano’s existence theorem for first order differential equations partly to fractional cases.

Keywords:

Fractional Derivative, Differential Equation, Initial Value Problem, Measure of Non-Compactness

1. Introduction

Let be a Banach space. We consider the nonlinear fractional differential equation

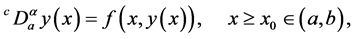(1.1)

with the initial value condition at an inner point (IVP for short)

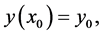(1.2)

where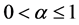, 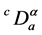is the Caputo fractional derivative, 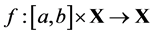is a given function satisfying some assumptions that will be specified later.

Fractional differential equations arise in many engineering and scientific disciplines as the mathematical modeling of systems and processes in the fields of physics, chemistry, biology, economics, control theory, signal and image processing, etc. which involve fractional order derivatives. Fractional differential equations also serve as an excellent tool for the description of hereditary properties of various materials and processes. Consequently, the subject of fractional differential equations is gaining much importance and attention (see [1] - [5] ). There are a large number of papers dealing with the existence or properties of solutions to fractional differential equations. For an extensive collection of such results, we refer the reader to the monograph [1] and [3] and references therein.

In the most of the mentioned works above, the initial value problems for fractional differential equations were studied with the initial conditions at the endpoints of the definition interval, recalling that the classical existence and uniqueness theorem are for first order differential equations, where the initial conditions are at any inner points of the considered interval. On the other hand, classical integer order derivatives at a point are determined by some neighbourhoods of this point, while the fractional derivatives are determined by intervals from the endpoints up to this point. Fractional derivatives at the same point with different endpoints of the definition intervals are in fact different derivatives. Let us investigate the fractional differential equations

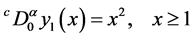(1.3)

and

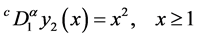(1.4)

with 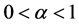and the same initial value condition

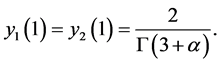
A direct computation deduces that the solutions to the above initial value problems are

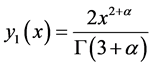
and

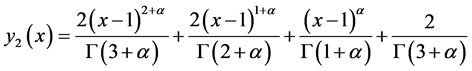
respectively. By a numerical method, we can find that 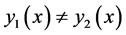for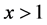. This example shows that and are two different “fractional derivatives”, and Equations (1.3) and (1.4) are two different equ- ations.

Motivated by the above comment, in this paper, we study the existence of solutions to the nonlinear Caputo fractional differential equation modeled as (1.1), with the initial conditions at inner points of the definition interval of the fractional derivative. In this case, the equivalent integral equation is a Volterra-Fredholm equation. Local existence results are obtained for the cases that the function f on the righthand side of the equation is Lipschitz and Caratheodory type, respectively. The theory of measure of non-compactness is employed to deal with the non-Lipschitz case. In this sense, the classical Peano’s theorem is extended to fractional cases.

2. Preliminaries and Lemmas

In this section we collect some definitions and results needed in our further investigations.

Let be the Banach space of all continuous functions with the norm

, and the Banach space of all measurable functions

such that are Lebesgue integrable, equipped with the norm with

.

Definition 2.1 ( [1] ): Let be a fixed number. The Riemann-Liouville fractional integral of order of the function is defined by

where denotes the Gamma function, i.e.,.

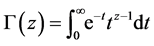
It has been shown that the fractional integral operator transforms the space into , and some other properties of are refered to [1] .

Definition 2.2 ( [1] ): Let, and. The Caputo fractional derivative of order of h at the point x is defined by

is also called the Caputo fractional differential operator.

Lemma 2.1 ( [1] ): Let and. Then

for.

In recent decades measures of noncompactness play very important role in nonlinear analysis [6] - [9] . They are often applied to the theories of differential and integral equations as well as to the operator theory and geo- metry of Banach spaces ( [10] - [15] ). One of the most important examples of measure of noncompactness is the Hausdorff’s measure of noncompactness, which is defined by

for bounded set B in a Banach space Y.

The following properties of Hausdorff’s measure of noncompactness are well known.

Lemma 2.2 ( [8] ): Let Y be a real Banach space and be bounded,the following properties are satisfied :

(1) B is pre-compact if and only if;

(2) where and mean the closure and convex hull of B respec- tively;

(3) when;

(4) where;

(5);

(6) for any;

(7) If the map is Lipschitz continuous with constant k then for any bounded subset, where Z be a Banach space;

(8), where

means the nonsymmetric (or symmetric) Hausdorff distance between B and C in Y;

(9) If is a decreasing sequence of bounded closed nonempty subsets of Y and, then is nonempty and compact in Y.

The map is said to be a if there exists a positive constant such that for any bounded closed subset, where Y is a Banach space.

Lemma 2.3 ( [8] ): (Darbo-Sadovskii) If is bounded closed and convex, the continuous map

is a -contraction, then the map Q has at least one fixed point in W.

In this paper we denote by the Hausdorff’s measure of noncompactness of X and by the Hausdorff’s measure of noncompactness of. To discuss the existence we need the following lemmas in this paper.

Lemma 2.4 ( [8] ): If is bounded, then

for all, where. Furthermore if W is equicontinuous on [a,b], then

is continuous on and

Lemma 2.5 ( [14] [15] ): If is uniformly integrable, then is measurable and

(2.1)

Lemma 2.6 ( [8] ): If is bounded and equicontinuous, then is continuous and

(2.2)

for all, where.

3. Existence Results

In this section, we study the initial value problem for nonlinear fractional differential equations with initial con- ditions at inner points. More precisely, we will prove a Peano type theorem of the fractional version. We begin with the definition of the solutions to this problem. Consider initial value problem

(3.1)

Since the fractional derivative of a function y at an inner point is determined by the values of y on the interval, for and, we get from Lemma 2.3 that

(3.2)

The initial condition then implies that

Inserting this into (3.2) we obtain

Based on the above analysis (see [1] ), we give the definition of mild solutions to the IVP (1.1)-(1.2).

Definition 3.1: A contionuous function is said to be a mild solution to (1.1)-(1.2) if it satisfies

(3.3)

where and.

We first give an existence result based on the Banach contraction principle.

Theorem 3.1: Let, and. Let be continuous and fulfil a Lipschitz con- dition with respect to the second variable with a Lipschitz constant L, i.e.

Then for with, there exist an with and a unique

mild solution to the IVP (1.1)-(1.2).

Proof. Since, we can take an with such that

(3.4)

We define a mapping by

for and. Then for any and, we have

It then follows that

with. Since, we get that. Thus an appli-

cation of Banach’s fixed point theorem yields the existence and uniqueness of solution to our integral equation (3.3).

Remark 3.1: The condition means that the point cannot be far away from a. How-

ever, the following example shows that we cannot expect that there exists a solution to (1.1)-(1.2) for each.

Example 3.1: Considering the differential equation with the Caputo fractional derivative

where is a constant. A direct computation shows that it admits a solution

whose existence interval is.

However, from the proof of Theorem 3.1 we can see that if the Lipschitz constant L is small enough, then can be extended to the whole interval. Thus we have the following result.

Theorem 3.2: Let, and. Let be continuous and fulfil a Lipschitz con-

dition with respect to the second variable with a Lipschitz constant L. If, then for every

, there exists an with and a unique mild solution to the IVP (1.1)-(1.2).

Next we want to study the case that f satisfies the Carathedory condition. For simplicity, we limit to the case that f is locally bounded. We list the hypotheses.

(H₁): satisfies the Carathedory condition, i.e. is measurable for every and is continuous for almost every xÎ[a,b].

(H₂): For every, there is a constant, such that for a.e. and with.

(H₃): There exists with such that

(3.5)

for a.e. and any bounded subset.

Theorem 3.3: Let and. Assume that the hypotheses (H₁)-(H₂) hold, and suppose satisfying

(3.6)

Further assume that there exists a real number solving the inequality

(3.7)

Then there exists an such that the IVP (1.1)-(1.2) has at least a solution.

Proof. On account of the hypothesis (3.8), we can find constants large enough and with

(3.8)

Due to the hypothesis (3.6), we can take small enough such that

(3.9)

Define an operator by

for and. It then follows from the hypotheses (H₁) − (H₂) as well as the Lebesgue dominated convergence theorem that T is well-defined, i.e., Ty is continuous on for every, and that T is continuous. Further, let. Then is a bounded closed subset of. For every and, we have

due to (H₂) and (3.8) which implie that.

Below we show that T satisfies the hypotheses of Darbo-Sadovskii Theorem (Lemma 2.5). We first prove that T maps bounded subsets in into bounded subsets. For this purpose we show that is bounded for every with fixed. Let. Then by (H₂), for every, we have

It follows that which is independent of. Hence is bounded.

Next we prove that T maps bounded subsets into equi-continuous subsets. Let be arbitrary and with. Then we have

which converges to 0 as, and the convergence is independent of. Thus is equi- continuous.

Now we verify that T is a -contraction. Take any bounded subset, then W is equi-continuous. So we get from Lemma 2.4, 2.6 and 2.8 that

(3.10)

The assumption implies that, which shows that the function with for every. Hence an employment of Hölder inequality yields

(3.11)

From the inequality (3.9), we deduce that, which means that T is a -con- traction on.

We have now shown that that T maps bounded subsets into bounded and equi-continuous subsets, and that T is a -contraction on. By Darbo-Sadovskii Theorem (Lemma 2.5), we conclude that T has at least a fixed point y in, which is the solution to (1.1)-(1.2) on, and the proof is completed.

Acknowledgements

This research was supported by the National Natural Science Foundation of China (11271316, 11571300 and 11201410) and the Natural Science Foundation of Jiangsu Province (BK2012260).

Cite this paper

Xiaoping Xu,Guangxian Wu,Qixiang Dong, (2015) Fractional Differential Equations with Initial Conditions at Inner Points in Banach Spaces. Advances in Pure Mathematics,05,809-816. doi: 10.4236/apm.2015.514075

References