Advances in Pure Mathematics
Vol.05 No.09(2015), Article ID:57755,6 pages
10.4236/apm.2015.59048
A Remark on the Uniform Convergence of Some Sequences of Functions
Guy Degla1,2
1Institut de Mathematiques et de Sciences Physiques (IMSP), Porto-Novo, Benin
2International Centre for Theoretical Physics (ICTP), Trieste, Italy
Email: gadegla@yahoo.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 May 2015; accepted 3 July 2015; published 6 July 2015
ABSTRACT
We stress a basic criterion that shows in a simple way how a sequence of real-valued functions can converge uniformly when it is more or less evident that the sequence converges uniformly away from a finite number of points of the closure of its domain. For functions of a real variable, unlike in most classical textbooks our criterion avoids the search of extrema (by differential calculus) of their general term.
Keywords:
Sequence of Functions, Uniform Convergence, Metric, Boundedness

1. Introduction
Let X be a nonempty set,  be a function and
be a function and  be a sequence of real-valued functions from X into
be a sequence of real-valued functions from X into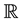 . Recall [1] - [3] that the sequence
. Recall [1] - [3] that the sequence 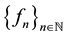 is said to converge uniformly to f on X, if
is said to converge uniformly to f on X, if
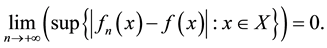
Obviously, if 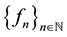 converges uniformly to f on X, then for each
converges uniformly to f on X, then for each 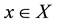 fixed, the sequence
fixed, the sequence 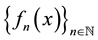 converges to
converges to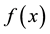 ; that is,
; that is, 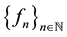 converges pointwise to f. It is also obvious that when X is finite and
converges pointwise to f. It is also obvious that when X is finite and 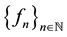 converges pointwise to f on X, then
converges pointwise to f on X, then 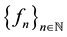 converges uniformly to f on X. However this converse
converges uniformly to f on X. However this converse
doesn’t hold in general for an arbitrary (infinite) set X; i.e., the pointwise convergence may not imply the uniform convergence when X is an arbitrary (infinite) set.
One can observe that in the mathematical literature, there are very few known results that give conditions under which a pointwise convergence implies the uniform convergence. Concerning sequences of continuous functions defined on a compact set, we have the following facts:
Proposition A. (Dini’s Theorem) [4]
If K is a compact metric space,  a continuous function, and
a continuous function, and  a monotone sequence of continuous functions from K into
a monotone sequence of continuous functions from K into  that converges pointwise to f on K, then
that converges pointwise to f on K, then  converges uniformly to f on K.
converges uniformly to f on K.
Proposition B. [5]
If E is a Banach space and 


(For the sake of completeness, we give the proof of this proposition in the Appendix Section).
Therefore our aim is to highlight a new basic criterion that shows in some way how a sequence of real-valued functions can converge uniformly when it is more or less obvious that the sequence converges uniformly away from a finite number of points of the closure of its domain. In the case of sequences of functions of a real variable, our criterion avoids, unlike in most classical textbooks [3] [6] , the search of extrema (by differential calculus) of their general terms. Several examples that satisfy the criterion are given.
2. The Main Result (Remark)
2.1. Theorem
Let 




Suppose that there exists a function f from 




Suppose furthermore that for each





Then the sequence of functions 

Proof
Let 
Thus
by the uniform convergence of 

And so
i.e.,
2.2. Observation
The boundedness condition (D) of the above theorem can not be removed as shown by the sequence of functions defined from 

where 





And we can see that 

3. Examples
We give some examples that illustrate the theorem.
(1) Let 



Then the sequence of functions 
converges uniformly to 
(2) Given an infinite metric space


i) the sequence of functions 
converges uniformly to 0 on E,
ii) the sequence of functions 
converges uniformly to 0 on E.
(3) Let 




i) Consider the sequence of functions 
Then 

ii) Consider the sequence of functions 
Then 

iii) Consider the sequence of functions 
Then 

(4) In real analysis, we can recover the facts that each of the following sequences converges uniformly to 0 on their respective domains:
Justifications (Proofs) of the examples
(1) For every
Therefore, on the one hand, for each
showing that 


On the other hand, we have
fulfilling condition (D) of the above theorem.
Thus 

(2) i) On the one hand, for each



and so 

On the other hand, we have
fulfilling condition (D) of the above theorem.
Thus 
ii) The uniform convergence of

Observe that the uniform convergence of 
(3) Note that for all natural number n, we have
because
following from
Therefore it suffices to prove that 

Let 

Then on the one hand, for each


and so 

On the other hand, we have
showing condition (D) of the above theorem.
Thus 

(4) i) Let us set 

On the one hand, we have for every
On the other hand, we have for every
showing that 

Therefore, by taking







ii) For 

On the one hand, we have for every
On the other hand, we have for every
showing that 

Therefore, by taking







iii) For 

On the one hand, we have for every
On the other hand, we have for every
showing that 


Therefore, by taking







iv) For 

On the one hand, we have for every
On the other hand, we have for every
showing that 


Therefore, by taking







v) The example of 






Cite this paper
GuyDegla,11, (2015) A Remark on the Uniform Convergence of Some Sequences of Functions. Advances in Pure Mathematics,05,527-533. doi: 10.4236/apm.2015.59048
References
- 1. Godement, R. (2004) Analysis I. Convergence, Elementary Functions. Springer, Berlin.
- 2. Munkres, J. (2000) Topology. 2nd Edition. Printice Hall, Inc., Upper Saddle River.
- 3. Ross, K.A. (2013) Elementary Analysis. The Theory of Calculus. Springer, New York.
http://dx.doi.org/10.1007/978-1-4614-6271-2 - 4. Godement, R. and Spain, P. (2005) Analysis II: Differential and Integral Calculus, Fourier Series, Holomorphic Fnctions. Springer, Berlin.
- 5. Ezzinbi, K., Degla, G. and Ndambomve, P. (in Press) Controllability for Some Partial Functional Integrodifferential Equations with Nonlocal Conditions in Banach Spaces. Discussiones Mathematicae Differential Inclusions Control and Optimization.
- 6. Freslon, J., Poineau, J., Fredon, D. and Morin, C. (2010) Mathématiques. Exercices Incontournables MP. Dunod, Paris.
Appendix
In this section, we prove Proposition B for the sake of completeness.
Proof of Proposition B
Let 




Also,
It follows that 
 .
.




































