Received 1 April 2015; accepted 30 April 2015; published 5 May 2015

ABSTRACT

In this paper, we prove the Hyers-Ulam stability of the following mixed additive-quadratic Jensen type functional equation:.

Keywords:

Hyers-Ulam Stability, Additive-Quadratic Jensen Type Functional Equation, Multi-Banach Spaces, Fixed Point Method

1. Introduction

In 1940, Ulam [1] proposed the stability problem of functional equations concerning the stability of group homomorphisms. Suppose that 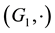is a group and that 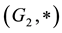is a metric group with the metric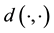. Given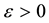, does there exist a 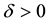such that if a mapping 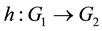satisfies the inequality

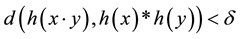
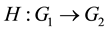for all, then a homomorphism exists with 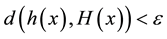for all?

The case of approximately additive functions was solved by Hyers [2] under the assumption that G₁ and G₂ are Banach spaces. In 1978, Rassias [3] proved a generalization of the Hyers theorem for additive mappings. The result of Rassias has provided a lot of influences during the past more than three decades in the development of a generalization of the Hyers-Ulam stability concept. This new concept is known as Hyers-Ulam-Rassias stability of functional equation.

The stability problems of several functional equations have been extensively investigated by a number of authors and there are many interesting results concerning this problem. A large list of references can be found in [4] -[11] .

Pinsker [12] characterized orthogonal additive functional equation on an inner product space. The orthogonal Cauchy functional equation

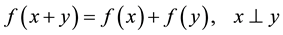
in which 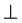is an orthogonality relation, is first investigated by Gudder and Strawther [13] . In 1985, Rätz [14] introduced a new definition of orthogonality by using more restrictive axioms than Gudder and Strawther. More- over, he investigated the structure of orthogonally additive mappings. Rätz and Szabό [15] investigated the pro- blem in a rather more general framework.

In [16] , Kenary and Cho proved the Hyers-Ulam-Rassias stability of mixed additive-quadratic Jensen type functional equation in non-Archimedean normed spaces and random normed spaces. In this paper, we prove the Hyers-Ulam stability of the following mixed additive-quadratic Jensen type functional equation:

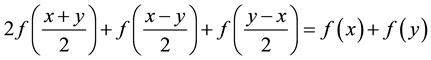(1)

in multi-Banach spaces.

The notion of multi-normed space is introduced by Dales and Polyakov [17] . This concept is somewhat similar to operator sequence space and has some connections with operator spaces and Banach lattices. Motivations for the study of multi-normed spaces and many examples are given in [17] . Also, the stability problems in multi-Banach spaces are studied by Dales and Moslehian [18] , Moslehian et al. ( [19] - [21] ) and Wang et al. [22] .

Now, let us recall some concepts concerning multi-Banach space.

Let be a complex normed space, and let. We denote by E^k the linear space consisting of k-tuples, where. The linear operations on E^k are defined coordinate wise. The zero element of either E or E^k is denoted by 0. We denote by the set and by the group of permutations on k symbols.

Definition 1.1 ( [17] ) A multi-norm on is a sequence

such that is a norm on E^k for each, for each, and the following axioms are satisfied for each with:

(A1);

(A2);

(A3);

(A4).

In this case, we say that is a multi-normed space.

Suppose that is a multi-normed space and take. We need two properties of multi-norms which can be found in [17] .

(a);

(b).

It follows from (b) that, if is a Banach space, then is a Banach space for each; in this case, is a multi-Banach space.

Now, we state two important examples of multi-norms for an arbitrary normed space E (see, for details, [17] ).

Example 1.2 ( [17] ) The sequence on defined by

is a multi-norm called the minimum multi-norm. The terminology “minimum” is justified by property (b).

Example 1.3 ( [17] ) Let be the (non-empty) family of all multi-norms on. For, set

.

Then is a multi-norm on, which is called the maximum multi-norm.

We need the following observation which can be easily deduced from the triangle inequality for the norm and the property (b) of multi-norms.

Lemma 1.4 [17] Suppose that and. For each, let be a sequence in E such that. Then for each, we have

.

Definition 1.5 [17] Let be a multi-normed space. A sequence in E is a multi-null

sequence if, for each, there exists such that

.

Let. We say that the sequence is multi-convergent to x in E and write

.

if is a multi-null sequence.

There are several orthogonality notations on a real normed space available. But here, we present the orthogonal concept introduced by Rätz [14] . This is given in the following definition.

Definition 1.6 Suppose that X is a vector space (algebraic module) with dim, and is a binary relation on X with the following properties:

1) Totality of for zero:, for all;

2) Independence: if and, then x and y are linearly independent;

3) Homogeneity: if and, then for all;

4) Thalesian properity: if P is a 2-dimensional subspace of X, and, which is the set of nonnegative real numbers, then there exists such that and.

The pair is called an orthogonality space (resp., module). By an orthogonality normed space (normed module) we mean an orthogonality space (resp., module) having a normed (resp., normed module) structure.

Definition 1.7 Let X be a set. A function is called a generalized metric on X if and only if d satisfies

(M1) if and only if;

(M2) for all;

(M3) for all.

Theorem 1.8 ([23] ) Let be a generalized complete metric space. Assume that be a stri- ctly contractive mapping with Lipschitz constant. Then, for all, either

for all nonnegative integers n or there exists a positive integer such that

1) for all;

2) the sequence converges to a fixed point of J;

3) is the unique fixed point of J in the set;

4) for all.

2. Hyers-Ulam Stability of Mixed Additive-Quadratic Jensen Type Functional Equation

Throughout this section, let, E be an orthogonality space and let be a multi-Banach space. For convenience, we use the following abbreviation for a given mapping,

for all with.

2.1. Hyers-Ulam Stability of Functional Equation (1): An Odd Case

In this section, using direct method, we prove the Hyers-Ulam stability of the functional Equation (1) in multi- Banach space.

Definition 2.1 An odd mapping is called an orthogonally Jensen additive mapping if

for all with.

Theorem 2.2 Suppose that α is a nonnegative real number and is an odd mapping satisfying

(2.1)

for all and. Then there exists a unique orthogonally Jensen additive mapping such that

(2.2)

for all.

Proof. Replacing by in (2.1), we get

(2.3)

for all since. Replacing by in (2.3) and dividing both sides by, we get

(2.4)

for all since. By using (2.4) and the principle of mathematical induction, we can easily get

(2.5)

for all, ,.

We now fix. We have

where we have used the Definition 1.1 and also replaced by in (2.5). It follows that

is a Cauchy sequence and so it is convergent in the multi-Banach spaces F. Set

for all. Hence, for each, there exists such that

for all. In particular, by property (b) of multi-norms, we have

. (2.6)

We next put in (2.5) to get

.

Letting and using Lemma 1.4 and (2.6), we obtain

.

Let and. Considering Definition 1.6, we have. Put, in (2.1) and divide both sides by. Then, using property (a) of multi-norms, we obtain

for all and. Taking, we get

for all and. Since f is an odd mapping, according to the definition of A, we know that A is an odd mapping. By Definition 2.1, the mapping A is an orthogonally additive mapping.

If is another orthogonally additive mapping satisfying (2.2), then

Taking, we get. This completes the proof.

2.2. Hyers-Ulam Stability of Functional Equation (1): An Even Case

In this section, we prove the Hyers-Ulam stability of the functional Equation (1) in multi-Banach space with the fixed point method.

Definition 2.3 An even mapping is called an orthogonally Jensen quadratic mapping if

for all with.

Theorem 2.4 Suppose that α is a nonnegative real number and is an even mapping satisfying

(2.7)

for all and and. Then there exists a unique orthogonally Jensen quadratic mapping such that

(2.8)

for all.

Proof. Letting in (2.7), we get

(2.9)

for all since. Replacing by and dividing both sides

by 4, we get

(2.10)

Let and introduce the generalized metric d defined on S by

Then it is easy to show that is a generalized complete metric space (see [5] , Lemma 2.1).

We now define an operator by

.

we assert that J is a strictly contractive operator. Given, let be an arbitrary constant with. From the definition of d, it follows that

for all. Therefore

for all. Hence, it holds that, i.e., for all. This means that J is a strictly contractive operator on S with the Lipschitz constant.

By (2.10), we have. According to Theorem 1.8, we deduce the existence of a fixed

point of J, that is, the existence of a mapping such that for all. Moreover, we have, which implies

for all. Also, implies the inequality

.

Let and. Considering Definition 1.6, we have. Set, in (2.7) and divide both sides by. Then, using property (a) of multi-norms, we obtain

for all and. Taking, we get

for all and. Since f is an even mapping, Q is an even mapping. According to Definition 2.3, we know that Q is an orthogonally quadratic mapping.

The uniqueness of Q follows from the fact that Q is the unique fixed point of J with the property that there exists such that

for all. This completes the proof of the theorem.

Acknowledgements

We thank the editor and the referee for their comments. Research is funded by the National Natural Science Foundation of China grant 11371119 and by Natural Science Foundation of Education Department of Hebei Province grant Z2014031.

References