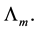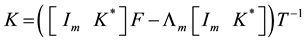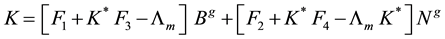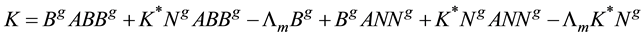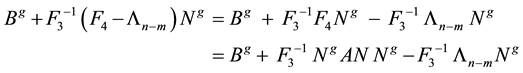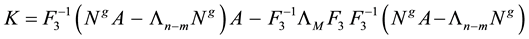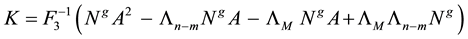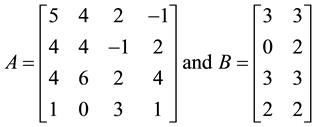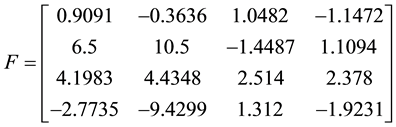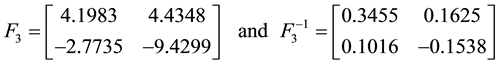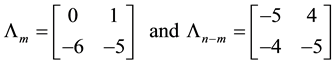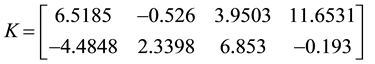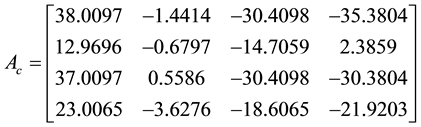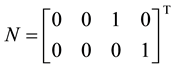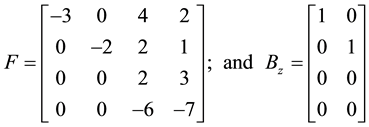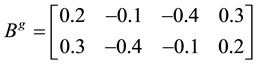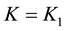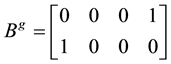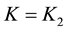Advances in Pure Mathematics
Vol.05 No.07(2015), Article ID:56793,6 pages
10.4236/apm.2015.57037
Simplified Methods for Eigenvalue Assignment
Omar Moh’d El-Basheer El-Ghezawi
Electrical Engineering Department, The University of Jordan, Amman, Jordan
Email: ghezawi@ju.edu.jo
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 March 2015; accepted 26 May 2015; published 29 May 2015
ABSTRACT
A state feedback method of reduced order for eigenvalue assignment is developed in this paper. It offers immediate assignment of 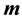 eigenvalues, with freedom to assign the remaining
eigenvalues, with freedom to assign the remaining 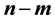 eigenvalues. The method also enjoys a systematic one-step application in the case where the system has a square submatrix. Further simplification is also possible in certain cases. The method is shown to be applicable to uncontrollable systems, offering the simplest control law when having maximum uncontrollable eigenvalues.
eigenvalues. The method also enjoys a systematic one-step application in the case where the system has a square submatrix. Further simplification is also possible in certain cases. The method is shown to be applicable to uncontrollable systems, offering the simplest control law when having maximum uncontrollable eigenvalues.
Keywords:
Eigenvalue Assignment, Pole Placement, Recursive Methods

1. Introduction
The problem of eigenvalue assignment is well established in control theory where numerous methods have been proposed―each with certain advantages and disadvantages. However, a need still arises for methods which are simple in concept and can be easily implemented. A fulfillment to such need is contributed by this paper.
As compared with some previous methods for eigenvalue assignment, this method doesn’t require specific transformations, knowledge of the open loop eigenvalues or the determination of the closed loop eigenvectors. The method utilizes submatrices stemming from a particular state transformation. The transformation is only needed in the development of the method and not the actual assignment of the eigenvalues.
The proposed method tackles eigenvalue assignment by manipulating lower order matrices, hence enjoying some numerical advantages. Furthermore, 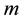 eigenvalues are assigned independently of the remaining
eigenvalues are assigned independently of the remaining  eigenvalues. The method is simplified when
eigenvalues. The method is simplified when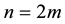 , where
, where 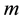 is the rank of
is the rank of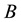 , resulting in a systematic feedback law requiring only the specification of two
, resulting in a systematic feedback law requiring only the specification of two 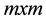 matrices. It can be further simplified in cases where the columns of
matrices. It can be further simplified in cases where the columns of  and
and 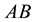 constitute an invertible matrix.
constitute an invertible matrix.
The method is also shown to apply to uncontrollable systems where certain features of some submatrices are pointed out, thus providing additional degrees of freedom in the control law. Furthermore, in the case of maximum number of uncontrollable eigenvalues, the controller is shown to exhibit its simplest form and offer arbitrariness which may be utilized in fulfilling a myriad of design objectives.
Finally, the systematic and straightforward nature of the method is demonstrated by two examples.
2. The Nonrecursive Feedback Law
The assignment law considered is a state feedback law of the form 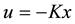 applied to the system
applied to the system
 (2.1)
(2.1)
where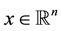 ,
, 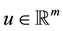 , the rank of
, the rank of 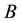 is
is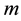 ,
, 
For the development of the simplified methods, a state transformation T is used where
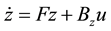
where

Such requirement on 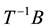
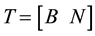
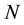
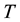

where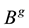

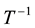
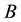


Using the terminology above, the submatrices become
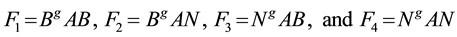
In addition

With reference to the recursive method of Hassan et al. [1] , 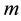
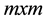
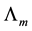

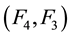

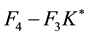

The recursive method [1] is now manipulated to result in a non-recursive feedback law.
According to [1] ; having undergone all recursive steps the final feedback matrix is given by

where
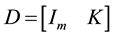
i.e.
substituting 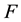
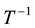
Substituting the values of 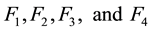
Using the fact that 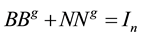
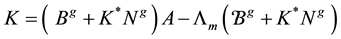
The advantage of this feedback law as given in (2.10) is that assignment of n eigenvalues is split into independent assignment of 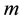
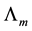

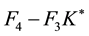
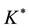

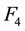

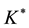
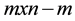

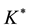
3. A Simplified Method When 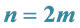
Although the previous development resulted in a controller which manipulates lower order matrices; the selection of 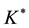
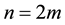
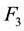
Due to the presence of identical terms within the parenthesis’s, we simplify one term in the state feedback matrix
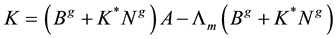
where 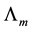
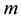
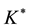

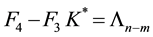
Assuming the nonsingularity of 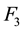

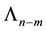

Substituting the value of 
Using (2.7), and recalling
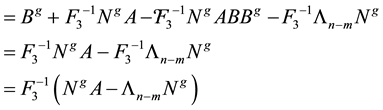
substituting this value for the two terms in the parenthesis’s in Equation (2.10) gives
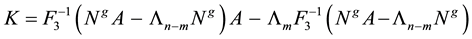
Some remarks regarding the control law are stated below.
A necessary condition for the invertibility of 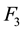
To see this, suppose 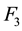
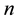
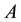
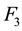
No need to do the state transformation. The determination of (2.4) is only needed to extract 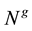

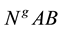
Assignment of 
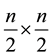
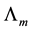
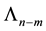
As compared with other assignments laws the highest power of 
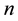
4. Further Simplification
Additional simplification can be done to the form of (3.4). By replacing 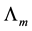

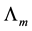
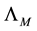
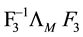
Ending up with a compact form for K as
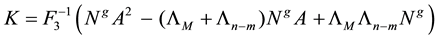
If 
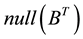
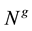

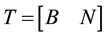
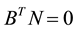
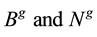
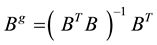
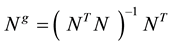
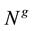
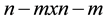
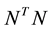

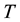

The choice of 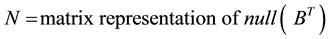
§ The selection of N is systematic.
§ Such choice gives the advantage of inverting an 
§ Further computational advantages are gained if the Gram-Schmidt ortho-normalization procedure is used (can be easily programmed on a digital computer and is already within the MATLAB function library). In this case, if 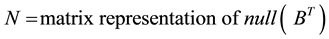
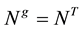
A further simplification to (4.1) is possible in the case where 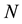
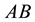

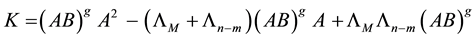
So, the design process now reduces to the selection of 
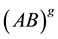
5. The Uncontrollable Case
The non-recursive feedback law can still be applied when the system is uncontrollable. In our case, and as has been shown by [11] , the pair 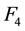
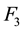
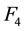
For the case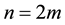
a) The matrix 
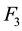
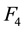
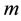

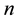
b) Since 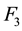
nations of each other. To see this, due to uncontrollability, the matrix 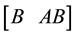
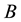

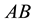
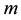
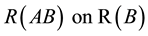
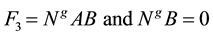
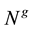
late

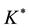
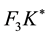
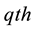


In the light of the above facts since a nonsingular 
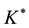
6. Justification of 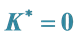
If the system has the maximum number of 
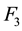
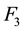

However, although (3.4) cannot be used to get the final feedback matrix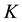

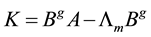
The justification for this form stems from the fact that in our case all uncontrollable eigenvalues are those of
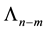




Seeing it differently, since in our case 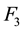

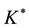
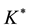

Note that 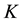

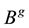
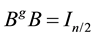
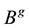
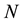
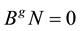
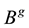

Note that 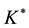
7. Examples
Example 1: Consider the controllable system given by
It is required to assign the eigenvalues −2, −3 and −5 ± j4.
To extract F3, MATLAB was used with 

Hence, to five significant digits
The matrices 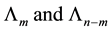
Using the control law given by (3.4) results in the following state feedback matrix
To check, the system closed loop matrix 
Which has the eigenvalues −2, −3, −5 + j4 and −5 − j4.
Example 2: Consider the following system [15] where
This system is uncontrollable with −1 and −4 being the uncontrollable eigenvalues. It is desired to assign the two eigenvalues −4 and −5.
So let
To expose the controllable and uncontrollable eigenvalues, we may take
Yielding
Which shows that
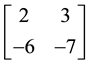
Besides, the inverse of T isn’t needed to extract


Using K as in (6.1) yields a state feedback K matrix, say
Another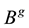
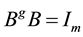
Which results in a different state feedback K matrix, say
Both 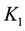
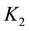
8. Conclusion
The paper has considered a method for eigenvalue assignment based on a scheme of recursive nature. The method involves algebraic manipulation of lower order matrices with an advantage of not requiring state transformation or eigenvectors determination. The method is further simplified in the case where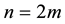

References
- Hassan, M.M. and Amin, M.H. (1987) Recursive Eigenstructure Assignment in Linear Systems. International Journal of Control, 45, 291-310. http://dx.doi.org/10.1080/00207178708933729
- Graybill, F.A. (1983) Matrices with Applications in Statistics. Wadsworth Publishing Company, Belmont.
- Green, P.E. and Carroll, J.D. (1976) Mathematical Tools for Applied Multivariate Analysis. Academic Press, New York.
- El-Ghezawi, O.M.E. (1991) A Two-Stage Method for Eigenvalueigen Vector Assignment. Dirasat, 17, 65-77.
- D’azzo, J.J. and Houpis, C.H. (1995) Linear Control Systems: Analysis and Design. 4th Edition, McGraw-Hill, New York.
- El-Ghezawi, O.M.E. (2010) Unification and Improvement of Certain Methods for Eigenvalue Assignment. Dirasat, 37, 206-213.
- Ackermann, J. and Utkin, V.I. (1998) Sliding Mode Control Design Based on Ackermann’s Formula. IEEE Transactions on Automatic Control, 43, 234-237. http://dx.doi.org/10.1080/00207178708933729
- Petkov, P., Christov, N. and Konstantinov, M. (1991) Computational Methods for Linear Control Systems. Prentice Hall, Upper Saddle River.
- Lancaster, P. and Tismentasky, M. (1985) The Theory of matrices with Applications. 2nd Edition, Academic Press, New York.
- Schott, J.R. (1997) Matrix Analysis for Statistics. John Wiley, Hoboken.
- El-Ghezawi, O.M.E. (1997) Recursive and Modified Recursive Eigenstructure Assignment of Uncontrollable Systems. Dirasat, 24, 620-628.
- Liu, G.P. and Patton, R.J. (1998) Eigenstructure Assignment for Control System Design. John Wiley & Sons, New York.
- White, B.A. (1995) Eigenstructure Assignment: A Survey. Proceedings of the Institution of Mechanical Engineers, 209, 1-11. http://dx.doi.org/10.1243/pime_proc_1995_209_357_02
- Sobel, K.M., Shapiro, E.Y. and Andry, A.N. (1994) Eigenstructure Assignment. International Journal of Control, 59, 13-37. http://dx.doi.org/10.1080/00207179408923068
- Friedland, B. (2005) Control System Design: Introduction to State Space Methods. Dover Publications, New York.