Advances in Pure Mathematics
Vol.04 No.10(2014), Article ID:50625,5 pages
10.4236/apm.2014.410061
Dual Quermassintegral Differences for Intersection Body
Lingzhi Zhao1, Jun Yuan2*
1School of Mathematics and Information Technology, Nanjing Xiaozhuang University, Nanjing, China
2College of Teacher Education, Nanjing Xiaozhuang University, Nanjing, China
Email: lzhzhao@163.com, *yuanjun_math@126.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 August 2014; revised 12 September 2014; accepted 19 September 2014
ABSTRACT
In this paper, we introduce the concept of dual quermassintegral differences. Further, we give the dual Brunn-Minkowski inequality and dual Minkowski inequality for dual quermassintegral differences for mixed intersection bodies.
Keywords:
Intersection Body, Dual Brunn-Minkowski Inequality, Dual Minkowski Inequality

1. Introduction
The projection body was introduced in 1934 by Minkowski [1] . The research on the projection body has attracted much attention. The intersection operator and the class of intersection bodies were introduced in 1988 by Lutwak [2] , who found a close connection between those bodies and famous Busemann-Petty problem (See [3] - [6] ).
In [2] , Lutwak presented the mysterious duality between projection and intersection bodies.
For convex bodies K and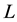 , let
, let
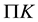 and
and
 denote the projection body of K and mixed projection body of K and
denote the projection body of K and mixed projection body of K and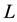 , respectively. In [7] , Lutwak established the following Brunn-Minkowski inequality for projection body and Minkowski inequality for mixed projection body:
, respectively. In [7] , Lutwak established the following Brunn-Minkowski inequality for projection body and Minkowski inequality for mixed projection body:
Theorem A. Let K and
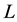 be convex bodies in
be convex bodies in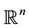 . Then
. Then
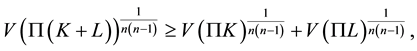 (1.1)
(1.1)
with equality if and only if K and
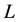 are homothetic.
are homothetic.
Theorem B. Let K and
 be convex bodies in
be convex bodies in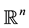 . Then
. Then
 (1.2)
(1.2)
with equality if and only if K and
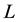 are homothetic.
are homothetic.
In [8] , Theorem A and Theorem B were extended to volume differences:
Theorem C. Suppose that K, L, and
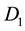 are convex bodies in
are convex bodies in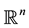 , and
, and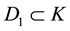 ,
,
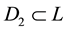 ,
,



with equality if and only if K and



Theorem D. Suppose that







with equality if and only if K and L are homothetic.
For star bodies K and



Theorem E. Let K and



with equality if and only if

Theorem F. Let K and



with equality if and only if

In this paper, we shall prove the dual forms of inequalities (1.3) and (1.4) for mixed intersection body. In this work new contributions that illustrate this mysterious duality will be presented. Our main results can be stated as follows:
Theorem 1.1. Let







with equality if and only if



Theorem 1.2. Let







with equality if and only if

Please see the next section for related definitions and notations.
2. Definitions and Notations
In this section, we will recall some basic results for dual quermassintegrals of star bodies. The reader is referred to Gardner [10] , Lutwak [2] [11] and Thompson [12] for the Brunn-Minkowski theory with its dual theory.
As usual, let










If

Two star bodies



The radial sum of two star bodies



For star bodies


If







Let









If



(See [13] for the concept of the volume difference of two compact domains).
The intersection body of a star body K,



where


Let





where


If









3. Inequalities for Dual Quermassintegral Differences
In this section, we will establish two inequalities for dual quermassintegral differences of star bodies, which are generalizations of Theorem 1.1 and Theorem 1.2 presented in introduction.
Theorem 3.1. Suppose that







with equality if and only if



Obviously, the case





Corollary 3.2. Let




with equality if and only if


Theorem 3.3. Suppose that




with equality if and only if



Obviously, the case

We will require some additional notations and two analytic inequalities to prove Theorem 3.1 and Theorem 3.3. Firstly, we define a function

where


Lemma 3.4. If



with equality holds if and only if the coordinates of

A proof of Lemma 3.4 can be found in [15] . The inequality (3.1) was first proved by Bellman [16] and is known as Bellman’s inequality.
Lemma 3.5. If




with equality if and only if
Proof. Consider the following function
Let
We get
On the other hand, if



This completes the proof.
Lemma 3.6. [15] Let




and

with equality if and only if


Proof of Theorem 3.1. For star bodies

with equality if and only if



Since
From (3.4) and (3.5), we obtain that
Then by Lemma 3.4, we get

Note that the equality holds in (3.4) if and only if L is a dilatate of K. By Lemma 3.4 we know that the equality holds in (3.6) if and only if L is a dilatate of K. and

This completes the proof.
Proof of Theorem 3.3. Applying inequality (3.3), we have
with equality if and only if


Hence, by Lemma 3.5, we obtain that
The proof is complete.
Acknowledgments
We thank the Editor and the referee for their comments. The research is supported by National Natural Science Foundation of China (11101216), Qing Lan Project and the Nanjing Xiaozhuang University (2010KYQN24, 2010KYYB13).
References
- Bonnesen, T. and Fenchel, W. (1987) Theory of Convex Bodies, BCS Associates, Moscow, ID; German Original: Springer, Berlin, 1934.
- Lutwak, E. (1988) Intersection Bodies and Dual Mixed Volumes. Advances in Mathematics, 71, 232-261. http://dx.doi.org/10.1016/0001-8708(88)90077-1
- Gardner, R.J. (1994) Intersection Bodies and the Busemann-Petty Problem. Transactions of the American Mathematical Society, 342, 435-445. http://dx.doi.org/10.1090/S0002-9947-1994-1201126-7
- Gardner, R.J. (1994) A Positive Answer to the Busemann-Petty Problem in Three Dimensions. Annals of Mathematics, 140, 435-447. http://dx.doi.org/10.2307/2118606
- Goodey, P., Lutwak, E. and Weil, W. (1996) Functional Analytic Characterizations of Classes of Convex Bodies. Mathematische Zeitschrift, 222, 363-381. http://dx.doi.org/10.1007/BF02621871
- Zhang, G.Y. (1999) A Positive Solution to the Busemann-Petty Problem in
. Annals of Mathematics, 149 535-543. http://dx.doi.org/10.2307/120974
- Lutwak, E. (1993) Inequalities for Mixed Projection Bodies. Transactions of the American Mathematical Society, 339, 901-916. http://dx.doi.org/10.1090/S0002-9947-1993-1124171-8
- Zhao, C.J. and Cheung, W.S. (2003) On P-Quermassintegral Differences Function. Proceedings of the Indian Academy of Science, 116, 221-231.
- Zhao, C.J. and Leng, G.S. (2005) Brunn-Minkowski Inequality for Mixed Intersection Bodies. Journal of Mathematical Analysis and Applications, 301, 115-123. http://dx.doi.org/10.1016/j.jmaa.2004.07.013
- Gardner, R.J. (2006) Geometric Tomography. 2nd Edition, Cambridge University Press, New York. http://dx.doi.org/10.1017/CBO9781107341029
- Lutwak, E. (1986) Volume of Mixed Bodies. Transactions of the American Mathematical Society, 294, 487-450. http://dx.doi.org/10.1090/S0002-9947-1986-0825717-3
- Thompson, A.C. (1996) Minkowski Geometry. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781107325845
- Leng, G.S. (2004) The Brunn-Minkowski Inequality for Volume Differences. Advances in Applied Mathematics, 32, 615-624. http://dx.doi.org/10.1016/S0196-8858(03)00095-2
- Zhang, G.Y. (1994) Centered Bodies and Dual Mixed Volumes. Transactions of the American Mathematical Society, 345, 777-801.
- Losonczi, L. and Páles, Z. (1997) Inequalities for Indefinite Forms. Journal of Mathematical Analysis and Applications, 205, 148-156. http://dx.doi.org/10.1006/jmaa.1996.5188
- Beckenbach, E.F. and Bellman, R. (1961) Inequalities. Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-64971-4
NOTES
*Corresponding author.



















 . Annals of Mathematics, 149 535-543.
. Annals of Mathematics, 149 535-543. 