Advances in Pure Mathematics
Vol.04 No.09(2014), Article ID:49454,6 pages
10.4236/apm.2014.49056
On Finite Rank Operators on Centrally Closed Semiprime Rings
J. C. Cabello1, R. Casas2, P. Montiel3
1Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, Granada, Spain
2Departamento de Didáctica de las Ciencias Experimentales, Facultad de Ciencias de la Educación, Universidad de Granada, Granada, Spain
3Departamento de Matemáticas, Centro de Magisterio La Inmaculada, Universidad de Granada, Granada, Spain
Email: jcabello@ugr.es, ricardocasas@ugr.es, pamonti@correo.ugr.es
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 July 2014; revised 2 August 2014; accepted 16 August 2014
ABSTRACT
We prove that the multiplication ring of a centrally closed semiprime ring R has a finite rank operator over the extended centroid C iff R contains an idempotent q such that qRq is finitely generated over C and, for each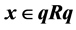 , there exist
, there exist
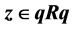 and e an idempotent of C such that
and e an idempotent of C such that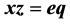 .
.
Keywords:
Ring, Semiprime Ring, Extended Centroid, Minimal Idempotent

1. Introduction
The symmetric ring of quotients
 of a semiprime ring
of a semiprime ring
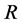 is probably the most comfortable ring of quotients of
is probably the most comfortable ring of quotients of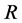 . This notion was first introduced by W.S. Martindale [1] for prime rings and extended to the semiprime case by Amitsur [2] . Recall that a ring
. This notion was first introduced by W.S. Martindale [1] for prime rings and extended to the semiprime case by Amitsur [2] . Recall that a ring
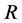 is said to be semiprime (resp. prime) if
is said to be semiprime (resp. prime) if
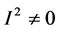 for every nonzero ideal
for every nonzero ideal
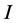 of
of
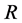 (resp. if
(resp. if
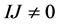 for all nonzero ideals
for all nonzero ideals
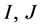 of
of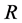 ). The center
). The center
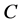 of
of
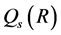 is called the extended centroid of
is called the extended centroid of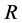 , and the
, and the

















“If the multiplication ring of a centrally closed prime ring






It is also well know that the extended centroid of a prime ring is a field, however, for a semiprime ring, we can only assert that said extended centroid is a von Neumann regular ring. This is the cause of the difficulty of extending this result. The starting point of this path relies on the fact that each subset




2. Tools
We shall assume throughout this paper that






In fact, [5] , Theorem 1.8 remains valid in case that


Given a








Next, we establish our main tool.
Proposition 1.1 Let









Proof. We denote




















such that




for all









Moreover, if there exists


then








Thus, the sum is direct. Note that

As a consequence, we have the following:
Corollary 1.2 Let






Proof. If








Note that if














S satisfies:




the sets




Corollary 1.3 Let






is


Proof. If






by Proposition 1.1, there exists



Corollary 1.4 If


such that
Proof. Let



It is clear that



Hence,
Therefore,




and so,
By repeating this procedure, there are

and hence,







and so,


elements of


Let












Recall that for a subset





Proposition 1.5 Let









Proof. Since



























We finalized this section with a desirable result, which is similar to the well-known result for minimal right ideals (see for instance [4] , Proposition 4.3.3).
Proposition 1.6 Let


1)



2) For every




Proof. (1)











(2)

Let I be a nonzero right ideal of R such that















A nonzero idempotent q of R is said to be

3. Theorem
In this section we will prove a semiprime extension of [3] , Theorem A.9. Concretely,
Theorem 2.1 Let R be a centrally closed semiprime ring. Then






We begin this proof with an another consequence of Proposition 1.1,which is an improvement of Corollary 1.2 to case

Lemma 2.2 Let










Proof. It is clear that

and

Hence,
If
that is,


Note that if



and



Hence,
If



Note that if





Therefore, denoting


and hence,

or even

Of course,




The next result is an immediate consequence of the Weak Density (see [4] , Theorem 2.3.3). We will denote by



Lemma 2.3 Let






Proof. Assume that



since

can suppose that








As a consequence:

First step in the proof of Theorem
Proposition 2.4 If





Proof. First of all, given a nonzero operator

form
for some












and




Second step in the proof of Theorem is a consequence of Lemma 2.2, and its proof can be obtained from a careful reading of the proof of [4] (Lemma 6.1.4).
Proposition 2.5 Let







Proof. Without loss of generality we can assume that
then


the sum is direct. Consider the set

It is clear that
















Primeness. Take


















so


Finally, the converse is obvious.
Funding
Supported by the Junta de Andaluca Grant FQM290.
References
- Martindale 3rd, W.S. (1969) Prime Rings Satisfying a Generalized Polynomial Identity. Journal of Algebra, 12, 576- 584. http://dx.doi.org/10.1016/0021-8693(69)90029-5
- Amitsur, S.A. (1972) On Rings of Quotiens. Symposia Mathematica, 8, 149-164.
- Bresar, M., Chebotar, M.A. and MartindalWe III, W.S. (2007) Functional Identities. Birkhauser Verlag, Basel-Boston- Berlin.
- Beidar, K.I., Martindale III, W.S. and Mikhalev, A.V. (1996) Rings with Generalized Identities. Marcel Dekker, New York.
- Cabello, J.C., Cabrera, M., Rodríguez, A. and Roura, R. (2013) A Characterization of π-Complemented Rings. Communications in Algebra, 41, 3067-3079. http://dx.doi.org/10.1080/00927872.2012.672604






































