Received 29 July 2014; revised 29 August 2014; accepted 15 September 2014

ABSTRACT

This paper provides derivation of some basic identities for complex four-component vectors defined in a complex four-dimensional spacetime frame specified by an imaginary temporal axis. The resulting four-vector identities take exactly the same forms of the standard vector identities established in the familiar three-dimensional space, thereby confirming the consistency of the definition of the complex four-vectors and their mathematical operations in the general complex spacetime frame. Contravariant and covariant forms have been defined, providing appropriate definitions of complex tensors, which point to the possibility of reformulating differential geometry within a spacetime frame.

Keywords:

Complex Spacetime Frame, Four-Vector Identities, Contravariant and Covariant Forms, Complex Tensors

1. Introduction

In a recent derivation [1] , the present author identified the unit wave vector 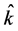to be the temporal unit vector within four-dimensional spacetime frame. The temporal direction is specified as an imaginary axis with unit vector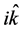, where is the imaginary number. General spacetime frame is then defined as a complex four-dimensional coordinate system spanned by the temporal unit vector and the three mutually perpendicular spatial unit vectors 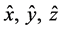specifying the x, y, z axes, respectively. We take the temporal unit vector 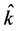to have general orientation relative to the spatial unit vectors according to

(1)

The usual assumption, implicit in conventional four-vector mathematics that the temporal axis is perpendicular to all the three mutually perpendicular spatial axes, with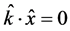, , 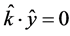, 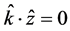may occur only as a special case to be specified. The basic elements of the complex spacetime frame are complex four-component vectors, which we generally call four-vectors. We define a general four-vector in the form

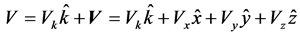(2a)

with the imaginary temporal component defined by

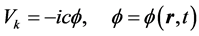(2b)

where is a scalar quantity specifying the nature of the temporal component of the four-vector. As usual, denotes time. In general, the temporal component of each four-vector occurs along the imaginary temporal axis, , multiplied by a factor, where is the speed of light. We follow standard convention denoting four- vectors by uppercase letters, e.g., , while the usual three-component spatial vectors are denoted with arrows over letter symbols, e.g.,.

According to the general definition in Equations (2a)-(2b), the spacetime displacement four-vector X takes the form

(3a)

while the corresponding event interval between two neighboring spacetime points, takes the form

(3b)

The spacetime derivative four-vector, is defined as

(4a)

where and is the usual three-component spatial gradient vector defined by

(4b)

Interpreting in Equation (4a) in terms of the general four-vector in Equations (2a)-(2b) gives

(4c)

We observe that the concept of imaginary temporal axis developed here, represents a rediscovery of the idea of imaginary time first introduced independently by Poincare [2] , Lorentz [3] and Einstein [4] in their original theories of electrodynamics or special relativity in a four-dimensional spacetime frame. These authors did not identify the temporal unit vector and therefore could not completely specify the complex spacetime frame and develop the full mathematical operations using complex four-vectors in the manner presented in this paper.

2. Mathematical Operations with Four-Vectors

The general four-component vector form in Equation (2a) with all unit vectors specified allows us to carry out four-vector mathematical operations in the complex spacetime frame in exactly the same manner as the standard mathematical operations with the familiar three-component vectors in three-dimensional space.

In developing the mathematical operations in general form, we shall take the temporal unit vector to be of general orientation relative to the spatial unit vectors, satisfying the conditions in Equation (1). We denote four-vectors with arrows, while the three-component spatial vectors are written in boldface as stated above. We use two general four-vectors and defined by

(5)

to develop the mathematical operations with four-vectors. The basic mathematical operations are essentially addition, subtraction, dot product, cross product, divergence and curl.

2.1. Addition and Subtraction

Four-vector addition and subtraction is straightforward, taking the form

(6)

2.2. The Dot Product

The dot product of the four-vectors and is obtained as

(7a)

which we expand term by term, maintaining the order of components in the products and then substitute, from Equation (5), to obtain the dot product in the final form

(7b)

2.3. The Cross Product

The cross product of the four-vectors and is obtained as

(8a)

which we expand term by term, using, and then substitute, from Equation (5) to obtain the cross product in the final form

(8b)

2.4. Divergence of a Four-Vector

Setting equal to the spacetime derivative four-vector according to

(9a)

with

(9b)

in the general four-vector dot product obtained in Equation (7b), we obtain the divergence of a general four- vector in the final form

(9c)

2.5. Curl of a Four-Vector

Setting equal to the spacetime derivative four-vector according to Equations (9a), (9b) in the general four-vector cross product obtained in Equation (8b), we obtain the curl of a general four-vector in the final form

(10)

3. Four-Vector Identities

We now derive some basic four-vector identities in complex four-dimensional spacetime frame, which generalize standard vector identities in three-dimensional Euclidean space [5] [6] .

3.1. Curl of Gradient Four-Vector

A gradient four-vector generated through application of the spacetime derivative four-vector on a scalar function is obtained as

(11a)

Setting the general four-vector equal to the gradient four-vector according to

(11b)

with

(11c)

in the general curl of a four-vector obtained in Equation (10), we obtain the curl of a gradient four-vector in the form

(11d)

which on using the standard three-dimensional space vector analysis results

(11e)

gives the final result

(12)

This shows that the curl of a gradient four-vector vanishes. This four-vector identity generalizes the corresponding vector identity in standard three-dimensional Euclidean space [5] [6] given in the first part of Equation (11e).

3.2. Divergence of Curl of a Four-Vector

Taking the divergence of the curl of the general four-vector in Equation (10), we obtain

(13a)

which on expanding term by term becomes

(13b)

Applying standard three-dimensional space vector analysis results

(13c)

we express Equation (13b) in the form

(13d)

Application of standard three-dimensional space vector identity

(13e)

gives

(13f)

which on using

(13g)

takes the final form

(13h)

Substituting Equation (13h) into Equation (13d) gives the final result

(14)

This shows that the divergence of curl of a four-vector vanishes. This four-vector identity generalizes the corresponding vector identity in standard three-dimensional Euclidean space [5] [6] given in the first part of Equation (13c).

3.3. General Vanishing Four-Vector Dot Product:

The important identity on the vanishing of the divergence of curl of a four-vector in Equation (14) can be generalized by taking the dot product of the four-vector and the cross product of the four-vectors and which on using the general result in Equation (8b) is obtained as

(15a)

which we expand term by term and use standard three-dimensional space vector identities

(15b)

to obtain

(15c)

Applying a three-dimensional space vector identity

(15d)

and using

(15e)

gives

(15f)

which we substitute into Equation (15c) to obtain the final result

(15g)

This result generalizes the divergence of curl of a four-vector obtained in Equation (14). It is a generalization of the corresponding vector identity in standard three-dimensional Euclidean space [5] [6] given in the first part of Equation (15b).

3.4. Divergence and Curl of

For a scalar function, we use the definitions of and from Equations (2a) and (4a) to obtain

(16a)

Expanding these term by term gives

(16b)

(16c)

which we reorganize to obtain the four-vector identities

(16d)

These four-vector identities generalize the corresponding vector identities in standard three-dimensional Euclidean space [5] [6] .

3.5. Divergence of Four-Vector Cross Product:

We use the general form of the curl of a four-vector from equation (10) to obtain

(17a)

(17b)

after applying standard three-dimensional space vector identities

(17c)

(17d)

(17e)

Subtracting Equation (17b) from Equation (17a) and applying standard three-dimensional vector identities, together with appropriate rules of differentiation of vector products, we obtain the final result

(17f)

We now use the four-vector cross product from Equation (8b) to obtain

(18a)

which we expand as appropriate and apply standard three-dimensional space vector identities

(18b)

to obtain the final result

(18c)

Substituting Equation (17f) into Equation (18c) gives the four-vector identity

(18d)

This four-vector identity generalizes the corresponding vector identity in standard three-dimensional Euclidean space [5] [6] given earlier in Equation (13e).

3.6. The Curl of a Four-Vector:

Let us start by taking the four-vector curl of the curl of the general complex four-vector in Equation (10) to obtain

(19a)

which we on expansion takes the form

(19b)

Next, we take the four-vector gradient of the divergence of the general complex four-vector in Equation (9c) to obtain

(19c)

which we expand in the form

(19d)

We apply standard three-dimensional Euclidean space vector identities giving

(19e)

(19f)

(19g)

which we substitute into Equation (19d) as appropriate to obtain the final form

(19h)

Subtracting Equation (19b) from Equation (19h) and using standard three-dimensional Euclidean space vector identities giving

(20a)

(20b)

we obtain

(20c)

which on reorganizing

(20d)

takes the form

(20e)

We easily obtain

(20f)

which we substitute into Equation (20c) to obtain

(20g)

Setting

(21a)

in the general four-vector dot product in Equation (7b) gives

(21b)

which we substitute into Equation (24e) and reorganize to obtain the four-vector identity

(22)

This four-vector identity generalizes the corresponding vector identity in standard three-dimensional Euclidean space [5] [6] given earlier in Equation (19g).

3.7. Gradient of Dot Product of Four-Vectors:

For general complex four-vectors, , we have

(23a)

(23b)

(23c)

(23d)

Expanding these term by term gives

(23e)

(23f)

We apply three-dimensional Euclidean space vector identities to obtain

(24a)

(24b)

(24c)

(24d)

(24e)

Substituting Equations (24a)-(24e) into Equation (23e), adding the result to Equation (23f) and reorganizing gives

(24f)

where we have applied a standard three-dimensional Euclidean space vector identity to introduce

(24g)

Rewriting

(25a)

(25b)

we express Equation (24f) in the form

(25c)

which on substituting the definition of the spacetime derivative four-vector from Equation (6a) and the four- vector dot product obtained in Equation (11c), gives the desired four-vector identity in the final form

(26)

This four-vector identity generalizes the corresponding vector identity in standard three-dimensional Euclidean space [5] [6] given earlier in Equation (24g).

3.8. Triple Cross Product of Four-Vectors:

We introduce a third four-vector defined by

(27)

and use the four-vector cross product to obtain

(28a)

which we expand as

(28b)

We apply standard three-dimensional Euclidean space vector identities to write

(28c)

(28d)

(28e)

(28f)

which we substitute into Equation (28b) and collect like terms to obtain

(28g)

We rewrite the last two terms in Equation (28g) by subtracting and adding appropriate terms according to

(29a)

(29b)

which we substitute back and collect like terms to express Equation (28g) in the form

(29c)

Finally, we apply the usual definitions of the four-vectors, and introduce the four-vector dot products

(29d)

in Equation (29c) to obtain the desired four-vector identity in the form

(30a)

This four-vector identity generalizes the corresponding vector identity in standard three-dimensional Euclidean space given earlier in Equation (28f).

We easily apply the four-vector identity obtained in Equation (30a) to establish the cyclic property of the triple four-vector cross product in the form

(30b)

which generalizes the corresponding vector identity in standard three-dimensional Euclidean space [5] [6] .

The four-vector identities derived in Equations (12), (14), (15g), (16d), (18d), (22), (26), (30a) and (30b) confirm the consistency of the definitions of the complex four-component vectors and corresponding mathematical operations within the complex four-dimensional spacetime frame. This means that complex four-dimensional spacetime frame characterized by complex four-component vectors is a consistent mathematical extension of the standard three-dimensional space characterized by the usual three-component vectors. The other four-vector identities can be derived following similar procedure.

4. Contravariant and Covariant Four-Vectors

To complete the mathematical formalism within complex four-dimensional spacetime frame, we introduce contravariant and covariant forms, which are useful in carrying out general mathematical operations with four-vec- tors. A contravariant four-vector is specified by positive spatial components, while a covariant four-vector is specified by negative spatial components. We represent the four-vector in a contravariant form by and in a covariant form by, where with 0 labeling the temporal component, while 1, 2, 3 label the spatial components, respectively. We define and below.

Denoting the four unit vectors by as presented in this paper, we define the contravariant coordinates of the general four-dimensional complex spacetime frame in the form [7] [8]

(31a)

The corresponding covariant coordinates are defined in the form

(31b)

We then express the contravariant spacetime displacement four-vector and the corresponding covariant form as

(31c)

which we introduce the position vector according to Equations (31a)-(31b) to express in the final forms

(31d)

The spacetime event interval takes the contravariant and covariant forms

(31e)

A general four-vector as defined earlier is expressed in contravariant and covariant forms according to

(32a)

(32b)

with

(32c)

which we express in the final forms

(32d)

The contravariant and covariant four-vectors are related through complex conjugation in the form

(32e)

We use this contravariant-covariant four-vector conjugation relation to obtain

(32f)

which provides the definition of the invariant length of the general four-vector or according to

(32g)

We express this in the general form

(32h)

Using, from Equation (32d), noting the relation in Equation (32e), we apply Equation (32g) or (32h) to obtain the invariant length in the explicit form

(32i)

which is modified by a factor arising from the general orientation of the temporal unit vector relative to the spatial unit vectors according to the definition

(32j)

The invariant length of the spacetime event interval is then modified according to

(32k)

where is the velocity, with speed defined as usual. This result has important implications for current theoretical and experimental research in physics [9] [10] .

Tensors in the Complex Spacetime Frame

We now develop the procedure for defining tensors [7] [8] within the general four-dimensional complex spacetime frame. To put the presentation in familiar form, we adopt the standard contravariant and covariant four- vector notation to express and from Equation (20d) in the form

(33a)

with complex conjugates taking the form

(33b)

where the usual four-vector mathematics is applied, but now taking account of the general orientation of the temporal unit vector relative to the spatial unit vectors to obtain the general results presented above.

Using the complex conjugation relation from Equation (33b) gives

(34a)

from which a definition of complex contravariant and covariant rank-2 tensors and follows according to

(34b)

In addition,

(34c)

provides a definition of complex rank-2 mixed tensors and in the form

(34d)

The definition of more general tensors of higher rank follows easily. Some mathematical properties of the rank-2 tensors defined above can be obtained by interchanging the indices, or taking complex conjugation or carrying out both operations simultaneously.

The complete definition of contravariant and covariant complex four-vectors, which can be used to define tensors of general ranks in contravariant, covariant or mixed forms, provides the necessary foundation for more general vector and tensor analysis, leading to reformulation of differential geometry a complex four-dimensional spacetime frame. This is indeed the origin of a new framework for studying physics, mathematics and related disciplines in the 21st-century and beyond. Some important implications for physics are presented in [1] .

5. Conclusion

All the basic four-vector identities which we have derived in this work take exactly the same form as the standard vector identities established in the familiar three-dimensional space. This confirms the consistency of the definition of complex four-component vectors and corresponding mathematical operations within a complex four-dimensional spacetime frame with an imaginary temporal axis. The contravariant and covariant forms introduced here lead to consistent definitions of complex tensors, which are the basic quantities for reformulation of differential geometry within complex spacetime frame. This new mathematical framework has important implications for various models of relativistic mechanics, quantum field theory and general relativity as a theory of gravitation and cosmology.

Acknowledgements

I thank Maseno University, Kenya, for supporting this work by providing facilities and working environment.

References