Advances in Pure Mathematics
Vol.4 No.6(2014), Article
ID:46583,5
pages
DOI:10.4236/apm.2014.46030
A New Integral Equation for the Spheroidal Equations in Case of m Equal to 1
Guihua Tian, Shuquan Zhong
University of Posts and Telecommunications, Beijing, China
Email: tgh-2000@263.net, tgh20080827@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 January 2014; revised 7 February 2014; accepted 15 February 2014
ABSTRACT
The spheroidal wave functions are investigated in the case $m = 1$. The integral equation is obtained for them. There are two kinds of eigenvalues in the differential and corresponding integral equations, and the relation between them is given explicitly. This is the great advantage of our integral equation, which will provide useful information through the study of the integral equation. Also an example is given for the special case, which shows another way to study the eigenvalue problem.
Keywords:Spheroidal Wave Functions, Integral Equation, Green Function

1. Introduction
The spheroidal wave equations are extension of the ordinary spherical equations. There are many fields where spheroidal functions play important roles just as the spherical functions do. So far, in comparison to simpler spherical special functions (the associated Lengdre’s functions), their properties are still difficult to study. The equations for them are
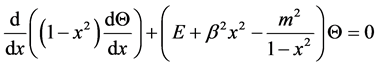 , (1)
, (1)
with −1 < x < 1 and the natural conditions that Θ is finite at the boundaries x = ±1. This is a kind of the singular Sturm-Liouville eigenvalue problem. To satisfy the boundaries condition, the parameter E can only take the values “ ,” which are called the eigenvalues of the Sturm-Liouville eigenvalue problem, and the corresponding solutions (the eigenfunctions)
,” which are called the eigenvalues of the Sturm-Liouville eigenvalue problem, and the corresponding solutions (the eigenfunctions) 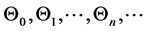 are called the spheroidal wave functions [1] -[3] .
are called the spheroidal wave functions [1] -[3] .
Under the condition β = 0, they reduce to the Spherical equations and the solutions to the Sturm-Liouville eigenvalue problem are the associated Legendre-functions Pml(x) (the spherical functions) with the eigenvalues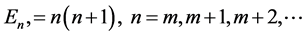 . The spheroidal equations only have one more term β2x2 than the spherical ones (the associated Lendgre’s equations). However, the extra term β2x2 in the equation presents many mathematical difficulties [1] -[3] . The difference between these two kinds of wave functions is far greater than their similarity. The former belongs to the Hune equations in contrast to that the spherical equations belong to the hyper-geometric equations. The Hune equations have four regular singularities; hence present much more difficulties in mathematical ground.
. The spheroidal equations only have one more term β2x2 than the spherical ones (the associated Lendgre’s equations). However, the extra term β2x2 in the equation presents many mathematical difficulties [1] -[3] . The difference between these two kinds of wave functions is far greater than their similarity. The former belongs to the Hune equations in contrast to that the spherical equations belong to the hyper-geometric equations. The Hune equations have four regular singularities; hence present much more difficulties in mathematical ground.
Usually, one studied the spheroidal equations by the perturbation method in the basis of the spherical functions and resulting in the continued fraction to determine the eigenvalues and eigenfunctions [1] -[3] . Recently, new methods are used to re-investigate the problems again [4] -[6] . The new methods mainly include the perturbation one in supersymmetry quantum mechanics (see [7] for the theory of supersymmetry quantum mechanics and more references in there), which give rise to many nice results [4] -[11] . Some of the results are the extension of the recurrence relation of the spherical functions to the spheroidal functions, and make the excited spheroidal functions available from the ground one. Other results might give new method in their numerical calculation [4] -[11] . There are also the integral equations, which provide another way to numerically study the spheroidal functions [1] . In [12] , the integral equations are extended to the spin-weighted spheroidal case.
In this paper, we mainly concern ourselves with the integral equations for them. For example, the integral equation for the prolate spheroidal wave equation is already existed [1] [12]
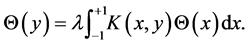 (2)
(2)
where the kernel 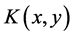 is
is
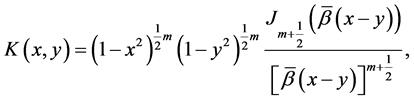 (3)
(3)
with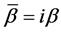 . There are two eigenvalues appear in the differential and the integral Equations (1), (2), that is, the quantities
. There are two eigenvalues appear in the differential and the integral Equations (1), (2), that is, the quantities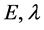 . However, the relation between the eigenvalues
. However, the relation between the eigenvalues  is unclear [1] [12] . In this letter, we will report a new integral equation for the spheroidal equation in the case of
is unclear [1] [12] . In this letter, we will report a new integral equation for the spheroidal equation in the case of . Because the integral equation is derived from the Green function of the Equations (1), it provides the concise relation between the eigenvalues
. Because the integral equation is derived from the Green function of the Equations (1), it provides the concise relation between the eigenvalues . This is the main advantage of the new integral equation.
. This is the main advantage of the new integral equation.
2. A New Integral Equation for the Spheroidal Equations
In order to obtain a new integral equation for the spheroidal equation with , we apply the transformation
, we apply the transformation
 (4)
(4)
to the Equation (1) and obtain the following
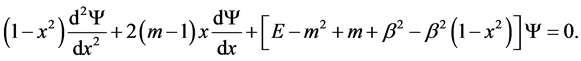 (5)
(5)
The above equation becomes very simple when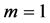 , that is,
, that is,
 (6)
(6)
where
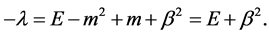 (7)
(7)
It is easy to find the Green function for the Equation (6), that is
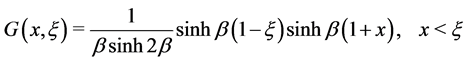 (8)
(8)
 (9)
(9)
The Green function  satisfies the following
satisfies the following
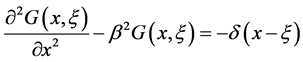 (10)
(10)
and the boundary conditions
 . (11)
. (11)
Hence the the Sturm-Liouville eigenvalue problem turns into the integral equation form:
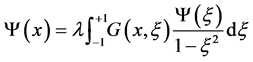 (12)
(12)
 (13)
(13)
The great advantage of the new integral Equation (12) lies in that the relation between the integral eigenvalues
 and
and  of the differential Equations (1) for the spheroidal is given explicitly by
of the differential Equations (1) for the spheroidal is given explicitly by
 (14)
(14)
Though the Green function 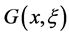 is symmetric with respect to the variables
is symmetric with respect to the variables , the kernal in the Equation (12) is not symmetrical at all. Nevertheless, it is easy to make the kernal be symmetry. That is, changing
, the kernal in the Equation (12) is not symmetrical at all. Nevertheless, it is easy to make the kernal be symmetry. That is, changing
 into
into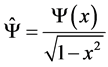 , the Equation (12) becomes
, the Equation (12) becomes
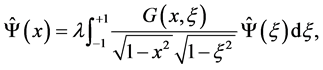 (15)
(15)
as desired by our requirement. It is well-known that one could easily to study the integral equations if their kernels are symmetry. Hence, the usual method to solve the integral equations could be used to treat the problem here too. We will stop here.
The Green function 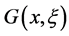 for the spheroidal equations in
for the spheroidal equations in  includes all cases of the parameter
includes all cases of the parameter 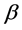 as a complex number. When
as a complex number. When 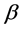 is pure imaginary, the corresponding equation is the prolate spheroidal equation and the Green function turns out as
is pure imaginary, the corresponding equation is the prolate spheroidal equation and the Green function turns out as
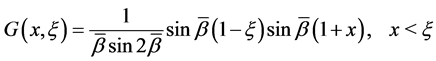
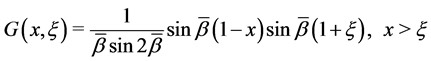 (16)
(16)
where  is real.
is real.
If one supposes the parameter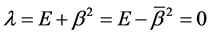 , the parameter
, the parameter 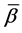 will stand in the position of the eigenvalues in the Sturm-Liouville eigenvalue problem. Of course, the parameter
will stand in the position of the eigenvalues in the Sturm-Liouville eigenvalue problem. Of course, the parameter  or
or 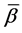 is no longer a fixed quantity in this case. Notice that the case is special because the parameter
is no longer a fixed quantity in this case. Notice that the case is special because the parameter 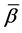 is not a fixed quantity in contrasting with the usual cases. In this special case, the original equation correspondingly becomes
is not a fixed quantity in contrasting with the usual cases. In this special case, the original equation correspondingly becomes
 (17)
(17)
The Green function in the Equation (16) will give much information about the eigenvalues and eigenfunctions in this special case. Now it could be regarded as the functions of the parameter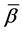 . One could expand this Green function in the form
. One could expand this Green function in the form
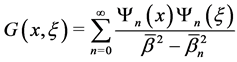 (18)
(18)
The eigenvalues are determined by the poles of the Green functions, that is
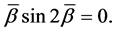 (19)
(19)
Hence,  ,
, 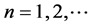 are the eigenvalues, and the residues of the corresponding pole are
are the eigenvalues, and the residues of the corresponding pole are
 (20)
(20)
and
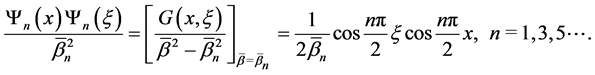 (21)
(21)
the nth eigenfunction is
 (22)
(22)
 (23)
(23)
Except for the normalization constants, these results are the same as those in Ref. [1] , though they are derived from the different way. As stated in Ref. [1] , the function
 (24)
(24)
are one kind of the eigenfunctions for the fixed parameter  of the original Equation (1) in case
of the original Equation (1) in case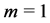 , so does
, so does
 (25)
(25)
for the fixed parameter .
.
The above example just provides some clues on the connection between the Green function and the solutions to the corresponding the Sturm-Liouville eigenvalue problem. If the Green function is the one corresponding with the parameter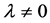 , they will more useful than just giving the integral equation. However, one could not obtain directly the information on the eigenvalues and eigenfunctions from the the Green function corresponding with the parameter
, they will more useful than just giving the integral equation. However, one could not obtain directly the information on the eigenvalues and eigenfunctions from the the Green function corresponding with the parameter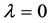 . In this situation, the useful information could be obtained through the study on the integral equation. Here the Green function
. In this situation, the useful information could be obtained through the study on the integral equation. Here the Green function  satisfies he Equation (10) rather than the following
satisfies he Equation (10) rather than the following
 . (26)
. (26)
This Green function  is connected with the eigenfunctions
is connected with the eigenfunctions 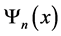 by
by
 (27)
(27)
Our Green function  related to
related to 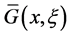 by
by
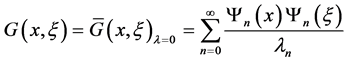 (28)
(28)
Of course,  contains much more useful information on the eigenvalues and eigenfunctions than that of
contains much more useful information on the eigenvalues and eigenfunctions than that of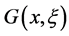 , but it is much harder to obtain. Even it is inferior to
, but it is much harder to obtain. Even it is inferior to ,
, 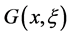 still could provide useful information through the integral equation, which will be our further study.
still could provide useful information through the integral equation, which will be our further study.
Acknowledgements
The work was partly supported by the National Natural Science of China (No. 10875018) and the Major State Basic Research Development Program of China (973 Program: No.2010CB923202).
References
- Flammer, C. (1956) Spheroidal Wave Functions. Stanford University Press, Stanford.
- Stratton, J., et al. (1956) Spheroidal Wave Functions. Wiley, New York.
- Li, L., Kang, X. and Leong, M. (2002) Spheroidal Wave Functions in Electromagnetic Theory. John Wiley and Sons, Inc., New York.
- Tian, G.H. and Zhong, S.Q. (2009) Arxiv: 0906.4687 V3: Investigation of the Recurrence Relations for the Spheroidal Wave Functions. Preprint.
- Tian, G.H. and Zhong, S.Q. (2009) Arxiv: 0906.4685 V3: Solve Spheroidal Wave Functions by SUSY Method. Preprint.
- Tian, G.H. (2010) New Method to Study the Spheroidal Functions. Chinese Physics Letter, 27, 030308. http://dx.doi.org/10.1088/0256-307X/27/3/030308
- Cooper, F., Khare, A. and. Sukhatme, U. (1995) Super-Symmetry and Quantum Mechanics. Physics Reports, 251, 267-385. http://dx.doi.org/10.1016/0370-1573(94)00080-M
- Tian, G.-H. and Zhong, S.-Q. (2010) The Recurrence Relations for the Spheroidal Functions. Science China G, 54, 393-400.
- Tian, G.H. and Li, Z.Y. (2011) Can All the Recurrence Relations for Spherical Functions Be Extended to Spheroidal Functions. Science China G, 54, 1775-1782. http://dx.doi.org/10.1007/s11433-011-4469-8
- Tang, W.L. and Tian, G.H. (2011) Solving Ground Eigenvalue and Eigenfunction of Spheroidal Wave Equation at Low Frequency by Supersymmetric Quantum Mechanics Method. Chinese Physics B, 20, Article ID: 010304.
- Tang, W.L. and Tian, G.H. (2011) Solving the Spin-Weighted Spheroidal Wave Equation with Small c by SUSYQM Method. Chinese Physics B, 20, Article ID: 050301.
- Tian, G.H. (2005) The Integral Equations for the Spin-Weighted Spheroidal Functions. Chinese Physics Letter, 22, 3013-3017.

