Advances in Pure Mathematics
Vol.4 No.1(2014), Article ID:41722,10 pages DOI:10.4236/apm.2014.41001
Contractions of Certain Lie Algebras in the Context of the DLF-Theory
Alexander Levichev*, Oleg Sviderskiy#Sobolev Institute of Mathematics, Novosibirsk, Russia
Email: *alevichev@gmail.com
Copyright © 2014 Alexander Levichev, Oleg Sviderskiy. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Alexander Levichev, Oleg Sviderskiy. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 12, 2013; revised December 11, 2013; accepted December 17, 2013
Keywords:Lie Algebras with Invariant Lorentzian Forms; Lorentzian Symmetric Spaces; Contractions of Lie Algebras; Conformal Lie Algebra; Segal’s Chronometric Theory; DLF-Theory
ABSTRACT
Contractions of the Lie algebras d = u(2), f = u(1 ,1) to the oscillator Lie algebra l are realized via the adjoint action of SU(2,2) when d, l, f are viewed as subalgebras of su(2,2). Here D, L, F are the corresponding (four-dimensional) real Lie groups endowed with bi-invariant metrics of Lorentzian signature. Similar contractions of (seven-dimensional) isometry Lie algebras iso(D), iso(F) to iso(L) are determined. The group SU(2,2) acts on each of the D, L, F by conformal transformation which is a core feature of the DLF-theory. Also, d and f are contracted to T, S-abelian subalgebras, generating parallel translations, T, and proper conformal transformations, S (from the decomposition of su(2,2) as a graded algebra T + Ω + S, where Ω is the extended Lorentz Lie algebra of dimension 7).
1. Introduction
As noticed by the first author (see [1,2]), there are precisely three four-dimensional non-abelian Lie algebras that admit a non-degenerate invariant bilinear form of Lorentzian signature:
the oscillator Lie algebra l, defined by the following commutation relations in a certain basis l1, l2, l3, l4:
![]() (1.1)
(1.1)
the Lie algebra d = u(2) generated by vectors X0, X1, X2, X3 with the following commutation relations:
 (1.2)
(1.2)
the Lie algebra 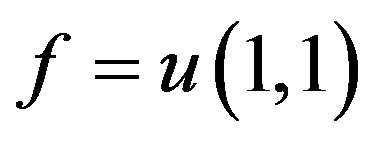 generated by vectors H0, H1, H2, H3, satisfying the following commutation relations
generated by vectors H0, H1, H2, H3, satisfying the following commutation relations
 (1.3)
(1.3)
Relations (1.2) are the same as the ones in [3].
Certain Lie groups (corresponding to the Lie algebras d, l, f), endowed with bi-invariant metrics of Lorentzian signature, provide so-called homogeneous solutions to Einstein’s equations of General Relativity Theory, GRT. We denote these solutions by the corresponding capital letters. They have been studied in [4]. In GRT literature (see [5]), D is known as the perfect fluid, F is a tachyonic fluid, and that L is a very special case of plane waves. Namely, it is an isotropic electromagnetic field determined by a covariantly constant light-like vector (see [6]). Groups defined by the oscillator Lie algebra l are also studied in detail on pp. 409-414 of [7].
Relations (1.1), (1.2), and (1.3) have been used in [8,9] where the basics of the DLF-approach have been presented (by A. L.). This DLF-theory can be briefly characterized as the LF-modification of Segal’s Chronometry (the latter one is based on D, see [3,9] and references therein).
It is known (see [9]) that these three space-times are conformally flat, and that in each case the isometry group of the corresponding Lorentzian manifold is of dimension 7. Each of d, l, f (as well as a four-dimensional abelian Lie algebra) can be realized as a subalgebra of the conformal algebra 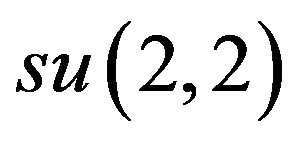 and these imbeddings will be specified below. Conventions about
and these imbeddings will be specified below. Conventions about  follow [3, p. 92]. Namely, a traceless four by four matrix m (with complex entries allowed) is in
follow [3, p. 92]. Namely, a traceless four by four matrix m (with complex entries allowed) is in 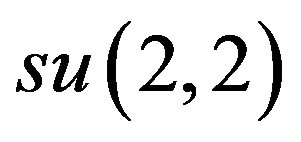 iff
iff
![]()
where s is a diagonal matrix:
 .
.
Also, commutation relations relative to a certain basis in su(2,2) are (3.1) of our Section 3.
The general subject of contractions (and deformations) of Lie algebras is important in physics (see, for example, Section IV.7 of [10]). It provides an explanation of one physical model being a limiting case of another one. In [10], it was the case of Newtonian world versus Minkowski space-time M. The findings of the present article (together with what has been already published by the first author) form the necessary base for investigation of similar relationships between space-times M, D, L, F.
The subject is also of interest from a pure mathematical point of view. Regarding contractions of Lie algebras, we follow [11].
2. Lie-Theoretical Contractions of d and f
Namely, we use the name Lie-theoretical contraction for the method defined by [11, p.2, (3)], where the commutation relations of a contracted Lie algebra are given by
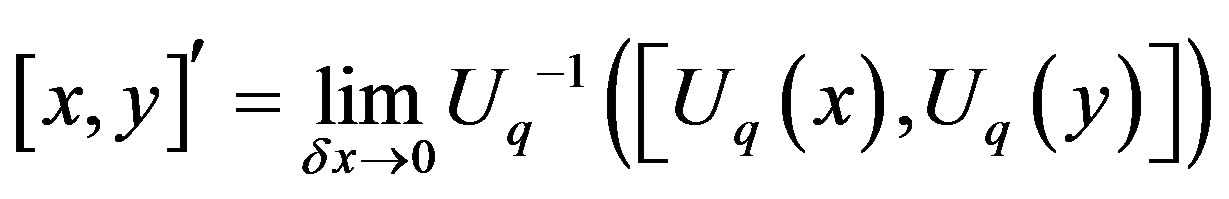 .
.
Here 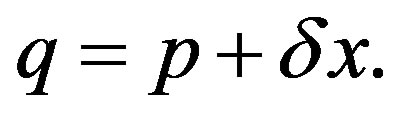 When q is not equal to p, Uq is a non-singular linear transformation of the original Lie algebra. When q = p, the inverse of the linear transformation Up does not exist.
When q is not equal to p, Uq is a non-singular linear transformation of the original Lie algebra. When q = p, the inverse of the linear transformation Up does not exist.
Theorem 2.1. There is a Lie-theoretical contraction of 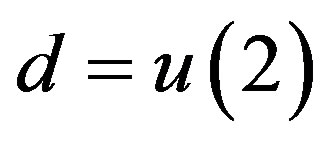 to the oscillator Lie algebra l.
to the oscillator Lie algebra l.
Proof. Consider the following vectors in d:

One can verify that for any non-zero value of α, the algebra generated by L1, L2, L3, L4, is isomorphic to d, since the Equations (2.1) are uniquely solvable for Xi.
The commutation relations for L1, L2, L3, L4, are as follows:

It can be easily seen that as α goes to zero, the commutation relations become (1.1), that is, of the oscillator Lie algebra l.
Remark 2.1. Alternatively, we can choose a different set of vectors in d:
![]()
It defines a Lie algebra isomorphic to d (when β is not zero). The commutation relations converge to those of the oscillator algebra when β goes to zero.
Theorem 2.2. There is a Lie-theoretical contraction of 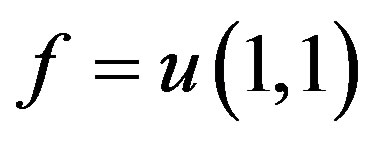 to the oscillator Lie algebra l.
to the oscillator Lie algebra l.
Proof. We apply similar contraction procedures to f as we did in the case of d. Let
![]()
Then, as α goes to 0, the commutation relations for L1, L2, L3, L4, become (1.1), that is, of the oscillator algebra l. Clearly, for any nonzero α, the Lie algebra generated by L1, L2, L3, L4, is isomorphic to f.
Remark 2.2. As noticed in [12], there always exists a (trivial) Lie-theoretical contraction of any Lie algebra to an abelian algebra.
3. Realization in su(2,2)
Our current goal is to realize the above-mentioned contractions of the Lie algebras d and f through the adjoint action of the group SU(2,2) on its Lie algebra su(2,2) of which all d, f and l are subalgebras. We will call such contractions the su(2,2)-inner contractions of the corresponding Lie algebras.
More specifically, we will conjugate the generators of d and f with elements of the maximal abelian subgroup A of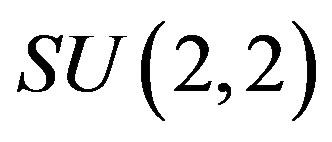 , from the Iwasawa decomposition
, from the Iwasawa decomposition .
.
Remark 3.1. A. L. thanks David Vogan for helpful discussions on the subject.
Remark 3.2. It is important to bear in mind (see [8,9]) that  acts on each of D, L, F. Joint consideration of the three worlds is the key feature of the DLF-theory.
acts on each of D, L, F. Joint consideration of the three worlds is the key feature of the DLF-theory.
In [13, p.135], the generic element a of the two-dimensional maximal abelian subalgebra A of 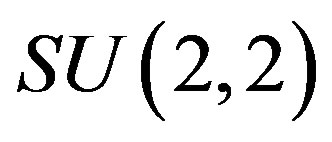 is chosen as
is chosen as
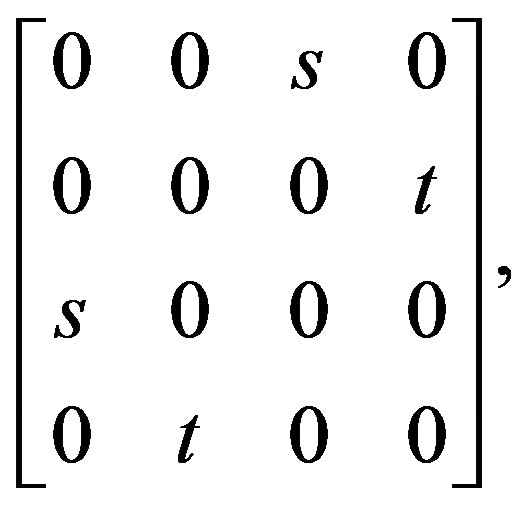
where s, t are real parameters. It thus can be written in terms of the generators Lij of 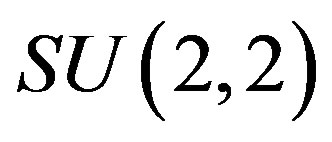 as
as

All fifteen matrices Lij (where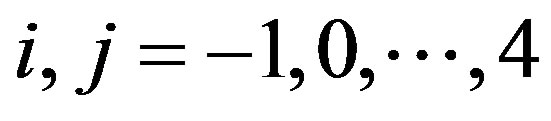 ) forming a (standard) basis of
) forming a (standard) basis of  can be found in [14]. Relative to this basis, the
can be found in [14]. Relative to this basis, the 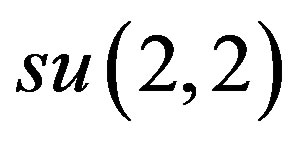 commutation relations are as follows
commutation relations are as follows
 (3.1)
(3.1)
where 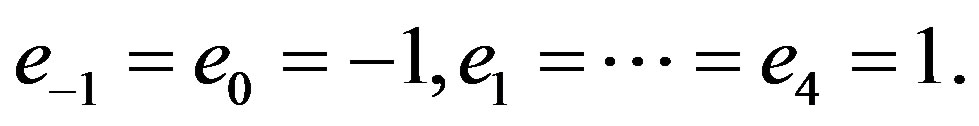
The generic element of the corresponding group A can then be written as

Clearly,

The following imbedding of 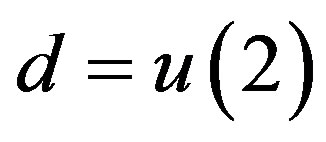 into
into 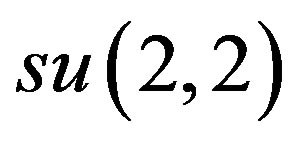 has been presented in [14, p.5262]:
has been presented in [14, p.5262]:
 (3.2)
(3.2)
Theorem 3.1. There exist  -inner contractions of d to oscillator subalgebras of
-inner contractions of d to oscillator subalgebras of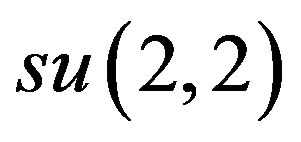 . Besides, there exist
. Besides, there exist 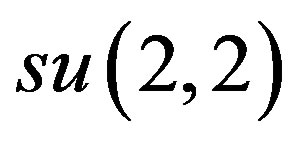 -inner contractions of d to abelian subalgebras of
-inner contractions of d to abelian subalgebras of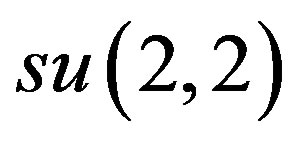 .
.
Proof. Choose the following basis for the Lie algebra d:

and conjugate the corresponding matrices with a generic element 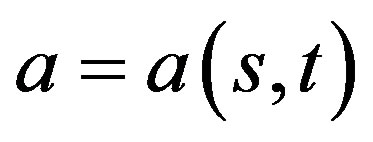 of the group A. Direct calculation shows that
of the group A. Direct calculation shows that
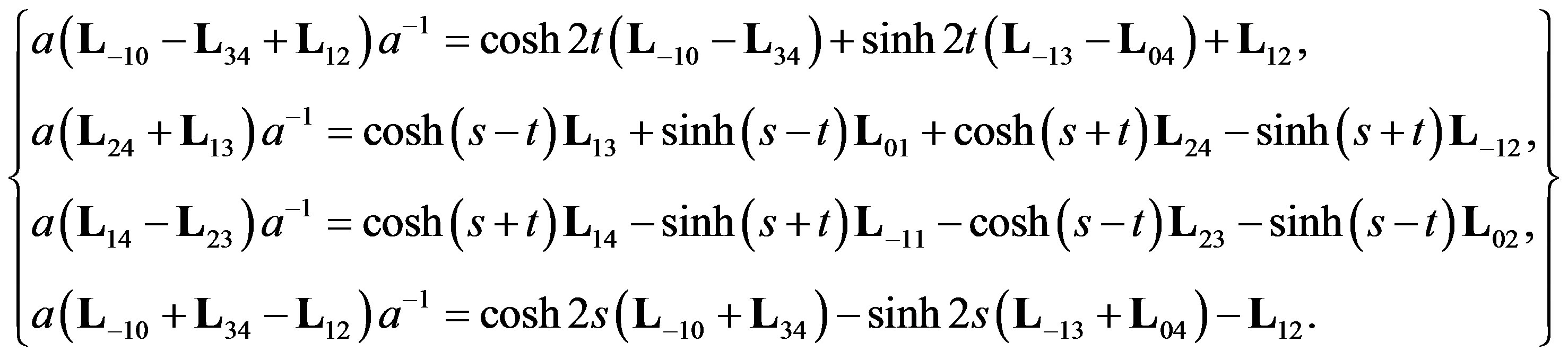 (3.3)
(3.3)
Set t = 0 in the above system and rewrite the equations as:

Now, introduce

from the equations above.
What we observe here is a special case of the contraction (2.1) with .
.
As s goes to infinity, the commutation relations become (1.1), which means that the outcome of the contraction is a subalgebra of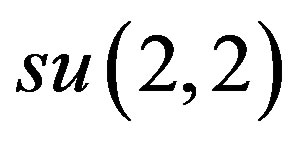 , isomorphic to the oscillator algebra l. Namely, basic matrices
, isomorphic to the oscillator algebra l. Namely, basic matrices
 (3.4)
(3.4)
of new subalgebra are the limits of the matrices ![]()
Alternatively, we can set s = 0 in system (3.3), and after a similar procedure, we get a limiting Lie algebra spanned by

It is also isomorphic to the oscillator Lie algebra, since the commutation relations are (1.1).
Finally, setting s = t in system (3.2), and repeating the procedure above, realizes a contraction of d to an abelian subalgebra of . The limiting algebra T (as s = t go to infinity) is generated by
. The limiting algebra T (as s = t go to infinity) is generated by
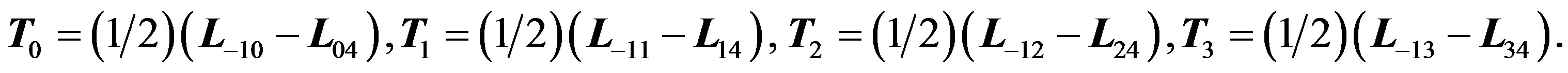
If we make s = t go to negative infinity, then the resulting abelian Lie algebra S is generated by
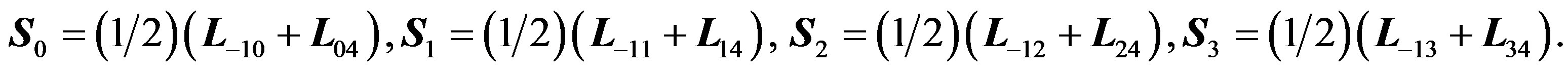
This finishes the proof of Theorem 3.1.
Remark 3.3. The (above) two subalgebras are known (in that order) as the Lie algebra of translations and the Lie algebra of “proper conformal transformations” of the Minkowski space-time: see [15], where su(2,2) is written as a graded algebra T + Ω + S with T, S being the two abelian algebras above, and Ω being the Lorentz Lie algebra extended by (infinitesimal) dilatations. The above choice of generators for T and for S has been made in Table V of [3].
In the remaining part of this section we arrange for similar procedures, as in the above, but for the case of . We realize it as a
. We realize it as a 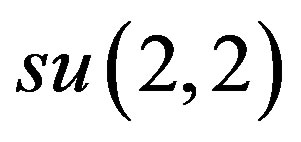 -subalgebra by choosing the following basis:
-subalgebra by choosing the following basis:
 (3.5)
(3.5)
This choice of the basis, with commutation relations (1.3), has been made in [8].
Theorem 3.2. There exists a 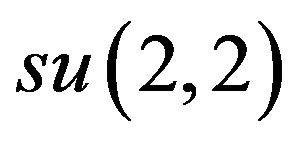 -inner contraction of this subalgebra f to a subalgebra of
-inner contraction of this subalgebra f to a subalgebra of  isomorphic to the oscillator Lie algebra l.
isomorphic to the oscillator Lie algebra l.
Proof. Choose one other basis for f:
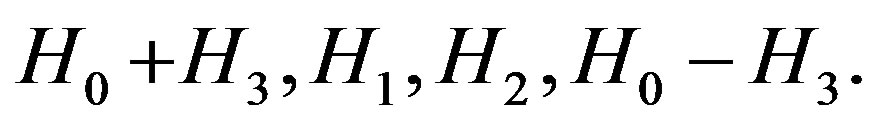 (3.6)
(3.6)
Conjugating these vectors with 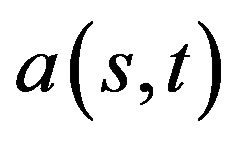 as in the proof of Theorem 3.1, we get the following:
as in the proof of Theorem 3.1, we get the following:
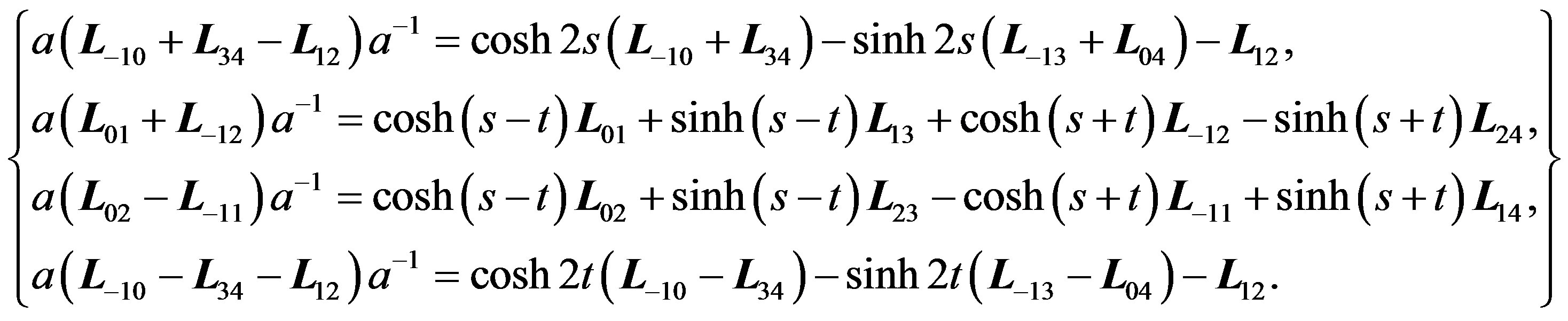 (3.7)
(3.7)
If we set t = 0 and perform a contraction analogous to that for d, we get in the limit as s goes to infinity, a subalgebra of  generated by the following set:
generated by the following set:
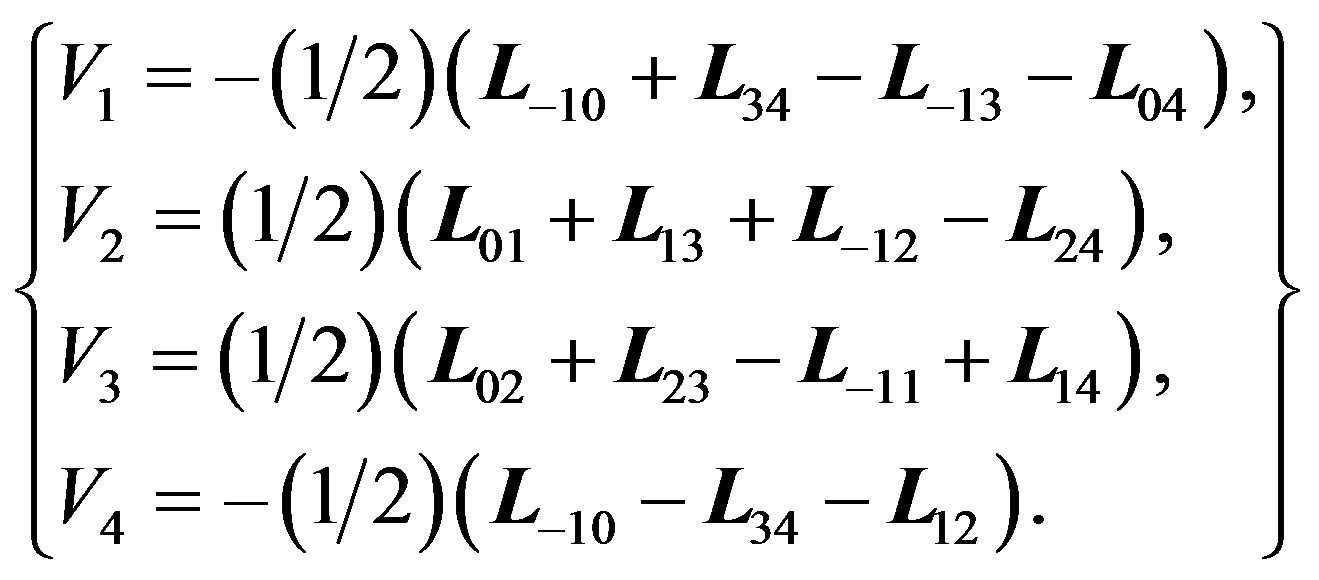 (3.8)
(3.8)
This subalgebra is isomorphic to the oscillator Lie algebra since the commutation relations are the same as (1.1).
4. Contractions of the Isometry Lie Algebras
As mentioned in the Introduction, the isometry groups of the Lorentzian manifolds, corresponding to the Lie algebras d, f, and l are of dimension 7. All three of these 7-dimensional Lie algebras, iso(D), iso(F), and iso(L) can be viewed as subalgebras of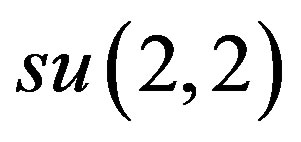 . The corresponding imbeddings are specified below (in Theorems 4.1, 4.2, 4.3), where
. The corresponding imbeddings are specified below (in Theorems 4.1, 4.2, 4.3), where 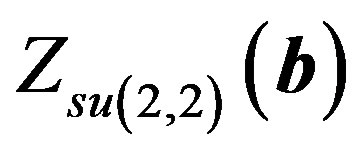 will denote the centralizer of a vector b in
will denote the centralizer of a vector b in . Considerable part of observations in this section has been known before, and we indicate a few references (see below). However, bringing together different methods and applying them to each of our main objects of study (space-times D, L, F), make the content of the section to a new ingredient of the mathematical presentation of the DLF-theory.
. Considerable part of observations in this section has been known before, and we indicate a few references (see below). However, bringing together different methods and applying them to each of our main objects of study (space-times D, L, F), make the content of the section to a new ingredient of the mathematical presentation of the DLF-theory.
According to [3], the following elements form a basis for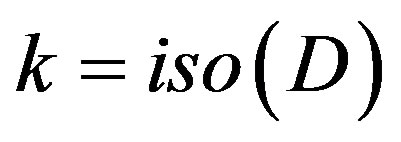 :
:
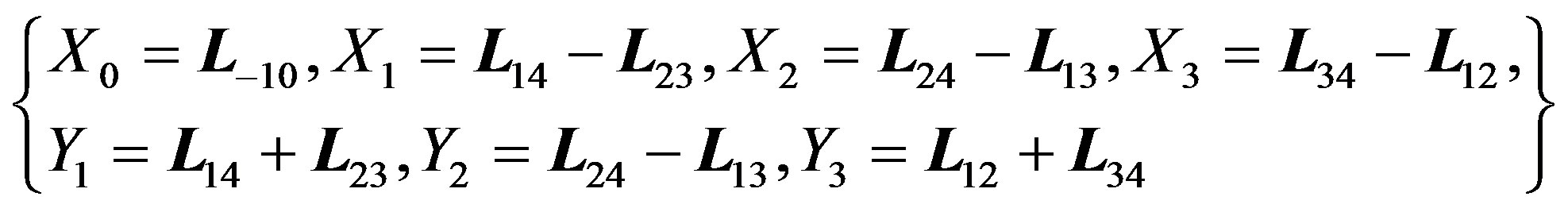 (4.0)
(4.0)
The two other isometry Lie algebras will be described below.
As it follows from (1.1), (1.2), (1.3), (3.1), (3.4), and (3.5), the centers of d, f, and of l are of dimension one, and they are generated by L−10, by L34, and by , respectively.
, respectively.
Theorem 4.1. The following is true for the Lie algebra iso(D):
 (4.1)
(4.1)
Theorem 4.2. The following is true for the Lie algebra iso(F):
 (4.2)
(4.2)
Theorem 4.3. The centralizer of l1 is a nine-dimensional Lie subalgebra of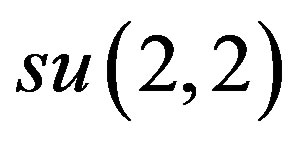 . More specifically, it is a two-dimensional nilpotent extension of iso(L).
. More specifically, it is a two-dimensional nilpotent extension of iso(L).
Proof of the theorem 4.1. It is a straightforward exercise, based on (3.1), to verify that the second equality in the above (4.1) holds. Regarding the first equality, it immediately follows from (4.0) that one of the two  blocks is generated by
blocks is generated by  and the other is generated by
and the other is generated by  The center {R} in (4.1) is generated by X0 = L−10 from (4.0).
The center {R} in (4.1) is generated by X0 = L−10 from (4.0).
Rather than to present other details from [3], one can use results from [16] to show that the basis (4.0) determines the Lie algebra iso(D). These results are based on the notion of a symmetric quadruple (k, q, p, B), where k is a finite dimensional real Lie algebra, q is a subalgebra of k, p is a non-zero, q-invariant, complementary vector subspace to q in k. B is a non-degenerate, q-invariant symmetric bilinear form on p. Also, [p, p] = q, and q contains no nonzero ideals of k. A certain involutive automorphism h of k is instrumental since q is its λ = 1 eigenspace, whereas p is its λ = −1 eigenspace.
It is shown in [16] that a simply connected pseudo-Riemannian symmetric space determines (up to an isomorphism) a symmetric quadruple. Given a symmetric quadruple, there exists a corresponding simply connected pseudo-Riemannian symmetric space. In our case iso(D) = k is reductive. To finish this alternative proof of equality (4.1), it is enough to present the corresponding symmetric quadruple (a Lorentzian one, due to the signature 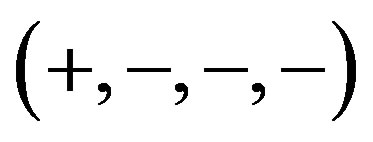 of the form B on p). To do so, introduce the following linear bijection h of the Lie algebra k: h is an identical transformation on the subalgebra q spanned by
of the form B on p). To do so, introduce the following linear bijection h of the Lie algebra k: h is an identical transformation on the subalgebra q spanned by , and h is negative 1 on the four-dimensional vector space p generated by
, and h is negative 1 on the four-dimensional vector space p generated by
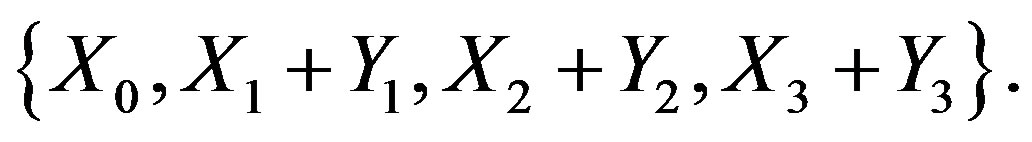
Clearly, q is isomorphic to su(2).
It is a straightforward exercise to verify that h is an involutive isomorphism of k. The form B on p is introduced as a “pull-back” of the following invariant Lorentzian form on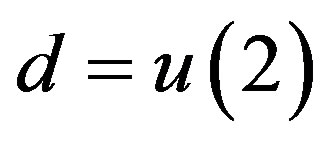 : vectors X0, X1, X2, X3 are orthonormal, their scalar squares being 1, −1, −1, −1, respectively. This finishes the proof of theorem 4.1.
: vectors X0, X1, X2, X3 are orthonormal, their scalar squares being 1, −1, −1, −1, respectively. This finishes the proof of theorem 4.1.
Let us now apply that last approach in the proof of theorem 4.2. The center R in (4.2) is generated by L34. One of the  -blocks is generated by H1, H2, H3 (these matrices have been introduced by (3.2) of Section 3); the other
-blocks is generated by H1, H2, H3 (these matrices have been introduced by (3.2) of Section 3); the other 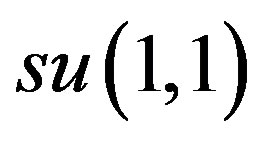 -block in (4.2) is a subalgebra of
-block in (4.2) is a subalgebra of  generated by
generated by

Let us show that the seven-dimensional subalgebra h spanned by
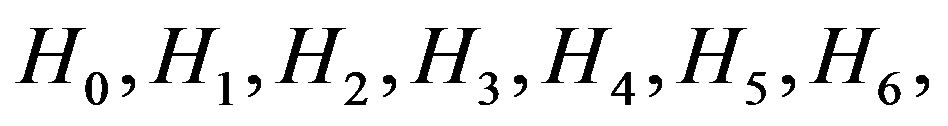 (4.3)
(4.3)
is the Lie algebra of the (reductive) Lie group Iso(F). The latter group is a subgroup of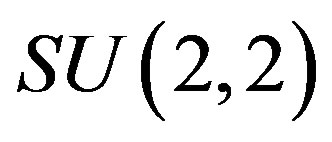 . Introduce the following linear bijection t of the Lie algebra h: t is an identity transformation on the subalgebra q generated by
. Introduce the following linear bijection t of the Lie algebra h: t is an identity transformation on the subalgebra q generated by
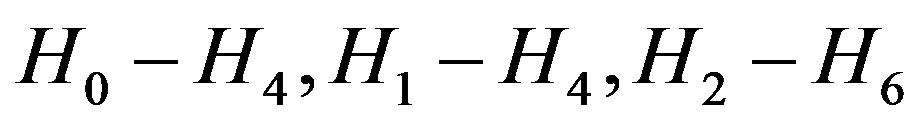
(clearly, q is isomorphic to ), and t is negative 1 on the four-dimensional vector space p generated by
), and t is negative 1 on the four-dimensional vector space p generated by

It is a straightforward exercise to verify that t is an involutive isomorphism of h. The form B on p is introduced as a “pull-back” of the following invariant Lorentzian form on : vectors H3, H0, H1, H2 are orthonormal, their scalar squares being 1, −1, −1, −1, respectively. The corresponding Lorentzian quadruple is now (h,q,p,B).
: vectors H3, H0, H1, H2 are orthonormal, their scalar squares being 1, −1, −1, −1, respectively. The corresponding Lorentzian quadruple is now (h,q,p,B).
Again, it is a straightforward exercise, based on (3.1), to verify that (4.2) holds, and that the above mentioned identity component of Iso(F) is the one of the block-diagonal subgroup of 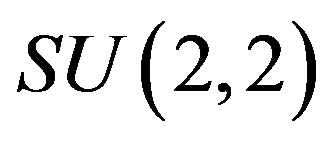 (see [9, Theorem 9]). Theorem 4.2 is proven.
(see [9, Theorem 9]). Theorem 4.2 is proven.
Proof of Theorem 4.3. It is known that the Lie algebra iso(L) is solvable and is of dimension 7. As a homogeneous symmetric Lorentzian manifold, L has been studied in [6]. The first author got to know the oscillator Lie group L from [17]. The L’s important property to admit a non-degenerate bi-invariant metric has only been noticed in early 80s: [1,2,18].
In paragraph 3 of [16] solvable Lorentzian quadruples are described in detail. That description includes a vector space w which is Euclidean in our case (the metric on w is chosen as a negative definite one). Also, a symmetric bilinear form A on w is part of the description. It is stated in [16] that if (k, q, p, B, w, A) is a solvable quadruple associated with a Lorentzian symmetric space L, then the full isometry Lie algebra iso(L) is the canonical semi-direct product of k with the algebra of skew-symmetric linear maps of w which commute with A. Here A is a linear operator associated with the form A. The operator A is defined by the formula
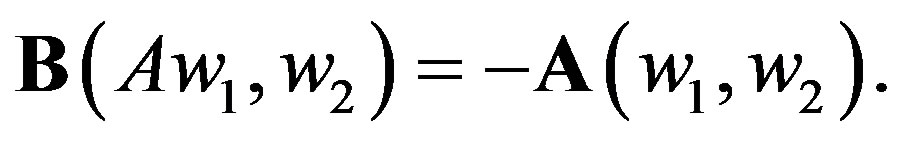
The approach of [6] was based on a choice of four left-invariant vector fields on the oscillator Lie group L (their commutation relations are (1.1) from the Introduction). In (1.1), the vector field l1 (which is also e1 of (4.4) below) is both left-, and right-invariant. There are three more linearly independent right-invariant vector fields (they commute with left-invariant vector fields on L). Overall, in the approach of [6], we get the following table
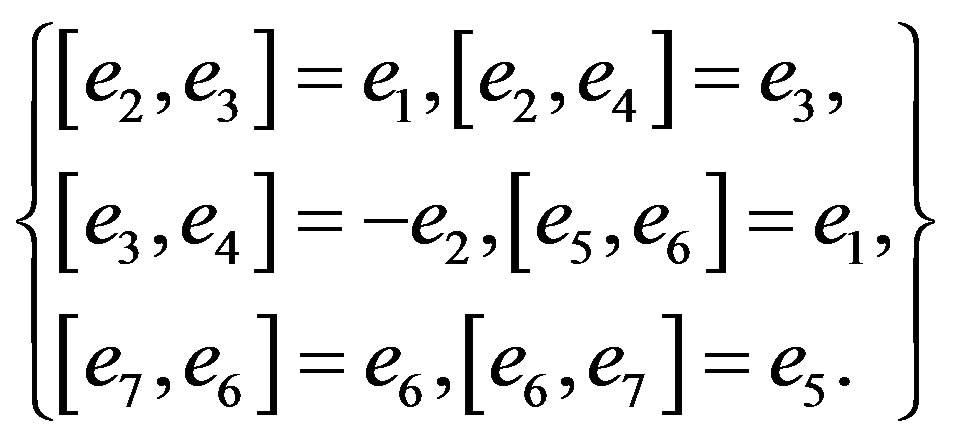 (4.4)
(4.4)
It determines the structure of the full isometry Lie algebra of the space-time in question. The seven generators, as elements of , can be chosen as follows (notice that this choice is different from the one in our Section 3):
, can be chosen as follows (notice that this choice is different from the one in our Section 3):
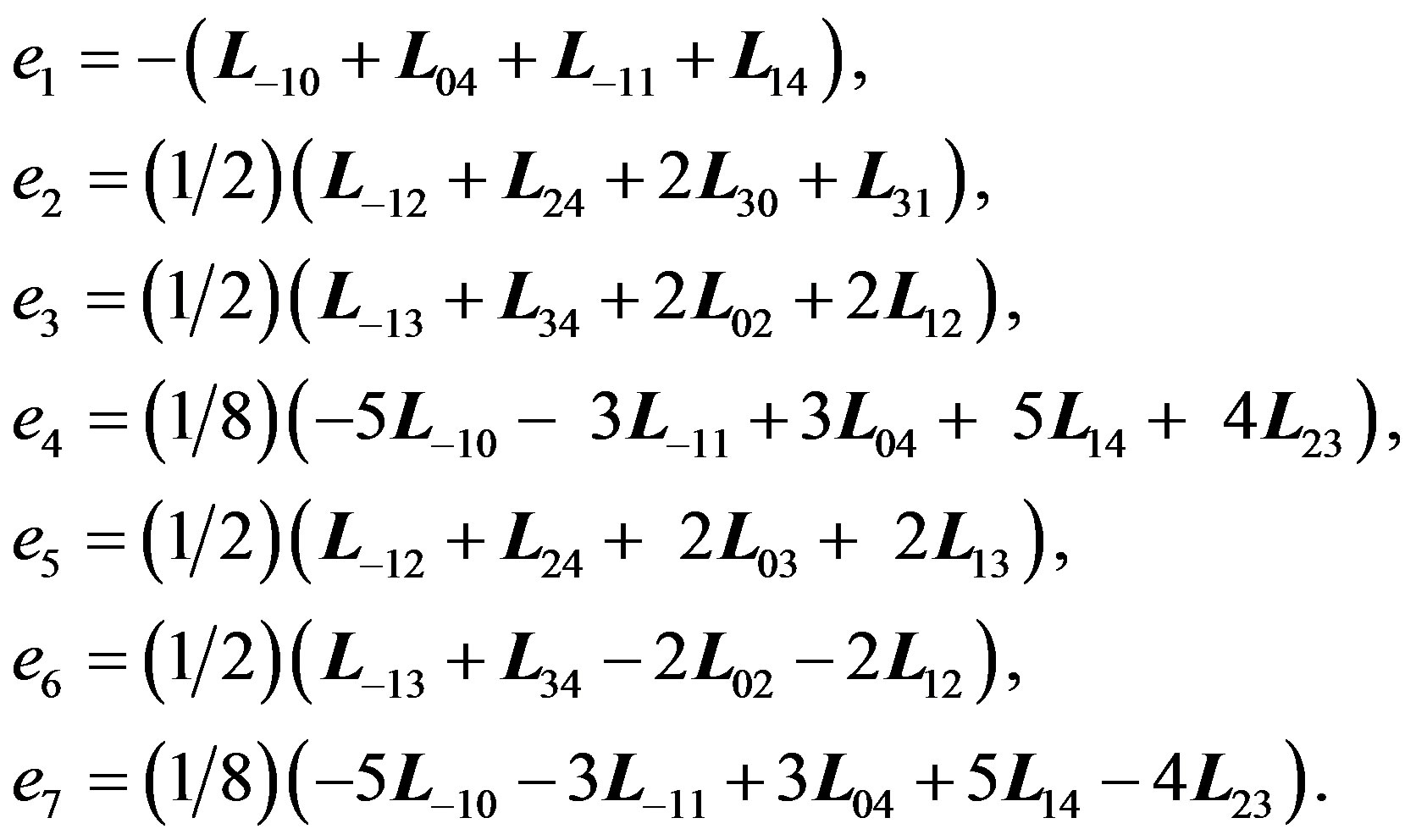
Starting with (4.4), introduce w with an orthonormal basis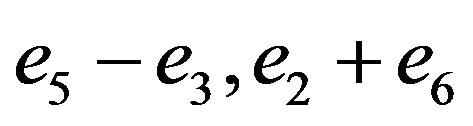 . Relative to this basis, the negative definite form
. Relative to this basis, the negative definite form![]() , to be of use below, is given by the diagonal matrix
, to be of use below, is given by the diagonal matrix
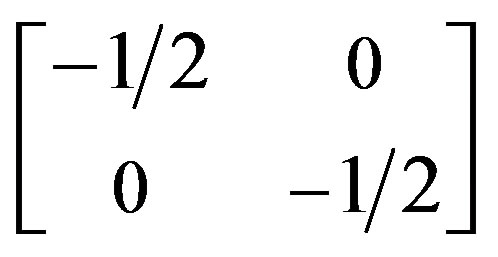 .
.
Introduce w* with a reciprocal basis . This involves a choice of a linear bijection between w and w*, with w* being the image of w, etc. Choose the form A given by the matrix
. This involves a choice of a linear bijection between w and w*, with w* being the image of w, etc. Choose the form A given by the matrix

relative to the same basis in w. Let us denote by R, 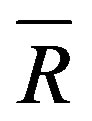 , one-dimensional vector spaces generated by e1, e4 + e7, respectively.
, one-dimensional vector spaces generated by e1, e4 + e7, respectively.
One can now verify that a six-dimensional

satisfies the following commutation table:
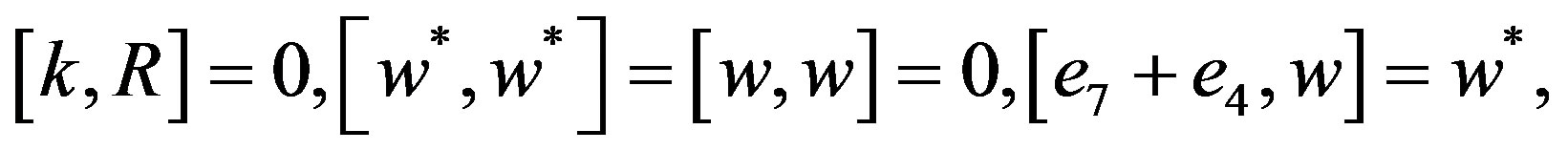
for w in w;
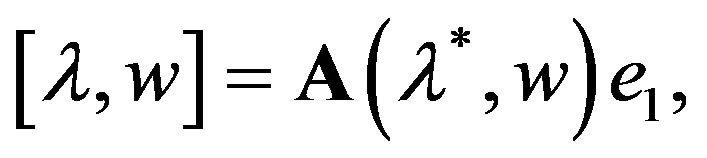
for ![]() in w*,
in w*, ![]() in w;
in w;
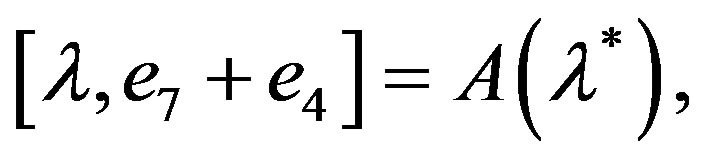
For ![]() in w.
in w.
Now,  ,
,  , and B is defined as follows: on w, B coincides with
, and B is defined as follows: on w, B coincides with![]() , from above,
, from above,
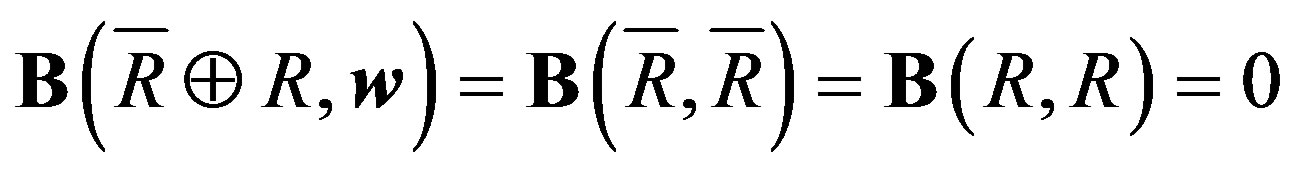 ,
,
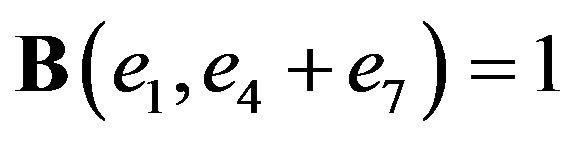 .
.
This is a particular case of commutation relations from p.588 of [2]. Vector 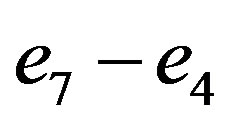 generates the algebra of those skew-symmetric linear maps of w which commute with A. We have thus applied results of [16] to show that the above seven-dimensional Lie algebra is the entire isometry Lie algebra of the corresponding symmetric Lorentzian space. To finish the proof of our theorem 4.3, we provide two more generators, L23, L−11 + L14 which (together with the above vectors
generates the algebra of those skew-symmetric linear maps of w which commute with A. We have thus applied results of [16] to show that the above seven-dimensional Lie algebra is the entire isometry Lie algebra of the corresponding symmetric Lorentzian space. To finish the proof of our theorem 4.3, we provide two more generators, L23, L−11 + L14 which (together with the above vectors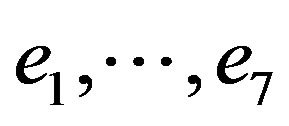 ) form the centralizer of e1. One can check the commutation relations to show that this nine-dimensional Lie subalgebra of
) form the centralizer of e1. One can check the commutation relations to show that this nine-dimensional Lie subalgebra of 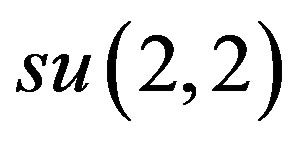 is a nilpotent extension of the seven-dimensional iso(L).
is a nilpotent extension of the seven-dimensional iso(L).
Remark 4.1. Presumably, if one adds the generator of a homothetic transformation (which acts non-trivially on e1), then the resulting 10-dimensional Lie algebra is the one discovered on p.130 of [19].
Remark 4.2. A centralizer of a non-zero element in su(2,2) may have dimension 3, 5, 7, or 9. It seems to be of interest to try to characterize those cases when the isometry Lie algebra coincides with the centralizer of a single element from the Lie algebra of all conformal transformations: it is so in theorems 4.1, 4.2 but it is not the case of theorem 4.3.
To continue, recall that k = iso(D) is defined by our (4.0).
Theorem 4.4. There exists an  -inner contraction of k to iso(L).
-inner contraction of k to iso(L).
Proof. As in (3.3), conjugate the involved matrices by 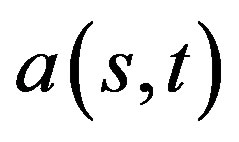 and set t = 0. Then choose the following seven vectors in the resulting Lie algebra aka−1:
and set t = 0. Then choose the following seven vectors in the resulting Lie algebra aka−1:
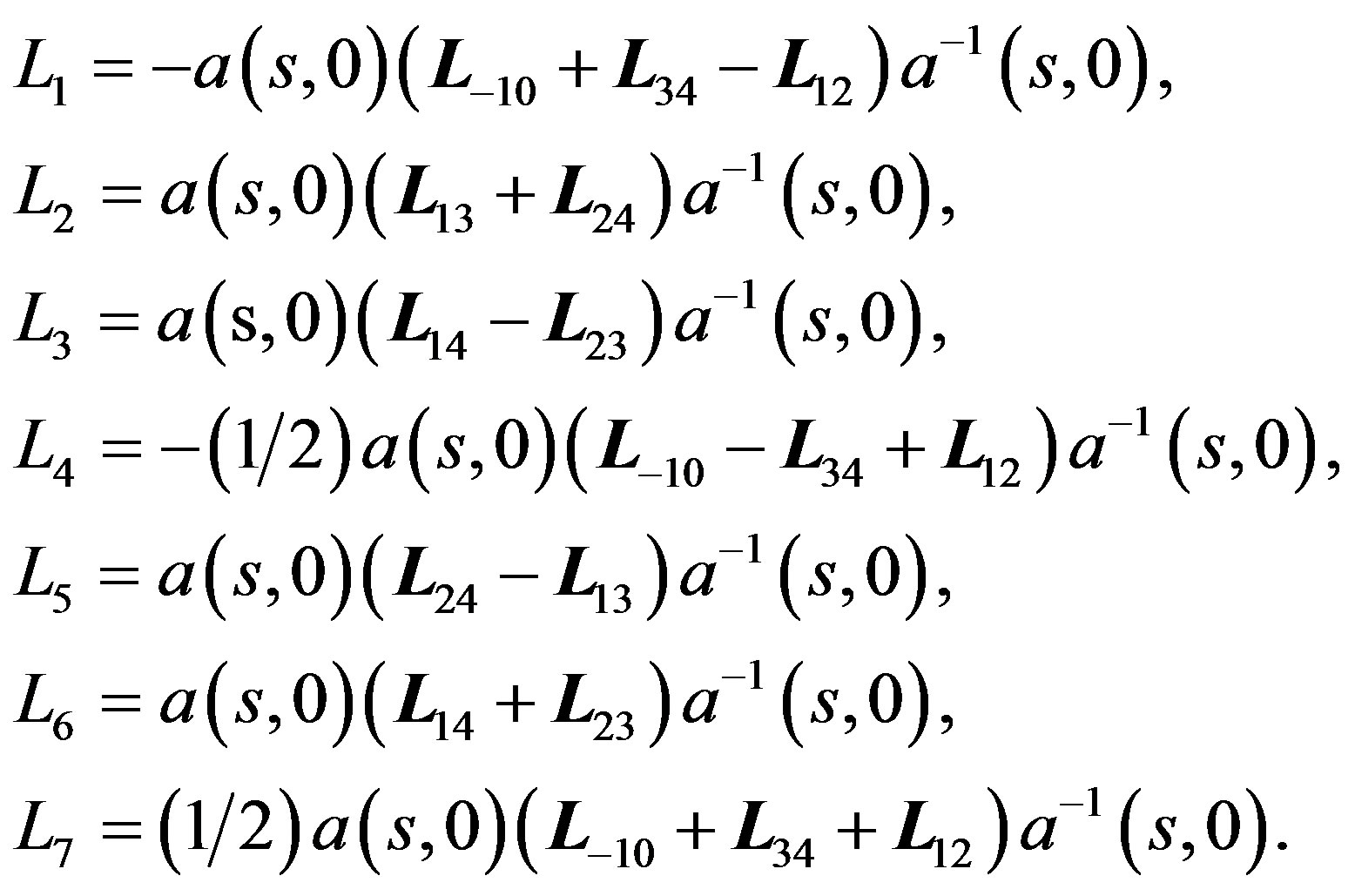
In the limit as s goes to infinity, the seven matrices form the following Lie subalgebra, isomorphic to iso(L):
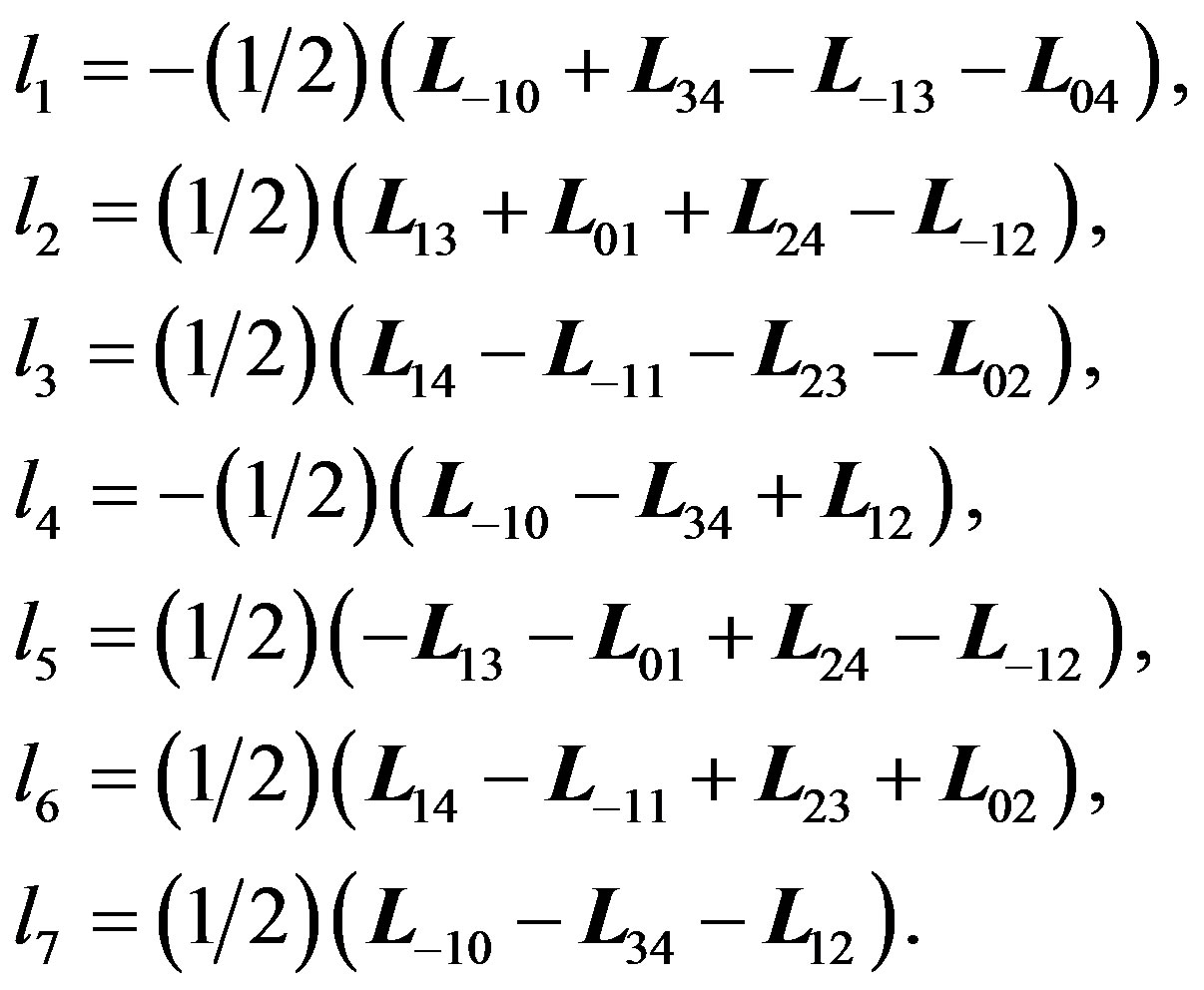 (4.5)
(4.5)
Remark 4.3. It is obvious that the Lie algebra (3.8) is a subalgebra of (4.5).
We can contract 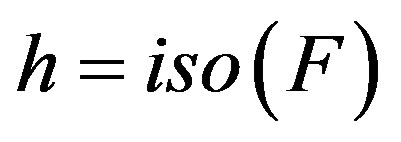 in, essentially, the same way we did the contraction of
in, essentially, the same way we did the contraction of 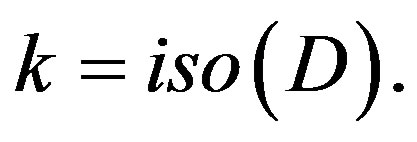 This h is
This h is 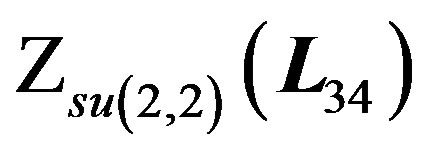 which is generated by the following vectors:
which is generated by the following vectors:

Theorem 4.5.There exists an 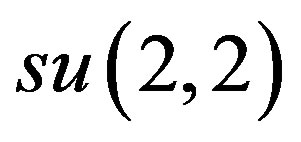 -inner contraction of h = iso(F) to iso(L).
-inner contraction of h = iso(F) to iso(L).
Proof. Complete basis (3.3) with vectors
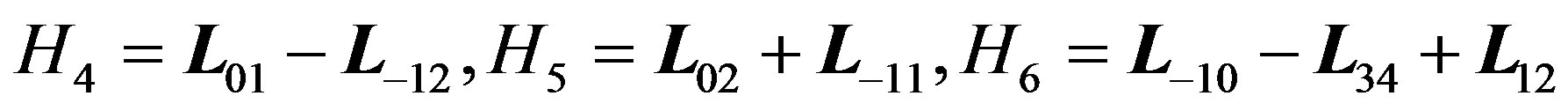
to obtain a basis for iso(F), and extend the contraction, defined earlier for f, to this algebra. Namely, conjugate

by  introduced in Section 3. Setting t = 0 and letting s go to infinity, we get a Lie algebra generated by the vectors
introduced in Section 3. Setting t = 0 and letting s go to infinity, we get a Lie algebra generated by the vectors

This last Lie algebra is (isomorphic to) iso(L).
Acknowledgements
A.L. thanks David Vogan for helpful discussions on the subject of Section 3, Ernest Vinberg for information on centralizers in su(2,2), and the comments for Referee.
REFERENCES
[1] A. K. Guts and A. V. Levichev, “On the Foundations of Relativity Theory,” Doklady Akademii Nauk SSSR, Vol. 277, No. 6, 1984, pp. 1299-1303. (in Russian)
[2] A. V. Levichev, “Causal Cones in Low-Dimensional Lie Algebras,” Siberian Journal of Mathematics, Vol. 26, No. 5, 1985, pp. 192-195. (in Russian)
[3] S. Paneitz and I. Segal, “Analysis in Space-Time Bundles I: General Considerations and the Scalar Bundle,” Journal of Functional Analysis, Vol. 47, No. 1, 1982, pp. 78-142. http://dx.doi.org/10.1016/0022-1236(82)90101-X
[4] A. V. Levichev, “Certain Symmetric General Relativistic Space-Times as the Solutions to the Einstein-Yang-Mills Equations,”, Proceedings Group Theoretical Methods in Physics (III International Seminar), Yurmala, 1985, pp. 145-150. (in Russian)
[5] D. Kramer, H. Stephani, M. MacCallum and E. Herlt, “Exact Solutions of Einstein’s Field Equations,” VEB Deutscher Verlag der Wissenschaften, Berlin, 1980.
[6] A. V. Levichev, “Chronogeometry of an Electromagnetic Wave Defined by a Bi-Invariant Metric on the Oscillator Lie Group,” Siberian Journal of Mathematics, Vol. 27, No. 2, 1986, pp. 237-245. http://dx.doi.org/10.1007/BF00969391
[7] J. Hilgert, K. H. Hofmann and J. D. Lawson, “Lie Groups, Convex Cones, and Semigroups,” Clarendon Press, Oxford, 1989.
[8] A. V. Levichev, “Three Symmetric Worlds Instead of the Minkowski Space-Time,” Transactions on RANS, series MMM&C, Vol. 7, No. 3-4, 2003, pp. 87-93.
[9] A. V. Levichev, “Pseudo-Hermitian Realization of the Minkowski World through the DLF-Theory,” Physica Scripta, Vol. 83, No. 1, 2011, pp. 1-9.
[10] V. Guillemin and S. Sternberg, “Geometric Asymptotics,” American Mathematical Society, Providence, 1977. http://dx.doi.org/10.1090/surv/014
[11] A. Fialowski and M. De Montigny, “On Deformations and Contractions of Lie Algebras,” SIGMA, Vol. 2, 2006, p. 10. http://www.emis.de/journals/SIGMA/2006/Paper048/
[12] I. Segal, “A Class of Operator Algebras Which Are Determined by Groups,” Duke Mathematical Journal, Vol. 18, No. 1, 1951, pp. 221-265. http://dx.doi.org/10.1215/S0012-7094-51-01817-0
[13] A. Knapp, “Representation Theory of Semisimple Groups: An Overview Based on Examples,” Princeton University Press, Princeton, 2001.
[14] I. E. Segal, H. P. Jakobsen, B. Orsted, S. M. Paneitz and B. Speh, “Covariant Chronogeometry and Extreme Distances: Elementary Particles,” Proceedings of the National Academy of Sciences, Vol. 78, No. 9, 1981, pp. 5261-5265. http://dx.doi.org/10.1073/pnas.78.9.5261
[15] S. Sternberg, “Chronogeometry and Symplectic Geometry,” Colloques Internationaux C.N.R.S. Geometrie Symplectique et Physique Mathematique, Vol. 237, 1975, pp. 45-57.
[16] M. Cahen, and N. Wallach, “Lorentzian Symmetric Spaces,” Bulletin of the American Mathematical Society, Vol. 76, No. 3, 1970, pp. 585-591. http://dx.doi.org/10.1090/S0002-9904-1970-12448-X
[17] R. F. Streater, “The Representations of the Oscillator Group,” Communications in Mathematical Physics, Vol. 4, No. 3, 1967, pp. 217-236. http://dx.doi.org/10.1007/BF01645431
[18] A. Medina and Ph. Revoy, “Les Groups Oscillateurs at Leurs Reseaux,” Manuscripta Mathematica, Vol. 52, No. 1-3, 1985, pp. 81-95. http://dx.doi.org/10.1007/BF01171487
[19] M. Cahen and Y. Kerbrat, “Champs des Vecteurs Conformes et Transformations Conformes des Espace Lorentziens Symmetriques,” Journal de Mathématiques Pures et Appliquées, Vol. 4, No. 57, 1978, pp. 99-132.
NOTES

*Corresponding author.
#Deceased.

