Advances in Pure Mathematics
Vol.3 No.9(2013), Article ID:40319,3 pages DOI:10.4236/apm.2013.39093
On the Behavior of Connectedness Properties in Isotonic Spaces under Perfect Mappings
Department of Mathematics, Egerton University, Egerton, Kenya
Email: machariastephen.y31@gmail.com, gichukih2002@yahoo.com, kewamoics@yahoo.com
Copyright © 2013 Stephen M. Gathigi et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Stephen M. Gathigi et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received October 25, 2013; revised November 25, 2013; accepted December 1, 2013
Keywords: Closure Operator; Closure Axiom; Isotonic Space; Perfect Mapping; Connectedness
ABSTRACT
The topological study of connectedness is heavily geometric or visual. Connectedness and connectedness-like properties play an important role in most topological characterization theorems, as well as in the study of obstructions to the extension of functions. In this paper, the behaviour of these properties in the realm of closure spaces is investigated using the class of perfect mappings. A perfect mapping is a type of map under which the image generally inherits the properties of the mapped space. It turns out that the general behaviour of connectedness properties in topological spaces extends to the class of isotone space.
1. Introduction
The concept of a topological space is generally introduced and studied in terms of the axioms of open sets. However, alternate methods of describing a topology are often used: neighborhood systems, family of closed sets, closure operator and interior operator. Of these, the closure operator—records [1], was axiomated by Kuratowski.
The class of continuous functions forms a very broad spectrum of mappings comprising of different subclasses with varying properties. In the spectrum of continuous functions is the class of perfect mappings which, although weaker than homeomorphisms, provides a general yet satisfactory means of investigating topological invariants and hence the equivalence of topological spaces.
In an attempt to extend the boundaries of topology, [2] has shown that topological spaces do not constitute a natural boundary for the validity of theorems and results in topology. Many results therefore, can be extended to closure spaces where some of the basic axioms in this space can be dropped. Many properties which hold in basic topological spaces hold in spaces possessing the isotonic property.
2. Literature Review
2.1. Closure Operator and Generalized Closure Space
A closure operator is an arbitrary set-valued, set-function 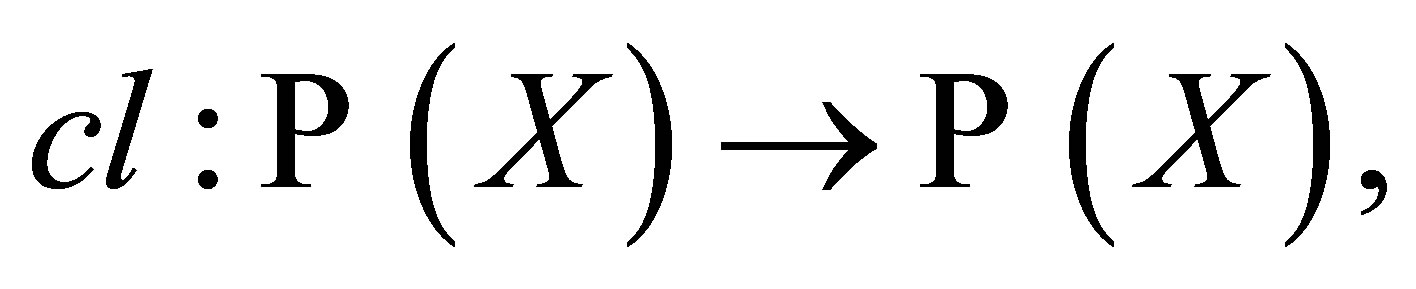 where
where 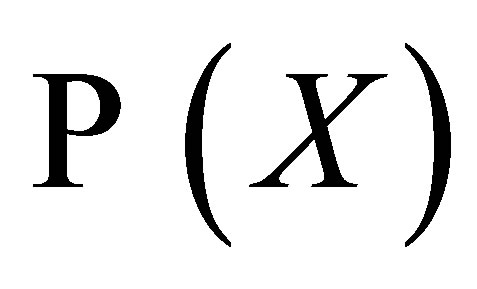 is the power set of a non-void set
is the power set of a non-void set , [3]. Let
, [3]. Let .
.
1) Grounded: 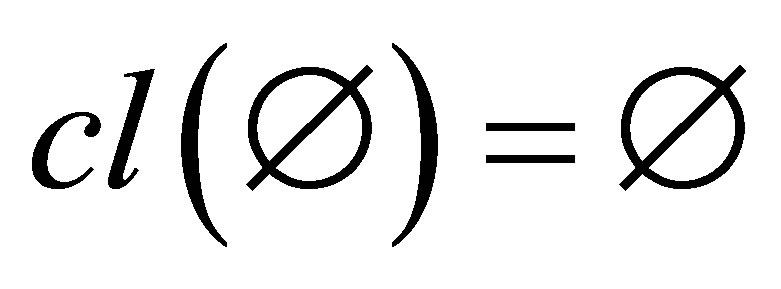
2) Expansive: 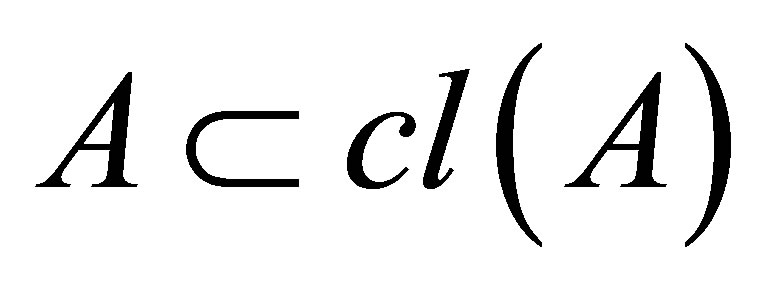
3) Sub-additive: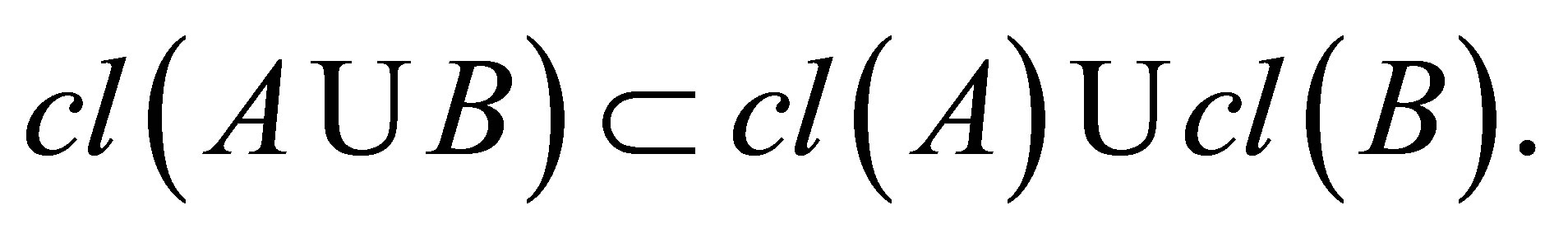 This axiom implies the Isotony axiom:
This axiom implies the Isotony axiom:  implies
implies 
4) Idempotent: 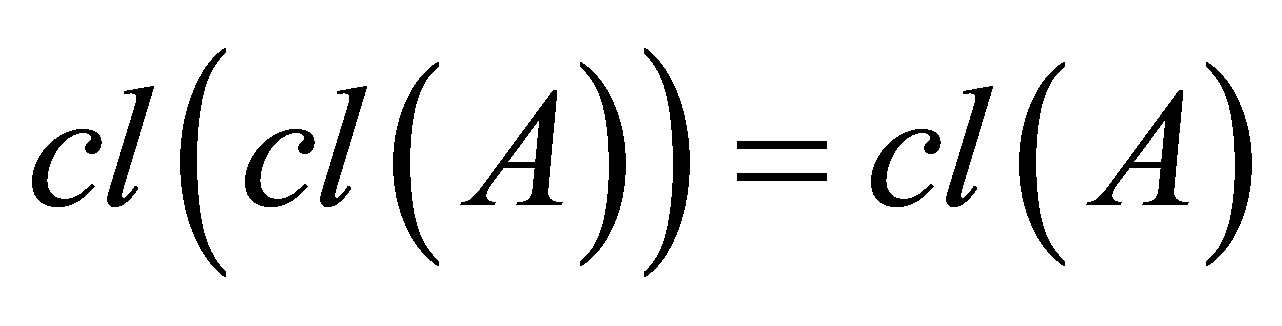
The structure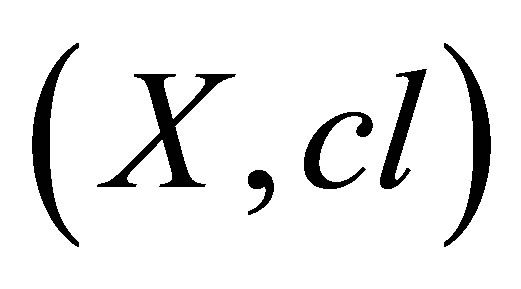 , where
, where 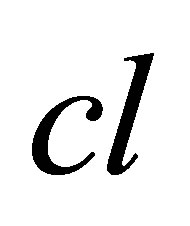 satisfies the first three axioms is called a closure space. If in addition the idempotent axiom is satisfied, then the structure is a topological space.
satisfies the first three axioms is called a closure space. If in addition the idempotent axiom is satisfied, then the structure is a topological space.
2.2. Isotonic Space
A closure space 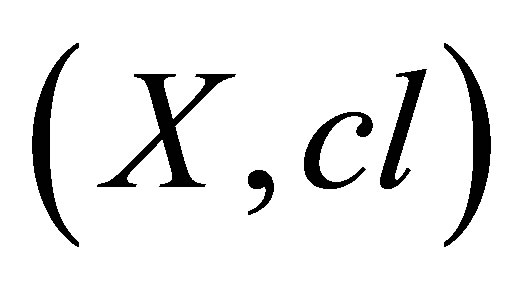 satisfying only the grounded and the isotony closure axioms is called an isotonic space [4].
satisfying only the grounded and the isotony closure axioms is called an isotonic space [4].
In the dual formulation, a space 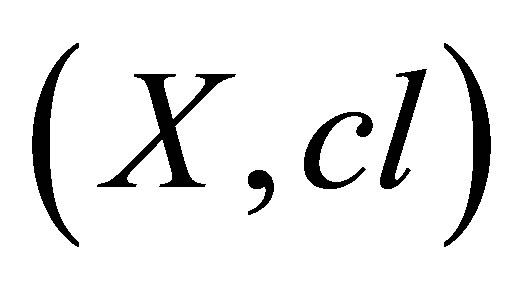 is isotonic if and only if the interior function
is isotonic if and only if the interior function 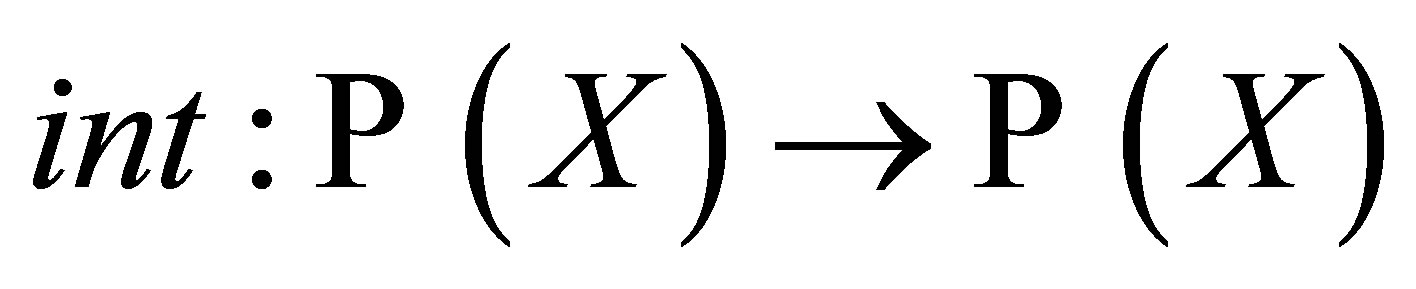 satisfies;
satisfies;
1)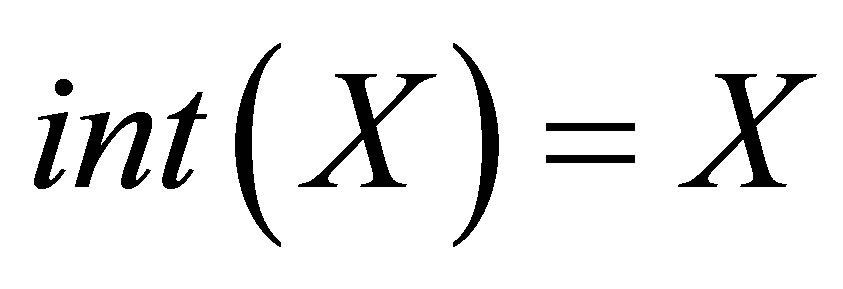 .
.
2) 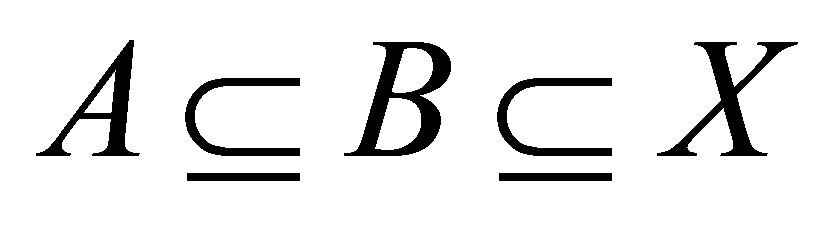 implies
implies 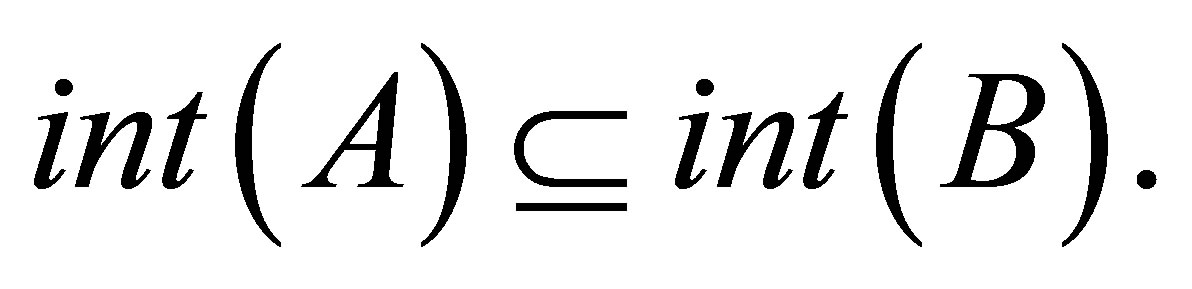
2.3. C-Compactness
Let 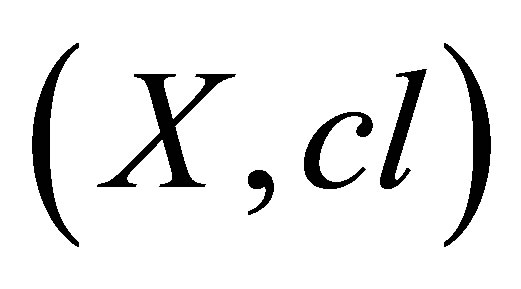 be a closure space. A family
be a closure space. A family 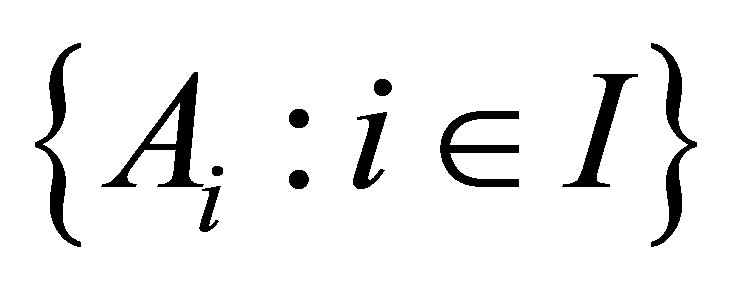 of subsets of
of subsets of 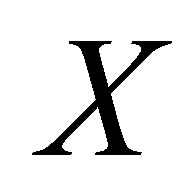 is called a c-cover of
is called a c-cover of 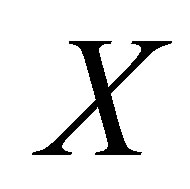 if
if 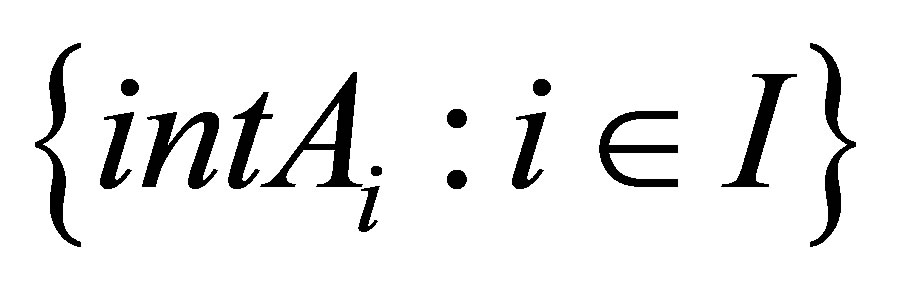 covers
covers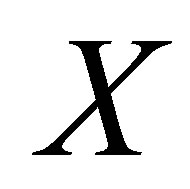 . A closure space is c-compact if every
. A closure space is c-compact if every  -cover of
-cover of  has a finite subcover, [3].
has a finite subcover, [3].
2.4. Connectedness
Various characterizations of connectedness exist in the realm of topological spaces. For instance, [5] described a space  to be connected if and only if for every decomposition of
to be connected if and only if for every decomposition of 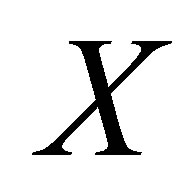 into two non-void closed sets
into two non-void closed sets  and
and , the condition
, the condition  is satisfied. In other words,
is satisfied. In other words, 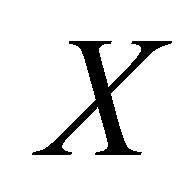 is connected if and only if it cannot be represented as a union of two non-empty, disjoint closed sets.
is connected if and only if it cannot be represented as a union of two non-empty, disjoint closed sets.
According to [4] an isotonic space 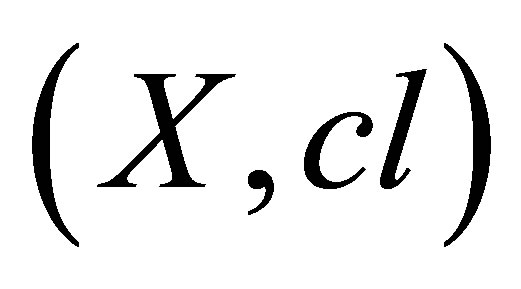 is connected if and only if for all
is connected if and only if for all  -isotonic doubleton spaces
-isotonic doubleton spaces , any continuous function
, any continuous function 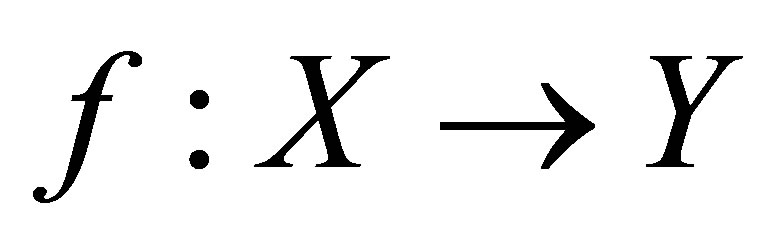 is a constant. This characterization of connectedness is an extension of an equivalent definition of connectedness in topological spaces that was given by [2] where
is a constant. This characterization of connectedness is an extension of an equivalent definition of connectedness in topological spaces that was given by [2] where 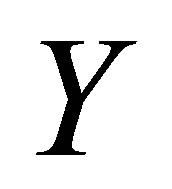 is a discrete space.
is a discrete space.
In topological spaces, connectedness is defined by means of open and closed sets. That definition can only be extended to closure spaces which have the expanding closure axiom; 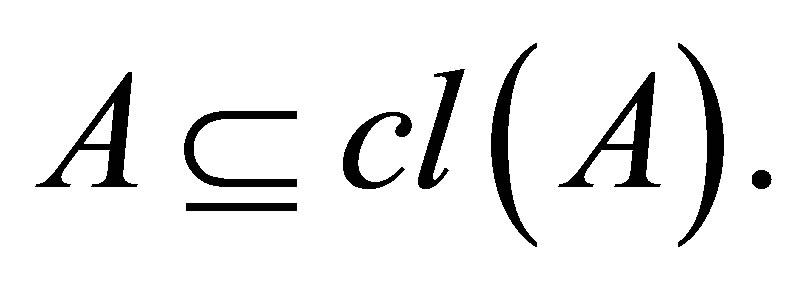 This is why the above definition is more suitable for isotonic spaces since it doesn’t involve open or closed sets.
This is why the above definition is more suitable for isotonic spaces since it doesn’t involve open or closed sets.
2.4.1. Total Disconnectedness
The component 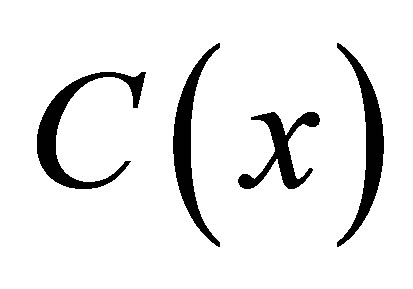 of
of 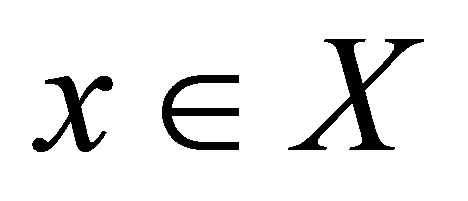 is the union of all connected subsets of
is the union of all connected subsets of 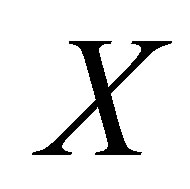 containing
containing 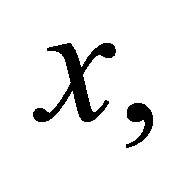 [5]. It is clear, from the fact that the union of any family of connected subsets having at least one point in common is also connected, that
[5]. It is clear, from the fact that the union of any family of connected subsets having at least one point in common is also connected, that 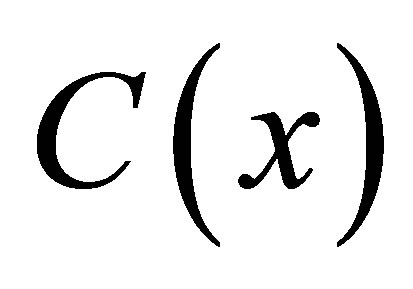 is connected.
is connected.
An isotonic space 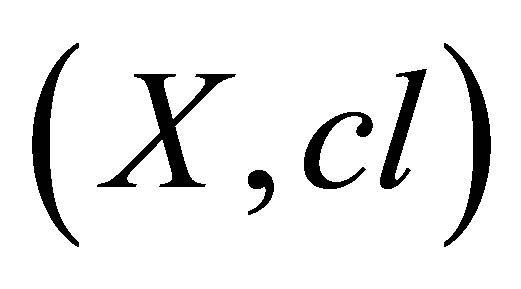 is said to be totally disconnected if for every
is said to be totally disconnected if for every , the component
, the component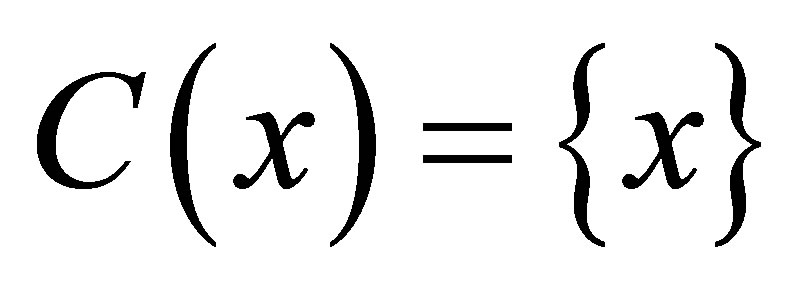 , [4]. Since the components of a space
, [4]. Since the components of a space 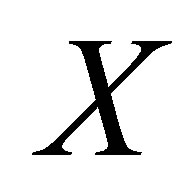 are closed, then every totally disconnected space is
are closed, then every totally disconnected space is 
2.4.2. Z-Connectedness
The concept of Z-connectedness, according to [6], is obtained by replacing the discrete space {0,1} in the characterization of connectedness, by some other space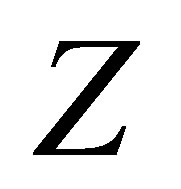 .
.
Let  be an isotonic space with more than one element. An isotonic space
be an isotonic space with more than one element. An isotonic space 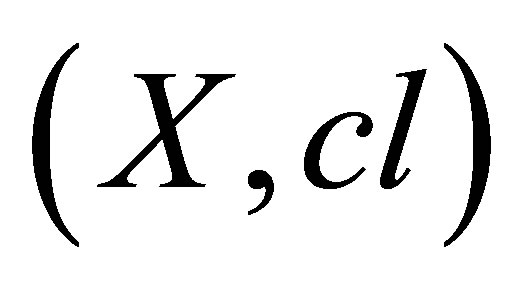 is called Z-connected if and only if any continuous function
is called Z-connected if and only if any continuous function 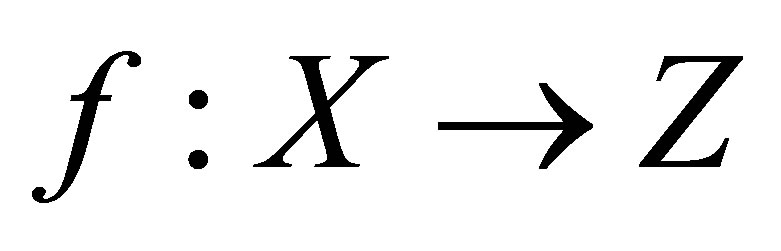 is constant, [5].
is constant, [5].
2.4.3. Strongly Connected
An isotonic space 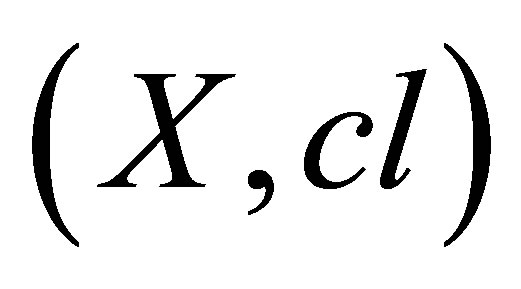 is strongly connected if there is no countable collection of pair-wise semi-separated sets
is strongly connected if there is no countable collection of pair-wise semi-separated sets 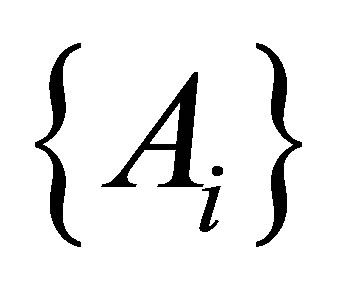 such that
such that . It follows from the definition that a strongly connected isotonic space is connected.
. It follows from the definition that a strongly connected isotonic space is connected.
2.5. Perfect Mappings
The class of perfect mappings is descended from the broader class of bi-quotient maps. A map 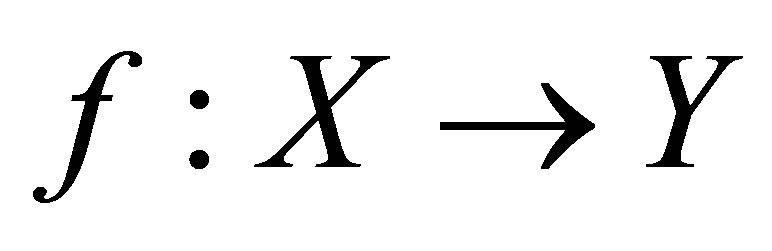 is called bi-quotient if whenever
is called bi-quotient if whenever 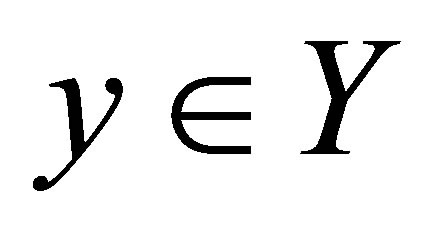 and
and  is a covering of
is a covering of  by open subsets of
by open subsets of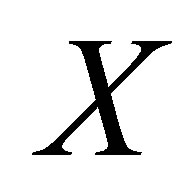 , then finitely many
, then finitely many 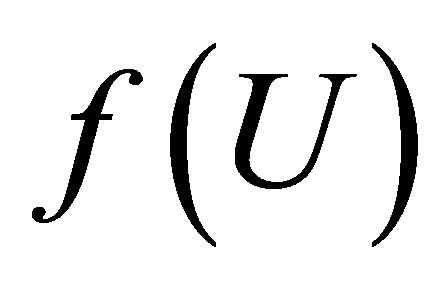 with
with  cover some neighbourhood of
cover some neighbourhood of 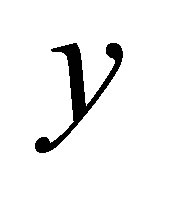 in
in 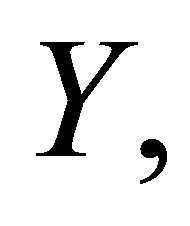 [7].
[7].
Let 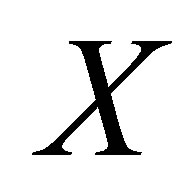 and
and 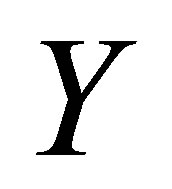 be topological spaces and
be topological spaces and 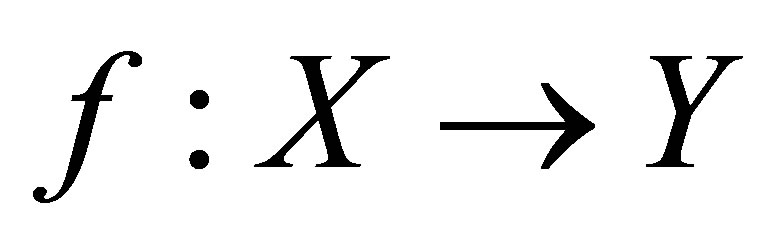 be a mapping. From [8]
be a mapping. From [8]
1) 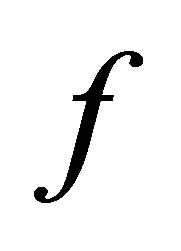 is called a compact mapping if
is called a compact mapping if 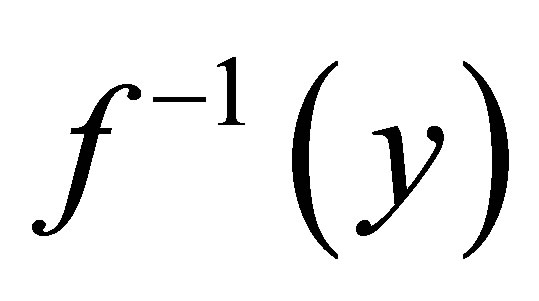 is a compact subset of
is a compact subset of  for each
for each 
2) 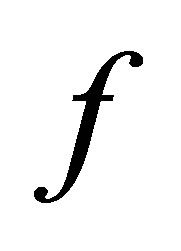 is called a perfect mapping if it is a closed and compact mapping.
is called a perfect mapping if it is a closed and compact mapping.
3)  is called an open perfect mapping if
is called an open perfect mapping if 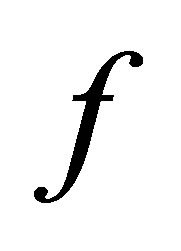 is an open and perfect mapping.
is an open and perfect mapping.
4) Every perfect mapping is a quotient map, where 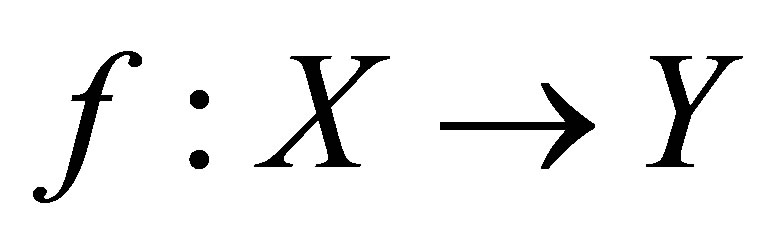 is a quotient map if
is a quotient map if  is open in
is open in 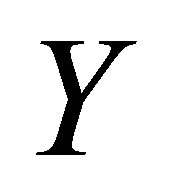 whenever
whenever 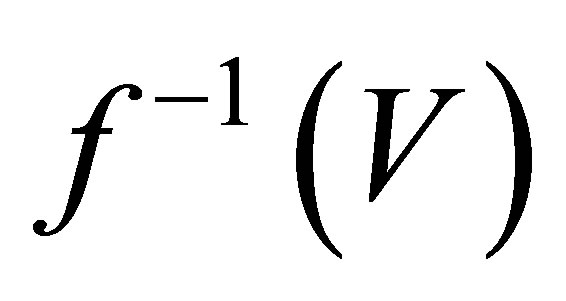 is open in
is open in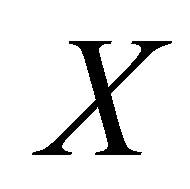 .
.
The class of perfect mappings may be used in substitution of homeomorphisms to investigate the invariance of topological properties. By investigating topological properties in isotonic spaces under the class of perfect mappings, which is a more general class of functions than homeomorphisms, the results and theorems obtained become a pointer of how general the concepts of topology can get.
3. Main Results
This section summarizes the results of this work.
3.1. Perfect Mappings on Isotonic Spaces
Let  and
and  be isotonic spaces and
be isotonic spaces and  be a continuous surjective mapping.
be a continuous surjective mapping. 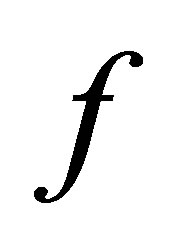 is called a c-compact mapping if
is called a c-compact mapping if 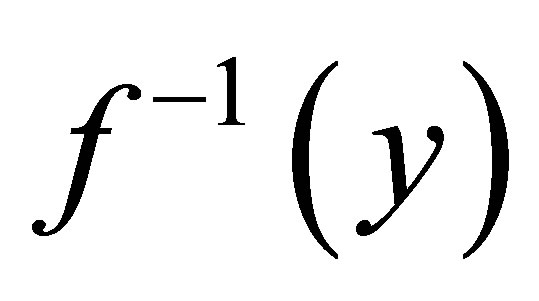 is a c-compact subset of
is a c-compact subset of .
.
A continuous surjective mapping between two isotonic spaces is said to be perfect if it is closed and 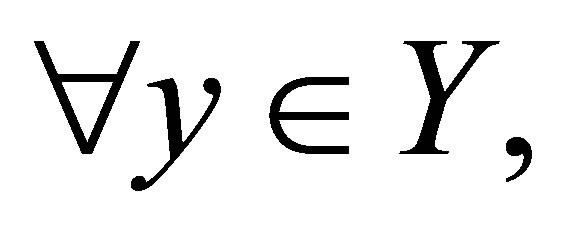
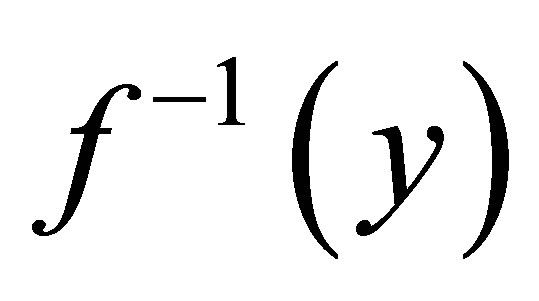 is a c-compact subset of
is a c-compact subset of .
.
These two definitions closely correlate with their definitions in general topological spaces, except for the fact that a different approach is employed while defining the foregoing topological notions.
3.2. Invariance of Connectedness Conditions
There are different forms of connectedness and disconnectedness that have been defined, both in topological spaces and in closure spaces. These definitions can be found under Section 2.3 of this paper. The next two theorems describe the behavior of the different forms of connectedness with respect to perfect mappings.
Theorem: Connectedness, Z-connectedness and strong connectedness are invariants of perfect mappings.
Proof: Let 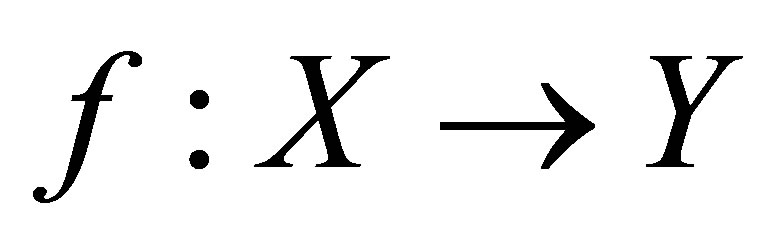 be a perfect mapping of a connected isotonic space
be a perfect mapping of a connected isotonic space 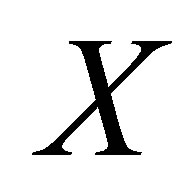 onto an isotonic space
onto an isotonic space . Since
. Since 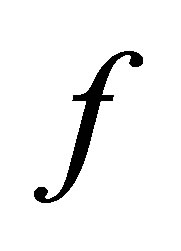 is a surjection, then
is a surjection, then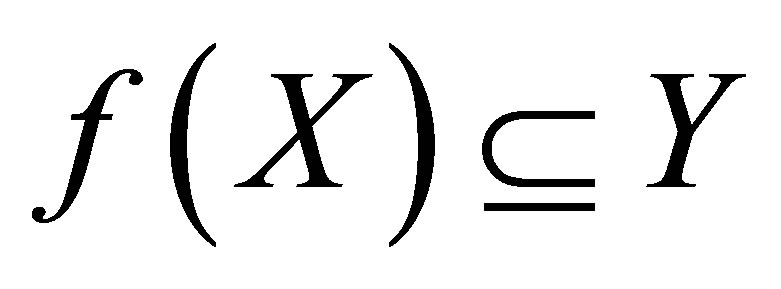 . Let
. Let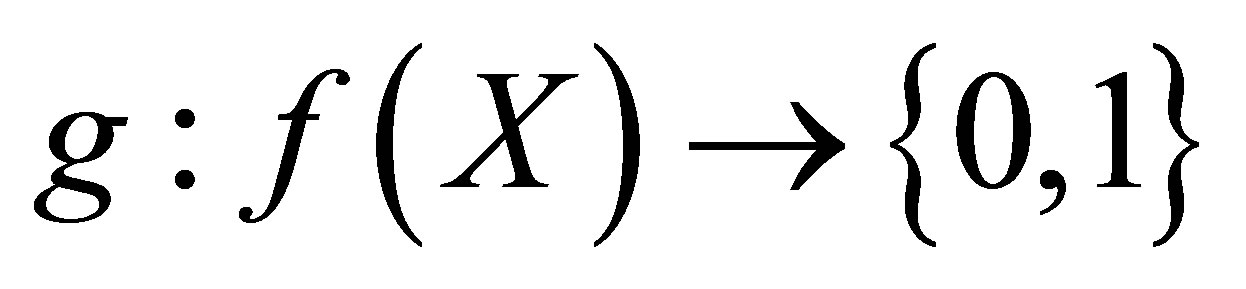 , be a perfect mapping, where
, be a perfect mapping, where 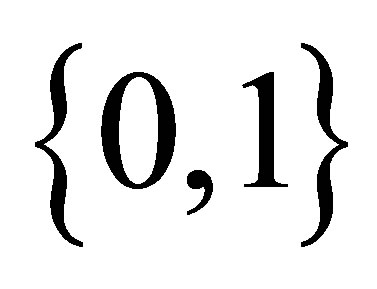 is a
is a  -doubleton isotonic space. Therefore,
-doubleton isotonic space. Therefore,  is perfect. Since
is perfect. Since 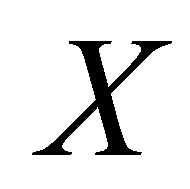 is connected,
is connected, 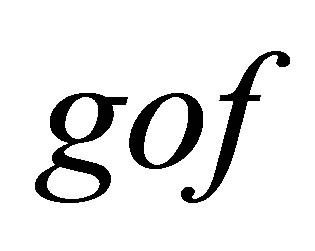 is a constant and hence
is a constant and hence 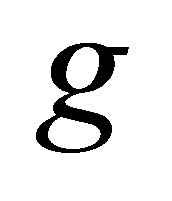 is also a constant function. This implies that
is also a constant function. This implies that 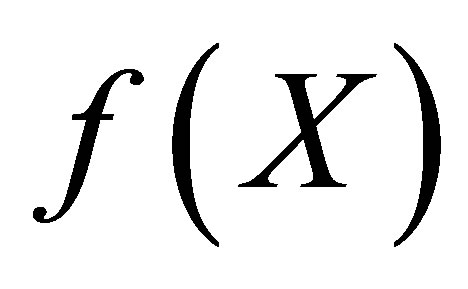 is connected.
is connected.
Let  be a Z-connected isotonic space and
be a Z-connected isotonic space and  be an isotonic space. Let
be an isotonic space. Let 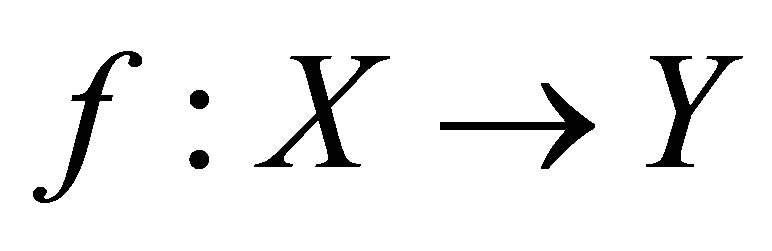 be a perfect mapping (f is a continuous surjection). If
be a perfect mapping (f is a continuous surjection). If 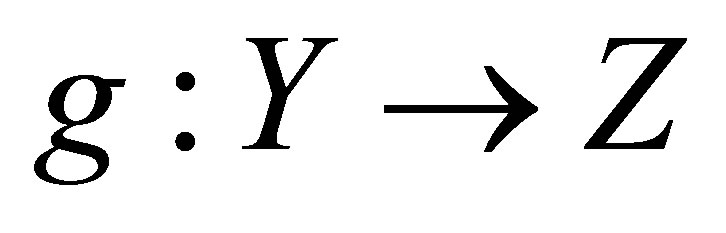 is a perfect mapping, where
is a perfect mapping, where 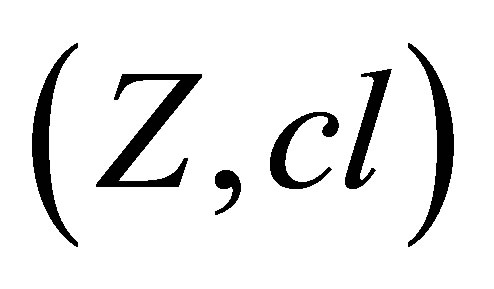 is an isotonic space with more than one element, then by Z-connectedness of
is an isotonic space with more than one element, then by Z-connectedness of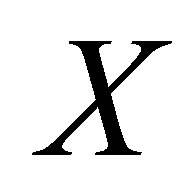 , the composition
, the composition 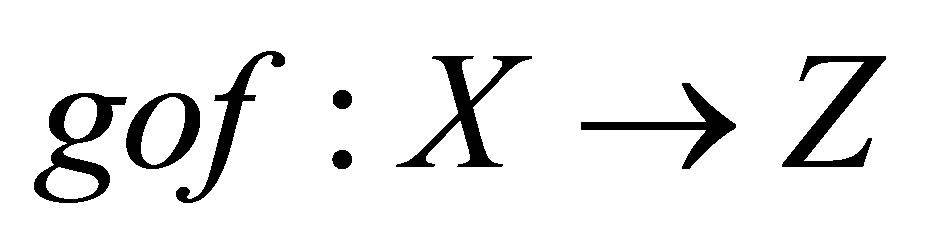 is a constant. It then follows that
is a constant. It then follows that 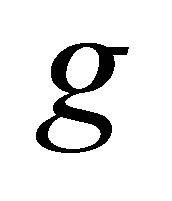 is also a constant and hence Y is Z-connected.
is also a constant and hence Y is Z-connected.
Let  be a perfect mapping between isotonic spaces. Suppose
be a perfect mapping between isotonic spaces. Suppose 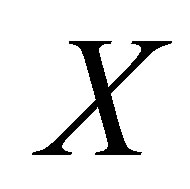 is strongly connected and
is strongly connected and 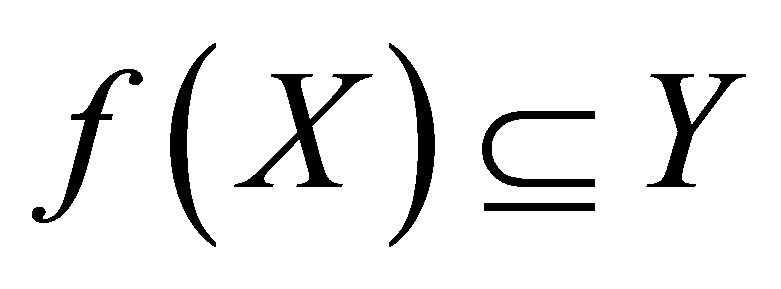 is not strongly connected. Then, there exists a countable collection
is not strongly connected. Then, there exists a countable collection  of pair-wise semi-separated sets such that
of pair-wise semi-separated sets such that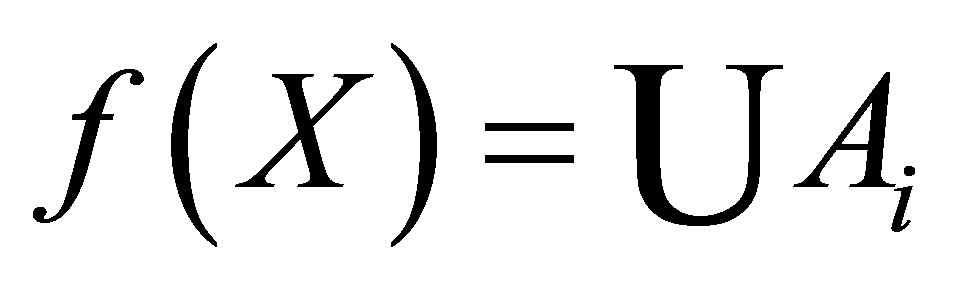 . The countable collection
. The countable collection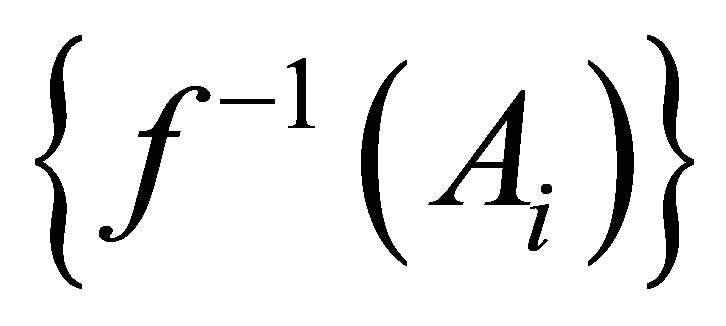 , is such that
, is such that
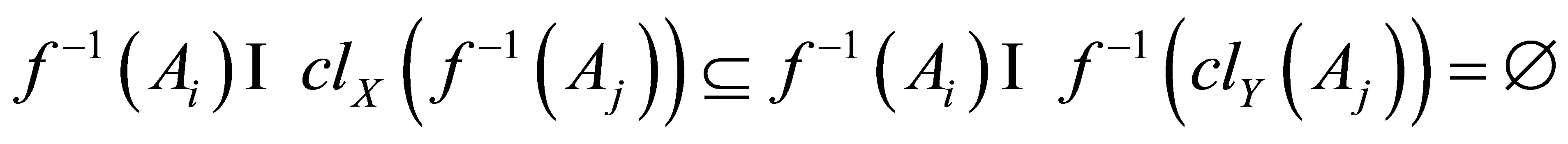
for all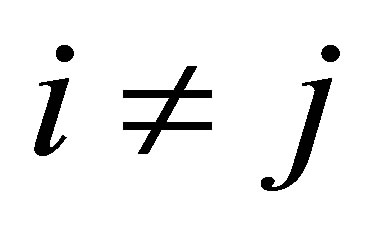 . Moreover,
. Moreover, . That is,
. That is, 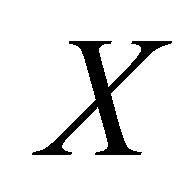 is not strongly connected which is a contradiction. The contrary,
is not strongly connected which is a contradiction. The contrary, 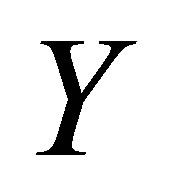 is strongly connected, is true.
is strongly connected, is true.
Theorem: Total disconnectedness and extremal disconnectedness are not invariants of perfect mapping.
Proof: Let 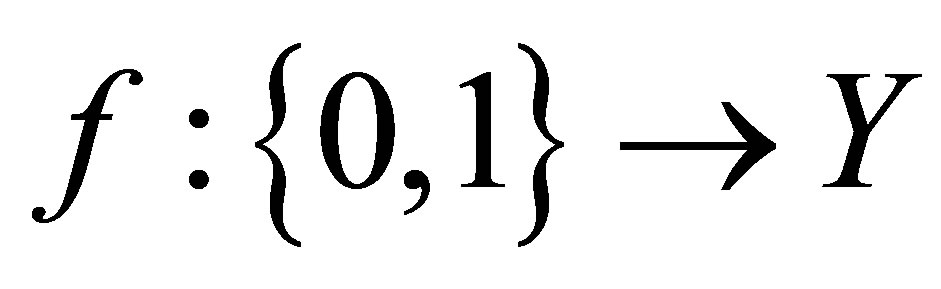 be a perfect mapping from the two-point isotonic space
be a perfect mapping from the two-point isotonic space 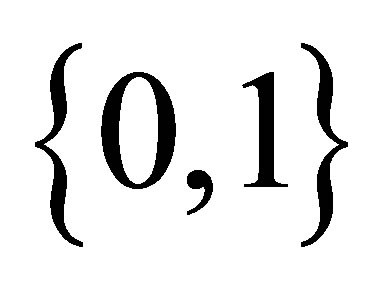 to any isotonic space
to any isotonic space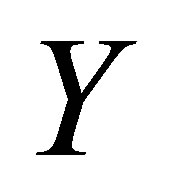 . Clearly,
. Clearly, 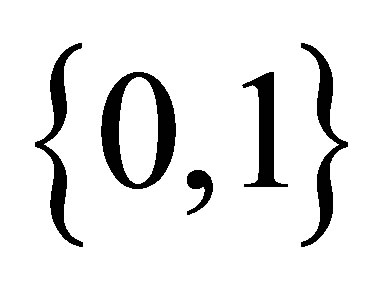 is totally disconnected while
is totally disconnected while  doesn’t have to be. Total disconnectedness is not invariant with respect to perfect mappings.
doesn’t have to be. Total disconnectedness is not invariant with respect to perfect mappings.
Since every extremally disconnected space is totally disconnected, then it follows that extremal disconnectedness is not an invariant of perfect mappings.
3.3. Local Connectedness
In this section, we localize the concept of connectedness. We say that a topological property holds locally at a point 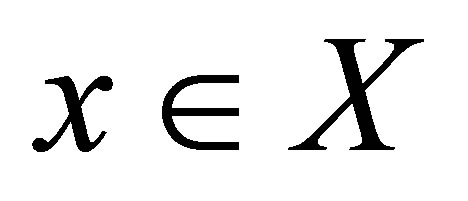 if there exists a neighborhood
if there exists a neighborhood  which has that property, whether the whole space
which has that property, whether the whole space 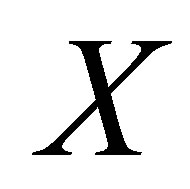 has that property or not.
has that property or not.
Definition
An isotonic space  is said to be locally connected at a point
is said to be locally connected at a point 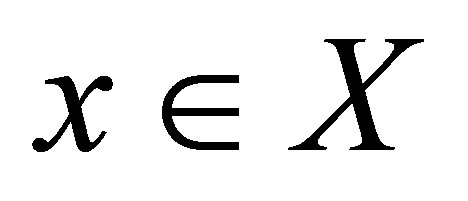 if for every neighborhood
if for every neighborhood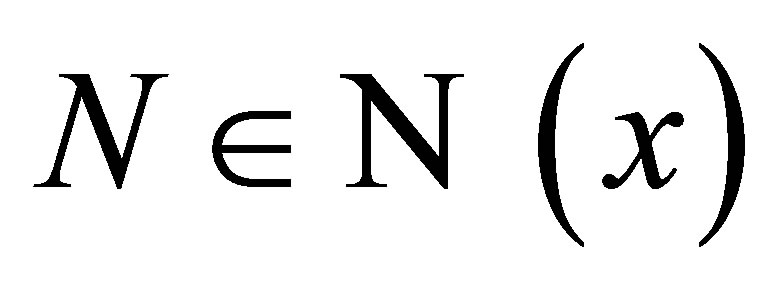 , there exists a connected neighborhood
, there exists a connected neighborhood 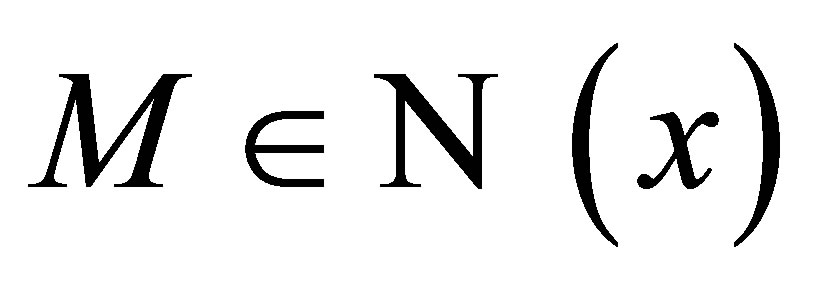 such that
such that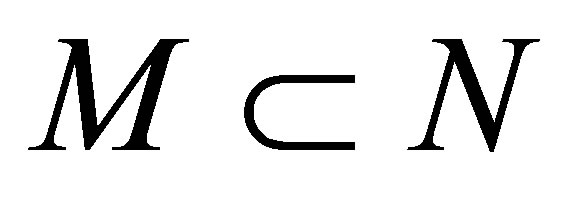 .
.  is said to be locally connected if it is locally connected at each of its points. This definition follows directly from general topological spaces.
is said to be locally connected if it is locally connected at each of its points. This definition follows directly from general topological spaces.
Theorem: Let 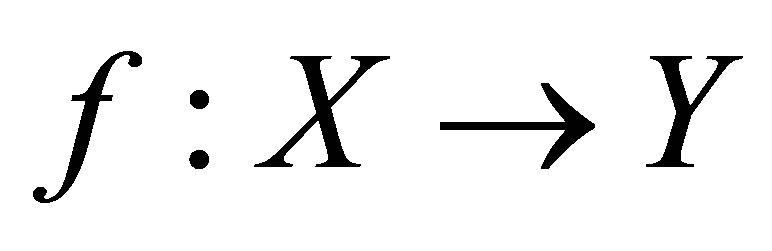 be a perfect map of a locally connected isotonic space onto an isotonic space
be a perfect map of a locally connected isotonic space onto an isotonic space . Then
. Then  is locally connected as well.
is locally connected as well.
Proof: If 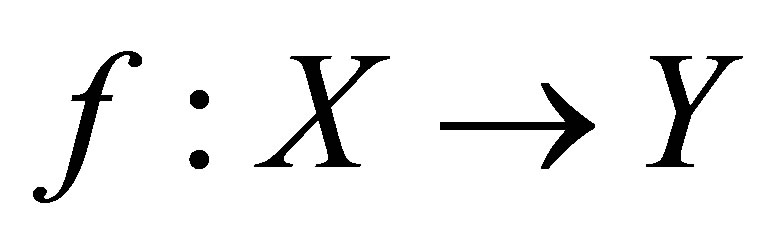 is perfect, then for every
is perfect, then for every 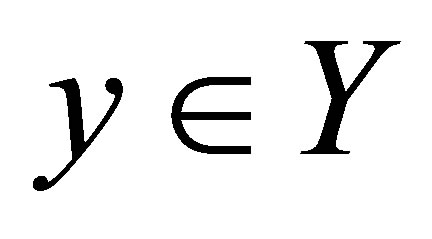 we have
we have  and since
and since 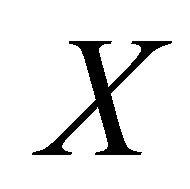 is locally connected, then for every
is locally connected, then for every , there exists a connected neighborhood
, there exists a connected neighborhood  such that
such that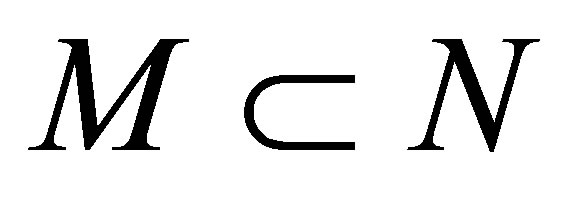 . Further
. Further 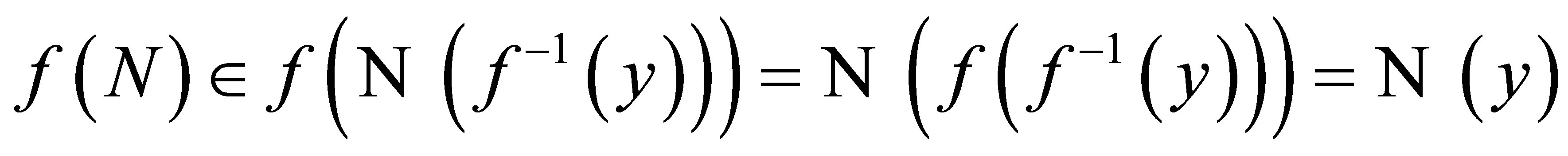 . Similarly
. Similarly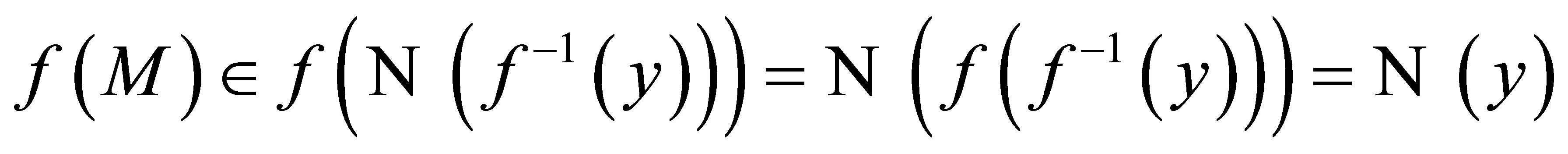 . Thus we have for every
. Thus we have for every 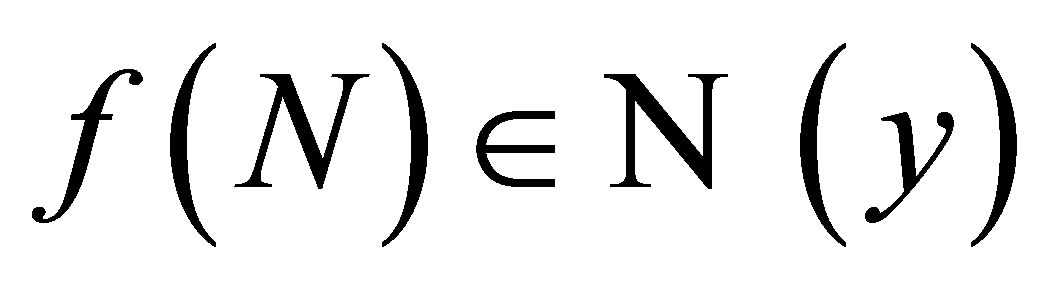 there exists
there exists 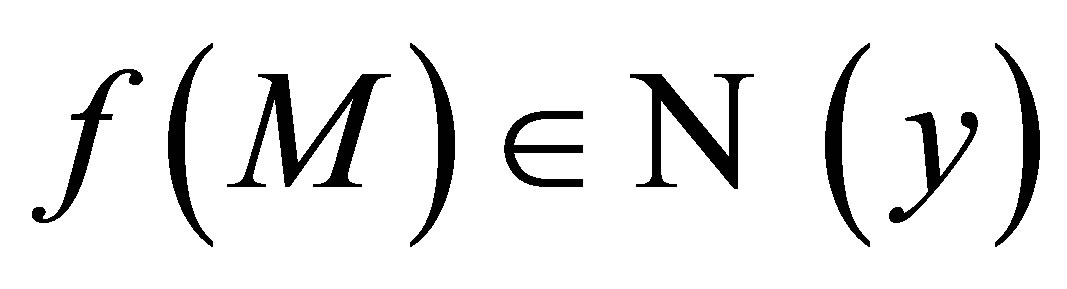 such that
such that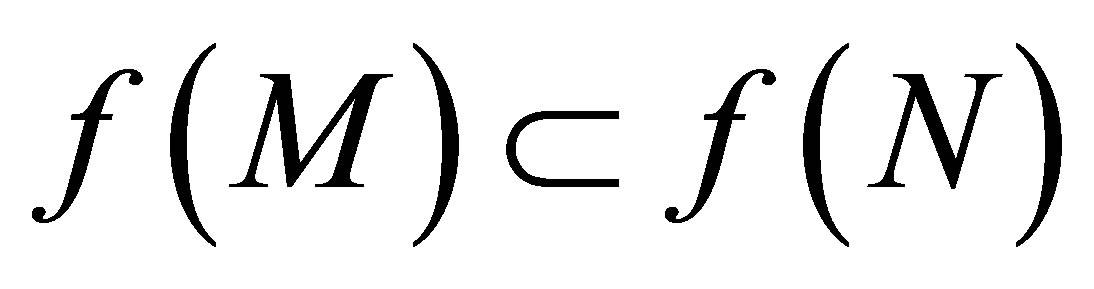 . Therefore
. Therefore  is locally connected.
is locally connected.
This result shows that local connectedness is an invariant of perfect mappings, despite the fact that the property is not an invariant of continuous functions.
4. Conclusion
The results obtained in this paper show that the invariance of connectedness properties in isotonic spaces under continuous functions extends to perfect mappings.
REFERENCES
- J. L. Kelley, “General Topology,” Springer, New York, 1955.
- A. S. Mashhour and M. H. Ghanim, “On Closure Spaces,” Indian Journal of Pure and Applied Mathematics, Vol. 106, No. 3, 1985, pp. 680-691.
- W. J. Thron, “What Results are Valid on Cech-closure Spaces”, Topology Proceedings. Vol 6, 1981, pp. 135-158.
- A. K. Elzenati and E. D. Habil, “Connectedness in Isotonic Spaces,” Turkish Journal of Mathematics, Vol. 30, No. 6 , 2006, pp. 247-262.
- K. Kuratowski, “Introduction to Set Theory and Topology,” Pergamon Press Ltd., London, 1961.
- B. Dai, “Strongly Connected Spaces,” National University of Singapore Journal, Vol. 12, No. 6, 2000, pp. 14-20.
- E. Michael, “Bi-Quotient Maps and Cartesian Product of Quotient Maps,” Anneles De l’institut Fourier, Vol. 18, No. 2, 1968, pp. 287-302.
- R. Engelking, “General Topology,” Haldermann Verlag, Berlin, 1989.

