Advances in Pure Mathematics
Vol.3 No.9A(2013), Article ID:40263,8 pages DOI:10.4236/apm.2013.39A1001
Classification of Single Traveling Wave Solutions to the Generalized Kadomtsev-Petviashvili Equation without Dissipation Terms in p = 2
Department of Mathematics, Northeast Petroleum University, Daqing, China
Email: xinghuadu@126.com
Copyright © 2013 Xinghua Du, Hua Xin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Xinghua Du, Hua Xin. All Copyright © 2013 are guarded by law and by SCIRP as a guardian
Received August 13, 2013; revised September 13, 2013; accepted September 21, 2013
Keywords: complete discrimination system for polynomial; traveling wave solution; generalized Kadomtsev-Petviashvili equation without dissipation terms
ABSTRACT
By using the complete discrimination system for the polynomial method, the classification of single traveling wave solutions to the generalized Kadomtsev-Petviashvili equation without dissipation terms in 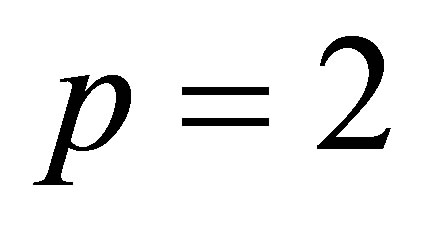 is obtained.
is obtained.
1. Introduction
In mathematics and physics, the Kadomtsev-Petviashvili (KP) equation is a partial differential equation to describe nonlinear wave motion. It can be used to model water waves of long wavelength with weakly nonlinear restoring forces and frequency dispersion [1]. A number of modified forms of the KP equation have been studied [2-6]. In [1,7], the generalized Kadomtsev-Petviashvili equation without dissipation terms was given by
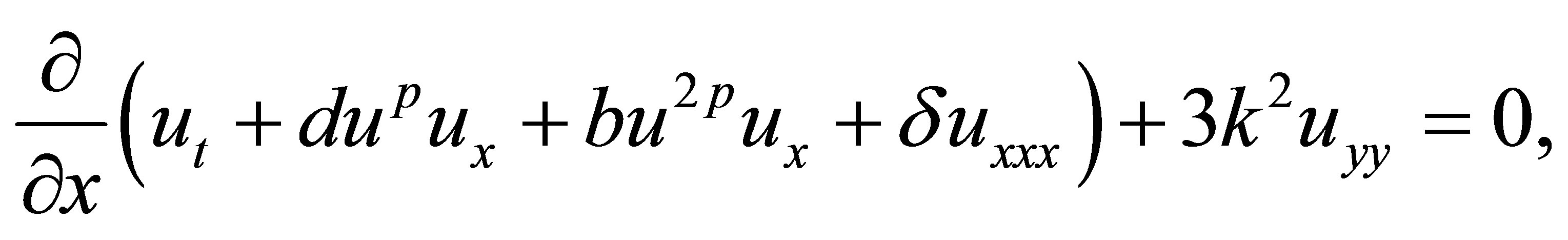 (1)
(1)
where  are constants,
are constants, 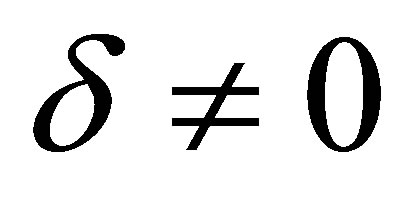 ,
,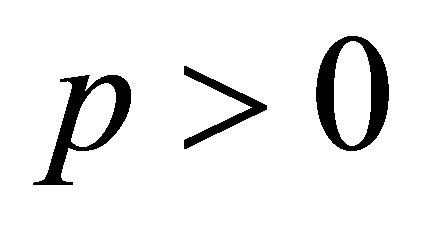 . Some of modified form of the KP equation can be written in the form of Equation (1).
. Some of modified form of the KP equation can be written in the form of Equation (1).
Many reliable methods are used in the literature to examine the completely integrable nonlinear evolution equations. The Hirota bilinear method, the Bäcklund transformation method, the inverse scattering method, the Painlevé analysis, the simplified Hirotas method established by Hereman et al. [8], and others were effectively used in [1-13]. Liu proposed a complete discrimination system for polynomial method [10-13]. That is, by using of elementary integral method and complete discrimination system for polynomial, the single wave solutions can be classified for some nonlinear differential equations which can be directly reduced to integral forms.
In this paper, we consider the following generalized Kadomtsev-Petviashvili equation without dissipation terms in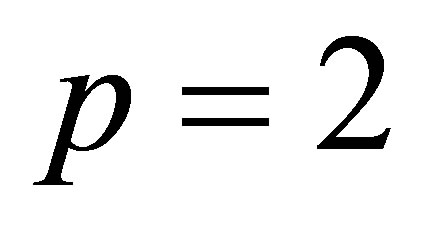 :
:
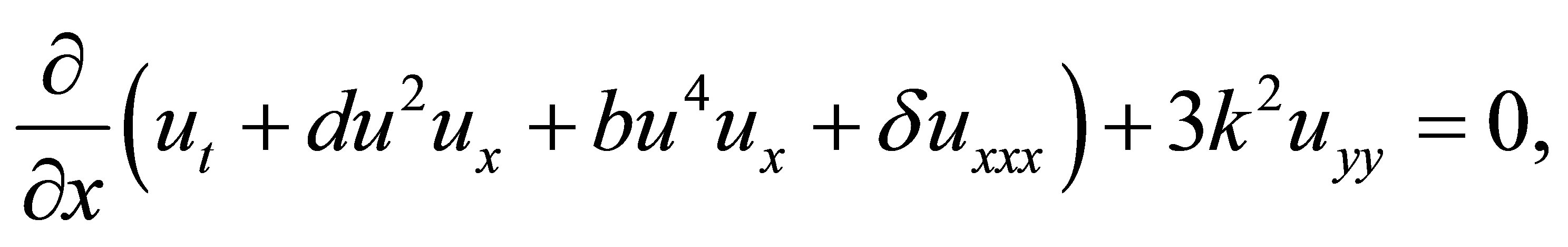 (2)
(2)
where 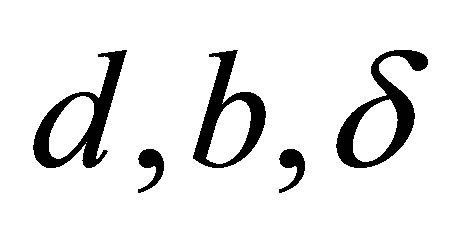 are constants,
are constants,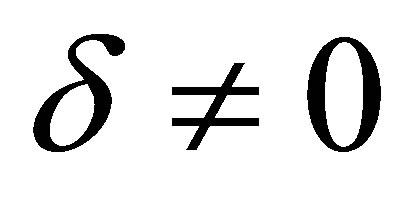 . By using Liu’s complete discrimination system for polynomial method, the classification of single traveling wave solutions to Equation (2) is obtained.
. By using Liu’s complete discrimination system for polynomial method, the classification of single traveling wave solutions to Equation (2) is obtained.
2. Classification of Solutions to Equation (2)
Take wave transformation
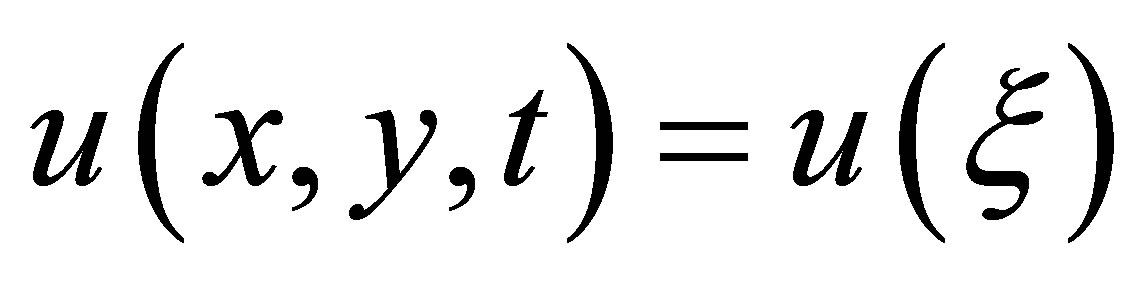 and
and 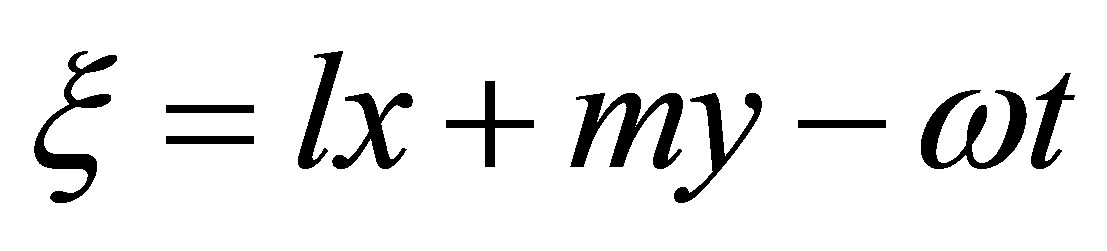
into Equation (1), the following nonlinear ordinary difference equation is given:
 (3)
(3)
Integrating Equation (3) once with respect to , and setting the integral constant to zero yields:
, and setting the integral constant to zero yields:
 (4)
(4)
Integrating Equation (4) twice yields
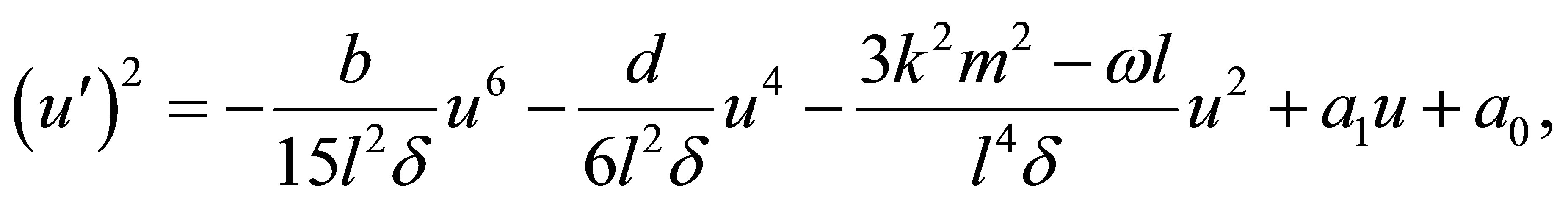 (5)
(5)
where 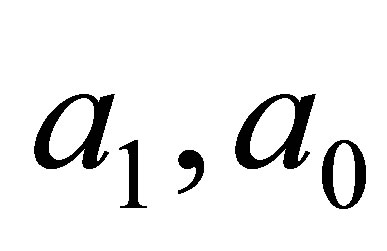 are arbitrary constants.
are arbitrary constants.
Case 2.1.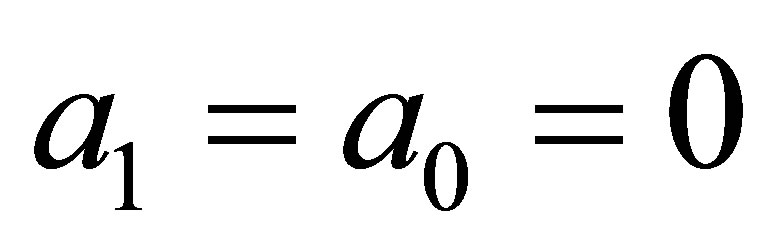 , we substitute the transformation
, we substitute the transformation
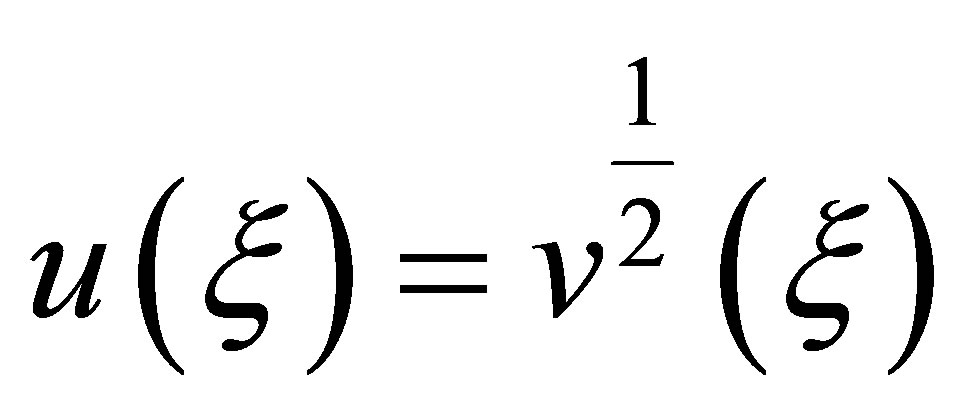
into Equation (5) yields
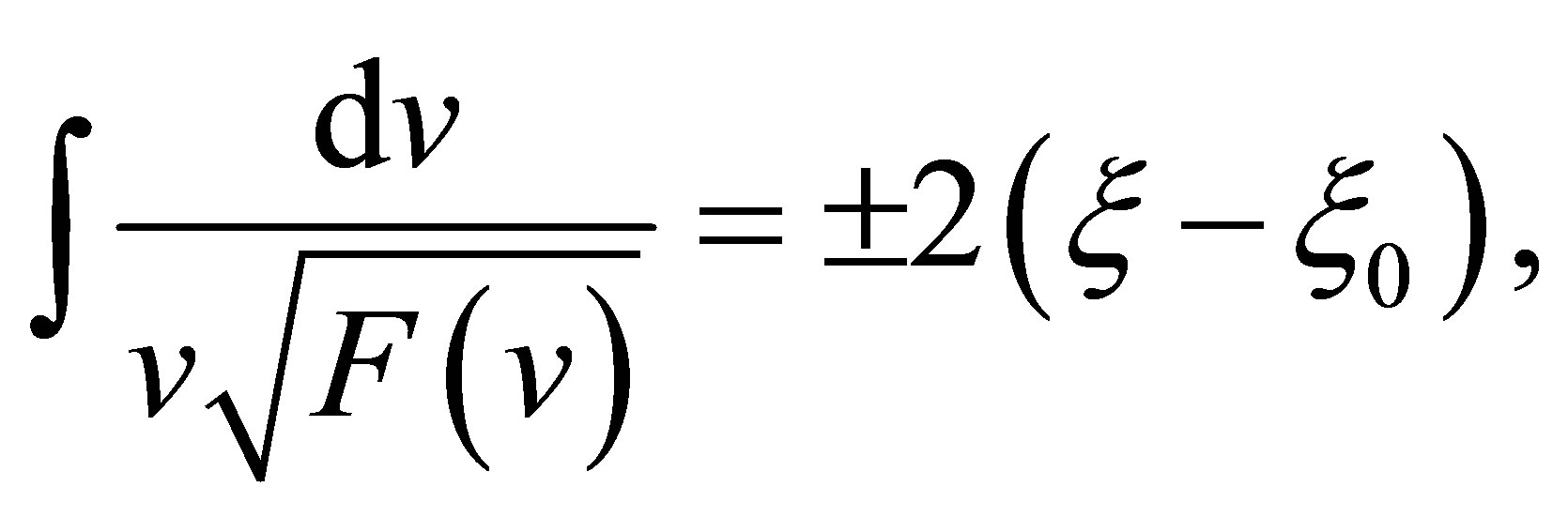 (6)
(6)
where
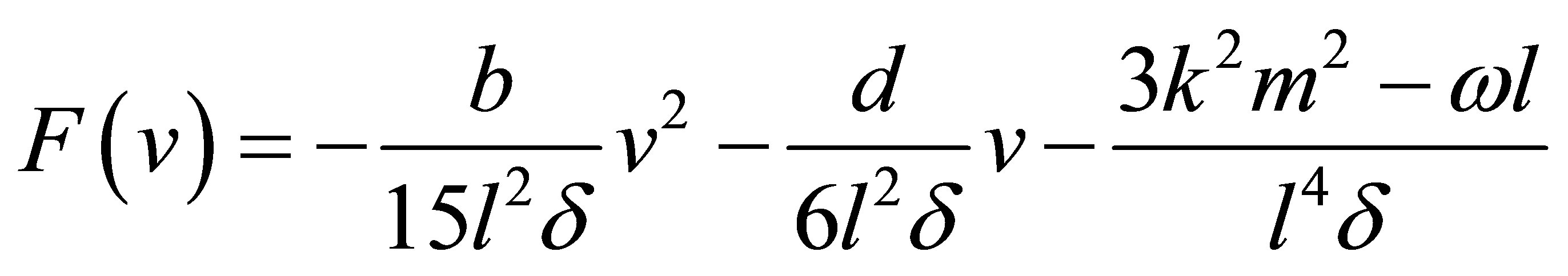 (7)
(7)
Let
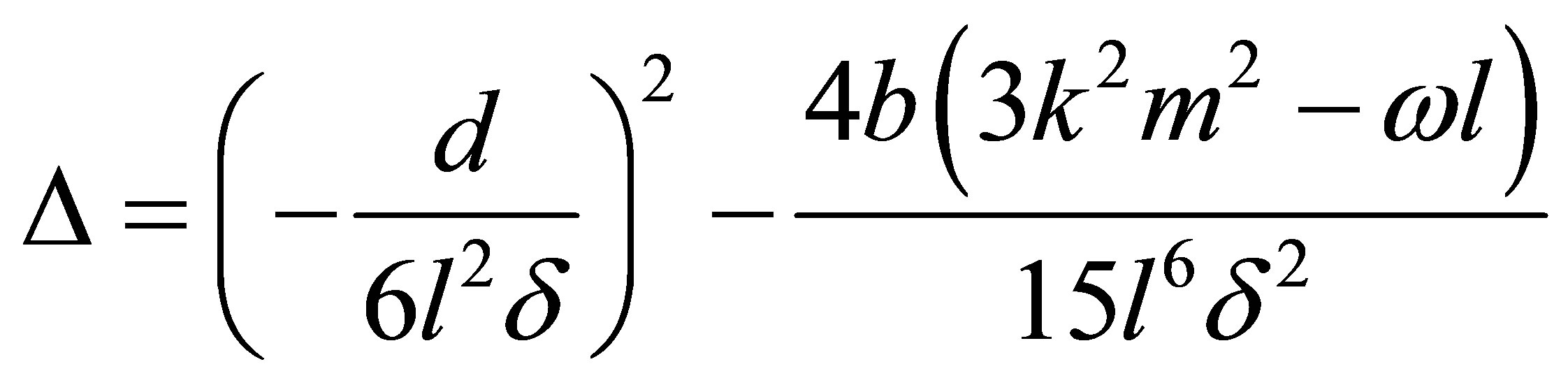 and
and ![]() is the discriminant of the polynomial
is the discriminant of the polynomial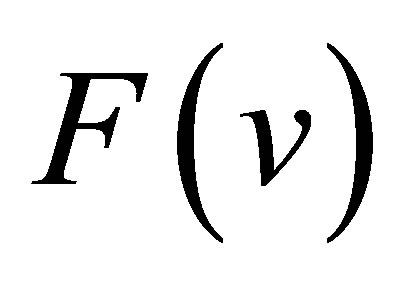 . According to the classification of the roots of
. According to the classification of the roots of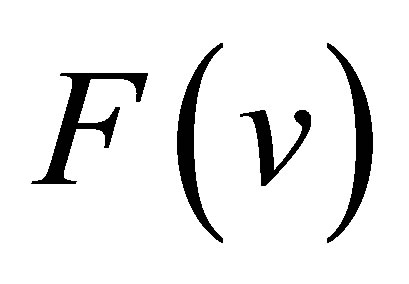 , there are three cases to be discussed.
, there are three cases to be discussed.
Case 2.1.1.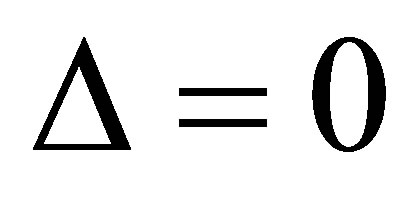 , when
, when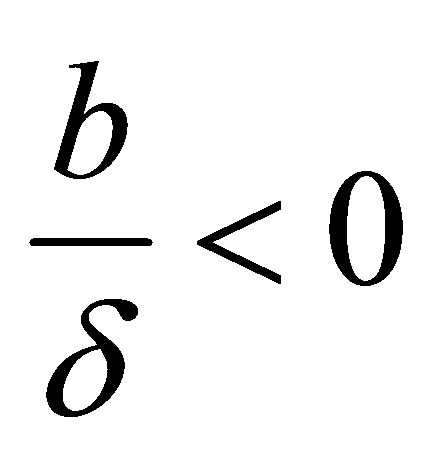 from Equation (6), we have
from Equation (6), we have
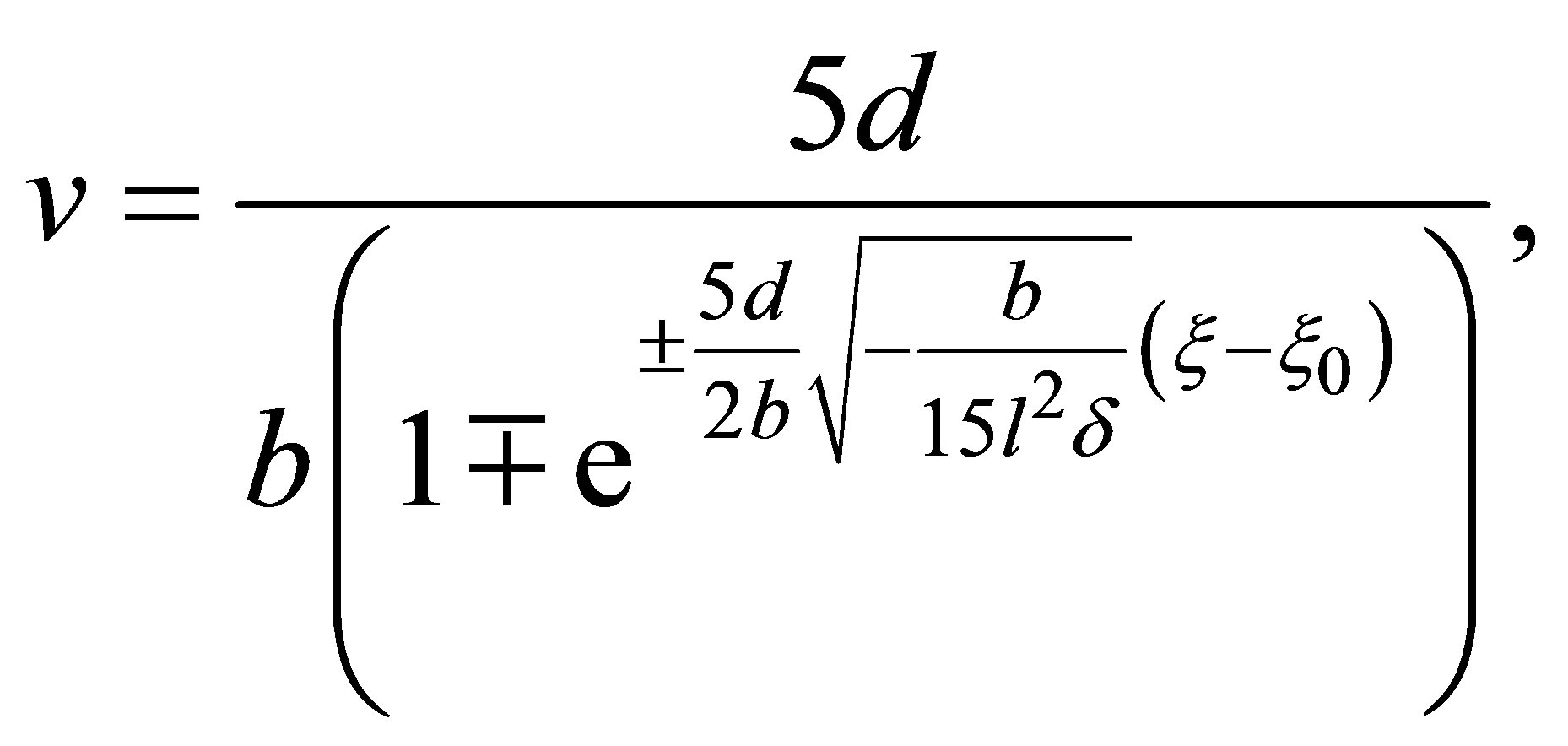 (8)
(8)
Case 2.1.2.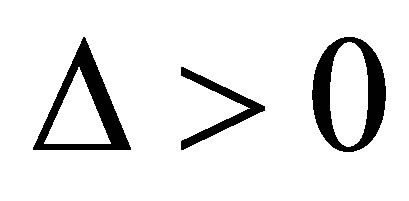 , when
, when
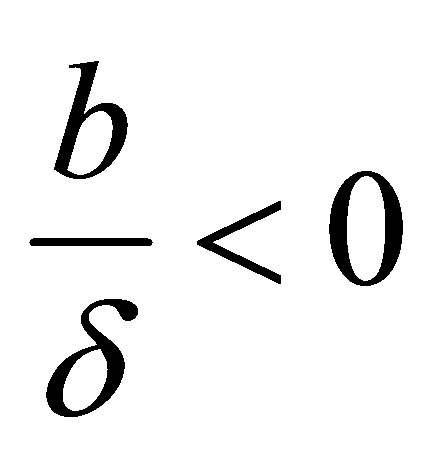 from Equation (6), we have
from Equation (6), we have
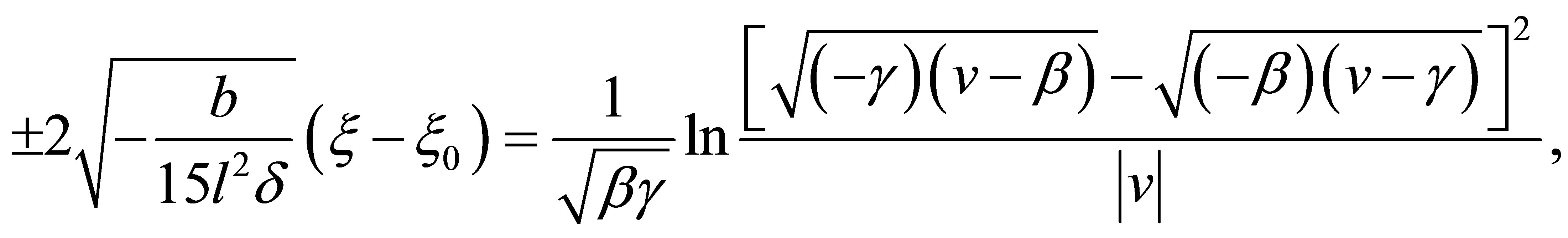 (9)
(9)
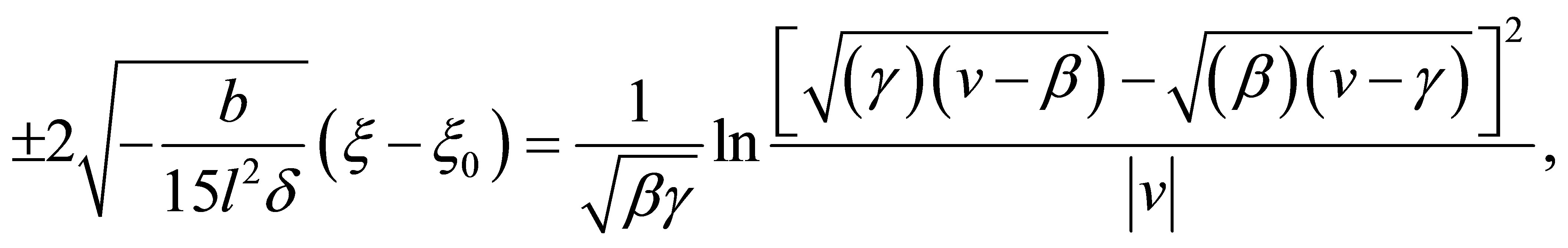 (10)
(10)
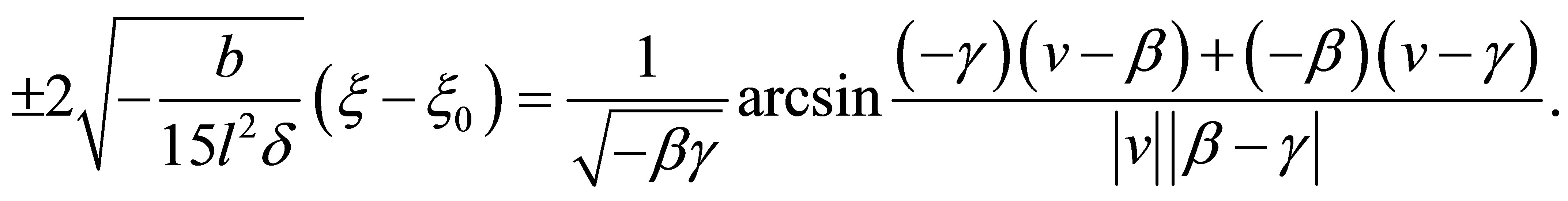 (11)
(11)
When
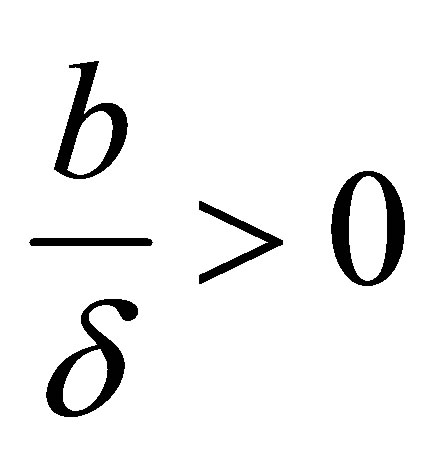 from Equation (6), we have
from Equation (6), we have
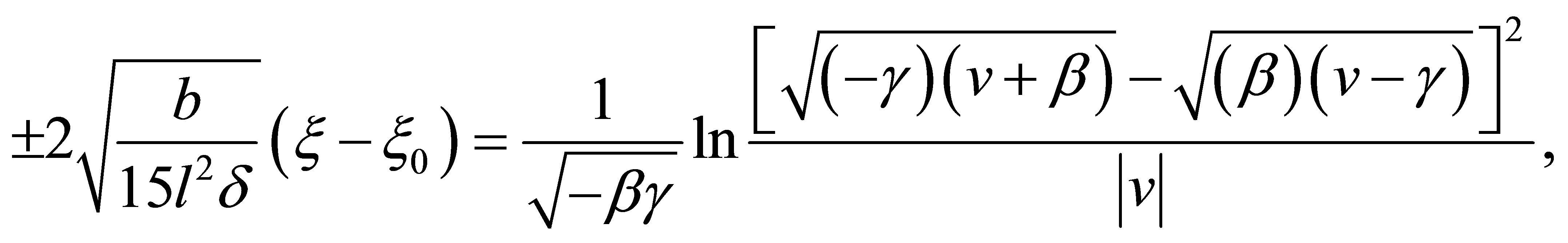 (12)
(12)
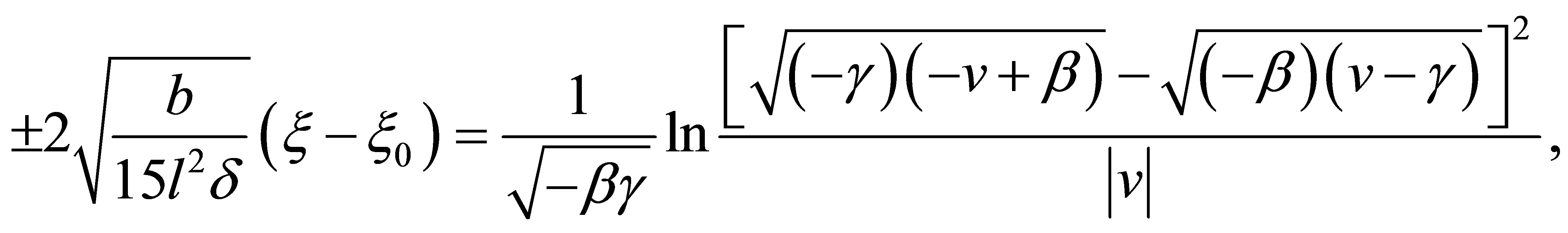 (13)
(13)
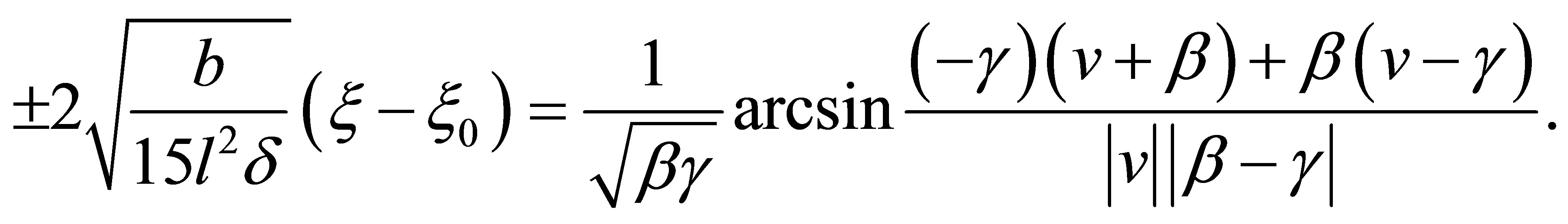 (14)
(14)
where
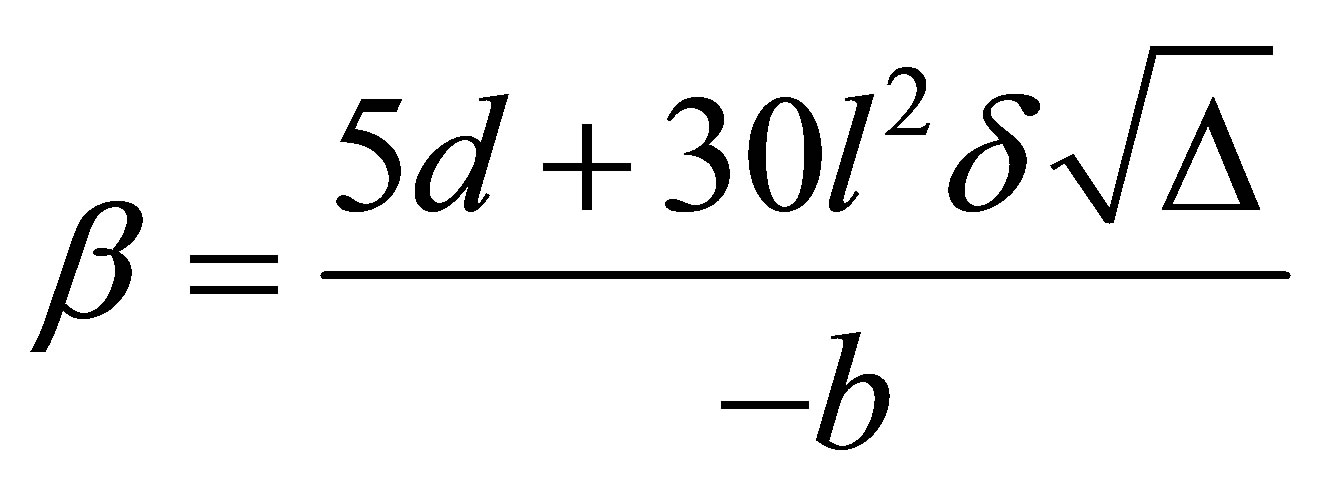 ,
,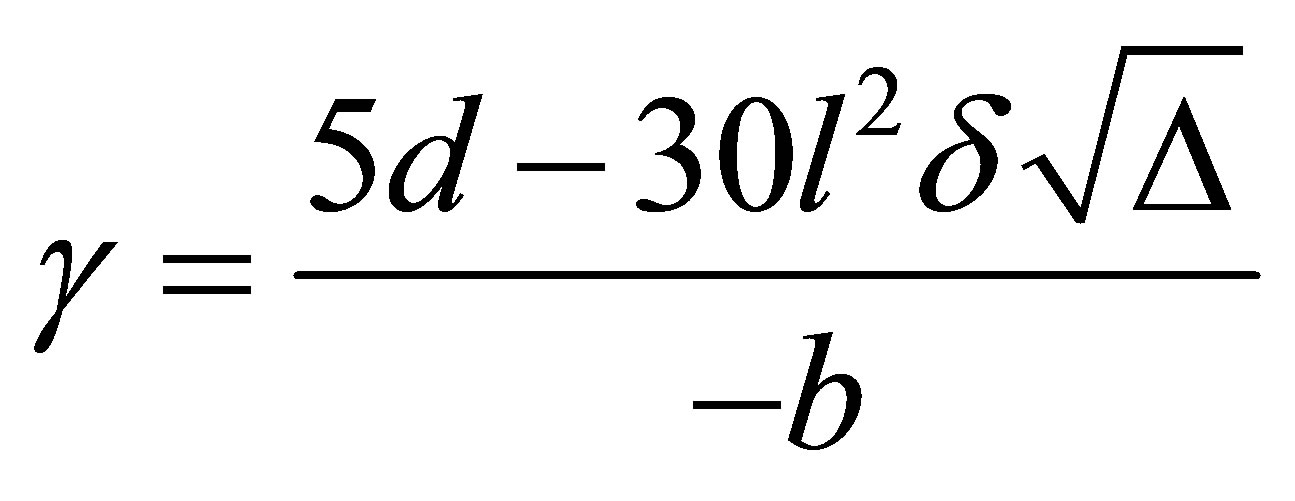 .
.
Case 2.1.3.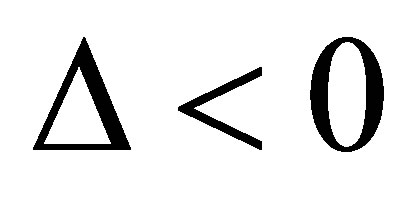 . From Equation (6), we have
. From Equation (6), we have
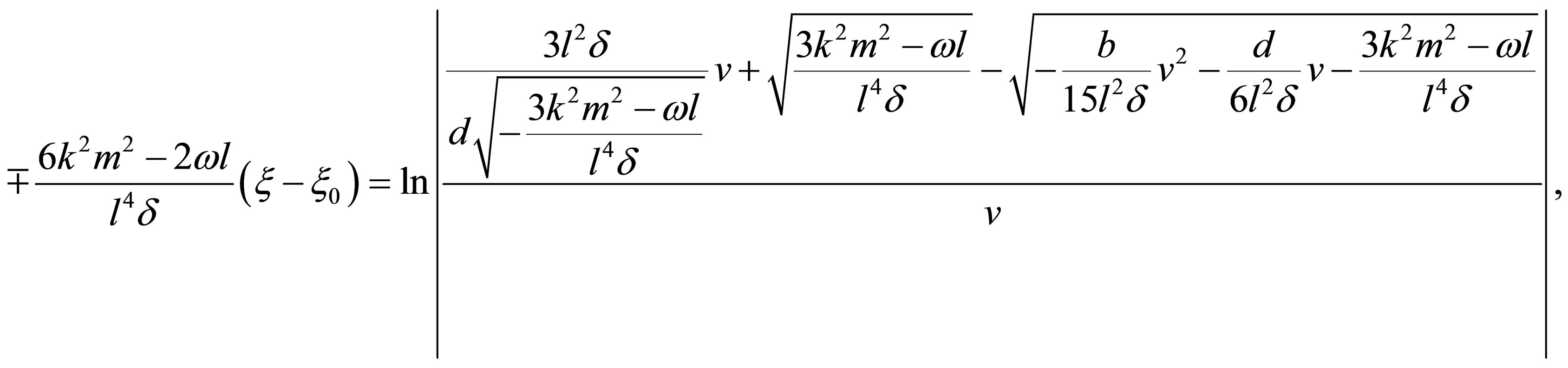 (15)
(15)
where
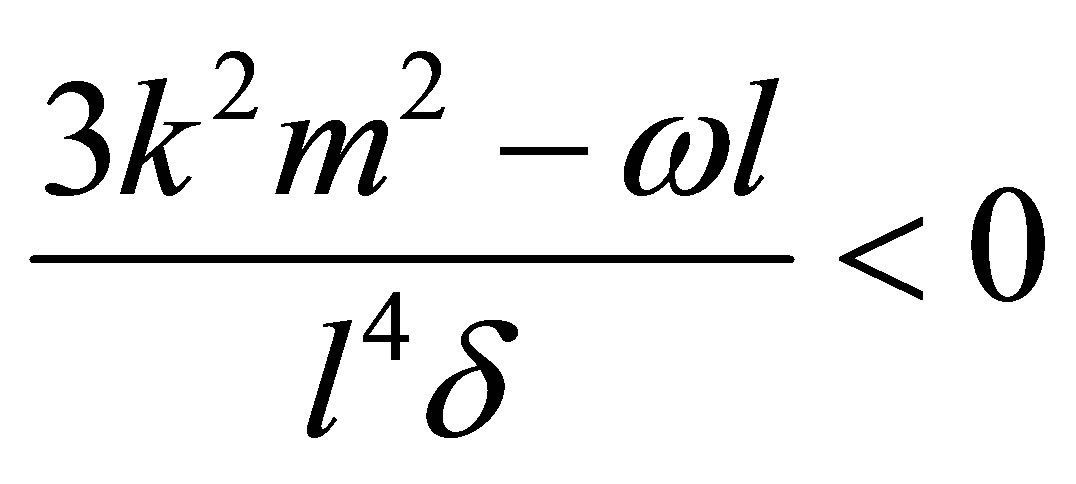 .
.
Case 2.2.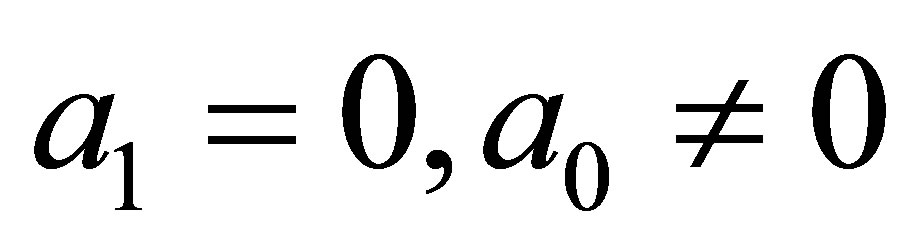 . Substituting the transformation
. Substituting the transformation
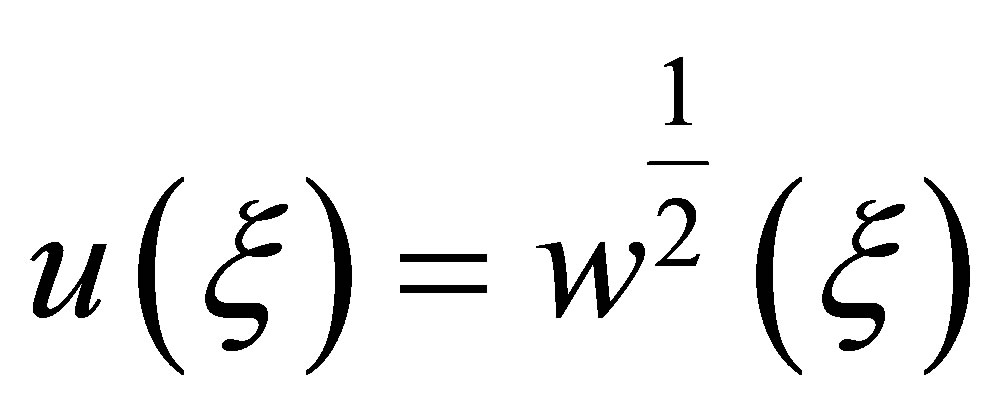
into Equation (5) yields
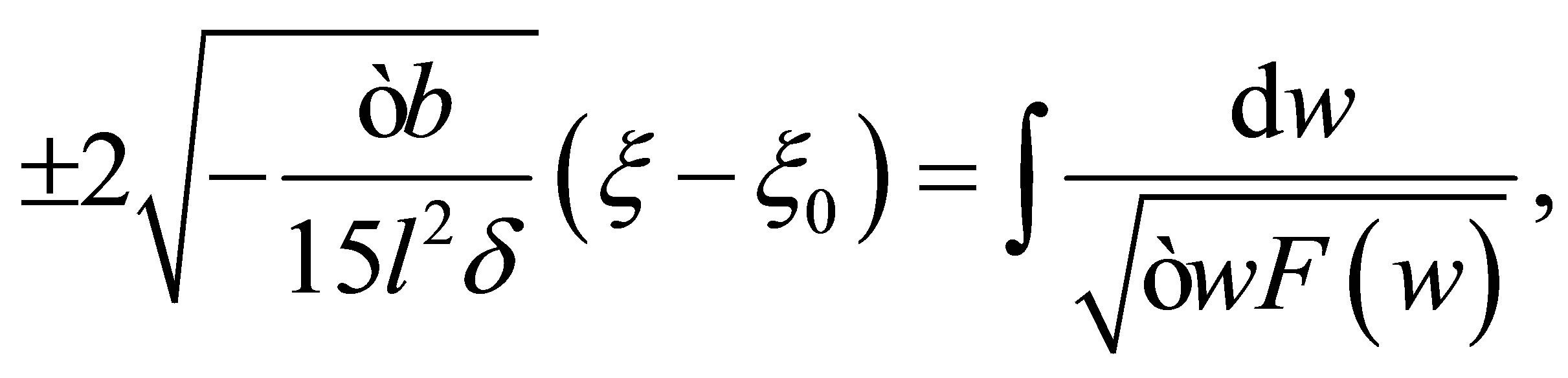 (16)
(16)
where
 (17)
(17)
If
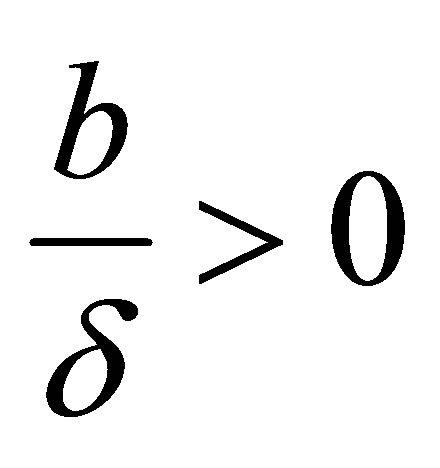 we take
we take
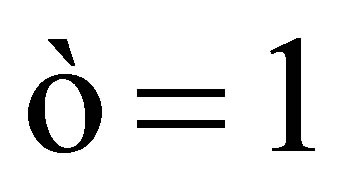 ; if
; if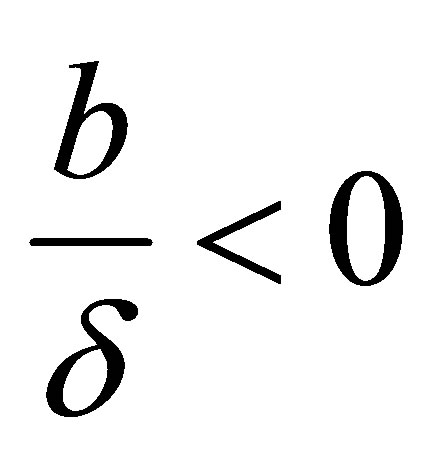 we take
we take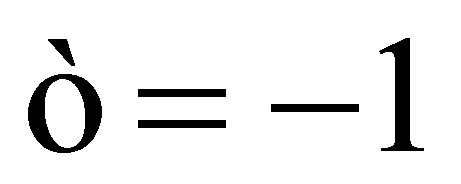 . The complete discrimination system for the third order polynomial
. The complete discrimination system for the third order polynomial 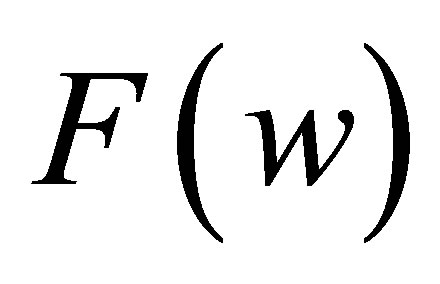 is given as follows:
is given as follows:
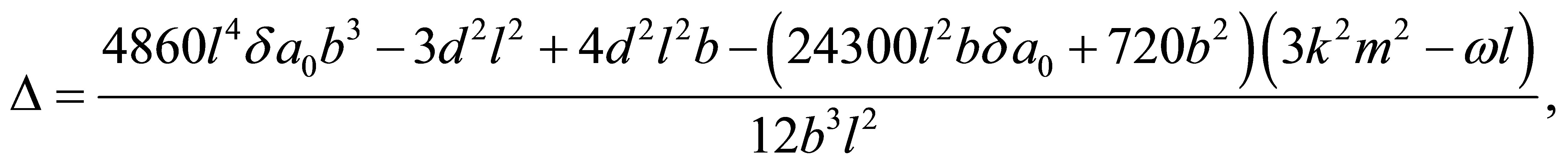
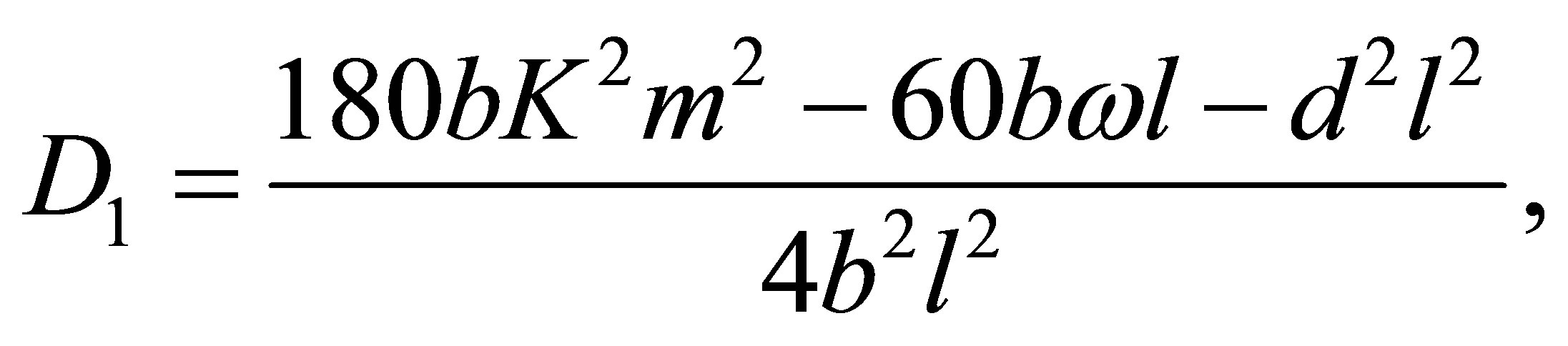 (18)
(18)
According to the classification of the roots of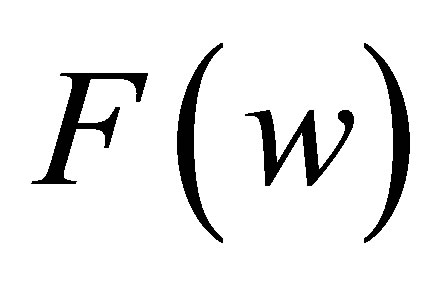 , there are four cases to be discussed.
, there are four cases to be discussed.
Case 2.2.1.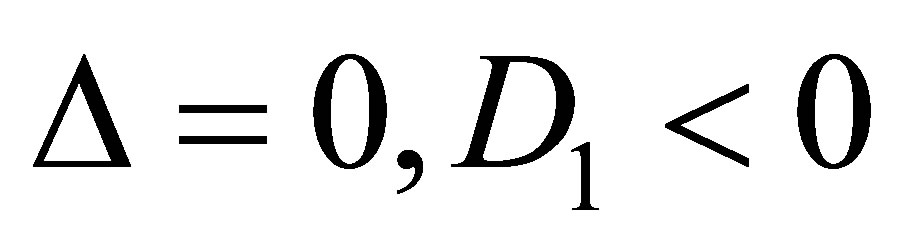 . Then
. Then
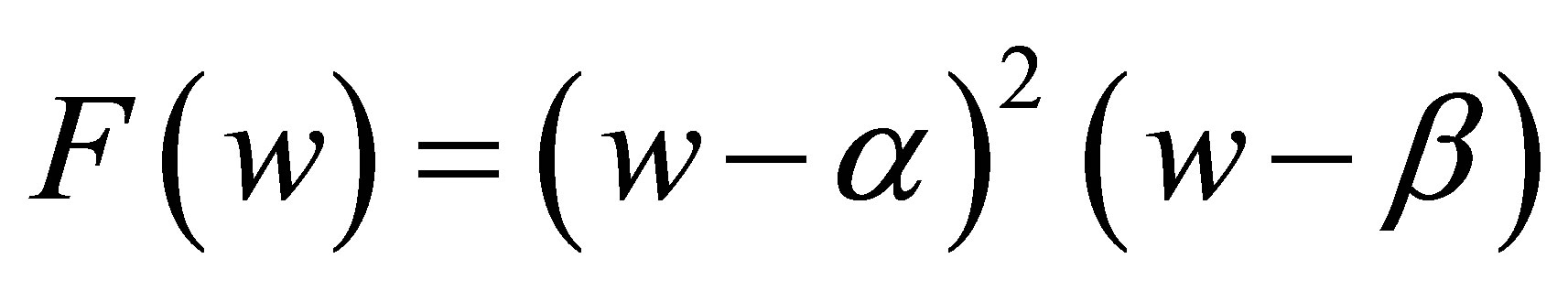 where
where 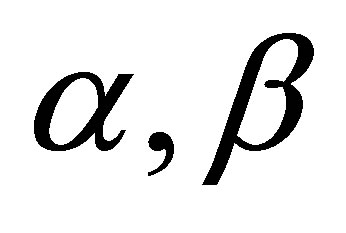 are real constants,
are real constants, 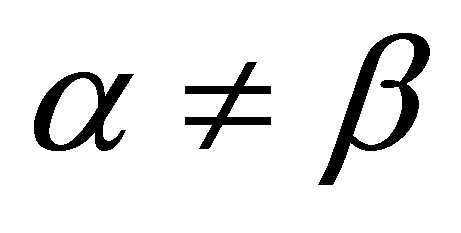 , and
, and 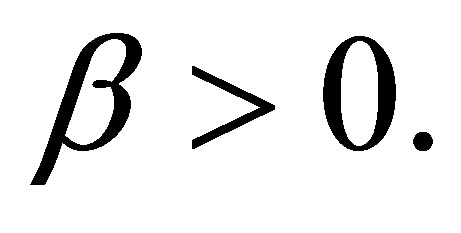 If
If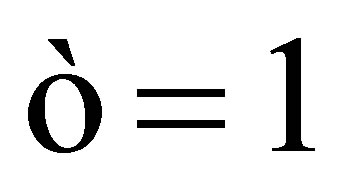 , when
, when 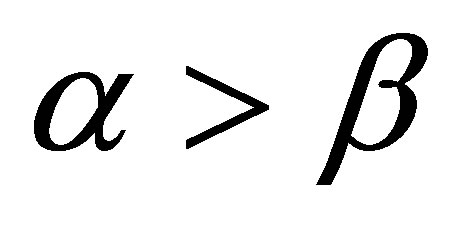 and
and , or when
, or when 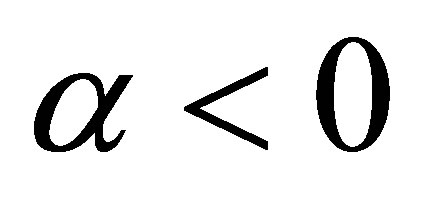 and
and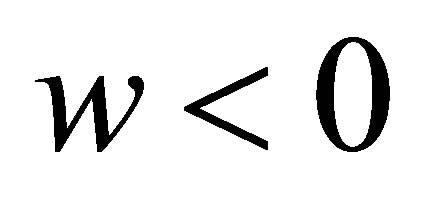 , from Equation (16), we have
, from Equation (16), we have
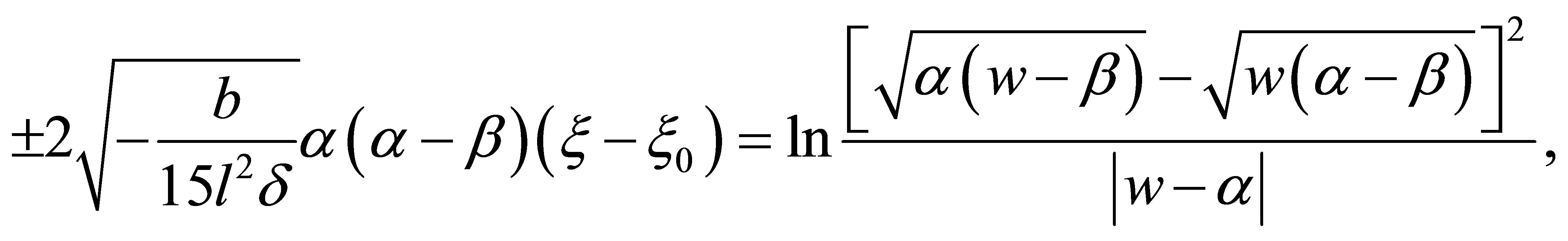 (19)
(19)
when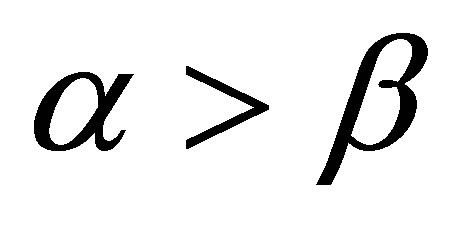 , and
, and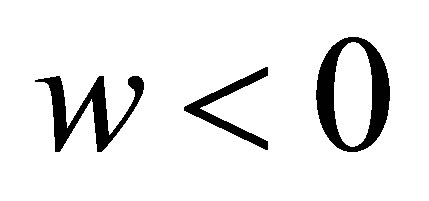 , or
, or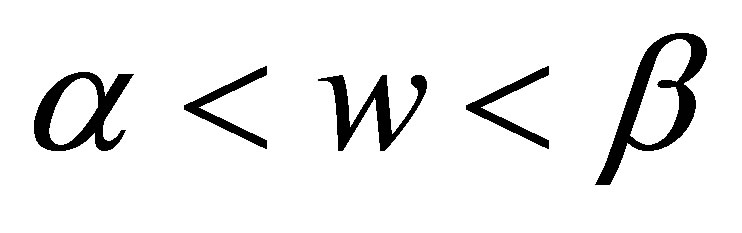 , we have
, we have
 (20)
(20)
when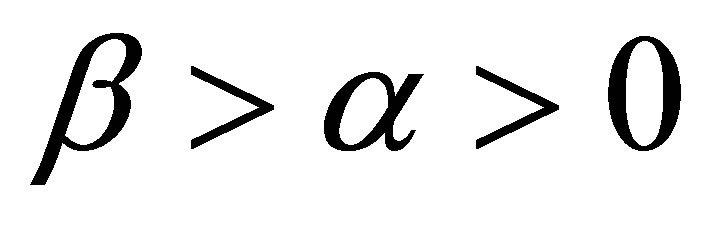 , we have
, we have
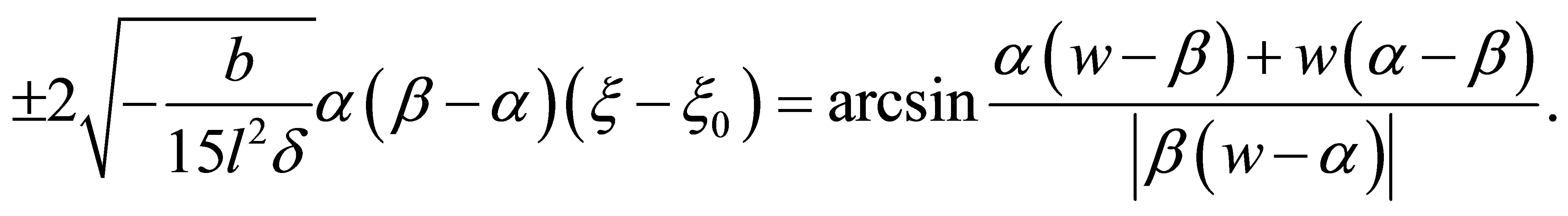 (21)
(21)
If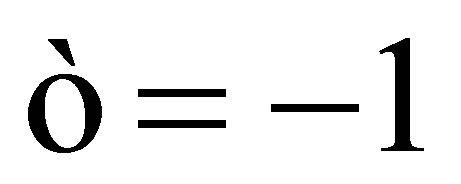 ,when
,when 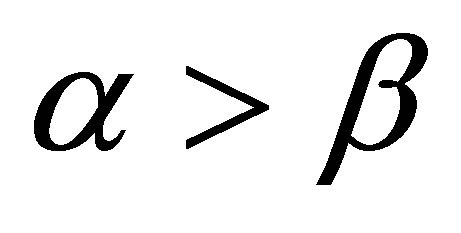 and
and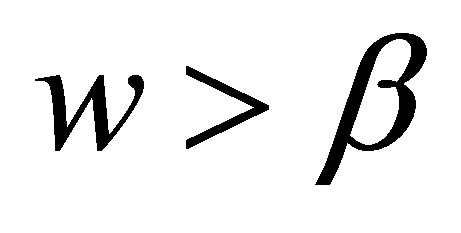 , or when
, or when 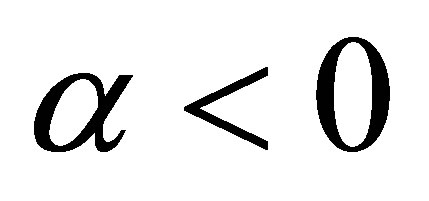 and
and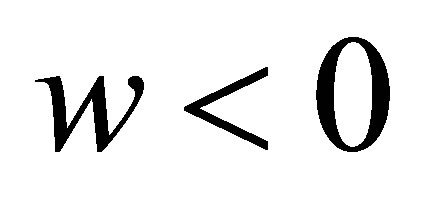 , from Equation (16), we have
, from Equation (16), we have
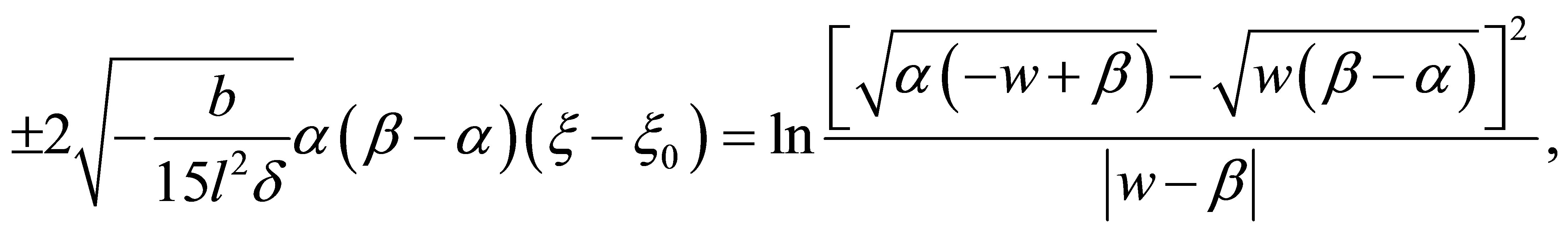 (22)
(22)
when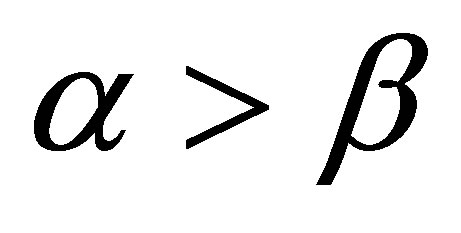 , and
, and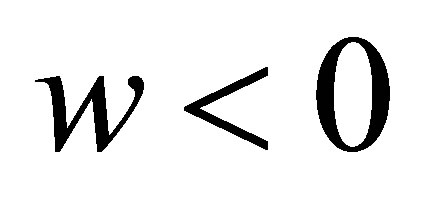 , or
, or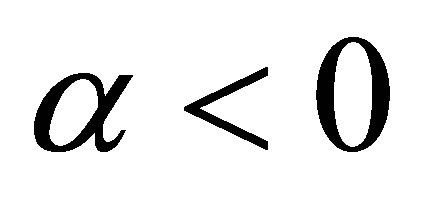 , and
, and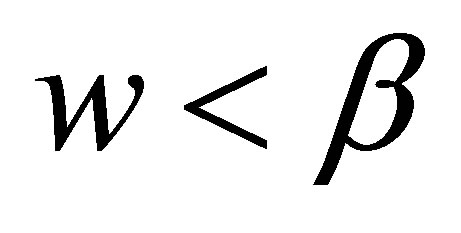 , we have
, we have
 (23)
(23)
when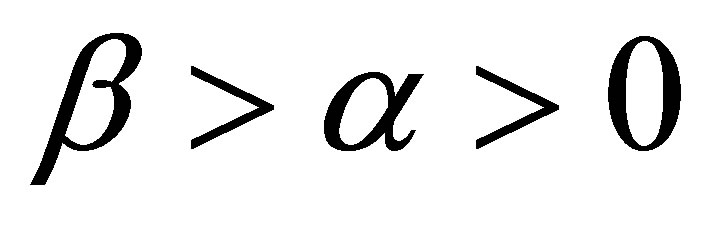 , we have
, we have
 (24)
(24)
Case 2.2.2. 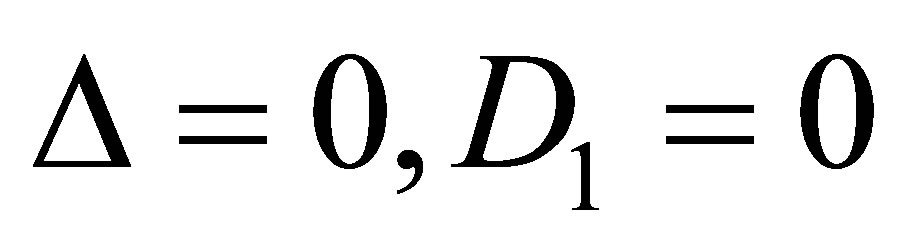 . Then
. Then
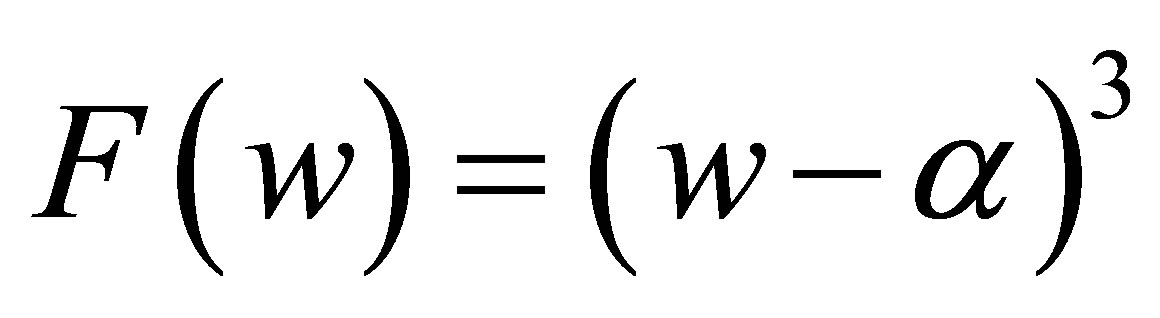 where
where ![]() is a real constant. If
is a real constant. If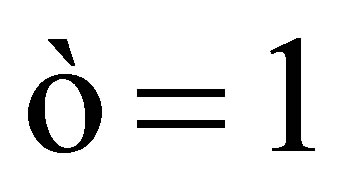 , when
, when![]() , and
, and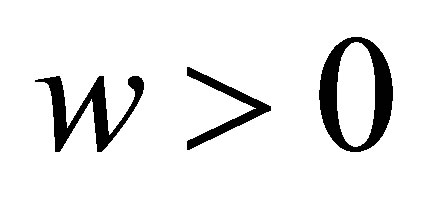 , or
, or![]() , and
, and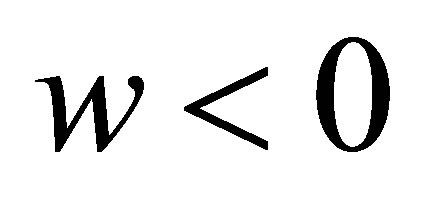 , we have
, we have
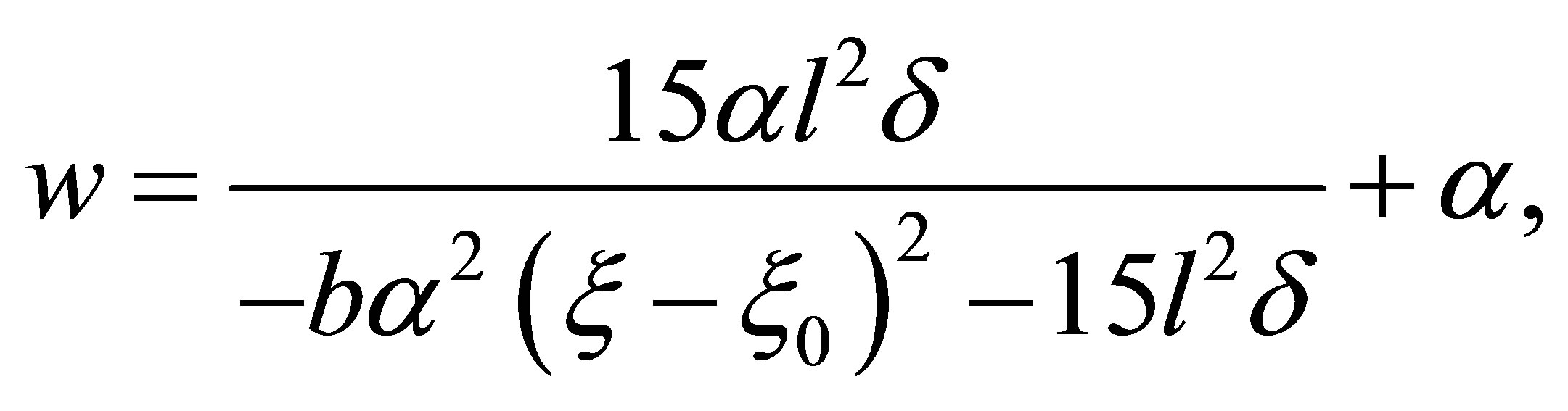 (25)
(25)
If , when
, when![]() , and
, and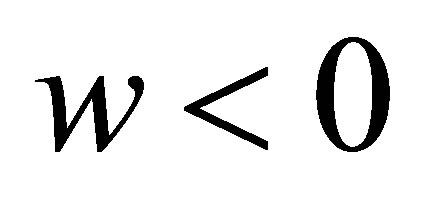 , or
, or![]() , and
, and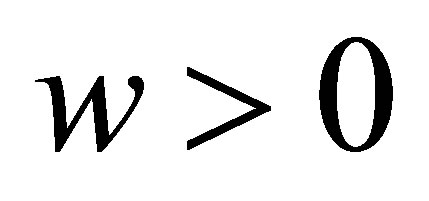 , we have
, we have
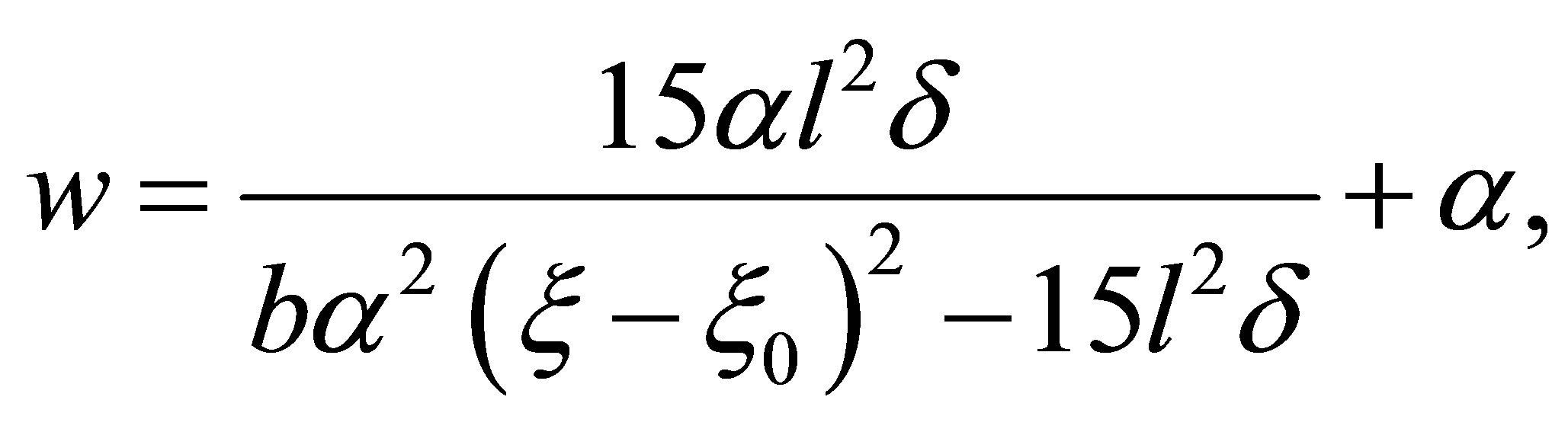 (26)
(26)
Case 2.2.3.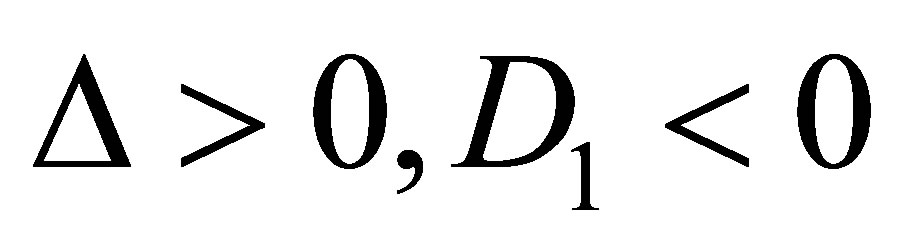 . Then
. Then
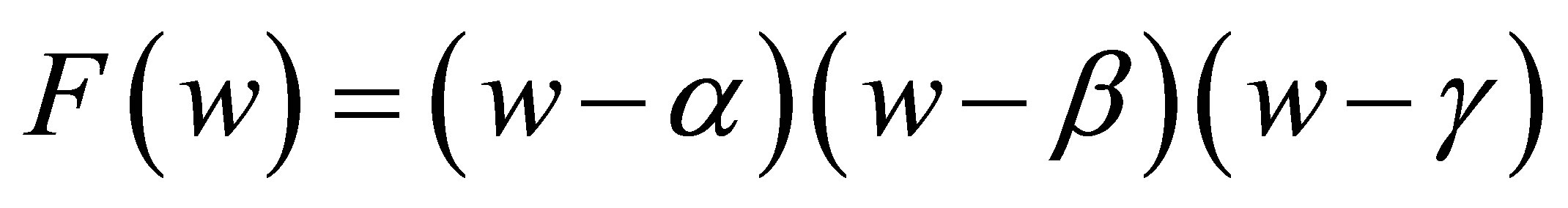 where
where 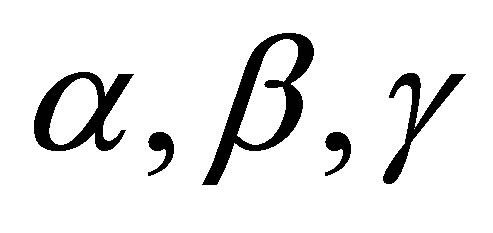 are different real constants. If
are different real constants. If , when
, when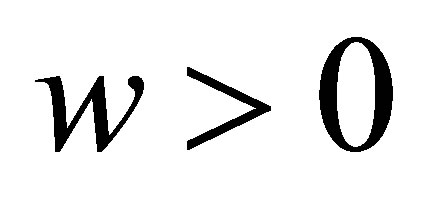 , or
, or , we have
, we have
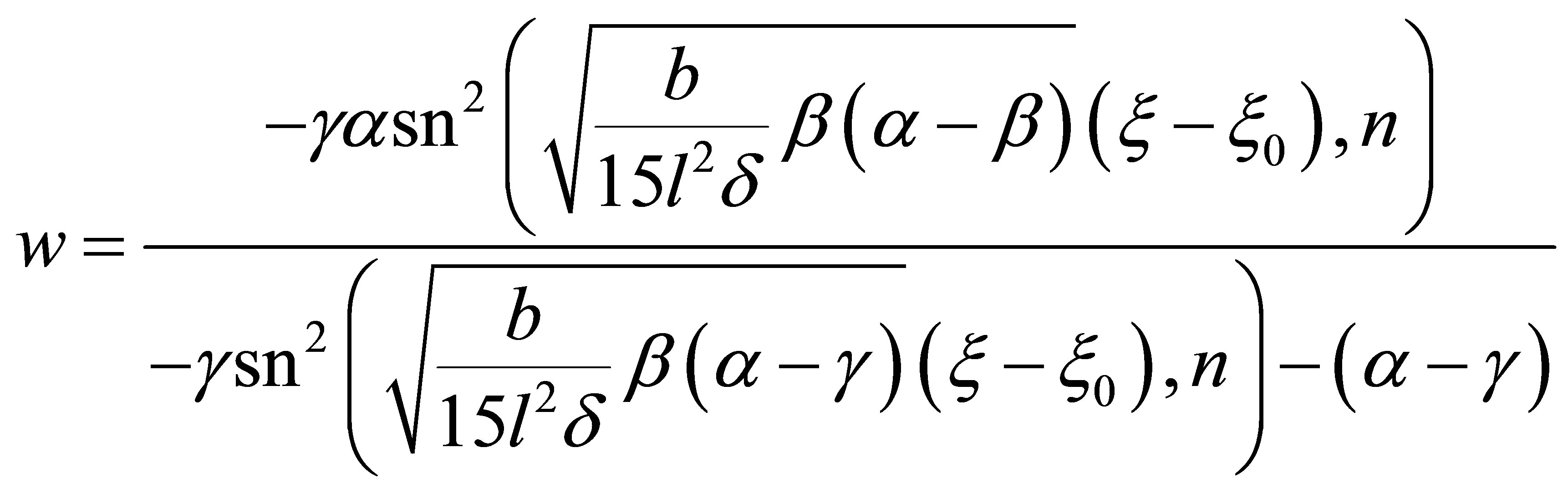 (27)
(27)
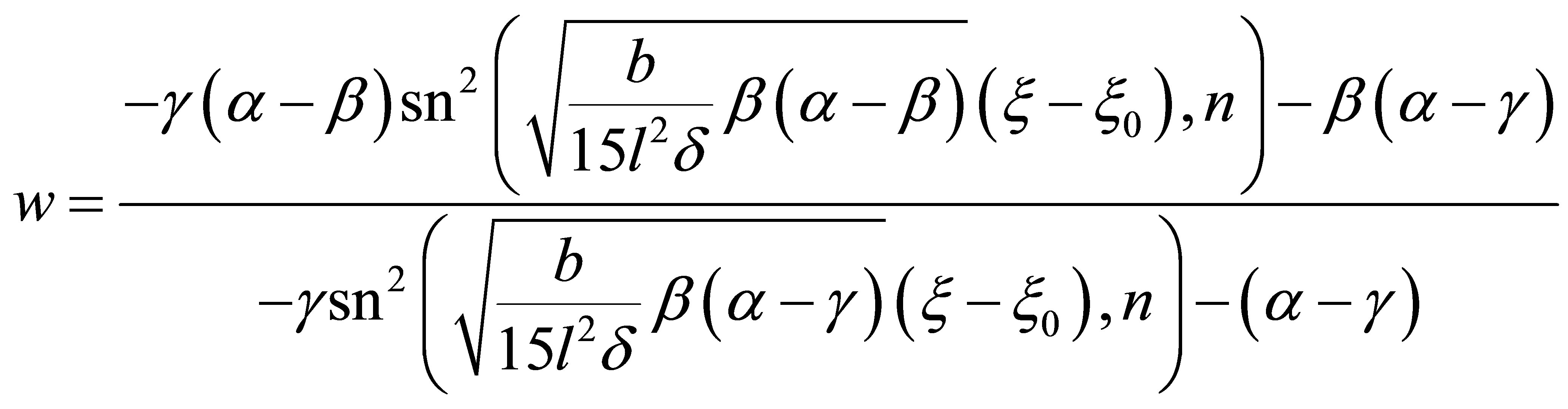 (28)
(28)
where
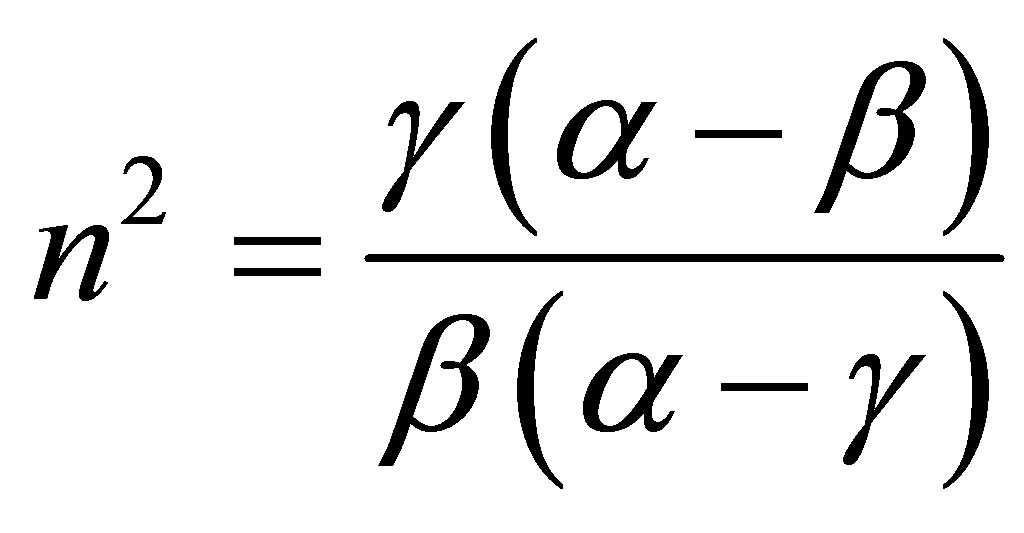 .
.
If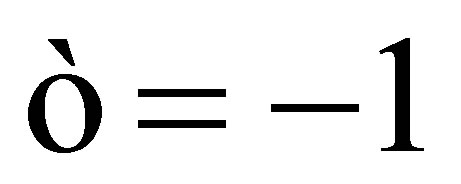 , when
, when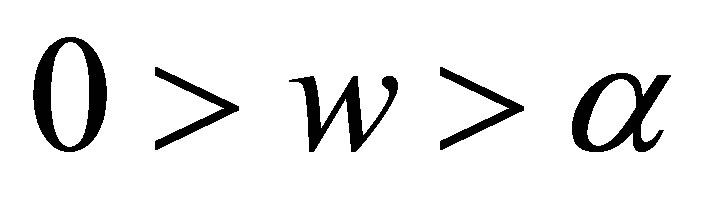 , and
, and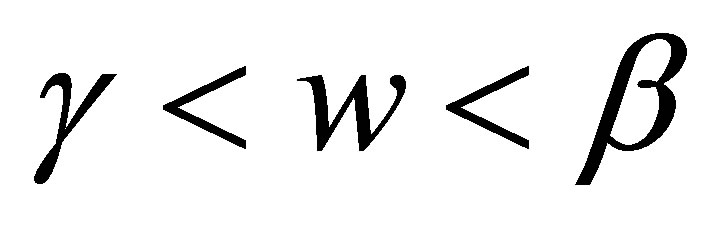 , we have
, we have
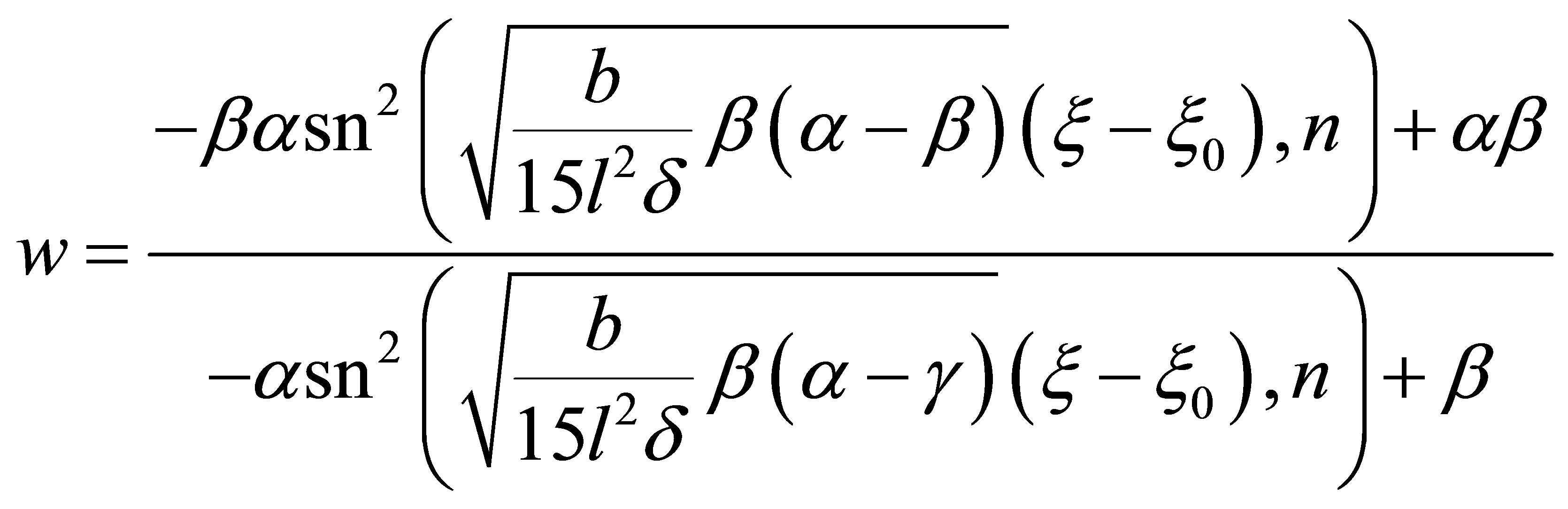 (29)
(29)
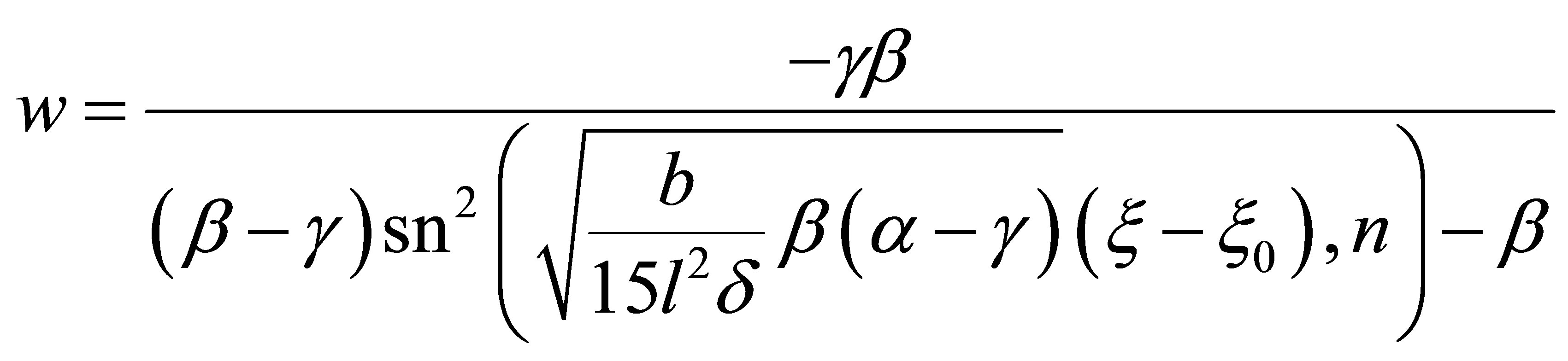 (30)
(30)
where
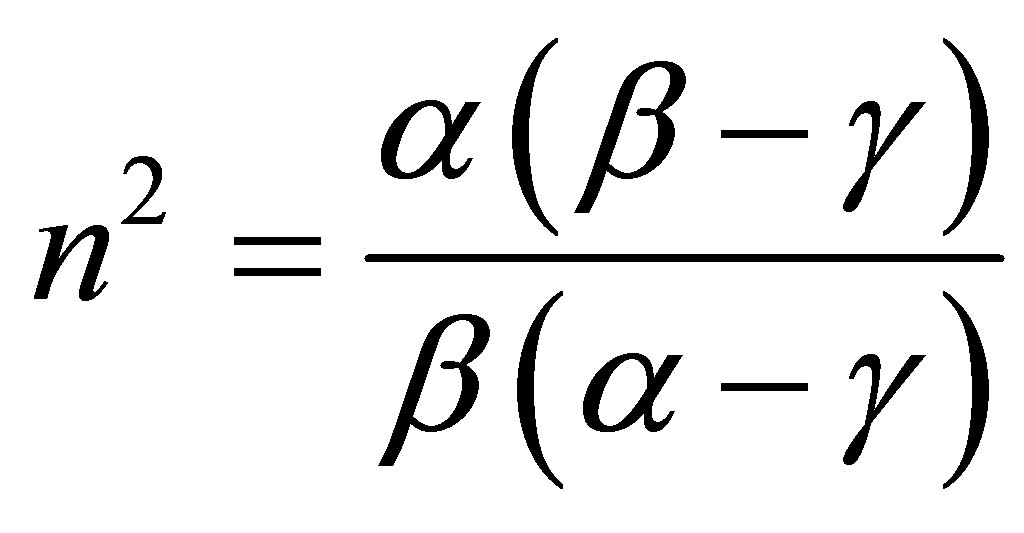 .
.
Case 2.2.4. 
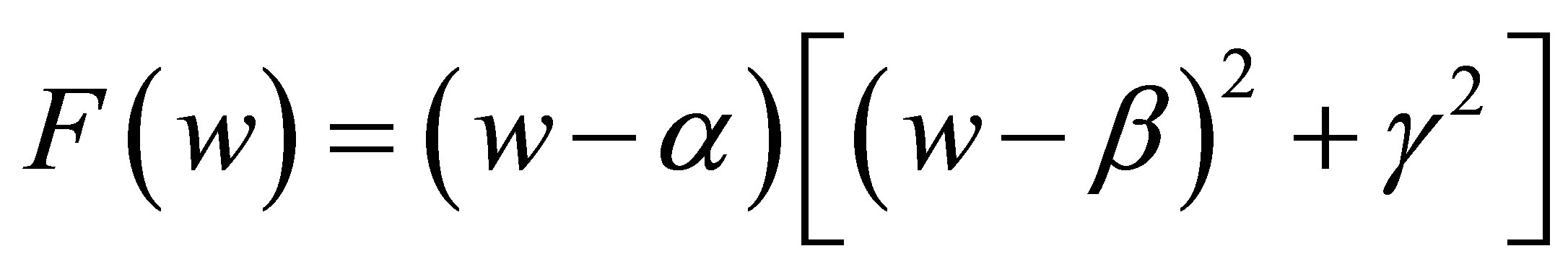 where
where 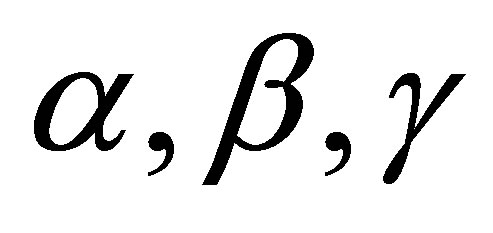 are all real constants, and
are all real constants, and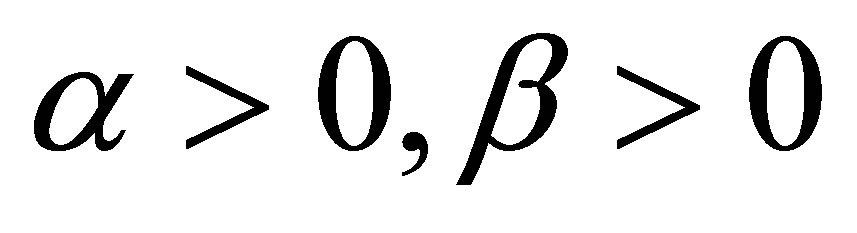 , and
, and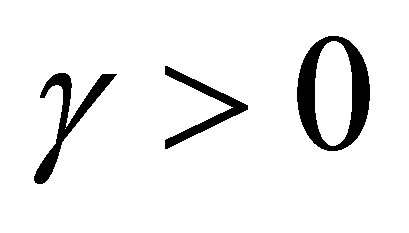 . we have
. we have
 (31)
(31)
where
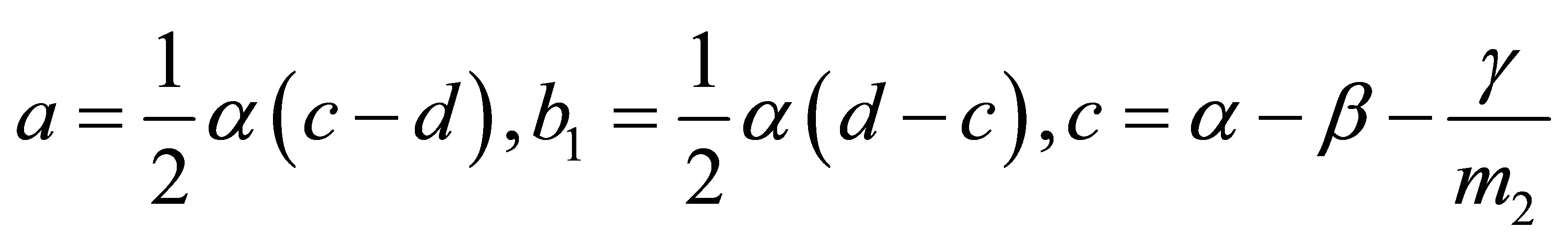 ,
,
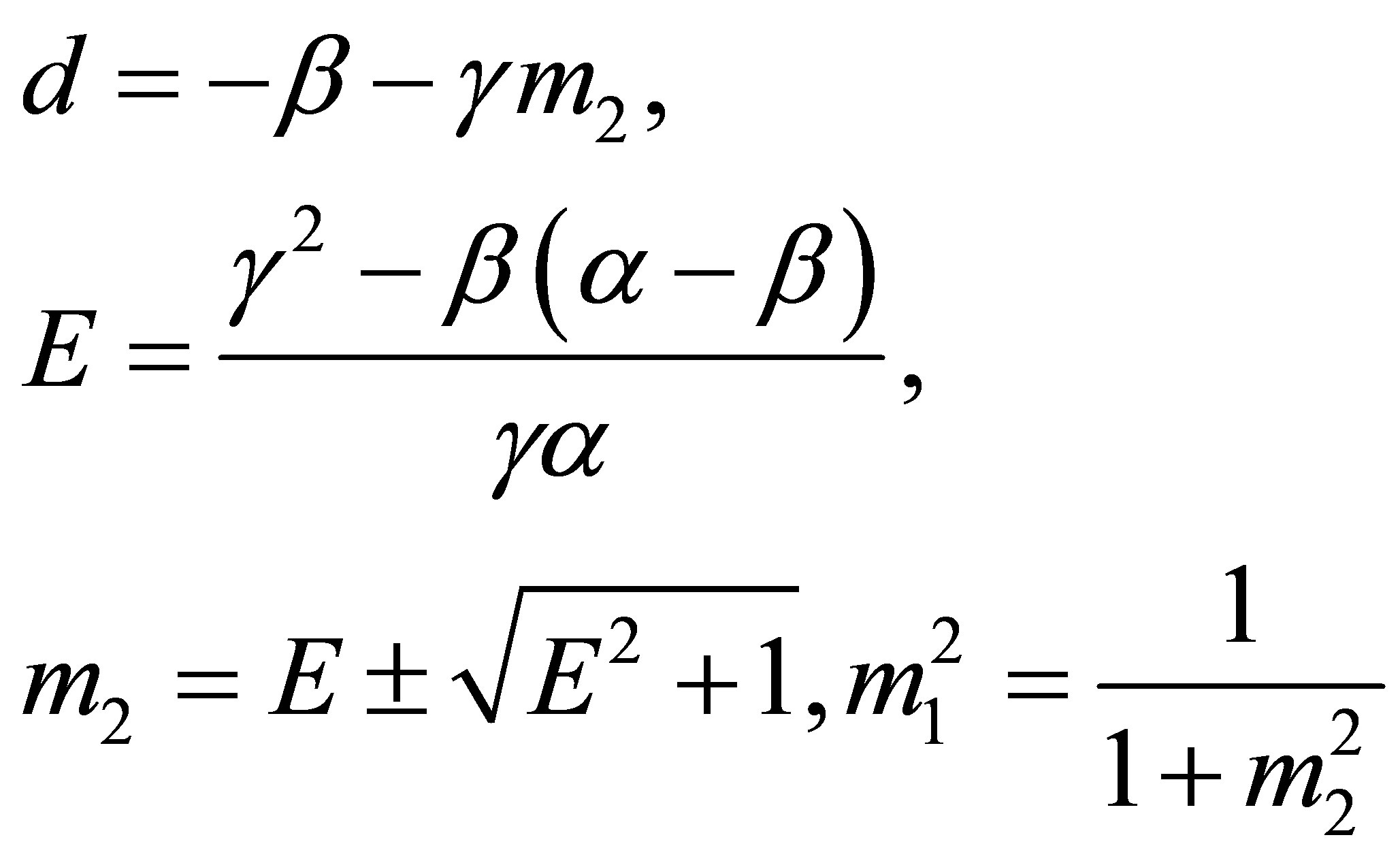 .
.
Case 2.3.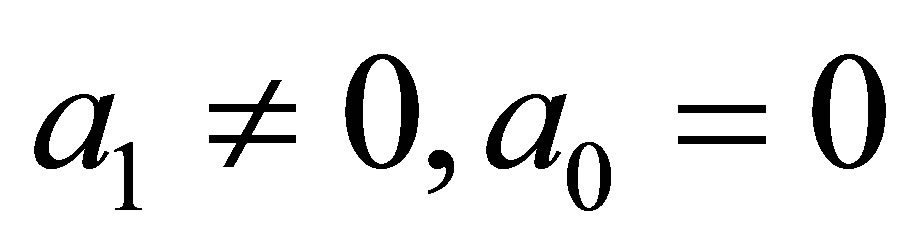 . The Equation (5) becomes
. The Equation (5) becomes
 (32)
(32)
where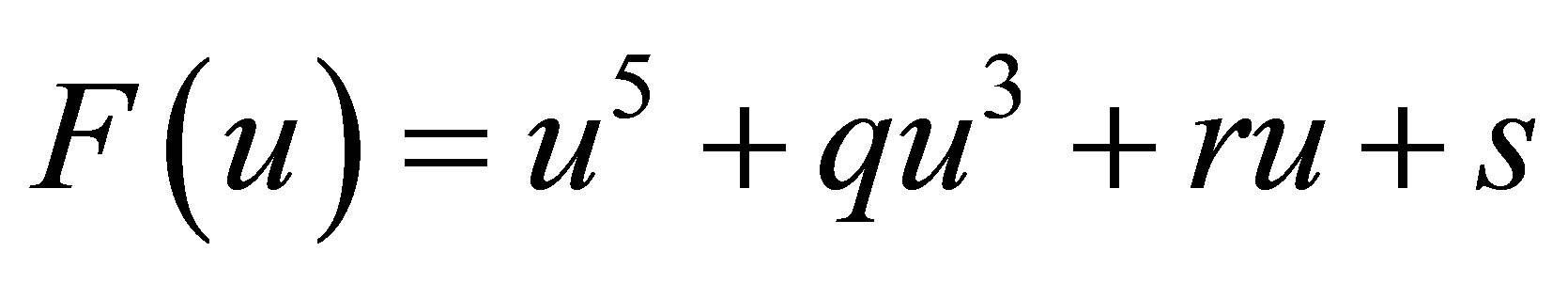 , and
, and
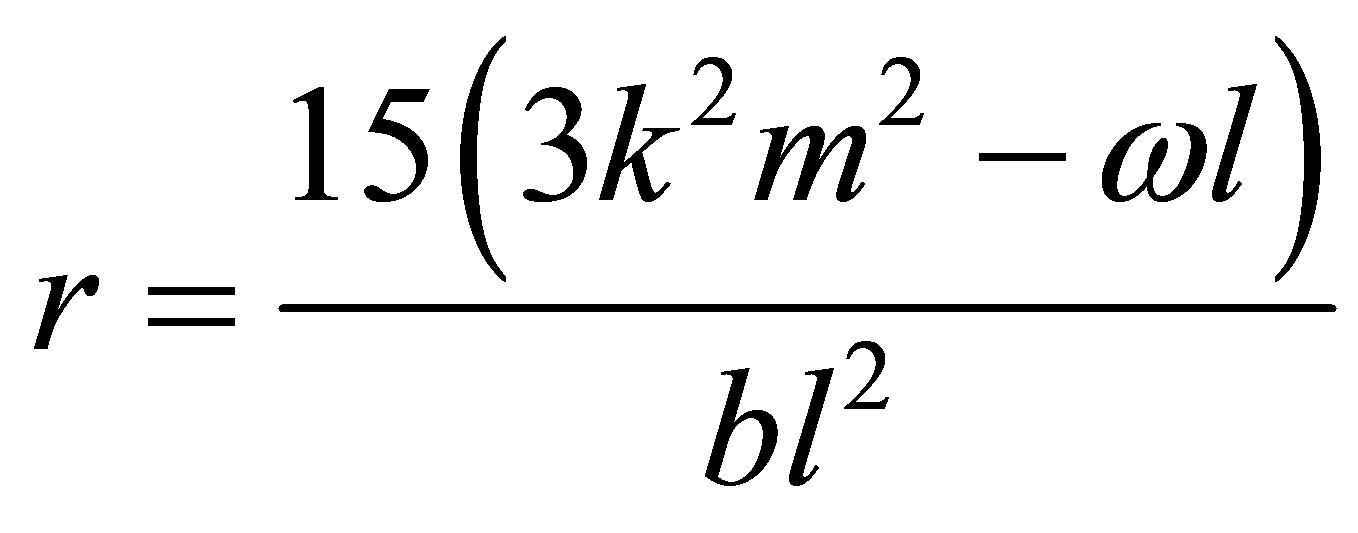
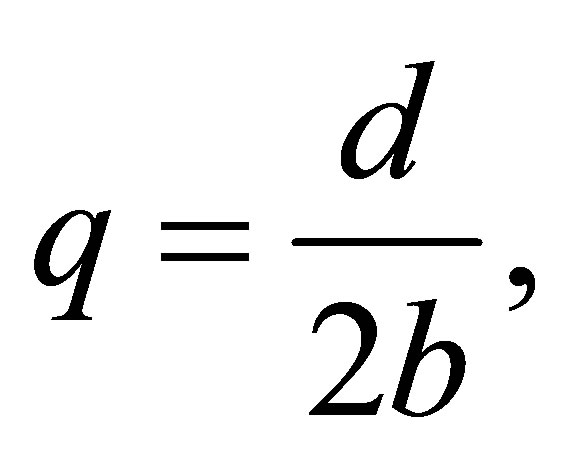 ,
,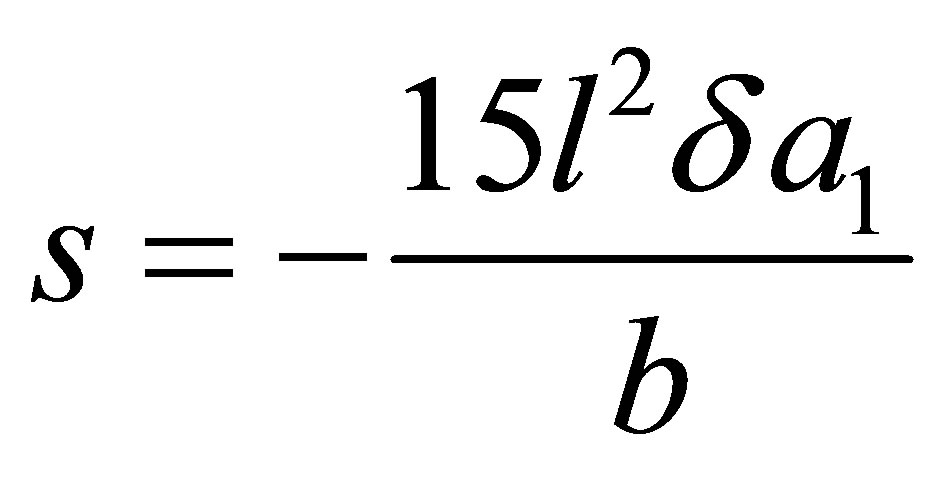 .
.
The complete discrimination system for the fifth order polynomial 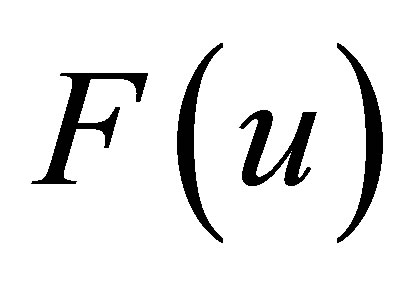 is given as follows:
is given as follows:
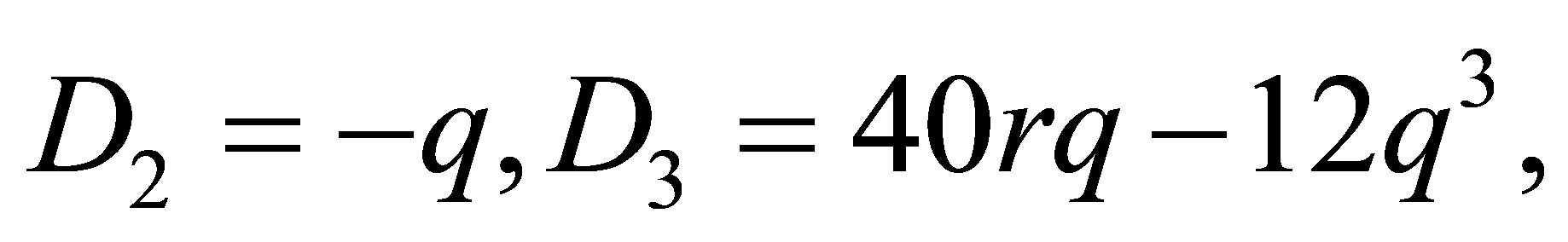
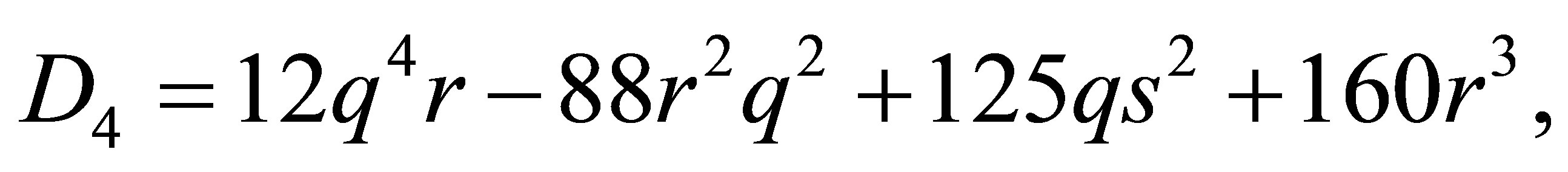
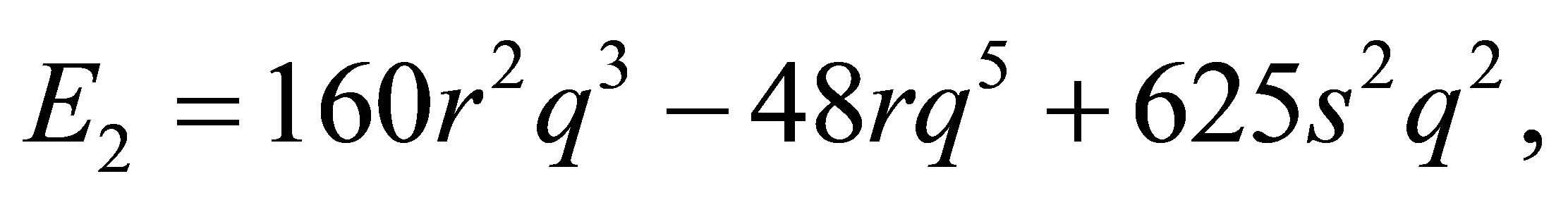
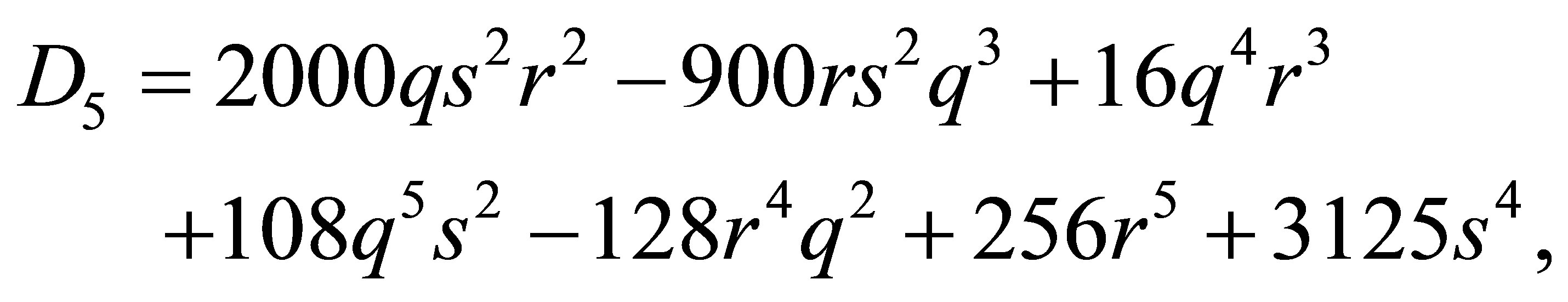
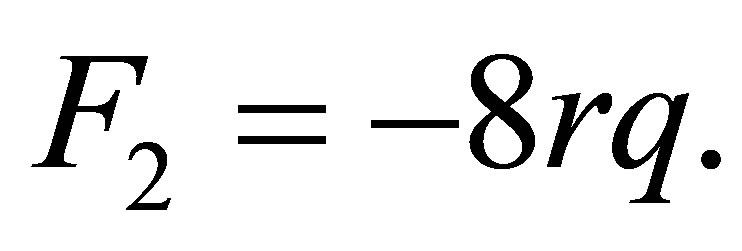 (33)
(33)
According to the classification of the roots of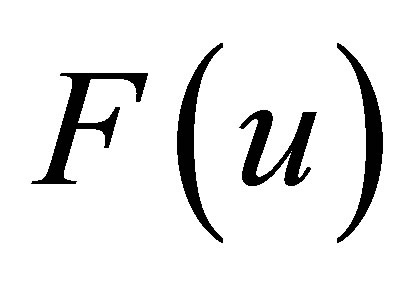 , there are seven cases to be discussed.
, there are seven cases to be discussed.
Case 2.3.1.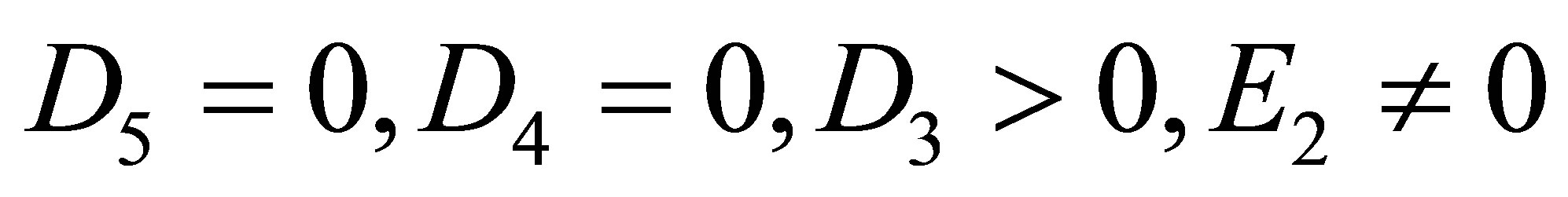 , then
, then
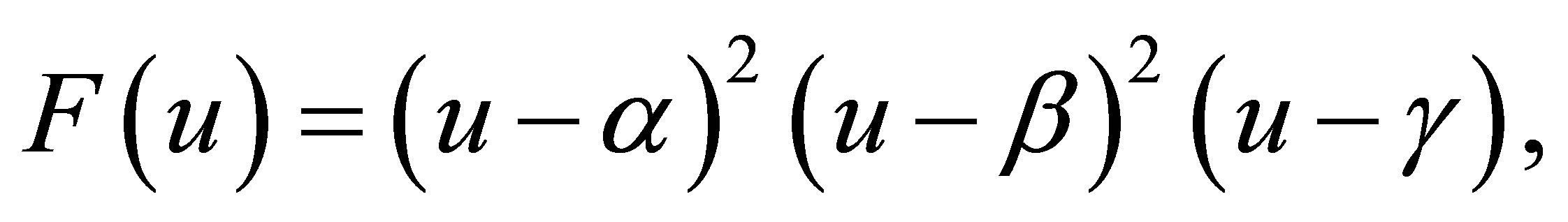
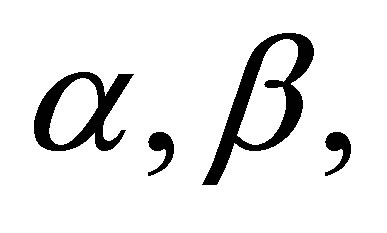 and
and 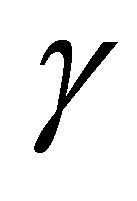 are real numbers,
are real numbers, 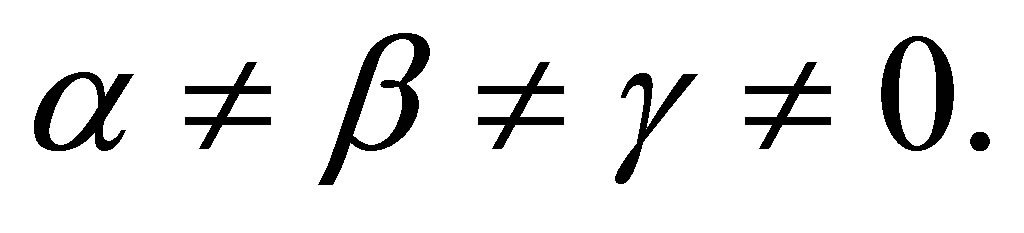 From Equation (32), we have
From Equation (32), we have
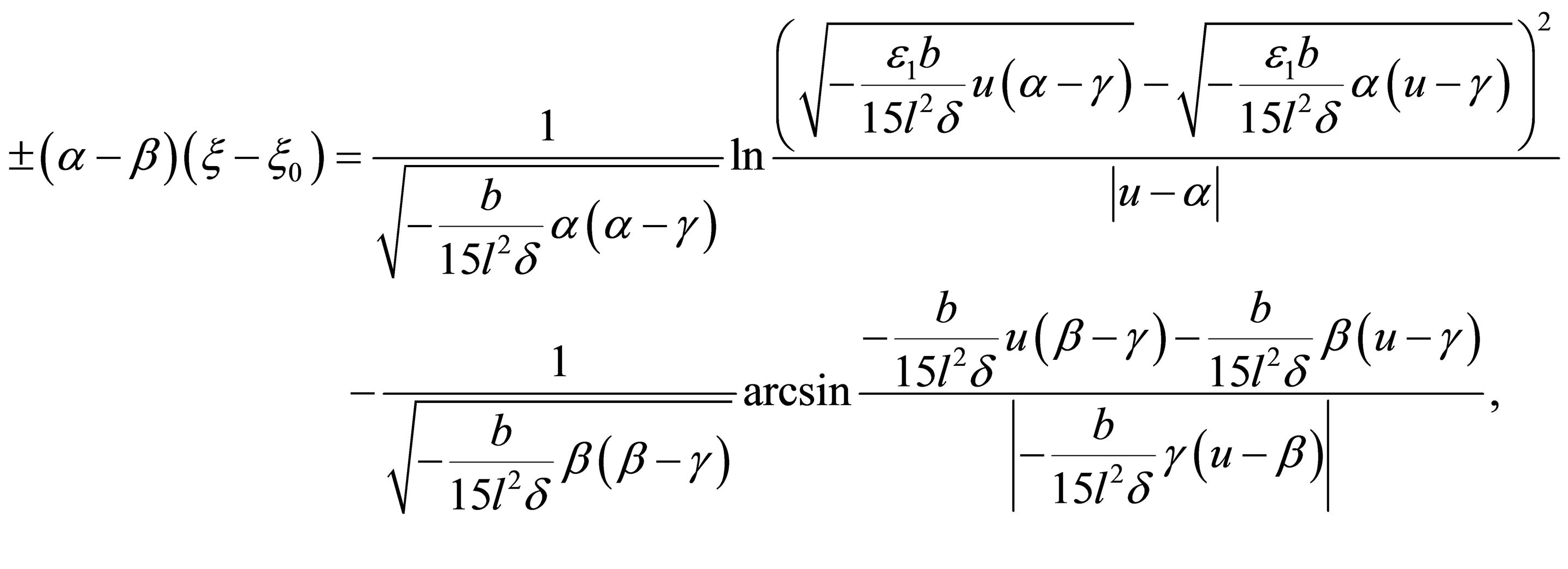 (34)
(34)
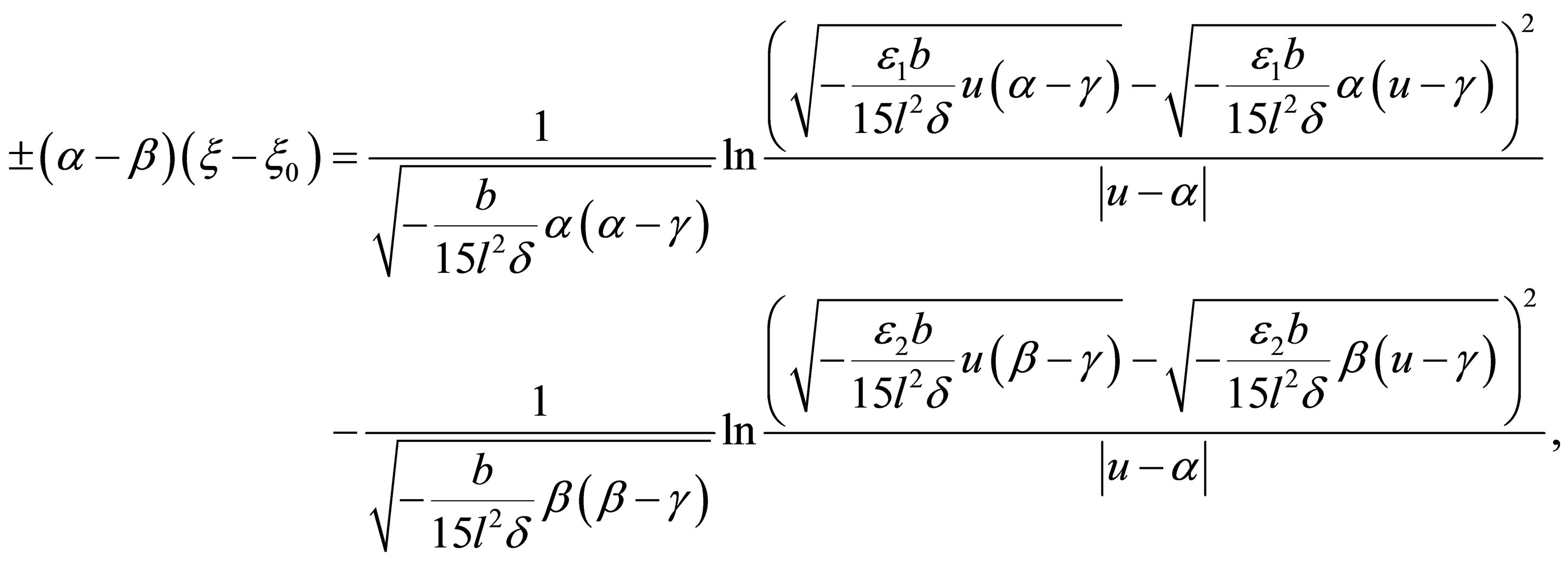 (35)
(35)
 (36)
(36)
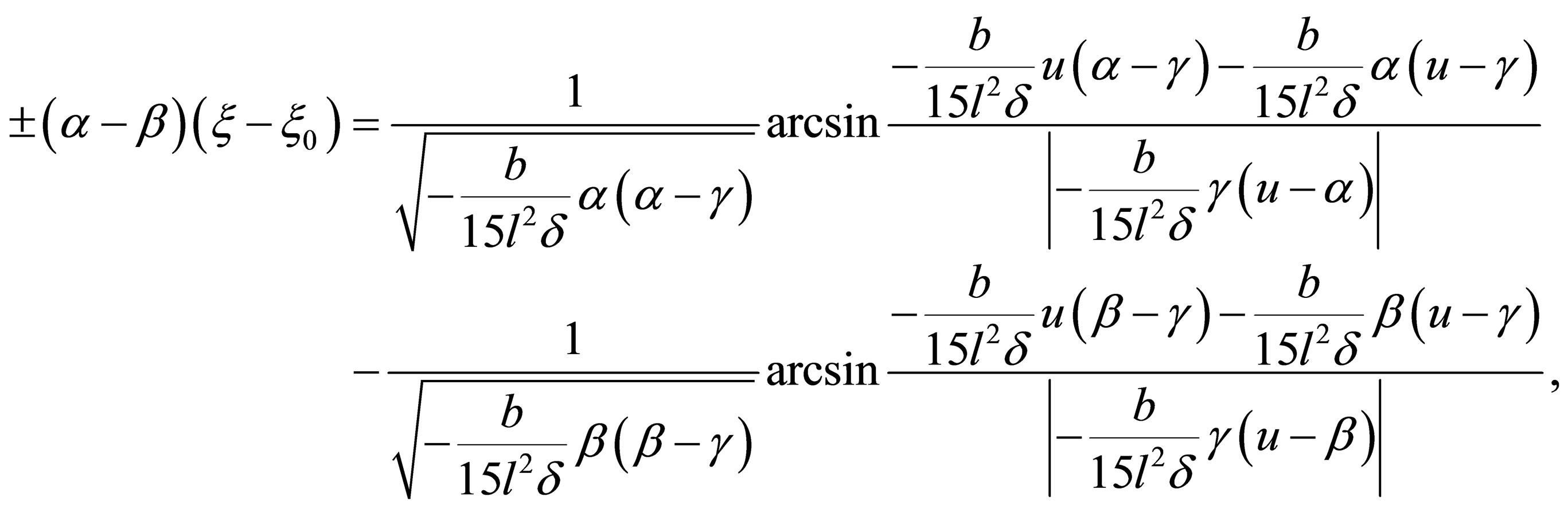 (37)
(37)
where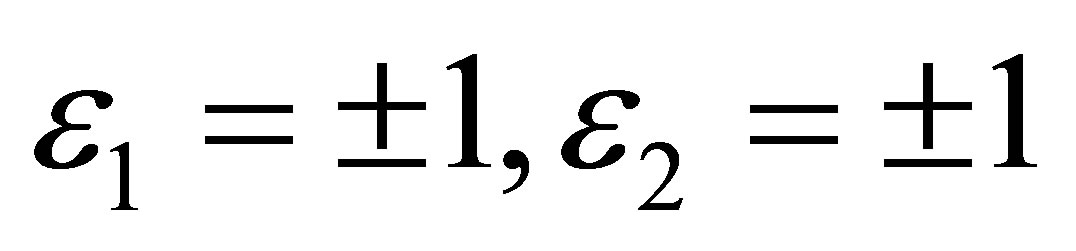 .
.
Case 2.3.2.
 ,
,
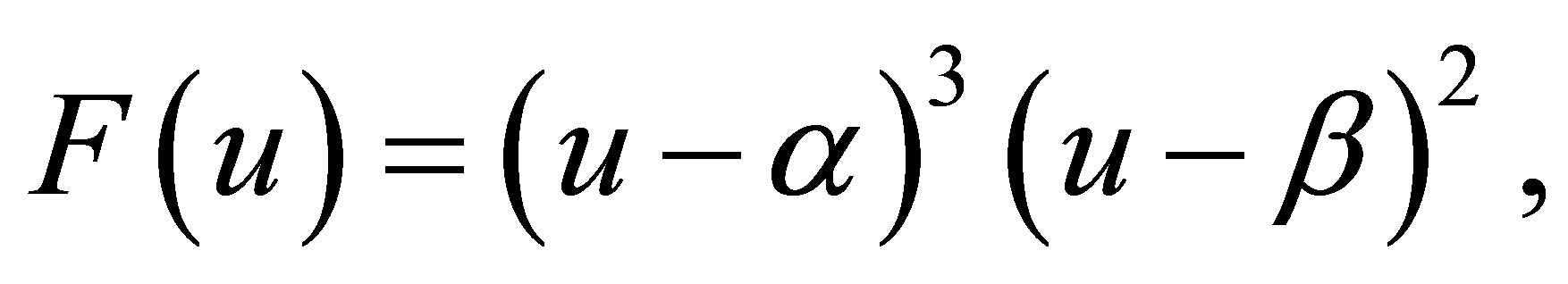
![]() and
and  are real numbers,
are real numbers,  From Equation (32), we have
From Equation (32), we have
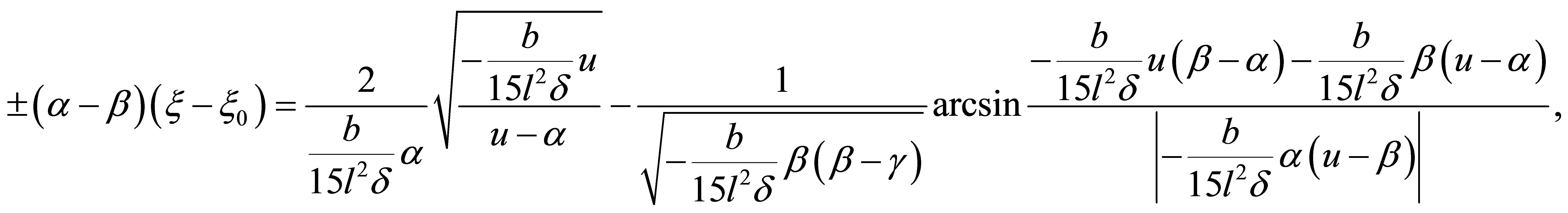 (38)
(38)
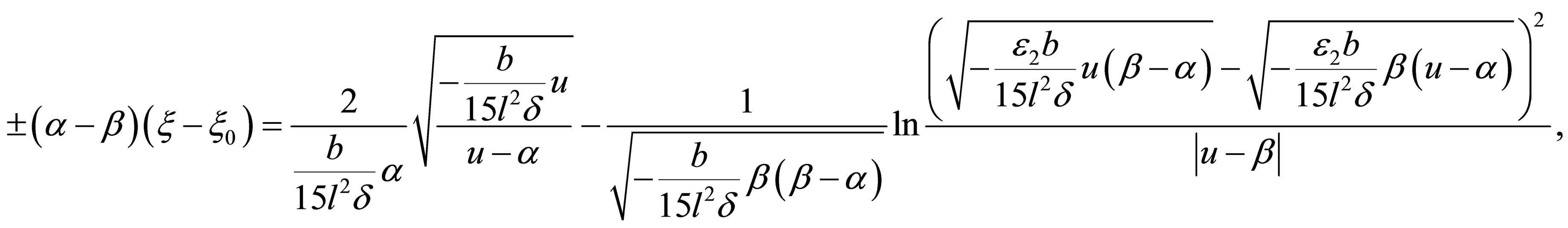 (39)
(39)
where 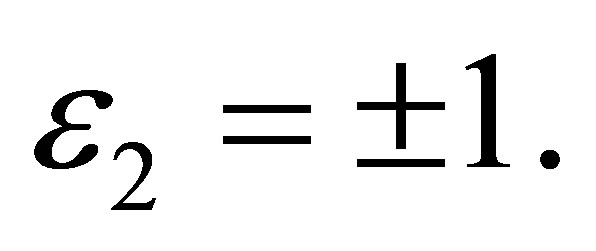
Case 2.3.3.
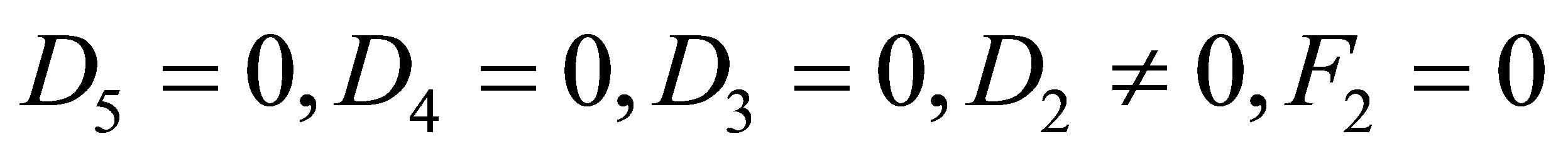 ,
,
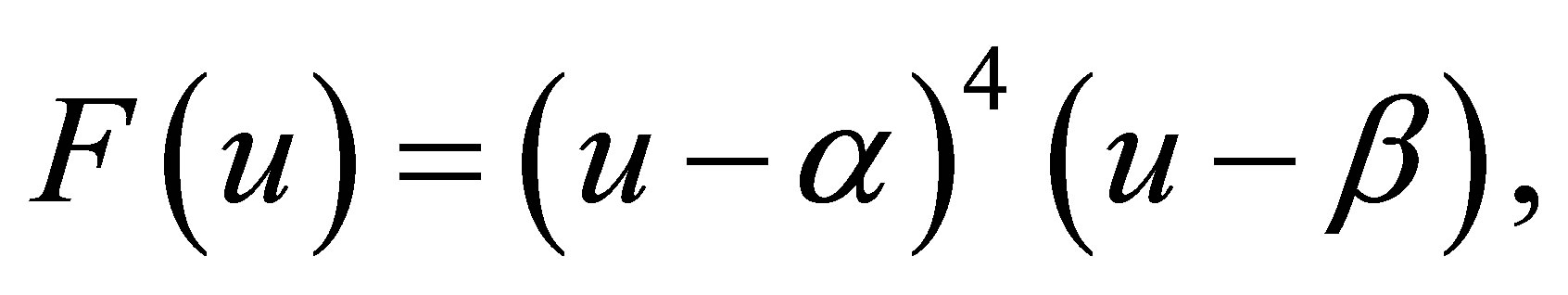
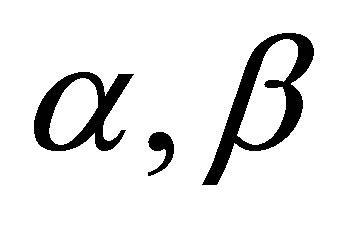 are real numbers,
are real numbers,  From Equation (32), we have
From Equation (32), we have
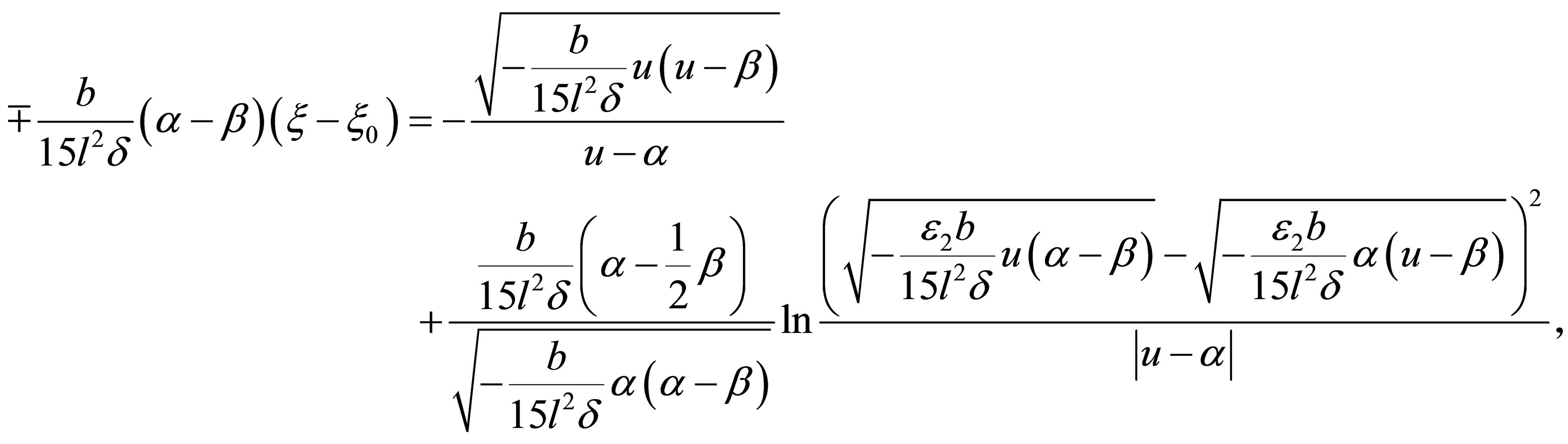 (40)
(40)
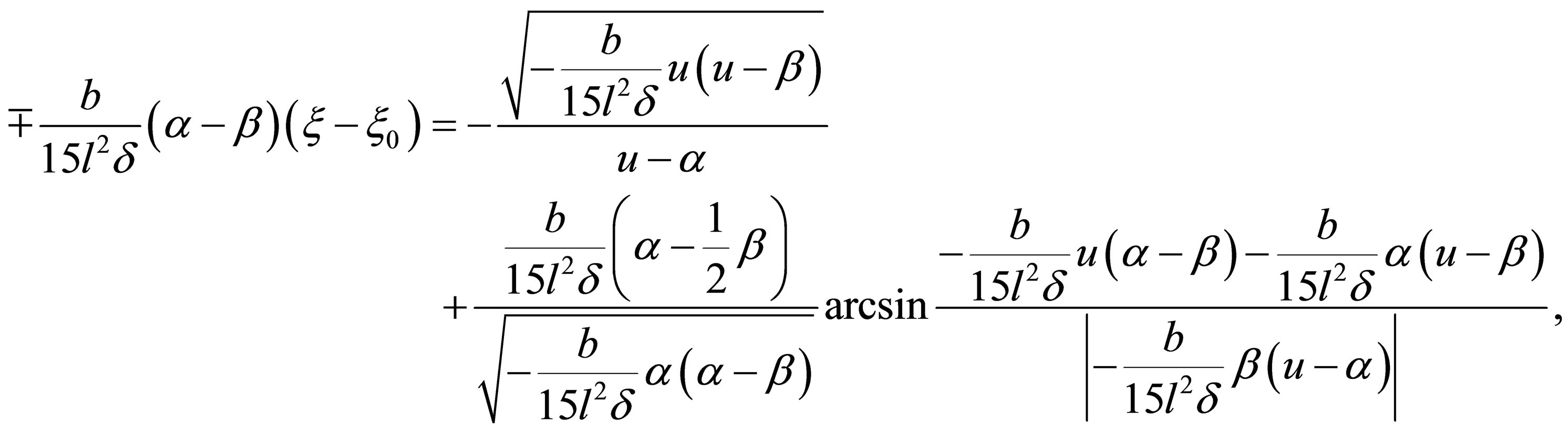 (41)
(41)
where 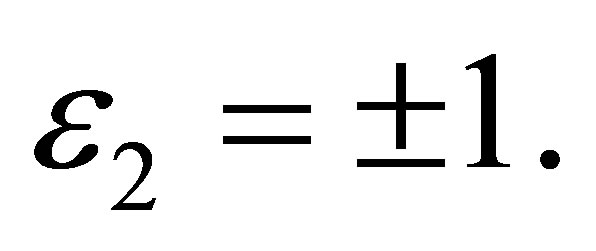
Case 2.3.4.
 ,
,
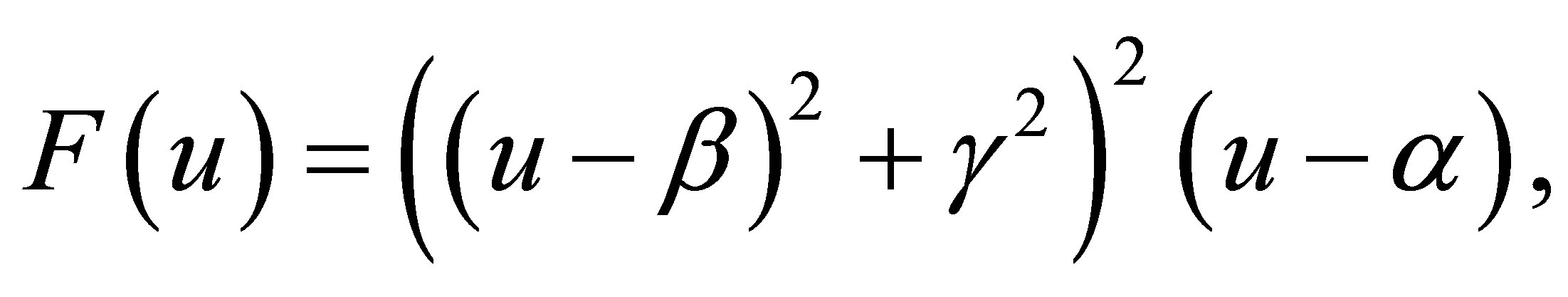 .
.
Respectively, from Equation (32), we have
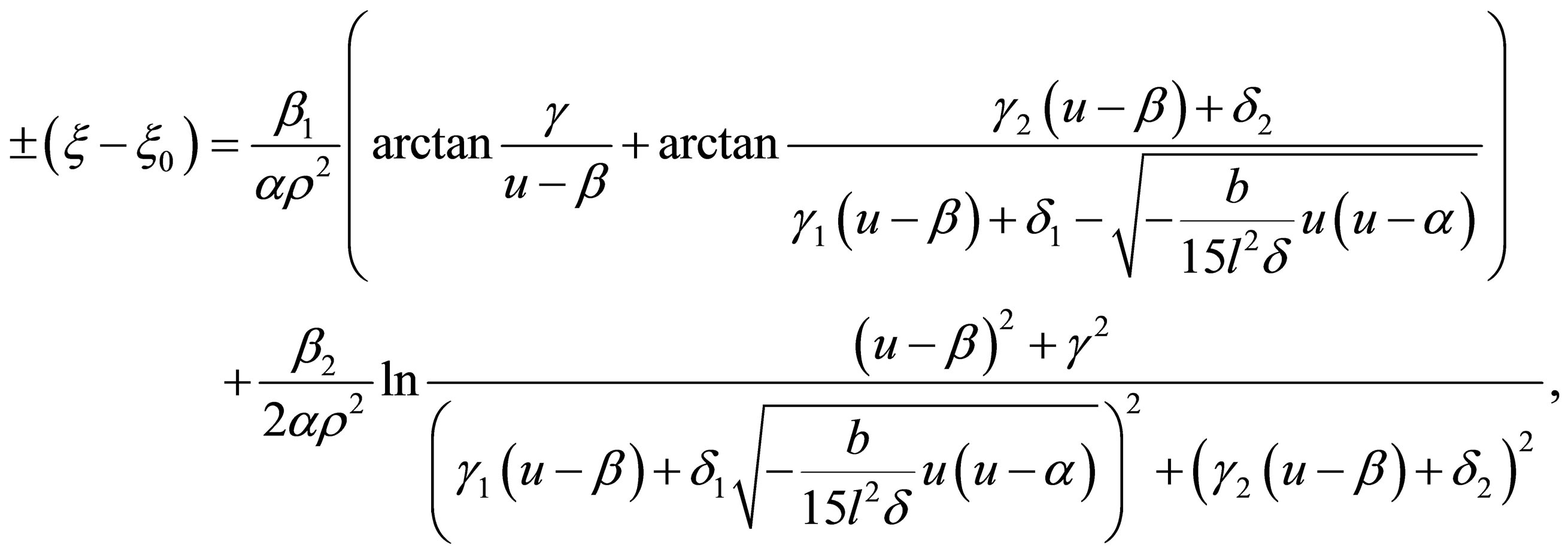 (42)
(42)
where
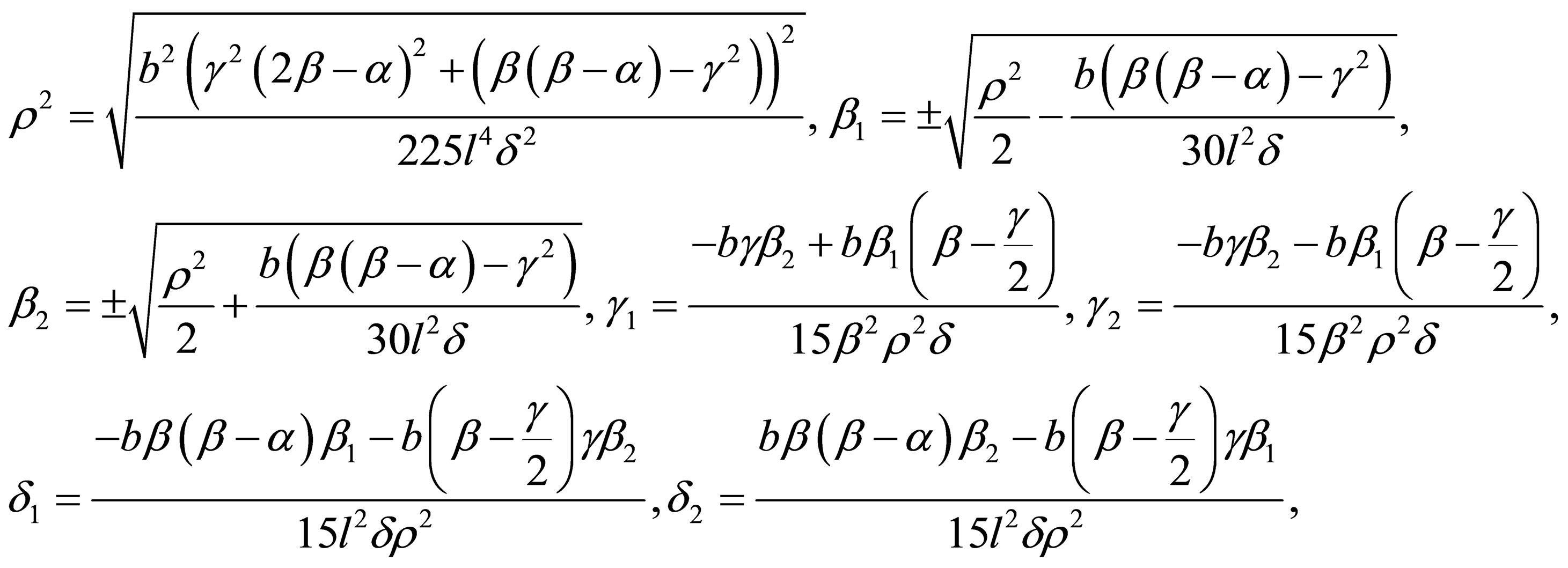 (43)
(43)
where the signs of  and
and 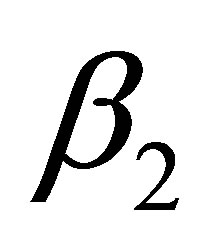 must satisfy
must satisfy
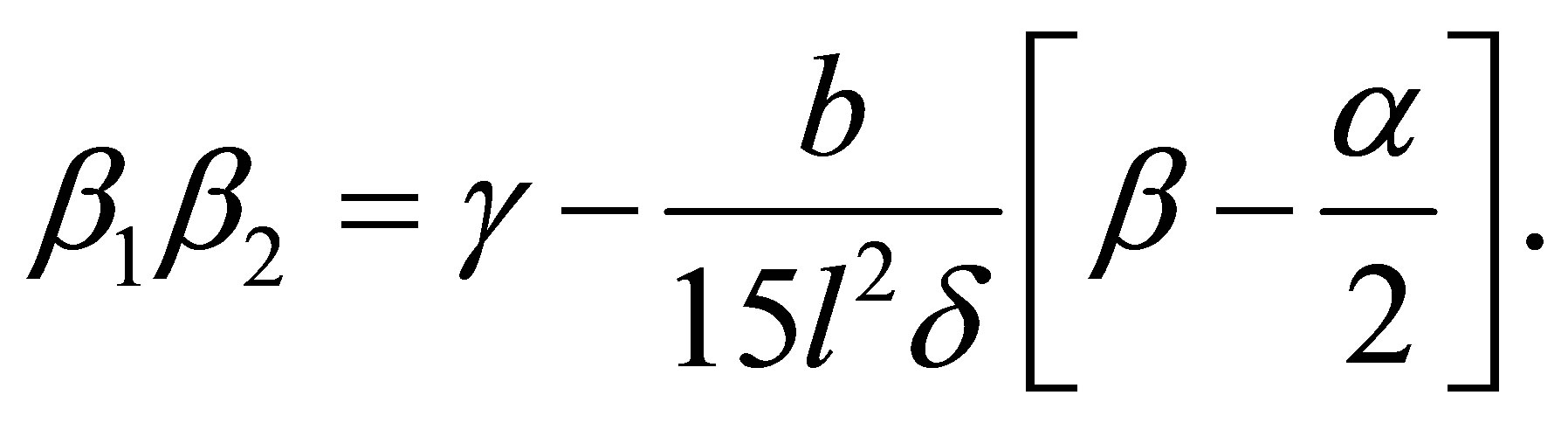
Case 2.3.5.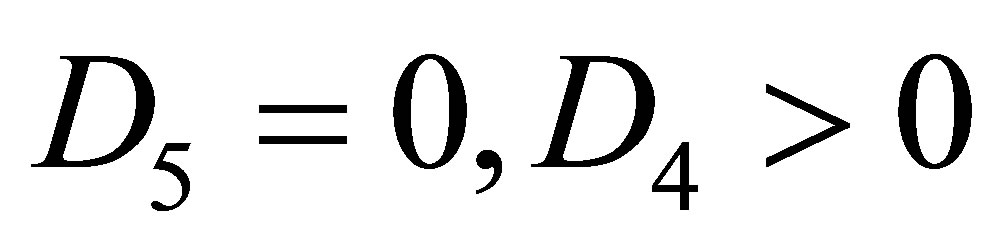 ,
,
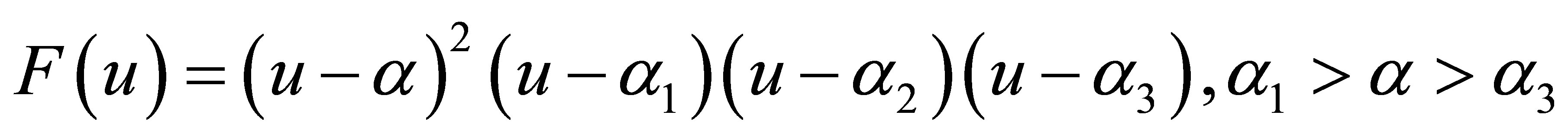 .
.
Respectively, from Equation (32), we have
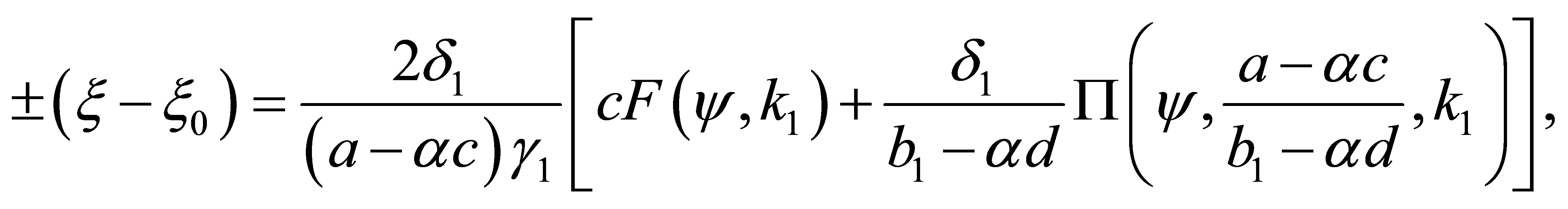 (44)
(44)
where we renew to queue the orders of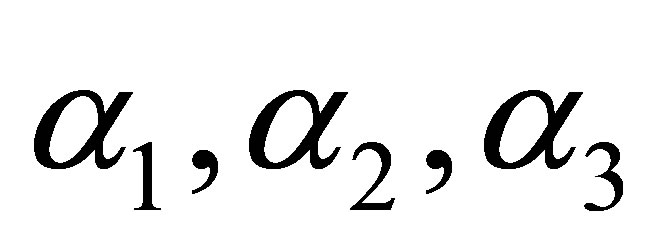 , and
, and , denote
, denote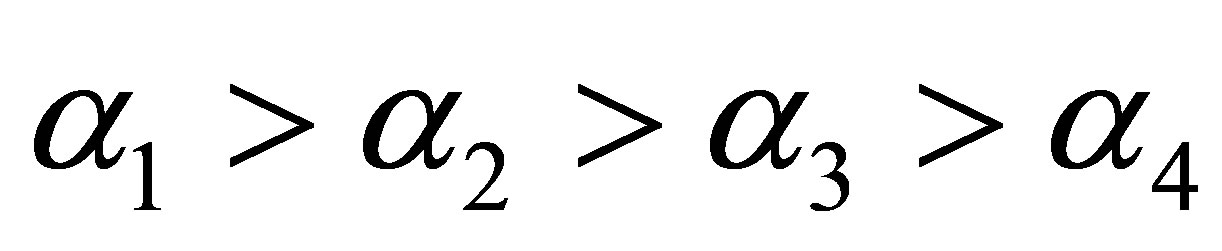 .When
.When
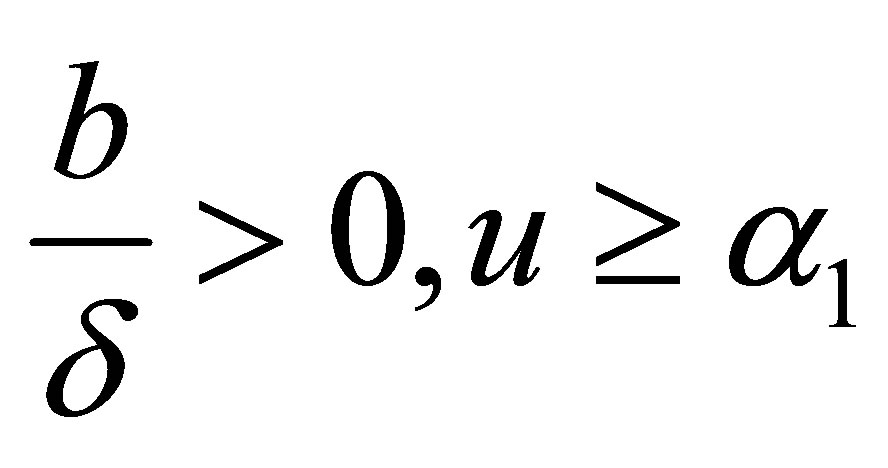 or
or 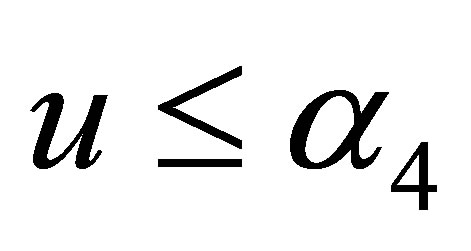
(other cases can be written similarly, they are omitted), the meaning of every parameter in Equation (44) are given as follows:
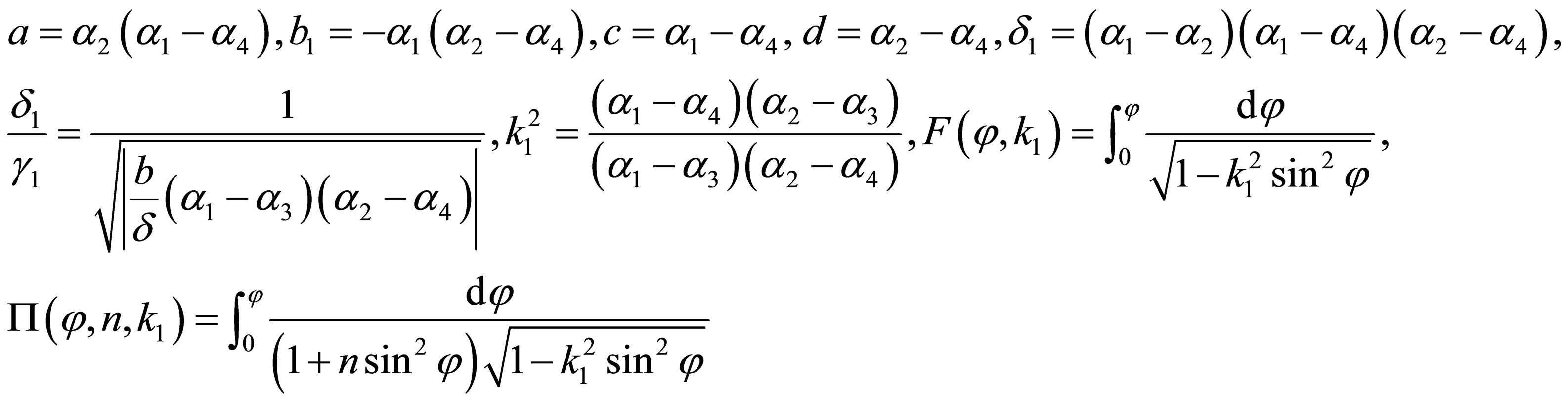 (45)
(45)
Case 2.3.6.
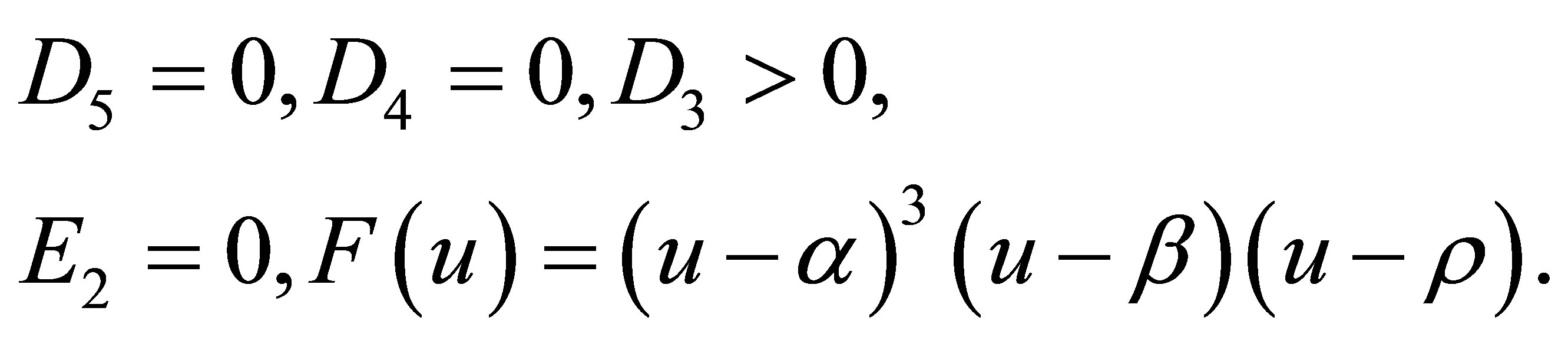
where we renew to queue the orders of 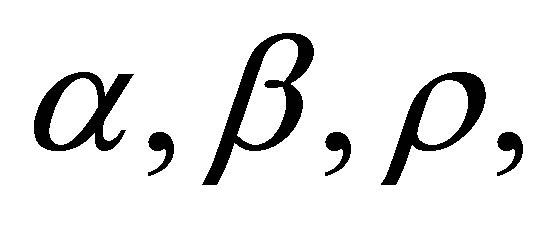 and 0, and denote
and 0, and denote 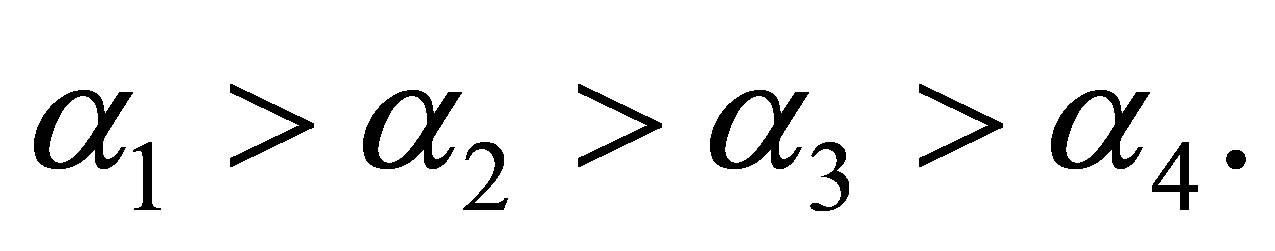 When
When
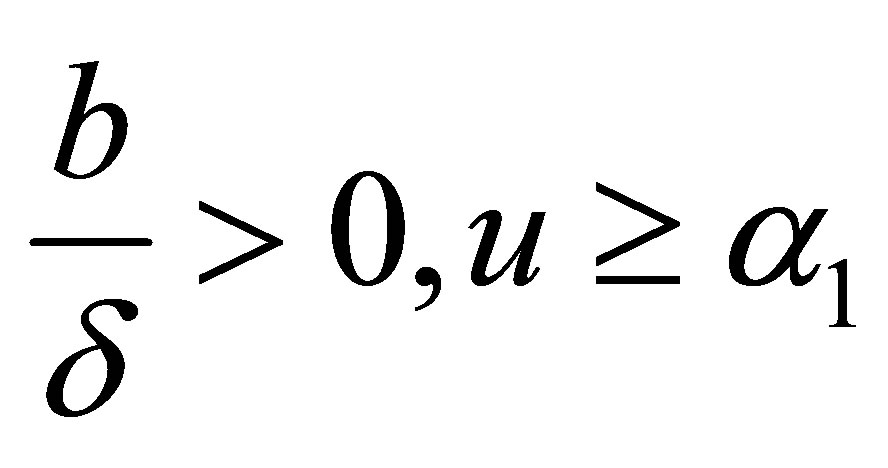 , or
, or 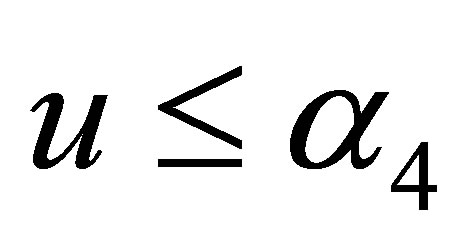
(other cases can be written similarly, they are omitted), we have
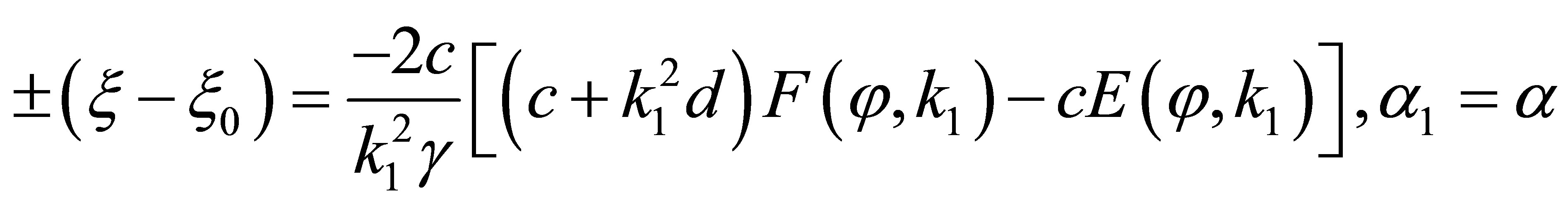 (46)
(46)
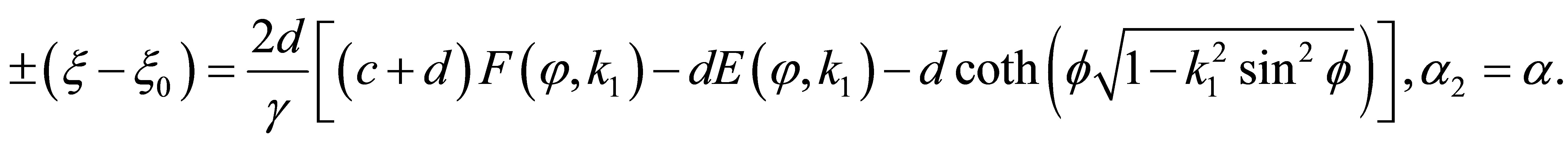 (47)
(47)
The signs are the same as the ones in Equation (45), furthermore,
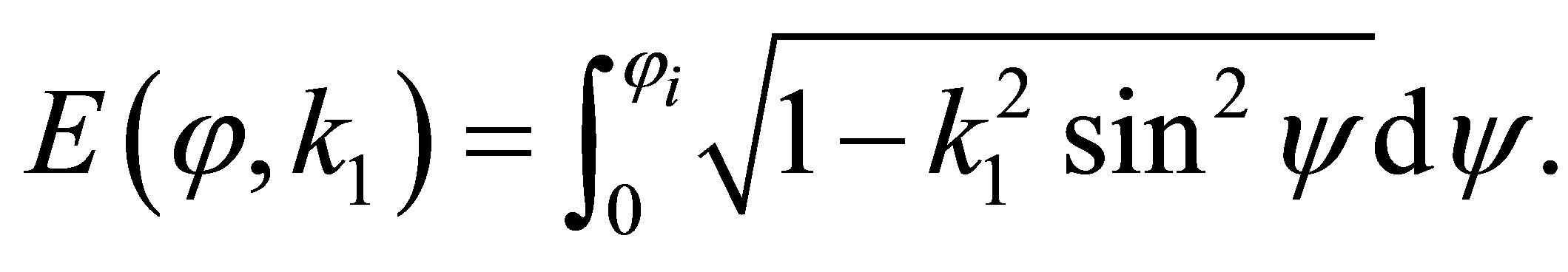 (48)
(48)
Case 2.3.7.
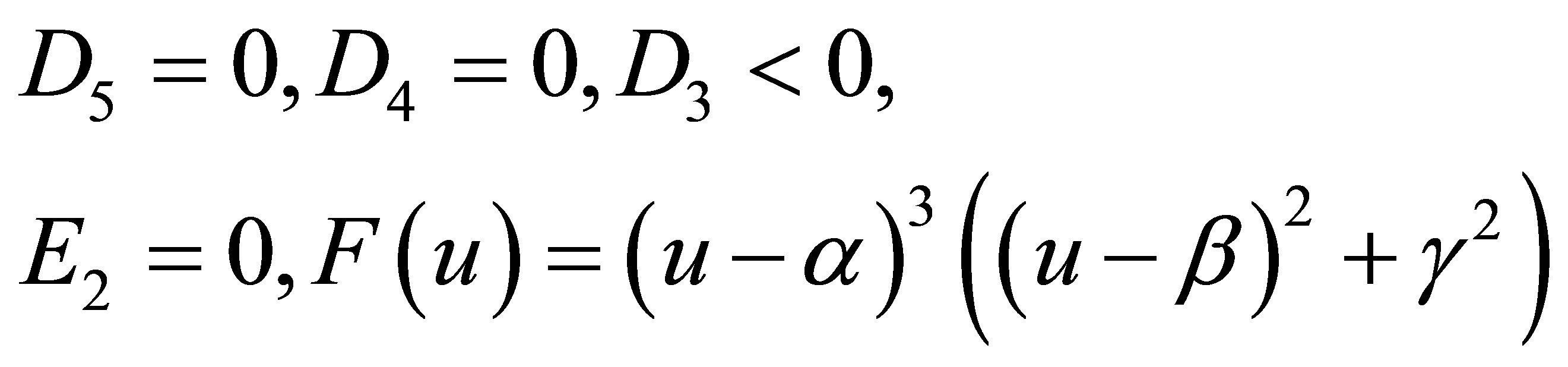
Now we renew to queue the orders of ![]() and 0, and denote
and 0, and denote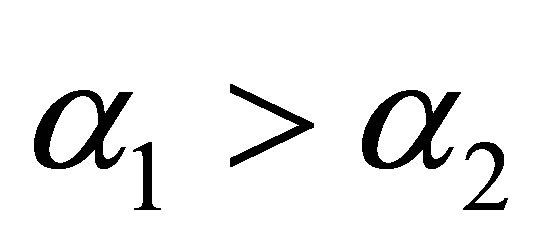 , we have
, we have
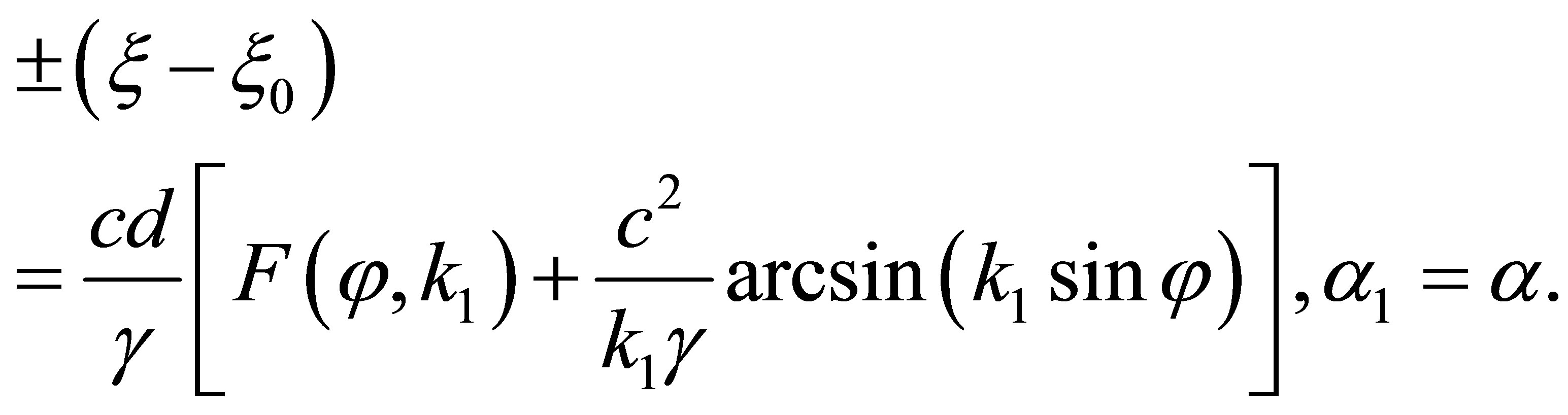 (49)
(49)
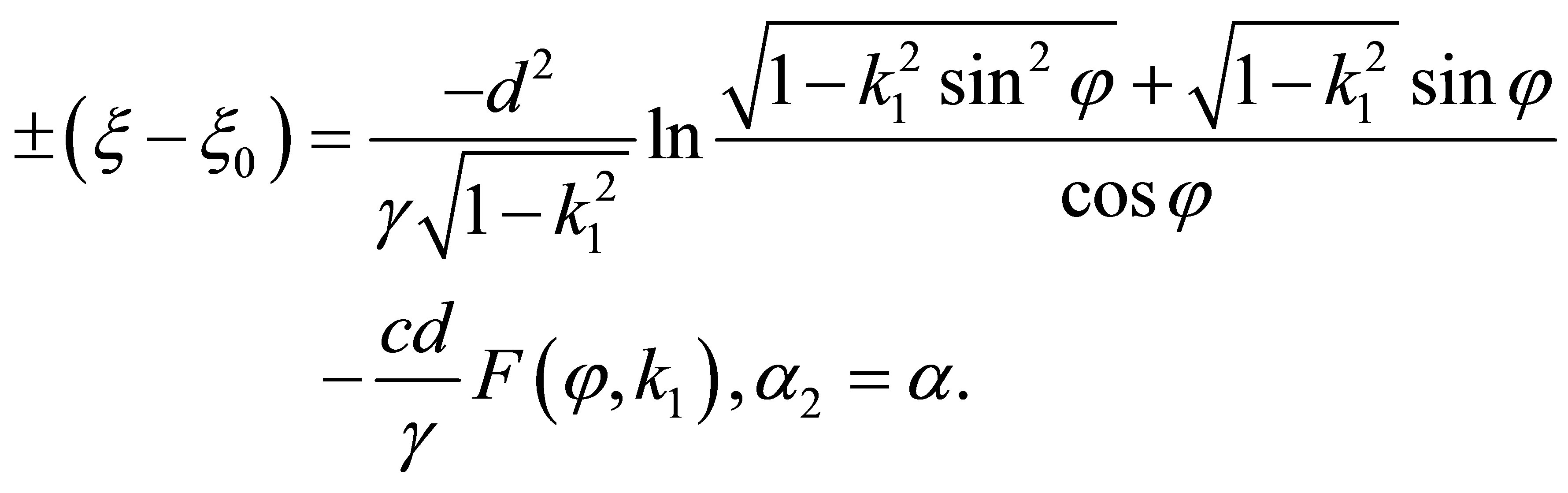 (50)
(50)
where
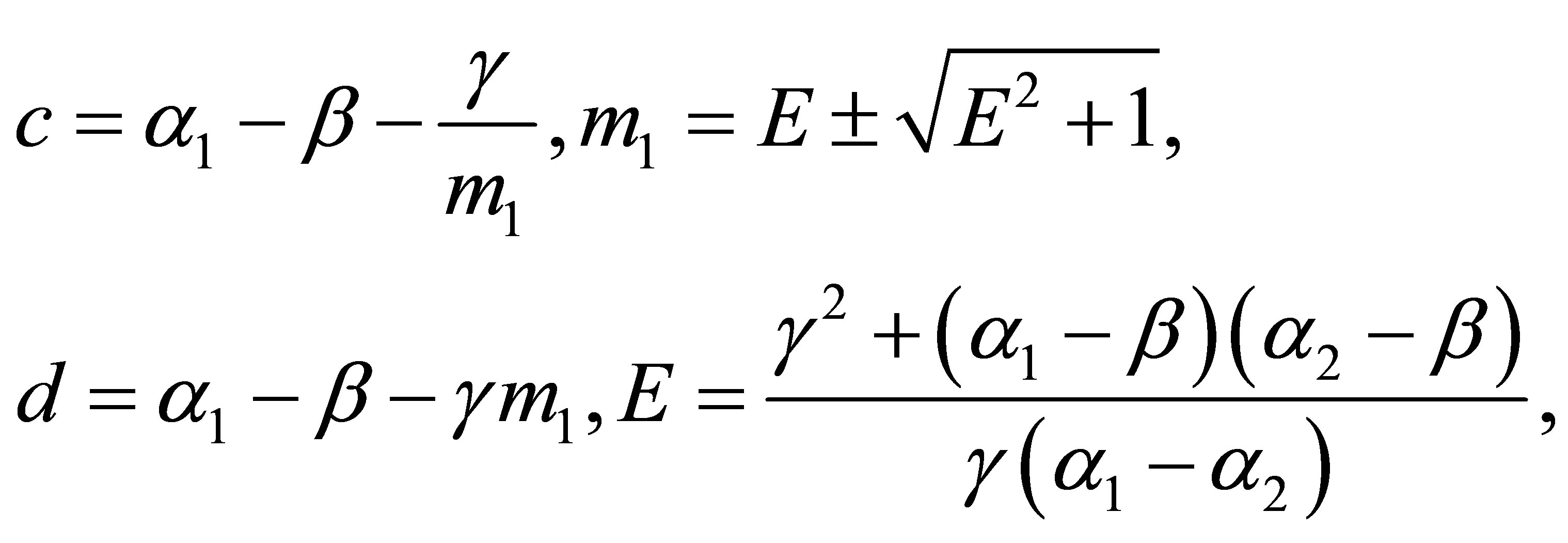 (51)
(51)
where the positive sign and negative sign for 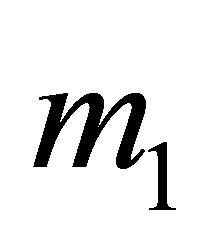 must satisfy
must satisfy
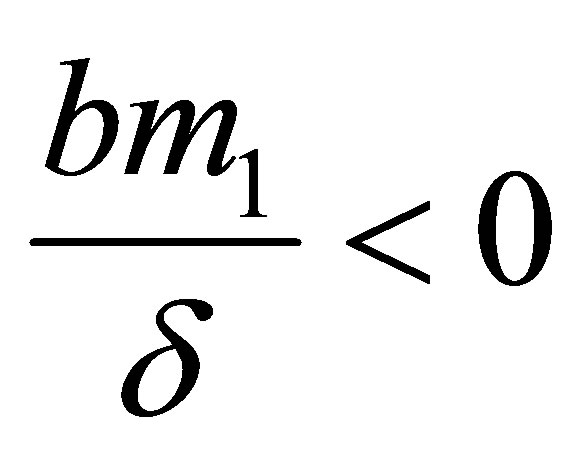 other signs are the same with the former.
other signs are the same with the former.
From the description above, using elementary integral method and complete discrimination system for polynomial, we have obtained the solutions of equations (6), (16) and (32) that can be expressed by elementary functions and elliptic functions. What’s more, some solutions are explicit, but some solutions are implicit functions. So we can write concretely the exact traveling wave solutions of Equation (5) in some special cases. They are omitted for simplicity.
3. Conclusion
Using the complete discrimination system for polynomial method, we have obtained the classification of single traveling wave solutions to the generalized KadomtsevPetviashvili equation without dissipation terms in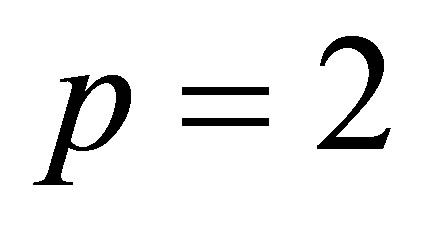 . With the same method, some of other evolution equations can be dealt with.
. With the same method, some of other evolution equations can be dealt with.
4. Acknowledgements
The project is supported by Scientific Research Fund of Education Department of Heilongjiang Province of China under Grant No. 12521049.
REFERENCES
- M. J. Ablowits, “Lectures on the Inverse Scattering Transform,” Studies in Applied Mathematics, Vol. 58, No. 11, 1978, pp. 17-94.
- G. C. Das and J. Sarma, “Evolution of Solitary Waves in Multicomponent Plasmas,” Chaos, Solitons and Fractals, Vol. 9, No. 6, 1998, pp. 901-911. http://dx.doi.org/10.1016/S0960-0779(97)00170-7
- X. Zhao, W. Xu, H. Jia and H. Zhou, “Solitary Wave Solutions for the Modified Kadomtsev-Petvisahvili Equation,” Chaos, Solitons, and Fractals, Vol. 74, 2007, pp. 465-475. http://dx.doi.org/10.1016/j.chaos.2006.03.046
- W. X. Ma, A. Abdeljabbar and M. G. Assad, “Wronskian and Grammian Solutions to a (3 + 1)-Dimensional Generalized KP Equation,” Applied Mathematics and Computation, Vol. 217, No. 24, 2011, pp. 10016-10023. http://dx.doi.org/10.1016/j.amc.2011.04.077
- A. M. Wazwaz, “Multiple-Soliton Solutions for a (3 + 1)-Dimensional Generalized KP Equation,” Communications in Nonlinear Science and Numerical Simulation, Vol. 17, No. 2, 2012, pp. 491-495. http://dx.doi.org/10.1016/j.cnsns.2011.05.025
- W. X. Ma and A. Abdeljabbar, “A Bilinear Bäcklund Transformation of a (3 + 1)-Dimensional Generalized KP Equation,” Applied Mathematics Letters, Vol. 25, No. 10, 2012, pp. 1500-1504. http://dx.doi.org/10.1016/j.aml.2012.01.003
- G. B. Whitham, “Linear and Nonlinaer Wave,” John Wiley, New York, 1974.
- W. Hereman and A. Nuseir, “Symbolic Methods to Construct Exact Solutions of Nonlinear Partial Differential Equations,” Mathematics and Computers in Simulation, Vol. 43, No. 1, 1997, pp. 13-27. http://dx.doi.org/10.1016/S0378-4754(96)00053-5
- W. X. Ma and A. Pekcan, “Uniqueness of the Kadomtsev-Petviashvili and Boussinesq Equations,” Zeitschrift für Naturforschung A, Vol. 66, 2011, pp. 377-382.
- C. S. Liu, “Applications of complete Discrimination System for Polynomial for Classifications of Traveling Wave Solutions to Nolinear Differential Equations,” Computer Physics Communications, Vol. 181, No. 2, 2010, pp. 317- 324. http://dx.doi.org/10.1016/j.cpc.2009.10.006
- C. S. Liu, “Classification of All Single Traveling Wave Solutions to Calogero-Focas Equation,” Communications in Theoretical Physics, Vol. 48, 2007, pp. 601-604. http://dx.doi.org/10.1088/0253-6102/48/4/004
- C. S. Liu, “Exact Traveling Wave Solutions for (1 + 1)-Dimentional Dispersive Long Wave Equation,” Chinese Physical Society, Vol. 14, No. 9, 2005, pp. 1710- 1716.
- C. S. Liu, “Direct Integral Method, Complete Discrimination System for Polynomial and Applications to Classifications of All Single Traveling Wave Solutions to Nonlinear Differential Equations: A Survey,” arXiv:nlin/ 0609058v1, 2006.

