Advances in Pure Mathematics
Vol.3 No.9B(2013), Article ID:41121,7 pages DOI:10.4236/apm.2013.39A2001
Riesz Means of Dirichlet Eigenvalues for the Sub-Laplace Operator on the Engel Group
Department of Applied Mathematics, Northwestern Polytechnical University, Xi’an, China
Email: xuejingjingsx@163.com
Copyright © 2013 Jingjing Xue. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 27, 2013; revised October 27, 2013; accepted November 5, 2013
Keywords: Engel Group; Sub-Laplace Operator; Eigenvalues; Riesz Mean
ABSTRACT
In this paper, we are concerned with the Riesz means of Dirichlet eigenvalues for the sub-Laplace operator on the Engel group and deriver different inequalities for Riesz means. The Weyl-type estimates for means of eigenvalues are given.
1. Introduction
The Engel group  is a Carnot group of step
is a Carnot group of step 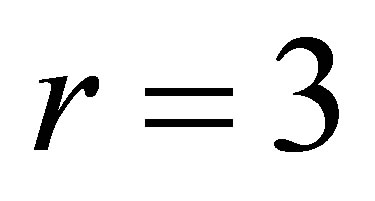 (see [1]), its Lie algebra is generated by the left-invariant vector fields
(see [1]), its Lie algebra is generated by the left-invariant vector fields
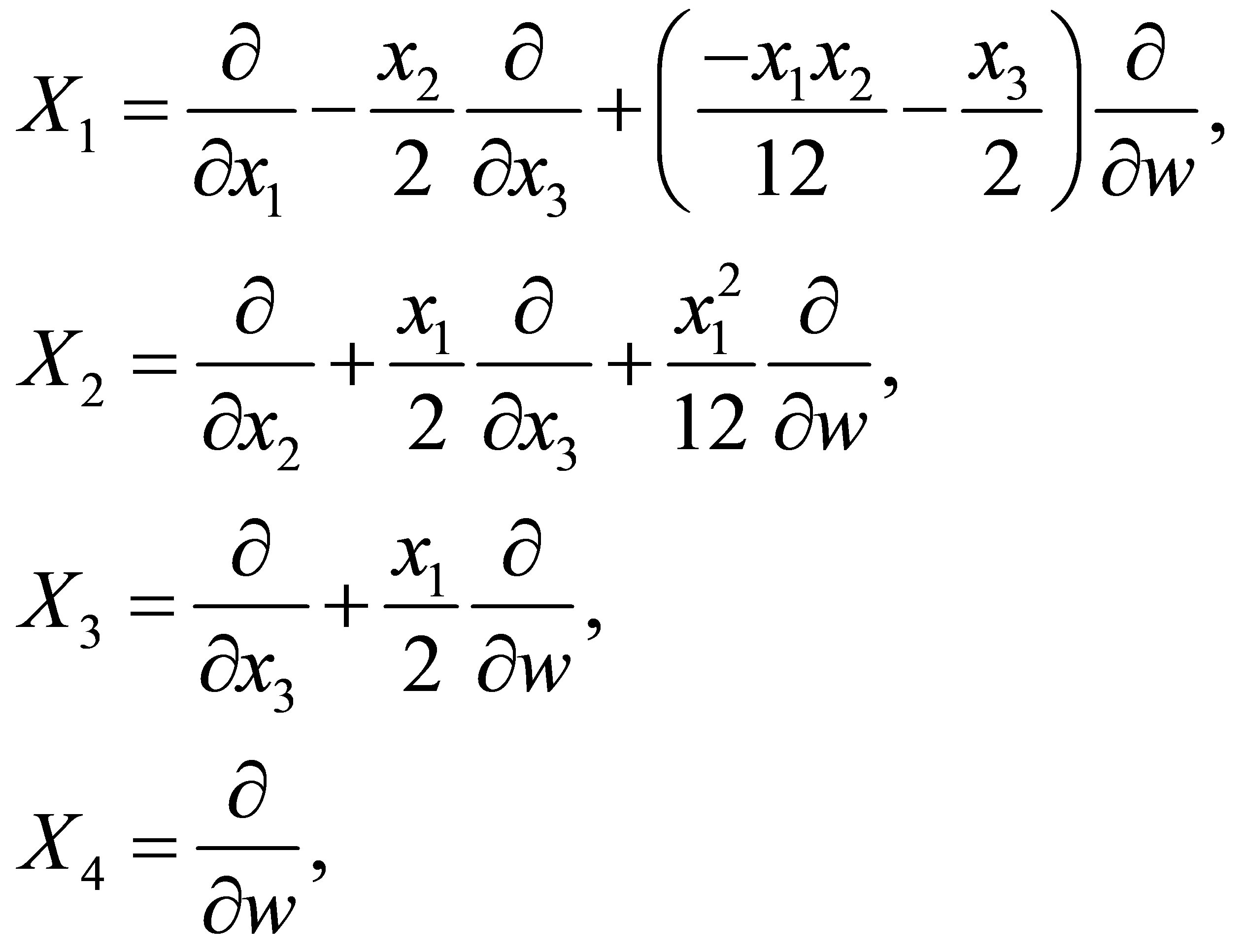
where 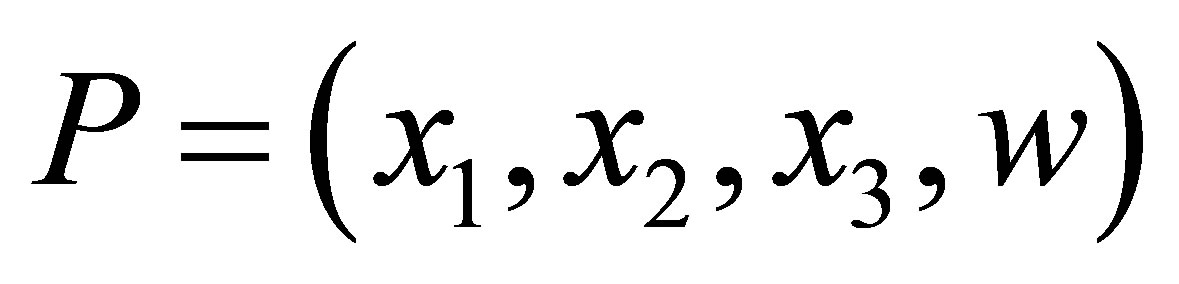 is a point of
is a point of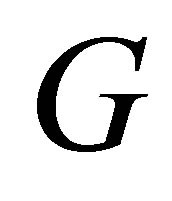 . It is easy to see that
. It is easy to see that
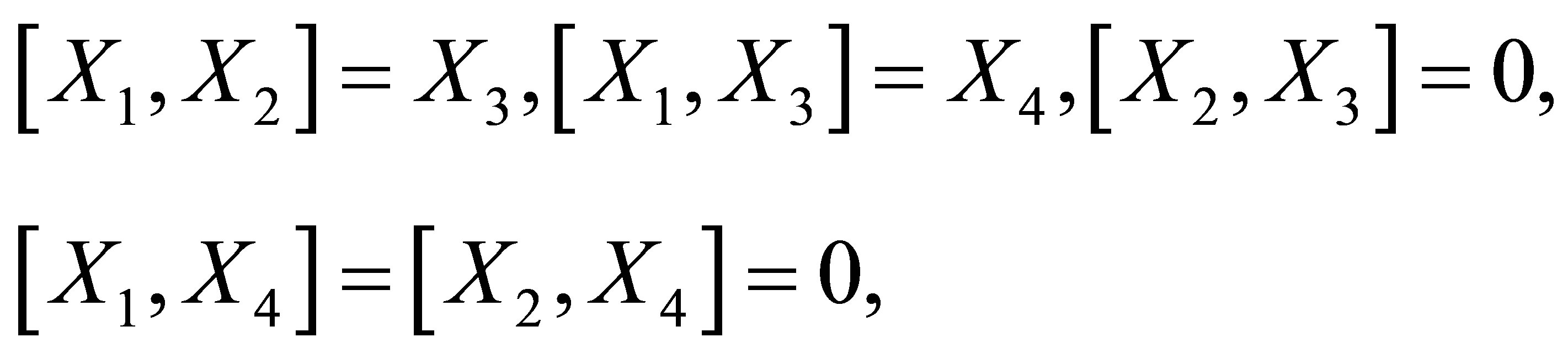
and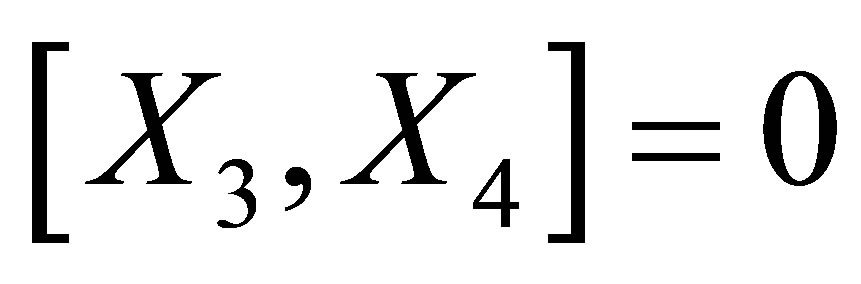 . So the Lie algebra of
. So the Lie algebra of 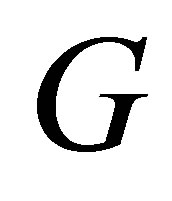 is
is
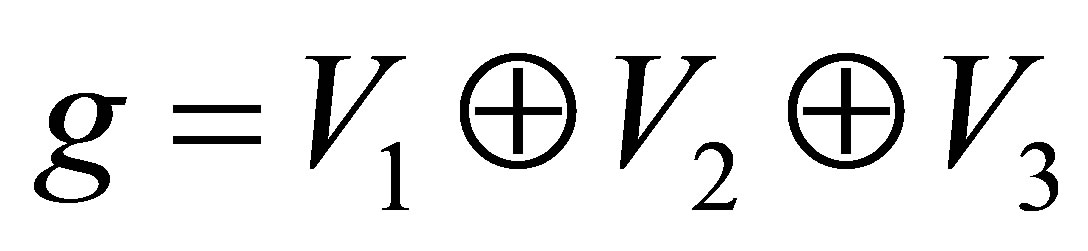 where
where 
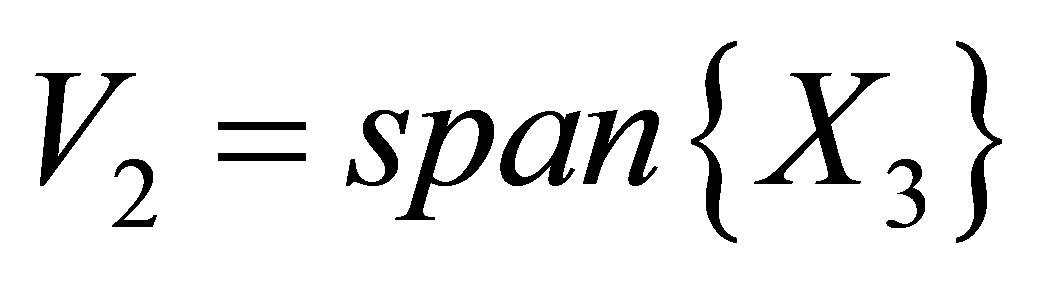 and
and
 . The sub-Laplace operator on
. The sub-Laplace operator on  is of the form
is of the form .
.
In the paper, we investigate the Riesz means of the Dirichlet problem
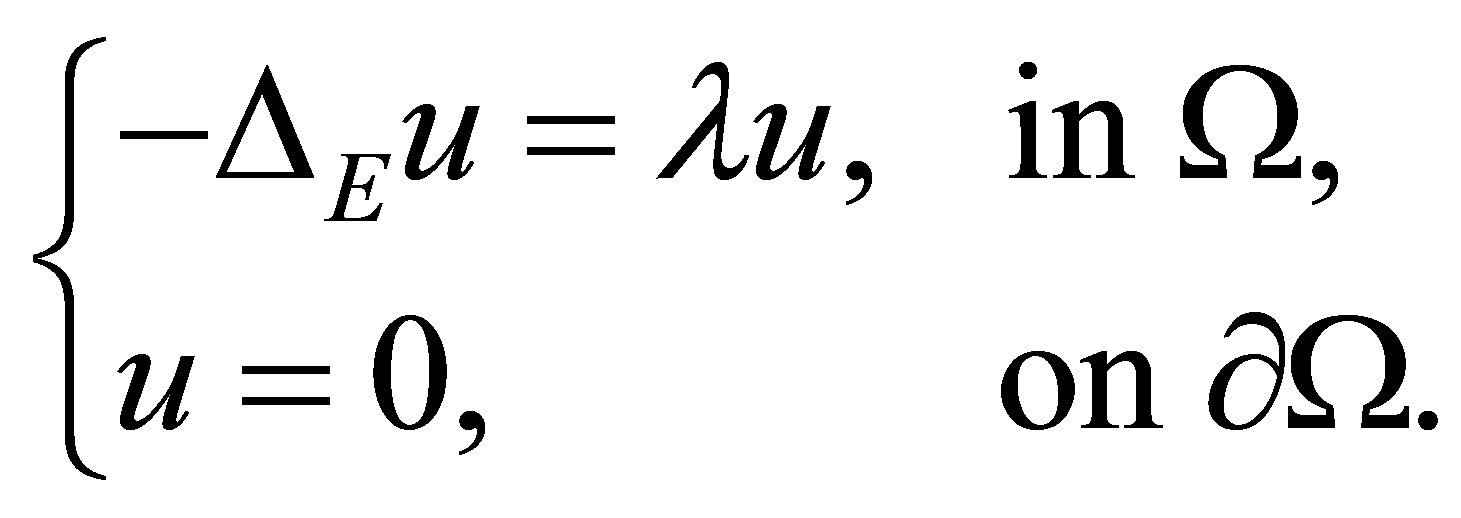 (1.1)
(1.1)
in the Engel group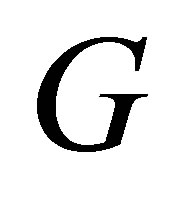 . Here
. Here  is a bounded and noncharacteristics domain in
is a bounded and noncharacteristics domain in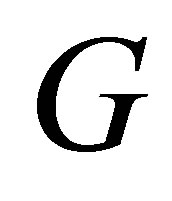 , with smooth boundary
, with smooth boundary . The existence of eigenvalues for (1.1) is from [2]. Let us by
. The existence of eigenvalues for (1.1) is from [2]. Let us by 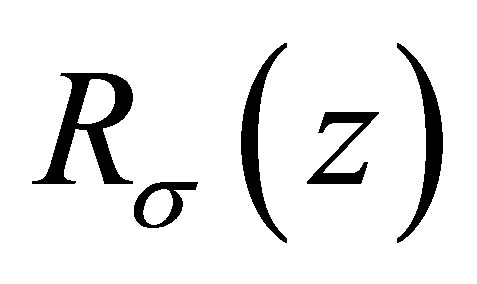 denote the Riesz means of order
denote the Riesz means of order  of the sequence
of the sequence 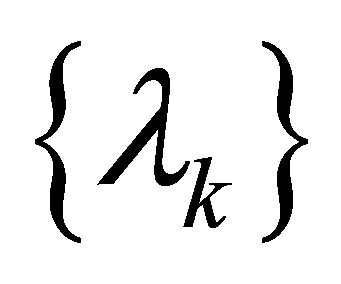 of eigenvalues of (1.1).
of eigenvalues of (1.1).
The Riesz means of Dirichlet eigenvalues for the Laplace operator in the Euclidean space have been extensively studied(see [3-5]). In recent years, E. M. Harrell II and L. Hermi in [6] treated the Riesz means 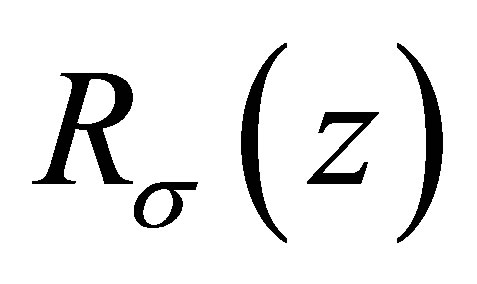 of order
of order  of
of 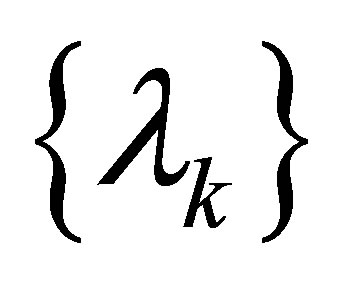 on the bounded domain
on the bounded domain  and pointed out that: for
and pointed out that: for 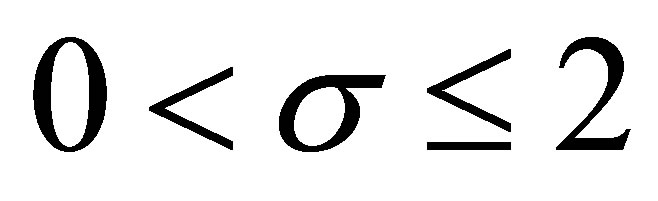 and
and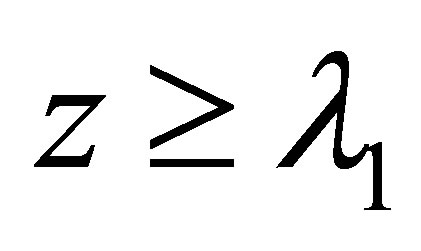 ,
,
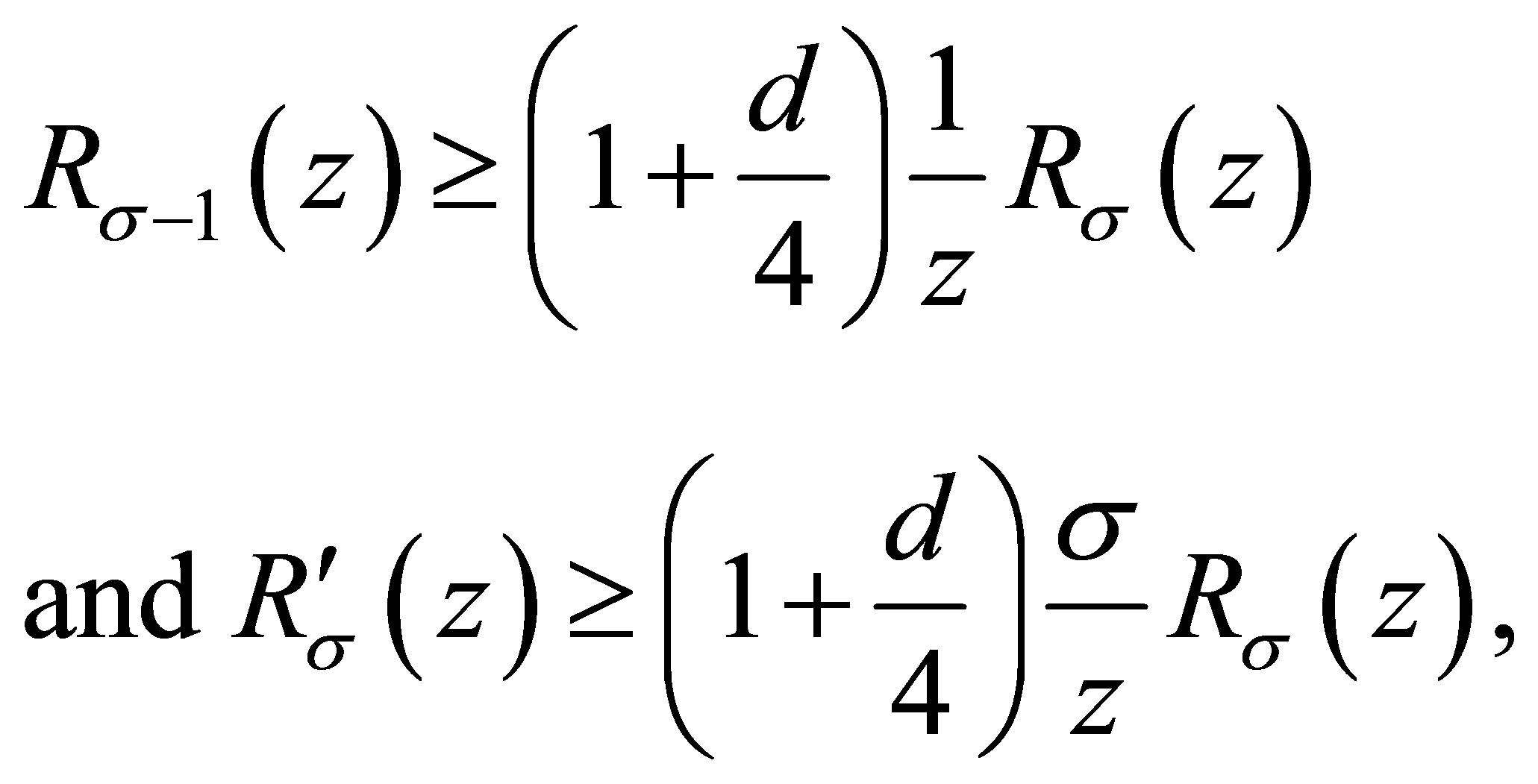 (1.2)
(1.2)
and 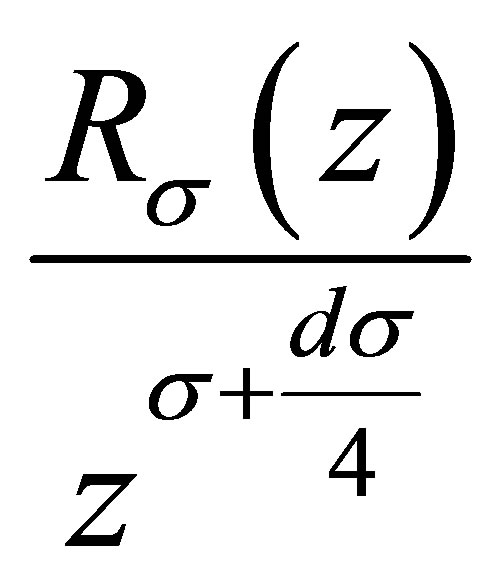 is a nondecreasing function of
is a nondecreasing function of ; for
; for
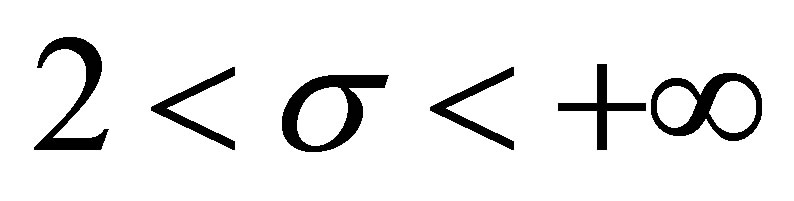 and
and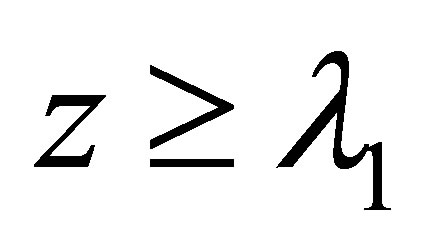 ,
,
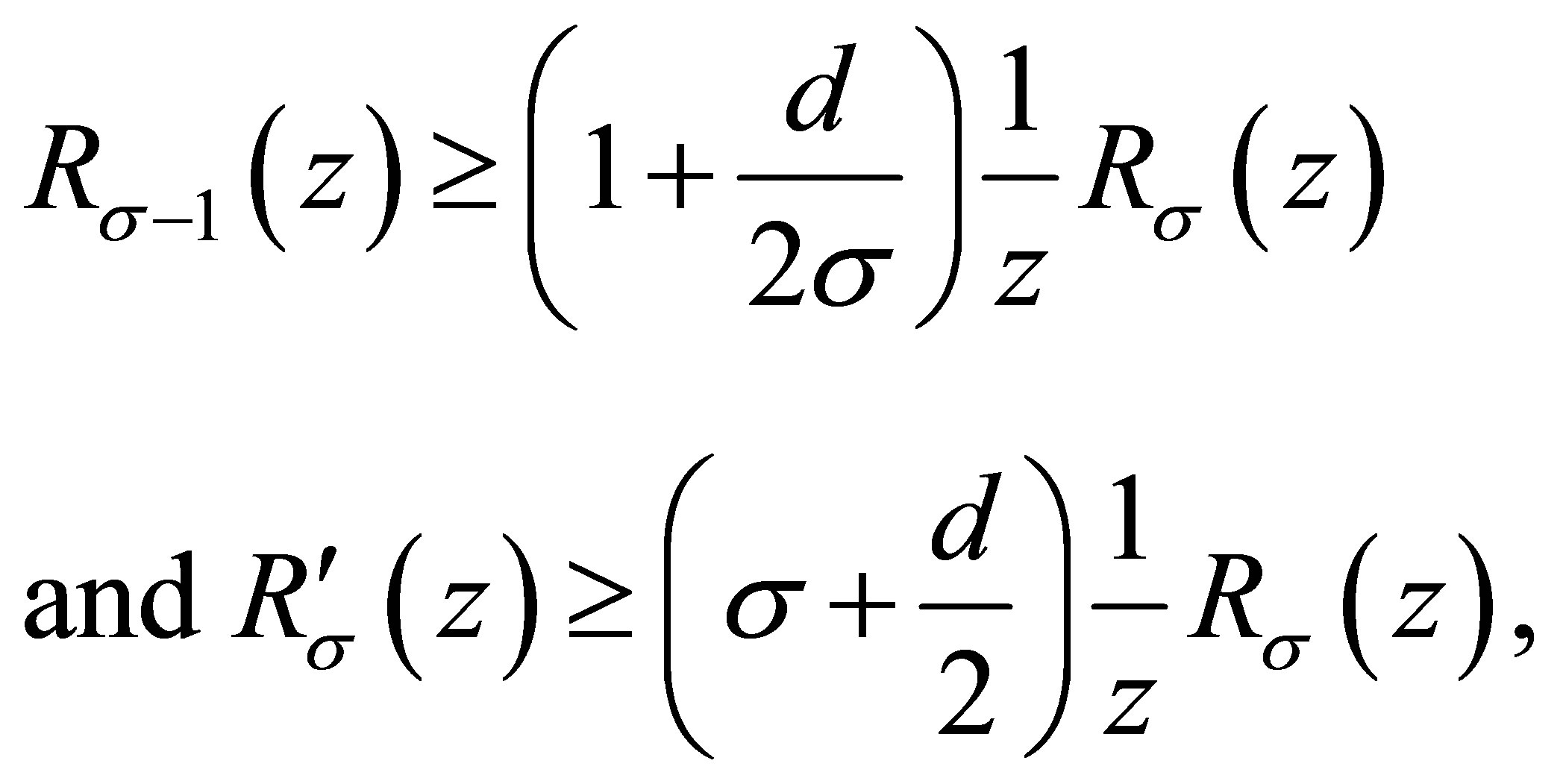 (1.3)
(1.3)
and 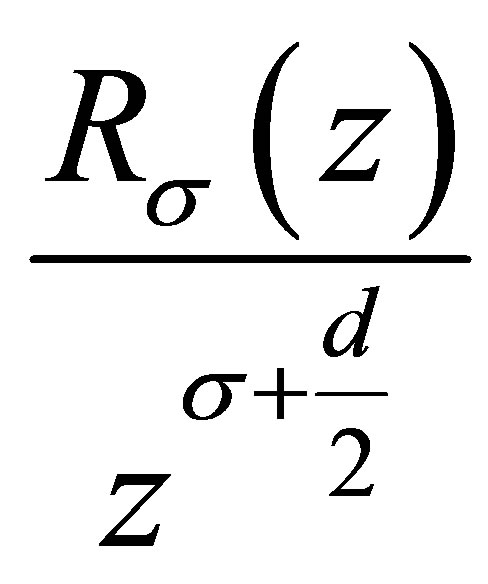 is a nondecreasing function of z, and then the Weyl-type estimates of means of eigenvalues is derived.
is a nondecreasing function of z, and then the Weyl-type estimates of means of eigenvalues is derived.
Jia et al. in [7] extended (1.2), (1.3) to the Heisenberg group.
The main results of this paper are the following.
Theorem 1.1 For 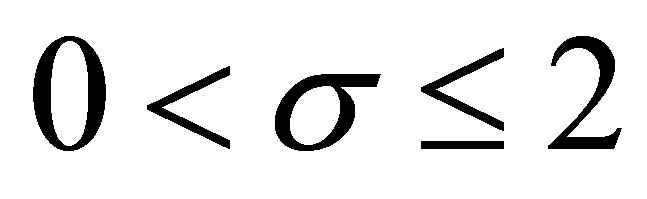 and
and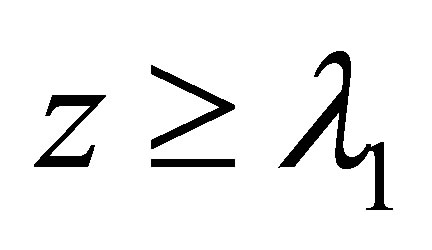 , we have
, we have
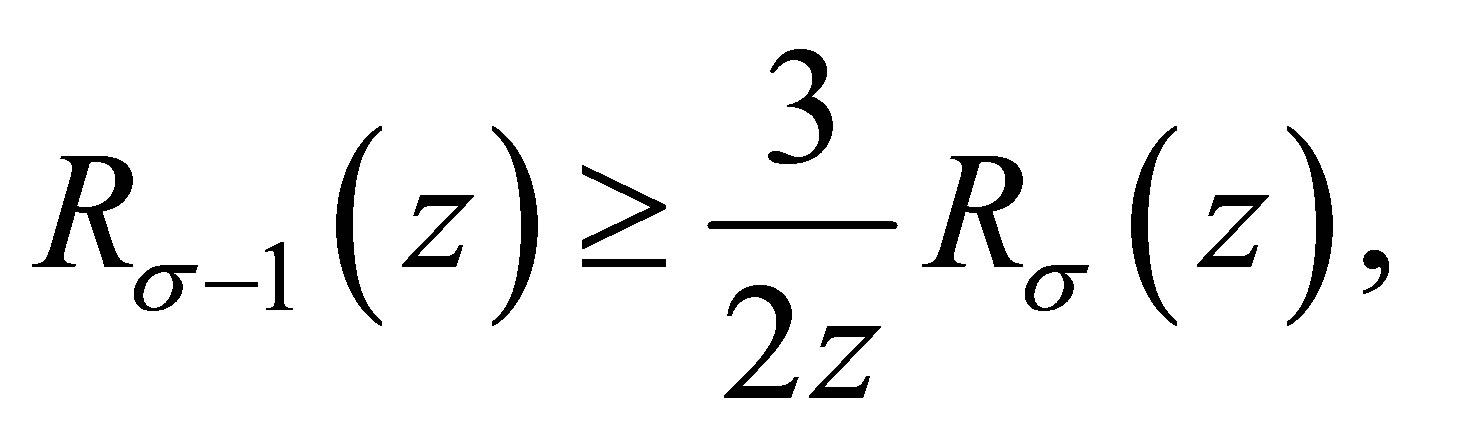 (1.4)
(1.4)
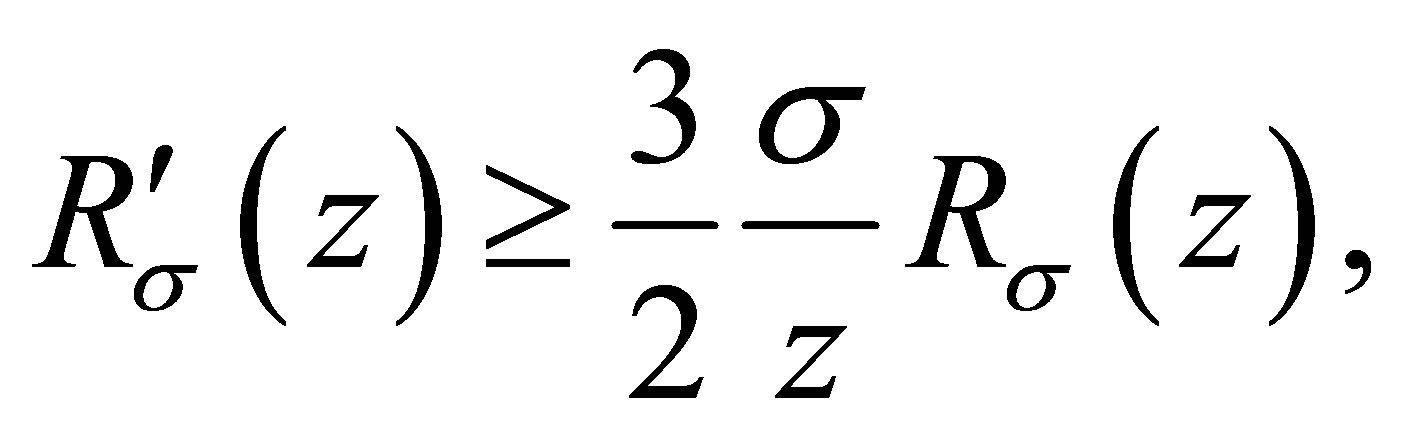 (1.5)
(1.5)
and 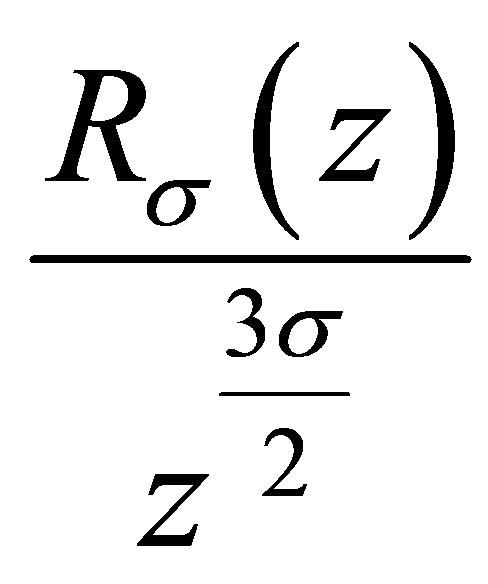 is a nondecreasing function of z; for
is a nondecreasing function of z; for
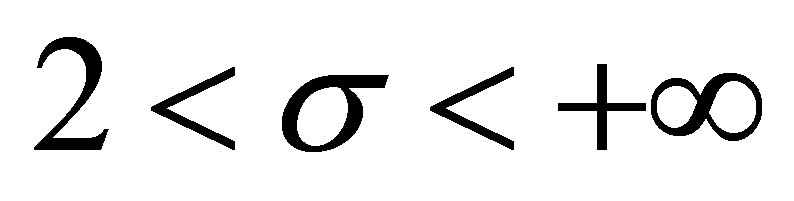 and
and , we have
, we have
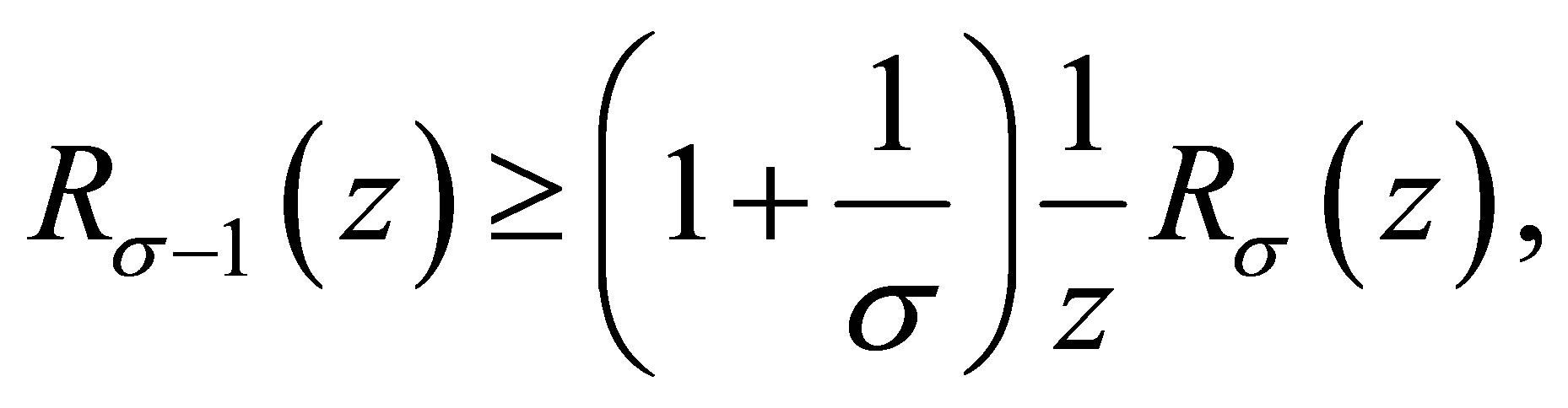 (1.6)
(1.6)
 (1.7)
(1.7)
and 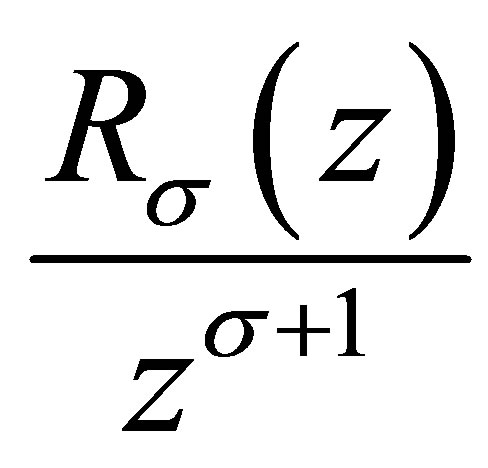 is a nondecreasing function of z.
is a nondecreasing function of z.
Theorem 1.2 Suppose that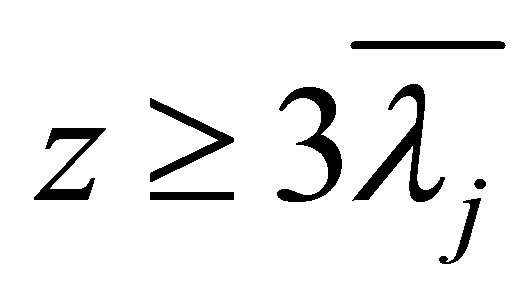 , then
, then
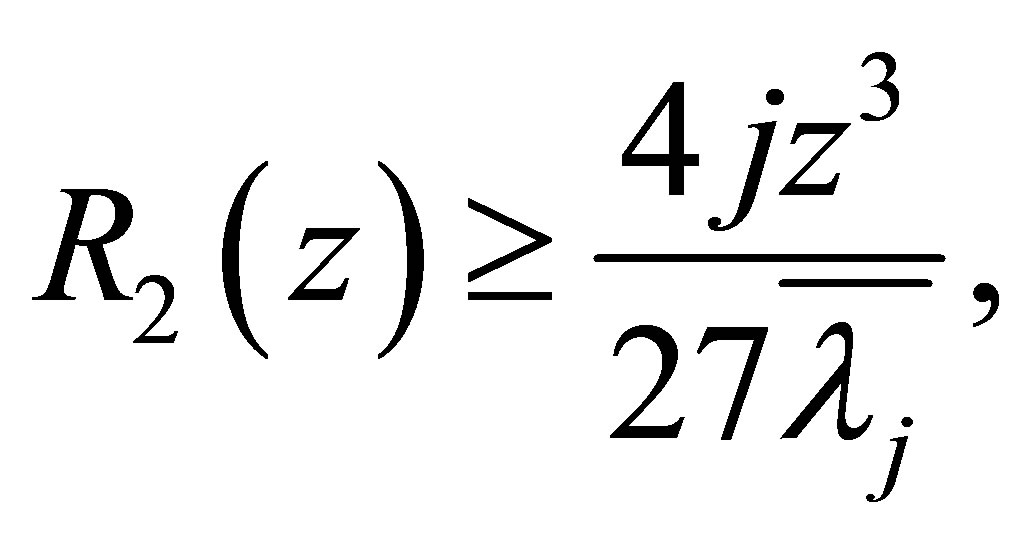 (1.8)
(1.8)
and therefore
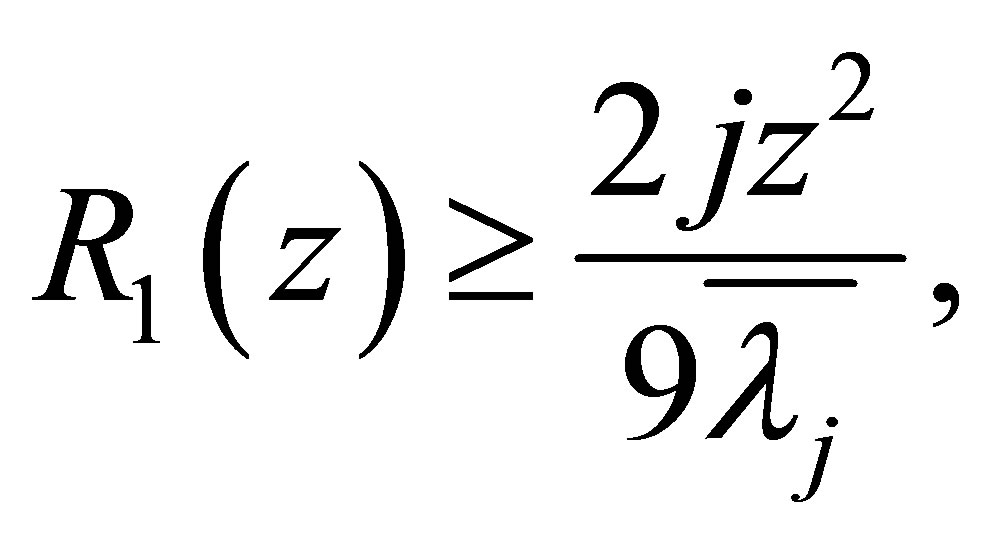 (1.9)
(1.9)
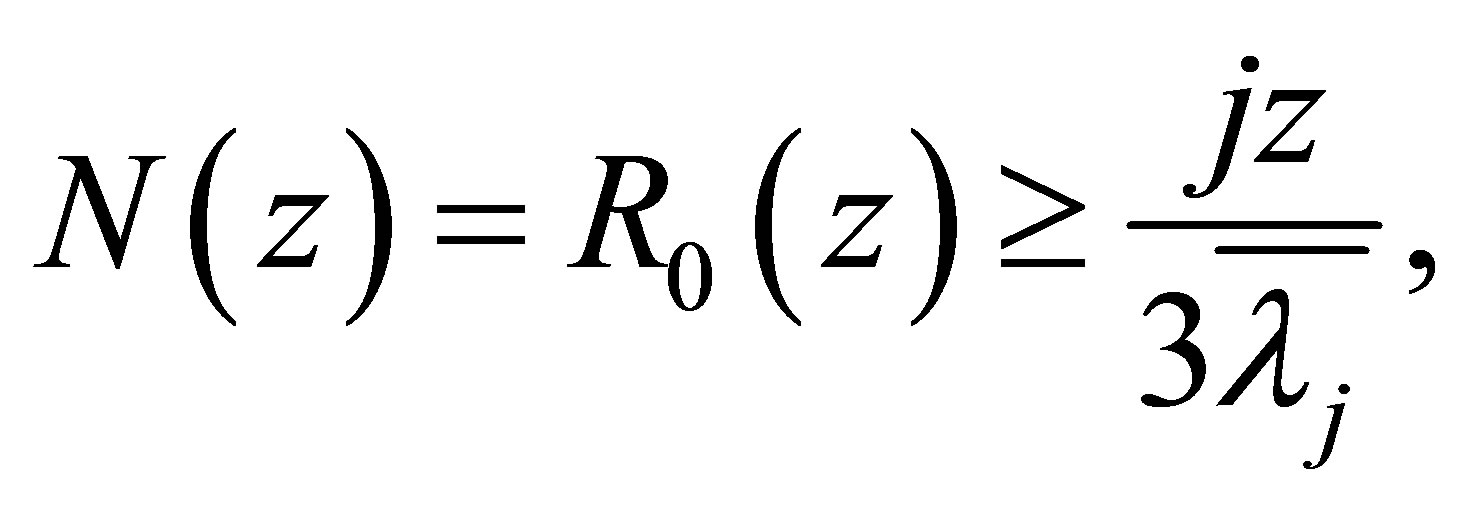 (1.10)
(1.10)
Moreover, for all , we have the upper bound
, we have the upper bound
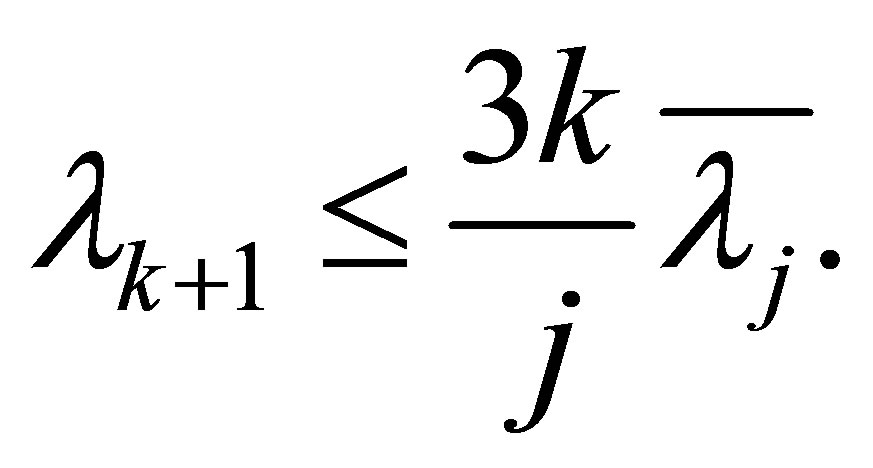 (1.11)
(1.11)
Theorem 1.3 For , we have
, we have
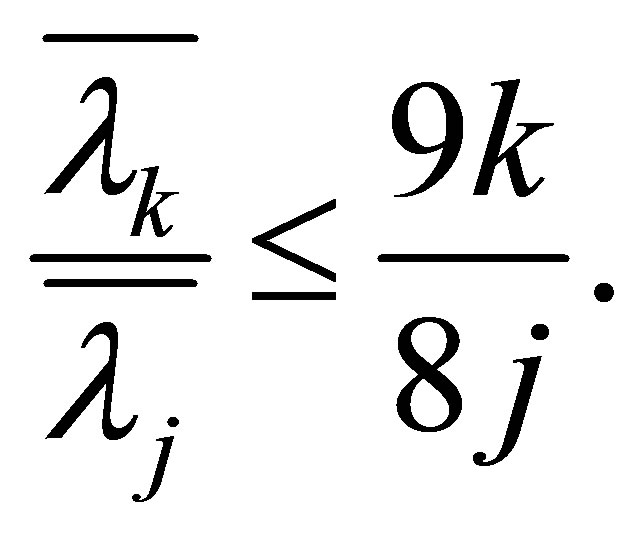 (1.12)
(1.12)
Authors in [6] combined the Weyl-type estimates of means of eigenvalues established in [6] and the result in [8] to obtain the Weyl-type estimates of eigenvalues. But it is not easy to extend the result in [8] to the Engel group. The Weyl-type estimates of eigenvalues for (1.1) still are open questions.
This paper is arranged as follows. In Section 2 the definition of Riesz means and Lemmas are described; Section 3 is devoted to the proof of Theorem 1.1. The proof of Theorem 1.2 is appeared in Section 4. In Section 5 the proof of Theorem 1.3 is given.
2. Preliminaries
Definition 2.1 For an increasing sequence 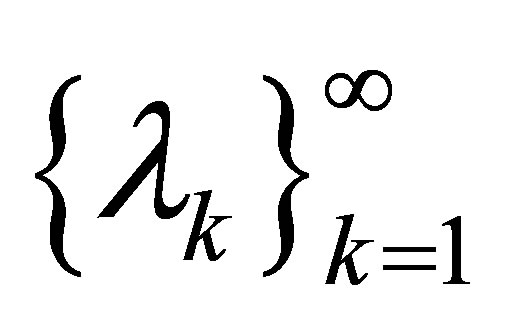 of real numbers and
of real numbers and , the Riesz means
, the Riesz means 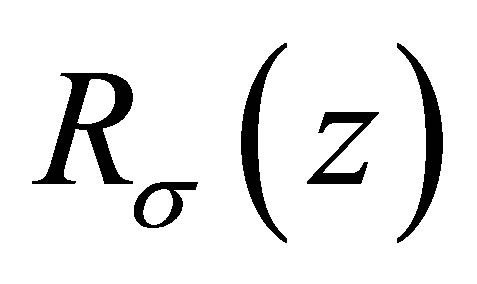 of order
of order 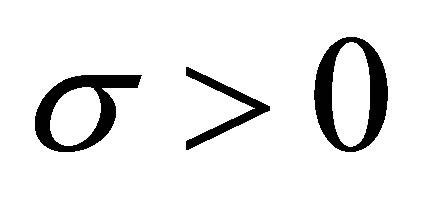 of
of 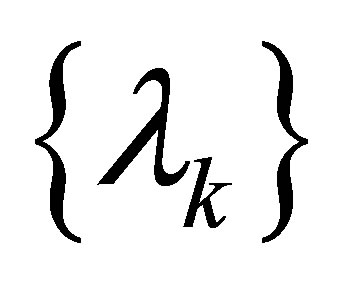 is defined by
is defined by
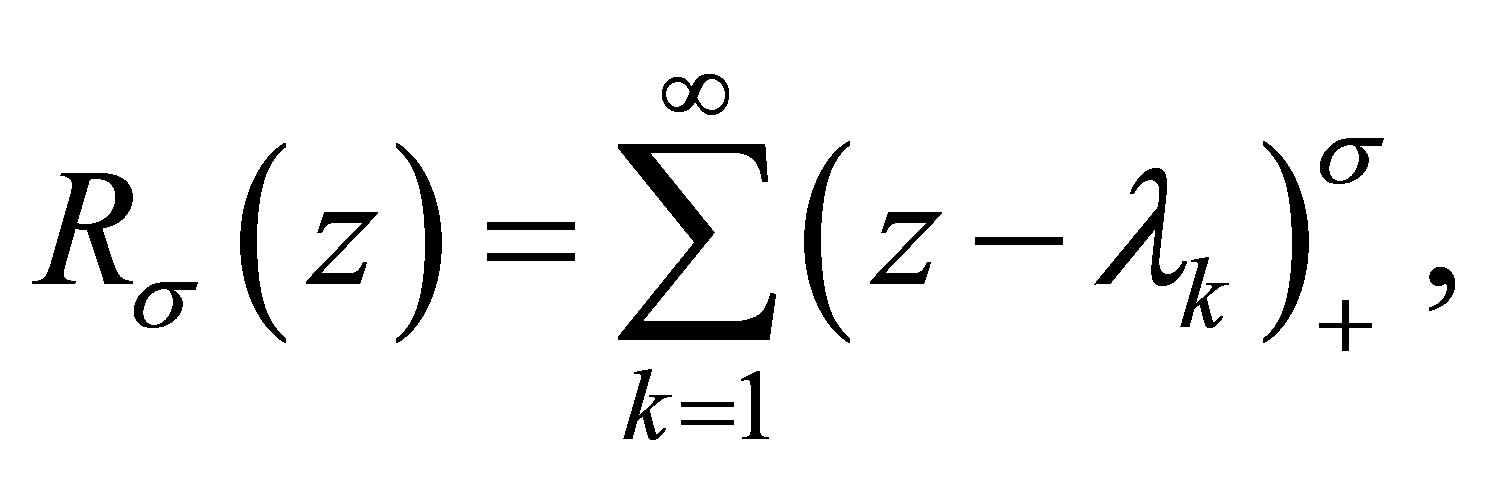
where 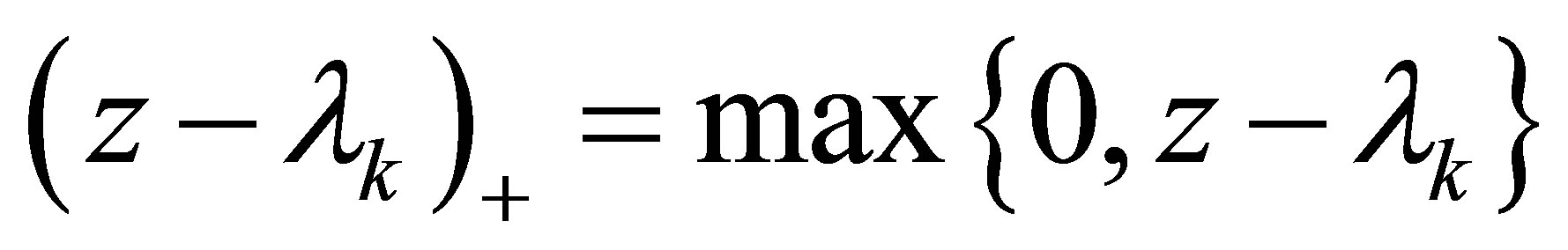 is the ramp function.
is the ramp function.
Clearly,
 (2.1)
(2.1)
Similarly to Theorem 1 of [9], we immediately have
Lemma 2.2 Denoting the  -normalized eigenfunctions of (1.1) by
-normalized eigenfunctions of (1.1) by , let
, let

for 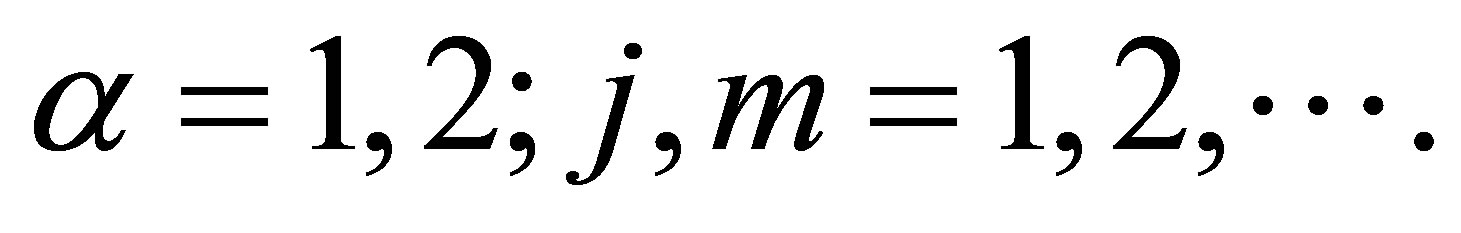 Then for each fixed
Then for each fixed , we have
, we have
 (2.2)
(2.2)
Lemma 2.3 ([10]) Let 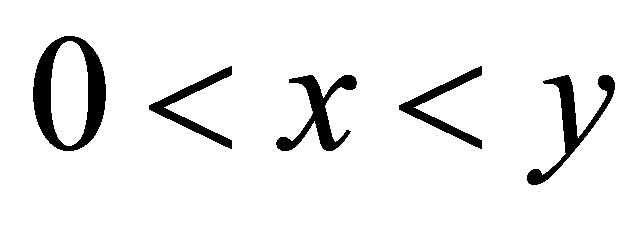 and
and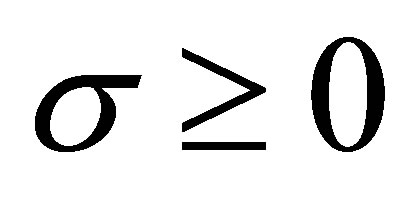 , then
, then
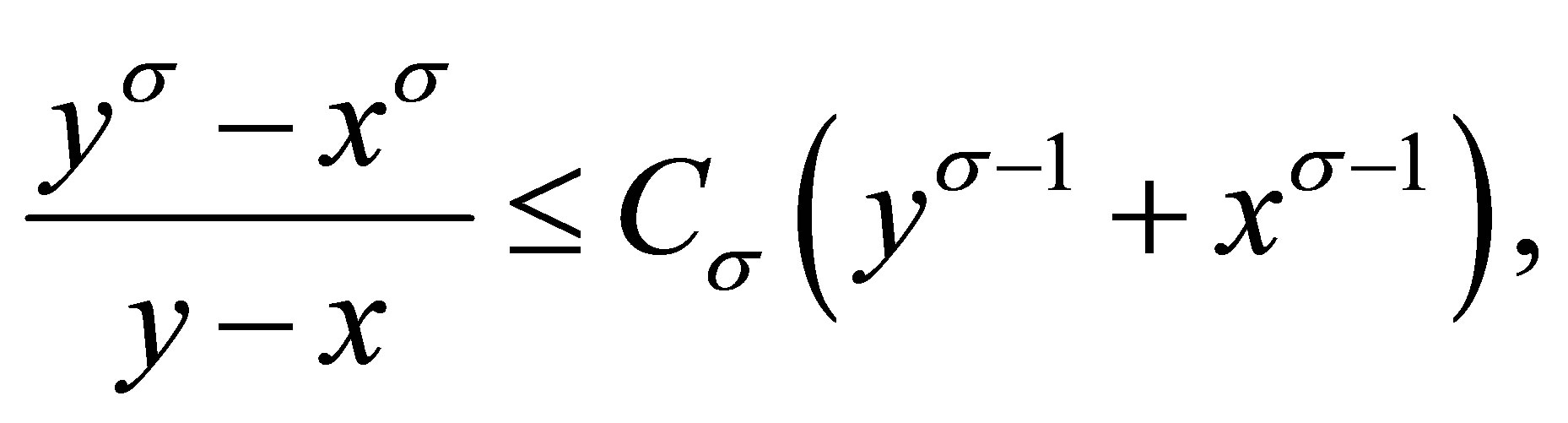
where
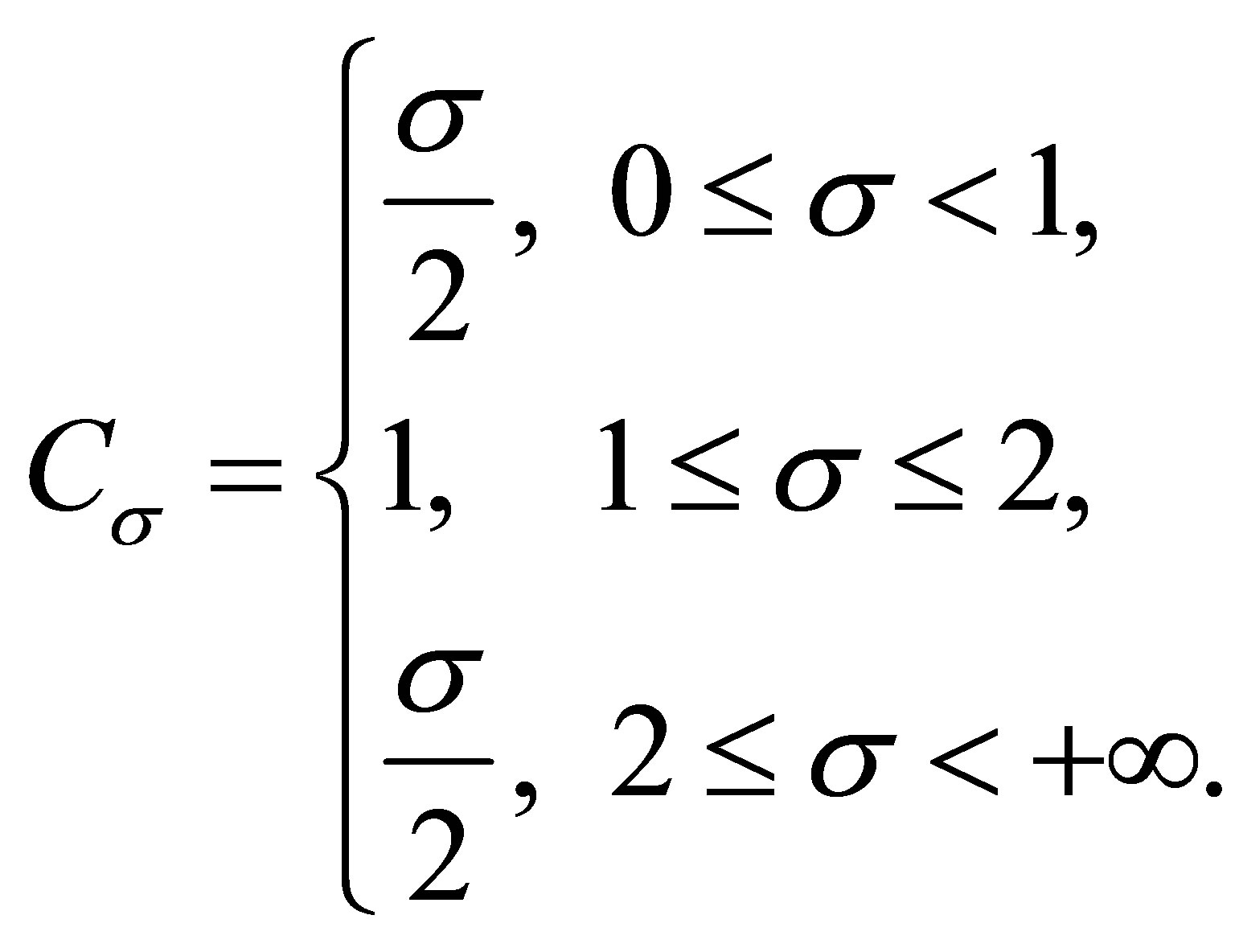
3. The Proof of Theorem 1.1
In this section, we prove Theorem 1.1 and two corollaries.
Proof. Let us use (2.2) and denote the first term on the right-hand side of (2.2) by . Applying Lemma 2.3 it follows
. Applying Lemma 2.3 it follows

here we used the symmetry on  and
and  in the last step.
in the last step.
Putting the above estimate into (2.2), we have
 (3.1)
(3.1)
where we denote
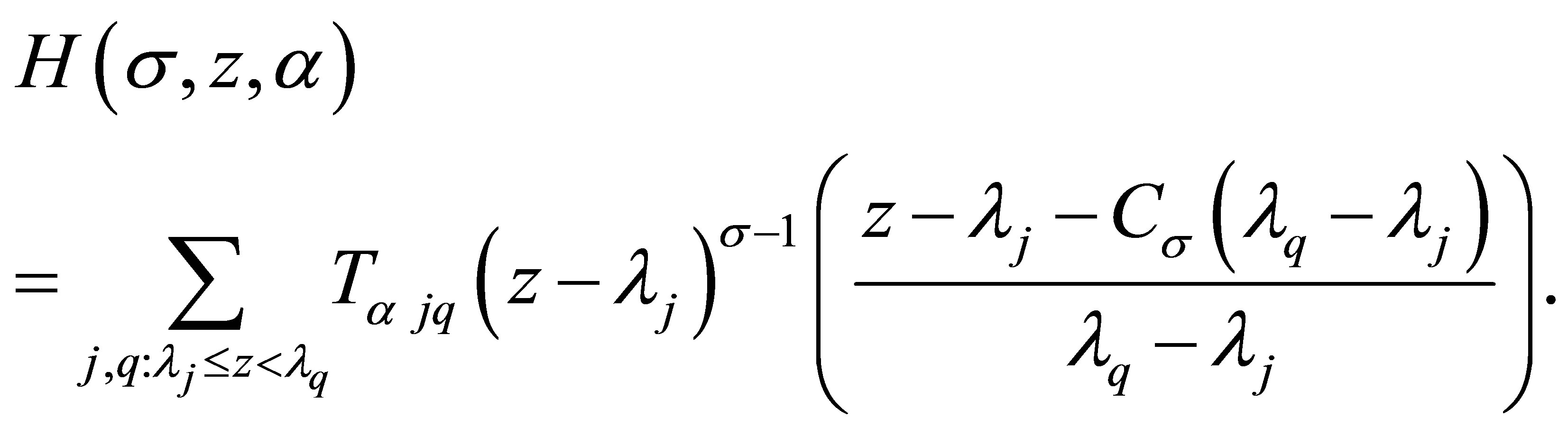 (3.2)
(3.2)
Since  is a complete orthonormal set, it follows
is a complete orthonormal set, it follows
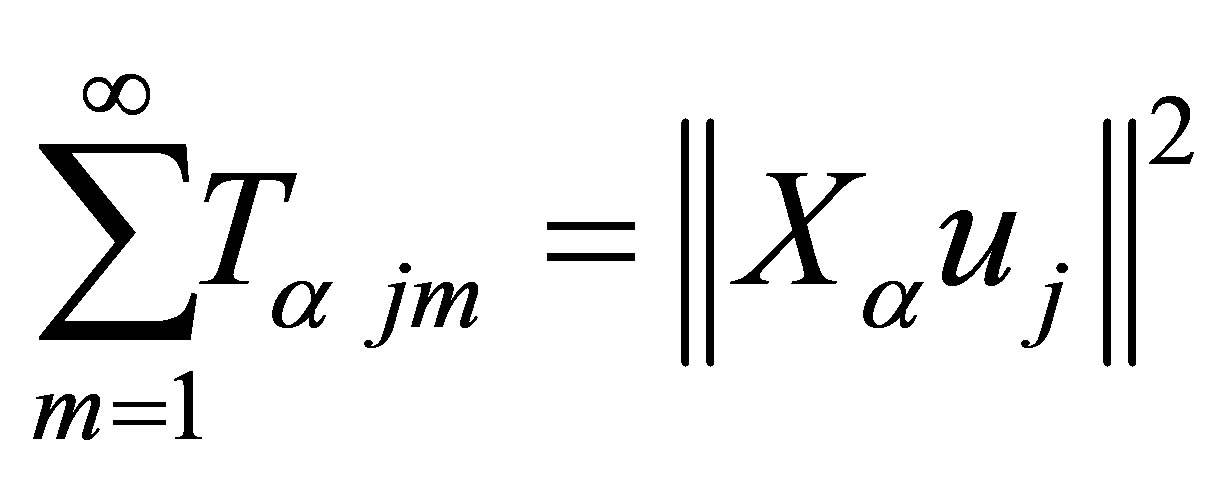
and

Returning to (3.1) with them, it yields
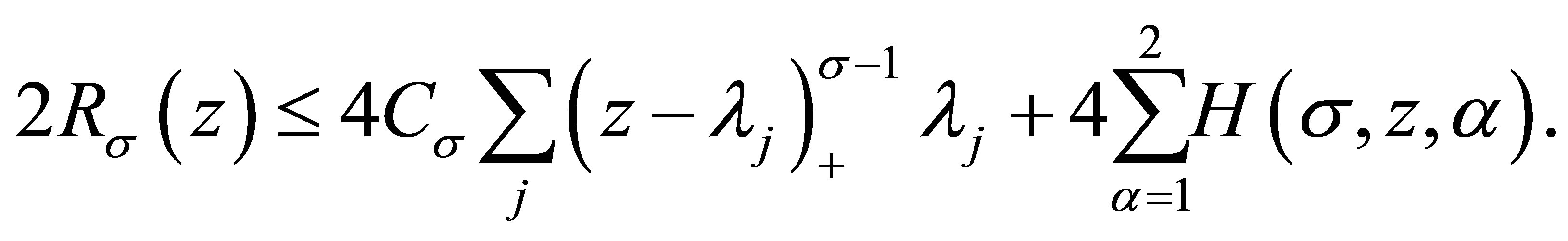 (3.3)
(3.3)
Since
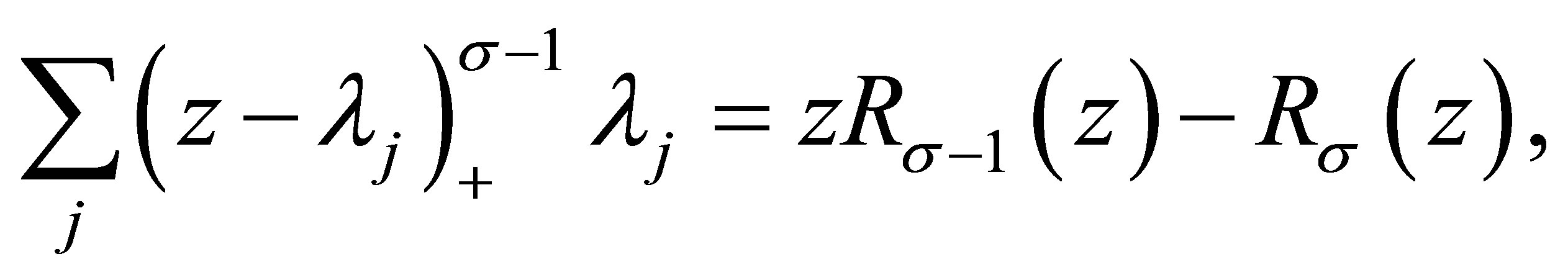
we have

namely,
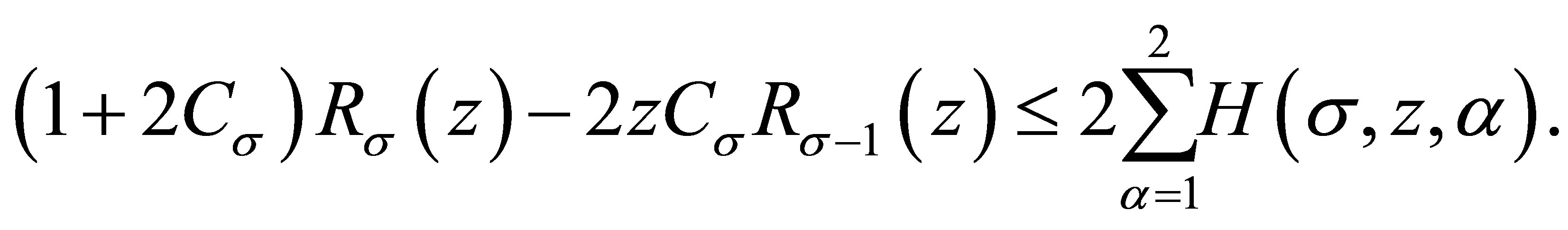 (3.4)
(3.4)
We consider three cases: 1) ; 2)
; 2)  and 3)
and 3)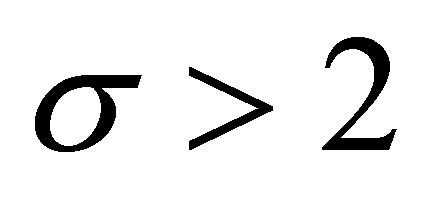 .
.
1)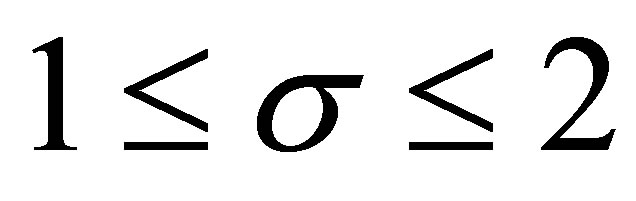 . In this case, it sees
. In this case, it sees  and
and

Since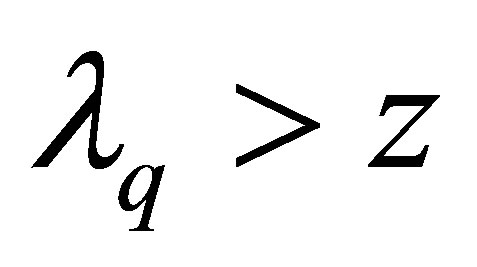 , it follows
, it follows

and therefore

Substituting this into (3.4), we obtain

and
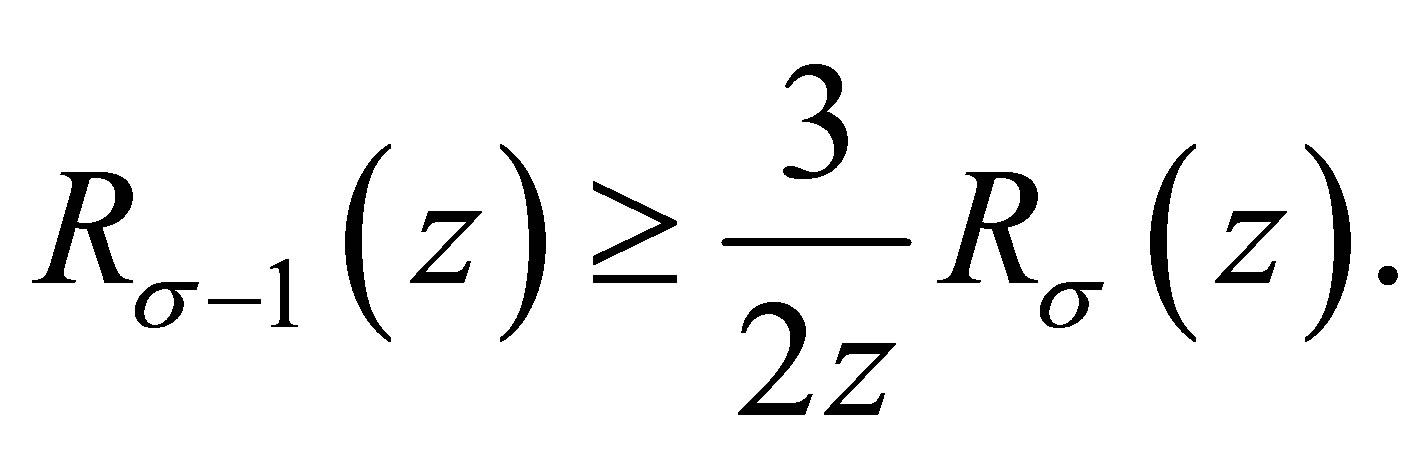
Now (1.4) is proved.
Using (2.1), we have

and (1.5) is proved.
Since
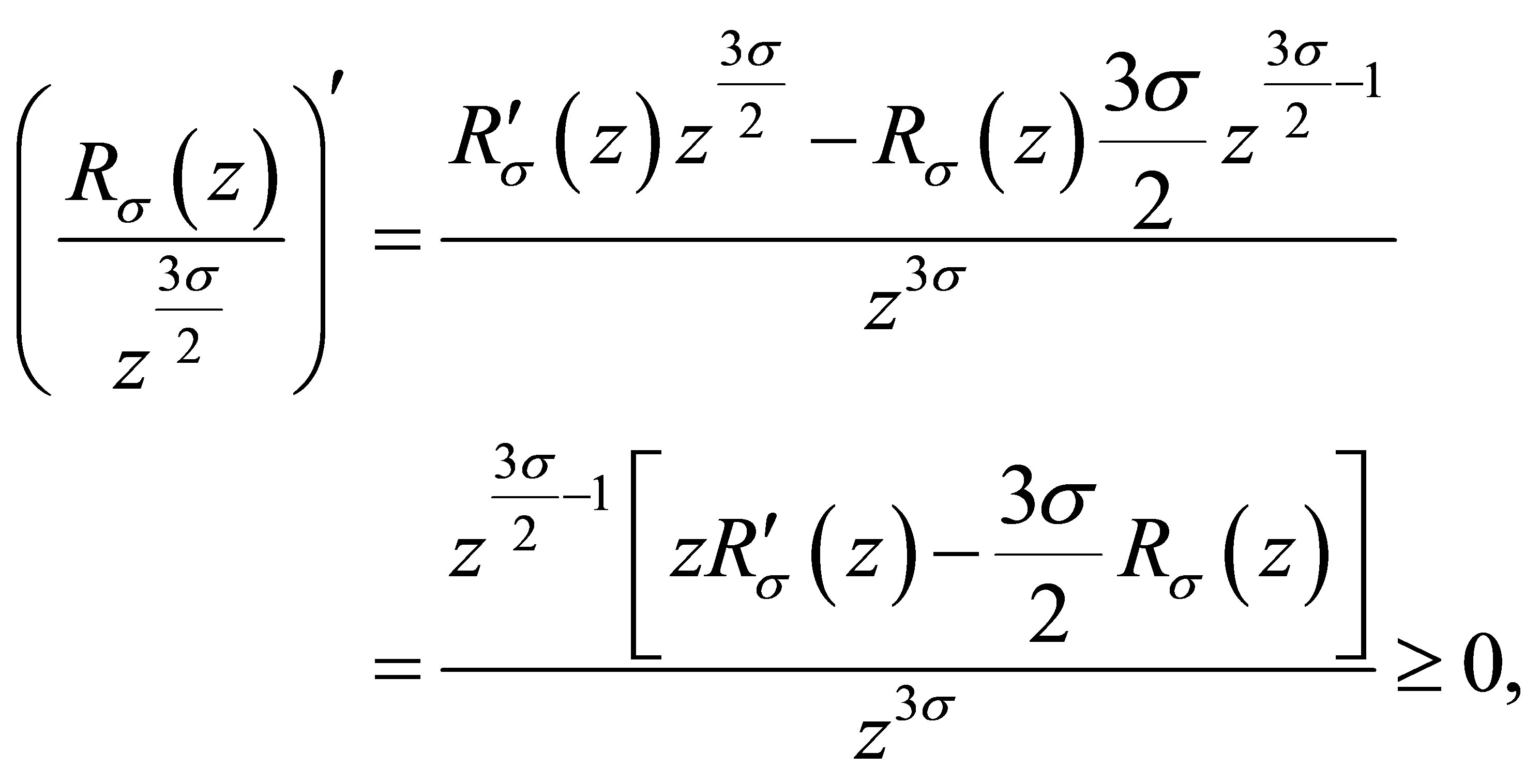
it follows that 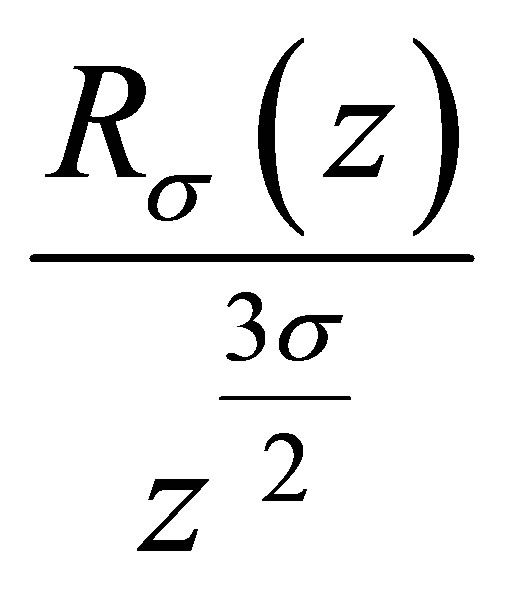 is a nondecreasing function of
is a nondecreasing function of .
.
2)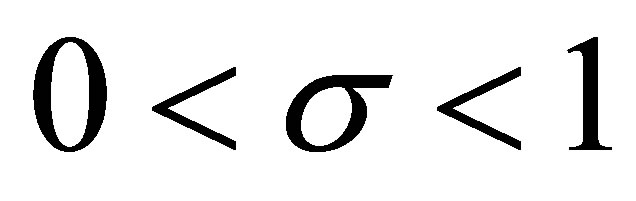 . Now
. Now , so
, so  and
and
 (3.5)
(3.5)
Then

and

Substituting this into (3.4), we obtain

namely,
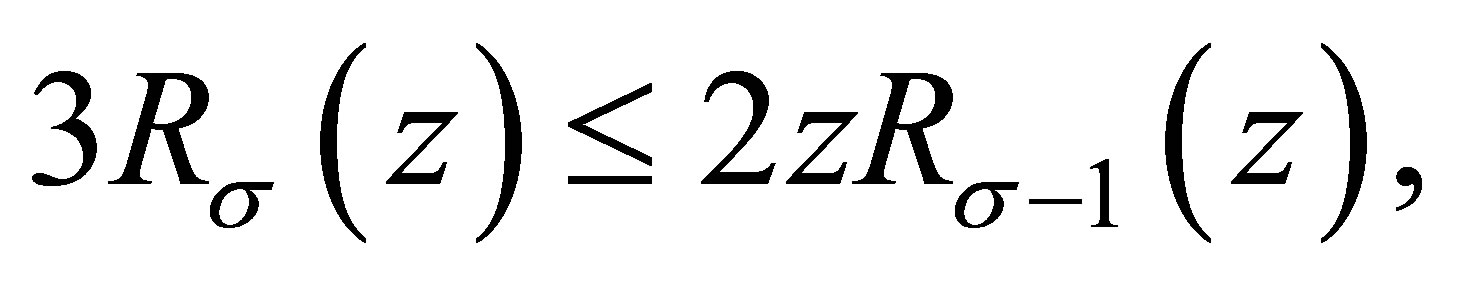
and (1.4) is proved.
The remainders are discussed similarly to 1).
3)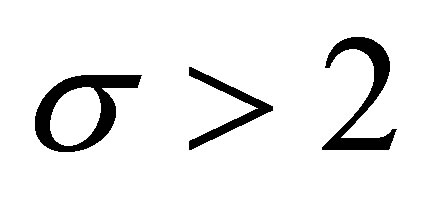 . In this case
. In this case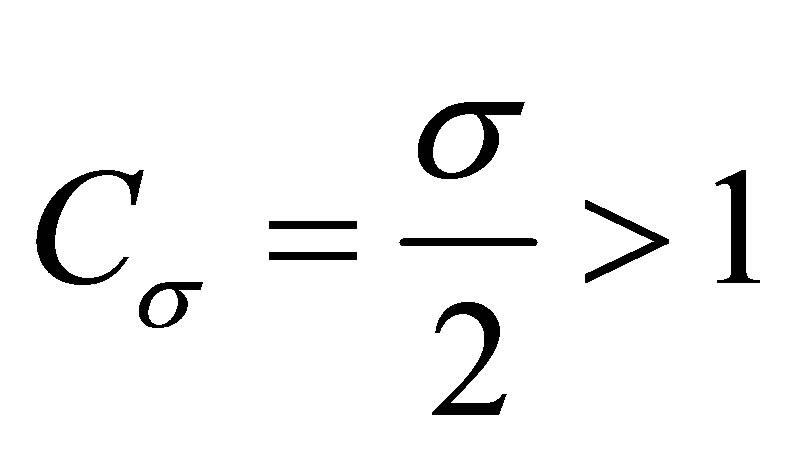 , so
, so 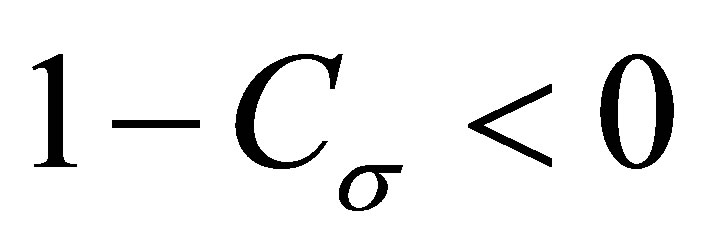 and
and
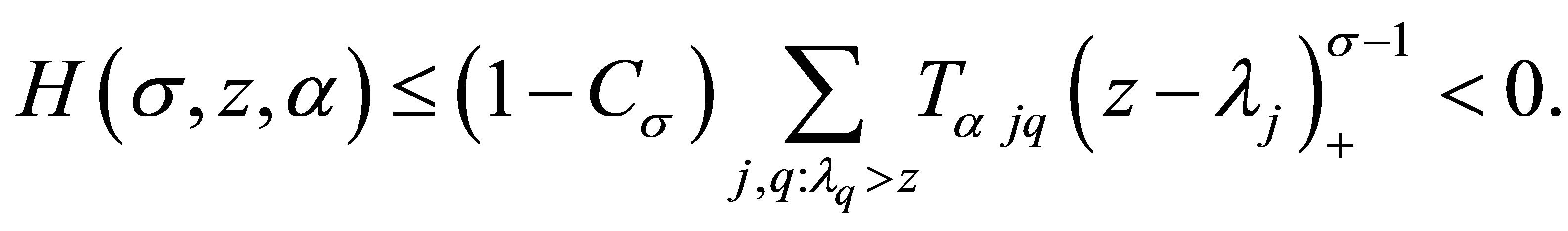
Substituting this into (3.4), we have
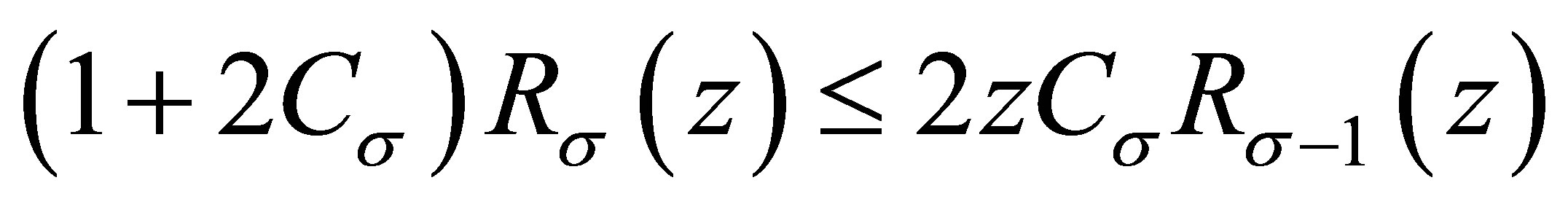
and (1.6) is proved.
Noting (2.1), it implies

and (1.7) is proved.
Similarly,

thus 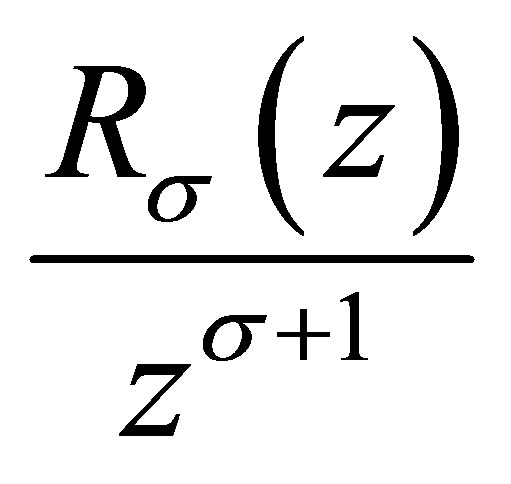 is a nondecreasing function of
is a nondecreasing function of .
.
Corollary 3.1 For all 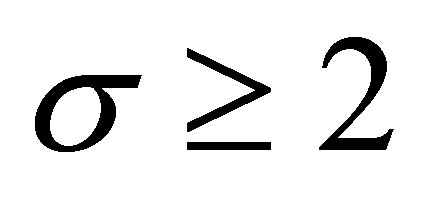 and
and ,
,
 (3.6)
(3.6)
where .
.
Proof. 1) Noting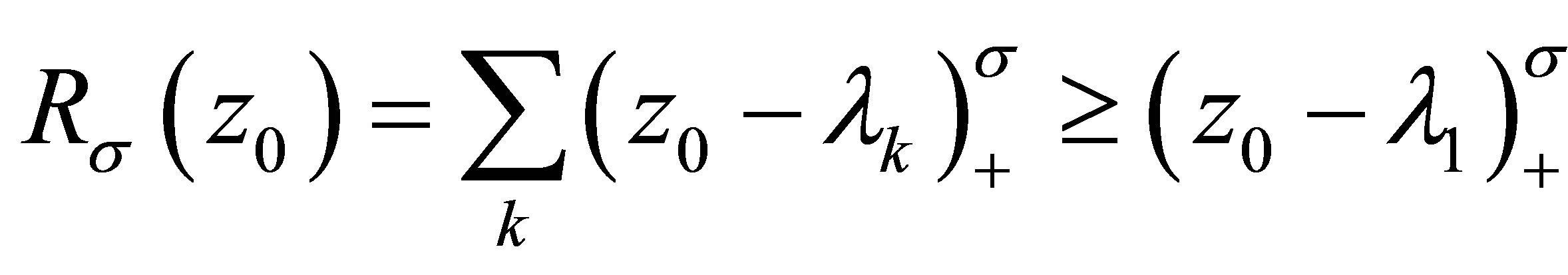 for any
for any , it follows from Theorem 1.1 that for all
, it follows from Theorem 1.1 that for all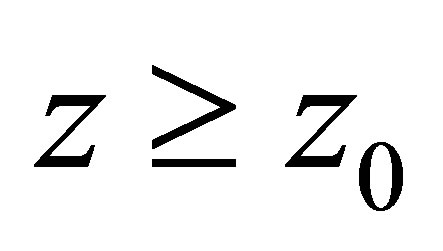 ,
,

So
 (3.7)
(3.7)
Since (3.7) holds for arbitrary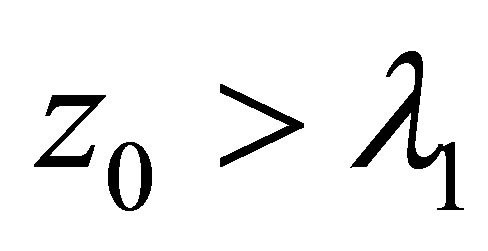 , it yields
, it yields
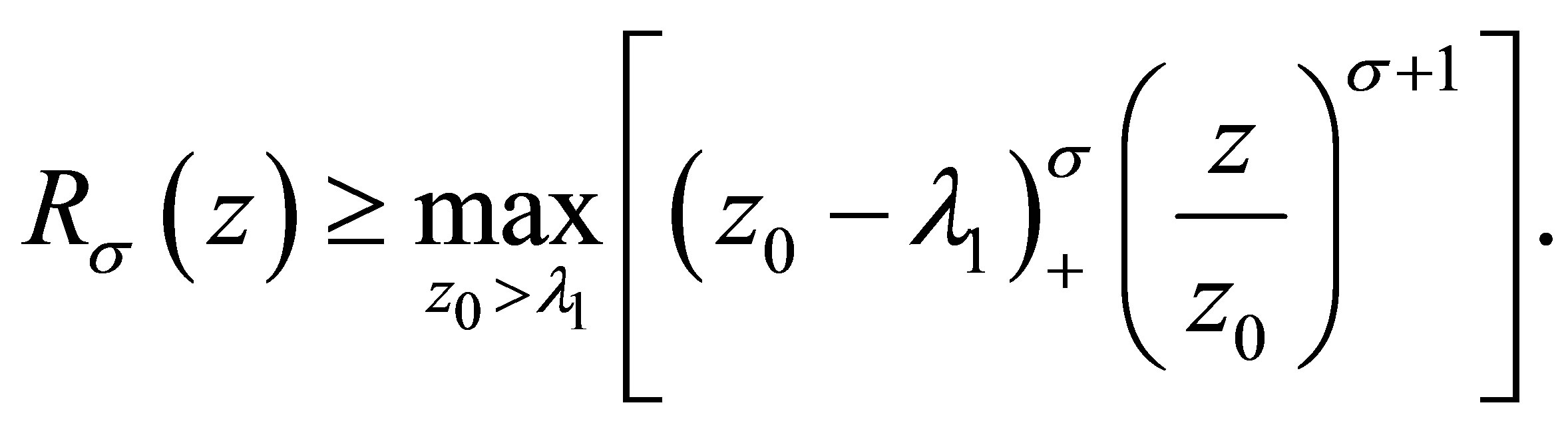
Due to
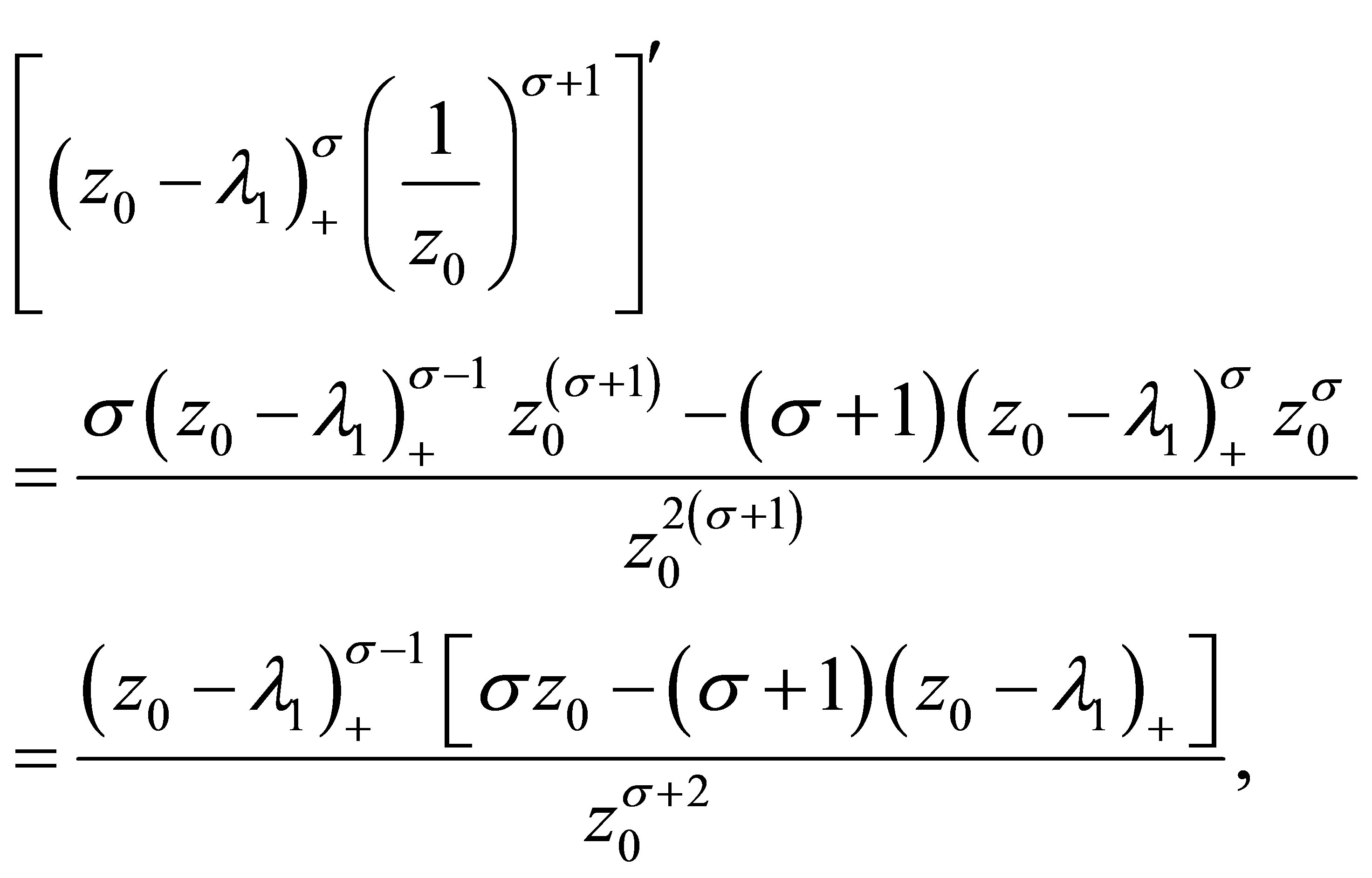
we see that when  , it gets
, it gets
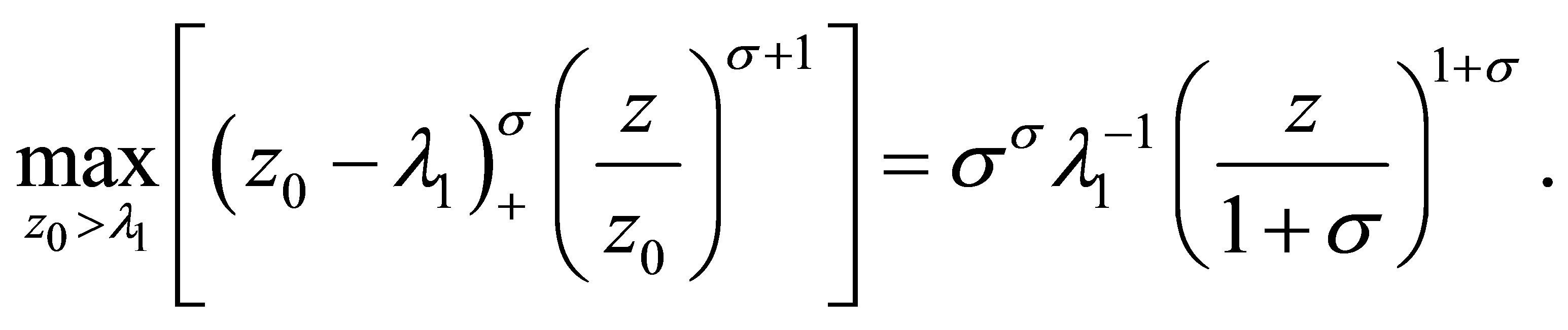
For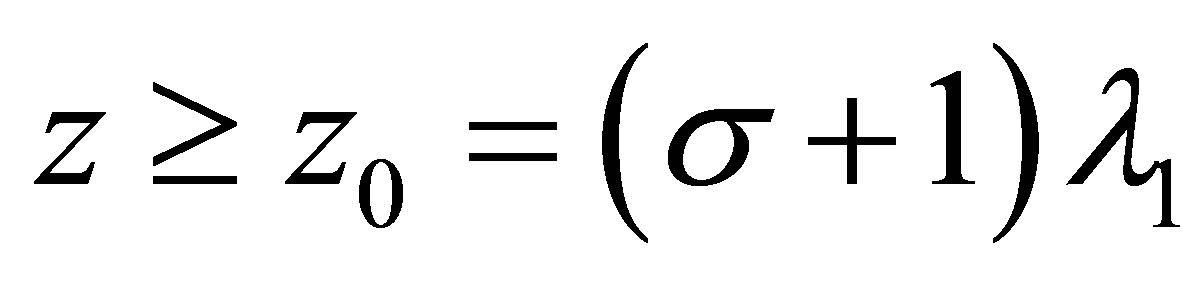 , we have
, we have
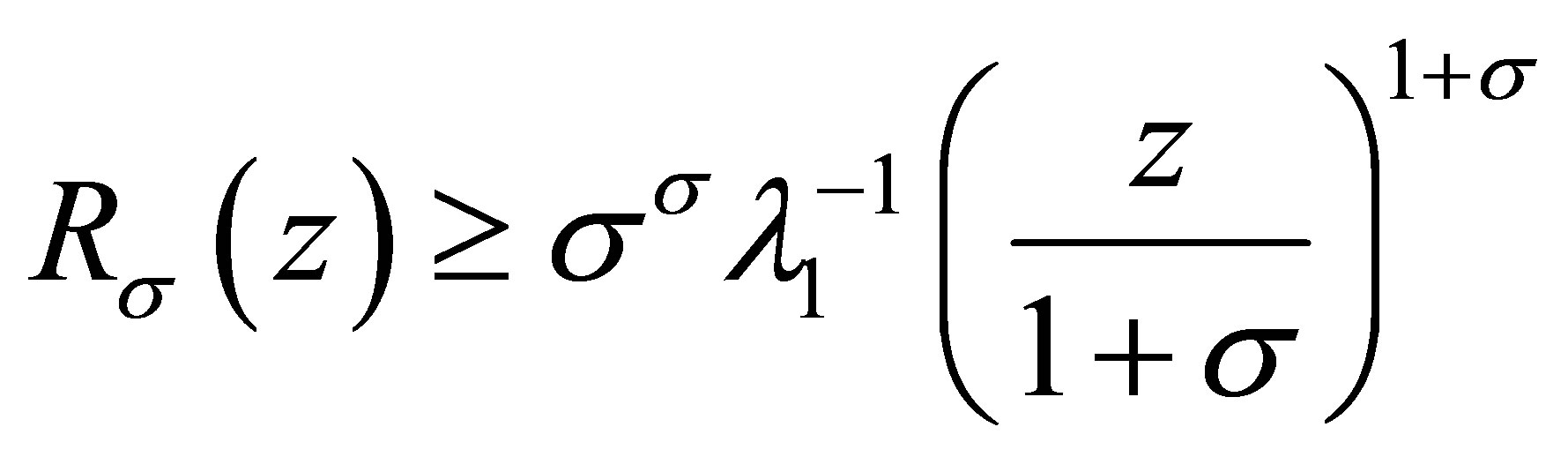
and the inequality in the left-hand side of (3.6) is valid.
2) By the Berezin-Lieb inequality (see [11]), we have

Notice that  is nondecreasing to
is nondecreasing to , it follows
, it follows

and the inequality in the right-hand side of (3.6) is proved.
Corollary 3.2 1) For  and
and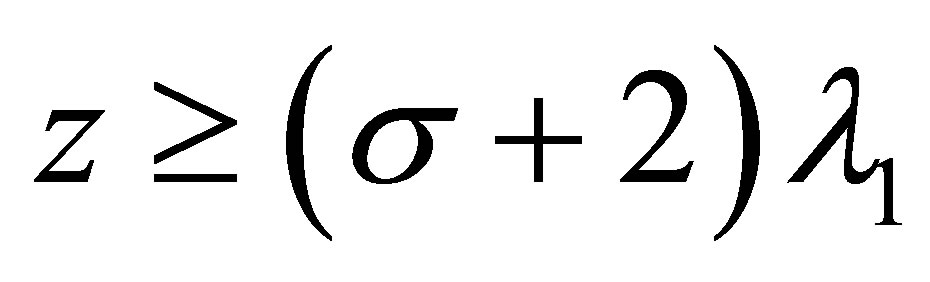 ,
,
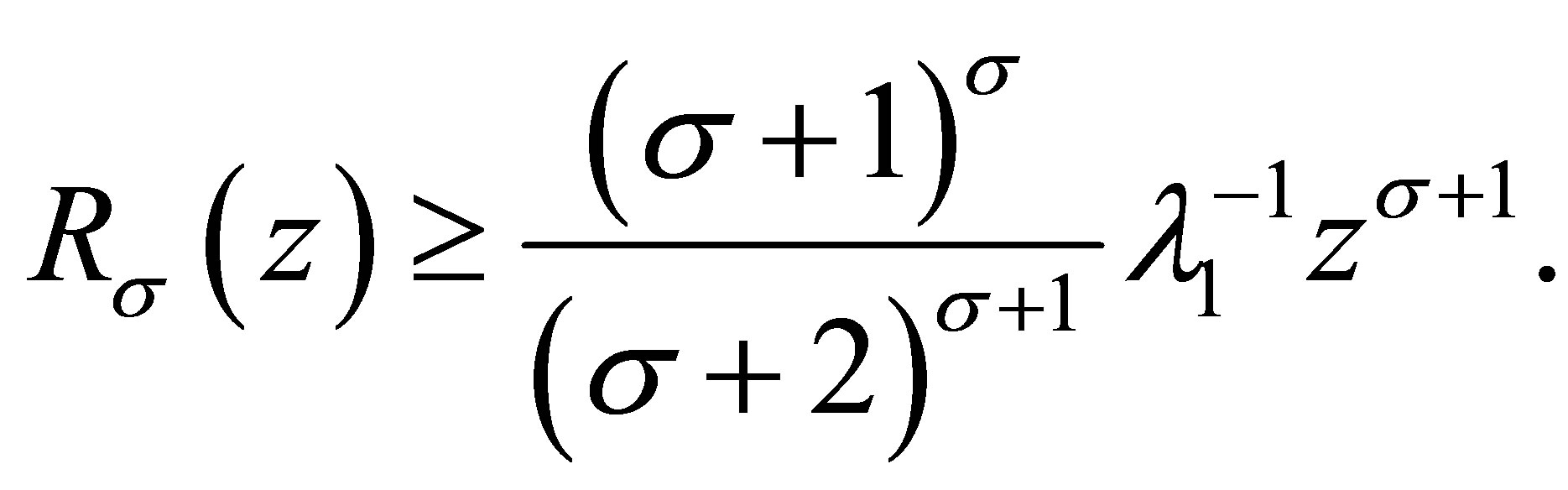 (3.8)
(3.8)
2) For 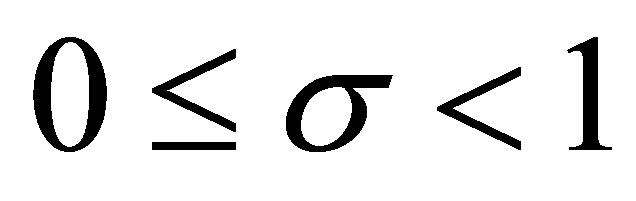 and
and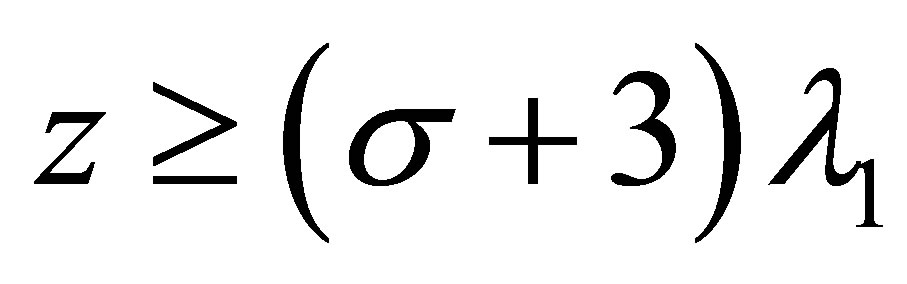 ,
,
 (3.9)
(3.9)
Proof. 1) By Corollary 3.1 we know that for  and
and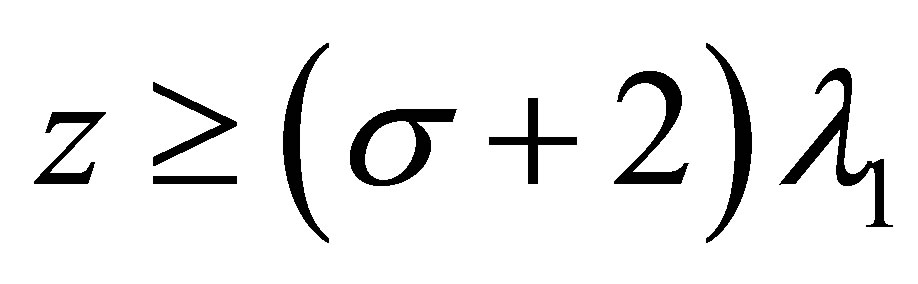 , it holds
, it holds
 (3.10)
(3.10)
Using Theorem 1.1, we have
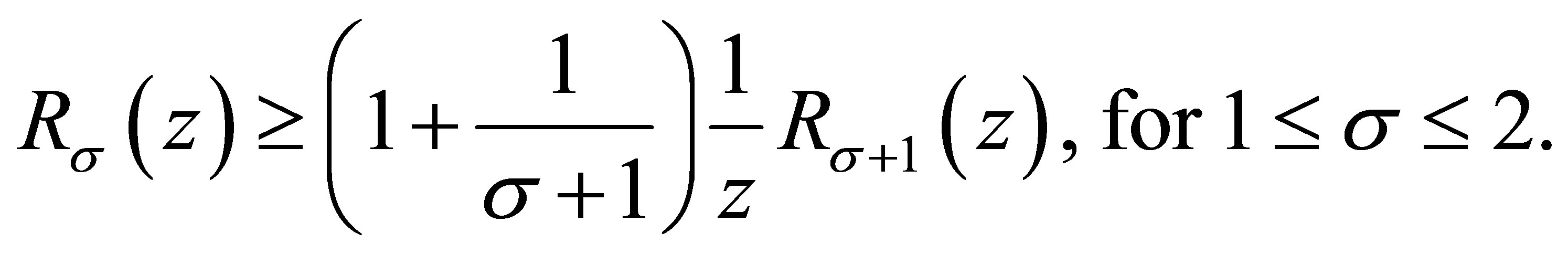 (3.11)
(3.11)
Combining (3.10) and (3.11), it follows

and (3.8) is proved.
2) By Corollary 3.1, it shows that for 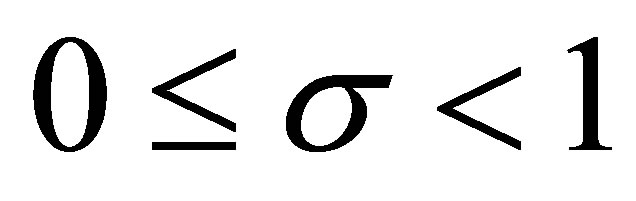 and
and , it holds
, it holds
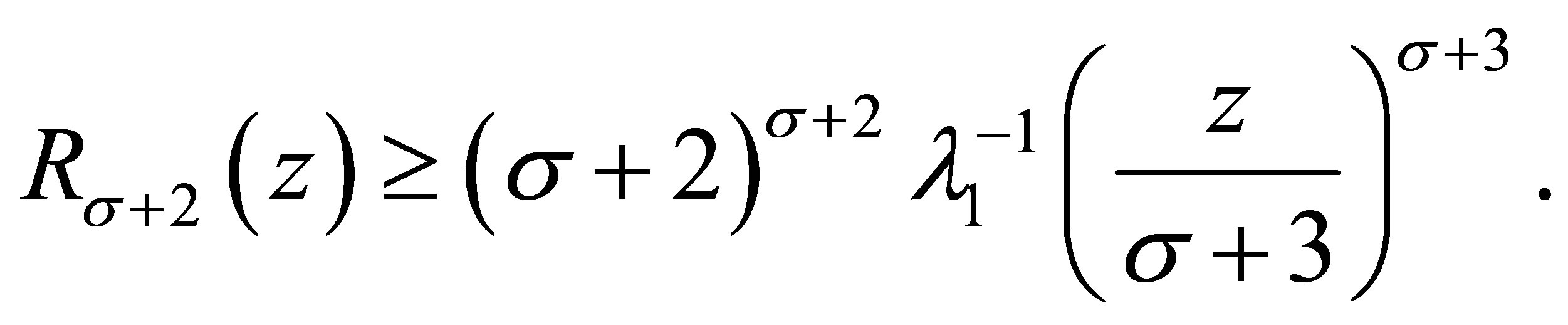 (3.12)
(3.12)
From Theorem 1.1, we see that for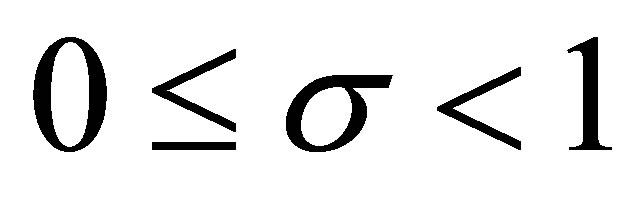 ,
,
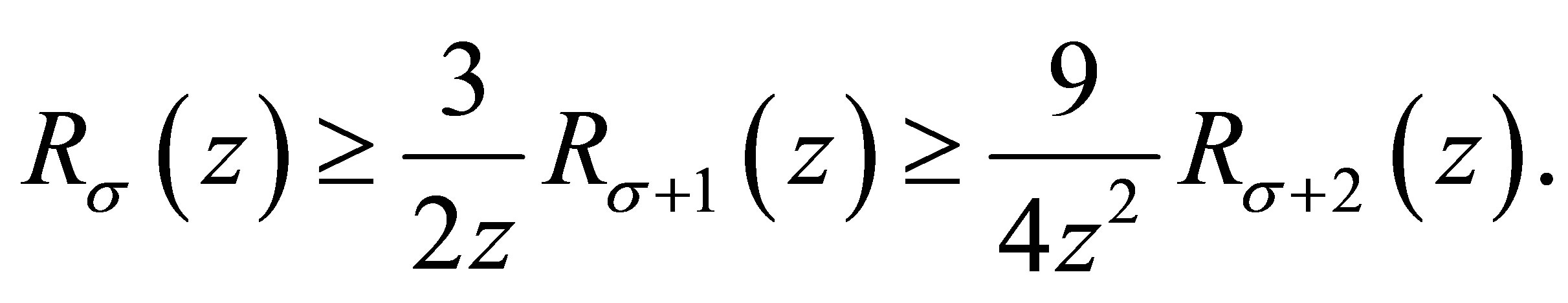 (3.13)
(3.13)
In the light of (3.12) and (3.13), it obtains

Noting that , for
, for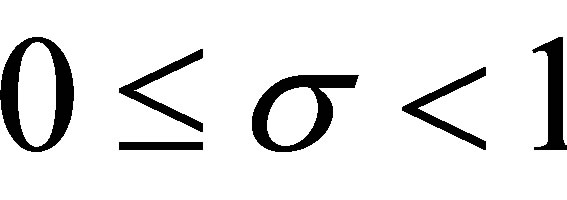 we have
we have
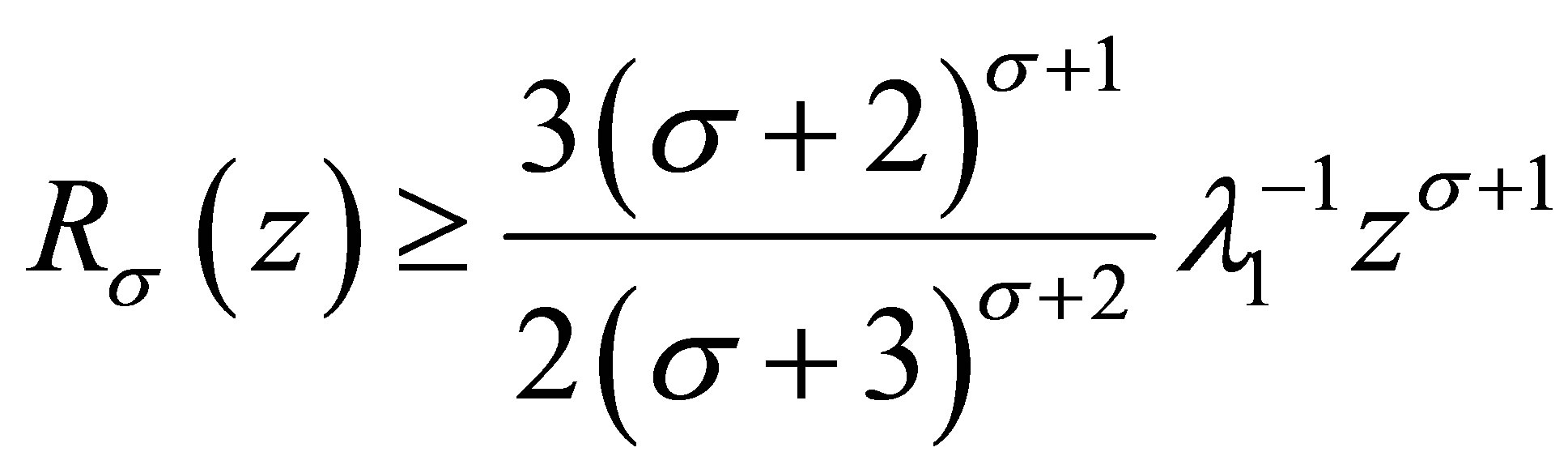
and (3.9) is proved.
Remark 3.3 Specially, we have
 (3.14)
(3.14)
 (3.15)
(3.15)
4. Proof of Theorem 1.2
Denote

and let  be the greatest integer
be the greatest integer  such that
such that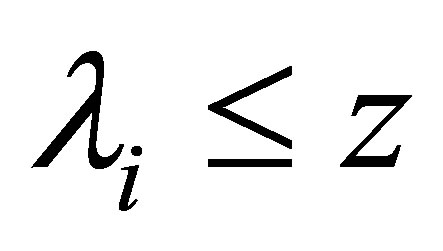 .
.
Let , it implies that
, it implies that 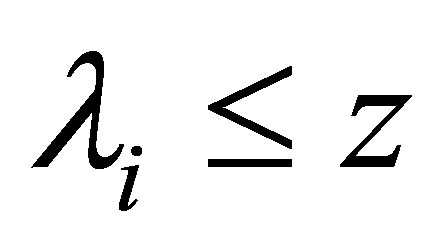 and
and , so
, so
 (4.1)
(4.1)
For any integer j and , it implies
, it implies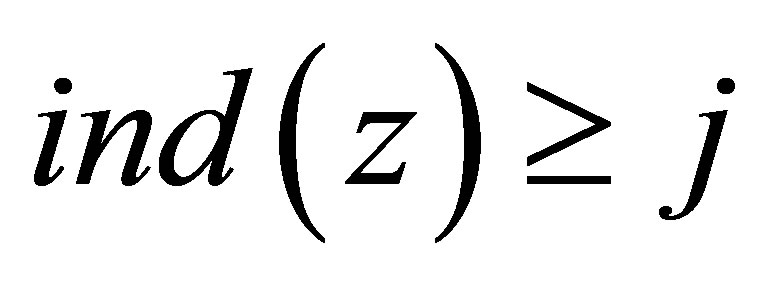 , and
, and

Using Theorem 1.1, we have that for ,
,

or
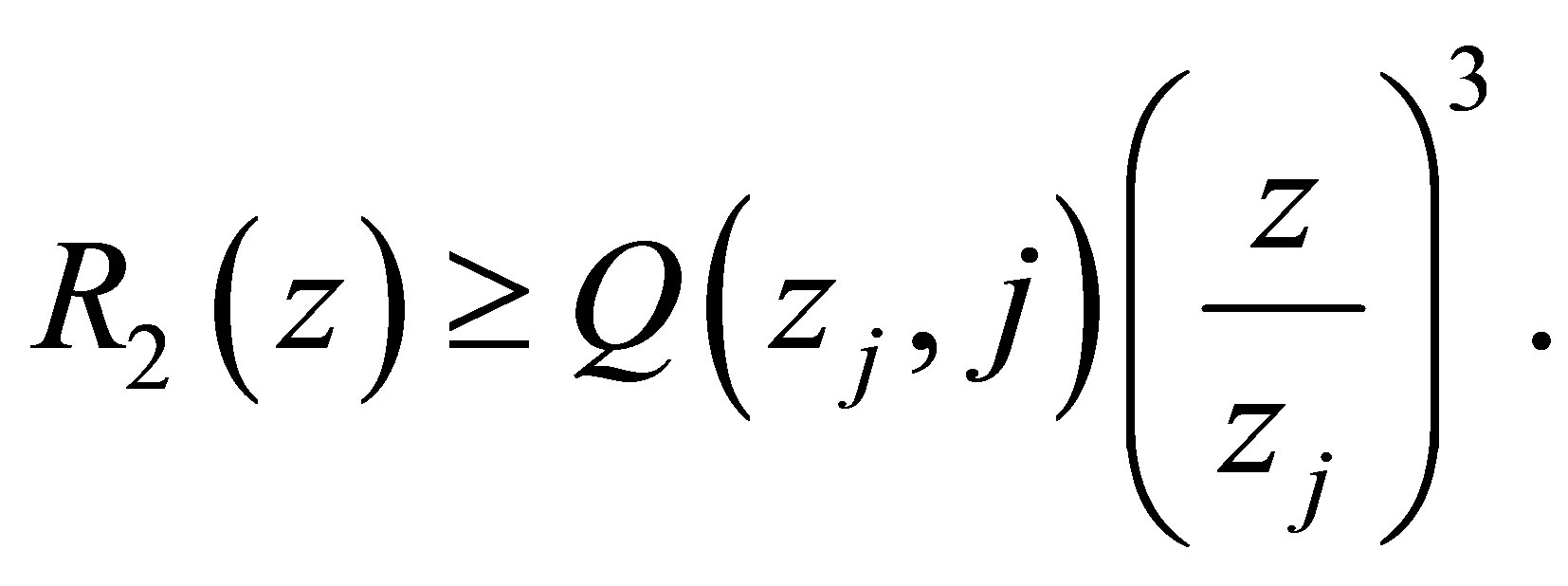 (4.2)
(4.2)
By the Cauchy-Schwarz inequality, it follows

and
 (4.3)
(4.3)
Proof of Theorem 1.2 1) Substituting 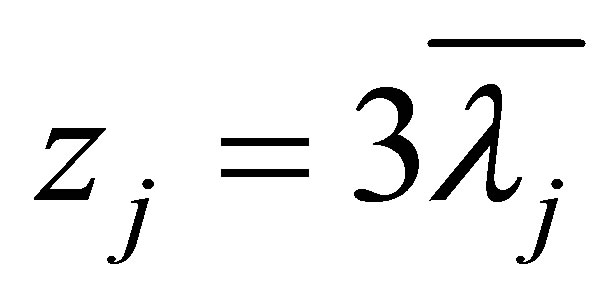 into (4.2) and noticing (4.3), we have
into (4.2) and noticing (4.3), we have

and (1.8) is proved.
2) We take (1.8) into (3.14) to obtain
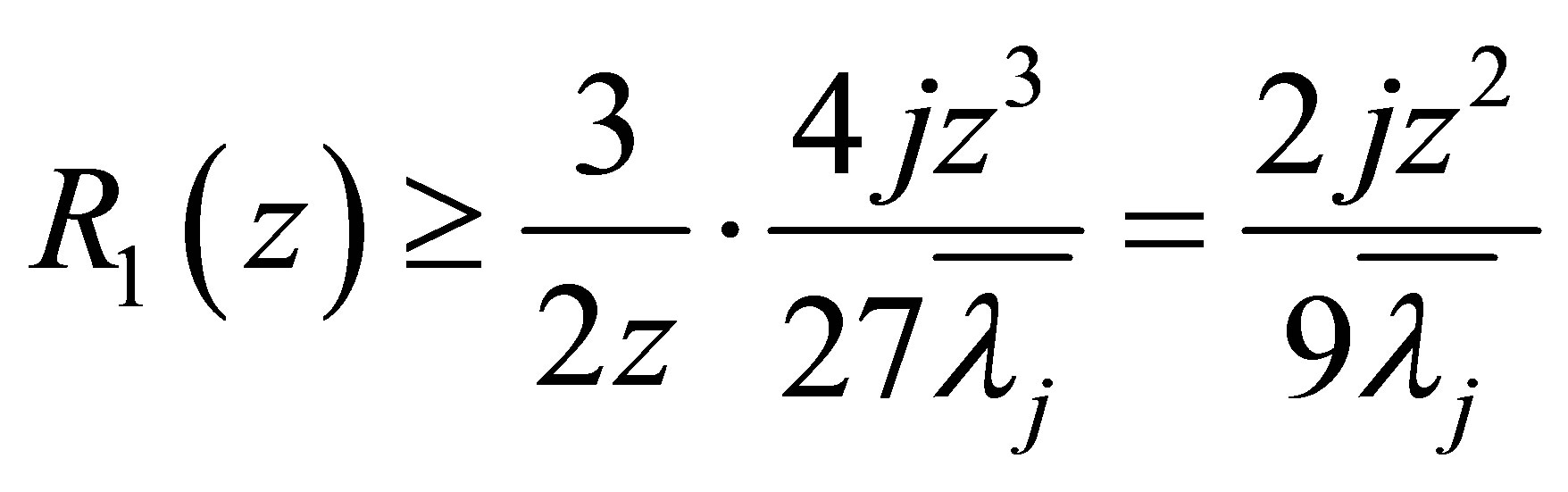
and (1.9) is proved.
3) Combining (1.8) and (3.15), it implies
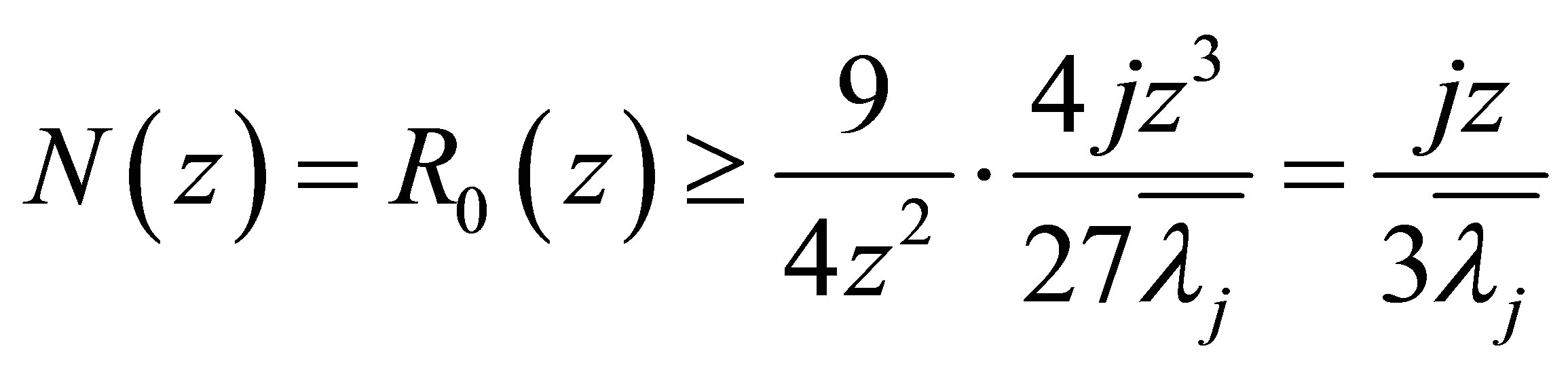
and (1.10) is proved.
4) If , then (1.11) is clearly valid; if
, then (1.11) is clearly valid; if
 , then (1.10) shows by letting
, then (1.10) shows by letting  that
that
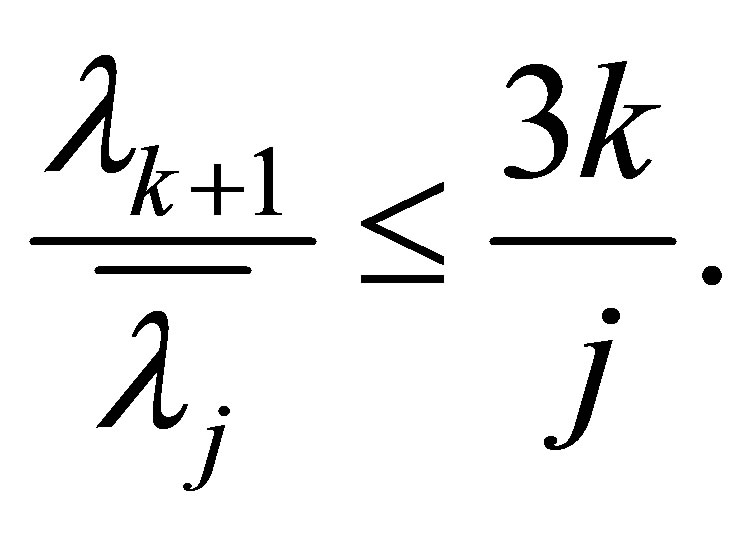
So (1.11) is proved and Theorem 1.2 is proved.
Corollary 4.1 We have
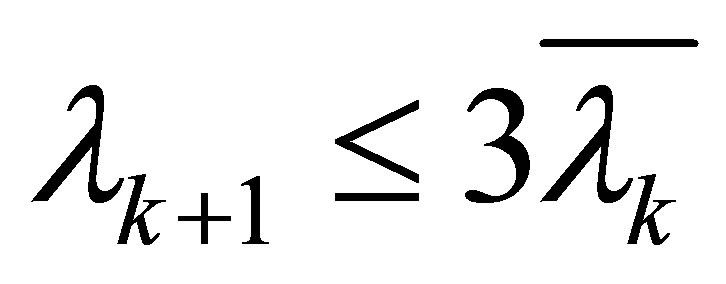
and
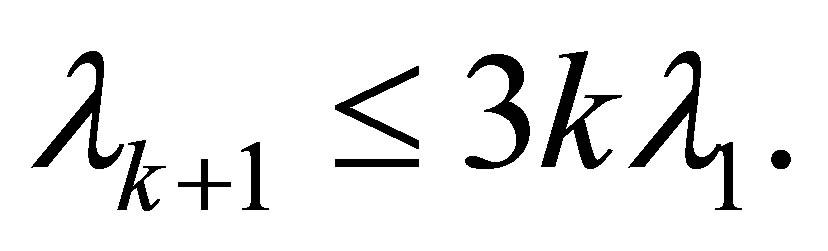 (4.4)
(4.4)
5. Proof of Theorem 1.3
We first recall the following definition before proving Theorem 1.3.
Definition 5.1 If 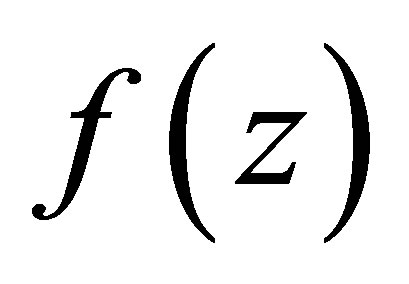 is superlinear in z as
is superlinear in z as , then its Legendre transform is defined by
, then its Legendre transform is defined by
 (5.1)
(5.1)
Remark 5.2 If  for all
for all , then
, then 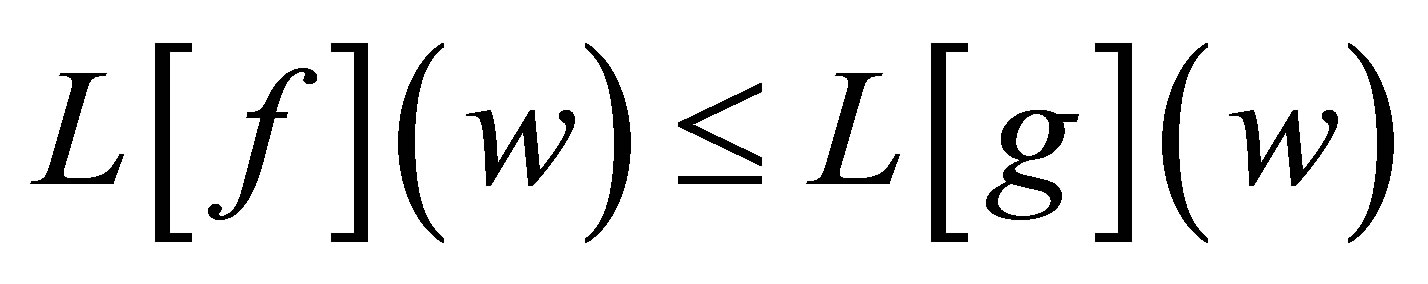 for all
for all ; Since the maximizing value of
; Since the maximizing value of  in (5.1) is a nondecreasing function of
in (5.1) is a nondecreasing function of , it follows that for
, it follows that for  sufficiently large, the maximizing
sufficiently large, the maximizing  exceeds
exceeds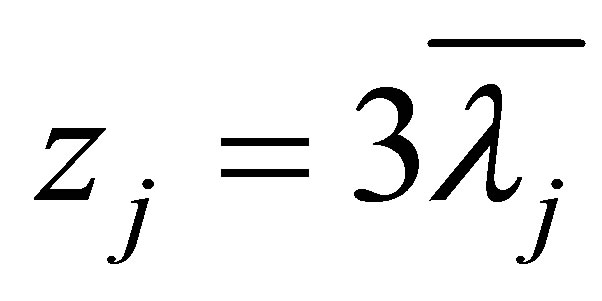 .
.
Proof of Theorem 1.3 From (1.9), we have
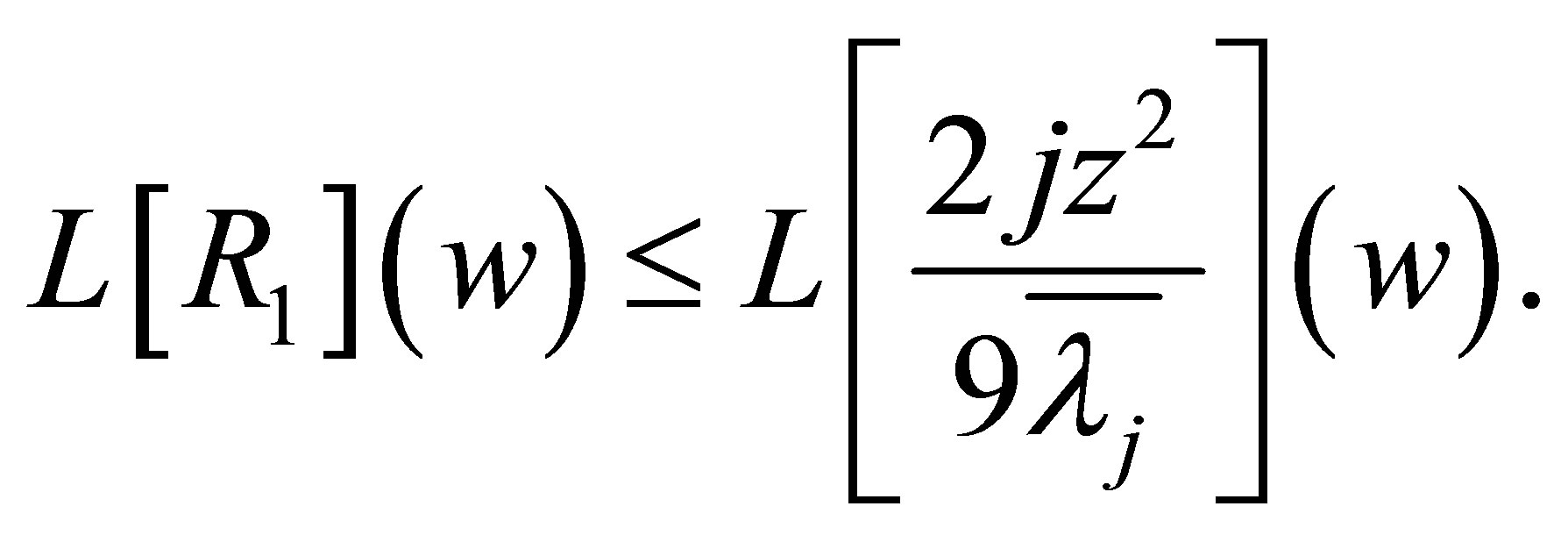 (5.2)
(5.2)
Now let us calculate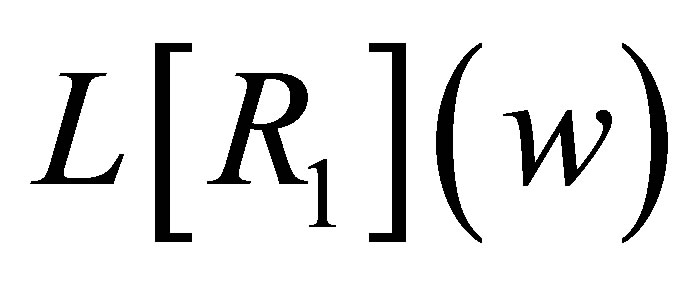 . Since
. Since

is piecewise linear function of , it implies that the maximizing value of
, it implies that the maximizing value of  in the Legendre transform of
in the Legendre transform of  is attained at one of the critical values.
is attained at one of the critical values.
In fact if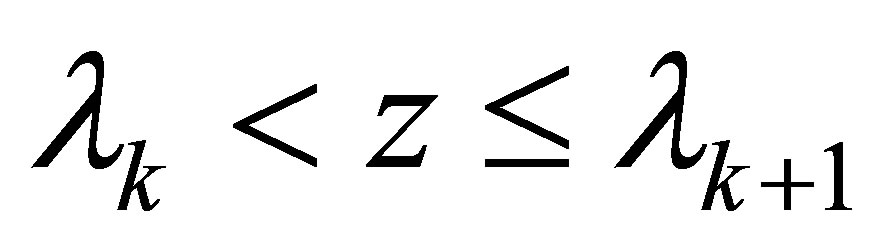 , then
, then

Noting that the maximizing value of  is a nondecreasing function of
is a nondecreasing function of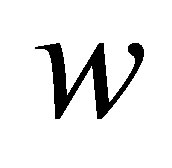 , we see
, we see , therefore the critical value
, therefore the critical value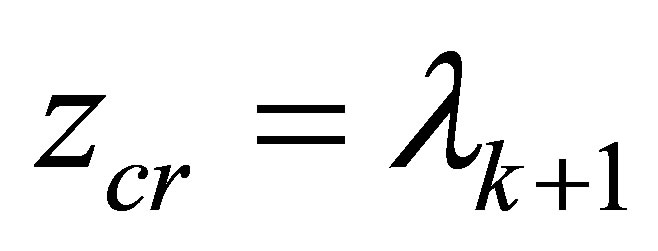 .
.
It is easy to check  and
and
 (5.3)
(5.3)
Next we calculate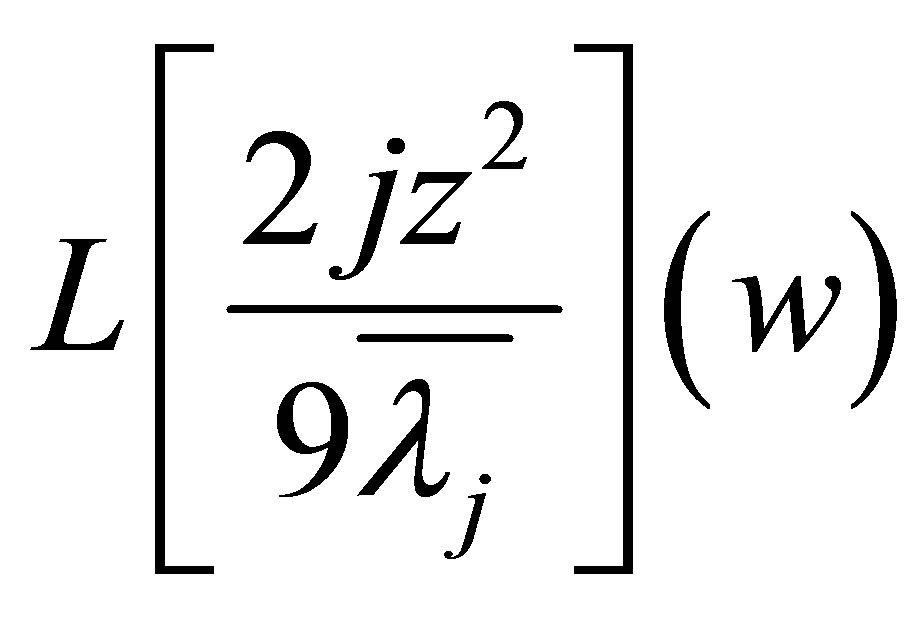 . Noting
. Noting

and letting
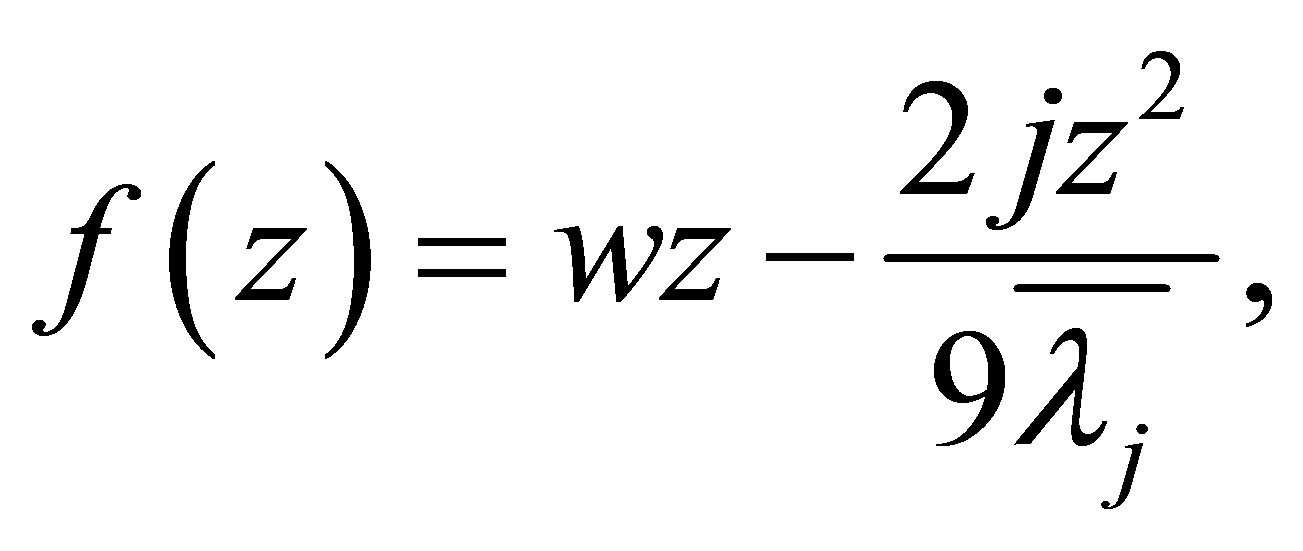
we know . By
. By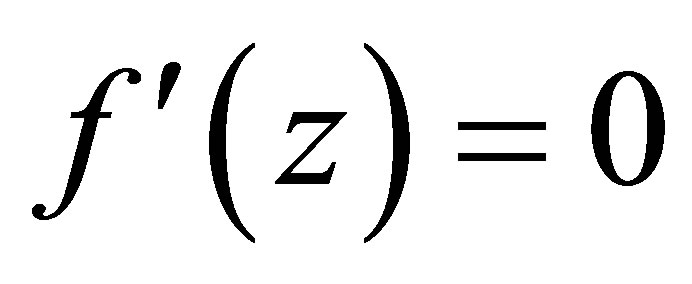 , it solves
, it solves
 (5.4)
(5.4)
Therefore
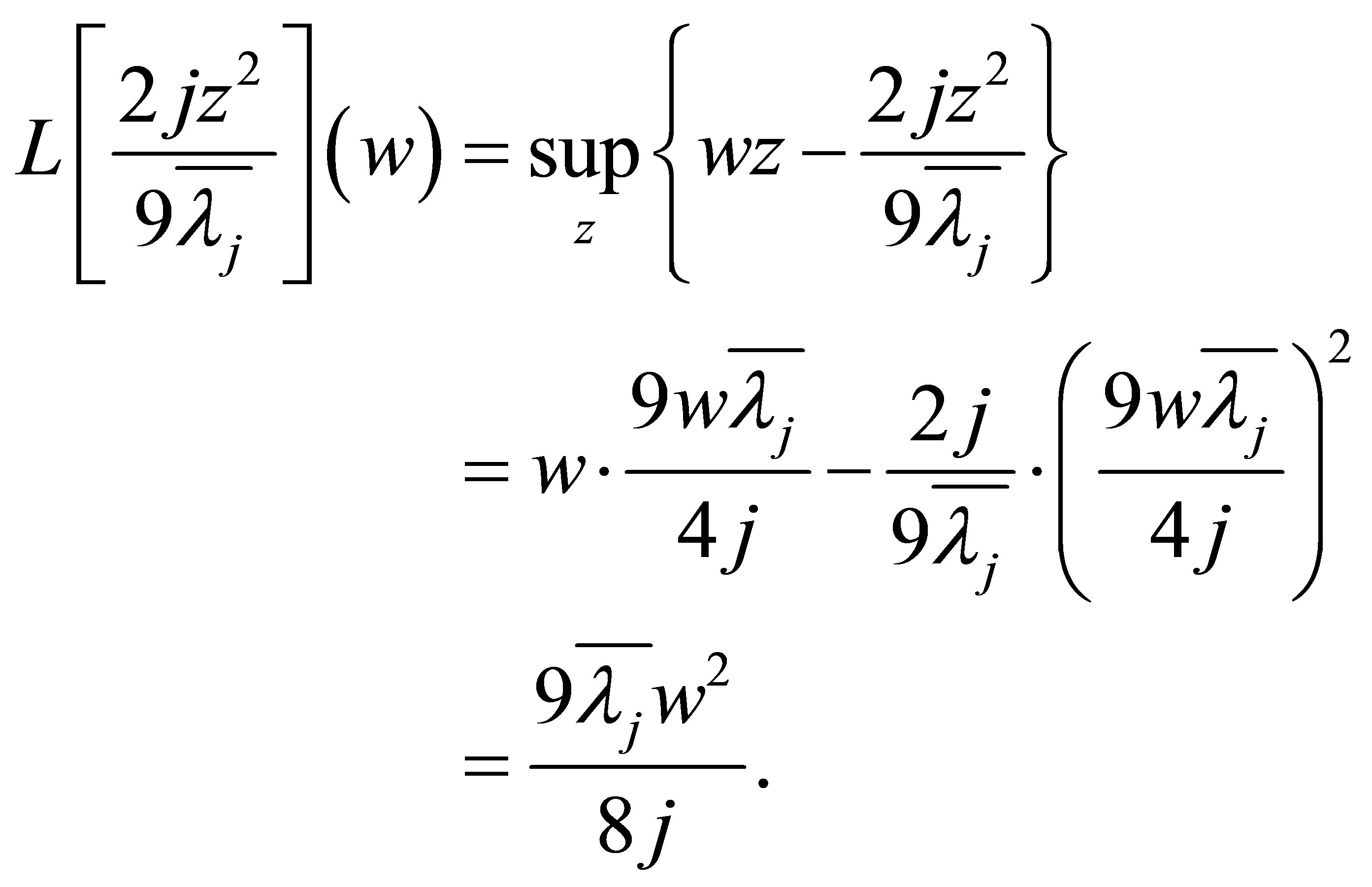 (5.5)
(5.5)
Taking (5.3) and (5.5) into (5.2), we have
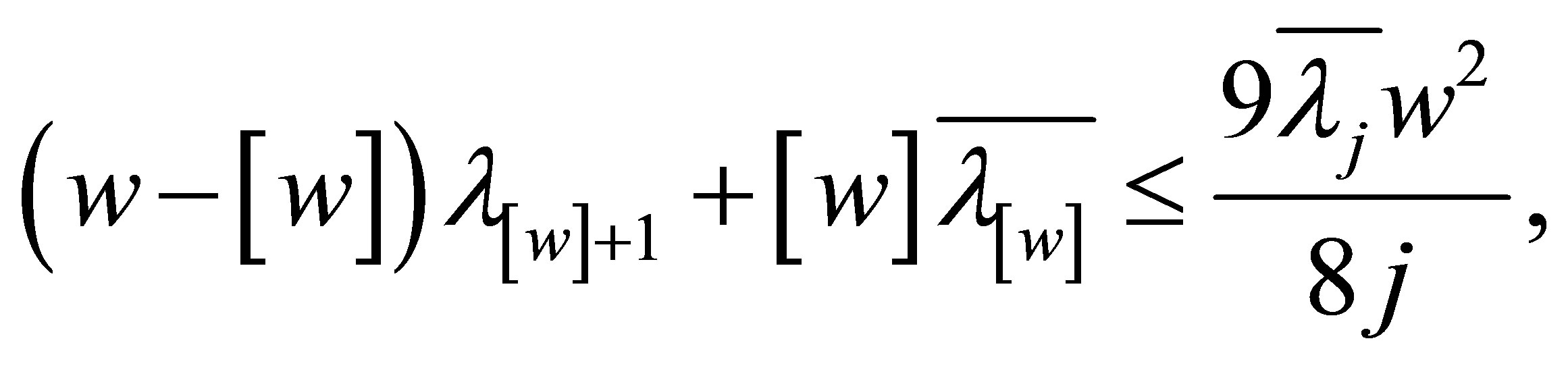 (5.6)
(5.6)
By (5.4), it has

From Theorem 1.2,  , so
, so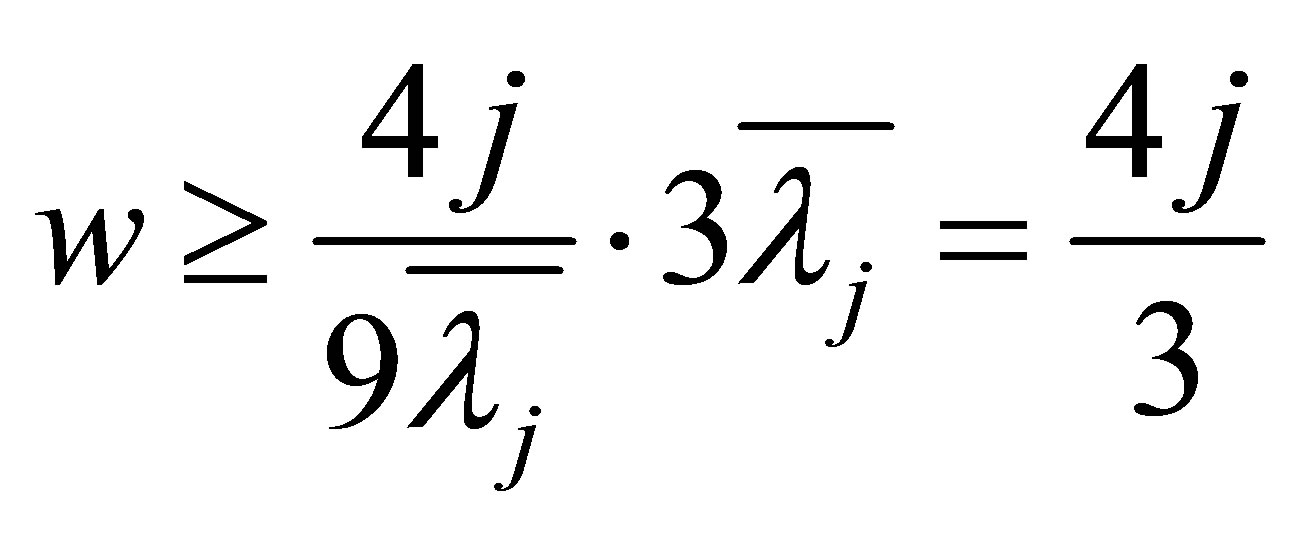 .
.
Then it follows that if w is restricted to the value then (5.6) is valid.
then (5.6) is valid.
Meanwhile, for any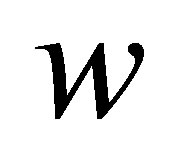 , we can always find an integer
, we can always find an integer  such that
such that  and
and
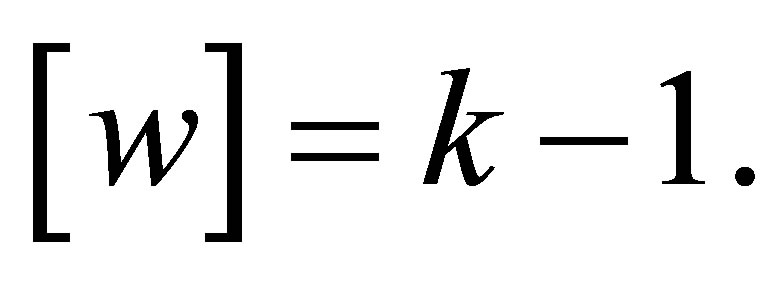
If 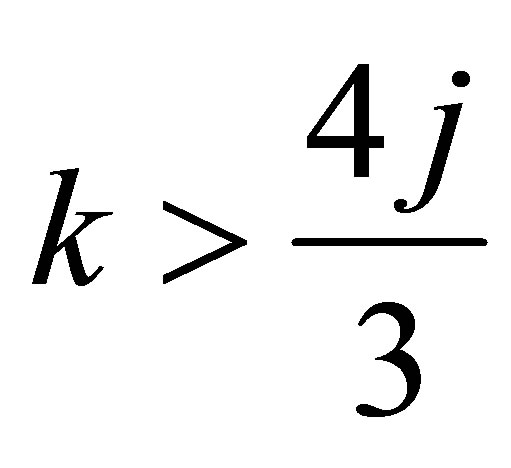 and
and 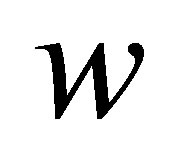 approaches to
approaches to  from belowthen we obtain from (5.5) that
from belowthen we obtain from (5.5) that

Therefore
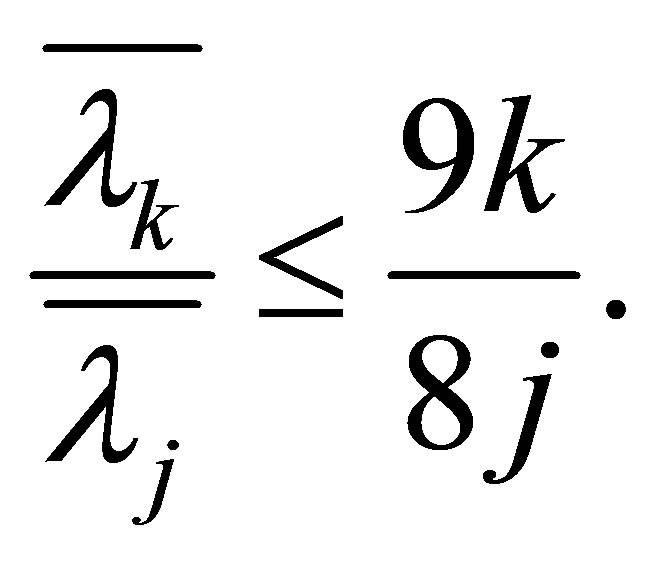
and Theorem 1.3 is proved.
Remark 5.3 If we let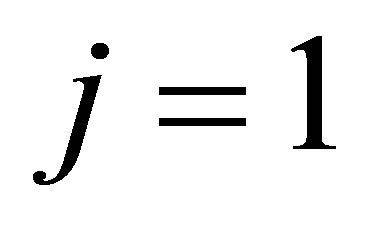 , then
, then
 (5.7)
(5.7)
We point out that (5.7) is sharper than (4.4). In fact, we get from (4.4) that

and
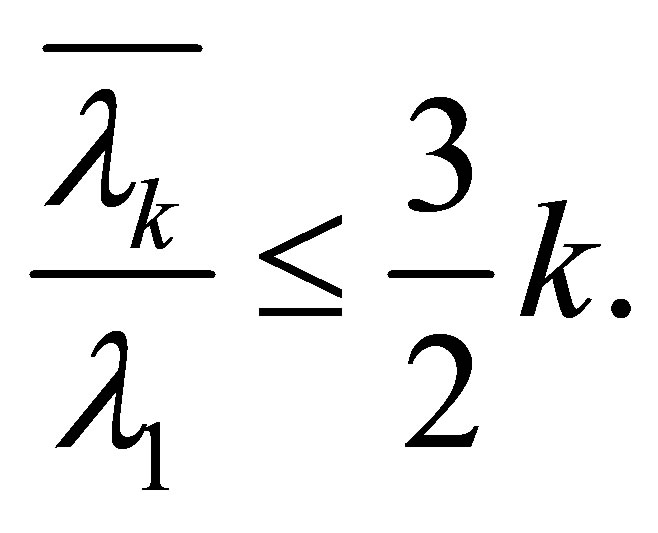
But  is always valid, so (5.7) is sharper than (4.4).
is always valid, so (5.7) is sharper than (4.4).
REFERENCES
- N. Garofalo and F. Tournier, “New Properties of Convex Functions in the Heisenberg Group,” Transactions of the American Mathematical Society, Vol. 358, No. 5, 2005, pp. 2011-2055. http://dx.doi.org/10.1090/S0002-9947-05-04016-X
- X. Luo and P. Niu, “Eigenvalues Problems for Square Sum Operators Consisting of Vector Fields,” Mathematica Applicata, Vol. 10, No. 4, 1997, pp. 101-104.
- E. M. Harrell and L. Hermi, “On Riesz Means of Eigenvalues,” Communications in Partial Differential Equations, Vol. 36, No. 9, 2011, pp. 1521-1543. http://dx.doi.org/10.1080/03605302.2011.595865
- Yu. G. Safarov, “Riesz Means of the Distribution Function of the Eigenvalues of an Elliptic Operator,” Journal of Soviet Mathematics, Vol. 49, No. 5, 1990, pp. 1210- 1212. http://dx.doi.org/10.1007/BF02208718
- B. Helffer and D. Robert, “Riesz Means of Bound States and Semicalassical Limit Connected with a Lieb-Thirring’s Conjecture,” Asymptotic Analysis, Vol. 3, No. 2, 1990, pp. 91-103.
- E. M. Harrell II and L. Hermi, “Differential Inequalities for Riesz Means and Weyl-Type Bounds for Eigenvalues,” Journal of Functional Analysis, Vol. 254, No. 12, 2008, pp. 3171-3191. http://dx.doi.org/10.1016/j.jfa.2008.02.016
- G. Jia, J. Wang and Y. Xiong, “On Riesz Inequalities for Subelliptic Laplacian,” Applied Mathematics, Vol. 2, No. 6, 2011, pp. 694-698. http://dx.doi.org/10.4236/am.2011.26091
- M. S. Ashbaugh and R. D. Benguria, “More Bounds on Eigenvalues Ratios for Dirichlet Laplacians in n Dimensions,” SIAM Journal on Mathematical Analysis, Vol. 24, 1993, pp. 1622-1651. http://dx.doi.org/10.1137/0524091
- E. M. Harrell II and J. Stubbe, “On Trace Identities and Universal Eigenvalues Estimates for Some Partial Differential Operators,” Transactions of the American Mathematical Society, Vol. 349, No. 5, 1997, pp pp. 1797- 1809. http://dx.doi.org/10.1090/S0002-9947-97-01846-1
- P. Lvy-Bruhl, “Rsolubilit Locale et Global d’Opra-Teurs Invariants du Second Order sur des Group de Lie Nilpotents,” Bulletin des Sciences Mathématiques, Vol. 104, No. 2, 1980, pp. 369-391.
- A. Laptev and T. Weidl, “Sharp Lieb-Thirring Inequalities in High Dimensions,” Acta Mathematica, Vol. 184, No. 1, 2000, pp. 87-111. http://dx.doi.org/10.1007/BF02392782

