Advances in Pure Mathematics
Vol.05 No.04(2015), Article ID:54865,12 pages
10.4236/apm.2015.54017
Crystallography in Spaces E2, E3, E4, E5 ・・・ N˚I Isomorphism Classes: Properties and Applications to the Study of Incommensurate Phase Structures, Molecular Symmetry Groups and Crystal Families of Space E5
R. Veysseyre1*, D. Weigel1, T. Phan1, H. Veysseyre2
1Laboratoire Mathématiques appliquées aux Systèmes, Ecole Centrale Paris, Paris, France
2Institut Supérieur de Mécanique de Paris, Paris, France
Email: *renee.veysseyre@normalesup.org
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 February 2015; accepted 3 March 2015; published 20 March 2015
ABSTRACT
This paper mainly consists of the classification of all crystallographic point groups of n-dimen- sional space with n ≤ 6 into different isomorphism classes. An isomorphism class is defined by a type of finite mathematic group; for instance, the different types of mathematic groups have been well defined and studied by Coxeter. This classification may be used in the investigation of several domains of crystallography such as the study of the incommensurate phases, the quasi crystals … Indeed, each mathematic substitution group characterizes an isomorphism class of crystallographic point groups (spaces E2 or E3), of point groups of super crystals (spaces E4 or E5), and of molecular symmetry groups (spaces E2 or E3). This mathematic group gives interesting information about: 1) the incommensurate phase structures and their phase transitions according to the Landau’s theory in their super spaces E4, E5, E6, ・・・; 2) the molecular symmetry group of chemisorbed molecules in space E2 (paragraph 2) or of the molecular crystal or solution in view of studying the molecule structure or its rotations or vibrationsin space E3; 3) the geometric polyhedron symmetry groups as the regular rhombohedron in space E3, the rhombotope 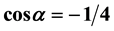 in space E4 or the rhombotope
in space E4 or the rhombotope 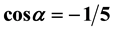 in space E5. Then, thanks to the isomorphism classes, we shall give properties of some crystal families that we have not published up to now. This formalism may be used to study crystal families in n-dimensional space with n > 6.
in space E5. Then, thanks to the isomorphism classes, we shall give properties of some crystal families that we have not published up to now. This formalism may be used to study crystal families in n-dimensional space with n > 6.
Keywords:
Crystallographic Point Groups, Isomorphism Classes, Incommensurate Phase Structures, WPV (Weigel Phan Veysseyre) Symbols of Point Groups

1. Introduction: Mathematics, Crystallography and Chemistry, Cayley’s Theorem
The crystallographers use Hermann-Mauguin’s symbols for the crystallographic point groups while the spectroscopists and the chemists use Schöenflies’s symbols in order to characterize the symmetry groups of the molecules which are crystallographic point groups too. For instance, the symbols 3 m (crystallographers) and C3v (chemists) are different symbols for isomorphic groups; it is the same property for the symbols 6 mm (crystallographers) and C6v (chemists).
From now, we use cr for crystallographic.
The point symmetries of a crystal are the cr point operations which are compatible with the translational symmetries of this crystal in a given space (E2 or E3). They are mainly described by means of group study based on the properties of finite mathematic groups together with a geometric approach. This process was used by Hermann and Mauguin, almost a century ago, when they established the cr symbols of point groups of two- and three-di- mensional spaces [1] . We recalled that Hermann and Mauguin were different scientists, one of them was rather crystallographer and the other one rather mathematician. Before explaining the properties of the WPV symbols and the isomorphism classes (Paragraphs 2-1 and 2-2), we give a first example of this mathematic approach. We select the finite mathematic dihedral group D4 of order 8 and the cr point group of the square 4 mm of order 8 in the space E2; the eight symmetry operations of group 4 mm are the following ones: two rotations of order 4 i.e. of angles 2p/4 and 3 × 2p/4, one rotation of order 2 i.e. of angle 2p/2, then 4 reflections denoted m and the identity. We write the set of these elements on the form 2(4) 5(2) 1(1), i.e. 2 elements of order 4, 5 elements of order 2 and the identity. Mathematic group D4 has elements of the same type. Hence, among the ten cr point groups of space E2, the group 4 mm is a realization of the group D4 in space E2. The two groups, D4 and 4 mm, were isomorphic as Hermann and Mauguin said. All the cr point groups isomorphic to mathematic group D4 are listed in Table 2 (Paragraph 5-1). Among the infinite set of symmetry groups of all the possible molecules of space E3, the symmetry group of the molecule BrF5 is a realization of this group D4. The chemists and the spectroscopists use the Schöenflies’s symbol C4v, the same point group as the group 4 mm with the same list of elements. Let’s note that the groups, C4v (BrF5 molecule), C3v (ammonia molecule) and C2v (molecule water) are polar groups.
As a second example, we consider the holohedry of the tetragonal family, i.e. the cr point group 4 mm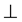 m of order 8 × 2 = 16, in space E3; the mark
m of order 8 × 2 = 16, in space E3; the mark 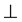 means that the group 4 mm
means that the group 4 mm m is the direct product of the two subgroups 4 mm and m. Moreover, these two subgroups act in two orthogonal subspaces of space E3: group 4 mm acts in a two-dimensional space, and group m acts in a one-dimensional space orthogonal to the first one. Group 4 mm
m is the direct product of the two subgroups 4 mm and m. Moreover, these two subgroups act in two orthogonal subspaces of space E3: group 4 mm acts in a two-dimensional space, and group m acts in a one-dimensional space orthogonal to the first one. Group 4 mm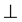 m has four elements of order 4, and seven elements of order 2 (five elements m, 2,
m has four elements of order 4, and seven elements of order 2 (five elements m, 2, ). This group is isomorphic to the mathematic group D4 × C2, direct product of the two groups D4 and C2 (Table 5, Paragraph 5-2).
). This group is isomorphic to the mathematic group D4 × C2, direct product of the two groups D4 and C2 (Table 5, Paragraph 5-2).
These two examples translate the Cayley’s theorem: any group G is isomorphic to a subgroup of the symmetric group S(G) of the permutations of this group. Especially, if the group G is a finite group of order n, it is isomorphic to a subgroup of the symmetric group Sn. The demonstration is summarized in the Annex.
The spectroscopists and the chemists add to the mathematical symbol a letter. For instance, the letter h in group C3h means that a horizontal plane of symmetry is added to the axis of rotation of group C3, and the letter v in group C3v means that three vertical planes of symmetry are added to the axis of rotation of group C3. So, for each cr point group and for each symmetry group of a molecule of spaces E3, E4 and E5, we give the mathematic symbol, i.e. the one of its isomorphism class and the Hermann-Mauguin’s symbol (spaces E2 and E3), or the WPV (Weigel Phan Veysseyre)’s symbol (spaces E4, E5, ・・・).
By the way, the real structure of the (mono, di and tri) incommensurate phases takes place in their superspace (E4, E5 and E6) where they become crystals, therefore for crystallographers these super spaces are real physical spaces. Hence, it is essential to use point and space groups in spaces E4, E5 and E6. Then, the section of this “physical” superstructure by the physical space, i.e. the three-dimensional space, gives the description of the structure. It is one of the main reasons which support our work. In this paper, we give an example of phase transition, between a mono incommensurate (inc) modulated phase and its basic structure (Paragraph 5-4).
When the physicists of the condensed matter will study the phase transitions of the inc phases in the super spaces systematically, these super spaces will be considered as real physical spaces. The space E3 is the crystal physical space while the spaces E4, E5 and E6 are the real crystal physical super spaces of the inc phases.
Thanks to the study of the isomorphism classes, we complete the description of the crystal families of space E5 that we have published previously. Five families are studied in the following paper (number II), i.e. the (monoclinic di iso squares)-al, decadic-al, (monoclinic di iso hexagons)-al, (rhombotopic )-al and rhombotopic
)-al and rhombotopic 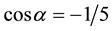 crystal families. Three more families, (di iso hexagons)-al, hypercube 4 dim.)-al and hyper- cube 5 dim., will be studied in a next paper. So, all the crystal families of space E5 will be studied.
crystal families. Three more families, (di iso hexagons)-al, hypercube 4 dim.)-al and hyper- cube 5 dim., will be studied in a next paper. So, all the crystal families of space E5 will be studied.
2. Properties of WPV (Weigel Phan Veysseyre) Geometric Symbols. Definition and Properties of the Isomorphism Classes. Example of the Class C6
2.1. WPV (Weigel Phan Veysseyre) Symbols. Definition and Properties
In order to study each crystal family of space E5, we used the geometric nature of the cell and the results given by the Scientific Software established by Veysseyre in [2] , we design this software by the expression SS E5.
This SS E5 gives for each of 32 crystal families of space E5:
・ The list of the cr point symmetry operations of order 2, 3, 4, ・・・ with their number for any subgroup of the holohedries.
・ The list of the subgroups of each subgroup of the holohedries.
The geometric approach allows us to give a name to the 32 crystal families of space E5.
The list of all the subgroups of each holohedry gives 955 cr point groups in the space E5. This list of the 955 cr point groups of space E5 contains the 10 cr point groups of space E2, the (32-10) cr point groups of space E3, the (227-32) crpoint groups of space E4. Moreover, thanks to the list of the cr point symmetry operations of order 2, of order 4, of order 5, ・・・, with their number, it is possible to assign to each cr point group a symbol as well as a mathematic symbol. These symbols are named “WPV symbols”, from the initials of this study’s authors (Weigel, Phan and Veysseyre [3] ).
The assigned WPV symbols to the cr point groups of space E5 are in agreement with the Hermann-Mauguin’s symbols of spaces E2 and E3 and they respect the International Sub-Commission Nomenclature recommendations in [4] . However, others rules must be given. Indeed, in spaces E4 and E5, several regular polytopes appear with symmetry operations compatible with the fourth and the fifth dimensions. In addition, for the study of the mono cubic families in [5] , we had to define and to study a new kind of symmetry operations that we called “iso cubic” operations.
The 955 cr point groups of space E5 are isomorphic to some mathematic groups. Most of these mathematic groups are the direct product of two or more cyclic groups. After the work of Fedorov and Schöenflies (1891) for the space groups in the three-dimensional space and the work of Brown in [6] for the cr point and space groups in four-dimensional space, we can cite the publications of Plesken in [7] - [9] which give a classification of the cr point and space groups respectively in 5 and 6 dimensions from a set of algorithms. The Cayley’s theorem (1854) specifies that all finite groups are isomorphic to a product of permutation groups. Thanks to the two lists named previously, i.e. the symmetry point operation and the subgroup lists, we are in position to give a complete classification of the cr point groups of five-dimensional space. So all the cr point groups isomorphic to a same mathematic group belong to an isomorphism class, these cr point groups are the cr realizations of the same mathematic group.
The WPV symbol contains more geometric information than the mathematic symbol and gives the geometric nature of the cell, the symmetry operations together with the supports of the group generators. A WPV symbol defines one and only one cr point group while the mathematic symbol is the same for all the groups of an isomorphism class.
2.2. Isomorphism Class, Definition and Properties
An isomorphism class is the infinite set of all point groups isomorphic to a mathematic group, either cr point groups or molecule symmetry groups or symmetry groups of polygons, polyhedrons, polytopes; these groups are the realizations of a mathematic group whatever the dimension of space is. The authors of the book [6] have given a mathematic type for all the 227 cr point groups of space E4; these types are characterized either by a mathematic symbol such as Cn 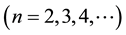 or Dn・・・ or by a number, for instance 128-1, and Plesken in [8] [9] gave the isomorphic types of all the holohedries of the crystal families of spaces E5 and E6.
or Dn・・・ or by a number, for instance 128-1, and Plesken in [8] [9] gave the isomorphic types of all the holohedries of the crystal families of spaces E5 and E6.
Indeed, any cr point group of a given space can be considered as the realization of one finite mathematic group; therefore, it is possible to gather all the cr point groups in different isomorphism classes. Of course, all the cr point groups of an isomorphism class have the same order and the same number of elements of each order i.e. the same arrangement of its elements. We recall that the order of an element g of a finite group is the smaller integer n such as the element gn equals the identity.
To sum up, an isomorphism class is characterized by:
1) A mathematic symbol for instance, Cn cyclic group, Dn dihedral group, Sn symmetric group, An alternate group, Dn × Cn direct product of the two groups Dn and Cn, Dicn or Qndicyclic group, or by a more complicate symbol defined in [10] . Some mathematicsymbols are explained in Annex.
2) A list of elements which is the same for all the cr point group of the class; this list gives the different symmetry elements classified order by order with their number.
Let’s give the cyclic group C6 as a simple example. The cyclic group C6 is isomorphic to the direct product of two cyclic groups C3 and C2, i.e. C6 = C3 × C2 because 3 and 2 are coprime. Each group of the class C6 has two elements of order 6, two elements of order 3, one element of order 2 and the identity. We write this list under the form 2(6) 2(3) 1(2). From now on, we omit the identity in the list of elements of a group. All the cr point groups which have two symmetry elements of order 6, two symmetry elements of order 3 and one symmetry element of order 2 belong to the isomorphism class C6. Table 1 listed all the groups isomorphic to group C6 which belong to four crystal families of space E5, i.e. the Hexagon triclinic, (Hexagon oblique)-al, (Diclinic de hexagons)-al and (Di hexagons)-al families; these groups belong to spaces E2, E3, E4, E5. This table lists the symbol of the holohedry and its order for each family. The name of the different families explains the construction of the cell, for instance (Hexagon oblique)-al, the cell is a right hyper prism (suffix al) and its base is the Cartesian product of a hexagon and a parallelogram.
Let be denoted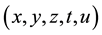 , the five axes of space E5. The group
, the five axes of space E5. The group 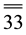 is the cyclic group generated by the
is the cyclic group generated by the
symmetry operation 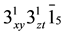 or by the equivalent operation
or by the equivalent operation 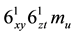 the six elements of the group
the six elements of the group  are the-
are the-
following ones:
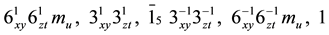




Remark
The cr point groups of an isomorphism class often belong to several crystal families.
Table 1. Crystallographic point groups of crystal families of space E5 isomorphicto mathematical group C6.
Table caption: First column: Family names. Second column: WPV symbol and order of the holohedries. Point groups isomorphic to group C6: of space E2.. Third column: of space E3. Fourth column: of space E4. Fifth column: of space E5 sixth column. SS E5 gives this information.
3. From Mathematic Groups to Crystallographic and Molecular Symmetry Point Groups. Realizations of Isomorphism Classes D3 and D3 × C2 in Spaces E2, E3, E4, E5 as cr Point Groups or Molecular Symmetry Groups
Let’s give the example of the isomorphism class D3 (dihedral group of order 6) with the list of elements 2(3) 3(2) and the one of the class D3 × C2 (of order 12) with the list of element 2(6) 2(3) 7(2). The realizations of these cr point groups belong to spaces E2, E3, E4, E5 in crystallography and to spaces E2, E3 in chemistry and spectroscopy.
Before start with these examples, it is useful to compare the arrangements of the two mathematic groups G and G × C2 where G is a finite group and C2 is the cyclic group of order 2. Let be denoted 



3.1. Isomorphism Class D3, in Space E3
The hexagonal crystal family (holohedry 6 mm
The Schöenflies’s symbol of these groups, used by the chemists, is C3v. As example, we can cite the crystal Fe2P (cr point group (3 2), space group P 321).
3.2. Isomorphism Class D3, in Space E4
Three crystal families of space E4 have cr point groups which belong to this isomorphism class. They are:
・ The hexagon rectangle crystal family (holohedry 6 mm
・ The hexagon oblique crystal family (holohedry 6 mm

・ The (monoclinic di hexagons) crystal family (holohedry (66 2 2), order 12), with the cr point (33 2).
3.3. Isomorphism Class D3, in Space E5
Three crystal families of space E5 have cr point groups which belong to this isomorphism class. They are:
・ The hexagon triclinic crystal family (holohedry 6 mm

・ The (hexagon oblique)-al crystal family (holohedry 6 mm


・ The (monoclinic di hexagons)-al crystal family (holohedry (66 2 2)

3.4. Example of the Molecule BF3 (Trifluoride Boron)
The set of the point groups of the equilateral triangle is isomorphic to mathematic group D3 (order 6) in space E2 and to group D3 × C2 (order 12) in space E3. The Schöenflies and H.M. symbols of each BF3 molecule are:
・ D3 or 3 m for the chemisorbed (mono layer) BF3 molecules on a very clean divided solid; indeed in this case, the plane of the molecule is not a reflection mirror, because from one side there are strong chemical bonds between the chemisorbed molecule and the solid while on the other side, there are weak chemical bonds between the chemisorbed molecule and the polylayerphysisorbed BF3 ones. So, here the chemisorbed molecules are strictly in space E2. Let us note that the three π rotations through three BH axes in a BF3 chemisorbed molecule are not possible just as the vibrations of this chemisorbed molecule orthogonal to the plane BF3 (one axis BH is the line which links the center B of the equilateral triangle of the molecule to one of its vertices).
・ D3h or 3 m
4. Realizations of Mathematic Classes A5, Order 60 and S5 (A5 × C2) Order 120 as Symmetry Groups in E3 (I, Ih) and as cr Point Groups of Super Crystals in E4 and E5, of Polyhedrons or Molecules in Spaces E3 or as cr Point Groups in Spaces E4 and E5
The list of the elements of the group A5 is the following one 24(5) 20(3) 15(2) and the one of the group S5 = A5 × C2 is 24(10) 24(5) 20(6) 20(3) 31(2), the relation between these two lists is explained in paragraph 3.
The mathematic substitution group A5 is the rotation group of the regular dodecahedron and of the regular icosahedron in space E3 and the group S5 is the point symmetry group of these polyhedrons. The regular dodecahedron has 20 vertices, 30 sides and 12 faces which are regular pentagons, three to each vertex. The Euler’s theorem is verified by these three numbers, indeed 20 − 30 + 12 = 2. The regular icosahedron has 12 vertices, 30 sides and 20 faces which are equilateral triangles, three to each vertex. The Euler’s theorem is verified by these three numbers 12 − 30 + 20 = 2. These two regular Platonic polyhedrons are dual to each other and their realizations as cr point groups in spaces E4 and E5 also.
These two polyhedrons are two geometric realizations of groups A5 and S5 in space E3. The group S5 has other realizations such as for instance the symmetry group of the two molecules C60 and C20H20. The group A5 has other realizations such as the rotation group of the two molecules C60 and C20H20. The Schoënflies symbol of this symmetry group is Ih.
So, the two molecules of space E3, the buckminsterfullerene C60 and the dodecahedrane C20H20 have the same rotation group of order 60, Schoenflies’s symbol I and the same symmetry group of order 120, Schoenflies’s symbol Ih. The groups I and Ih are two “molecular” realizations in space E3 of the mathematic groups A5 and S5.
More details about groups A5 and S5 are given in the paper number II with the study of the two crystal families (rhombotopic

5. Isomorphism Classes D4 Order 8, D4 × C2 Order 16 and D4 × C2 × C2 Order 32 in Spaces E2, E3, E4, E5. Application to the Study of the Mono Incommensurate NbTe4 Phase Transition in Its Super Space
5.1. Isomorphism Class D4, One of the Five Types of Mathematic Groups of Order Eight
Sixteen cr point groups of space En 
The symmetry elements of group D4 are the following ones: 2(4) 5(2), i.e. this group has two symmetry operations of order 4 and five symmetry operations of order 2 besides the identity.
The inversion has for symbol m in space E1, 2 in space E2, 



5.1.1. Remarks about Table 2
・ The WPV symbols are very similar to the Hermann-Mauguin’s symbols 4 mm, 422. It is easy to verify that all these groups have the same distribution of elements, 2(4) 5(2) and the identity. These results are in agreement with the SS E5 lists.
・ These sixteen cr point groups belong to one crystal family of space E2, the square family, to one crystal family of space E3, the tetragonal family, to three crystal families of space E4, the square oblique, the square rectangle and the monoclinic di squares families and to four crystal families of space E5, the triclinic square, the (square oblique)-al, the square orthorhombic and the (monoclinic di squares)-al families.
・ As for every isomorphism class, the number of cr point groups of class D4 depends on the dimension of the studied space. For instance, one group acts in space E2 strictly, two in E3, five in E4 and eight in E5.
・ Thanks to the geometric approach which has been rarely used in the crystallography in the super space and to the WPV symbols which in fact generalize Hermann-Mauguin’s symbols, it is possible to predict the existence of cr point groups and crystal families in space En with 

5.1.2. Remark about Table 3
・ The geometrical supports of cr point groups of spaces E6, E7 can be obtained from those of space E5:
Table 2. Crystallographic point groups isomorphic to mathematic group D4 in spaces E2, E3, E4 and E5.
Table caption: First column: WPV symbol and geometric supports of the symmetry operations. (x y z t u) is a basis of space E5. The axes x and y on the one hand and z and t on the other hand are orthogonal, the axis u is orthogonal to space E4. Second column: Names of the crystal families. SS E5 gives this information.
Table 3. Crystallographic point groups of isomorphism class D4 in spaces E2, ・・・, E7.
Table caption: First column: Spaces. Second column: WPV symbol point groups. Third column: Names of the crystal families. Fourth column: WPV symbol of the holohedries. Fifth column: Order of the holohedries.
Space E6 
Space E7 
5.1.3. Complement about the Family Numbered I
C2 is the only mathematic group of order 2. In space En, it contains the two elements 1 and


5.2. Isomorphism Class D4 × C2
The symmetry elements of group D4 × C2 of order 16 are the following ones 4(4) 11(2), this group has four symmetry operations of order 4 and eleven symmetry operations of order 2, besides the identity. Table 5 lists the cr point group of this class. As previously, SS E5 gives this information.
5.3. Isomorphism Class D4 × C2 × C2
The symmetry elements of group D4 × C2 × C2 of order 32 are the following ones: 8(4) 23(2), i.e. 8 symmetry operations of order 8 and 23 symmetry operations of order 2 besides the identity. Among the 227 cr point groups of space E4, only one group belongs to this isomorphism class, it is the holohedry of the crystal family square rectangle, the group 4 mm
5.4. Study in the Super Space E4 of a Mono Incommensurate Modulated Phase NbTe4 and of Its Phase Transitions, between Itself (50 K < T < 793 K), Its Basic Structure and Its Lock-in Phase (L.IN) T < 50 K
The diffraction experiments prove that the inc phase NbTe4 is a mono inc phase so the super space of this structure is the four-dimensional space E4.
Table 4. Crystal families numbered I.
Table caption: Firstcolumn: Spaces. Second column: Geometric names of the family. Third column: Names of the crystal cells. Fourth column: Number of length parameters. Fifth column: Number of angular parameters.
Table 5. Crystallographic point groups isomorphic to mathematical group D4 × C2.
Table caption: First column: Family names and spaces. Second column: WPV symbol of the point groups isomorphic to the mathematic group D4 × C2. SS E5 gives this information.
As early as 1984, Van Smaalen in [11] determined the structure of this inc. phase in its super space E4. They proved that the cr point group of this structure is the group 
・ As a crystal in the usual three-dimensional space


・ As well as a crystal in the four-dimensional space 
So, we have to consider two “out of phase operators”. A linear operator which does not bring any new information, i.e. the element identity of the binary group mt. One antilinear operator which “reverses the phase of the inc phase”, i.e. the element mt, reflection in the super space E4 

To sum up, if we consider the BS of NbTe4 in space E4, its cr point group is



Now, we prove that the point group of the BS of NbTe4 in space E4 is the cr point group


To sum up, the group subgroup relation between the cr point group of the BS and the cr point group of the inc phase in their common super space E4 is the following one

If we are not afraid to work in the super space E4, the Landau’s theory of second order phase transition is verified.
6. Conclusions
As early as 1854, Arthur Cayley proved that any finite group G is isomorphic to a subgroup of the permutation group of G.
In this paper, we show that the geometric, physical, chemical and crystallographic isometry point groups which are isomorphic to the same mathematic group of permutations can be gathered together in one isomorphism class. As the cr point groups of an isomorphism class have the same mathematic structure, their Hermann-Mauguin’s symbols or Weigel Phan Veysseyre’s symbols are very similar and they have the same list of elements (arrangements). For instance, the symmetry group Ih of order 120 of the dodecahedron molecule C20H10 is isomorphic to the cr point group [5] ×


Actually, these isomorphic cr point groups are either the symmetry groups of polytopes in geometry (spaces E2, E3, E4, E5, ・・・) or the cr point groups (spaces E2, E3, E4, E5, ・・・) or the chemistry molecular symmetry groups (spaces E2 and E3) or the magnetic point groups (space E4, ・・・) or the inc phase point groups (in their super spaces, E4 for the mono, E5 for the di, and E6 for the tri inc phases).
For instance, a mathematic group, such as D6, characterizes an isomorphism class in physics, chemistry, ・・・; the groups of this class are either molecular symmetry groups such as C6v for the chemisorbed molecule C6H6 in the space E2 or cr point groups such as 6 mm in space E2 (identical to C6v) or geometric point groups of the Platon’s polyhedrons such as 6 mm for the regular hexagon of the space E2.
Yet, it is no sense to speak about an isomorphism class without specifying the spaces where these groups act. Indeed, if we do not limit the dimension of the space, an isomorphism class can contain an infinite number of groups.
Schöenflies [13] and Fedorov [14] proved that there were ten cr point groups in space E2 and thirty-two in space E3. Carl Hermann and Victor Mauguin gave the mathematic and crystallographic structures through the symbols called Hermann-Mauguin symbols. These thirty-two cr point groups of space E3 are the realizations of twenty mathematic permutation finite groups only. To sum up, they belong to the following isomorphic classes:
C1, C2, C2 × C2, C2 × C2 × C2 in the triclinic, monoclinic and orthorhombic crystal families;
C4, C4 × C2, D4, D4 × C2 in the tetragonal crystal family;
C3, C3 × C2, D3, D3 × C2, C6, C6 × C2, D6, D6 × C2 in the hexagonal crystal family;
A4, A4 × C2, S4, S4 × C2 in the cubic crystal family.
Therefore, the thirty-two cr point groups of space E3 are built from a set of twenty generators (the generators are the subgroups which allow to building the group) and there are only twenty types of Hermann-Mauguin symbols, i.e. twenty mathematical structures for the thirty-two cr point groups of space E3.
Then, the spectroscopists and the theorist chemists used the molecular symmetry groups with the Schöenflies’s molecular symbols and they simplified the theoretical approach of the bonds, of the rotations and of the vibrations of the molecules.
Of course, some of them, the cr point group Oh of SF6 in space E3, are identical to a cr point group, e.g. Cu in space E3, while the others are not identical to any cr point group of space E3 but they are identical to one cr point group of the 227 cr point groups of space E4. The group Ih of the molecule C60 in space E3 is identical to the group [5] ×

After that, when Shubnikov [15] and Bertaut [16] [17] studied the magnetic crystals in their super space E4, they used the primed symmetry operators or antisymmetry operators or time reversal operators along the fourth dimension; the time’s inversion in space E4 was actually the reflection through the mirror physical space
Let us give an example. A finite mathematic group such as C2 × C2 × C2 of order 8 can realize itself in the magnetic point group of space E4 22.1’, (1’ is the binary group with the conservation of the time 1 and the inversion of the time 1’) in the set of the 122 magnetic point groups of space E4.
We see that a ferromagnetic mono inc. phase will be a super crystal in space E5 where the time’s inversion will be a reflection through the super space E4
The first structure determinations of inc phases which were super crystals in their super spaces were made by De Wolf in [18] , Janner and Janssen [19] , and Grébille, Weigel, Veysseyre and Phan [20] .
Now, the super crystallographers find the mono, di and triinc phase structures in the superspaces E4, E5 and E6 and soon they will study their physical properties and their transitions of phases in these same super spaces.
Acknowledgements
Many thanks to the super crystallography’s pioneers who have inspired us:
Alexey Vassilyevich Schubnikov† for the long and fruitful discussion in this Moskow Institute in 1966.
E. F. Bertaut† for his constant support, all the work together and the gift of his friendship.
Aloyso Janner and Ted Janner for fruitful discussions, especially in Nijmegen and in Paris.
Hubert Curien, crystallographer, the father of the European Spatial Program and also French Minister of the Research and Technology.
A. J. C. Wilson† (Symmetry I.T.C.) who reproached us not to have begun earlier that geometric approach because he should have done it with us. What honour!
The theorist Chemists and Spectroscopists of the Chemistry Departement of “Ecole Polytechnique” Palaiseau France.
References
- International Tables for Crystallography (1996) Vol. A Edited by T. Hahn. Kluwer Academic Publishers, Dordrecht/ Boston/London.
- Veysseyre, R. and Veysseyre, H. (2002) Crystallographic Point Groups of Five-Dimensional Space 1. Their Elements and Their Subgroups. Acta Crystallographica Section A, 58, 429-433.
- Weigel, D., Phan, T. and Veysseyre, R. (1987) Crystallography, Geometry and Physics in Higher Dimensions. III. Geometrical Symbols for the 227 Crystallographic Point Groups in Four-Dimensional Space. Acta Crystallographica Section A, 43, 294-304. http://dx.doi.org/10.1107/S0108767387099367
- Janssen, T., Birman, J.L., Koptsik, V.A., Senechal, M., Weigel, D., Yamamoto, A., Abrahams, S.C. and Hahn, T. (1999) Symmetry Elements in Space Groups and Point Groups. Acta Crystallographica Section A, 55, 761-782.
- Weigel, D., Phan, T. and Veysseyre, R. (2008) Crystal Families and Systems in Higher Dimensions, and Geometrical Symbols of Their Point Groups. II. Cubic Families in Five- and n-Dimensional Spaces. Acta Crystallographica Section A, 64, 687-697. http://dx.doi.org/10.1107/S0108767308028766
- Brown, H., Bulöw, R., Neubüser, J., Wondratschek, H. and Zassenhaus, H.J. (1978) Crystallographic Groups of Four- Dimensional Space. Wiley, New York.
- Plesken, W. (1981) Bravais Groups in Low Dimensions. Communications in Mathematical Chemistry, 97-119.
- Plesken, W. and Hanrath, W. (1984) The Lattices of Six-Dimensional Euclidean Space. Mathematics of Computation, 43, 573-587. http://dx.doi.org/10.1090/S0025-5718-1984-0758205-5
- Plesken, W. and Schulz, T. (2000) Counting Crystallographic Groups in Low Dimensions. Experimental Mathematics, 9, 407-411.
- Coxeter, H.S.M. and Moser, W.O.J. (1965) Generators and Relations for Discrete Groups. Springer-Verlag, Berlin, Göttingen, Heidelberg, New York, 117-133.
- Van Smaalen, S., Bronsema, K.D. and Mahy, J. (1986) The Determination of the Incommensurately Modulated Structure of Niobium Tetratelluride. Acta Crystallographica B, 42, 43-50.
- Chen, Z.Y. and Walker, M.B. (1989) Superspace Symmetry Modes and Incommensurate-to-Incommensurate Phase Transition in NbTe4. Physical Review B, 40, 8983-8994. http://dx.doi.org/10.1103/PhysRevB.40.8983
- Schöenflies, A. (1984) Krystallsysteme und Krystallstructur. Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-61740-9
- Fedorov, E.S. (1891) The Symmetry of Regular Systems of Figures (in Russian). Proceedings of the Imperial St. Petersburg Mineralogical Society, 28, 1-146.
- Shubnikov, A.V. and Belov, N.V. (1964) Colored Symmetry. Pergamon Press, Oxford.
- Bertaut, E.F. (1950) Raies de Debye-Scherrer et repartition des dimensions des domaines de Bragg dans les poudres polycristallines. Acta Crystallographica, 3, 14-18. http://dx.doi.org/10.1107/S0365110X50000045
- Bertaut, E.F. (1952) Sur la correction de la transformée de Fourier d’une raie de Debye-Scherrer dans la mesure de dimensions cristallines. Acta Crystallographica, 5, 117-121. http://dx.doi.org/10.1107/S0365110X5200023X
- de Wolff, P.M. (1974) The Pseudo-Symmetry of Modulated Crystal Structures. Acta Crystallographica, A30, 777-785. http://dx.doi.org/10.1107/S0567739474010710
- Janner, A. and Janssen, T. (1977) Symmetry of Periodically Distorted Crystals. Physical Review B, 15, 643-651. http://dx.doi.org/10.1103/PhysRevB.15.643
- Grébille, D., Weigel, D., Veysseyre, R. and Phan, T. (1990) Crystallography, Geometry and Physics in Higher Di- mensions. VII. The Different Types of Symbols of the 371 Mono-Incommesurate Superspace Groups. Acta Crystal- lographica Section A, 46, 234-240.
Annex
Abstract Mathematic Groups
We summarize the main properties of some types of abstract groups. The used notations are those of Coxeter for the greatest part.
E is the unit element of the group, and the mark × is used for a direct product.
Cyclic Group Cn
A cyclic group Cn is a group of order n generated by only one element g such as
Dihedral Group Dn
The dihedral group Dn is a group of order 2n; it is the group of the n rotations and of the n symmetries of a plane which preserve a regular polygon to n vertices. This group is generated by two elements T and R such as:
Particular cases of dihedral groups
・ If 
・ D2 = D1 × C2 = C2 × C2.
Symmetric Group Sn
The symmetric group Sn is the permutation group of the n vertices of a regular simplex in the (n-1)-dimensional space; it is of order n!
Alternating Group An
The alternating group An is the group of the even permutation of n objects; it is of order n!/2.
Dicyclic Group
The dicyclic group 

Of course, the symbol 

Quaternion Group
The smallest dicyclic group is the group

Cayley’s Theorem
“Any group G is isomorphic to a subgroup of the symmetric group
If the group G is a finite group of order n, this group G is isomorphic to a subgroup of Sn
Demonstration
Let be g an element of the group G. We consider the application 

This application is bijective, indeed:





As the law of the group G is associative, it is possible to write:
Therefore, this application is a permutation and the application 

is a morphism of group, then the picture of

As the application of G in 
If the order of G is finite, the picture of G is a subgroup of Sn (n order of G)
NOTES
*Corresponding author.













