ABSTRACT

The notion of preordering, which is a generalization of the notion of ordering, has been introduced by Serre. On the other hand, the notion of round quadratic forms has been introduced by Witt. Based on these ideas, it is here shown that 1) a field is formally real n-pythagorean iff the nth radical, is a preordering (Theorem 2), and 2) a field 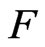is n-pythagorean iff for any n-fold Pfister form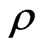. There exists an odd integer such that 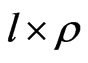is a round quadratic form (Theorem 8). By considering upper bounds for the number of squares on Pfister’s interpretation, these results finally lead to the main result (Theorem 10) such that the generalization of pythagorean fields coincides with the generalization of Hilbert’s 17th Problem.

1. Introduction

In the latter half of the twentieth century, a consideration for the generalization of pythagorean fields has been made by many researchers, e.g., Elman and Lam [1], Becker [2], Koziol, Szymiczek, and Yucas [3-6], Kijima and Nishi [7], and so on.

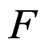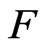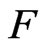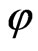Throughout the paper, let be a field of characteristic different from 2 and be the multiplicative group of. A field is said to be pythagorean if. For a quadratic form over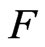, we put and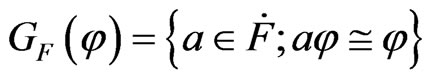. Witt [8] defined a round quadratic form 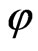as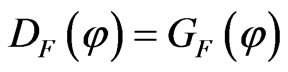. Recall that Pfister forms are round ([8], Satz 4. (c)).

The class of fields with the following property has been proposed by Elman and Lam [1]:

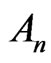: Any torsion n-fold Pfister form over F is hyperbolic.

Furthermore, they made a hypothesis that if a field 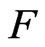satisfies the property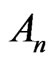, then the ideal 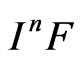is torsionfree, where is the ideal of even dimensional forms in the Witt ring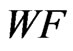. Szymiczek [5] replaced this hypothesis with a problem of rigid elements that if, then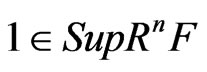, and had studied this problem for amenable fields, linked fields, abstract Witt rings of elementary type, and so on. When a field satisfies the property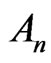, it is clear that 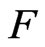also satisfies the property.

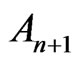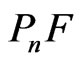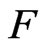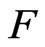We denote by the set of n-fold Pfister forms over and by the nth radical of, which is given by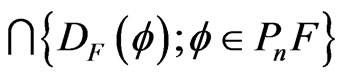. This radical defined by Yucas [6] shows a generalization of Kaplansky’s radical 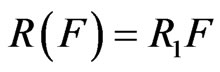[9].

Later, Koziol [3] has proposed the class of npythagorean fields with the following property as every n-fold Pfister form represents all sums of squares over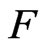, that is,.

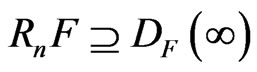Pythagorean fields are -pythagorean and the class of 1-pythagorean fields is the same as the class of quasipythagorean fields defined by Kijima and Nishi [7]. In fact, the class of n-pythagorean fields is the same as the class of fields which satisfy the property 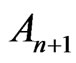([3], Proposition 2.3).

On the other hand, a generalization of Hilbert’s 17th Problem has been accomplished by Artin [10]. Later, an interpretation of this generalization has been made by Pfister [11], who has proposed the class of 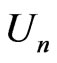-fields with the following property as for any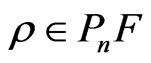, holds, where

.

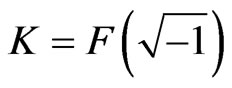Furthermore, he showed implicitly in ([11], chapter 6, Theorem 3.5) that if a field is a -field, then 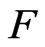is n-pythagorean.

Unexplained notation and terminology refer to [12,13].

2. Preorderings and Round Quadratic Forms

Pfister [11] has derived upper bounds for the number of squares on Hilbert’s 17th Problem. Hence, the following can be shown by results of Artin [10] and Pfister ([11], chapter 6, Corollary 3.4).

Theorem 1. Let be the rational function field in n variables over a real closed field R and 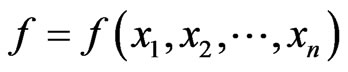be an element of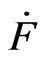. Then the following statements are equivalent:

1) 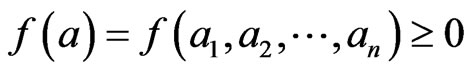for all 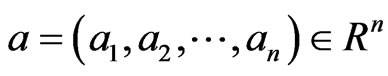where is defined.

2) holds.

3) is a totally positive element.

We shall prove some results by use of the notions of preorderings (Serre [14]) and round quadratic forms. By Proposition 2.3 in [3] and Lemma 3.1 in [15], the following can be shown.

Theorem 2. (([16], Proposition 1), ([17], Proposition 2.1)). For a field F, the following statements are equivalent:

1) F is n-pythagorean.

2) holds for all.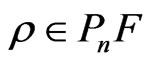

In particular, if F is formally real, these statements are further equivalent to the condition.

3) The nth radical 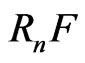is a preordering.

If a field 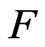is n-pythagorean, then 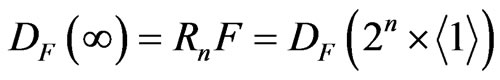. Thus, the following can be obtained.

Corollary 3. (cf. [13], Corollary 11.4.11). For any formally real n-pythagorean field F, every totally positive element of F is a sum of 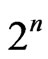squares.

Remark 4. Corollary 3 shows a generalization of Hilbert’s 17th Problem. The notion of preordering and nth radical play an important role for this Problem. A typical example of n-pythagorean field is a field of transcendence degree n over a real closed field. Many examples of n-pythagorean fields are known. For example, n-Hilbert fields are so in [4]. Also, Kijima [18] has constructed many such examples by use of some results of Kula [19].

Next, we shall discuss about the generalization of pythagorean fields. The following result is well-known.

Theorem 5. (cf. [8], Satz 3. (g)). Let be a field and l 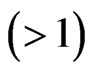be an odd integer. Then the following statements are equivalent:

1) The form 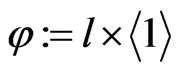is round.

2) 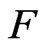is pythagorean.

In particular, if the form 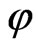is anisotropic, then 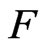is a formally real field.

Proposition 6. ([16, Proposition 3]). Let be an n-fold Pfister form over F and l 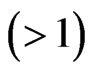be an odd integer. If 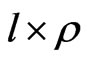is a round quadratic form, then 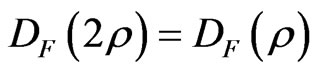holds.

Proof. For any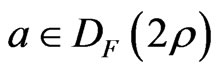, it is sufficient to show that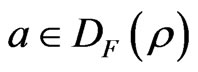. The round form 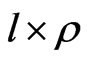means that. Since is an odd integer, we put 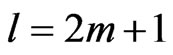for some integer. Hence it follows that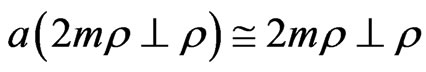. On the other hand, since 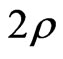is a Pfister form, 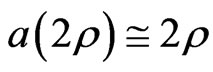holds and then. Thus 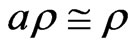follows from Witt’s Cancellation Theorem. This implies that.

Corollary 7. ([16, Proposition 3]). If there exist an integ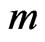er and an odd integer 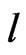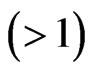such that the form is anisotropic round, then F is formally real.

Proof. Since the form 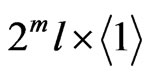is round, it follows from Proposition 6 that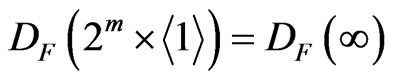. If a field 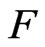is non-real, then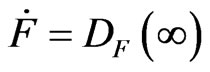. This contradicts the assumption that 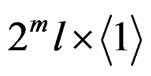is anisotropic.

As a characterization of an n-pythagorean property, the following generalization of pythagorean fields can be presented.

Theorem 8. ([16], Proposition 3). For a field F, the following statements are equivalent:

1) F is n-pythagorean.

2) For any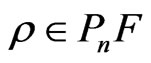, there exists an odd integer such that 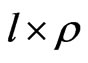is a round quadratic form.

Proof. (1) => (2): If a field 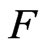is n-pythagorean, then 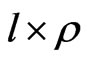is a round quadratic form for any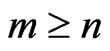, any positive integer 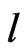and any.

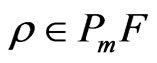(2) => (1): This follows from Theorem 2 and Proposition 6.

Theorem 9. The n-pythagorean field is the generalization of pythagorean field and the Pythagoras number of this field is at most.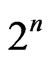

Proof. If a field is m-pythagorean, then 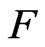is (m + 1)-pythagorean. Thus, it follows from Theorem 5 and Theorem 8.

Finally, the main result of this paper has been established as follows.

Theorem 10. The generalization of pythagorean fields coincides with the generalization of Hilbert’s 17th Problem.

Proof. If a field is non-real, then 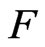has no ordering and moreover holds. Therefore, Hilbert’s 17th Problem results in a problem that if a field is non-real, then does an equality hold? Thus, the required result can be established by use of Corollary 3 and Theorem 9.

Incidentally, the notion of round quadratic forms is connected with the torsion-freeness of the ideal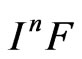. We shall extend Proposition 2.3 in [7] to an npythagorean field.

Proposition 11. ([17, Proposition 3.1]). Let 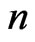be an integer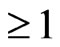. If F is an n-pythagorean field, then the following statements hold.

1)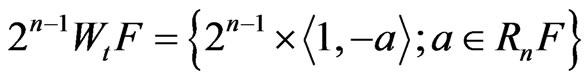, where 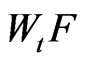is the maximal torsion subgroup of.

2) 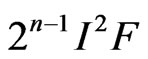is torsion-free.

Proof. 1) For any element 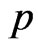of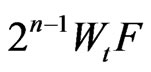, there exists an element 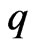of 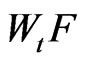such that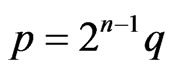. By ([20], Satz 22), we can find and 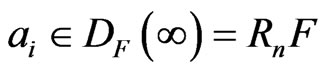such that

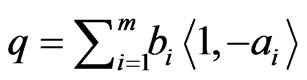in. Because of

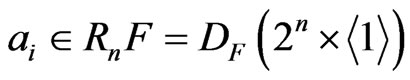, the Pfister form is universal and round. Hence and in.

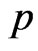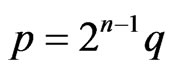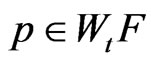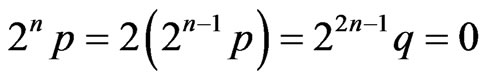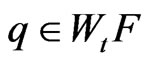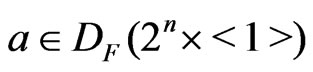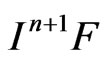2) For any element of, it is sufficient to show that p = 0. Now there exists an element of such that. Since, it follows from 1) that. Therefore and then for some element from 1). Since is an element of, it follows from ([13], Hauptsatz 10.5.1) that p = 0.

Remark 12. In case of 1-pythagorean fields, statements 1) and 2) of Proposition 11 are equivalent (see Remark 2.4 in [7]). As a characterization of 1-pythagorean fields, Corollary 4.4 of Krawczyk [21] is beautiful and can be extended to 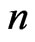-pythagorean fields. This will be given in the forthcoming paper [22].

3. Concluding Remark

Becker [2] has used the terminology of n-pythagorean field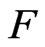s as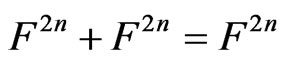. Therefore, for the field with the property 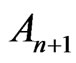defined by Elman and Lam [1], the following name shall be recommended as Hilbert-Pythagoras field of level n.

4. Acknowledgements

The author would like to express his deep appreciation to the late Professor M. Nishi for leading to the quadratic form theory. Also, he is very grateful to Professor S. Kageyama and the late Dr. T. Iwakami for their valuable advices.

REFERENCES