Advances in Pure Mathematics
Vol.4 No.3(2014), Article ID:44336,5 pages DOI:10.4236/apm.2014.43011
Filtered Ring Derived from Discrete Valuation Ring and Its Properties
M. H. Anjom Shoa*, M. H. Hosseini
University of Birjand, Birjand, Iran
Email: *ajomshoamh@birjand.ac.ir, mhhosseini@birjand.ac.ir
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 7 January 2014; revised 7 February 2014; accepted 15 February 2014
ABSTRACT
In this paper we show that if 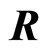 is a discrete valuation ring, then
is a discrete valuation ring, then 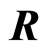 is a filtered ring. We prove some properties and relation when
is a filtered ring. We prove some properties and relation when  is a discrete valuation ring.
is a discrete valuation ring.
Keywords:Commutative Ring; Valuation Ring; Discrete Valuation Ring; Filtered Ring; Graded Ring; Filtered Module; Graded Module

1. Introduction
In commutative algebra, valuation ring and filtered ring are two most important structures (see [1] -[3] ). If  is a discrete valuation ring, then
is a discrete valuation ring, then  has many properties that have many usages for example decidability of the theory of modules over commutative valuation domains (see [1] -[3] ), Rees valuations, and asymptotic primes of rational powers in Noetherian rings, and lattices (see [4] ). We know that filtered ring is also a most important structure since filtered ring is a base for graded ring especially associated graded ring, completion, and some results like on the Andreadakis Johnson filtration of the automorphism group of a free group (see [5] ) on the depth of the associated graded ring of a filtration (see [6] ). So, as important structures, the relation between these structures is useful for finding some new structure. In this article, we show that we can make a filtration with a valuation. Then we explain some new properties for it. On the other hand, we show this is a strongly filtered ring, then we explain some new properties for it.
has many properties that have many usages for example decidability of the theory of modules over commutative valuation domains (see [1] -[3] ), Rees valuations, and asymptotic primes of rational powers in Noetherian rings, and lattices (see [4] ). We know that filtered ring is also a most important structure since filtered ring is a base for graded ring especially associated graded ring, completion, and some results like on the Andreadakis Johnson filtration of the automorphism group of a free group (see [5] ) on the depth of the associated graded ring of a filtration (see [6] ). So, as important structures, the relation between these structures is useful for finding some new structure. In this article, we show that we can make a filtration with a valuation. Then we explain some new properties for it. On the other hand, we show this is a strongly filtered ring, then we explain some new properties for it.
2. Preliminaries
In this paper the ring 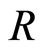 means a commutative ring with unit.
means a commutative ring with unit.
Definition 2.1 A subring 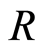 of a field
of a field 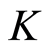 is called a valuation ring of
is called a valuation ring of , if for every
, if for every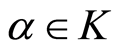 ,
, 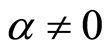 , either
, either  or
or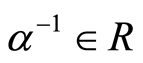 .
.
Definition 2.2 Let 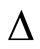 be a totally ordered abelian group. A valuation
be a totally ordered abelian group. A valuation  on
on  with values in
with values in 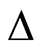 is a mapping
is a mapping  satisfying:
satisfying:
i)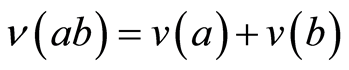 ;
;
ii)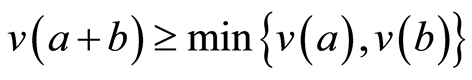 .
.
Definition 2.3 Let 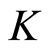 be field. A discrete valuation on
be field. A discrete valuation on 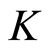 is a valuation
is a valuation 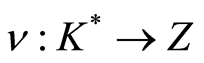 which is surjective.
which is surjective.
Definition 2.4 A fractionary ideal of  is an
is an 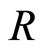 -submodule
-submodule  of
of  such that
such that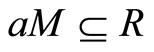 , for some
, for some ,
,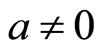 .
.
Definition 2.5 A fractionary ideal 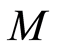 is called invertible, if there exists another fractionary ideal
is called invertible, if there exists another fractionary ideal 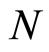 such that
such that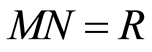 .
.
Proposition 2.1 Let 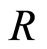 be a local domain. Every non zero fractionary ideal of
be a local domain. Every non zero fractionary ideal of 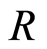 is invertible if and only if
is invertible if and only if 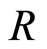 is DVR (see [3] ).
is DVR (see [3] ).
Theorem 2.1 Let 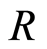 be a Noetherian local domain with unique maximal ideal
be a Noetherian local domain with unique maximal ideal  and
and 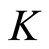 the quotient field of
the quotient field of . The following conditions are equivalent.
. The following conditions are equivalent.
i)  is a discrete valuation ring;
is a discrete valuation ring;
ii) 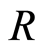 is a principal ideal domain;
is a principal ideal domain;
iii) 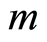 is principal;
is principal;
iv)  is internally closed and every non-zero prime ideal of
is internally closed and every non-zero prime ideal of  is maximal;
is maximal;
v) Every non-zero ideal of  is power of
is power of 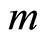 (see [3] ).
(see [3] ).
Definition 2.6 Let 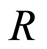 be a ring together with a family
be a ring together with a family 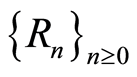 of subgroups of
of subgroups of 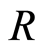 if satisfying the following conditions:
if satisfying the following conditions:
i) ;
;
ii) 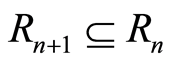 for all
for all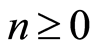 ;
;
iii) 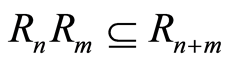 for all
for all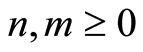 ;
;
Then we say 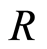 has a filtration.
has a filtration.
Definition 2.7 Let 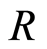 be a ring together with a family
be a ring together with a family 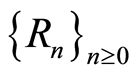 of subgroups of
of subgroups of 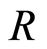 if satisfying the following conditions:
if satisfying the following conditions:
i) ;
;
ii)  for all
for all ;
;
iii) 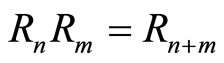 for all
for all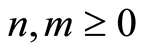 ;
;
Then we say 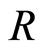 has a strong filtration.
has a strong filtration.
Example 2.1 Let  be an ideal of
be an ideal of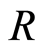 , then
, then  is a filtration that is called
is a filtration that is called 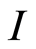 adic filtration ring.
adic filtration ring.
Definition 2.8 Let 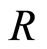 be a filtered ring. A filtered
be a filtered ring. A filtered 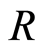 -module
-module 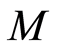 is an
is an  -module together with family
-module together with family 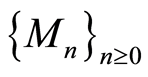 of subgroup
of subgroup  of satisfying:
of satisfying:
1.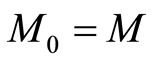 ;
;
2. 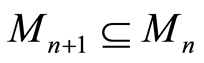 for all
for all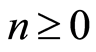 ;
;
3.  for all
for all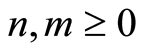 .
.
Then we say  has a filtration.
has a filtration.
Definition 2.9 A map 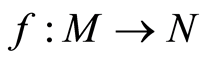 is called a homomorphism of filtered modules, if: i)
is called a homomorphism of filtered modules, if: i) 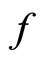 is
is 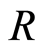 -module an homomorphism and ii)
-module an homomorphism and ii) 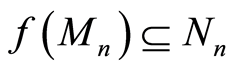 for all
for all .
.
Definition 2.10 A graded ring 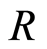 is a ring, which can expressed as a direct sum of subgroup
is a ring, which can expressed as a direct sum of subgroup  i.e.
i.e. 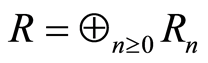 such that
such that 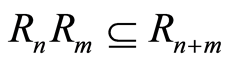 for all
for all 
Definition 2.11 Let 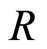 be a graded ring. An
be a graded ring. An  -module
-module 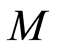 is called a graded
is called a graded 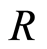 -module, if
-module, if 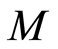 can be expressed as a direct sum of subgroups
can be expressed as a direct sum of subgroups 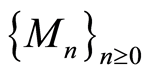 i.e.
i.e. 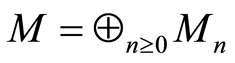 such that
such that 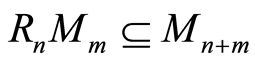 for all
for all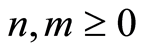 .
.
Definition 2.12 Let  and
and 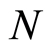 be graded modules over a graded ring
be graded modules over a graded ring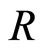 . A map
. A map 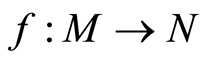 is called homomorphism of graded modules if: i)
is called homomorphism of graded modules if: i) 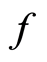 is
is  -module an homomorphism and ii)
-module an homomorphism and ii) 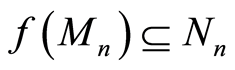 for all
for all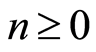 .
.
Definition 2.13 Let 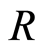 be a filtered ring with filtration
be a filtered ring with filtration . Let
. Let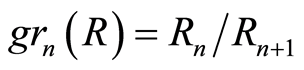 , and
, and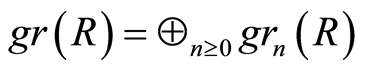 . Then
. Then 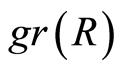 has a natural multiplication induced from
has a natural multiplication induced from 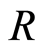 given
given
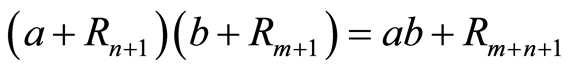
where . This makes
. This makes 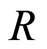 in to a graded ring. This ring is called the associated graded ring of
in to a graded ring. This ring is called the associated graded ring of .
.
Definition 2.14 Let 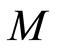 be a filtered
be a filtered  -module over a filtered ring
-module over a filtered ring 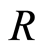 with filtration
with filtration 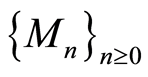 and
and 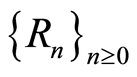 respectively. Let
respectively. Let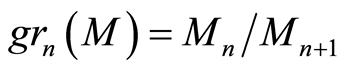 , and
, and . Then
. Then 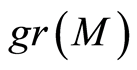 has a natural
has a natural
 -module structure given by
-module structure given by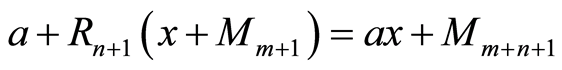 , where
, where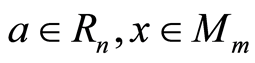 .
.
3. Filtered Ring Derived from Discrete Valuation Ring and Its Properties
In this section we proved that, if  is a discrete valuation ring, then
is a discrete valuation ring, then 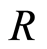 is a filtered ring. And we prove some properties for
is a filtered ring. And we prove some properties for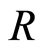 .
.
Let  be a field which
be a field which 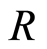 be a domain and a discrete valuation ring (DVR) for
be a domain and a discrete valuation ring (DVR) for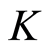 . The map
. The map 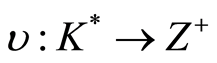 is valuation of
is valuation of .
.
Lemma 3.1 By above definition, the set 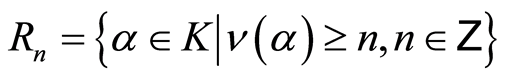 is an ideal of
is an ideal of .
.
Proof. (see [3] )
Theorem 3.1 If  is a discrete valuation ring with valuation
is a discrete valuation ring with valuation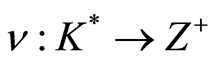 . Then
. Then 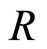 is a filtered ring with filtration defined by
is a filtered ring with filtration defined by
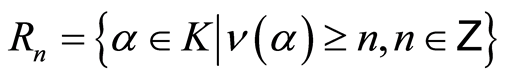
where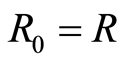 .
.
Proof. By definition of valuation ring, it is obvious that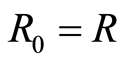 . For the second condition for filtration ring we have
. For the second condition for filtration ring we have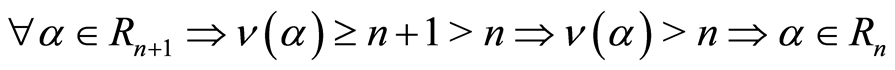 , So we have
, So we have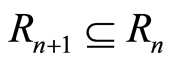 .
.
For the third condition, we have for every 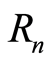 and
and  without losing generality. Since
without losing generality. Since  and
and 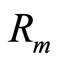 are ideals of
are ideals of 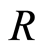 so
so

is an ideal of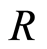 .
.
Now let 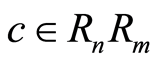 then
then  for
for  and
and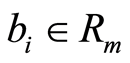 .
.
Thus

Consequently we have 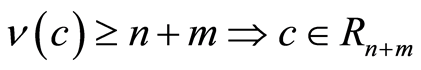 hence
hence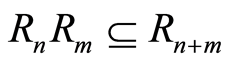 . Therefore
. Therefore 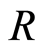 is a filtered ring.
is a filtered ring.
Proposition 3.1 Let 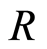 be a local domain. If every non-zero fractionary ideal of
be a local domain. If every non-zero fractionary ideal of 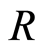 invertible, then
invertible, then  is filtered ring.
is filtered ring.
Proof. By proposition 2.1 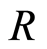 is DVR then by theorem 3.1
is DVR then by theorem 3.1  is filtered ring.
is filtered ring.
Proposition 3.2 Let 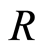 be a Noetherian local domain with unique maximal ideal
be a Noetherian local domain with unique maximal ideal 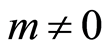 and
and 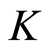 the quotient field of
the quotient field of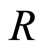 . Then
. Then  is filtered ring if one of following conditions is held i)
is filtered ring if one of following conditions is held i) 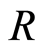 is a principal ideal domain;
is a principal ideal domain;
ii) 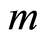 is principal;
is principal;
iii)  is integrally closed and every non-zero prime ideal of
is integrally closed and every non-zero prime ideal of 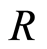 is maximal.
is maximal.
Proof. It follows from theorem (3.1) and theorem (2.1).
Definition 3.1 Let  be a ring, and let
be a ring, and let 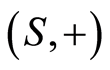 be a totally ordered cancellative semigroup having identity
be a totally ordered cancellative semigroup having identity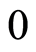 . A function
. A function 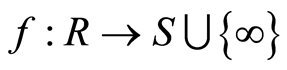 is a filtration if
is a filtration if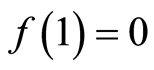 ,
, 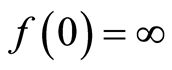 and for all
and for all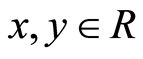 i)
i)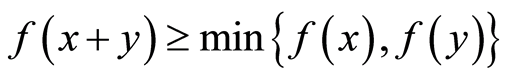 , and ii)
, and ii) , then
, then  is called a filtration.
is called a filtration.
For this filtration we have 1) 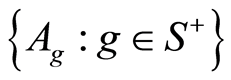 the set of ideals;
the set of ideals;
2)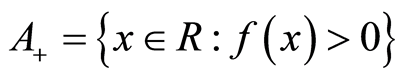 ;
;
3)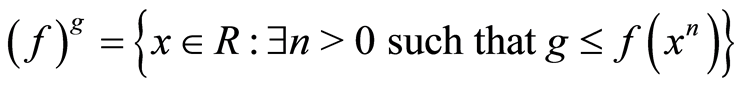 ;
;
4)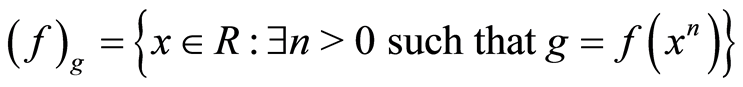 .
.
Lemma 3.2 Let  be a filtration and let
be a filtration and let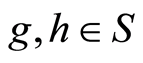 . Then:
. Then:
i)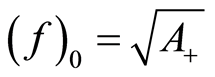 ;
;
ii)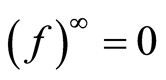 ;
;
iii) ;
;
iv) if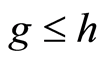 , then
, then 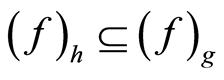 and
and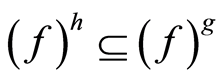 .
.
Proof. See lemma 3.3 of [7] .
Proposition 3.3 If  be a discrete valuation ring, then there exists a totally ordered cancellative semigroup
be a discrete valuation ring, then there exists a totally ordered cancellative semigroup , and
, and 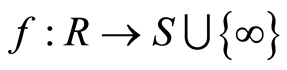 such that:
such that:
i) ;
;
ii)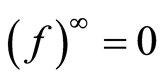 ;
;
iii)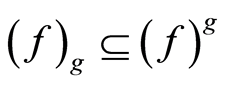 ;
;
iv) if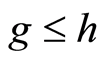 , then
, then , and
, and .
.
Proof. By theorem 3.1 there exists a filtration for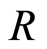 , then by lemma 2.1 we have the all above conditions.
, then by lemma 2.1 we have the all above conditions.
Proposition 3.4 Let 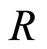 be a filtered ring,
be a filtered ring, 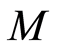 ,
, 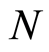 filtered
filtered  -modules, and
-modules, and  homomorphism of filtered
homomorphism of filtered  -modules. If the induced map
-modules. If the induced map 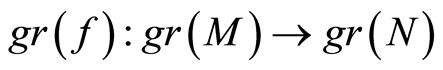 is injective, then
is injective, then 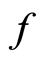 is injective provided
is injective provided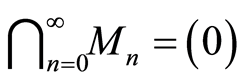 . (see [3] )
. (see [3] )
Corollary 3.1 Let 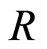 be a valuation ring,
be a valuation ring, 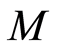 ,
, 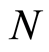 filtered
filtered 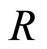 -modules, and
-modules, and 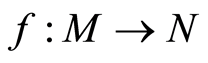 homomorphism of filtered
homomorphism of filtered  -modules. If the induced map
-modules. If the induced map 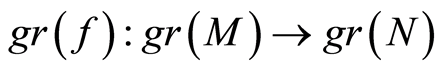 is injective, then
is injective, then 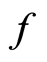 is injective provided
is injective provided .
.
Proposition 3.5 If 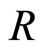 is a discrete valuation ring with valuation
is a discrete valuation ring with valuation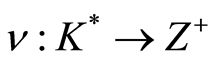 , Then
, Then 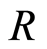 is a strongly filtered ring with filtration defined by
is a strongly filtered ring with filtration defined by
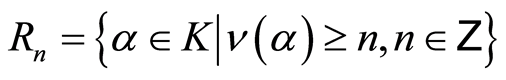
where .
.
Proof. By theorem 3.1 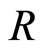 is a filtered ring. Now we show
is a filtered ring. Now we show  for all
for all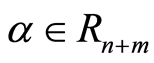 . Since
. Since 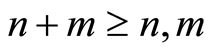 so
so

Consequently , and
, and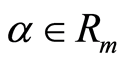 . Therefore
. Therefore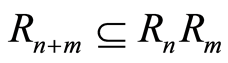 .
.
Proposition 3.6 Let  be a discrete valuation ring, and
be a discrete valuation ring, and . If
. If 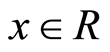 and
and , then
, then
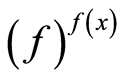 is smallest prime ideal in
is smallest prime ideal in  which contains
which contains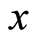 , and
, and 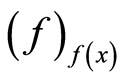 is largest prime ideal in
is largest prime ideal in 
which does not contains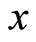 .
.
Proof. By proposition 3.5 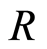 is strongly filtered ring, then by proposition 4.2. of [7] -[9] we have If
is strongly filtered ring, then by proposition 4.2. of [7] -[9] we have If  and
and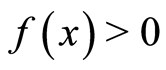 , then
, then 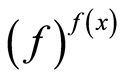 is smallest prime ideal in
is smallest prime ideal in 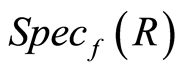 such that contains
such that contains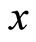 , and
, and 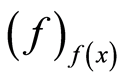 is the largest prime ideal in
is the largest prime ideal in  such that does not contains
such that does not contains .
.
Remark 3.1 Given a strong filtration  on a ring
on a ring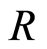 , we say that a prime
, we say that a prime 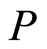 in
in 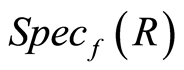 is branched in
is branched in , if
, if 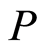 cannot be written as union of prime ideals in
cannot be written as union of prime ideals in 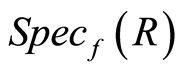 such that properly contained in
such that properly contained in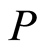 .
.
Corollary 3.2 Let  be a discrete valuation ring and
be a discrete valuation ring and . Then a prime ideal
. Then a prime ideal 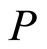 in
in 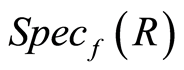 is branched in
is branched in  if and only if
if and only if 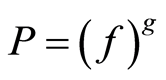 for some
for some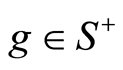 .
.
Proof. By proposition 3.5 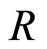 is strongly filtered ring, then by proposition 4.5. of [7] a prime ideal
is strongly filtered ring, then by proposition 4.5. of [7] a prime ideal 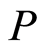 in
in 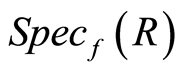 is branched in
is branched in , if and only if,
, if and only if, 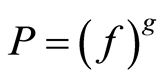 for some
for some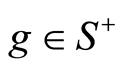 .
.
References
- Atiyah, M.F. and Macdonald, L.G. (1969) Introduction to Commutative Algebra. Addison-Wesley Publishing Company.
- Bourbaki, N. (1972) Commutative Algebra. Originally Published as Elements de Mathematique, Algebra Commutative 1964, 1965, 1968, 1969 by Hermann, Paris.
- Gopalakrishnan, N.S. (1983) Commutative Algebra. Oxonian Press, PVT, LTD, New Delhi.
- Puninskia, G., Puninskayab, V. and Toffalorib, C. (2007) Decidability of the Theory of Modules over Commutative Valuation Domains. Annals of Pure and Applied Logic, 145, 258-275. http://dx.doi.org/10.1016/j.apal.2006.09.002
- Cohen, F.R. and Heap, A. (2011) Alexandra Pettet on the Andreadakis Johnson Filtration of the Automorphism Group of a Free Group. Journal of Algebra, 329, 72-91. http://dx.doi.org/10.1016/j.jalgebra.2010.07.011
- Levy, R., Loustauna, P. and Shapiro, J. (1991) The Prime Spectrum of an Infinite Product of Copies of Z. Fundamenta Mathematicae, 138, 155-164.
- Nishida, K. (2005) On the Depth of the Associated Graded Ring of a Filtration. Journal of Algebra, 285, 182-195. http://dx.doi.org/10.1016/j.jalgebra.2004.10.026
- Olberding, B., Saydam, S. and SHapiro, J. (2005) Complitions, Valuations and Ultrapowers of Noetherian Domain. Journal of Pure and Applied Algebra, 197, 213-237. http://dx.doi.org/10.1016/j.jpaa.2004.09.002
NOTES

*Corresponding author.

