Advances in Pure Mathematics
Vol.3 No.2(2013), Article ID:28551,5 pages DOI:10.4236/apm.2013.32033
Hilbert Boundary Value Problem with an Unknown Function on Arbitrary Infinite Straight Line
Mathematics College, Northeast Petroleum University, Daqing, China
Email: caolixia98237@163.com
Received December 9, 2012; revised January 11, 2013; accepted January 29, 2013
Keywords: arbitrary infinite straight line; symmetric extension; Hilbert boundary Value problem; unknown function; Riemann boundary value problem
ABSTRACT
We consider a Hilbert boundary value problem with an unknown parametric function on arbitrary infinite straight line passing through the origin. We propose to transform the Hilbert boundary value problem to Riemann boundary value problem, and address it by defining symmetric extension for holomorphic functions about an arbitrary straight line passing through the origin. Finally, we develop the general solution and the solvable conditions for the Hilbert boundary value problem.
1. Introduction
Various kinds of boundary value problems (BVPs) for analytic functions or polyanalytic functions have been widely investigated [1-8]. The main approach is to use the decomposition of polyanalytic functions and their generalization to transform the boundary value problems to their corresponding boundary value problems for analytic functions. Recently, inverse Riemann BVPs for generalized holomorphic functions or bianalytic functions have been investigated [9-12].
In this paper, we consider a kind of Hilbert BVP with an unknown parametric function. We first define the symmetric extension of holomorphic function about an infinite straight line passing through the origin, and discuss its several important properties. And after, we propose a Hilbert BVP with an unknown parametric function on arbitrary half-plane with its boundary passing through the origin. Then, we transform the Hilbert BVP into a Riemann BVP on the infinite straight line using the defined symmetric extension. Finally, we discuss the solvable conditions and the solution for the Hilbert BVP.
2. A Hilbert Boundary Value Problem with an Unknown Function
Let ![]() be an infinite straight line with an inclination
be an infinite straight line with an inclination 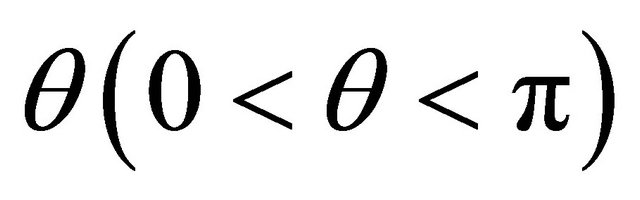 in the complex plane, passing through the origin and being oriented in upward direction. Let
in the complex plane, passing through the origin and being oriented in upward direction. Let 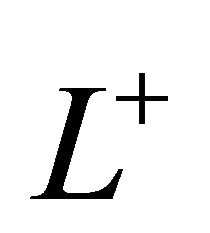 and
and 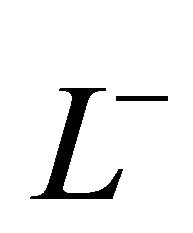 denote the upper half-plane and the lower halfplane cut by
denote the upper half-plane and the lower halfplane cut by![]() .
.
Our objective is to find a pair of functions 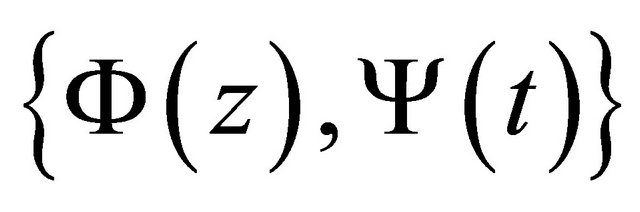 , where
, where 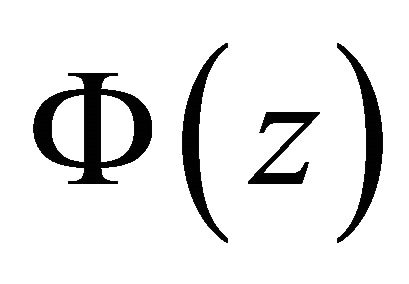 is holomorphic in the domain
is holomorphic in the domain 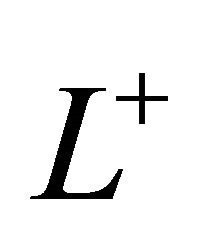 and continuously extendable to its boundary
and continuously extendable to its boundary![]() , and
, and 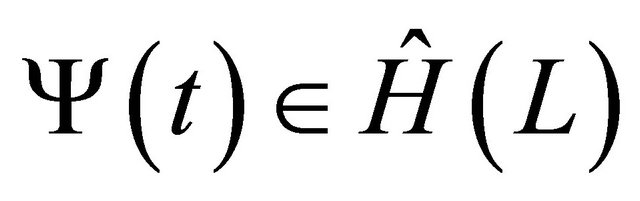 is real-valued and Holder continuous on
is real-valued and Holder continuous on![]() , satisfying the following boundary conditions
, satisfying the following boundary conditions
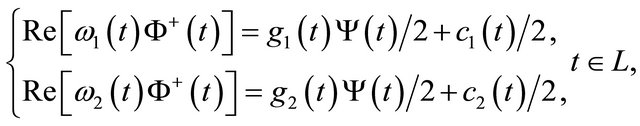 (1)
(1)
where
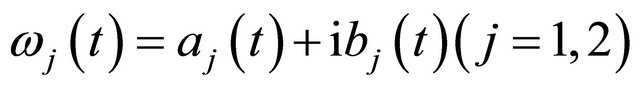 and
and
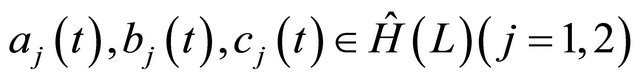
are given functions.
3. Symmetric Extension of Holomorphic Functions about an Infinite Straight Line
An important step in solving problem (1) is to define a symmetric extension of holomorphic functions about the infinite straight line ![]() with an inclination
with an inclination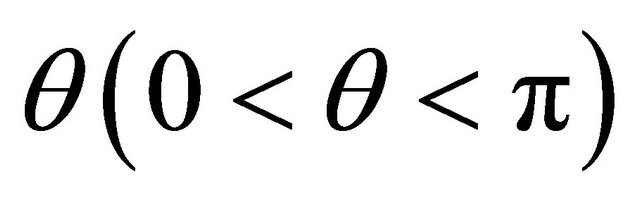 .
.
For a holomorphic function  in the simplyconnected domain
in the simplyconnected domain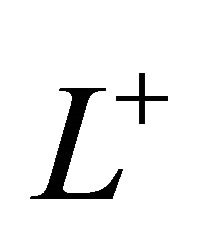 , we define the symmetric extension of
, we define the symmetric extension of  about
about ![]() as follows:
as follows:
 , (2)
, (2)
where 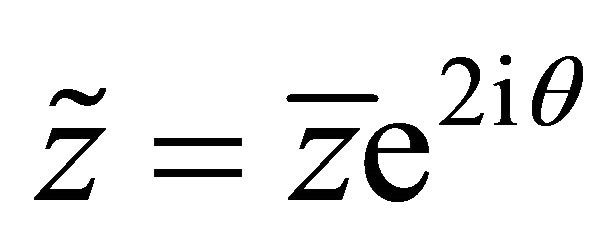 is the symmetric point of
is the symmetric point of  about
about![]() . For simplicity, we express
. For simplicity, we express 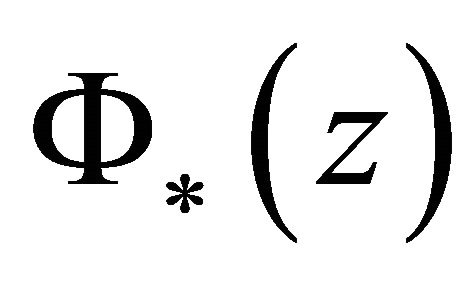 as
as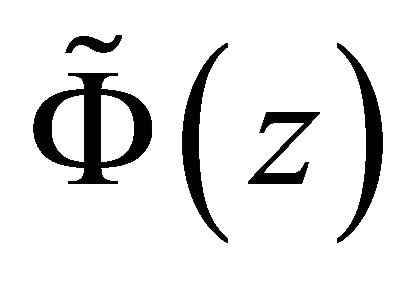 . From definition (2), we may establish that 1)
. From definition (2), we may establish that 1) ;
;
2) If 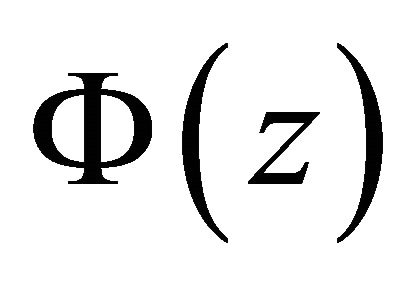 is defined in
is defined in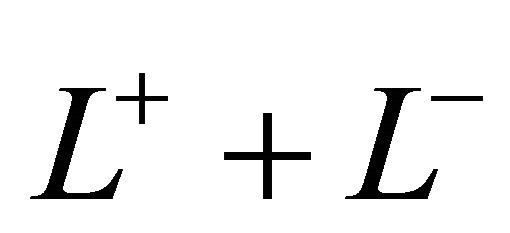 , then
, then 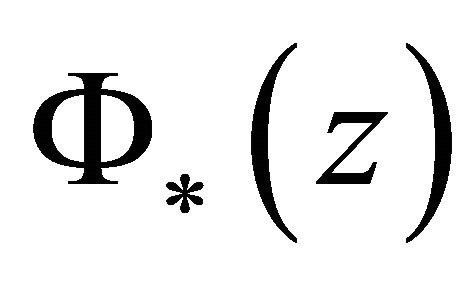 is also defined in
is also defined in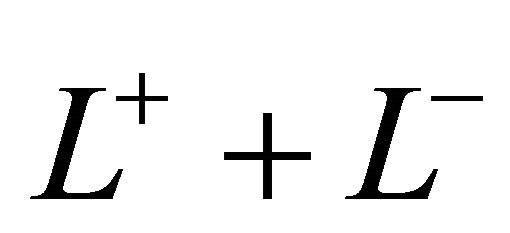 ;
;
3) If 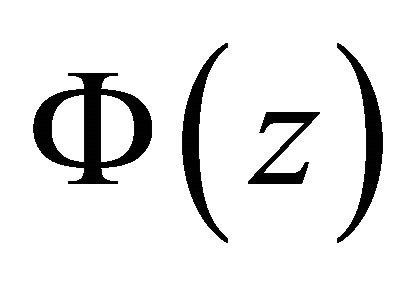 is holomorphic in
is holomorphic in , then
, then 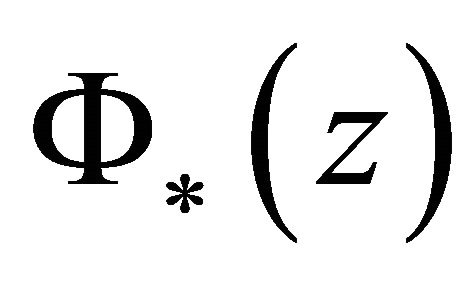 is holomorphic in
is holomorphic in 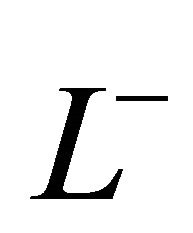 because of
because of
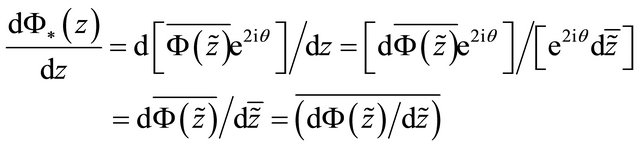 ;
;
4) If a holomorphic 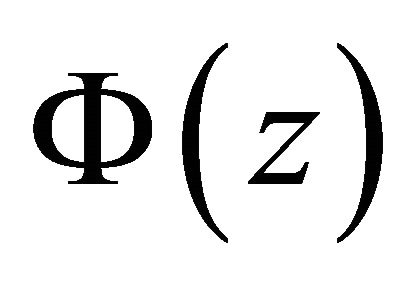 in
in 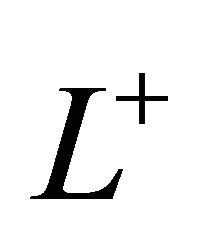 can be continuously extended to
can be continuously extended to![]() , then
, then  in
in 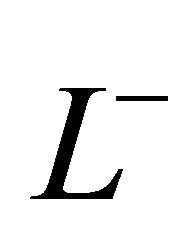 can be continuously extended to
can be continuously extended to![]() , and their boundary value on
, and their boundary value on ![]() satisfies the following equality
satisfies the following equality
![]() ; (3)
; (3)
5) If 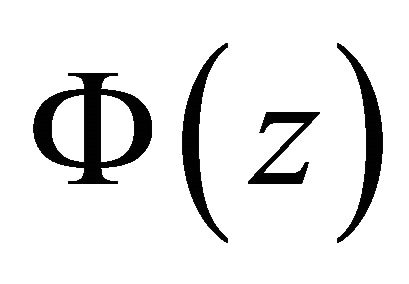 is holomorphic in
is holomorphic in 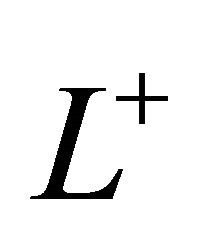 and continuous on
and continuous on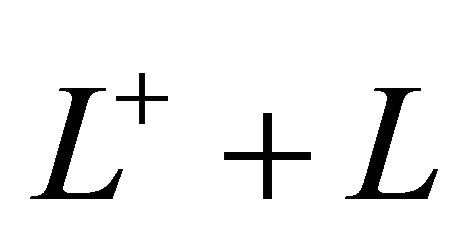 , then
, then
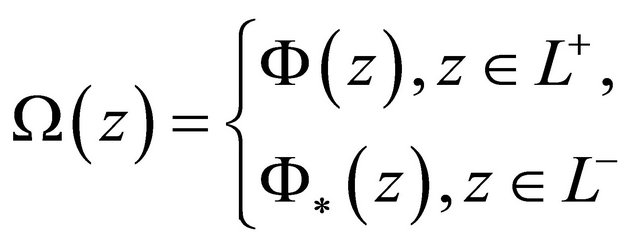 (4)
(4)
is a sectionally holomorphic function that jumps on ![]() with
with 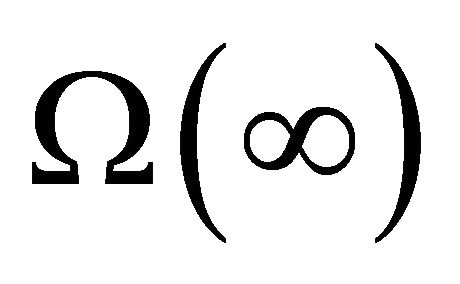 finite, and
finite, and 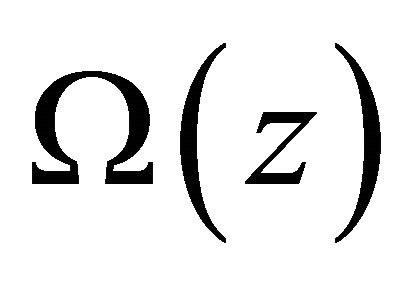 possesses the following properties:
possesses the following properties:
![]() (5)
(5)
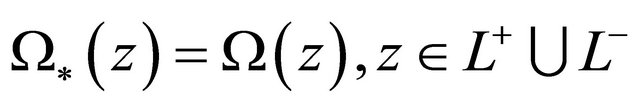 (6)
(6)
![]() (7)
(7)
6) Let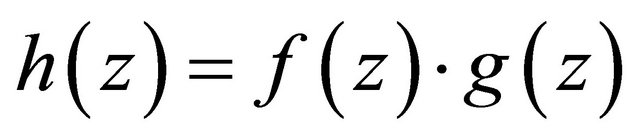 , where
, where 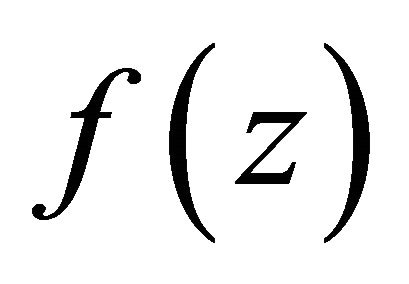 and
and  are holomorphic in
are holomorphic in 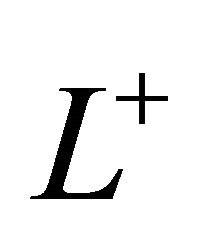 (
(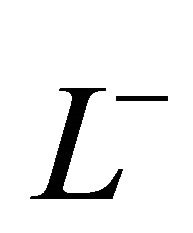 or
or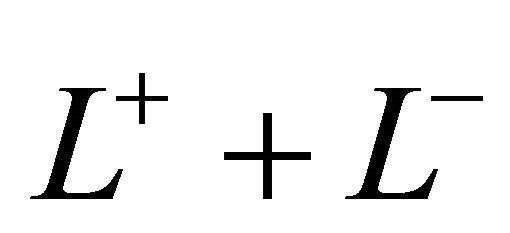 ). It is not necessarily true that
). It is not necessarily true that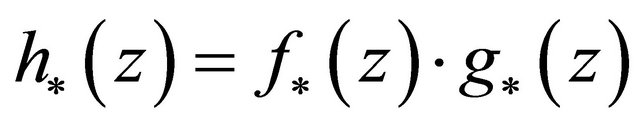 .
.
Problem (1) is normal only if 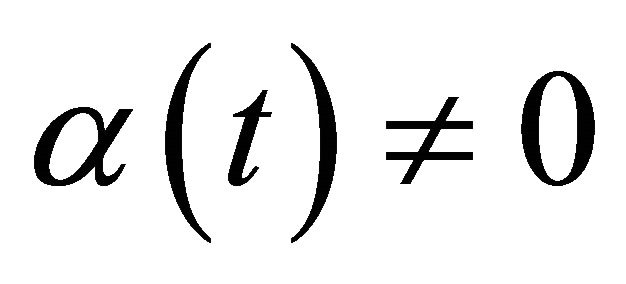 on
on![]() .
.
4. Transformation of Problem (1)
In this section, we develop a general method to solve boundary value problem (1) or similar problems. Let
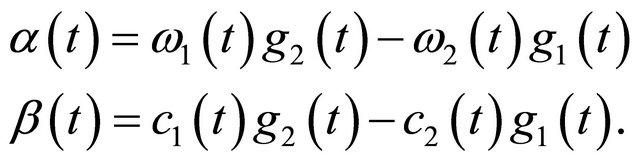
Multiplying the first and the second equation in (1) by  and
and 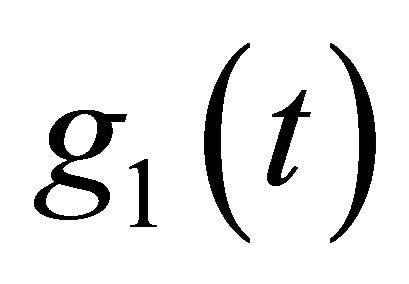 respectively, we obtain the Riemann boundary problem
respectively, we obtain the Riemann boundary problem
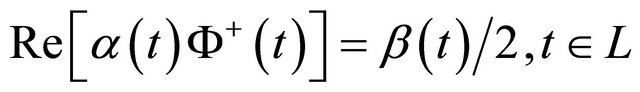 (8)
(8)
or
![]() . (9)
. (9)
By extending  to
to  about the straight line
about the straight line![]() , we obtain a sectionally holomorphic function
, we obtain a sectionally holomorphic function  as (4) with jump
as (4) with jump![]() , satisfying the boundary conditions
, satisfying the boundary conditions
![]() .
.
Thus (9) can be rewritten in the form
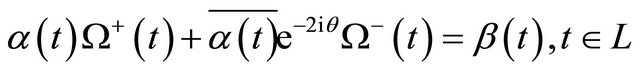 . (10)
. (10)
Due to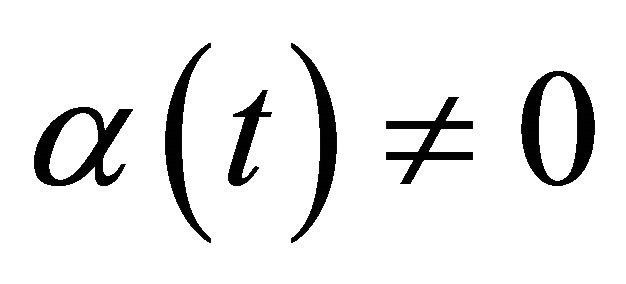 , (10) can be written as R problem
, (10) can be written as R problem
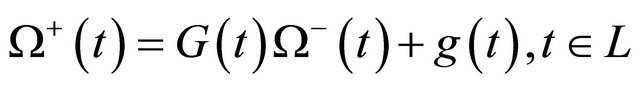 , (10)’
, (10)’
where
 (11)
(11)
and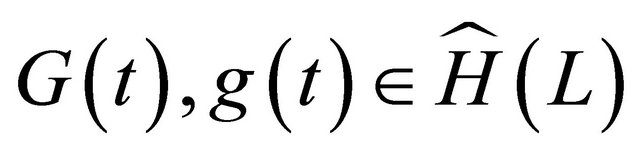 ,
, on
on![]() .
.
If 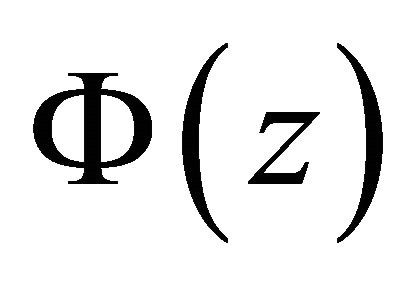 is a solution of problem (1), then
is a solution of problem (1), then 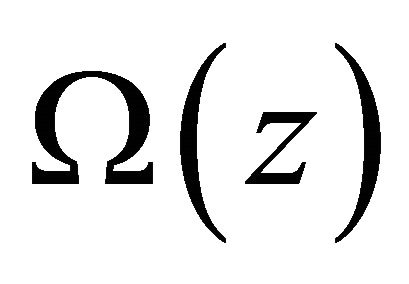 extended from
extended from 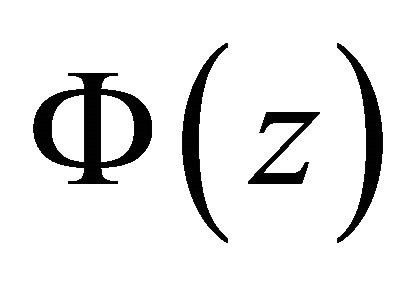 by (4) must be a solution of (10) or (10)’ in
by (4) must be a solution of (10) or (10)’ in 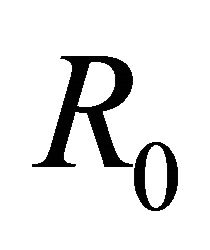 (namely
(namely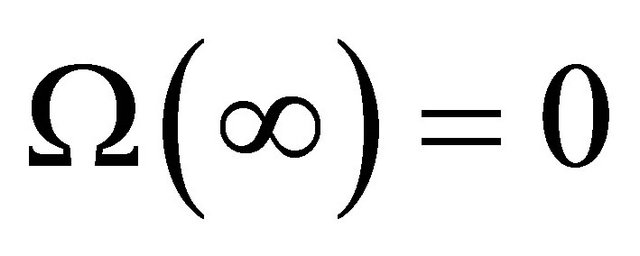 ) and satisfies the boundary condition (5). On the other hand, if the solution
) and satisfies the boundary condition (5). On the other hand, if the solution 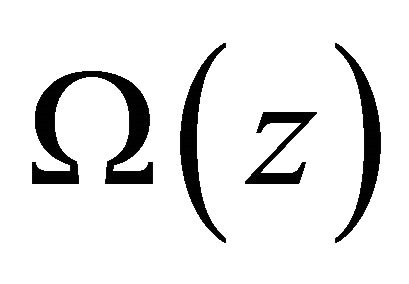 of R problem (10)’ in
of R problem (10)’ in 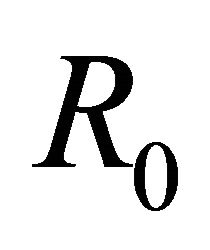 satisfies the boundary condition (5), then
satisfies the boundary condition (5), then 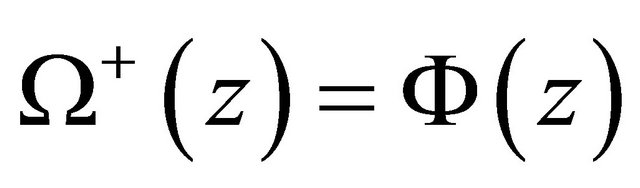 is really a solution of problem (1). Consequently, problem (1) is equivalent to R problem (10)’ in
is really a solution of problem (1). Consequently, problem (1) is equivalent to R problem (10)’ in  together with the additive condition (5).
together with the additive condition (5).
Assume that 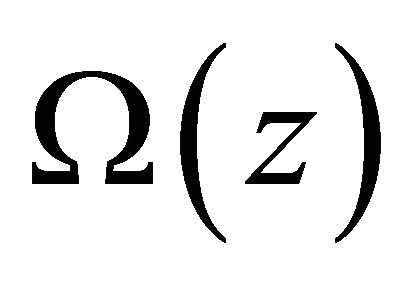 is a solution of (10) in
is a solution of (10) in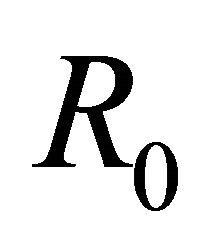 , by making conjugate for (10) we obtain
, by making conjugate for (10) we obtain
![]() .
.
We read from relation (7) that  is also a solution of (10)’ in
is also a solution of (10)’ in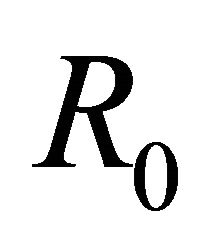 , so that
, so that
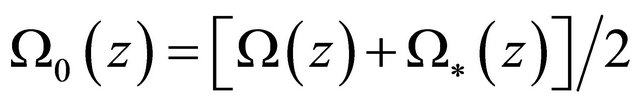
is a solution of (10)’ in class 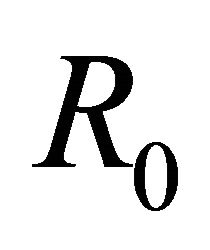 and satisfies the additive condition (5). So that, whenever we find out the solution
and satisfies the additive condition (5). So that, whenever we find out the solution 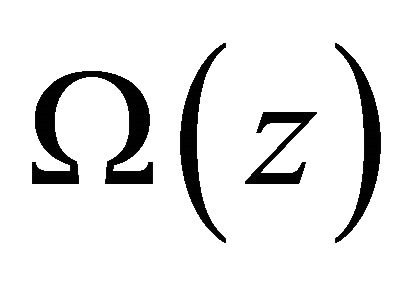 of problem (10)’ in class
of problem (10)’ in class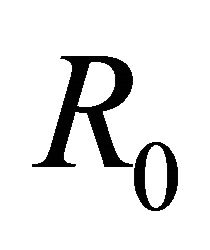 , and write out
, and write out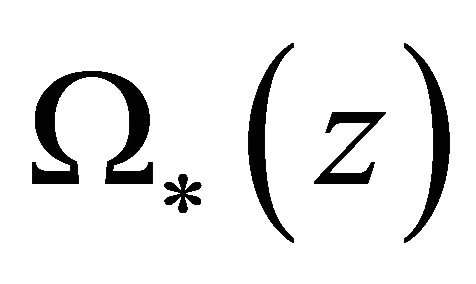 , then
, then
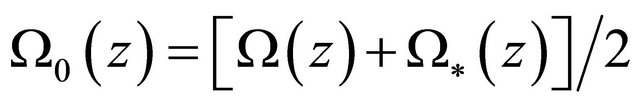
is actually the solution of problem (1).
Let
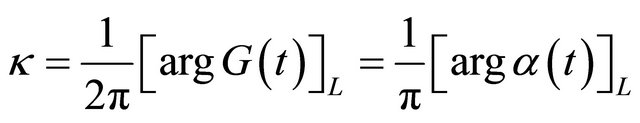 .
.
By 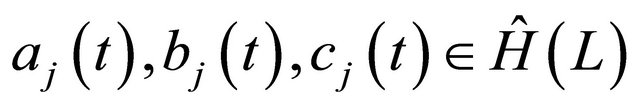 we know that
we know that ![]() is even.
is even.
5. Solution of the Hilbert Boundary Value Problem with an Unknown Function
Here, we only consider the problem (1) in the normal case. The nonnormal case can be solved similarly.
5.1. Homogeneous Problem
The homogeneous problem of (1) is as follows
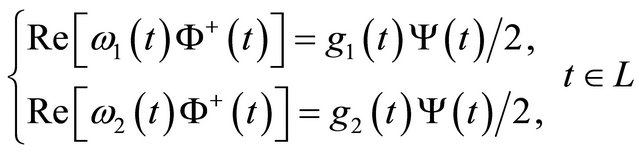 . (12)
. (12)
By canceling the unknown function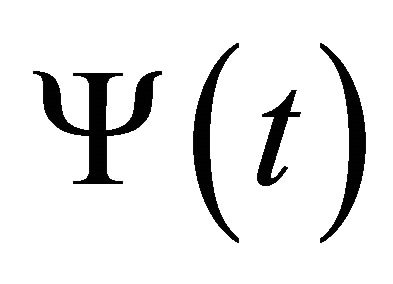 , problem (12) becomes
, problem (12) becomes
 , (13)
, (13)
which corresponds to the homogeneous problem of R problem (10)’
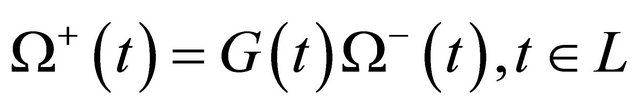 . (14)
. (14)
Setting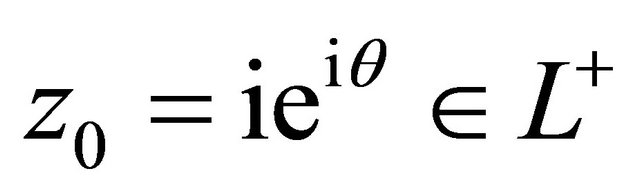 , we have
, we have
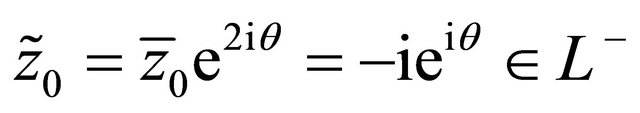 .
.
If we let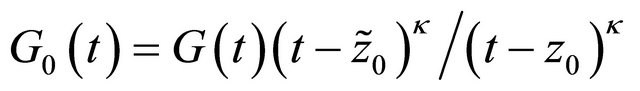 , then we know
, then we know 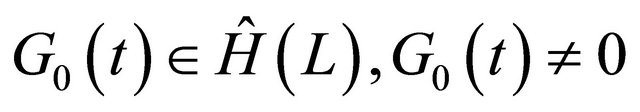 on
on ![]() with
with
 , and
, and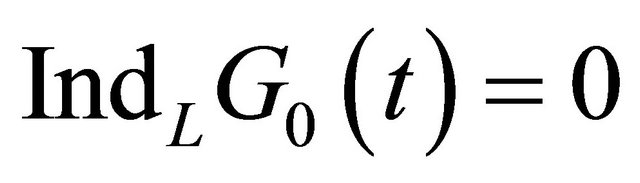 . By letting
. By letting
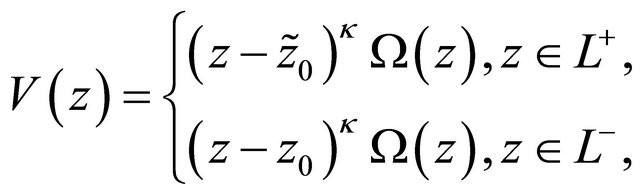
we can rewrite (14) as follows
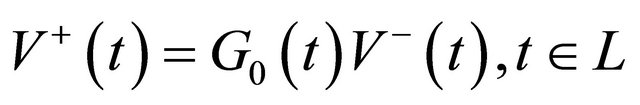 . (15)
. (15)
Let us introduce the function
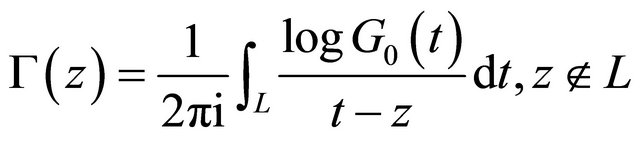 .
.
Since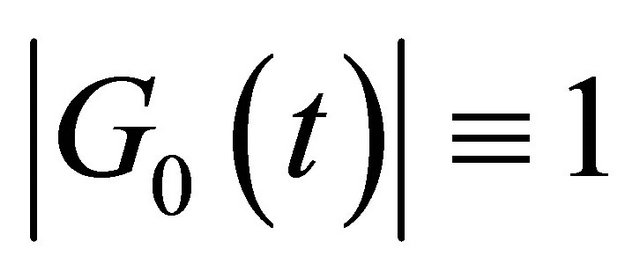 , we have
, we have
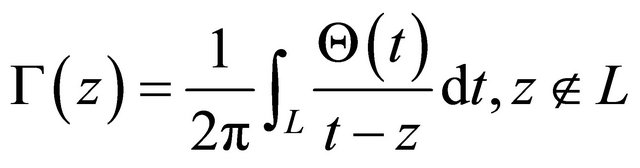 , (16)
, (16)
where

is real-valued on ![]() and
and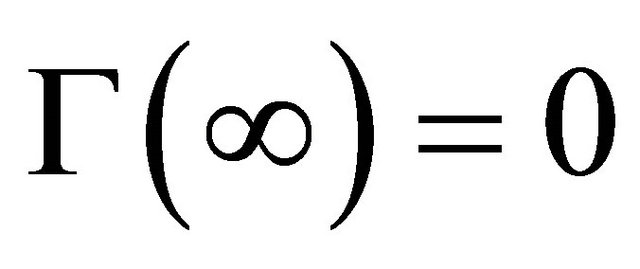 . Now the canonical function of R problem (15) or (14) can be taken as
. Now the canonical function of R problem (15) or (14) can be taken as
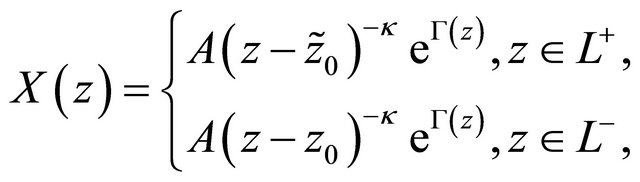 (17)
(17)
where  is an unknown complex constant. We can see from (17) that
is an unknown complex constant. We can see from (17) that , thus R problem (15) can be transferred to the following problem
, thus R problem (15) can be transferred to the following problem
 . (18)
. (18)
So 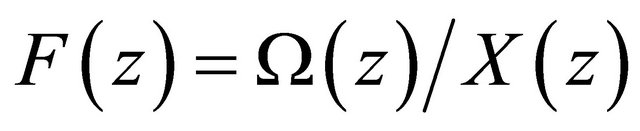 is holomorphic on the whole complex plane and has
is holomorphic on the whole complex plane and has ![]() order at
order at . From [5] we know that the general solution of R problem (14) in
. From [5] we know that the general solution of R problem (14) in 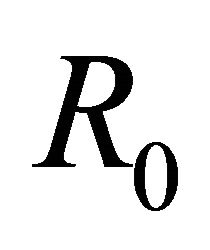 takes the form
takes the form
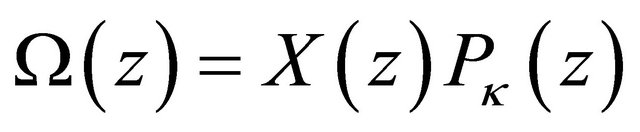 , (19)
, (19)
where 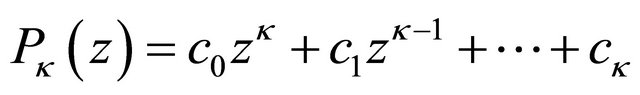 is an arbitrary polynomial of degree
is an arbitrary polynomial of degree ![]() with
with  if
if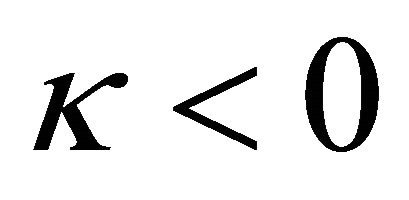 .
.
According to (16), we know
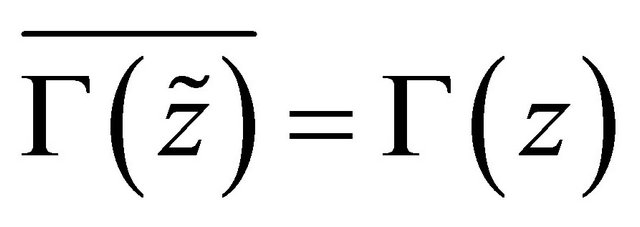 (20)
(20)
and hence
![]() . (21)
. (21)
From (17) and (20) it can be seen that
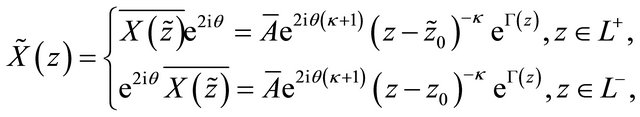
which implies that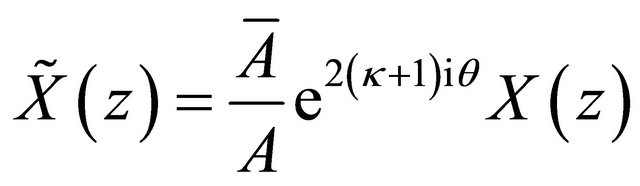 . By taking
. By taking
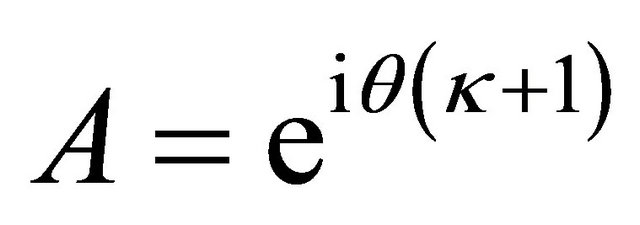 (22)
(22)
we obtain
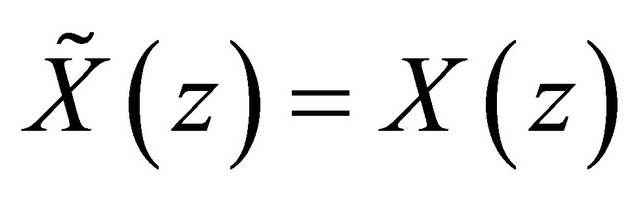 (23)
(23)
and

Consequently, we see that 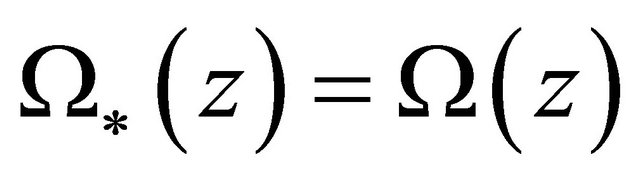 if and only if
if and only if
 (24)
(24)
Then when condition (24) is satisfied, the solution of H problem (13) is given by (19).
Now putting the solution 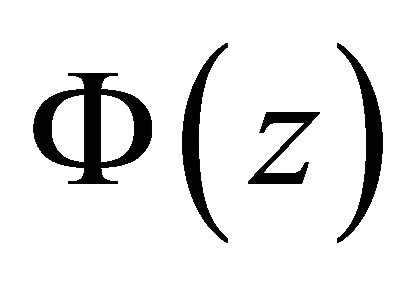 of H problem (13) given by (19) into the first equation (or the second equation) in (12), we get
of H problem (13) given by (19) into the first equation (or the second equation) in (12), we get
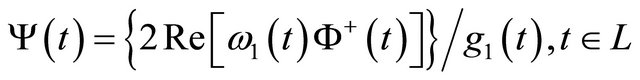 . (25)
. (25)
Thus we get the following results.
Theorem 5.1. For the homogeneous problem (12), the following two cases arise.
1) When , its general solution is
, its general solution is , where
, where 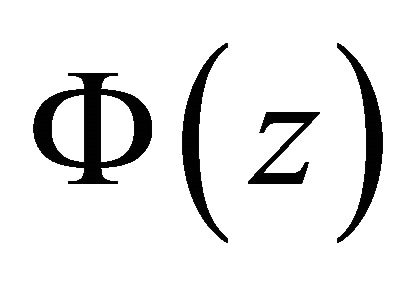 and
and 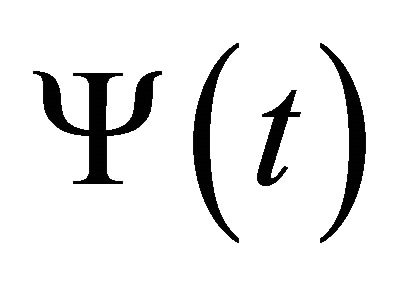 are given by (19) and (25) respectively, in which condition (24) is satisfied for
are given by (19) and (25) respectively, in which condition (24) is satisfied for , and
, and  is given by (22) (a real constant factor is permitted for
is given by (22) (a real constant factor is permitted for ).
).
2) When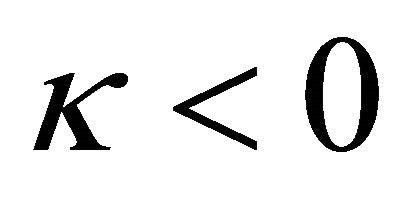 , it only has zero-solution
, it only has zero-solution
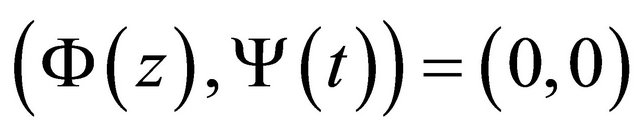 .
.
5.2. Nonhomogeneous Problem
In order to solve the n nonhomogeneous problem (1), we only need to find out a particular solution for problem (1).
According to [5], we know that when 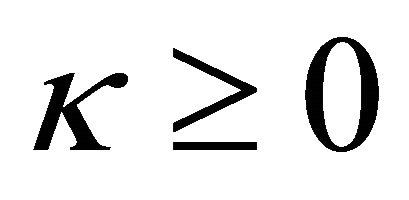 the R problem (10)’ a particular solution in class
the R problem (10)’ a particular solution in class  as follows
as follows
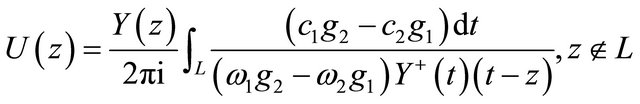 . (26)
. (26)
Therefore  is actually the particular solution of problem (1), where
is actually the particular solution of problem (1), where
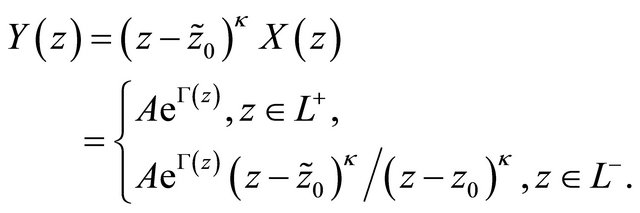 (27)
(27)
And from (20) we obtain
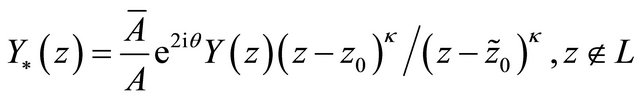 . (28)
. (28)
It follows from (3) that ![]() and from (20) and (21) that
and from (20) and (21) that
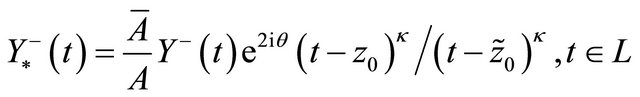 .
.
While due to  and (28) we have
and (28) we have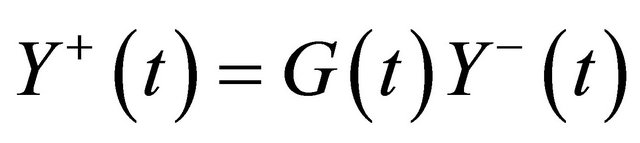 , so we obtain
, so we obtain
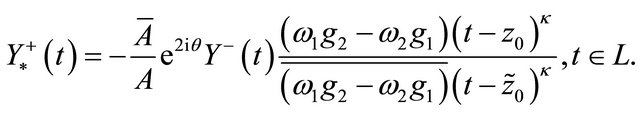 (29)
(29)
Therefore, we obtain
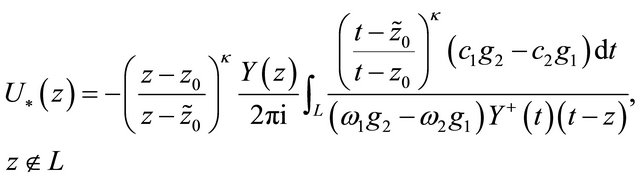 (30)
(30)
and
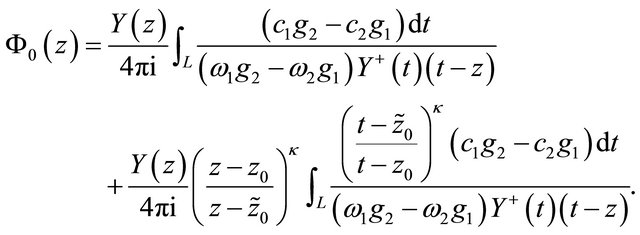 (31)
(31)
When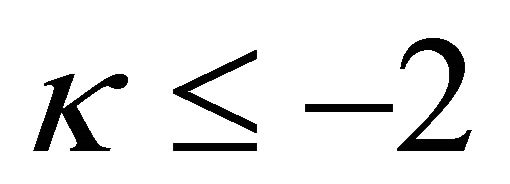 ,
, 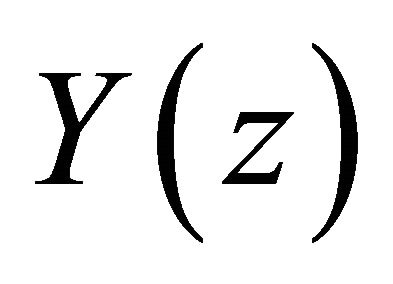 has singularity of order
has singularity of order 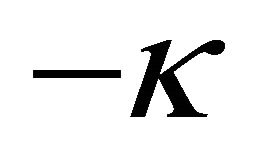 at
at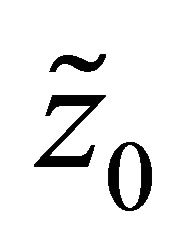 . Now we aim to cancel the singularity of
. Now we aim to cancel the singularity of 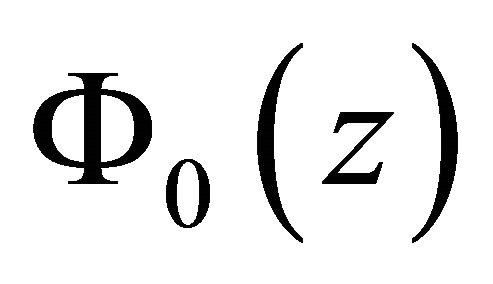 at
at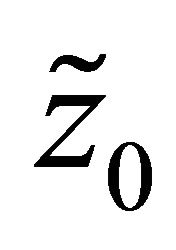 . From [5], we know that R problem (10)’ is solvable in
. From [5], we know that R problem (10)’ is solvable in 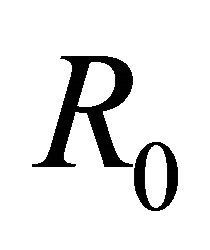 if and only if
if and only if
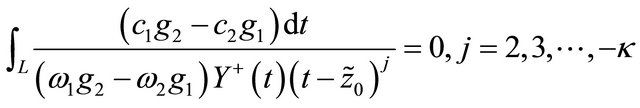 (32)
(32)
and its unique solution takes the form
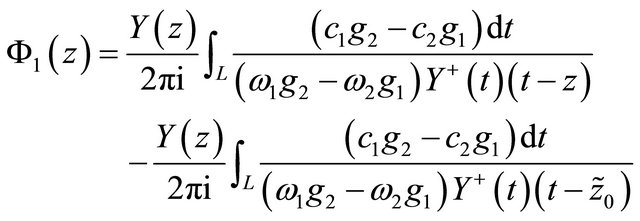 . (33)
. (33)
For the case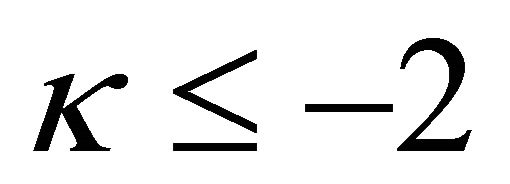 , since the solution for (10)’ in
, since the solution for (10)’ in 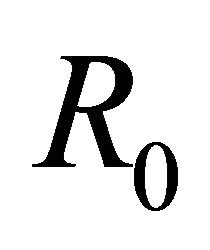 is unique and
is unique and 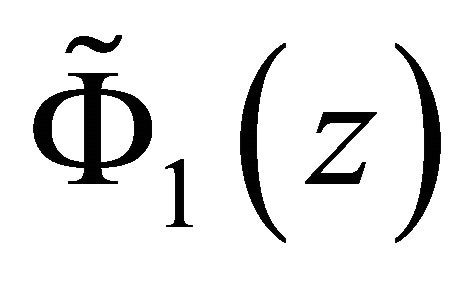 must be a solution of (10)’ in
must be a solution of (10)’ in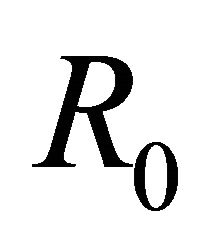 , we conclude that
, we conclude that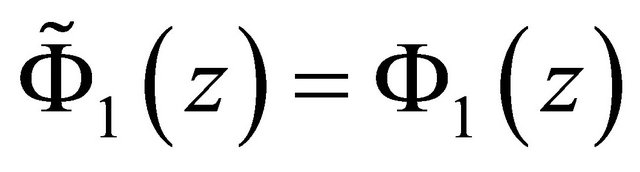 , thus (33) is actually the unique solution of nonhomogeneous problem (8).
, thus (33) is actually the unique solution of nonhomogeneous problem (8).
Combining the particular solution of nonhomogeneous problem (8) and the general solution of homogeneous problem (14), we known that when , the general solution of R problem (8) is
, the general solution of R problem (8) is
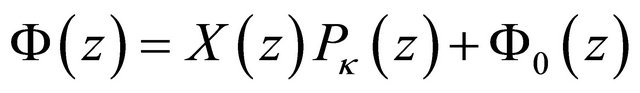 (34)
(34)
where  satisfies condition (24) and
satisfies condition (24) and 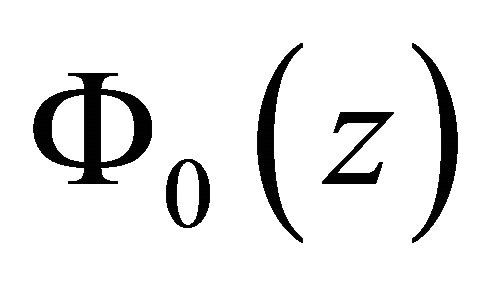 is given by (31); when
is given by (31); when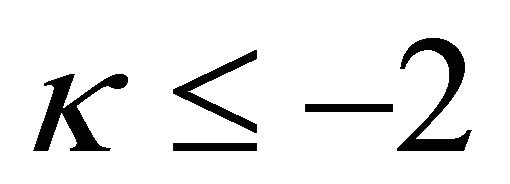 , R problem (8) is solvable if and only if (32) is satisfied and the unique solution is given by (33).
, R problem (8) is solvable if and only if (32) is satisfied and the unique solution is given by (33).
Putting the solution  into the first equation in (1), we obtain
into the first equation in (1), we obtain
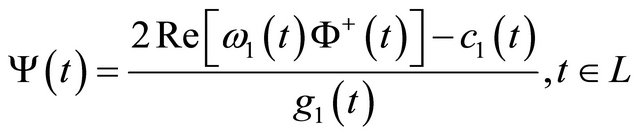 . (35)
. (35)
Therefore, we derive the following results.
Theorem 5.2. If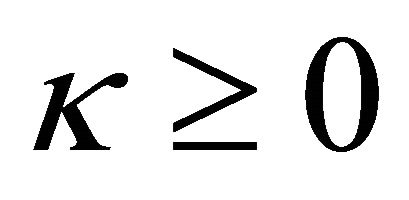 , the nonhomogeneous problem (1) is always solvable and its general solution is
, the nonhomogeneous problem (1) is always solvable and its general solution is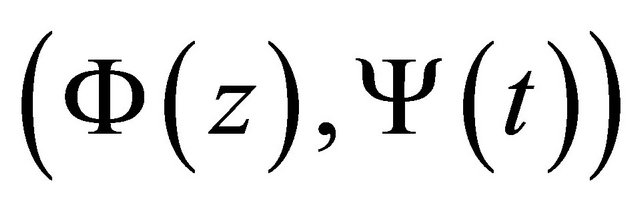 , where
, where 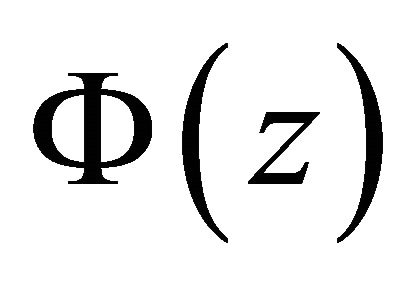 is given by (34) with
is given by (34) with 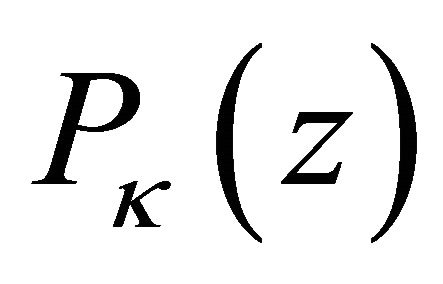 satisfying condition (24) and
satisfying condition (24) and  being given by (22) (a real constant factor is permitted for
being given by (22) (a real constant factor is permitted for ), while
), while 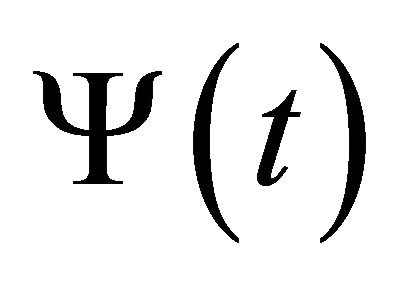 is given by (35). If
is given by (35). If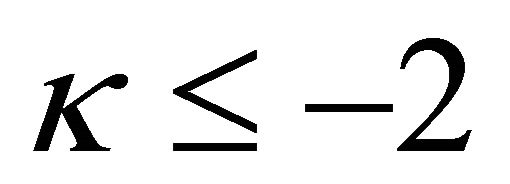 , under the necessary and sufficient condition (32), the nonhomogeneous problem (1) has unique solution
, under the necessary and sufficient condition (32), the nonhomogeneous problem (1) has unique solution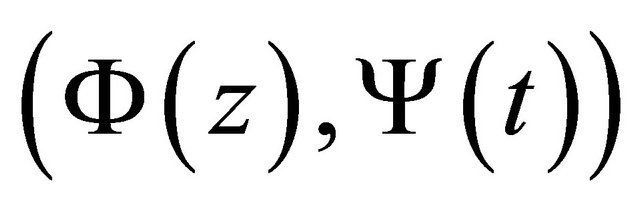 , where
, where 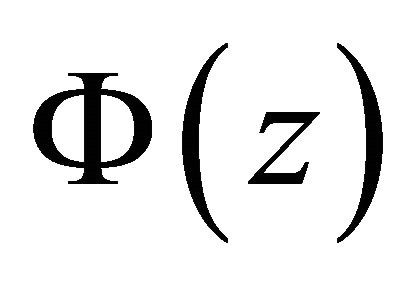 and
and 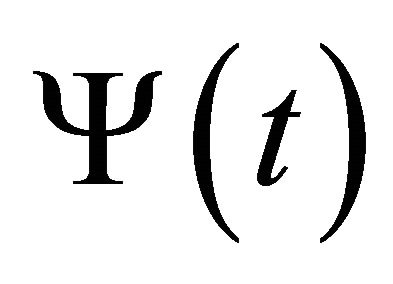 are given by (33) and (35) respectively.
are given by (33) and (35) respectively.
REFERENCES
- M. B. Balk, “Polyanalytic Functions,” Akademie Verlag, Berlin, 1991.
- H. Begehr and A. Kumar, “Boundary Value Problems for the Inhomogeneous Polyanalytic Equation I,” Analysis: International Mathematical Journal of Analysis and Its Application, Vol. 25, No. 1, 2005, pp. 55-71.
- D. Jinyuan and W. Yufeng, “On Boundary Value Problems of Polyanalytic Functions on the Real Axis,” Complex Variables, Vol. 48, No. 6, 2003, pp. 527-542. doi:10.1080/0278107031000103412
- B. F. Fatulaev, “The Main Haseman Type Boundary Value Problem for Metaanalytic Function in the Case of Circular Domains,” Mathematical Modelling and Analysis, Vol. 6, No. 1, 2001, pp. 68-76.
- J. K. Lu, “Boundary Value Problems for Analytic Functions,” World Scientific, Singapore, 1993.
- A. S. Mshimba, “A Mixed Boundary Value Problem for Polyanalytic Function of Order n in the Sobolev Space Wn, p(D),” Complex Variables, Vol. 47, No. 12, 2002, pp. 278-1077.
- N. I. Muskhelishvili, “Singular Integral Equations,” World Scientific, Singapore, 1993.
- W. Yufeng and D. Jinyuan, “Hilbert Boundary Value Problems of Polyanalytic Functions on the Unit Circumference,” Complex Variables and Elliptic Equations, Vol. 51, No. 8-11, 2006, pp. 923-943. doi:10.1080/17476930600667692
- L. Xing, “A Class of Periodic Riemann Boundary Value Inverse Problems,” Proceedings of the Second Asian Mathematical Conference, Nakhon Ratchasima, 1995, pp. 397-400.
- M. H. Wang, “Inverse Riemann Boundary Value Problems for Generalized Analytic Functions,” Journal of Ningxia University of Natural Resources and Life Sciences Education, Vol. 27, No. 1, 2006, pp. 18-24.
- X. Q. Wen and M. Z. Li, “A Class of Inverse Riemann Boundary Value Problems for Generalized Holomorphic Functions,” Journal of Mathematical, Vol. 24, No. 4, 2004, pp. 457-464.
- L. X. Cao, P.-R. Li and P. Sun, “The Hilbert Boundary Value Problem With Parametric Unknown Function on Upper Half-Plane,” Mathematics in Practice and Theory, Vol. 42, No. 2, 2012, pp. 189-194.

