World Journal of Mechanics
Vol. 1 No. 6 (2011) , Article ID: 9103 , 8 pages DOI:10.4236/wjm.2011.16033
Study of Surface Instability of Kelvin-Helmholtz Type in a Fluid Layer Bounded above by a Porous Layer and below by a Rigid Surface
1UGC-Centre for Advanced Studies in Fluid Mechanics, Department of Mathematics, Bangalore University, Bangalore, India
2Department of Mathematics, Government First Grade College Yellapur (U.K), Karnataka State, India
3Department of Science and Humanities, PES Institute of Technology, Bangalore, India
E-mail: rudraiahn@hotmail.com, shivakumarais@gmail.com, ckrishna2002@yahoo.com
Received September 11, 2011; revised October 8, 2011; accepted October 28, 2011
Keywords: Electrohydrodynamics, KHI, Magnetic Field, BJ-Slip Condition, Porous Layer
ABSTRACT
The surface instability of Kelvin-Helmholtz type bounded above by a porous layer and below by a rigid surface is investigated using linear stability analysis. Here we adopt the theory based on electrohydrodynamic as well as Stokes and lubrication approximations. We replace the effect of boundary layer with Beavers and Joseph slip condition. Here we have studied the combined effect of electric and magnetic fields on Kelvin-Helmholtz instability (KHI) in a fluid layer bounded above by a porous layer and below by a rigid surface. The dispersion relation is obtained using suitable boundary and surface conditions and results are depicted graphically. Also the ratio Gm is numerically computed for different values of We and M given in the Table 1. From this it is clear that the combined effect of electric and magnetic fields with porous layer are more effective than the effect of compressibility in reducing the growth rate of RTI. Also, these results shows that with a proper choice of magnetic field it is possible to control the growth rate of Electrohydrodynamic KHI (EKHI) and hence can be restored the symmetry of IFE target.
1. Introduction
KHI occurs when we consider the character of the equilibrium of a stratified heterogeneous fluid in which different layers are in relative motion. The most important case is when two superposed fluids flow one over the other with a relative horizontal velocity, the instability of the plane interface between the two fluids when it occurs in this instance, is known as “Kelvin-Helmholtz Instability”. The KHI of a Newtonian incompressible fluid in a composite layer bounded by a densely packed fluid saturated porous lining on one side and another side by an impermeable rigid surface is investigated in this paper. This can occur when velocity shear is present at the interface within a continuous fluid or when there is sufficient velocity difference across the interface between two fluids. The stability analysis can be used to predict the onset of instability and transition from laminar to turbulent flow in fluids of different densities moving at various speeds. Helmholtz [1] studied the dynamics of two fluids of different densities when a small disturbance such as a wave is introduced at the boundary connecting the fluids. If surface tension can be ignored, and for some short enough wavelengths, two fluids in parallel motion with different velocities and densities yielded an interface that is unstable for all speeds. The existence of surface tension stabilizes the short wavelength instability however, and theory then predicts stability until a velocity threshold is reached. The theory with surface tension included broadly predicts the onset of wave-formation in the important case of wind-over-water. Also the study of this instability becomes applicable to inertial confinement fusion and plasma-Beryllium interface. The KHI in a composite layer differs from the KHI in two fluid layers. The KHI arises when two uniform fluids, separated by a horizontal boundary, are in relative motion. Because of its relevance to astrophysical, geophysical and laboratory situations, this problem has been analyzed by several authors (Shore [2], Chandrasekhar [3]). Without surface tension, this streaming is unstable no matter how small the velocity difference between the layers may be. It was shown by Kelvin [4,5] that the surface tension will suppress the instability if the difference in velocity is sufficiently small. From an industrial view point, the momentum transfer and the KHI in composite region provides impetus for effective design of porous bearings in lubrication process, particularly in the slider bearings and in the effective design of target in inertial fusion energy (IFE). Because of these importances the KHI is investigated in this paper using the linear stability analysis. Chandrasekhar [3] gave an introduction to classical KHI. He discussed the effects of surface tension, variable density, streaming velocity, rotation and applications of magnetic field on the instability behaviour. The experimental observation of KHI has been given by Francis [6]. The effect of rotation and a general oblique magnetic field on the KHI has been studied by Sharma and Srivastava [7]. The study of electrohydrodynamic (EHD) KHI of free surface charges, separating two semi-infinite dielectric fluids and influenced by an electric field, has been discussed by Melcher [8]. The main difference between KH and RT instabilities in inclusion of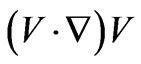 , which is a non-linear term, in the perturbation equations.
, which is a non-linear term, in the perturbation equations.
Elhefnawy [9] studied the non-linear KHI problem under the influence of an oblique electric field by employing the method of multiple scales. He combined the cases of normal and tangential fields. He found that the nonlinear effects may be stabilized or destabilized depending on both density and dielectric constant. Mehta and Bhatia [10] investigated KHI of two viscous, superposed, rotating and conducting fluids. Singh and Khare [11] have investtigated the stability of two semi-infinite homogenous gravitating streams of infinite conductivity under uniform horizontal magnetic field and uniform rotation. Bhatia and Hazarika [12] discussed this stability problem for superposed viscous gravitating fluids. The importance of the KHI problem has been demonstrated by Benjamin and Bridges [13] who have given an excellent reappraisal of the classic KHI problem in hydrodynamics. They have shown that the problem admits of a canonical Hamiltonian formulation and obtained several new results. More recently Sharma and Kumar [14] have studied the RTI of two superposed conducting Walter’s B' electroviscoelastic fluids in hydromagnetics while Allah [15] has investigated the effects of magnetic field and heat and mass transfer on the KHI of superposed fluids. To our knowledge KHI in a composite layer namely a thin fluid layer bounded by a porous layer has not been given any attention in spite of its importance in IFE.
We also note that the flow through porous medium has been of considerable importance in recent years particularly among geophysical fluid dynamicists and petroleum engineers. The physical properties of comets, meteorites and interplanetary dust strongly suggest the significance of the effects of porosity in astrophysical context (see McDonnel [16] and Rudraiah and Srimani [17]). Sunil and Chand [18] have investigated the effects of permeability of the porous medium on different stability problems. In this paper the flow in the porous layer is governed by the Darcy equation and that in a thin fluid film is governed by Navier-Stokes equation. Following Babchin et al., [19] and Rudraiah et al., [20], a simple theory based on Stokes and lubrication approximations is used in this study by replacing the effect of the boundary layer with a Beavers and Joseph [21] slip condition, with the primary objective of using porous layer to suppress the growth rate of KHI. In the above studies the fluid has been considered to be Newtonian. The electrohydrodynamic Kelvin-Helmholtz instability of the interface between two uniform superposed Rivlin-Ericksen viscoelastic dielectric fluid-particle mixtures in porous medium is investigated by El-Sayed [22]. El-Dib and Matoog [23] have studied the Electrorheological Kelvin-Helmholtz instability of a fluid sheet. This work deals with the gravitational stability of an electrified Maxwellian fluid sheet shearing under the influence of a vertical periodic electric field. The field produces surface charges on the interfaces of the fluid sheet. Due to the rather complicated nature of the problem a mathematical simplification is considered where the weak effects of viscoelastic fluids are taken into account. Khalil Elcoot [24] has studied the new analytical approximation forms for non-linear instability of electric porous media. In this work, we have examined the effects of stability of the normal electric field on the porous media, in view of the non-linear theory. The main purpose is to discuss a modulation instability of a finite wavetrain solution by using the method of multiple scales perturbation, and comparing the results with the linear instability theory. Non-linear electrohydrodynamic Kelvin-Helmholtz instability (EKHI) was developed in the parallel flow of two statically stable fluids through porous media for Darcian and non-Darcian flows. The interface separating two semi-infinite dielectric fluids were influenced by a normal electric field in the absence of surface charges. The objective of this paper is to predict the combined effects of electric and magnetic fields on electrohydrodynamic KHI with porous layer.
2. Mathematical Formulation
The physical configuration is shown in Figure 1. We consider a thin target shell in the form of a thin film of unperturbed thickness h (Region 1) filled with an incomepressible, viscous, poorly electrically conducting light fluid of density  bounded below by a rigid surface at y = 0 and above by an incompressible, viscous poorly
bounded below by a rigid surface at y = 0 and above by an incompressible, viscous poorly
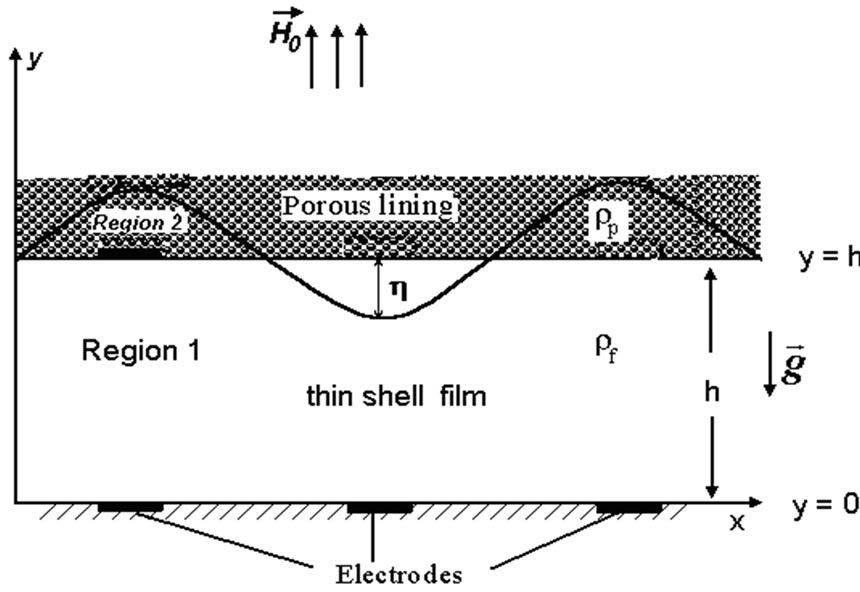
Figure 1. Physical configuration.
conducting heavy fluid of density  saturating a dense nanostructured porous layer of large extent compared to the shell thickness h. Also, the electrodes are embedded at the rigid surface y = 0 as well as at the interface y = h and there by an electric field is generated in fluid-porous medium composite system in addition with transverse magnetic field. The fluid in the thin film is set in motion by acceleration normal to the interface. The small perturbations are amplified when acceleration is directed from the lighter fluid in the thin film to the heavier fluid in the porous lining. KHI can occur when there is sufficient velocity difference across the interface between two fluids. To investigate this KHI, we consider a rectangular coordinate system (x, y) with the x-axis parallel to the film and y-axis normal to it. The perturbed interface
saturating a dense nanostructured porous layer of large extent compared to the shell thickness h. Also, the electrodes are embedded at the rigid surface y = 0 as well as at the interface y = h and there by an electric field is generated in fluid-porous medium composite system in addition with transverse magnetic field. The fluid in the thin film is set in motion by acceleration normal to the interface. The small perturbations are amplified when acceleration is directed from the lighter fluid in the thin film to the heavier fluid in the porous lining. KHI can occur when there is sufficient velocity difference across the interface between two fluids. To investigate this KHI, we consider a rectangular coordinate system (x, y) with the x-axis parallel to the film and y-axis normal to it. The perturbed interface  is along the y direction.
is along the y direction.
The basic equations for clear fluid layer (region 1) and those for porous layer (region 2) are as given below:
Region-1:
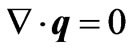 (2.1)
(2.1)
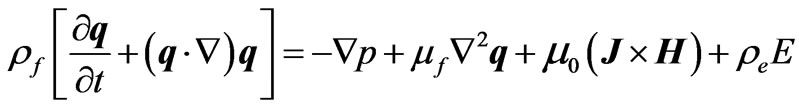 (2.2)
(2.2)
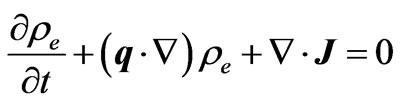 (2.3)
(2.3)
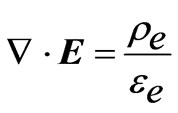 (2.4a)
(2.4a)
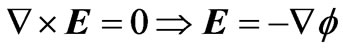 (2.4b)
(2.4b)
 (2.4c)
(2.4c)
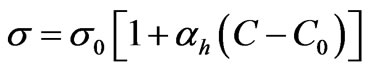 (2.4d)
(2.4d)
Region-2:
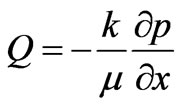 (2.5)
(2.5)
where 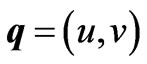 the fluid velocity, E the electric field, H the magnetic field, J the current density,
the fluid velocity, E the electric field, H the magnetic field, J the current density, 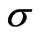 the electrical conductivity,
the electrical conductivity, 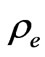 the density of charges,
the density of charges,  the dielectric constant, k the permeability of the porous medium,
the dielectric constant, k the permeability of the porous medium,  the electric potential, p the pressure, C the concentration,
the electric potential, p the pressure, C the concentration, 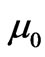 magnetic permeability,
magnetic permeability, 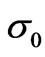 the electrical conductivity at the reference concentration C0,
the electrical conductivity at the reference concentration C0, 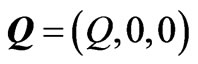 the uniform Darcy velocity, ah is the volumetric expansion coefficient of
the uniform Darcy velocity, ah is the volumetric expansion coefficient of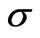 ,
, 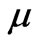 the fluid viscosity and
the fluid viscosity and 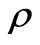 the fluid density.
the fluid density.
The electrical conductivity s varies with concentration C of DT as in Equation (2.4d). Then assuming negligible advection of concentration, we have
 (2.4)
(2.4)
with C = C0 at y = 0(2.4g)
C = C1 at y = h.(2.4h)
Solving Equation (2.4f) using the above conditions and substituting the solution so obtained in Equation (2.4d), we get
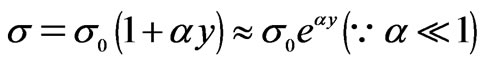 (2.4i)
(2.4i)
where a = ahDC and DC = C1 – C0. We assume the frequency of charge distribution is smaller than the corresponding relaxation frequency of the electric field, and hence the time derivative of 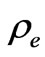 is negligible compared to
is negligible compared to 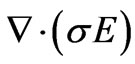 in Equation (2.3). From this, we get
in Equation (2.3). From this, we get
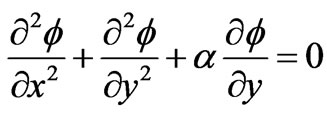 (2.5)
(2.5)
The above equation has to be solved subject to the boundary conditions
 (2.6a)
(2.6a)
 (2.6b)
(2.6b)
where 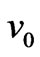 is the applied electric potential. These conditions arise due to embedded electrodes at y = 0 and y = h and permits a linear variation of
is the applied electric potential. These conditions arise due to embedded electrodes at y = 0 and y = h and permits a linear variation of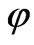 with x.
with x.
The basic equations are simplified using the following Stokes and lubrication and electrohydrodynamic approximations (See Rudraiah et al. [20]):
1) The electrical conductivity of the liquid, s, is negligibly small, i.e., .
.
2) The film thickness h is much smaller than the thickness H of the dense fluid above the film. That is

3) The surface elevation h is assumed to be small compared to film thickness h. That is

4) The Strauhal number S, a measure of the local acceleration to inertial acceleration in Equation (2.2), is negligibly small.
That is
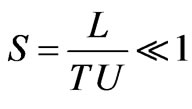
where 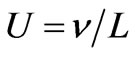 is the characteristic velocity, v the kinematic viscosity,
is the characteristic velocity, v the kinematic viscosity, 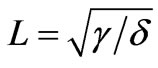 the characteristic length and
the characteristic length and  the characteristic time.
the characteristic time.
Under these approximations Equations (2.1) and (2.2) for fluid in the film, after making dimensionless using
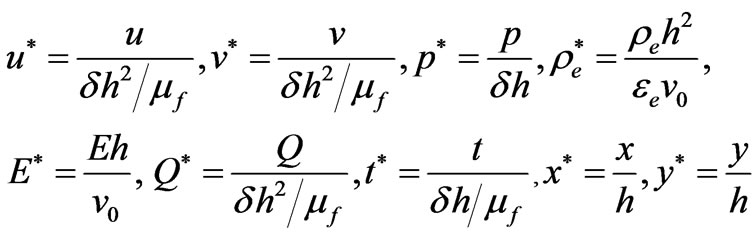 (2.7)
(2.7)
become (after neglecting the asterisks for simplicity).
Region 1:
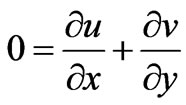 (2.8)
(2.8)
 (2.9)
(2.9)
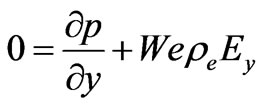 (2.10)
(2.10)
where  is the electric number and
is the electric number and 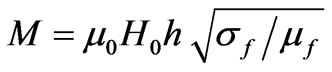 is the Hartmann number.
is the Hartmann number.
Region 2:
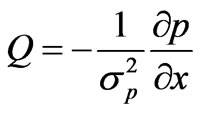 (2.11)
(2.11)
where  is the porous parameter.
is the porous parameter.
Substituting the Equation (2.7) in Equation (2.5) and in the boundary conditions (2.6), we obtain
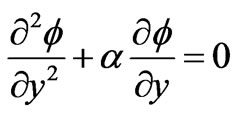 (2.12)
(2.12)
with boundary conditions
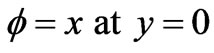 (2.13)
(2.13)
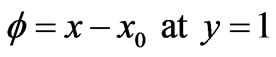 (2.14)
(2.14)
The solution of Equation (2.12), using the above boundary conditions, is
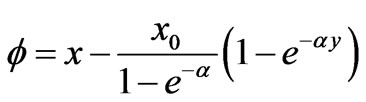 (2.15)
(2.15)
Equation (2.4a), using Equation (2.15), becomes
 (2.16)
(2.16)
and hence
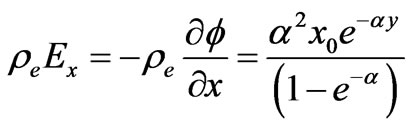 (2.17)
(2.17)
3. Dispersion Relation
To find the dispersion relation, first we have to find the velocity distribution from Equation (2.9) using the following boundary and surface conditions:
 (3.1)
(3.1)
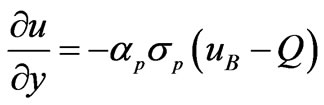 at y = 1 where
at y = 1 where
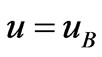 at y = 1
at y = 1
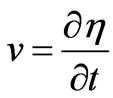 at y = 1(3.3)
at y = 1(3.3)
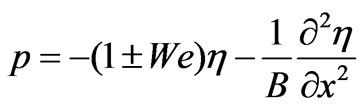 at y = 1(3.4)
at y = 1(3.4)
Here 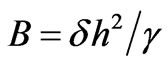 is the Bond number and
is the Bond number and  is the elevation of the interface.
is the elevation of the interface.
The solution of (2.9) subject to the above conditions is
 (3.5)
(3.5)
where


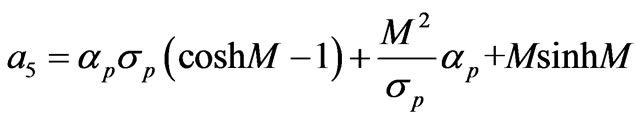
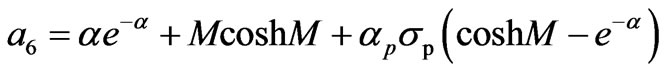
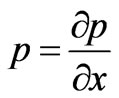
After integrating Equation (2.8) with respect to y between y = 0 and 1 and using Equation (3.5), we get
 (3.6)
(3.6)
where
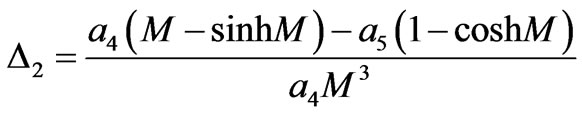
Then Equation (3.3), using Equations (3.6) and (3.4), becomes
 (3.7)
(3.7)
To investigate the growth rate, n, of the periodic perturbation of the interface, we look for solution of Equation (3.7) in the form
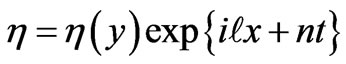 (3.8)
(3.8)
where 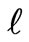 is the wave number and
is the wave number and  is the amplitude of perturbation of the interface.
is the amplitude of perturbation of the interface.
Substituting Equation (3.8) into (3.7), we obtain the dispersion relation in the form
 (3.9)
(3.9)
The positive or negative sign in the second term in Equation (3.9) will depends on whether voltage difference is applied in the same direction of the gravity or opposite direction. So that the Equation (3.9) takes the form
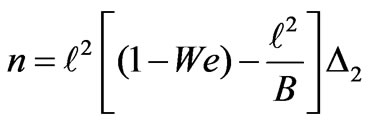 (3.10)
(3.10)
From Equation (3.10) we can obtain the results as particular cases for suitable choice of the parameters in Equation (3.10) as given below.
Case 1: KHI in a poorly conducting region bounded by porous layer and absence of magnetic field (i.e., M = 0), 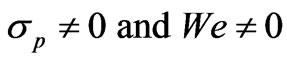 , Equation (3.10) reduces to
, Equation (3.10) reduces to
 (3.11)
(3.11)
where

Case 2: KHI in magnetohydrodynamics (MHD) without electric field bounded by porous layer. In this case, 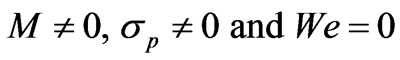 , Equation (3.10) reduces to
, Equation (3.10) reduces to
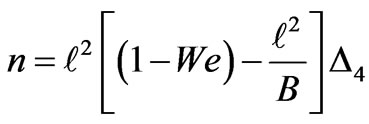 (3.12)
(3.12)
where
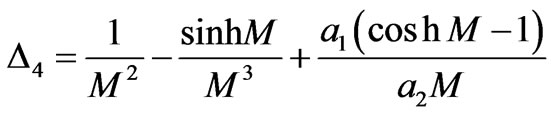
Case 3: KHI in the magnetohydrodynamics (MHD) case in the absence of porous layer. In this case, 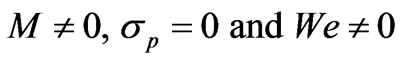 , Equation (3.10) reduces to
, Equation (3.10) reduces to
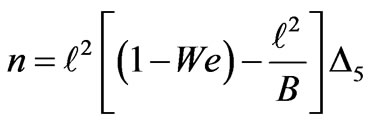 (3.13)
(3.13)
where

Also, Equation (3.10) can be expressed as
 (3.14)
(3.14)
where

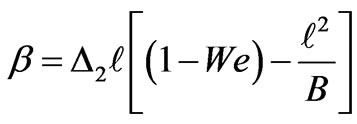

Setting n = 0 in Equation (3.10), we obtain the cut-off wavenumber, 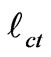 in the form
in the form
 (3.15)
(3.15)
because 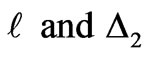 are non-zero.
are non-zero.
The maximum wavenumber, 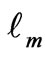 obtained from Equation (3.10) by setting
obtained from Equation (3.10) by setting 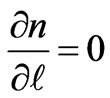 is
is
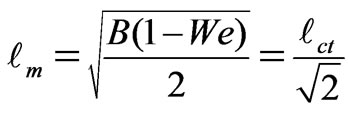 (3.16)
(3.16)
because  are different from zero.
are different from zero.
The corresponding maximum growth rate, nm, is
 (3.17)
(3.17)
Similarly, using , we obtain
, we obtain
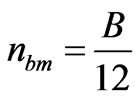 (3.18)
(3.18)
and hence
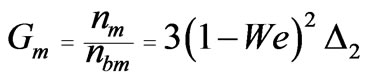 (3.19)
(3.19)
To know the reduction in growth rate of the IFE target, the analytical expression for Gm is computed for different values of We by fixing  and
and  and the results are tabulated in Table 1. The growth rate given by Equation (3.10) is also computed numerically for different values of parameters and the results are presented graphically in Figures 2-5.
and the results are tabulated in Table 1. The growth rate given by Equation (3.10) is also computed numerically for different values of parameters and the results are presented graphically in Figures 2-5.
4. Results and Discussion
In this study we have shown the surface instability of KH type in a fluid layer bounded above by a porous layer and below by a rigid surface is affected by the combined effect

Table 1. Reduction in growth rate for different values of We and M.
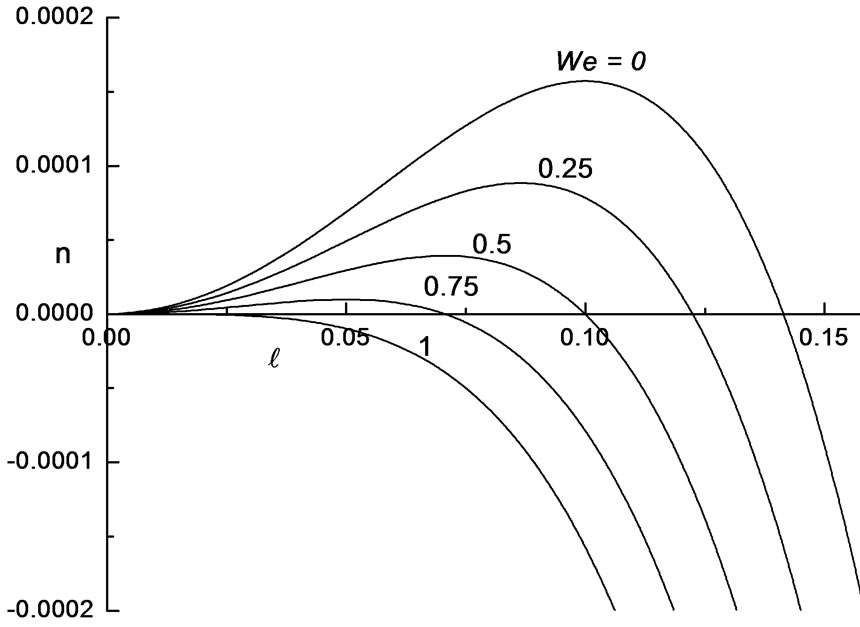
Figure 2. Growth rate, n versus the wavenumber,  for different values of electric parameter We when ap = 0.1, sp = 4, B = 0.02 and M = 5.
for different values of electric parameter We when ap = 0.1, sp = 4, B = 0.02 and M = 5.
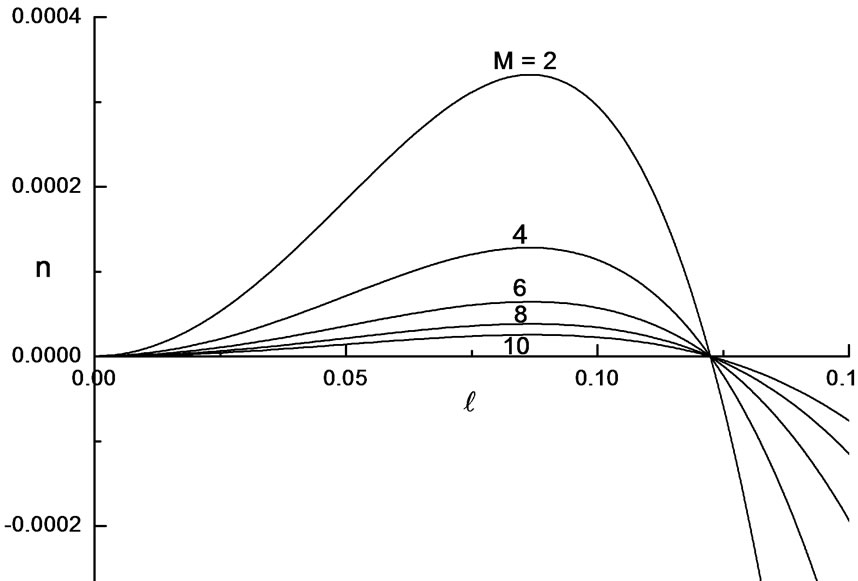
Figure 3. Growth rate, n versus the wavenumber,  for different values of Hartmann number M when ap = 0.1, sp = 4, B = 0.02 and We = 0.25.
for different values of Hartmann number M when ap = 0.1, sp = 4, B = 0.02 and We = 0.25.
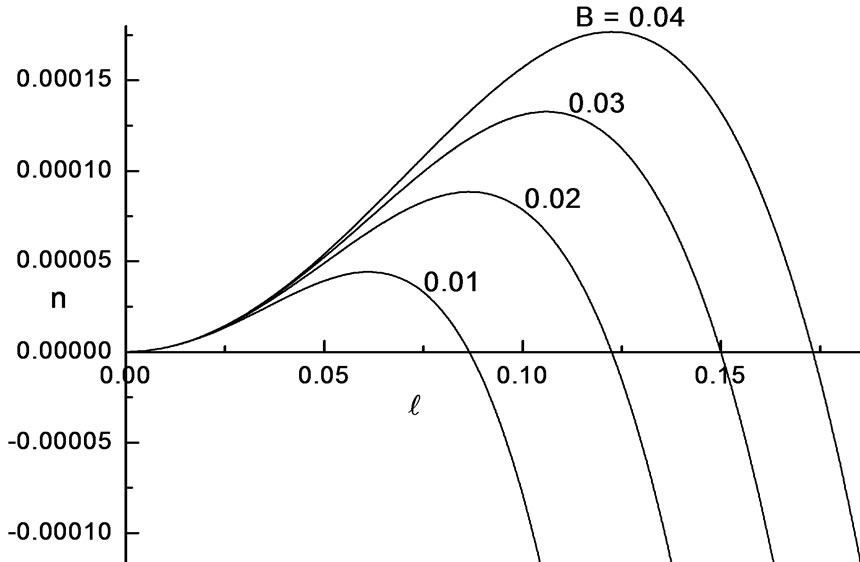
Figure 4. Growth rate, n versus the wavenumber,  for different values of Bond number B when ap = 0.1, sp = 4, M = 5 and We = 0.25.
for different values of Bond number B when ap = 0.1, sp = 4, M = 5 and We = 0.25.

Figure 5. Growth rate, n versus the wavenumber,  for different values of porous parameter sp when ap = 0.1, B = 0.02, M = 5 and We = 0.25.
for different values of porous parameter sp when ap = 0.1, B = 0.02, M = 5 and We = 0.25.
of electric and magnetic fields. The dispersion relation given by Equation (3.10) is so general that we obtained the three cases. The Equation (3.19) is numerically computed for different values of We and M and results are tabulated in Table 1.
From this table, it is clear that combined effect of electric and magnetic fields in a fluid layer bounded above by a porous layer and below by rigid surface are more effective than the effect of compressibility in reducing the growth rate of KHI. In particular for We = 1, complete symmetry can be maintained because nm = 0 and hence Gm = 0 for We = 1. Also from this table we conclude that the reduction of growth rate is considerable when the Hartmann number M is small. For example 64% reduction in nm compared to  for M = 10–1, 50% reduction when M = 1, 31% reduction when M = 2 and 16% reduction when M = 5 as defined in Table 1. These shows that with a proper choice of magnetic field it is possible to control the growth rate of KHI and hence can be restored the symmetry of IFE target.
for M = 10–1, 50% reduction when M = 1, 31% reduction when M = 2 and 16% reduction when M = 5 as defined in Table 1. These shows that with a proper choice of magnetic field it is possible to control the growth rate of KHI and hence can be restored the symmetry of IFE target.
The growth rate n given by the relation (3.10) is numerically computed for different values We, M, B and . The results are depicted in the Figures 2 to 5 of growth rate n versus the wave number,
. The results are depicted in the Figures 2 to 5 of growth rate n versus the wave number, . From Figure 2 we found that the growth rate decreases with increase in the values of We = 0, 0.25, 0.5, 0.75 and 1. It is clear that the growth rate decreases with increase in the electric energy compared to in absence of electric field. Also, Figure 3 shows that the increase in the Hartmann number M decreases the growth rate in the range of M = 2, 4, 6, 8, 10. From this we conclude that the increase in M makes the system more stable towards stability and hence stabilizes the system. From Figure 4, it is observe that the growth rate increases with increase in the Bond number in the range of 0.04 to 0.01. The Bond number B being the reciprocal of surface tension implies that an increase in surface tension decreases the growth rate and hence makes the interface more stable. Finally, from Figure 5 we found that as
. From Figure 2 we found that the growth rate decreases with increase in the values of We = 0, 0.25, 0.5, 0.75 and 1. It is clear that the growth rate decreases with increase in the electric energy compared to in absence of electric field. Also, Figure 3 shows that the increase in the Hartmann number M decreases the growth rate in the range of M = 2, 4, 6, 8, 10. From this we conclude that the increase in M makes the system more stable towards stability and hence stabilizes the system. From Figure 4, it is observe that the growth rate increases with increase in the Bond number in the range of 0.04 to 0.01. The Bond number B being the reciprocal of surface tension implies that an increase in surface tension decreases the growth rate and hence makes the interface more stable. Finally, from Figure 5 we found that as  increases from 4 to 100 the growth rate decreases and move towards neutral stability. We conclude that an increase in
increases from 4 to 100 the growth rate decreases and move towards neutral stability. We conclude that an increase in  also stabilizes the EKHI due to the resistance offered by the solid particles of the porous layer to the fluid.
also stabilizes the EKHI due to the resistance offered by the solid particles of the porous layer to the fluid.
5. Acknowledgements
The work supported by ISRO under the research projects no. ISRO/RES/2/338/2007-08 & ISRO/RES/2/335/2007-08. ISRO’s financial support to carry out this research is gratefully acknowledged. One of us (KBC) wishes to thank the Principal, Government First Grade College, Yellapur (U.K) for their encouragement and support. Also, BMS wishes to thank the Principal and Management, PES Institute of Technology, Bangalore for their kind support and encouragement.
REFERENCES
- H. Helmholtz, “On Discontinuous Movements of Fluids,” Philosophical Magazine Series 4, Vol. 36, 1868, pp. 337- 346.
- S. N. Shore, “An Introduction to Astrophysical Hydrodynamics,” Academic Press, New York, 1992.
- S. Chandrasekhar, “Hydrodynamic and Hydromagnetic Stability,” Dover Publications, New York, 1961.
- L. Kelvin, “Hydrokinetic Solutions and Observations, On the Motion of Free Solids through a Liquid,” Mathematical and Physical Papers IV, Hydrodynamics and General Dynamics, Cambridge, 1910, pp. 69-75.
- L. Kelvin, “Influence of Wind and Capillary on Waves in Water Superposed Frictionless,” Mathematical and Physical Papers IV, Hydrodynamics and General Dynamics, Cambridge, 1910, pp. 76-85.
- J. R. D. Francis, “Wave Motions and the Aerodynamic Drag on a Free Oil Surface,” Philosophical Magazine Serials 7, Vol. 45, No. 366, 1954, pp. 695-702.
- R. C. Sharma and K. M. Srivastava, “Effect of Horizontal and Vertical Magenetic Fields on Rayleigh-Taylor Instability,” Australian Journal of Physics, Vol. 21, No. 6, 1968, pp. 923-930. doi:10.1071/PH680923
- J. R. Melcher, “Field Coupled Surface Waves,” MIT Press, Cambridge, 1963.
- A. R. F. Elhefnawy, “Nonlinear Electrohydrodynamics Kelvin-Helmholtz Instability under the Influence of an Oblique Electric Field,” Physica A, Vol. 182, No. 3, 1992, pp. 419-435. doi:10.1016/0378-4371(92)90352-Q
- V. Mehta and P. K. Bhatia, “Kelvin-Helmholtz Instability of two Viscous Superposed Rotating and Conducting Fluids,” Astrophysics and Space Science, Vol. 141, No. 1, 1998, pp. 151-158. doi:10.1007/BF00641921
- R. P. Singh and H. C. Khare, “Stability of Rotating Gravitating Superposed Streams in a Uniform Magnetic Field,” Proceedings of National Academy of Sciences, New Delhi, Vol. 43, 1991, pp. 49-55.
- P. K. Bhatia and A. B. Hazarika, “Gravitational Instability of Partially Ionized Plasma in an Oblique Magnetic Field,” Physica Scripta, Vol. 51, No. 6, 1995, pp. 775- 779.
- T. B. Benjamin and T. J. Bridges, “Reappraisal of the Kelvin-Helmholtz Problem. Part-2: Interaction of the KelvinHelmholtz Superharmonic and Benjamin-Feir Instabilities,” Journal of Fluid Mechanics, Vol. 333, 1997, pp. 327-373. doi:10.1017/S0022112096004284
- R. C. Sharma and P. Kumar, “On the Stability of Two Superposed Walters B' Viscoelastic Liquid,” Czechoslovak Journal of Physics, Vol. 47, No. 2, 1996, pp. 197-204.
- M. H. O. Allah, “The Effects of Magnetic Field and Mass and Heat Transfer on Kelvin-Helmholtz Stability,” Proceedings of National Academy of Sciences, Vol. 68, No. 2, 1998, pp. 163-173.
- J. A. M. McDonnel, “Cosmic Dust,” John Wiley and Sons, Toronto, 1978.
- N. Rudraiah and P. K. Srimani, “Thermal Convection of a Rotating Fluid through a Porous Media,” Vignana Bharti, Vol. 2, No. 2, 1976, pp. 11-17.
- Sunil and T. Chand, “Effects of Rotation on the RayleighTaylor Instability of Two Superposed Magnetized Conducting Plasma,” Indian Journal of Physics, Vol. 71, 1997, pp. 95-105.
- A. J. Babchin, A. L. Frenkel, B. G. Levich and G. I. Sivashinsky, “Nonlinear Saturation of Rayleigh-Taylor Instability in Thin Films,” Physics of Fluids, Vol. 26, No. 11, 1983, pp. 3159-3161. doi:10.1063/1.864083
- N. Rudraiah, R. D. Mathad and H. Betigeri, “The RTI of Viscous Fluid Layer with Viscosity Stratification,” Current Science, Vol. 76, No. 6, 1997, pp. 391-398.
- G. S. Beavers and D. D. Joseph, “Boundary Conditions at a Naturally Permeable Wall,” Journal of Fluid Mechanics, Vol. 30, No. 1, 1967, pp. 197-207. doi:10.1017/S0022112067001375
- M. F. El-Sayed, “Effect of Variable Magnetic Field on the Stability of a Stratified Rotating Fluid Layer in Porous Medium,” Czechoslovak Journal of Physics, Vol. 50, No. 5, 2002, pp. 607-614. doi:10.1023/A:1022854217365
- Y. O. El-Dib and R. T. Matoog, “Electrorheological Kelvin-Helmholtz Instability of a Fluid Sheet,” Journal of Colloid and Interface Science, Vol. 289, No. 1, 2005, pp. 223-241. doi:10.1016/j.jcis.2005.03.054
- A. E. Khalil Elcoot, “New Analytical Approximation Forms for Non-Linear Instability of Electric Porous Media,” International Journal of Non-Linear Mechanics, Vol. 45, No. 1, 2010, pp. 1-11. doi:10.1016/j.ijnonlinmec.2009.08.011

