World Journal of Mechanics
Vol.07 No.05(2017), Article ID:76487,17 pages
10.4236/wjm.2017.75013
Artificial Neural Networks Based Integrated Predictive Modelling of Quality Characteristics in CNC Turning of Cantilever Bars
D. M. Davakan, A. El Ouafi
Mathematics, Computer Science and Engineering Department, University of Quebec at Rimouski, Rimouski, Canada

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 16, 2017; Accepted: May 23, 2017; Published: May 26, 2017
ABSTRACT
The objective of this study is to develop an effective approach for product quality prediction in Computer Numerical Control turning of cantilever bars. A systematic predictive modelling procedure based on experimental investigations, neural network modelling and various statistical analysis tools is designed to produce the most accurate, practical and cost-effective prediction model. The modeling procedure begins by exploring the relationships between cutting parameters known to have an influence on quality characteristics of machined parts, such as dimensional errors, form errors and surface roughness, as well as their sensitivity to the process conditions. Based on these explorations and using numerous statistical tools, the most relevant variables to include in the prediction model are identified and fused using several artificial neural network architectures. An application on CNC turning of cantilever bars demonstrates that the proposed modeling procedure can be effectively and advantageously applied to quality characteristics prediction due to its simplicity, accuracy and efficiency. The experimental validation reveals that the resulting prediction model can correctly predict the quality characteristics of machined parts under variable machining conditions.
Keywords:
Machining, CNC Turning, Cantilever Bar, Product Quality, DOE, Predictive Modelling, Artificial Neural Networks

1. Introduction
Turning is one of the most commonly used metal cutting processes because of its ability to remove material faster, giving reasonably good quality for cylindrical parts. The turning process is used in a variety of manufacturing industries including the aerospace and automotive sectors where quality is an important factor. The quality of finished products plays a crucial role in the functional capacity of the part and, therefore, a great deal of attention should be paid to maintaining consistent geometrical and dimensional tolerances and acceptable surface roughness. Producing a part with the desired specifications presents both technological and economic issues. The production processes used to reach the appropriate specifications affect not only the functional attributes of the product but also the manufacturing costs. Working under ideal conditions, engineers can control the product quality by controlling the cutting process parameters. Usually, engineers set these parameters based on experience or handbook data. In the case of turnings tiff materials clamped in a chuck, it is known that it is possible to arrive at a good precision for diameter, surface roughness and geometrical forms only if the length to diameter ratio of the work piece is relatively low. Otherwise, the turning operation could result in poor specifications and fail to meet the required tolerances.
Effectively, the quality characteristics of machined parts (QCMP) may deviate from the expected values due to many factors: geometric machine errors, thermally induced distortions of machine tool elements, static deflections of the machine-fixture-workpiece-tool system (MFWTS) under cutting forces, and other error sources such as tool attributes variation (geometry, material, fixture, tool wear, etc.), workpiece attributes change (material, hardness, dimension, geometry, fixture, etc.), machining process parameters (cutting speed, feed rate, depth of cut, etc.), and machining operation conditions (cutting forces, temperature, MFWTS vibration, cutting fluid, and other dynamic variables. The complex correlations between these factors make it difficult to develop an intuitive quality control and improvement approach based only on human experience. All of these factors must be considered simultaneously in order to build up an appropriate and successful process quality enhancement plan. An intelligent integration strategy of the most influential factors and the most significant information sources is the key element in developing an effective approach to quality control and an efficient prediction system for the CNC turning process.
The quality of machined parts is recognized as a key element for competitive production, due to tolerance requirements of mechanical parts designed for high precision applications [1] . Many research works have been conducted in order to improve the performance of the machining processes [2] - [8] . Among the most reported works are several studies based on the development of modelling approaches using analytical models, finite element method models, regression models, response surface models and Taguchi analyses to estimate, predict and improve the performances of the machining process [9] - [15] . In recent years, artificial neural networks, fuzzy logic, sensor fusion and genetic algorithms are increasingly used to develop predictive models for various part quality characteristics [16] - [22] . Some of these modelling techniques are combined with various measurement techniques. The main measurements that have been identified as major indicators of machined part quality include cutting forces, cutting torque, vibrations, acoustic emissions, temperature and motor current [23] - [28] . Other direct measuring methods such as touch trigger probes, proximity sensors, optical and electrical resistance measurement techniques have also been reported, but their reliability under real conditions is limited [29] [30] [31] [32] . Generally, these models are focused on particular applications and materials with a limited range of experimental conditions, and oriented to specific types of errors and tolerances. These models are therefore ill-adapted to many applications. Other efforts have also been made to develop a number of on-line measurement techniques to assess the QCMP using sophisticated instrumentations. The analysis of data from these measurements demonstrated the difficulties involved in extracting representative sets of all quality characteristics from only one source of information. Data simultaneously acquired from several sensors is needed. This analysis also shows that two main requirements need to be satisfied when developing predictive models: the measurements must reflect the process behavior under its varied operating conditions and the generated data must allow for some refinement in order to discriminate the effect of various cutting parameters and conditions. The integration of several sensors can greatly improve the accuracy and efficiency of the modeling process in various applications. This approach remains nevertheless a tributary to the used processing and modeling methods.
The literature review clearly shows that there is no structured approach or comprehensive and integrated predictive approach combining dimensional errors, form errors and surface roughness at the same time. This research proposes an effective approach for dimensional error, form error and surface roughness prediction in the CNC turning of cantilever bars. After a structured experimental investigation, relationships and interactions between cutting parameters, cutting conditions and the quality characteristics of specific machined parts are analysed, and their sensitivity to the process conditions is evaluated. Based on the experimental results and various statistical tools, the variables most relevant to the prediction model are identified and fused using several artificial neural network (ANN) architectures. An application to CNC turning of cantilever bars is developed to illustrate the feasibility and the effectiveness of the proposed modeling procedure.
2. Machined Part Quality Characteristics
To demonstrate the proposed predictive modelling procedure, three parts quality characteristics are considered: diametral errors (De), circularity errors (Ce), and surface roughness (Ra). Note that the dimensional and geometrical specifications of the final parts are expressed in drawings in terms of dimensional and geometrical tolerances. There is no direct relationship between deviations resulting from the cutting process and tolerance values. However, it is important to understand these interdependencies for analysing the effects of machining parameters on the machined part dimensional and geometrical specifications.
As illustrated in Figure 1, a bar with an initial diameter (Di) is considered for turning operation using a nominal depth of cut d in a cantilever mounting con-
Figure 1. Typical deflections in turning of cantilever bars: (a) Cantilever mounting configuration and (b) Typical workpiece deflections.
figuration (Figure 1(a)). The machined parts dimensional and form errors are basically estimated from the defections of the MFWTS in the cross-section containing the cutting point. The workpiece deflection and the machine center deviation of are predominantly due to the cutting forces (radial and tangential forces). The tool deflections in X and Y directions are due to radial and tangential force components respectively. The effects of tool and workpiece axial deflections on the radial deviations, due to the axial cutting force, are negligible. Because of all these deflections, dimensional and form errors appear on the machined part surfaces as soon as the cutting forces disappear and the axis of the part returns to its normal position. These errors appear proportional to stresses and deflections received. Consequently, the turning of cylindrical surfaces leads, in the case of cantilever mounting configuration, to surfaces with an apparent polynomial profile (Figure 1(b)).
The diametral error can bedefined as the deviations between the desired and actual profiles of the workpiece. For the cantilever bar turning process, the diametral error is expressed as:
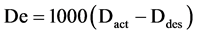
where De is the diametral error (µm), Dact is the actual (measured) diameter (mm) and Ddes is the desired diameter (mm). The desired and actual diameters are virtually equal at the fixed end of the workpiece. Due to the increase in part deflection, Degrows along the length of part and reaches its maximum value at the cantilever free end. In other hand, the ISO definition of circularity or roundness is based on the ratio between the inscribed and the circumscribed circles (maximum and minimum sizes for circles that are just sufficient to fit inside and to enclose the shape). The circularity error (Ce) or out of roundness can therefore be defined as the difference between the radius of the two circles. The first circle is drawn outside the profile as to wholly enclose it, and the other is drawn inside the roundness profile so that it just inscribes the profile. The unit used for Ce is the micrometre. Finally, the surface roughness Ra (mean roughness) is the arithmetic average of the absolute values of the roughness profile. Ra is one of the most effective surface roughness measurements commonly adopted in engineering practice. Ra gives a good description of the height variations of the surface. The unit used for Ra is the micrometre.
3. Experimental Study
Numerous factors have an important influence on machined part dimensional and geometric accuracy during tuning operations. This study will employthirteen of them to illustrate the proposed approach. The first five factors are related to cutting parameters and workpiece geometry: cutting speed (S), cutting feed rate (f), depth of cut (d), workpiece diameter (Di), and workpiece length (L). The eight other input factors are related to the process’ dynamic conditions, and are recognized to have a significant influence on diametral errors (De), circularity errors (Ce) and surface roughness (Ra). These factors are: radial, tangential and axial cutting forces (Fx, Fy, Fz), radial and axial machine-workpiece-tool vibrations (Vbx and Vbz), acoustic emission (AE), and radial and axial workpiece deflections (dfx and dfz).
3.1. Experimental Design
In any experiment, the quality of the acquired data depends mainly on the data collection method. In a lot of cases, full factorial experiments are conducted. However, this design cannot be implemented when there are too many factors under consideration because the number of repetitions required would lead to prohibitive costs. By contrast, the use of a strategy such as orthogonal arrays (OAs), developed by Taguchi, can led to an efficient and robust fractional factorial design of experiments that can collect all of the statistically significant data with the minimum possible number of repetitions [33] . Accordingly, OAs will be used in this paper for the design of experiment and the modelling procedure.
The experiments are carried out on a CNC turning machine tool using a carbide insert for turning aluminum 6061-T6. The cutting tool is fixed on a Kistler piezoelectric dynamometer fixed rigidly on the tool turret so that the three components of the cutting force could be measured. A three-component accelerometer and an acoustic emission transducer mounted close to the cutting zone measured, respectively, the accelerations due to the MFWTS vibrations and the acoustic emissions generated by the machining operation. Two capacitance probes mounted close to the tool holder measured the tool deflections in the feed and speed directions.
Experiments are performed in two stages using L32 and L16 orthogonal arrays. In the first stage, a set of 32 experimental tests is performed to obtain the input data for training the ANN in the modelling procedure. In the second stage, an additional set of 16 experimental tests is performed to obtain the input data for evaluating and confirming the capacity of the resulting model. Cutting parameters used in both first and second stage experiments are summarized in Table 1. In order to ensure the validity of the experimental results, all 48 tests are repeated three times. Single pass cuts are executed according to the factor levels of
Table 1. Factors and levels chosen for the experiments.
each repetition. Feed and cutting speed levels are chosen within the range recommended by the manufacturer. The cutting depth is limited under 3.5 mm to represent finishing and semi-finishing conditions. The inserts are changed regularly in order to maintain small cutting tool wear and to avoid tool wear as additional factor.
All sensor signals are acquired and conditioned so that only the steady-state portions are retained. For each repetition, the min, max and mean values of the radial, tangential and axial cutting forces (Fx, Fy, Fz), MFWTS vibrations in the X and Z directions (Vbx and Vbz), acoustic emission (AE), and tool radial and axial deflections (dfx and dfz) in the steady state portions are calculated. The max values are considered to be the most representative. The machined parts are inspected for the three considered quality characteristics. The diametral and circularity errors are measured using a 3-axis moving bridge type coordinate measuring machine with an accuracy to less than 1 μm. The machined parts are measured at six uniformly distributed locations along its length to determine the form and dimensional errors. Each measurement, taken over a specific area, is repeated three times and the average values are considered. The surface roughness is inspected on three separate profiles using an accurate Mitutoyo Surftest profilometer, and again the average of three readings is recorded. The average dimensional, circularity and surface roughness errors obtained after inspection as well as other sensor measurement data are used to evaluate de the cause and effect relationships between machining parameters, machining conditions and QCMP. Figure 2 presents 12 typical profiles selected from the 32 profiles obtained using experimental factors presented in Table 1 for turning of cantilever bars.
3.2. Analysis Strategy
The experimental data is analyzed using three statistical tools: the graph of the average effects of each factor level, the percent contribution of factors extracted from the analysis of variance (ANOVA), and the correlation between the QCMP and various factors and sensor measurements. The percent contribution of a factor reflects the portion of the total variation observed in the experiment that is attributed to that factor. Ideally, the total percent contribution of all considered factors must add up to 100. Any difference from 100 represents the contribution of other uncontrolled factors and experimental errors. As the experiments are designed using an OA, the estimates of the average effects of a given factor on various responses will not be biased. Two ANOVA are performed in
Figure 2. Typical dimentional errors along workpiece axis in cantilever mounting.
this analysis. The first ANOVA is performed using machining parameters (S, f, d, Diand L) as inputs and sensor measurements (Fx, Fy, Fz, Vx, Vz, AE, dfx and dfz) as outputs in order to evaluate the effects of machining parameters on theprocess dynamic conditions. The second ANOVA is performed using machining parameters (S, f, d, Di and L) as input factors and QCMP (De, Ce and Ra) as outputs to identify the parameters that have the highest impact on part quality and to estimate their effects. ANOVAs are completed by a correlation analysis to evaluate the type and the strength of relationships between machining parameters, machining conditions and QCMP.
3.3. Experimental Data Analysis
Figure 3 shows that various QCMP are affected at different degrees by the machining process parameters. The factors most affecting part quality are the cutting feed and the cut depth. These results are expected, since the cutting forces, which are recognized to have a significant effect on part quality, are more sensitive to changes in feed and cut depth than to cutting speed variations (Figures 4(a)-(c)). Unlike Ra, De and Ce, depend significantly on Di and L. De and Ce are relatively large when Di is low and L is large. These results can be explained by the increased rigidity of the part as the diameter increases and by the increase in part deformation as the distance from the chuck increases (Figures 4(g)-(h)). Cutting speed appears to be the factor that has the least influence on De and Ce.
The factors that most affect Ra are S, f and d. The effects of Di and L are insignificant. These results are anticipated since vibrations and acoustic emissions, which are known to have an important effect on surface roughness, are less sensitive to changes in Di and L than they are to S, f and d variations (Figures 4(d)-(f)).
On the other hand, De, Ce and Ra show a strong dependency on cutting feed. The correlation analysis reported in Table 2 indicates that feed is correlated to De, Ce and Ra by up to 75%, while Di is correlated to De, Ce and Ra by less than
Figure 3. Effects of cutting parameters on quality characteristics of the machined parts.
25%. Accordingly, one can presume that De and Ce can be controlled using f, d and L, while Ra can be controlled using S, f and d. Similar conclusions can be clearly established from the percent contributions analysis. The percent contributions analysis also confirms that the contributions of these factors to the variation of De, Ce and Ra exceed 95%. The error remains within acceptable levels (less than 5%), implying that the most important process conditions influencing these QCMP are all included in the experiment. Figure 4 shows the average effects of process cutting parameters on sensor measurements data.
The cutting forces and workpiece deflection are strongly affected by f and d. The radial deflection appears to be more sensitive to L than the axial deflection. Acoustic emissions and vibrations are much more affected by cutting speed than cutting feed. However, the error associated with these sensor measurements is high, indicating that other factors, such as tool wear and variations in the characteristics of the workpiece and cutting tools could perturb the generated acoustic emissions and vibrations during the cutting operations. Accordingly, these variables cannot be reliably used to control globally the considered QCMP.
Furthermore, correlation analysis results in Table 2 shows that the QCMP is correlated to different degrees with various machining parameters and conditions. Thus one can expect to use all of these factors in any modelling procedure.
Figure 4. Effects of cutting parameters on sensor measurements.
Table 2. Correlations between cutting parameters, cutting conditions and quality characteristics the machined parts.
However, even if these factors could be selected based on the above analysis, it still remains expensive to implement. Thus, a systematic and rigorous procedure to select the best combination of variables to include in the model is required.
4. Building the Prediction Model
4.1. Proposed Modelling Strategy
Turning operations are dynamic processes with various nonlinearities and stochastic disturbances. The difficulty of building an effective prediction model lies in the selection of the appropriate modelling technique and the variables to be included in the model. These choices represent the basic ingredients of any modelling methodology. Selecting the model form and the modelling technique is not sufficient to produce the best model. Since deterministic models are typically valid only for a limited range of cutting conditions, ANNs present the best modelling alternative. While various neural techniques can be used in this approach, a multilayer feed forward network seems to be one of the most appropriate choices because of its simplicity and flexibility. In order to determine the best combination of variables to be included in the modelling procedure in a fast and cost effective way, OAs are used again. The selection of variables is based on analyzing the effect of each combination of variables on the performance of the designed models, as well as the contribution of each variable to modelling, validation and prediction errors.
Many criteria can be used to assess whether a reduced model adequately represents the relationship between the QCMP and the cutting parameters under various process conditions. Measuring the performance of fitted models is based on the principle of reducing several statistical criteria. These include the residual sum of squared errors (SSE), the residual mean square error (MSE), the total squared error (Mallow’s Cp), and the coefficient of determination (R2). For the majority of modelling techniques, the model is determined by minimizing the residual sum of squares (SSE). All of the criteria, MSE, Cp, and R2, are a linear function of the SSE. The combination of variables that minimizes the SSE creates MSE and Cp as the minimum and R2 as the maximum under a fixed number of variables. Among these criteria, R2 does not have an extreme value and shows a gradual increasing trend when the number of variables in the model is increased. Thus, the use of R2 as a criterion for the selection of variables can allow some subjectivity. If p variables among q variables are selected, the residual mean square is MSEp = SSEp/(n − p − 1), where n is the total number of observations. The terms SSEp and n-p both decrease with an increase in the number of independent variables p. Therefore, MSEp have the ability to show an extreme value. In this study, the judgment function used consists in minimizing the training residual mean square error (MSEt) and the validation residual mean square error (MSEv) for each quality characteristic, as well as the total residual mean square error (MSEtot).
4.2. Application of the Proposed Strategy
To illustrate the proposed modelling approach, twelve variables are considered. Before selecting the variables and training the ANN models, it is important to establish the size of the hidden layer and to optimize the training performances. The idea is to approximate the relationship between the size of the hidden layer, the number of input variables and the complexity of the parameters to be estimated. For all trained models, an average error of less than 1% is used, irrespective of the hidden layer size. Consequently, to avoid long training and over-fit- ting that could affect accuracy, the [NP*2NP + 1*3] network structure is selected (NP: number of inputs). For variable selection, the procedure begins by selecting the OA for the model design. The OA that best fits this modelling procedure is a L16. The procedure used for models design is illustrated in Table 3. The (1) and (0) numbers indicate whether the variables are used as input to the model or not, respectively.
To reduce the number of variables and simplify the variable selection procedure, the variables Di and L are combined into a single variable identified as L/D and defined as workpiece length/diameter ratio. The data structure used to produce the designed models is showed in Table 4. Typical results representing the performances of the designed models as a function of the seven selection criteria are presented in Table 5.
Table 5 shows that all models fit the data relatively well, as indicated by the MSE values. Using these results, the average effect of each variable on each model’s performance is evaluated. The graphs of average effects demonstrate that the
Table 3. Designed models for the variables selection procedure.
Table 4. Typical training and testing data sets for prediction model building.
Table 5. Typical modelling performances for variables selection using MSEt, MSEv and MSEtot.
variables having the most positive effects on the designed models are feed rate, cutting depth, L/D ratio, cutting forces (Fx and Fz) and workpiece deformation (dfx and dfz). The presence of speed, vibrations and acoustic emission in the model increase the MSE values. These results are confirmed by the average effect of each variable in terms of percent contribution to improving model accuracy. Table 6 reveals that the variables significantly reducing MSE values are f, d, L/D, Fx, Fz, dfx and dfz. These ascertainments suggest that there are many options to consider in building an efficient part quality prediction model. However, given the dominant and robust relationships that link dfx and dfz to f, d, L/D and cutting forces, added to the strong correlation between deformations and QCMP, it is obviously desirable to include f, d, dfx and dfz in the proposed quasi-optimal model (QOM). Accordingly, the model including the selected variables is built using a multilayer feedforward network. The topology of the ANN implemented is described in Figure 5. The network configuration selected have 4 neurons in the input layer corresponding to feed rate (f), depth of cut (d) and workpiece radial and axial deflections (dfx and dfz), and 3 neurons in the output layer corresponding to diametral errors (De), circularity errors (Ce) and
Table 6. % contributions of cutting parameters and conditions in the modelling performances of the designed models.
Figure 5. Artificial neural network architecture.
surface roughness (Ra).
Figure 6 shows the variation of the network’s prediction accuracy for the three quality characteristics. The maximum prediction errors are less than 3.50%, 4.75% and 5.75% respectively for De, Ce and Ra, and present an excellent distribution of predicted points. Thus, it can be concluded that the ANN is able to learn complex relationships very well and can be used as an effective predictive tool. The model is then used for prediction using the validation data. Figure 7 shows the variation of the QOM’s prediction accuracy for the three quality characteristics. The maximum prediction errors are under 10%.
A global evaluation of the achieved results demonstrates that the resultant model successfully estimates the QCMP during CNC turning of cantilever bars.
Figure 6. Predicted vs measured quality characteristics of the parts in the modelling phase: (a) diametral errors, (b) circularity errors and (c) surface roughness.
Figure 7. Predicted vs measured quality characteristics of the parts in the prediction phase:(a) diametral errors, (b) circularity errors and (c) surface roughness.
The proposed quality prediction approach can successfully contribute to a reducing machined part error by approximately 90%. This model demonstrates that it is not necessary to massively instrument the machine tool in order to find the relevant information needed for modelling the quality characteristics of machined parts. Only two sensors probing the tool deflections in the feed and speed directions are necessary. These deformations can be eventually estimated with good precision using a simplified model based simply on the cutting parameters.
5. Conclusion
The present study is devoted to the development of an integrated model for quality prediction in CNC turning of cantilever bars. A systematic modelling procedure based on experimental investigations, ANN modelling and various statistical tools is designed to produce the most accurate and effective prediction model. The effects of several cutting parameters and conditions on the quality characteristics of the machined parts are analyzed, and their correlation with diametral errors, circularity errors and surface roughness are investigated under various practical process conditions. Based on these results and using various statistical analysis tools, the most relevant variables to be included in the prediction model are identified and fused using several ANN architectures. Four variables are methodically selected from thirteen possible variables, including cutting parameters, cutting forces, deflections, vibration and acoustic emission. Among all these variables, feed rate, depth of cut and workpiece deflections are found to provide the needed information for an accurate and efficient prediction model. Using these variables, a quasi-optimal model is produced by training an ANN using data obtained from structured experiments conducted under a large variety of cutting parameters and conditions. The achieved results are very encouraging. The dimensional errors, circularity errors and surface roughness are predicted with a global error fluctuating between 3.50% and 10% under variable machining conditions. These results demonstrate that the proposed modeling procedure can be effectively applied to quality prediction and monitoring due to its simplicity, accuracy and robustness.
Cite this paper
Davakan, D.M. and El Ouafi, A. (2017) Artificial Neural Networks Based Integrated Predictive Modelling of Quality Characteristics in CNC Turning of Cantilever Bars. World Journal of Mechanics, 7, 143-159. https://doi.org/10.4236/wjm.2017.75013
References
- 1. Bedworth, D.D., Anderson, M.R. and Wolfe, P.M. (1991) Computer-Integrated Design and Manufacturing. McGraw-Hill, New York.
- 2. Kurtoglu, A. and Sohlenius, G. (1990) The Accuracy Improvement of Machine Tools. CIRP Annals, 39, 417-419.
- 3. Li, X. (2001) Real-Time Prediction of Workpiece Errors for a CNC Turning Centre, Part 1. Measurement and Identification. International Journal of Advanced Manufacturing Technology, 17, 649-653.
https://doi.org/10.1007/s001700170128 - 4. Li, X. and Du, R. (2002) Analysis and Compensation of Workpiece Errors in Turning. International Journal of Production Research, 40, 1647-1667.
https://doi.org/10.1080/00207540110100685 - 5. Rafai, N.H. and Islam, M.N. (2009) An Investigation into Dimensional Accuracy and Surface Finish Achievable in Dry Turning. Machining Science and Technology, 13, 571-589.
https://doi.org/10.1080/10910340903451456 - 6. Benardos, P.G. and Vosniakos, G.C. (2003) Predicting Surface Roughness in Machining: A Review. International Journal of Machine Tools and Manufacture, 43, 833-844.
- 7. Jawahir, I.S., et al. (2011) Surface Integrity in Material Removal Processes: Recent Advances. CIRP Annals, 60, 603-626.
- 8. Abellan-Nebot, J.V. and Subirón, F.R. (2010) A Review of Machining Monitoring Systems Based on Artificial Intelligence Process Models. International Journal of Advanced Manufacturing Technology, 47, 237-257.
https://doi.org/10.1007/s00170-009-2191-8 - 9. Van Luttervelt, C.A., et al. (1998) Present Situation and Future Trends in Modelling of Machining Operations Progress Report of the CIRP Working Group—Modelling of Machining Operations. CIRP Annals, 47, 587-626.
- 10. Arrazola, P.J., Özel, T., Umbrello, D., Davies, M. and Jawahir, I.S. (2013) Recent Advances in Modelling of Metal Machining Processes. CIRP Annals, 62, 695-718.
- 11. Ehmann, K.F., Kapoor, S.G., DeVor, R.E. and Lazoglu, I. (1997) Machining Process Modeling: A Review. Journal of Manufacturing Science and Engineering, 119, 655-663.
https://doi.org/10.1115/1.2836805 - 12. Carrino, L., Giorleo, G., Polini, W. and Prisco, U. (2002) Dimensional Errors in Longitudinal Turning Based on the Unified Generalized Mechanics of Cutting Approach. Part II: Machining Process Analysis and Dimensional Error Estimate. International Journal of Machine Tools and Manufacture, 42, 1517-1525.
- 13. Masset, L. and Debongnie, J.F. (2004) Machining Processes Simulation: Specific Finite Element Aspects. Journal of Computational and Applied Mathematics, 168, 309-320.
- 14. Rajasekaran, T., Palanikumar, K. and Arunachalam, S. (2013) Investigation on the Turning Parameters for Surface Roughness Using Taguchi Analysis. Procedia Engineering, 51, 781-790.
- 15. Asiltürk, I. and Cunkas, M. (2011) Modeling and Prediction of Surface Roughness in Turning Operations Using Artificial Neural Network and Multiple Regression Method. Expert Systems with Applications, 38, 5826-5832.
- 16. Chandrasekaran, M., Muralidhar, M., Krishna, C.M. and Dixit, U.S. (2010) Application of Soft Computing Techniques in Machining Performance Prediction and Optimization: A Literature Review. International Journal of Advanced Manufacturing Technology, 46, 445-464.
https://doi.org/10.1007/s00170-009-2104-x - 17. Li, X., Venuvinod, P.K., Djorjevich, A. and Liu, Z. (2001) Predicting Machining Errors in Turning Using Hybrid Learning. International Journal of Advanced Manufacturing Technology, 18, 863-872.
https://doi.org/10.1007/PL00003954 - 18. Jiao, Y., Lei, S., Pei, Z.J. and Lee, E.S. (2004) Fuzzy Adaptive Networks in Machining Process Modeling: Surface Roughness Prediction for Turning Operations. International Journal of Machine Tools and Manufacture, 44, 1643-1651.
- 19. El Ouafi, A. and Barka, N. (2014) An ANN Based Multi-Sensor Integration Approach for In-Process Monitoring of Product Quality in Turning Operations. Journal of Automation and Control Engineering, 2, 289-293.
https://doi.org/10.12720/joace.2.3.289-293 - 20. Suresh, P.V.S., Rao, P.V. and Deshmukh, S.G. (2002) A Genetic Algorithmic Approach for Optimization of Surface Roughness Prediction Model. International Journal of Machine Tools and Manufacture, 42, 675-680.
- 21. Reddy, B.S., Kumar, J.S. and Reddy, K.V.K. (2009) Prediction of Surface Roughness in Turning Using Adaptive Neuro-Fuzzy Inference System. Journal of Mechanical and Industrial Engineering, 3, 252-259.
- 22. Kumanan, S., Jesuthanam, C.P. and Kumar, R.A. (2008) Application of Multiple Regression and Adaptive Neuro Fuzzy Inference System for the Prediction of Surface Roughness. International Journal of Advanced Manufacturing Technology, 35, 778-788.
https://doi.org/10.1007/s00170-006-0755-4 - 23. Vacharanukul, K. and Mekid, S. (2005) In-Process Dimensional Inspection Sensors. Measurement, 38, 204-218.
- 24. Dimla, D.E. (2000) Sensor Signals for Tool-Wear Monitoring in Metal Cutting Operations—A Review of Methods. International Journal of Machine Tools and Manufacture, 40, 1073-1098.
- 25. Risbood, K.A., Dixit, U.S. and Sahasrabudhe, A.D. (2003) Prediction of Surface Roughness and Dimensional Deviation by Measuring Cutting Forces and Vibrations in Turning Process. Journal of Materials Processing Technology, 132, 203-214.
- 26. Li, X. (2001) Real-Time Prediction of Workpiece Errors for a CNC Turning Centre, Part 3. Cutting Force Estimation Using Current Sensors. International Journal of Advanced Manufacturing Technology, 17, 659-664.
https://doi.org/10.1007/s001700170130 - 27. Benardos, P.G., Mosialos, S. and Vosniakos, G.C. (2006) Prediction of Workpiece Elastic Deflections under Cutting Forces in Turning. Robotics and Computer-Inte-grated Manufacturing, 22, 505-514.
- 28. Da Silva, M.B. and Wallbank, J. (1999) Cutting Temperature: Prediction and Measurement Methods—A Review. Journal of Materials Processing Technology, 88, 195-202.
- 29. Jiang X.J. and Whitehouse, D.J. (2012) Technological Shifts in Surface Metrology. CIRP Annals, 61, 815-836.
- 30. Ramesh, S. and Ramamoorthy, B. (1996) Measurement of Surface Finish Using an Optical Diffraction Technique. Wear, 195, 148-151.
- 31. Ostafiev, V.A. (1999) Machining Precision Augmented by Sensors. International Journal of Production Research, 37, 91-98.
https://doi.org/10.1080/002075499191931 - 32. Nobel, G., Donmez, M.A. and Burton, R. (1990) Real-Time Compensation for Tool Form Errors in Turning Using Computer Vision. SPIE Proceedings, 1335, 186-193.
https://doi.org/10.1117/12.22864 - 33. Ross, P.J. (1996) Taguchi Techniques for Quality Engineering: Loss Function, Orthogonal Experiments, Parameter and Tolerance Design. McGraw-Hill Professional, New York.









