World Journal of Mechanics
Vol.06 No.11(2016), Article ID:71485,23 pages
10.4236/wjm.2016.611030
Study on Periodic MHD Flow with Temperature Dependent Viscosity and Thermal Conductivity past an Isothermal Oscillating Cylinder
Rubel Ahmed, Reaz Uddin, B. M. Jewel Rana, Rafrafin Selim, Sarder Firoz Ahmmed
Mathematics Discipline, Khulna University, Khulna, Bangladesh

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 9, 2016; Accepted: October 22, 2016; Published: October 25, 2016
ABSTRACT
Temperature dependent viscosity and thermal conducting heat and mass transfer flow with chemical reaction and periodic magnetic field past an isothermal oscillating cylinder have been considered. The partial dimensionless equations governing the flow have been solved numerically by applying explicit finite difference method with the help Compaq visual 6.6a. The obtained outcome of this inquisition has been discussed for different values of well-known flow parameters with different time steps and oscillation angle. The effect of chemical reaction and periodic MHD parameters on the velocity field, temperature field and concentration field, skin-friction, Nusselt number and Sherwood number have been studied and results are presented by graphically. The novelty of the present problem is to study the streamlines by taking into account periodic magnetic field.
Keywords:
Chemical Reaction, Periodic MHD, Oscillating Cylinder, Variable Viscosity, Thermal Conductivity

1. Introduction
In recent, the study of unsteady free convective flows through an oscillating cylinder evinces a vital role in chemical engineering, turbo machinery, and aerospace technology. The occurrence of heat and mass transfer is too general in chemical process industries such as the production of polymer and food processing. The study of MHD incompressible viscous flows has several vital engineering applications in devices such as MHD power generators, electrical components transmission lines, cooling of nuclear reactors, geothermal systems, forming metal, crystal growing, aerodynamic processes, and heat exchange designs. The focus of a huge number of researchers has drowned by MHD due to its various applications such as pumps, bearings. Implicit finite-difference scheme of Crank-Nicolson type has been used to solve radiation and mass transfer effects on unsteady MHD free convection flow of an incompressible viscous fluid past a moving vertical cylinder which has been analyzed by Reddy et al. (2009) [1] . When the radiation parameter increases the velocity and temperature decrease in the boundary layer which has been founded by them. Unsteady natural convection of air with a variable viscosity over an isothermal vertical cylinder has been solved with the help of implicit finite-difference method by Rani et al. (2010) [2] . The objective of the work was to investigate the viscosity effects on the free convective flow of the air along a semi-infinite vertical cylinder and by analyzing they found that velocity profiles near the wall decrease with the increasing kinematic viscosity variation parameter also noticed that the decrease in the viscosity-variation parameter leads to the increase in the average heat transfer rate and to the decrease in the average skin friction. Conduction-radiation effects on periodic MHD flow along a vertical surface have been analyzed by Siddiqa et al. (2012) [3] . Radiation, chemical reaction, and magnetic parameters have been used by Machireddy (2013) [4] to investigate chemically reactive species and radiation effects on MHD convective flow past a moving vertical cylinder. By using implicit finite difference method he founded that the transient velocity increases with an increase in thermal Grashof number or mass grashof number. With the increasing values of magnetic field, parameter decreases the transient velocity. Gauss-Seidel iteration method has been used by Babu et al. (2014) [5] to investigate the effects of chemical reaction and radiation and by considering two concentric cylinders of different radius. They worked on the effects of chemical reaction and radiation absorption on mixed convective flow in a circular annulus at constant heat and mass flux.
Unlike other fluid, Cintaginjala et al. (2014) [6] considered the Jeffrey’s fluid, By taking Jeffrey’s fluid Gauss-Seidel iteration method have been used to investigate the effects of chemical reaction and radiation absorption on mixed convective heat and mass transfer flow through a cylindrical annulus with heat generating sources and non- linear density temperature relation which have been done by Cintaginjala et al. (2014) [6] and they also used two concentric cylinders to investigate the problem. An explicit finite numerical analysis has been carried out by taking temperature as a variable by Mondal et al. (2015) [7] . By using magnetic parameter, permeability parameter, Schmidt number, thermal Grashof number, mass Grashof number and accelerated parameter they worked on free convection and mass transfer flow through a porous medium with variable temperature. Also, they assumed that there were no effects of temperature and concentration on the fluid. The velocity increases with the decreasing of the magnetic parameter and Schmidt number whereas the velocity profiles increase with increasing the Permeability parameter, thermal Grashof number, mass Grashof number and accelerated parameter in case of cooling of the plate which has been investigated by Mondal et al. (2015) [7] . A numerical study on unsteady natural convection flow past an isothermal vertical cylinder with temperature dependent viscosity has been analyzed by Hossain et al. (2015) [8] . They also worked on the effect of viscosity variation parameter on isotherms and streamlines. By taking binary fluid mixture a regular perturbation method has been used to solve MHD flow, heat and mass transfer due to auxiliary moving cylinder in the presence of thermal diffusion, radiation and chemical reactions by Sharma et al. (2015) [9] . They used regular perturbation method to solve the above problem and with the increases in the value of magnetic field parameter decreases velocity which has been concluded by Sharma et al. (2015) [9] . In a porous medium by using Darcy-Forchheimer model the main aim of that work was to investigate the effects of radiation, chemical reaction, thermal-diffusion and diffusion-thermo on MHD heat and mass transfer free convection flow near the lower stagnation point of an isothermal horizontal circular cylinder. In the presence of Soret and Dufour effects, hydro-magnetic flow of viscoelastic fluid over porous oscillatory stretching sheet with thermal radiation has been investigated by Ali et al. (2016) [10] . An implicit finite-dif- ference method of Crank-Nicolson type have been employed to investigate the chemical reaction and temperature oscillation effect on unsteady MHD free convective flow over moving semi-infinite vertical cylinder by Rajesh et al. (2016) [11] . They found that velocity increases with the increasing thermal Grashof number, mass Grashof number and decreases with the increasing values of the magnetic parameter, Prandtl number, Schmidt number. Recently, MHD flow and heat transfer of couple stress fluid over an oscillatory stretching sheet with heat source/sink in porous medium have been carried out by Ali et al. (2016) [12] . Chemical reaction and radiative MHD heat and mass transfer flow with temperature dependent viscosity past an isothermal oscillating cylinder have been investigated by Ahmed et al. (2016) [13] . Recently, magnetic field and thermal radiation effect on heat and mass transfer of air flow near a moving infinite plate with a constant heat sink has been investigated by Arifuzzaman et al. (2016) [14] .
By considering temperature dependent viscosity and thermal conducting heat and mass transfer flow with chemical reaction and magnetic field past an isothermal oscillating cylinder have been studied. Unlike other researchers, we have used magnetic field periodically. The main aim of this paper is to investigate the effects of chemical reaction, periodic magnetic field on velocity field, temperature field and concentration field, skin-friction, Nusselt number, Sherwood number and stream-lines with different time steps, oscillation angle and also compared with the absence of a non-periodic magnetic field. The partial dimensionless equations governing the flow are solved numerically by using explicit finite difference method with the help of Compaq visual 6.6a.
2. Mathematical Model
In the presence of periodic magnetic field unsteady two-dimensional free convective flow of a viscous incompressible electrically conducting fluid past a semi-infinite oscillating cylinder of radius r0 have been investigated. Here, the x-axis is taken along the axis of cylinder in the vertical direction and the radial coordinate r is considered as normal to the cylinder. Initially the fluid and the cylinder are at the same temperature 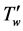 and concentration
and concentration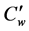 . At time t' the cylinder starts moving in the vertical direction with a uniform velocity u0.
. At time t' the cylinder starts moving in the vertical direction with a uniform velocity u0.
The temperature of the surface of the oscillating cylinder is increased to 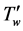 concentration
concentration 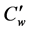 are maintained constantly thereafter. A uniform periodic magnetic field (B0) is imposed to the oscillating cylinder which is presented in Figure 1. It is further assumed that there is no applied voltage, so that electric field is absent [4] . It is also assumed that there exists a homogeneous first order chemical reaction between the fluid and species concentration. But here we assume the level of species concentration to be very low and hence heat generated during chemical reaction can be neglected. Hence, any convective mass transport to or from the surface due to a net viscous dissipation effects in the energy equation are assumed to be negligible. It is also assumed that all the fluid properties are constant except that of the influence of the density variation with temperature and concentration in the body force term. The foreign mass present in the flow is assumed to be at low level, and Soret and Dufour effects are negligible. By considering the above assumptions, the boundary layer equations governing flow past an oscillating cylinder with Boussinesq’s approximation can be expressed in the following form. Then, the flow under consideration is governed by the following system of equations:
are maintained constantly thereafter. A uniform periodic magnetic field (B0) is imposed to the oscillating cylinder which is presented in Figure 1. It is further assumed that there is no applied voltage, so that electric field is absent [4] . It is also assumed that there exists a homogeneous first order chemical reaction between the fluid and species concentration. But here we assume the level of species concentration to be very low and hence heat generated during chemical reaction can be neglected. Hence, any convective mass transport to or from the surface due to a net viscous dissipation effects in the energy equation are assumed to be negligible. It is also assumed that all the fluid properties are constant except that of the influence of the density variation with temperature and concentration in the body force term. The foreign mass present in the flow is assumed to be at low level, and Soret and Dufour effects are negligible. By considering the above assumptions, the boundary layer equations governing flow past an oscillating cylinder with Boussinesq’s approximation can be expressed in the following form. Then, the flow under consideration is governed by the following system of equations:
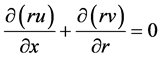 (1)
(1)
Figure 1. Flow model and physical co-ordinate.
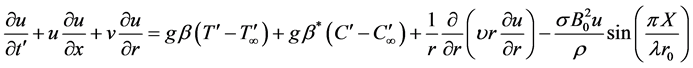 (2)
(2)
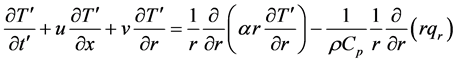 (3)
(3)
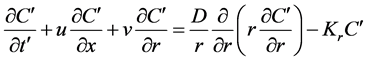 (4)
(4)
With boundary conditions,
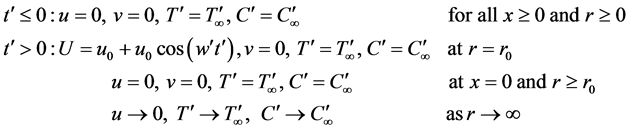 (5)
(5)
It is necessary to make the Equations (1) to (4) with boundary conditions (5) dimensionless. For this intention we introduce the following dimensionless quantities
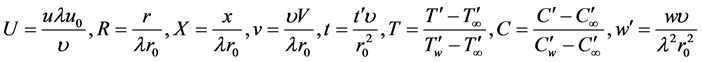 (6)
(6)
If γ and ε denotes the non-dimensional viscosity variation parameter and thermal conductivity then 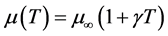 and
and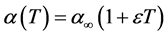 . By putting the non- dimensional quantities of (6) (Sadia et al. [3] ) into the Equations (1) to (4) along with (5), then we obtain the following no-dimensional Equations (7) to (10) with boundary conditions (11).
. By putting the non- dimensional quantities of (6) (Sadia et al. [3] ) into the Equations (1) to (4) along with (5), then we obtain the following no-dimensional Equations (7) to (10) with boundary conditions (11).
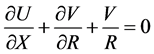 (7)
(7)
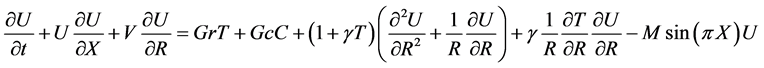 (8)
(8)
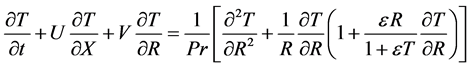 (9)
(9)
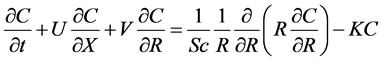 (10)
(10)
The corresponding boundary conditions in terms of non-dimensional variables are
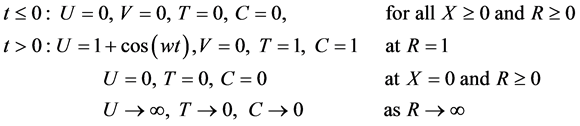 (11)
(11)
Skin friction coefficient, the rare of heat transfer rate and Sherwood number are expressed as follows



3. Numerical Technique
An explicit finite difference method has been devoted to solve the nonlinear partial differential Equations (7)-(10) along with boundary condition (11). The finite difference equations for the Equations (7)-(10) have been recounted by the Equations (15) to (18) respectively




To get the finite difference equations the region of the periodic MHD flow is divided into the grids or meshes of lines parallel to X and R is taken normal to the axis of the oscillating cylinder. Here we consider that the height of the cylinder is Xmax = 20.0 i.e. X varies from 0 to 20 and regard Rmax = 50.0 as corresponding to R → ∞. In the above Equations (15) to (18) the subscripts i and j designate the grid points along the X and R coordinates, respectively, where X = iΔX and
4. Results and Discussion
In order to obtain the corporal insight of the problem of the study, the velocity profile, temperature profile and concentration profile are reveal by assigning numerical values to different parameters encountered into the corresponding equations. The value of Schmidt number (Sc) are chosen for Hydrogen gas diffusing in electrically-conducting Air (Sc = 0.20), Helium (Sc = 0.30), steam (Sc = 0.60), Oxygen (Sc = 0.66), NH3 (Sc = 0.78),CO2 at 250C (Sc = 0.94), Methanol (Sc = 1.00) and high viscous fluid (Sc = 5.00). The value of Prandtl number (Pr) are chosen for air (Pr = 0.71), Nitrogen (Pr = 0.78), water (Pr = 7.0) and water at 40C (Pr = 11.62).
With the increases of viscosity variation parameter (γ) the velocity decreases which elucidates in the Figure 2. Peak velocity for γ = 2.00 is 12.0615% greater than peak velocity for γ = 5.00. Similarly, peak velocity for γ = 1.00 is 29.564%greater than peak velocity for γ = 2.00. It has been noticed that there is a major change of peak velocity for γ = 1.00, γ = −0.50 which occurs very drastically and that is 113.629%. However, there is no effect of viscosity variation parameter (γ) on the velocity at R = 4.5 (ap- proximately) which is indicated by the circle. Figure 3, evinces the velocity curve for
Figure 2. Velocity profiles for different values of γ.
Figure 3. Velocity profiles for different values of time steps(t) and M.
different time steps. The velocity of the fluid is increasing with the increasing of time steps and low periodic magnetic field indicates more smooth curves than the higher magnetic field. Due to the increasing values of Prandtl number (Pr) and Scmidth number (Sc) increases the viscosity of the fluid and decrease the molecular diffusivity which decreases the velocity of fluid. For the increasing values of Prandtl number (Pr), Scmidth number (Sc) and magnetic parameter (M) the velocity curves let on a different shape and its decreasing which have been indicated in Figure 4. The black long dashed line shows that there is no effect of the periodic magnetic parameter and the smoothness is decreasing with the increasing of the magnetic parameter (M). With the decreases of viscosity variation parameter (γ), thermal conductivity (ε) and magnetic parameter (M) the velocity increases which appeared in the Figure 5. Figure 6, indicates the velocity profile for different values of oscillation angle (ϕ), Gr, Gc and M. we have taken the oscillation range,
Figure 4. Velocity profiles for different values of Pr, Sc and M.
Figure 5. Velocity profiles for different values of γ, ε and M.
Figure 6. Velocity profiles for different values of Gr, Gc and M.
Figure 7. Velocity profiles for different values of time steps(t) and Pr.
71.512%, 19.57% respectively. Figure 8, let on a different shape for different values of thermal conductivity parameter. It has noticed that with the increasing values of thermal conductivity the values of velocity are also increasing. At ε = 2.00 then the height velocity is 1.36589. 1.34891 for ε = 1.00. Height velocity 1.34481 at ε = 0.50 and so on. For the increasing of Scmidth number decreases the molecular diffusivity. That’s why velocity curves downward due to increasing the Schmidt number (Sc) which is revealed the Figure 9. According to the descending order of Scmidth number 1.538, 1.905 and 45.455 through percentages are the difference of velocity between two curves.
Figure 10, evinces the temperature profile for different values of Prandtl number (Pr). With the increases of Prandtl number results in low thermal conductivity, as a result, conduction even thermal boundary layer thickness decreases. That’s, result to decrease the temperature. There is a significant effect of Pr on the temperature profile at R = 1.55556 (approximately). From above, by ascending order of curves at same point R = 1.55556, percentages of the difference of temperature between two curves are 35.514, 8.513 and 0.688 respectively. Figure 11, elucidates the temperature profiles for different values of thermal conductivity parameter. By descending order of thermal conductivity (ε), the difference of temperature between two curves is 13.497%, 12.942% and 16.52% respectively. Temperature profiles decreases for the combine increasing values of Pr, Sc and M which is indicated in Figure 12. When the values of Scmidth number (Sc) changes then the concentration curves let on different curves for the fixed values of the rest parameters as shown in Figure 13. By investigating Figure 13, it is
Figure 8. Velocity profiles for different values of ε.
Figure 9. Velocity profiles for different values of Sc.
Figure 10. Temperature profiles for different values of Pr.
Figure 11. Temperature profiles for different values of ε.
Figure 12. Temperature profiles for different values of Pr, Sc and M.
Figure 13. Concentration profiles for different values of Sc.
apparent that the curves are upward direction with the decreasing values of Scmidth number (Sc). By descending order of Scmidth number (Sc) at same point R = 2.333, the difference of temperature between two curves are 6.9225%, 38.56% and 23.18% respectively.
Increase of chemical reaction (K) significantly alerts the concentration boundary layer thickness but does not alerts momentum boundary layer. Due to the increasing values of Sc, Pr and K the concentration curves let on different curves for fixed values rest parameters as shown in Figure 14. By analyzing Figure 14, it is apparent that the curves are upward direction with the decreasing values of Sc, Pr and K. So, our presented problem indicates the destructive chemical reaction problem. Velocity gradient increases with the increases of Prandtl number (Pr) and Scmidth number (Sc). As a result, with the increasing values of Prandtl number (Pr) the values of skin-friction decreases which are exhibited in Figure 15. The percentages of the difference of skin- friction as the descending order of Prandtl number are 1.9769 and 2.68054. Skin friction increases for the increasing values of Scmidth number (Sc) while it decreases with an increase in magnetic parameter (M), through-out the transient period which has been indicated as in the Figure 15. The real fact is that the magnetic Field results in damping effect on velocity of the fluid by creating drag force i.e. the increase values of magnetic parameter create a drug force known as Lorentz force that opposes the fluid motion which is indicated in Figure 16. Also the boundary layer thickness decreases with an increase of magnetic parameter. Smaller values of Prandtl number (Pr) are
Figure 14. Concentration profiles for different values of Pr, Sc and ε.
Figure 15. Skin-friction for different values of Pr.
Figure 16. Skin-friction for different values of Pr, Sc and M.
equivalent to increase the thermal conductivities and therefore heat is able to diffuse from the cylinder more rapidly than higher values of Prandtl number. For the increasing values of Prandtl number the values of Nusselt number increases which is displayed in Figure 17. Nusselt number increases with the increases of Prandtl number (Pr), Scmidth number (Sc) and thermal conductivity (ε) which is uncovered in the Figure 18. At time t = 0.99900 the values of Nusselt number as the ascending order of curves are 0.96152, 0.87027 and 0.79517. Figure 19, Elucidates the Sherwood number for different values Prandtl number (Pr), Scmidth number (Sc). Sherwood number are decreasing for the decreasing values Prandtl number (Pr), Scmidth number (Sc) and there is a significant effect of Sherwood number at t = 0.1(approximately). Figure 20 and Figure 21 show the streamlines for different values of the magnetic parameter. The smooth solid lines in Figure 19 indicates the value of M = 0.00 i.e., there is no effect of the periodic magnetic field. Higher magnetic field (M) indicates the non-smooth curves which are indicated in the Figure 21. With the increases of viscosity variation parameter (γ) and thermal conductivity (ε) increases the values of the stream which as spectacled in Figure 22 and Figure 23. Streamlines for γ = 2.0 is 6.08% higher than γ = −0.5 and at the same point streamlines decrease for the increasing values of thermal conductivity (ε). Streamlines for ε = 2.0 is 0.40% lower than ε = 0.5.
Finally, a comparison of the present results with the published results (Machireddy [4] ) is elucidated in Table 1. The desired accuracy of the present results is qualitatively as well as qualitatively good in case of flow parameters.
Figure 17. Nusselt number for different values of Pr.
Figure 18. Nusselt number for different values of Pr, Sc and ε.
Figure 19. Sherwood number for different values of Pr and Sc.
Figure 20. The streamlines for different values of M.
Figure 21. The streamlines for different values of M.
Figure 22. The streamlines for different values of γ.
Figure 23. The streamlines for different values of ε.
Table 1. Comparison of the accuracy of the present results with the previous results.
5. Conclusions
An elaborated numerical analysis has been performed for the effects of the chemical reaction of the first order on the periodic MHD free convective flow for a gas past a moving semi-infinite oscillating cylinder with variable kinematic viscosity and thermal conductivity. The partial dimensionless equations governing the flow have been solved numerically by applying explicit finite difference method with the help Compaq visual 6.6a. The obtained outcome of this inquisition has been discussed for different values of well-known flow parameters with different time steps and oscillation angle. By analyzing the problem, the concluding remarks have been carried out as follows:
・ The velocity decreases with an increase of Scmidth number (Sc), Prandtl number (Pr) and periodic magnetic field (M) also higher magnetic field indicate more non- smooth curves than the lower periodic magnetic field (M). i.e. the wavy curves occurs only when we impose the magnetic field (M) periodically.
・ Higher oscillation angle (ϕ) indicates the lower point on the wall than lower oscillation angle (ϕ) at which the initial velocity starts.
・ With the decreasing of chemical reaction parameter (K), viscosity variation parameter (γ), result to increasing the velocity profiles while velocity increases with the increases of thermal conductivity (ε).
・ For the decreasing values of Scmidth number (Sc) and Prandtl number (Pr), the temperature increases while temperature increases for increasing values of thermal conductivity (ε).
・ The concentration increases with the decreasing values of Scmidth number (Sc), Prandtl number (Pr) and chemical reaction parameter (K).
・ Nusselt number increases for the increasing values of Prandtl number (Pr), Scmidth number (Sc) and skin-friction decreases for the increasing values of the periodic magnetic field (M), Prandtl number (Pr).
・ Sherwood number increases with the increasing values of Scmidth number (Sc).
・ With the increases of viscosity variation parameter (γ) and thermal conductivity (ε) increases the values of stream-lines also lower periodic magnetic field (M) indicates the more smooth streamlines than the higher periodic magnetic field (M).
Acknowledgements
We acknowledge the ministry of National Science and Technology (NST), Dhaka, Bangladesh and thank for providing financial support for this research work as a fellowship in 2015-2016.
Cite this paper
Ahmed, R., Uddin, R., Jewel Rana, B.M., Selim, R. and Ahmmed, S.F. (2016) Study on Periodic MHD Flow with Temperature Dependent Viscosity and Thermal Conductivity past an Isothermal Oscillating Cylinder. World Journal of Mechanics, 6, 419-440. http://dx.doi.org/10.4236/wjm.2016.611030
References
- 1. Reddy, M.G. and Reddy, M.B. (2009) Radiation and Mass Transfer Effects on Unsteady MHD Free Convection Flow of an Incompressible Viscous Fluid past a Moving Vertical Cylinder. Theoretical and Applied Mechanics, 3, 239-260.
- 2. Rani, H.P. and Kim, C.Y. (2010) A Numerical Study on Unsteady Natural Convection of Air with Variable Viscosity over an Isothermal Vertical Cylinder. Korean Journal of Chemical Engineering, 27, 759-765.
http://dx.doi.org/10.1007/s11814-010-0211-x - 3. Sadia, S., Hossain, M.A. and Golra, R.S.R. (2012) Conduction-Radiation Effects on Periodic MHD Flow along a Vertical Surface. International Journal of Thermal Science, 53, 119-129.
http://dx.doi.org/10.1016/j.ijthermalsci.2011.10.002 - 4. Machireddy, G.R. (2013) Chemically Reactive Species and Radiation Effects on MHD Convective Flow past a Moving Vertical Cylinder. Ain Shams Engineering Journal, 4, 879-888.
http://dx.doi.org/10.1016/j.asej.2013.04.003 - 5. Babu, K.R., Venkateswarlu, B. and Satyanarayana, P.V. (2014) Effects of Chemical Reaction and Radiation Absorption on Mixed Convective Flow in a Circular Annulus at Constant Heat and Mass Flux. Advances in Applied Science Research, 5, 122-138.
- 6. Cintaginjala, P.K., Rao, U.R. and Rao, D.R.V.P. (2014) Effect of Chemical Reaction and Radiation Absorption on Mixed Convective Heat and Mass Transfer Flow of a Jeffrey’s Fluid in a Cylindrical Annulus with Heat Generating Sources and Non-Linear Density-Temperature Relation. International Journal of Mathematical Archive, 5, 158-168.
- 7. Mondal, R.K., Hossain, M.A., Ahmed, R. and Ahmmed, S.F. (2015) Free Convection and Mass Transfer Flow through a Porous Medium with Variable Temperature. American Journal of Engineering Research, 4, 100-106.
- 8. Hossain, M.A., Mondal, R.K., Ahmed, R. and Ahmmed, S.F. (2015) A Numerical Study on Unsteady Natural Convection Flow with Temperature Dependent Viscosity past an Isothermal Vertical Cylinder. International Journal of Advanced Research in Engineering & Management, 1, 91-98.
- 9. Sharma, B.R. and Konwar, H. (2015) MHD Flow, Heat and Mass Transfer Due to Auxiliary Moving Cylinder in Presence of Thermal Diffusion, Radiation and Chemical Reactions in a Binary Fluid Mixture. International Journal of Computer Applications, 110, 52-59.
http://dx.doi.org/10.5120/19396-1074 - 10. Ali Nasir Khan, S.U., Abbas, Z. and Sajid, M. (2016) Soret and Dufour Effects on Hydromagnetic Flow of Viscoelastic Fluid over Porous Oscillatory Stretching Sheet with Thermal Radiation. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 1-14.
- 11. Rajesh, V., Beg, A. and Sridev, C. (2016) Finite Difference Analysis of Unsteady MHD Free Convective Flow over Moving Semi-Infinite Vertical Cylinder with Chemical Reaction and Temperature Oscillation Effects. Journal of Applied Fluid Mechanics, 9, 157-167.
- 12. Ali, N., Khan, S.M. and Abbas, Z. (2016) MHD Flow and Heat Transfer of Couple Stress Fluid over an Oscillatory Stretching Sheet with Heat Source/Sink in Porous Medium. Alexandria Engineering Journal, 55, 915-924.
http://dx.doi.org/10.1016/j.aej.2016.02.018 - 13. Ahmed, R., Rana, B.M.J., Uddin, R., Islam, M.M. and Ahmmed, S.F. (2016) Chemical Reaction and Radiative MHD Heat and Mass Transfer Flow with Temperature Dependent Viscosity past an Isothermal Oscillating Cylinder. Physical Science International Journal, 12, 1-9.
http://dx.doi.org/10.9734/PSIJ/2016/28008 - 14. Arifuzzaman, S.M., Dhali, S.K., Azad, M.A.K. and Roy, B. (2015) Magnetic Field and Thermal Radiation Effect on Heat and Mass Transfer of Air Flow near a Moving Infinite Plate with a Constant Heat Sink. World Journal of Mechanics, 5, 235-248.
http://dx.doi.org/10.4236/wjm.2015.512022

























