World Journal of Mechanics
Vol.06 No.08(2016), Article ID:69453,15 pages
10.4236/wjm.2016.68018
Vibration Control Using Heat Actuators
Ilhan Tuzcu
Department of Mechanical Engineering, California State University, Sacramento, CA, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 July 2016; accepted 1 August 2016; published 4 August 2016
ABSTRACT
This paper focuses on theoretical investigation of active vibration control of a cantilever beam using heat actuation. The actuator is a thin metal bar rigidly bonded to the beam on one face and subject to heat input on the opposite face. The actuator then works like a piezoelectric actuator, and expands and contracts in response to applied heat. We assume that the actuator is insulated so that no heat is transferred to the beam, ensuring that the heat does not alter the beam’s thermal state. To avoid necessity of cooling, we consider two actuators working together at the same span- wise location, one on the upper and one on the lower face of the beam. Then, the beam can be bent up and down by applying heat to the lower and upper actuators, respectively. The governing equations are partial differential equations for one-dimensional heat conduction of the actuators and the bending vibration of the beam with attached actuators. For an approximate solution, Rayleigh-Ritz method replaces the partial differential equations with a system of ordinary differential equations. A control model is obtained from a low-dimensional representation of the system, and used to design feedback control and observer by means of LQR and Kalman-Bucy filtering techniques. The control signal obtained is introduced into the plant model, a high-dimensional representation of the system, to mimic the true system as closely as possible. In a numerical application, the response of the beam to an initial excitation is simulated, which demonstrates that the heat actuators are in fact effective in active vibration control of the beam.
Keywords:
Vibration Control, Heat Actuator, Temperature Control, Euler-Bernoulli Beam, Output Control

1. Introduction
Suppression of vibration in flexible structures remains to be a challenging problem in the related technical com- munity. The current trend is to use active means to suppress the vibration. The active control of vibration in structures is implemented by means of sensors, actuators, an accurate mathematical model of the whole system (flexible structure + sensors + actuators), and a computer to carry out all required computations in real time.
Sensors do all measurements, but usually the states of the system cannot be measured directly. Hence, the mathematical model of the system is used to estimate all of the states based on the available measurements, provided that the system is observable. The mathematical model is also used to compute the control signal to be inputed to the actuator based on these estimates of the states. The actuator produces what is needed to affect the true system to suppress the vibration. This can be force, moment, strain, etc. The actuators widely used in vibration control are hydraulic, pneumatic, and piezo-electric, with each having its own benefits and disadvantages depending on the specific applications in which they are used [1] . A special attention has been given to piezoelectric actuators in the recent years. These actuators are bonded on surfaces of structures at some discrete locations to alter the local strain therein by the application of proper voltage signals to actuators [2] .
Another type of actuation that has started receiving some attention in vibration control is simple heat. Considering a structure initially at room temperature, an applied load causes temperature to vary over the body of the structure nonuniformly. Areas of the structure under tension are now cooler and areas under compression are hotter than the room temperature, creating a temperature gradient in the structure. This in turn causes a heat flow by conduction from hotter areas to cooler areas. Hence, a portion of the mechanical energy introduced to the structure is converted to heat through this process. Since the heat flow created is irreversible, the portion of the mechanical energy converted to heat is dissipated. This phenomenon is known as thermoelastic damping [3] . With this fact, question remains as to whether vibration in a structure can be suppressed by artificially introducing a thermal gradient in the body by means of some external heat actuation. Some earlier studies had shown that, when applied properly, external heat actuation could in fact introduce significant amount of thermoelastic damping in structures [4] - [9] .
Pioneering research by Edberg [4] considers control of vibration in a beam using a thermoelectric actuator, which has an ability to heat or cool the beam to produce a thermal gradient across the thickness of the beam. Experimental results reported in the paper show that with a simple lead compensation, damping ratio for the first vibrational mode of a cantilever beam is increased by more than nine times. Another work by Murozono and Sumi [5] also investigates active vibration control of a cantilever beam, but this time by heat input into the beam through the upper and lower surfaces, solely for creating a temperature gradient across the beam section. Foil strain gauges bonded on the surfaces are used as heat actuators. The heat input is through the upper or lower surface, depending on the direction of the gradient needed. Experiments reveal that the damping ratio for the first vibration mode is increased by about ten times. A computational study by Tuzcu et al. [6] considers a uniform rod in longitudinal vibration and shows that control of both vibration and temperature can be achieved by heat input through thermoelectric actuators bonded on the lower and upper surfaces of the rod. Tuzcu and Gonzalez-Rocha [7] extended the work of Tuzcu et al. [6] to a beam in bending. Both vibration and temperature are controlled simultaneously using thermoelectric actuators. Zhang et al. [8] proposes a vibration control of thermally induced vibration in space structures. Actuators are heaters bounded on the spacecraft structure at some optimal positions. Tuzcu et al. [9] explores the idea of using heat patches as actuators working in pairs on the upper and lower surfaces at some discrete spanwise locations of a uniform beam to simultaneously control vibration and temperature in the beam. A numerical example shows the presence of thermoelastic damping and demonstrates simultaneous control of elastic displacement and temperature gradient using a set of displacement measurements.
References [4] - [9] have a major disadvantage: all use heat actuation that requires heating the flexible structure to be controlled, which has a potential to alter the thermal state of the structure significantly, which in turn can prevent the structure from functioning properly. To overcome this problem, this paper proposes a simple design of an actuator which includes a thin metal bar bonded to the structure to be controlled on one face and subject to heat input on the opposite face, as seen in Figure 1. Then, the actuators will work somewhat like piezoelectric actuators, expanding and contracting in response to applied heat, instead of electric voltage in the case of piezoelectric actuators. For more effective control of the structure, multiple of these actuators can be rigidly bonded to the upper and lower surfaces of the beam in pairs at a desired number of spanwise locations. It is assumed that the actuators are insulated so that no heat is transfered to the flexible structure. Since each actuator and the structure are rigidly attached to each other, extension in an actuator due to the application of heat is transferred directly to the host structure. The beam will then bend down if heat is applied to one or more upper actuators, and it will bend up if heat is applied to one or more lower actuators. Hence, the beam's deflection can be controlled by choosing proper heat inputs to the actuators.
Figure 1. Cantilever beam with heat actuators.
2. Modeling
We will demonstrate our modeling and control approach on a cantilever beam, which is a fundamental element commonly encountered in structures. To make the presentation of our approach more clear and focus, we limit ourselves to a simple model by assuming the beam is uniform and there is only one pair of actuators, as shown in Figure 1. The beam is slender so that Euler-Bernoulli beam theory is valid. The upper and lower actuators are assumed to be rigidly bonded to the beam, which means the displacements of the beam and the actuators are equal at every point on the bonding surfaces. We define the displacement field in the beam as
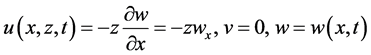 (1)
(1)
where 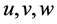 are the displacement components in
are the displacement components in  -directions, respectively, and subscript x denotes a partial derivative with respect to x. Displacement components of a typical point P on the beam are illustrated in Figure 1. The beam’s left-end is fixed and its right-end is free so that w is subject to the boundary conditions:
-directions, respectively, and subscript x denotes a partial derivative with respect to x. Displacement components of a typical point P on the beam are illustrated in Figure 1. The beam’s left-end is fixed and its right-end is free so that w is subject to the boundary conditions:
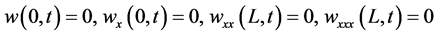 (2)
(2)
where each subscript x indicates a partial derivative with respect to x. Then, the strain components of the beam can be expressed as
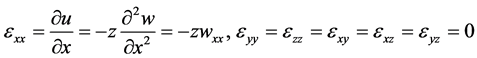 (3)
(3)
Since the ends of the actuators are free, the normal strains of the actuators will be constant at beam’s strains at its interface with the actuators [10] , which means
 (4)
(4)
Assuming a linear stress-strain relation, we can express the only nonzero stress component in beam as
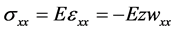 (5)
(5)
where E is the Young’s modulus of the beam. On the other hand, the normal stresses in the actuators are
 (6)
(6)
where 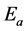 is the Young’s modulus and
is the Young’s modulus and 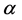 the coefficient of thermal expansion for the actuator material, and
the coefficient of thermal expansion for the actuator material, and 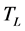 and
and 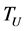 are the temperature deviations from the ambient temperature
are the temperature deviations from the ambient temperature 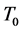 in the lower and upper actuators, respectively. We assume the actuators are insulated on all faces except the ones that are subject to the heat inputs
in the lower and upper actuators, respectively. We assume the actuators are insulated on all faces except the ones that are subject to the heat inputs 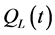 and
and






We approximate w, 


where

are the matrices consisting of m and n number of shape functions and

are the vectors of generalized coordinates for elastic displacement, and temperatures of the upper and lower actuators. Note that we use the same matrix of shape functions for the upper and lower actuators because we assume the actuators are identical and placed symmetrically about the x axis. We choose the shape functions 

where 






Let us now express the total potential energy, which is the summation of potential energies of the beam and the lower and upper actuators:

where 


the volumes of the actuators, and 
Equation (7) into Equation (11), we rewrite the potential energy expression as

where

We note that K is the stiffness matrix.
Kinetic energy of the beam is

where the mass matrix is

where 

Generalized force is obtained from the virtual work:

where 


is the generalized force vector.
The equations of motion of the beam can be derived by means of Lagrange’s equations of motion, which can be written in the vector as

where 

Equation (19) governs the elastic deflection of the beam. Since this equation is coupled with the temperature difference
The heat conduction in the upper actuator is described by the boundary-value problem defined by the following partial differential equation and boundary conditions:

where 




Substituting the second of Equation (7), premultiplying both sides by

Similarly, substituting the second of Equations (7) into the boundary conditions, we get

Using the integration by parts, the second integral in Equation (22) can be written as

Substituting Equation (24), Equation (22) can be rewritten in the compact form

where

Equation (25) completely describes the temperature in the upper actuator for prescribed heat input

which then leads to the following scalar equations for the individual generalized coordinates:

Hence, the eigenvalues of the heat conduction are 




The heat conduction in the lower actuator is similarly described by the boundary-value problem

Following the same steps, Equation (22) through Equation (24), we get

which governs the temperature in the lower actuator for prescribed heat input



2.1. Plant Model
Equations (19), (25) and (30) completely describe the motion of the uniform cantilever beam with the upper and lower actuators for prescribed inputs



which can be rewritten in the state-space form

where

are the state and input vectors, and

are the coefficient matrices. Note that the dimensions of





We will call the state-space model of Equation (32) the plant model, which, in absence of an experimental model, will be used to simulate the behavior of the actual system and to test the performance of our control design. In order for this model to approximate the behavior of the actual system better, we will choose m and n (the number of shape functions used in the expansions of Equations (7)) as high as possible. Control design, on the other hand, will be based on a control model that uses a less number of shape functions, as explained next.
Our objective in this paper is to control the deflection of the beam using 





where











2.2. Control Model
Control design must be as simple as possible for easy implementation and fast real-time computations. This in turn requires a low-order control model. To that end, we first note that the second integral of the expression for 

which clearly means the first column is the only non-zero column in








where

are the control state vector and the control input, and

The dimensions of









3. Output Feedback Control Design
The system to be controlled is inherently underactuated because cantilever beam is a distributed-parameter system with infinite degrees of freedom while the number of control inputs that can be used must always be finite. This inherent property of the system remains a fact even though we use a finite-order approximation of the actual system, namely the control model, because the order of the control model is 


where 




where 

The control design described above assumes that the state vector 








where 






in which V is the state excitation noise intensity matrix.
We assume deflection measurements at the points 


where

is the output matrix relating the actual state to the output. The estimate of the output, on the other hand, is written as

where

is the output matrix relating the estimated state to the estimated output.
Once 




4. Numerical Application
The modeling approach and the control design presented above will be numerically demonstrated for a uniform cantilever beam. We will use the same cantilever beam and the related parameters used in [9] so that we can compare the results from this paper directly to the ones from [9] . Physical parameters of the beam and the actuators are listed in Table 1. For most effective actuators, we choose 






The matrices



To demonstrate the simulation of the closed-loop system, we choose 











where “diag” means diagonal matrix and 


The corresponding eigenvalues of open-loop plant and control models, closed-loop control model, and ob- server dynamics are listed in Table 2. The open-loop plant model has 34 eigenvalues while the control model has only 7. The zero and the negative real eigenvalues of the plant correspond to the heat conduction of the actuators, as explained earlier, and purely complex ones correspond to the vibration of the beam. The control model has a zero eigenvalue and three pairs of purely complex conjugate eigenvalues. The third and the fourth columns of Table 2 show how these eigenvalues are stabilized by the control and observer designs, respectively. However, the question remains as to whether the control and observer designs stabilize the plant. This question
Table 1. Physical parameters.
Table 2. System eigenvalues.
will be answered by the simulation of the closed-loop plant.
Block diagram shown in Figure 2 completely describes how the control of the plant is implemented. We will test the performance of our control design by simulating the response of the closed-loop plant to the same initial conditions used in [9] , namely

Figure 2. Block diagram of the closed-loop system.
so that the beam is initially at rest in the shape of 


Figure 4 shows the heat inputs to the lower and upper actuators needed to achieve this damping. Considering that the amplitude of the vibration in this numerical example is high, these heat inputs seem to be reasonable. Even though [9] uses heat actuators in two spanwise locations, the required heat inputs are quite similar to those of this paper.
In this paper, we assume each actuator is insulated in all faces except the face that is subject to the heat, including the faces normal to x and y axes. This assumption clearly means the temperatures everywhere in the actuators increase monotonically until the heat inputs are ceased after vibration amplitude reduces to a desired value. As an example, temperatures 



We can also compare the total heat injected into the volumes in the two papers. we compute the total heat input to the actuators within t seconds as the integral of total heat rate:




5. Conclusions
This paper investigates active vibration control of a structure using a new type of actuator. The structure of interest is a cantilever beam. The actuator, on the other hand, is a thin metal bar rigidly bonded to the beam on one face and subject to heat input on the opposite face. The actuator then can work like a piezoelectric actuator, and expand and contract in response to applied heat. We assume that the actuator is insulated so that no heat is transferred to the beam. This ensures that the heat applied to the actuator does not alter the thermal state of the beam. One problem that needs to be addressed is that expansion of the actuator requires heating while contraction requires cooling. However, cooling is not practical, and to avoid it, we consider two actuators working together at the same spanwise location, one on the upper and one on the lower face of the beam. Then, the beam can be bent down by applying heat to the upper actuator, and bent up by applying heat to the lower actuator.
Figure 3. Outputs: elastic displacement at 

Figure 4. Heat inputs to the lower and upper actuators.
Figure 5. Actuator temperatures.
In the first part of the paper, we obtain a comprehensive model of the system that can be used to design control and simulate the response of the closed-loop system. Euler-Bernoulli beam theory is assumed to be valid to describe the motion of the beam with the attached actuators. Then, the Lagrange’s equations of motion are used to derive the governing equations for the vibration of the beam with the actuators. Since we assume the elastic motions of the actuators only depend on the elastic motion of the beam, the actuators do not bring any additional elastic degrees of freedom into the governing equations. One-dimensional heat conduction equation is used as
Figure 6. Total heat introduced into the actuators.
the equation governing the temperature in each actuator. We also assume the temperatures of the actuators are not affected by the elastic motion. The governing equations are a set of three partial differential equations, each of which has an infinite dimension. For an approximate solution, we use Rayleigh-Ritz method to replace the partial differential equations with a desired number of ordinary differential equations, obtaining a finite, but otherwise high-dimensional system. The higher the dimension, the more accurate the model is.
We obtain the plant model by using a high-dimensional representation of the system so that it can be repre- sented as accurately as possible. On the other hand, we obtain the control model by using a low-dimensional representation of the system so that estimates of the states as well as control inputs can easily be computed in real time. Since we do not have an experimental model, we use the plant model to mimic the true system as closely as possible, which is the reason to choose a high dimensional model. The control model is used to design feedback control and observer by means of LQR and Kalman-Bucy filtering techniques. The observer design is based on only two displacement measurements, one in the middle and one at the free end of the beam.
In a numerical application, control signal is computed using the control and observer gains based on the control model, and inputted into the plant. Then, the response of the beam to an initial excitation is simulated. The numerical simulation demonstrates that the actuators are in fact effective in active vibration control of the beam. The results obtained are comparable to some of the results of [9] . For comparison reason, the feedback control is designed so that approximately the same damping factor as that of [9] is achieved. However, we show that the total heat input needed to achieve this damping is much smaller than that of [9] , from which we conclude that the actuators of this paper are more effective than those of [9] .
For simplicity of the models, we assume that each actuator is insulated in all faces except the face it is subject to heat. With this assumption, the heat conduction is one-dimensional (only in z-direction), and also we do not have to make assumptions about the convection and/or radiation heat transfer from the faces normal to x and y axes to outside. However, in real-life applications, this assumption is hard to enforce and it must be relaxed. Our future work will aim to make design alterations to relax this assumption to make the work more applicable to real-life situations.
Acknowledgements
The author thanks the editor and the referee for their comments.
Dedication
This paper is dedicated to the memory of Prof. Leonard Meirovitch.
Cite this paper
Ilhan Tuzcu, (2016) Vibration Control Using Heat Actuators. World Journal of Mechanics,06,223-237. doi: 10.4236/wjm.2016.68018
References
- 1. Huber, J.E., Fleck, N.A. and Ashby, M.F. (1997) The Selection of Mechanical Actuators Based on Performance Indices. Proceedings of the Royal Society A, 453. 2185-2205.
http://dx.doi.org/10.1098/rspa.1997.0117 - 2. Jalili, N. (2010) Piezoelectric-Based Vibration Control: From Macro to Micro/Nano Scale Systems. Springer, New York.
- 3. Nowinski, J.L. (1978) Theory of Thermoelasticity with Applications. Sijthoff & Noordhoff International Publishers.
http://dx.doi.org/10.1007/978-94-009-9929-9 - 4. Edberg, D.L. (1987) Control of Flexible Structures by Applied Thermal Gradients. AIAA Journal, 25, 877-883.
http://dx.doi.org/10.2514/3.9715 - 5. Murozono, M. and Sumi, S. (1994) Active Vibration Control of a Flexible Cantilever Beam by Applying Thermal Bending Moment. Journal of Intelligent Material Systems and Structures, 5, 21-29.
http://dx.doi.org/10.1177/1045389X9400500103 - 6. Tuzcu, I., Asmatulu, R. and Hasanyan, D. (2003) Control of the Vibration and Temperature in a Thermoelastic Rod. Proceedings of 5th International Congress on Thermal Stresses and Related Topics, Blacksburg, 8-11 June 2003.
- 7. Tuzcu, I. and Gonzalez-Rocha, J. (2013) Modeling and Control of Thermoelastic Beam. Proceedings of the ASME Dynamic Systems and Control Conference, Palo Alto, 21-23 October 2013, V001T06A004.
http://dx.doi.org/10.1115/dscc2013-4025 - 8. Zhang, J., Xiang, Z. and Liu, Y. (2014) Control of the Thermally Induced Vibration of Space Structures by Using Heaters. Journal of Spacecraft and Rockets, 51, 1454-1463.
http://dx.doi.org/10.2514/1.A32601 - 9. Tuzcu, I., Moua, J.K. and Olivares, J.G. (2016) Control of a Thermoelastic Beam Using Heat Actuation. Journal of Vibration and Control, in press.
http://dx.doi.org/10.1177/1077546316629251 - 10. Crawley, E.F. and de Luis, J. (1987) Use of Piezoelectric Actuators as Elements of Intelligent Structures. AIAA Journal, 25, 1373-1385.
http://dx.doi.org/10.2514/3.9792 - 11. ÖziSik, M.N. (1980) Heat Conduction. John Wiley & Sons, Inc., New York.
- 12. Meirovitch, L. (1990) Dynamics and Control of Structures. John Wiley & Sons, New York.












